本文链接：https://www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2024.04.130

随着各种先进复合材料以及轻质合金在工业领域的广泛使用，胶粘连接凭借着被胶件的适用材料广、连接质量小、密封性能良好等优点成为重要的装配连接手段之一^[1]。尤其在精密惯性仪表等高精度仪器中，内部组件大多采用胶接结构。

很多学者关注了胶接结构的连接性能对装配体的影响。自20世纪40年代起，国外学者从模型构建与解析、实验设计等方面进行了研究。如：Volkersen^[2]首次考虑了被粘物的弹性变形问题并建立了胶粘接头的剪切模型，但采用的是一维杆模型，并未考虑胶接结构的复杂工况；Goland等^[3]考虑到加载过程中的偏心会造成被粘物弯曲，因而在模型中引入弯曲效应，建立了包括剥离应力的一维梁G-R模型；Hart-Smith^[4]在假设被粘物为弹性材料、胶层为弹塑性材料的前提下，采用叠层梁分析方法对胶粘接头进行理论分析，使得分析结果更加符合实际；Ojalvo等^[5]考虑了胶层厚度对胶层剪切应力分布的影响，将被粘物和胶层视为理想弹性体，推导出胶层剪切应力沿胶层厚度方向变化的表达式；Tsai等^[6]采用叠层梁单元理论研究了胶接结构中基底的剪切变形，预测了该剪切变形对胶层剪切应力分布特性的影响；Allman等^[7-8]基于胶粘接头的端部效应，构建了胶粘接头的解析模型，得到了接头端部较为理想的应力分布，发现应力峰值未出现在接头边缘，符合预测结果。除此之外，还有许多解析模型被构建，Renton等^[9-14]构建的解析模型都具有代表性，极大推动了胶粘接头解析模型的发展。近年来，国内学者也进行了相关研究，同样取得了较大的进展。如：Luo等^[15-17]基于线性和非线性分析建立了胶接结构的解析模型；Wang等^[18]进一步把胶层横向位移作为独立的影响因素，构建了胶粘接头的三参数弹性解析模型；Zhao等^[19]基于一维梁理论模型研究了求解单搭接胶接结构胶层端部载荷的新方法。

随着有限元仿真技术的不断发展，利用有限元仿真软件对胶接结构进行分析的研究逐渐增多。如：Darwish等^[20-22]运用线弹性模型对胶接结构进行有限元仿真，得到了不同基底材料胶接结构的应力分布；Osnes等^[23-25]运用非线性模型研究了几何和材料的非线性对单搭接胶粘接头剥离强度的影响；Sulu^[26]对嵌入式双搭接胶接结构的失效载荷进行了仿真，分析了取向角和连接方式对胶接结构的影响，得到了双搭接胶接结构的最优参数及与零件的连接方式。

目前，对胶接结构连接性能的研究开始采用胶粘模型，并在实验中考虑了动态载荷。如：Wang等^[27-28]研究了超声振动对复合材料胶接结构力学性能的影响，结果表明，通过超声振动促进胶黏剂流动而填充黏合间隙，可以有效提高结构的剪切强度；Wang等^[29]研究了加载速率对复合材料胶接结构力学性能的影响，结果表明，提高加载速率可使结构的剪切强度增大。

综上所述，国内外学者对胶接结构的连接性能进行了多方面研究，其主要采用理想的搭接模型，较少考虑实际胶接零件的几何结构对其性能的影响，且通常着重于分析胶接结构的静态性能。为了使研究更贴合实际，本文构建了高精度陀螺仪浮子组件胶接结构的模型，并开展数值分析与仿真计算，分析了胶层厚度、胶层长度、浮筒厚度和胶层形状等对胶层静动态性能的影响，以期为胶接结构的设计提供理论依据。

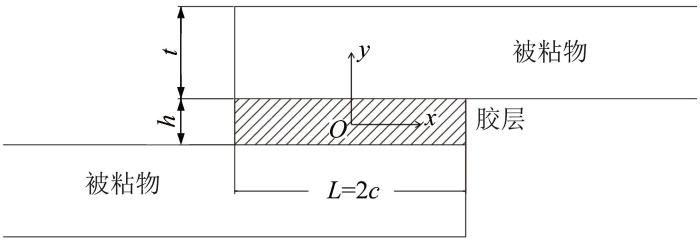
在Ojalvo弹性解析模型中，假设单搭接胶粘接头呈平面应力状态，胶层的纵向应力忽略不计，胶层变形沿厚度方向呈线性分布，所得二维简化模型如图1所示。图中，直角坐标系xOy的原点O位于胶层中心。

首先采用有限元方法对单搭接胶粘接头进行仿真分析，然后通过Ojalvo解析模型得到相同结构尺寸下单搭接胶粘接头中胶层的应力分布趋势，通过对比两者的应力曲线，来验证有限元分析模型的准确性。

单搭接胶粘接头的胶层剪切应力τ可以表示为：

式中：A、B为剪切应力解常数，c为胶层长度的一半。

式中：Ga为胶层剪切弹性模量，L为胶层长度，E为被粘物的弹性模量，t为被粘物厚度，h为胶层厚度。

单搭接胶粘接头的胶层剥离应力σ可以表示为：

式中：C、D为剥离应力解常数。

式中：Ea为胶层有效厚度拉伸刚度。

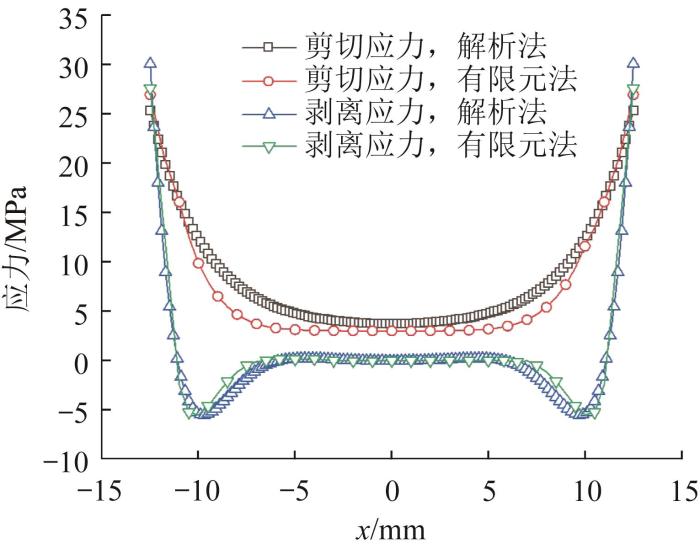
单搭接胶粘接头有限元仿真模型的参数设置：胶层的厚度为0.2 mm，宽度为40 mm，长度为25 mm，泊松比为0.35，弹性模量为4.89 GPa；被粘物的厚度为1.5 mm，宽度为40 mm，长度为100 mm，泊松比为0.3，弹性模量为206 GPa；拉伸载荷为8 000 N。通过有限元法和解析法求解单搭接胶粘接头的胶层剪切应力和剥离应力，结果如图2所示。由图可知，通过有限元法和解析法得到的胶层剪切应力的最大误差为6.2%，剥离应力的最大误差为8.1%，应力曲线基本吻合，验证了有限元仿真方法的准确性。

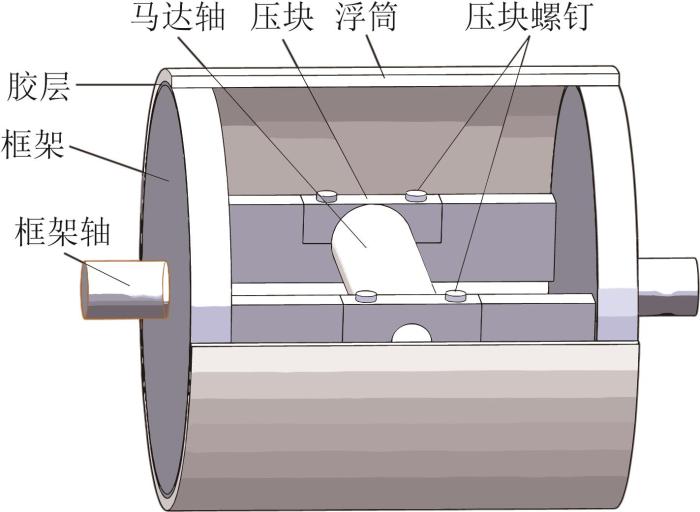
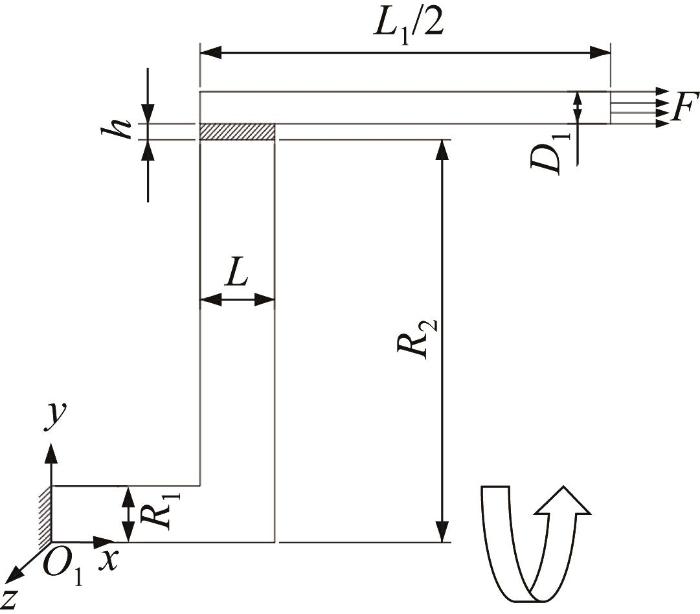
陀螺仪浮子组件的结构如图3所示。将浮子组件中对胶接结构影响较小的马达轴、压块和压块螺钉省略，仅留下组成胶接结构的浮筒、胶层、框架和框架轴。由于组件结构具有对称性，为了提高运算效率，选取实际结构的一半建立有限元模型，其二维简化结构如图4所示。图中：框架轴半径R₁=7 mm，框架半径R₂=50 mm，胶层厚度h=0.2 mm，胶层长度L=10 mm，浮筒厚度D₁=3 mm，浮筒长度L₁=110 mm。以框架轴左端面为yO₁z面，框架轴轴线方向为x向，建立坐标系。

上文已验证了单搭接胶粘接头有限元分析结果的准确性。因此，根据单搭接模型的边界条件及材料属性参数等，构建陀螺仪浮子组件胶接结构的有限元模型。

1）几何模型构建。

根据图4所示的简化结构，以框架轴为旋转轴线，旋转拉伸360°，形成三维胶接结构，其中胶层夹在浮筒与框架之间。胶接结构和胶层的有限元模型如图5所示。为了保证胶层应力仿真结果的准确性，将胶层划分为多层网格单元，网格类型为实体185，采用六面体单元。进行网格无关性分析，最终模型包含495 636个单元、533 856个节点。

2） 边界条件设置。

为了模拟实际工况，进行边界条件设置。设置框架轴端面为固定约束，对浮筒截面施加10 000 N的拉伸面载荷；胶层与浮筒、胶层与框架之间的接触类型设置为绑定接触，接触算法选择默认的罚函数法。

3） 材料参数设置。

设置框架和浮筒材料的弹性模量为220 GPa，泊松比为0.3；胶层材料的弹性模量为1.42 GPa，泊松比为0.35。

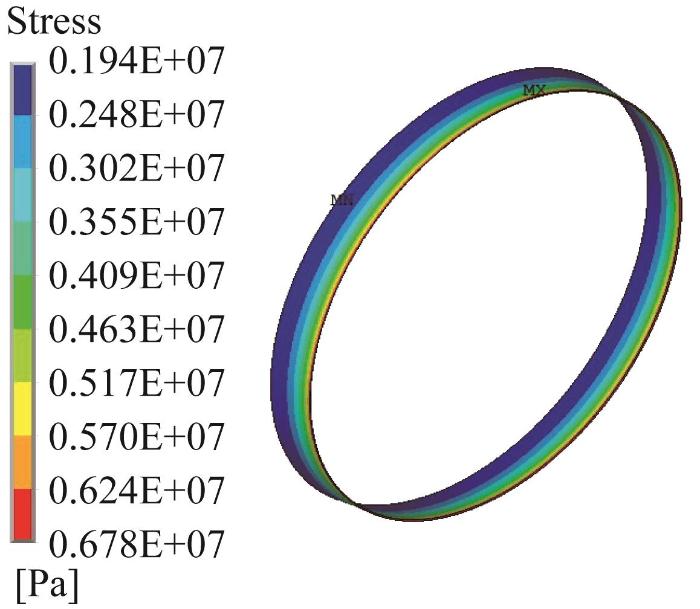
仿真得到胶接结构的胶层剪切应力分布云图，如图6所示。由图可知：剪切应力沿胶层周向基本保持不变，与单搭接模型下的应力分布有明显不同；在胶层轴向，剪切应力有逐渐增大的趋势。

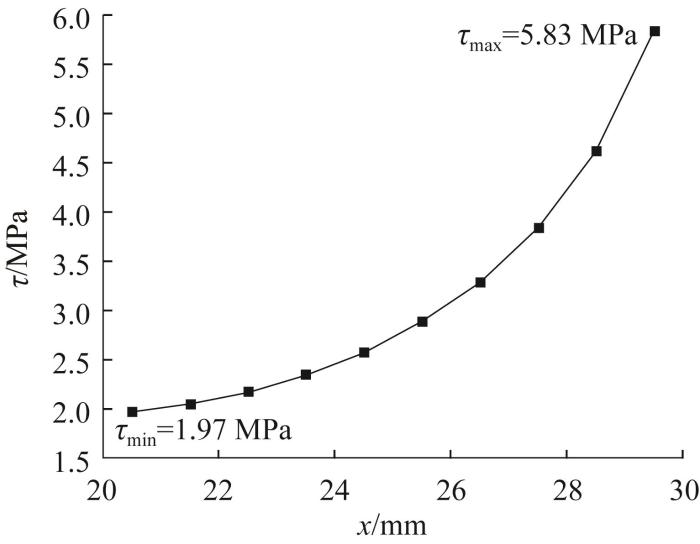
胶层轴向剪切应力变化曲线如图7所示。由图可知：胶层两端的剪切应力分别达到最小值1.97 MPa和最大值5.83 MPa，剪切应力与x呈正相关，其变化大致呈二次曲线形状，剪切应力的方差为1.60 MPa²；在x=20~26 mm的粘接区域内，胶层的剪切应力相对较小，极小值约仅为右端峰值的36.3%；当x>26 mm时，剪切应力随着x的增大而快速增大。

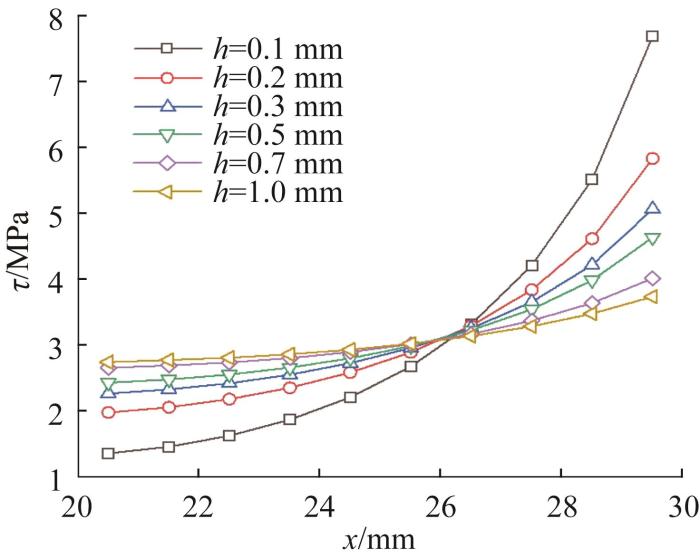
选取h=0.1, 0.2, 0.3, 0.5, 0.7, 1.0 mm，保持其他参数不变，研究不同胶层厚度对胶层剪切应力分布的影响。不同胶层厚度下胶层剪切应力的变化曲线如图8所示。由图可知：在不同胶层厚度下，胶层剪切应力的变化趋势基本相同，剪切应力均沿着胶层轴向逐渐增大；随着胶层厚度的增大，剪切应力的变化逐渐趋于平缓。在实际工作过程中，剪切应力达到最大值的60%以上为优势承载区域。当h=1.0 mm时，优势承载区域占比为100.0%，远大于h=0.1 mm时的26.4%，说明增大胶层厚度有助于扩大胶层的优势承载区域，提高应力分布的均匀性。

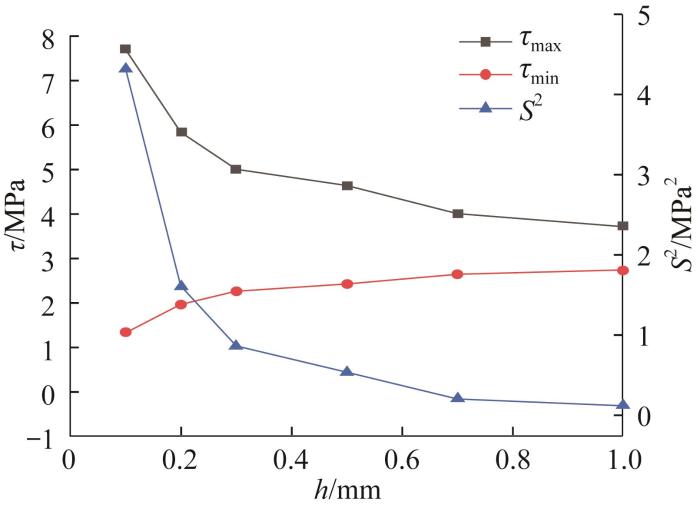
可以用剪切应力的方差S₂来衡量剪切应力的离散程度。不同胶层厚度下胶层剪切应力极值和方差的变化曲线如图9所示，具体数值如表1所示。由图和表可知：随着胶层厚度的增大，胶层最大剪切应力下降了51.6%，而最小剪切应力增大了102.9%，表明随着胶层厚度的增大，剪切应力的变化逐渐趋于平缓，且最大和最小剪切应力逐渐接近某一中间值；剪切应力的方差由初始的4.31 MPa²下降到0.11 MPa²，降低了97.5%。增大胶层厚度有助于改善剪切应力的分布情况，提高粘接性能，而随着厚度的增大，改善效果越来越差，所以，应控制胶层厚度，避免因厚度过大而劣化粘接结构的其他性能。

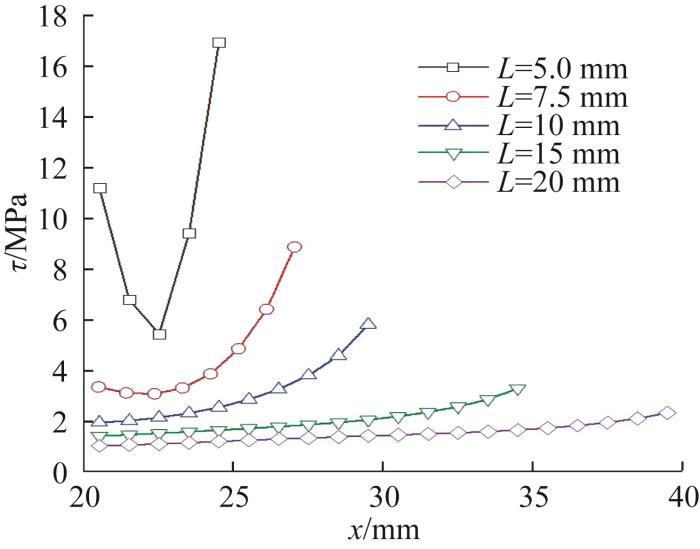
选取L=5.0, 7.5, 10, 15, 20 mm，保持其他参数不变，研究不同胶层长度对胶层剪切应力分布的影响。不同胶层长度下胶层剪切应力的变化曲线如图10所示。由图可知：当L=5.0, 7.5 mm时，剪切应力呈先减小后增大的不对称U形分布趋势；当L=10, 15, 20 mm时，剪切应力为单调增大，说明在7.5 mm与10 mm之间存在某个长度，使得剪切应力的变化趋势发生转变；当L=20 mm时，优势承载区域占比达到57.5%，大于L=5 mm时的40.6%，说明增大胶层长度有利于扩大胶层的优势承载区域。

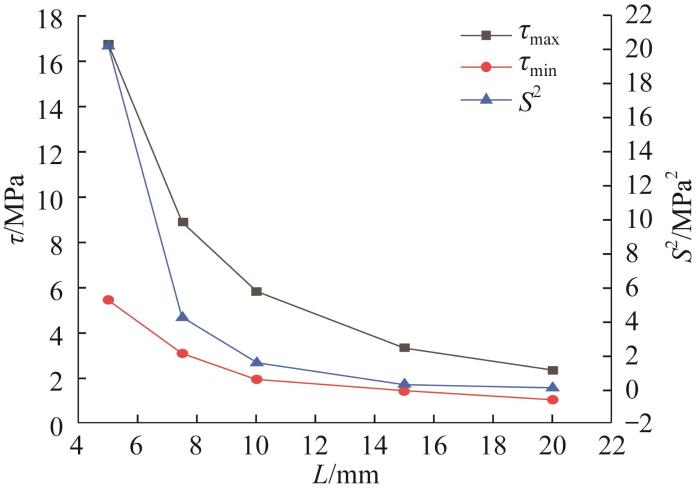
不同胶层长度下胶层剪切应力极值和方差的变化曲线如图11所示，具体数值如表2所示。由图和表可知：随着胶层长度的增大，胶层最大剪切应力由16.75 MPa下降到2.36 MPa，降低了85.9%；最小剪应力由5.47 MPa下降到1.06 MPa，降低了80.6%；剪切应力方差由20.19 MPa²下降到0.12 MPa²，降低了99.4%。结果表明，胶层长度对三者变化趋势的影响与胶层厚度有着明显不同，均随着长度的增大而单调递减且变化逐渐趋于平缓。因此，增大胶层长度有助于减小剪切应力的极值，使应力分布更加均匀。

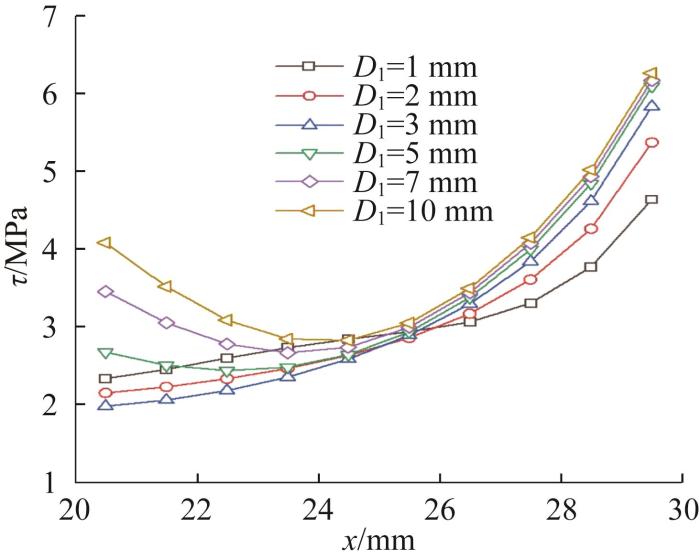
选取D₁=1, 2, 3, 5, 7, 10 mm，保持其他参数不变，研究不同浮筒厚度对胶层剪切应力分布的影响。不同浮筒厚度下胶层剪切应力的变化曲线如图12所示。由图可知：当D₁=1, 2, 3 mm时，胶层剪切应力单调增大，且随着D₁的增大，应力变化曲线更加陡峭；当D₁=5, 7, 10 mm时，剪切应力先减小后增大，应力变化曲线呈不对称的U形；当D₁=10 mm时，优势承载区域占比为42.1%，小于D₁=1 mm时的65.3%，说明增大浮筒厚度并不能提高优势承载区域的占比。

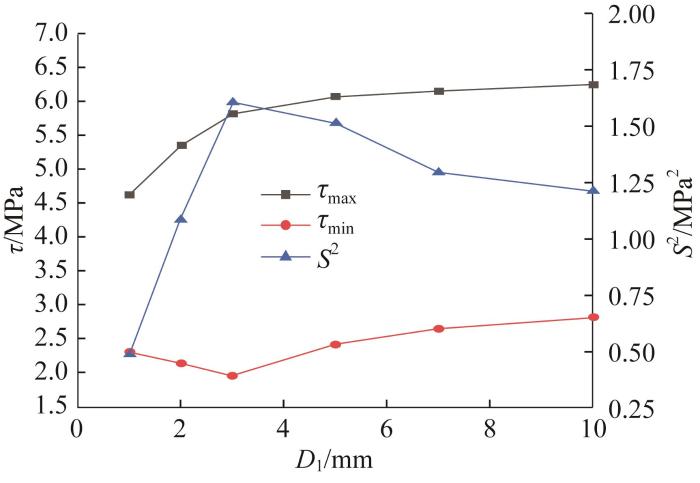
不同浮筒厚度下胶层剪切应力极值和方差的变化曲线如图13所示，具体数值如表3所示。由图和表可知：随着浮筒厚度的增大，胶层最大剪切应力不断增大，共增大了35.1%；最小剪切应力先减小后增大，最终增大了21.5%；剪切应力方差先快速增大后逐渐降低，由0.48 MPa²变化到1.21 MPa²，增大了152.1%。浮筒厚度对剪切应力分布的影响并不明显，改变浮筒厚度并不能有效改善剪切应力分布的均匀性，反而随着浮筒厚度的增大劣化粘接结构的其他性能。

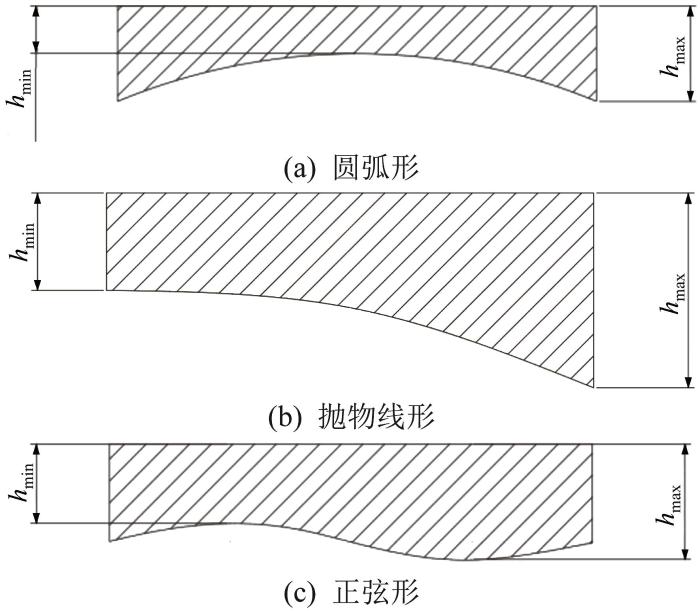
选取圆弧形、抛物线形和正弦形胶层，研究胶层形状对胶层剪切应力分布的影响。胶层形状如图14所示。胶层截面尺寸：胶层长度L=10 mm，胶层最大厚度h_max=1 mm，选取胶层最小厚度h_min=1.00, 0.75, 0.50, 0.25 mm。

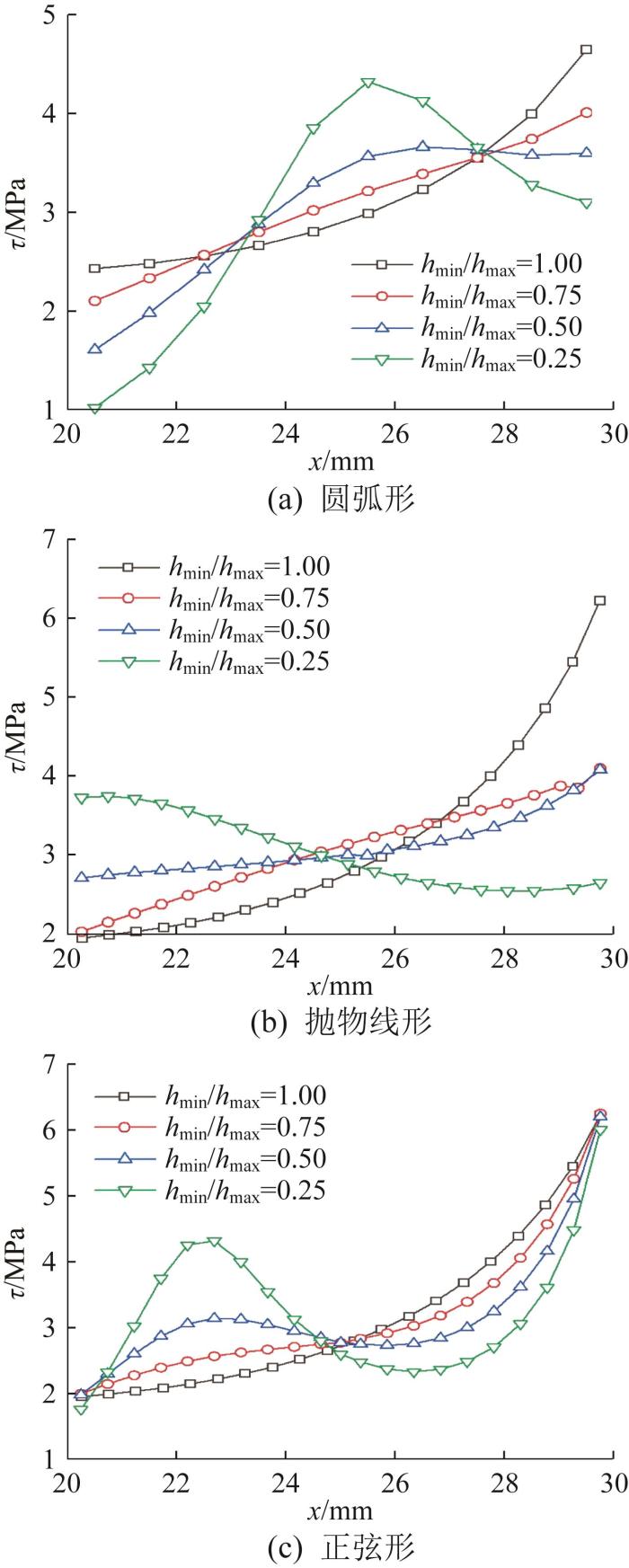
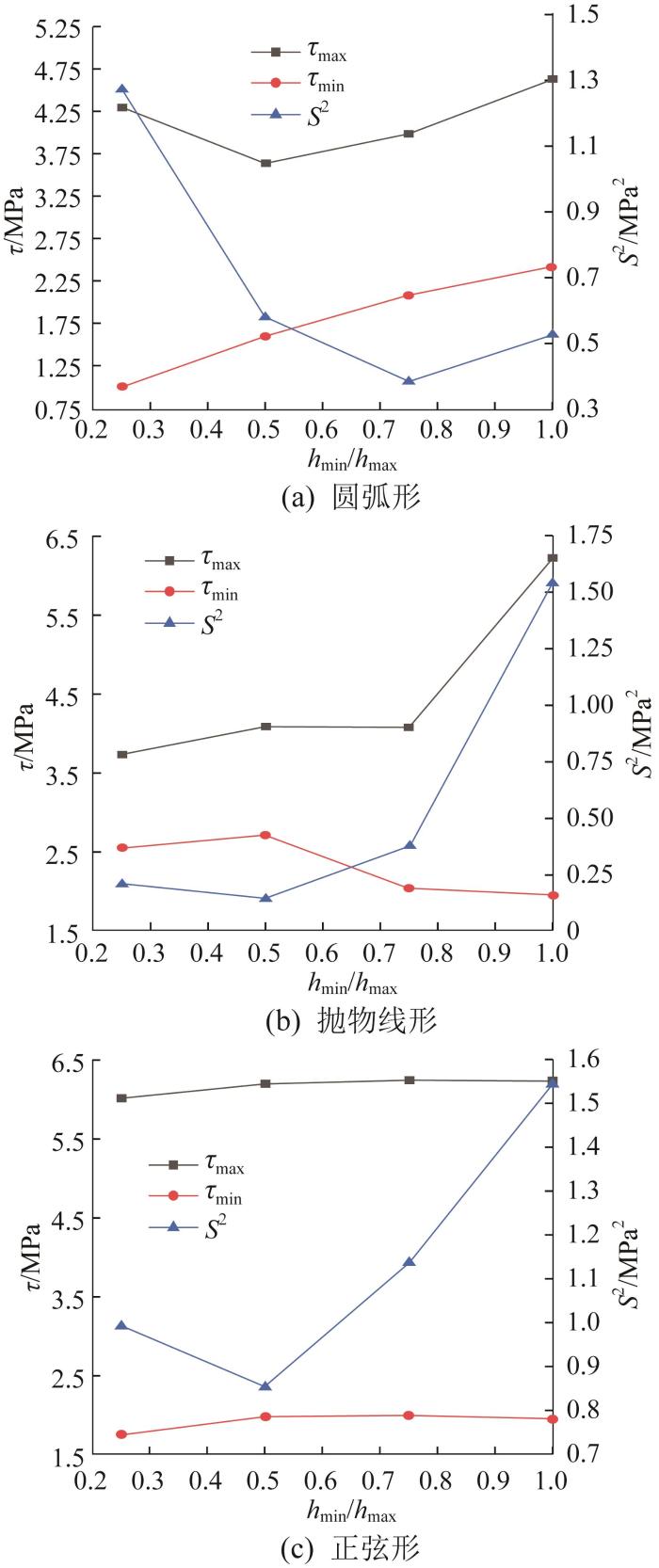
以h_min/h_max为变量，不同h_min/h_max下胶层剪切应力的变化曲线如图15所示，应力极值和方差的变化曲线如图16所示，具体数值如表4所示。由图和表可知：随着h_min/h_max减小，圆弧形胶层的剪切应力曲线逐渐变凸且应力最小值不断下降，而方差先减小后迅速增大，当h_min/h_max=0.25时达到1.28 MPa²，剪切应力分布均匀性变差；随着h_min/h_ma减小，抛物线形胶层剪切应力的变化逐渐平缓，胶层右端的剪切应力迅速减小，左端的应力缓慢增大，应力方差也迅速降低，当h_min/h_ma=0.50时达到最小值0.14 MPa²，应力分布均匀性得到有效改善；对于正弦形胶层而言，其两端的剪切应力基本不变，但随着h_min/h_max减小，整体上由单调增大逐渐变为近似正弦变化，当h_min/h_max=0.50时应力方差达到最小值0.85 MPa²，相比抛物线形胶层，应力分布均匀性改善并不明显。

通过对上述3种胶层剪切应力的分析可知，剪切应力都随着胶层厚度的变化而变化，在胶层厚度大的部位剪切应力较小，在胶层厚度小的部位剪切应力较大。以h_min/h_max=0.25为例来看，圆弧形胶层中间部位的胶层厚度最小，两端最大，剪切应力在中间达到极大值，靠近两端则不断减小；抛物线形胶层的厚度左端最小，右端最大，则剪切应力的极大值及极小值分别出现在胶层的左端及右端；正弦形胶层的剪切应力也呈现与胶层厚度相反的变化趋势。

模态分析是动力学分析的重要组成部分，用于确定系统的固有频率和振型。胶接结构模态分析模型为上文所构建的有限元模型。在分析模型中，对框架轴两端施加固定约束，采用Block Lanczos法的特征值求解器进行模态分析。分别改变胶层厚度、胶层长度、浮筒厚度中的1个参数，保持其他参数不变，来研究该参数对胶接结构固有频率的影响。

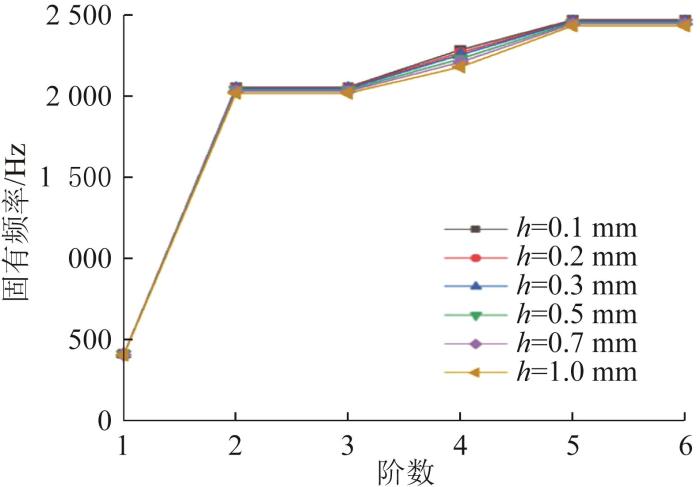
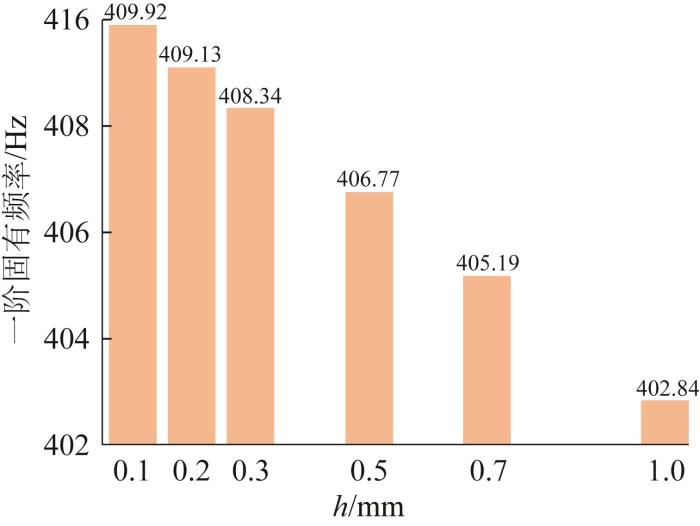
不同胶层厚度下胶接结构前六阶固有频率的对比及一阶固有频率的变化分别如图17和图18所示。由图可知：当h=0.1~1.0 mm时，胶接结构前六阶固有频率的变化趋势基本一致，只有四阶固有频率有较大出入；随着胶层厚度增大，胶接结构一阶固有频率近似线性减小，由409.92 Hz下降到402.84 Hz，约下降了1.73%。可见，胶层厚度对胶接结构固有频率的影响较小，可以忽略。

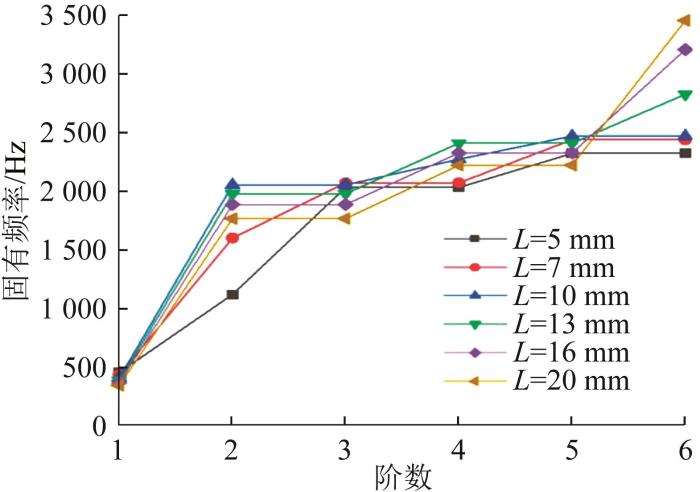
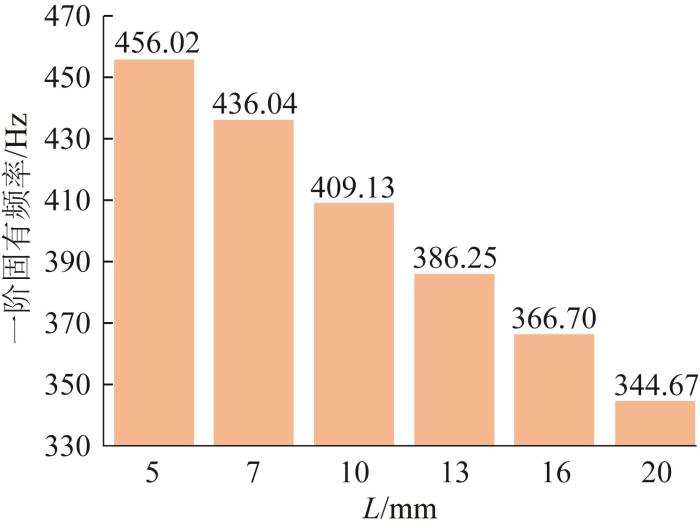
不同胶层长度下胶接结构前六阶固有频率的对比及一阶固有频率的变化分别如图19和图20所示。由图可知：当L=5~20 mm时，胶接结构前六阶固有频率变化较剧烈；随着胶层长度增大，二阶到五阶固有频率没有明显变化，一阶和六阶固有频率逐渐减小，一阶固有频率近似线性减小，由456.02 Hz下降到344.67 Hz，约下降了24.42%。可见，相比于胶层厚度，改变胶层长度对结构固有频率的影响较为明显。

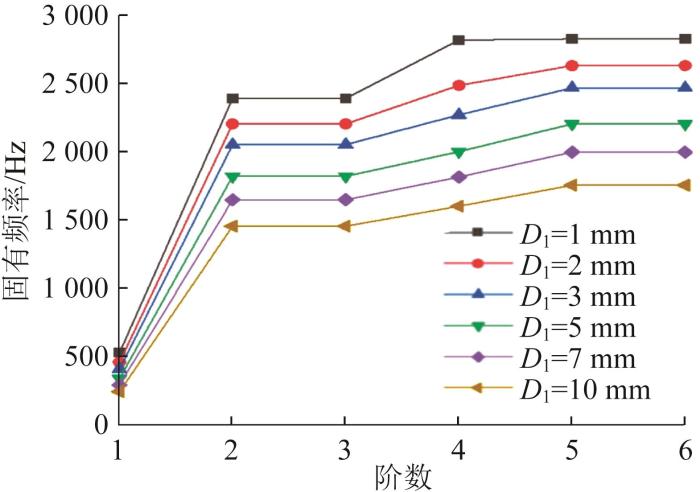
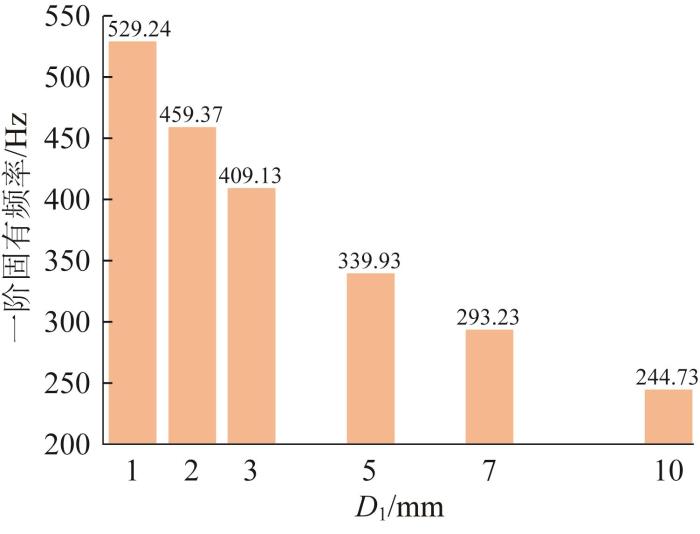
不同浮筒厚度下胶接结构前六阶固有频率的对比及一阶固有频率的变化分别如图21和图22所示。由图可知：当D₁=1~10 mm时，胶接结构前六阶固有频率的变化十分明显；随着浮筒厚度增大，前六阶固有频率均呈现逐渐下降的趋势，一阶固有频率由529.24 Hz下降到244.73 Hz，约下降了53.76%，阶数越大，下降幅度越大。

综上所述，对于胶接结构而言，胶层长度及浮筒厚度对其固有频率的影响较大，胶层厚度的影响较小。增大该3种结构尺寸均使结构的一阶固有频率减小，结构的动态性能下降。研究结果对后续综合考虑动静态性能的胶接结构的多目标优化具有指导作用。

1）本文采用解析法对单搭接胶粘接头应力的有限元仿真结果进行了验证，证明了有限元方法分析胶粘接头应力分布的准确性，为进一步分析陀螺仪浮子组件胶接结构奠定了基础。

2）建立了陀螺仪浮子组件胶接结构的有限元模型，分析了胶层厚度、胶层长度、浮筒厚度及胶层形状对胶接结构静动态性能的影响规律，得到如下结论。

在静态性能方面，增大胶层厚度和长度可以有效改善胶层剪切应力分布的均匀性，但随着参数值增大，改善效果逐渐减弱。同时，胶层整体结构尺寸变大，可能会严重影响胶接结构的其他性能。而增大浮筒厚度并不能有效改善胶层剪切应力分布的均匀性。

设计了3种不同形状的胶层。相比正弦形和圆弧形胶层，抛物线形胶层对胶层剪切应力分布均匀性的改善比较明显。此外，胶层不同部位的剪切应力随着该部位胶层厚度的变化而变化，厚度越大，应力越小。

在动态性能方面，胶层长度和浮筒厚度对胶接结构的前六阶固有频率有着明显影响，胶层厚度的影响则较小。增大浮筒厚度可以减小结构前六阶固有频率，而增大胶层长度只会使结构的一阶和六阶固有频率下降。就一阶固有频率而言，胶层厚度、胶层长度、浮筒厚度对其作用规律相同，都随着结构尺寸的增大而逐渐减小，其中浮筒厚度的影响最大。