缝隙节流液体静压轴承油膜刚度系数的研究

doi:10.3785/j.issn.1006-754X.2024.04.120

缝隙节流液体静压轴承油膜刚度系数的研究

田助新^,^,¹^,³, 齐思田¹, 程春彦², 鹿怀庆^,²^,³

1.三峡大学机械与动力学院，湖北宜昌 443002

2.黄河水利职业技术学院机械工程学院，河南开封 475004

3.华中科技大学数字制造装备与技术国家重点实验室，湖北武汉 430074

Research on oil film stiffness coefficient of slot throttling hydrostatic bearing

TIAN Zhuxin^,^,¹^,³, QI Sitian¹, CHENG Chunyan², LU Huaiqing^,²^,³

1.College of Mechanical and Power Engineering, China Three Gorges University, Yichang 443002, China

2.School of Mechanical Engineering, Yellow River Conservancy Technical Institute, Kaifeng 475004, China

3.State Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan 430074, China

通讯作者: 鹿怀庆（1985—），男，讲师，博士，从事机床误差分析和诊断研究，E-mail: huaiqinglu@163.com

收稿日期: 2024-03-04 修回日期: 2024-04-07

基金资助:

国家重点研发计划资助项目. 2020YFB2007600

Received: 2024-03-04 Revised: 2024-04-07

作者简介 About authors

田助新（1987—），男，副教授，硕士生导师，博士，从事流体静压及动压支承系统研究，E-mail:zhuxintian1987@sina.com,https://orcid.org/0000-0002-5286-5714 , E-mail：zhuxintian1987@sina.com

摘要

油膜刚度系数是液体静压轴承的关键性能参数之一。针对缝隙节流液体静压轴承，推导了其油膜承载力的解析表达式，并在此基础上进一步推导了油膜刚度系数的解析表达式。相比于传统经验公式，采用该表达式的计算结果与实验结果更吻合。通过分析应用案例可知：油膜承载力与节流参数、主轴离心率均呈正相关关系；油膜正向刚度系数随着离心率的增大而减小，油膜交叉刚度系数随着离心率的增大而增大，并且正向刚度系数明显大于交叉刚度系数。利用该轴承油膜刚度系数的表达式，可以通过测量轴承运行过程中的轴心位置，实时得到轴承油膜刚度系数，从而对缝隙节流液体静压轴承的运行进行有效监控。

关键词： 液体静压轴承 ; 缝隙节流 ; 油膜刚度系数 ; 油膜承载力 ; 轴心位置

Abstract

Oil film stiffness coefficient is one of the key performance parameters of hydrostatic bearing. In the context of slot throttling hydrostatic bearing, the analytical expression for the oil film load capacity was deduced, and the analytical expression for the oil film stiffness coefficient was further derived on this basis. Compared with conventional empirical formula, the calculated results from this expression were in better agreement with the experimental results. Through the analysis of application cases, it could be seen that the oil film load capacity was positively correlated with throttling parameters and spindle eccentricity. The positive oil film stiffness coefficient decreased with the increase of eccentricity, whereas the cross oil film stiffness coefficient increased with the increase of eccentricity, and the positive stiffness coefficient was obviously greater than the cross stiffness coefficient. By using the expression for oil film stiffness coefficient of bearing, the oil film stiffness coefficient can be obtained in real time by measuring the bearing shaft center position in the running process of the bearing, and the operation of the slot throttling hydrostatic bearing can be effectively monitored.

Keywords： hydrostatic bearing ; slot throttling ; oil film stiffness coefficient ; oil film load capacity ; journal center position

PDF (1707KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

田助新, 齐思田, 程春彦, 鹿怀庆. 缝隙节流液体静压轴承油膜刚度系数的研究[J]. 工程设计学报, 2024, 31(5): 634-640 doi:10.3785/j.issn.1006-754X.2024.04.120

TIAN Zhuxin, QI Sitian, CHENG Chunyan, LU Huaiqing. Research on oil film stiffness coefficient of slot throttling hydrostatic bearing[J]. Chinese Journal of Engineering Design, 2024, 31(5): 634-640 doi:10.3785/j.issn.1006-754X.2024.04.120

本文链接：https://www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2024.04.120

液体静压轴承具有刚度大、磨损小及承载能力强的优点，被广泛应用于车床、磨床等的旋转机械设备中^[1-3]。液体静压轴承是各类机床主轴的关键部件，其性能直接影响着机床的整体加工性能。

为了改善液体静压轴承的动静态特性，国内外学者对其开展了大量研究。如：Singh等^[4]通过有限元方法求解液体静压轴承油膜的Reynolds方程，发现轴承结构和离心率是影响轴承油膜承载力的关键因素；袁梓馨^[5]讨论了供油压力对油膜刚度和阻尼系数的影响，并对静压轴承的结构参数进行了优化；考虑到润滑剂的非牛顿性，Verma等^[6]发现非牛顿流体的润滑剂能明显影响液体静压轴承的承载力和流量等静态特性；Nicodemus等^[7]讨论了润滑剂的非牛顿性对有磨损的液体静压轴承静态特性的影响。除了有限元方法外，还有不少其他方法也能用来分析液体静压轴承的特性。如：Liang等^[8]基于高斯数值积分公式提出了一种求解精度较高的解析方法来求解液体静压轴承的静态特性；陈淑江等^[9]联立液体静压轴承的Reynolds方程和流量方程，构建了静压主轴轴心位置的计算模型；熊万里等^[10]基于固液界面滑移重新建立了更精确的轴承压力流量模型；Wang等^[11]提出了一种比有限元方法更高效的液体静压轴承油膜承载力数值计算方法。除液体静压轴承之外，Voitus等^[12]以气液混合静压轴承为研究对象，通过数值计算方法求得了轴承油膜的刚度和阻尼系数，发现空气洁净度会影响轴承的4个刚度系数和4个阻尼系数。

在上述研究中，液体静压轴承的油腔结构均为矩形。为了探究不同油腔结构对液体静压轴承动静态特性的影响，Nicodemus等^[13]对具有矩形、圆形、椭圆形和三角形油腔结构的液体静压轴承的静态特性进行了对比分析，发现油腔结构对轴承动静态特性具有明显的影响；Ren等^[14]分析了具有瓣式油腔结构的液体静压轴承的动静态特性，发现半径间隙、油腔深度、供油压力和小孔节流器直径等均明显影响着轴承运行的稳定性。

上述研究在求解液体静压轴承动静态性能时，都采用数值计算方法。其优点是计算精度高，但存在计算程序收敛困难及计算时间长等缺点。如采用传统的经验公式^[15-16]，计算速度快，但计算精度较低。针对计算精度和计算速度难以兼顾的问题，Liang等^[17]提出了一种计算液体静压轴承油腔压力的解析方法，在保证计算精度的前提下，极大地提升了计算速度；在该方法的启示下，Zhang等^[18]进一步改进了液体静压轴承静态特性的求解方法。

上述研究中的液体静压轴承所使用的节流器均为小孔式和毛细管式。这2种节流器是实际工程中使用较多的固定式节流器，其节流参数在轴承运行过程中保持不变，因此在工作过程中不能通过调整其节流参数来控制轴承的承载性能，而基于合理设计的缝隙节流器能有效实现这一功能^[19-20]。因此，本文以缝隙节流液体静压轴承为研究对象，探究其油膜刚度系数的影响因素，为液体静压轴承在运行过程中的性能调控提供一定的参考。

1 油膜刚度系数理论分析

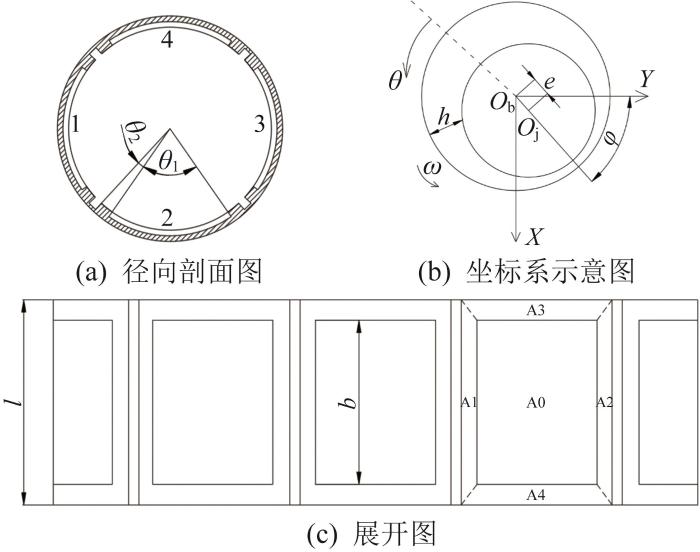
所研究的轴承为带有周向回油槽的四油垫液体静压轴承，其结构如图1所示。4个油垫的结构相同，每个油垫都分成5个区域：油腔区域A0、周向封油面区域A1和A2以及轴向封油面区域A3和A4。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 液体静压轴承结构示意图

Fig.1 Schematic diagram of structure of hydrostatic bearing

轴承几何结构尺寸的量纲为mm，轴承封油面油膜厚度的量纲为μm，为了减小计算过程中的截断误差，采用无量纲量。具体的无量纲变换如下：

\begin{array}{l} a^{*} = \frac{a}{r}, b^{*} = \frac{b}{r}, l^{*} = \frac{l}{r}, F^{*} = \frac{F}{p_{s} r^{2}}, h^{*} = \frac{h}{c}, \\ K^{*} = \frac{c}{p_{s} r^{2}} K, p^{*} = \frac{p}{p_{s}}, x^{*} = \frac{x}{c}, y^{*} = \frac{y}{c}, z^{*} = \frac{z}{r}, \\ Q^{*} = \frac{12 η}{p_{s} c^{3}} Q, ω^{*} = \frac{6 η r^{2}}{p_{s} c^{2}} ω, δ_{s} = \frac{b_{s} {h_{s}}^{3}}{L_{s} c^{3}} \end{array}

式中：l为轴承长度；b为油腔沿轴承轴向的长度；a为轴向封油边长度，a=(l-b)/2；r为轴承半径；F为油膜力；p_s为供油压力；h为封油面区域的油膜厚度；c为半径间隙；K为油膜刚度系数；p为油膜压力；Q为润滑剂流量；η为润滑剂黏度；ω为主轴转动的角速度；δ_s为缝隙节流器的节流参数；L_s、b_s、h_s分别为节流缝隙的长度、宽度、厚度；以轴承中心O_b为原点，分别以轴承径向平面的水平方向和竖直方向为X、Y向，轴承轴向为Z向，建立坐标系。

1.1　封油面区域油膜厚度的计算

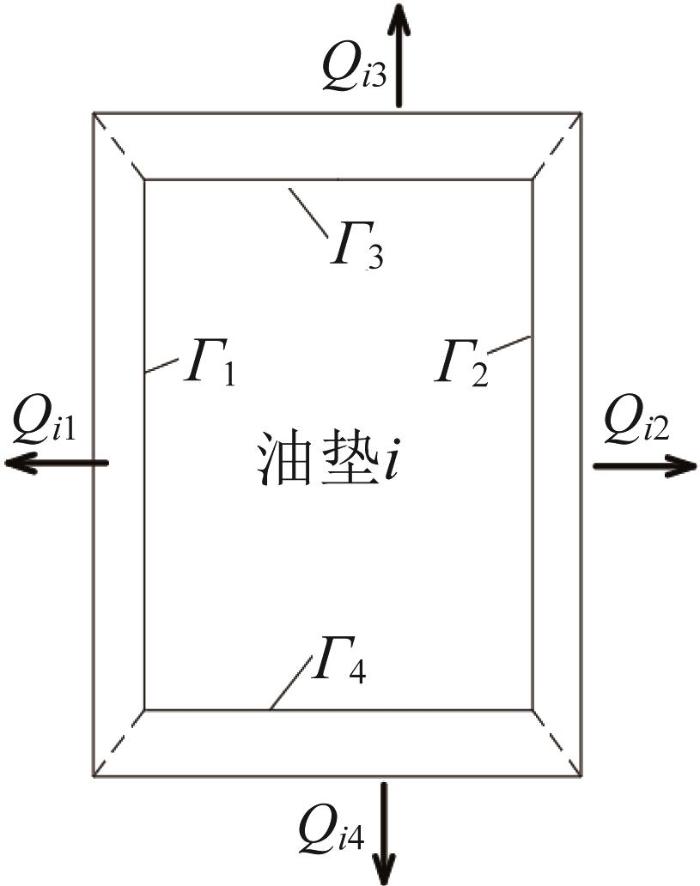
油垫i (i=1, 2, …, 4)上润滑剂的流出如图2所示，其中Γ_i 表示油腔区域的边界线。润滑剂在油垫周向封油面区域A1和A2的油膜厚度h^*_i₁和h^*_i₂可分别表示为：

h_{i 1}^{*} = 1 + ε c o s (φ - \frac{θ_{1}}{2} + \frac{i - 1}{2} π)

(1)

h_{i 2}^{*} = 1 + ε c o s (φ + \frac{θ_{1}}{2} + \frac{i - 1}{2} π)

(2)

式中：ε为轴承离心率，φ为轴承偏位角，θ₁为油腔区域的包角。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 油垫上润滑剂流出示意图

Fig.2 Schematic diagram of lubricant flowing from oil cushion

不考虑安装误差，即认为主轴中心线与轴承中心线平行，则润滑剂在油垫轴向封油面区域A3和A4的油膜厚度h^*_i₃和h^*_i₄可分别表示为：

h_{i 3}^{*} = h_{i 4}^{*} = (1 + ε c o s θ) |_{θ \in (φ - \frac{θ_{1}}{2} + \frac{i - 1}{2} π, φ + \frac{θ_{1}}{2} + \frac{i - 1}{2} π)}

(3)

式中：θ为轴承转角。

1.2　润滑剂流量计算

从区域A1和A2流出的润滑剂的流量Q^*_i₁和Q^*_i₂可分别表示为：

Q_{i 1}^{*} = \int_{Γ_{1}} (\frac{h^{3}}{12 η} \frac{\partial p}{r \partial θ} |_{Γ_{1}} - \frac{r ω h}{2}) d z = b^{*} (\frac{{h_{i 1}^{*}}^{3} p_{r i}^{*}}{θ_{2}} - h_{i 1}^{*} ω^{*})

(4)

Q_{i 2}^{*} = \int_{Γ_{2}} (\frac{h^{3}}{12 η} \frac{\partial p}{r \partial θ} |_{Γ_{2}} + \frac{r ω h}{2}) d z = b^{*} (\frac{{h_{i 2}^{*}}^{3} p_{r i}^{*}}{θ_{2}} + h_{i 2}^{*} ω^{*})

(5)

式中：θ₂为周向封油面的包角，p_r_i^* 为油垫i的油腔压力。

从区域A3和A4流出的润滑剂的流量相等，可表示为：

\begin{array}{l} Q_{i 3}^{*} = Q_{i 4}^{*} = \int_{Γ_{3}} (\frac{h^{3}}{12 η} \frac{\partial p}{\partial z} |_{Γ_{3}}) r d θ = \int_{Γ_{3}} \frac{{h_{i 3}^{*}}^{3} p_{r i}^{*}}{a^{*}} |_{Γ_{3}} d θ = \\ \frac{p_{r i}^{*}}{a^{*}} \int_{φ - \frac{θ_{1}}{2} + \frac{i - 1}{2} π}^{φ + \frac{θ_{1}}{2} + \frac{i - 1}{2} π} {(1 + ε c o s θ)}^{3} d θ = \frac{p_{r i}^{*}}{a^{*}} f_{i 3} (ε, φ) \end{array}

(6)

其中：

\begin{array}{l} f_{i 3} (ε, φ) = \frac{3}{2} {(- 1)}^{i - 1} ε^{2} c o s 2 φ s i n θ_{1} + θ_{1} (1 + \frac{3}{2} ε^{2}) + \\ ε \{6 + \frac{ε^{2}}{3} [4 - c o s θ_{1} + {(- 1)}^{i - 1} (2 c o s θ_{1} + 1) \\ \overset{}{c o s^{^{^{^{^{}}}}} 2 φ]}\} \times c o s (φ + \frac{i - 1}{2} π) s i n \frac{θ_{1}}{2} \end{array}

(7)

流出油垫i的润滑剂总流量 $Q_{i}^{*}$ 为：

Q_{i}^{*} = Q_{i 1}^{*} + Q_{i 2}^{*} + Q_{i 3}^{*} + Q_{i 4}^{*}

(8)

将式(4)至式(6)代入式(8)，可得：

Q_{i}^{*} = f_{i} (ε, φ) p_{r i}^{*} + f_{i 1} (ε, φ)

(9)

其中：

f_{i} (ε, φ) = \frac{b^{*}}{θ_{2}} f_{i 2} (ε, φ) + \frac{2}{a^{*}} f_{i 3} (ε, φ)

(10)

f_{i 1} (ε, φ) = 2 b^{*} ω^{*} ε s i n (φ + \frac{i - 1}{2} π) s i n \frac{θ_{1}}{2}

(11)

\begin{array}{l} f_{i 2} (ε, φ) = 2 + 3 ε^{2} [1 + {(- 1)}^{i - 1} c o s 2 φ c o s θ_{1}] + ε \cdot \\ \{6 + ε^{2} [2 - c o s θ_{1} + {(- 1)}^{i - 1} c o s 2 φ \\ (2 c o s θ_{1} - 1)]\} \times c o s (φ + \frac{i - 1}{2} π) c o s \frac{θ_{1}}{2} \end{array}

(12)

1.3　油垫的油腔压力计算

所研究的液体静压轴承使用的是缝隙节流器，每个油垫均配备一个节流器。流经节流器进入油垫i的润滑剂的流量Q^*_i 可表示为：

Q_{i}^{*} = δ_{s} (1 - p_{r i}^{*})

(13)

轴心位置无量纲直角坐标x^*和y^*可表示为：

x^{*} = ε s i n φ, y^{*} = ε c o s φ

(14)

将式(14)代入式(9)，并联立式(9)和式(13)，可求得到缝隙节流液体静压轴承油垫i的油腔压力为：

p_{r i}^{*} = \frac{- f_{i 1} (x, y) + δ_{s}}{f_{i} (x, y) + δ_{s}}

(15)

1.4　油膜承载力计算

由图1可知，油垫2和4均关于X轴对称，因此其油膜承载力的方向均为X向。同理，油垫1和3油膜承载力的方向均为Y向。因此，油垫i油腔区域A0的油膜承载力F^*_i₀可表示为：

F_{i 0}^{*} = \int_{- \frac{θ_{1}}{2}}^{\frac{θ_{1}}{2}} b^{*} p_{r i}^{*} c o s θ d θ = 2 b^{*} p_{r i}^{*} s i n \frac{θ_{1}}{2}

(16)

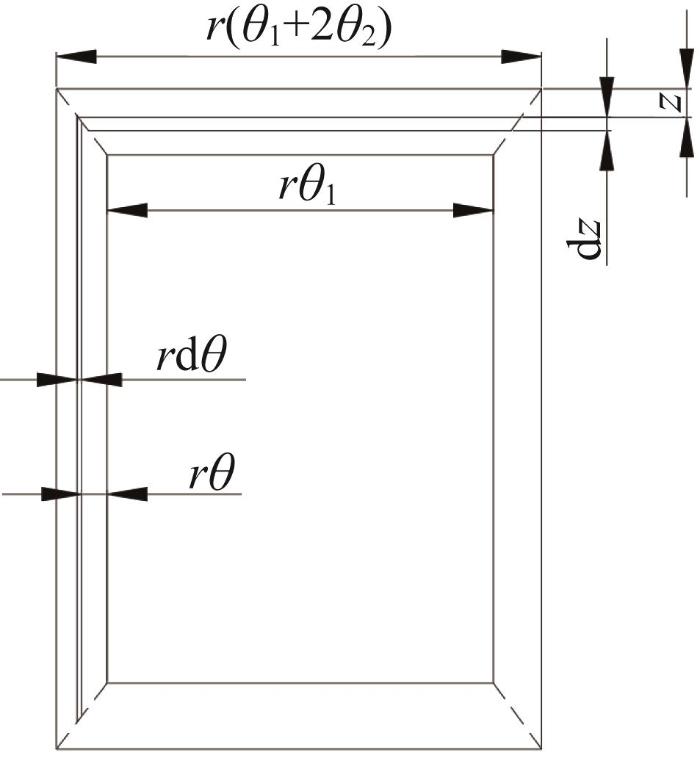
油垫结构的尺寸如图3所示。由于油垫周向封油面包角θ₂较小，可以认为区域A1和A2的油膜承载力是线性变化的。因此，A1和A2的油膜承载力F^*_i₁和F^*_i₂可表示为：

F_{i 1}^{*} = F_{i 2}^{*} = \int_{0}^{θ_{2}} [b^{*} + \frac{θ}{θ_{2}} (l^{*} - b^{*})] p_{r i}^{*} \frac{θ_{2} - θ}{θ_{2}} c o s (θ + \frac{θ_{1}}{2}) d θ = \frac{p_{r i}^{*} b^{*}}{2} θ_{2} c o s \frac{θ_{1}}{2}

(17)

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 油垫结构尺寸示意图

Fig.3 Schematic diagram of structure size of oil cushion

对于一般的液体静压轴承，θ₂ $≪$ θ₁，因此A3和A4的油膜承载力F^*_i₃和F^*_i₄可表示为：

\begin{array}{l} F_{i 3}^{*} = F_{i 4}^{*} = \int_{0}^{\frac{l^{*} - b^{*}}{2}} \frac{4 z^{*}}{l^{*} - b^{*}} p_{r i}^{*} s i n [\frac{θ_{1}}{2} + (1 - \frac{2 z^{*}}{l^{*} - b^{*}}) θ_{2}] d z^{*} = \\ \frac{p_{r i}^{*} (l^{*} - b^{*})}{2} s i n \frac{2 θ_{1} + θ_{2}}{4} \end{array}

(18)

则油垫i的总油膜承载力 $F_{i}^{*}$ 为：

F_{i}^{*} = F_{i 0}^{*} + F_{i 1}^{*} + F_{i 2}^{*} + F_{i 3}^{*} + F_{i 4}^{*} = g (l^{*}, b^{*}, θ_{1}, θ_{2}) p_{r i}^{*}

(19)

其中：

\begin{array}{l} g (l^{*}, b^{*}, θ_{1}, θ_{2}) = 2 b^{*} s i n \frac{θ_{1}}{2} + b^{*} θ_{2} c o s \frac{θ_{1}}{2} + \\ (l^{*} - b^{*}) s i n \frac{2 θ_{1} + θ_{2}}{4} \end{array}

(20)

液体静压轴承在X和Y向的油膜承载力F^*_x 和F^*_y 分别为：

F_{x}^{*} = F_{2}^{*} - F_{4}^{*} = g (l^{*}, b^{*}, θ_{1}, θ_{2}) (p_{r 2}^{*} - p_{r 4}^{*})

(21)

F_{y}^{*} = F_{3}^{*} - F_{1}^{*} = g (l^{*}, b^{*}, θ_{1}, θ_{2}) (p_{r 3}^{*} - p_{r 1}^{*})

(22)

液体静压轴承的油膜总承载力F^* 可表示为：

F^{*} = \sqrt[]{{F_{x}^{*}}^{2} + {F_{y}^{*}}^{2}}

（23）

1.5　油膜刚度系数计算

将F^*_x 和F^*_y 分别关于轴心位置坐标x^*和y^*求导，即可得到液体静压轴承的4个油膜刚度系数：

\begin{array}{l} [\begin{matrix} \begin{array}{l} K_{x x}^{*} \\ K_{y x}^{*} \end{array} & \begin{array}{l} K_{x y}^{*} \\ K_{y y}^{*} \end{array} \end{matrix}] = - [\begin{matrix} \begin{array}{l} \frac{\partial F_{x}^{*}}{\partial x^{*}} \\ \frac{\partial F_{y}^{*}}{\partial x^{*}} \end{array} & \begin{array}{l} \frac{\partial F_{x}^{*}}{\partial y^{*}} \\ \frac{\partial F_{y}^{*}}{\partial y^{*}} \end{array} \end{matrix}] = \\ [\begin{matrix} \begin{array}{l} \frac{\partial p_{r 4}^{*}}{\partial x^{*}} - \frac{\partial p_{r 2}^{*}}{\partial x^{*}} \\ \frac{\partial p_{r 1}^{*}}{\partial x^{*}} - \frac{\partial p_{r 3}^{*}}{\partial x^{*}} \end{array} & \begin{array}{l} \frac{\partial p_{r 4}^{*}}{\partial y^{*}} - \frac{\partial p_{r 2}^{*}}{\partial y^{*}} \\ \frac{\partial p_{r 1}^{*}}{\partial y^{*}} - \frac{\partial p_{r 3}^{*}}{\partial y^{*}} \end{array} \end{matrix}] g (l^{*}, b^{*}, θ_{1}, θ_{2}) \end{array}

(24)

其中：

\begin{array}{l} \frac{\partial p_{r i}^{*}}{\partial j^{*}} = p_{r i}^{*} [\frac{1}{f_{i 1} (x^{*}, y^{*}) - δ_{s}} \frac{\partial f_{i 1}}{\partial j^{*}} - \frac{1}{f_{i} (x^{*}, y^{*}) + δ_{s}} \frac{\partial f_{i}}{\partial j^{*}}] \\ (i = 1, 2, \dots, 4; j = x, y) \end{array}

(25)

2 油膜刚度系数理论计算结果的验证

为了验证上述油膜刚度系数理论计算结果的正确性，采用文献[19]中液体静压轴承的结构参数和运行工况，进行油膜刚度系数计算，并将计算结果与文献[19]中的计算结果、实验结果进行对比。文献[19]采用是传统经验公式。油腔压力和油膜刚度系数随供油压力的变化曲线如图4所示。由图可知：相比于采用传统的经验公式，本文的计算结果与实验结果更吻合。此外，相比于利用有限元或有限差分等数值计算方法求解Reynolds方程而得到液体静压轴承的油膜刚度系数，本研究直接给出了油膜刚度系数的解析表达式，极大地提高了计算效率。因此，本文的计算方法可以在保证计算精度的前提下，有效提高计算效率。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 油腔压力和油膜刚度系数随供油压力的变化曲线

Fig.4 Variation curves of oil chamber pressure and oil film stiffness coefficient with oil supply pressure

3 油膜刚度系数影响因素分析

基于上述理论推导，本节分析节流参数、主轴离心率对油膜承载力和油膜刚度系数的影响。轴承结构如图1所述，为四油腔带周向回油槽的液体静压轴承，其相关参数如表1所示。

表1 液体静压轴承的相关参数

Table 1 Relevant parameters of hydrostatic bearing

参数	数值
轴承半径r/mm	50
轴承长度l/mm	100
半径间隙c/mm	0.5
供油压力p_s/MPa	2
轴向封油边长度a/mm	10
周向封油面的包角θ₂/(º)	12
油腔区域的包角θ₁/(º)	60
油腔数量/个	4
油腔形状	矩形
节流器类型	缝隙节流
节流参数δ_s	10, 20, 30, 40
轴承转速n/(r/min)	1 500
轴承偏位角φ/(º)	30
润滑剂黏度η/(Pa·s)	0.008 7
润滑剂密度ρ/(kg/m³)	870

新窗口打开| 下载CSV

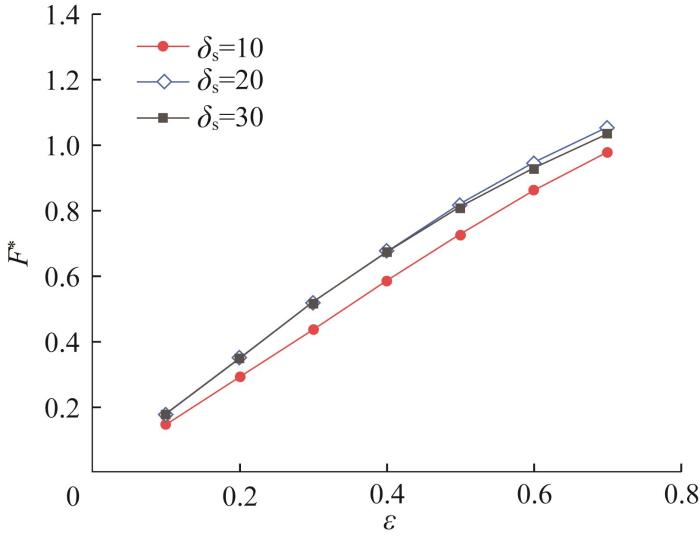
不同节流参数下油膜承载力随主轴离心率的变化曲线如图5所示。由图可知：节流参数越大，油膜承载力越大，而当节流参数大于20时，其对油膜承载力的影响变得较微弱；主轴离心率越大，油膜承载力越大。这是由于随着主轴离心率增大，主轴与油垫封油面区域的间隙减小，导致该油垫的卸油流量减小，由于节流参数和供油压力不变，由式(13)可得，该油腔的压力会变大，进而使得油膜承载力变大。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同节流参数下油膜承载力随主轴离心率的变化曲线

Fig.5 Variation curves of oil film load capacity with spindle eccentricity under different throttling parameters

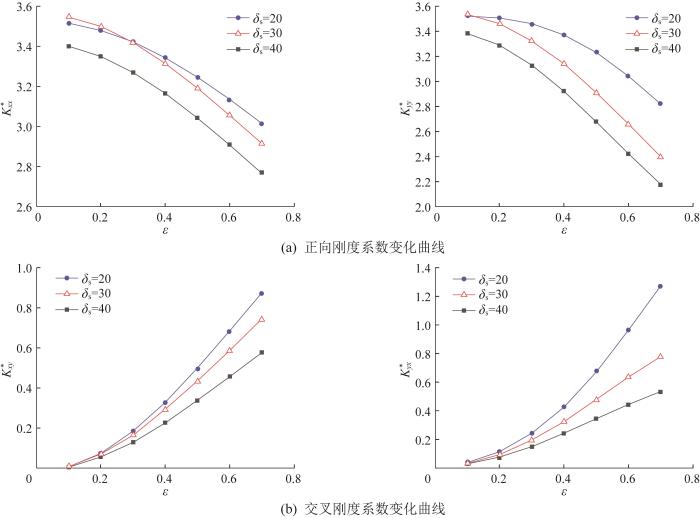
不同节流参数下油膜刚度系数随主轴离心率的变化曲线如图6所示。由图可知：油膜正向刚度系数 $K_{x x}^{*}$ 和 $K_{y y}^{*}$ 随着离心率的增大而减小，油膜交叉刚度系数 $K_{x y}^{*}$ 和 $K_{y x}^{*}$ 随着离心率的增大而增大，且 $K_{x x}^{*}$ 和 $K_{y y}^{*}$ 明显大于 $K_{x y}^{*}$ 和 $K_{y x}^{*}$ ；对于 $K_{x y}^{*}$ 和 $K_{y x}^{*}$ ，节流参数越大，其值越小；对于 $K_{x x}^{*}$ 和 $K_{y y}^{*}$ ，当离心率较大（如离心率大于0.3）时，节流参数越大，其值越小；当离心率较小、节流参数小于30时，会出现离心率越小而正向刚度系数越大的情况。节流参数越大，正向刚度系数随离心率的变化率越大，而交叉刚度系数随离心率的变化率则越小。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同节流参数下油膜刚度系数随主轴离心率的变化曲线

Fig.6 Variation curves of oil film stiffness coefficient with spindle eccentricity under different throttling parameters

4 应用案例

由式(24)可知，油膜刚度系数与轴心位置、轴承几何结构参数及节流器几何结构参数等相关。因此，基于轴承运行过程中的轴心位置可以实时求解油膜刚度系数。

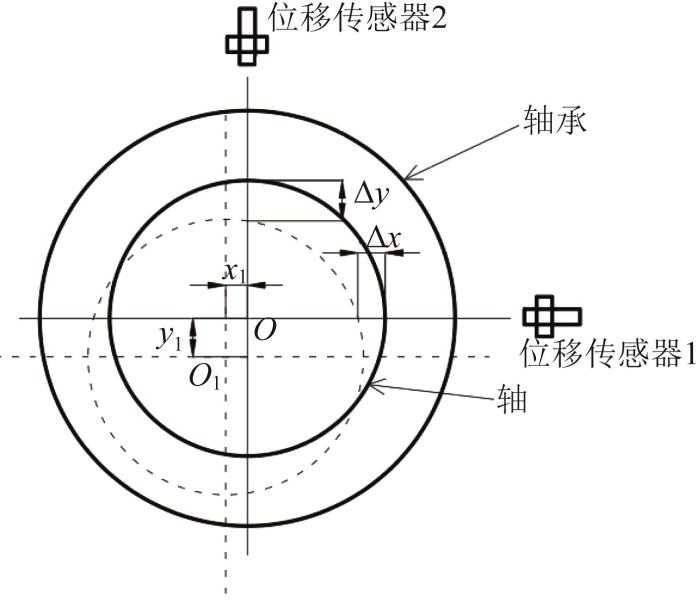
轴承轴心位置的测量如图7所示。在轴承圆周方向间隔90º布置2个位移传感器；以轴承中心为坐标原点O，O点与2个位移传感器的连线为x、y轴，建立坐标系。当轴颈与轴承同心时，将位移传感器的读数清零。在轴承工作过程中，轴颈中心会偏离轴承中心至O₁点，此时位移传感器的读数Δx、Δy即为轴颈在x、y向的位移，则O₁点坐标(x₁, y₁)与位移传感器读数(Δx, Δy)存在如下关系^[21]：

x_{1} = Δ x + \frac{{(Δ x)}^{2} - {(Δ y)}^{2}}{4 [R - (Δ x + Δ y)]}

y_{1} = Δ y + \frac{{(Δ y)}^{2} - {(Δ x)}^{2}}{4 [R - (Δ x + Δ y)]}

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 轴承轴心位置测量示意图

Fig.7 Schematic diagram of bearing shaft center position measurement

将式(26)和(27)代入式(24)，结合轴承和所用缝隙节流器的几何结构参数，即可得到轴承运行过程中的实时油膜刚度系数。

5 结论

1）本文给出了缝隙节流液体静压轴承油膜承载力和油膜刚度系数的解析式，并将计算结果与采用传统经验公式的计算结果和实验结果进行了对比。相比于传统经验公式，本文的计算结果与实验结果更吻合。相比于通过数值方法求解Reynolds方程而得到油膜刚度系数，采用本文方法能够有效提高油膜刚度系数的计算效率。

2）缝隙节流液体静压轴承的油膜承载力与节流参数、主轴离心率均呈正相关关系，当节流参数大于20时，节流参数对油膜承载力的影响变得较微弱。油膜正向刚度系数 $K_{X X}^{*}$ 和 $K_{Y Y}^{*}$ 随着离心率的增大而减小，油膜交叉刚度系数 $K_{X Y}^{*}$ 和 $K_{Y X}^{*}$ 随着离心率的增大而增大，并且 $K_{X X}^{*}$ 和 $K_{Y Y}^{*}$ 明显大于 $K_{X Y}^{*}$ 和 $K_{Y X}^{*}$ 。

3）利用油膜刚度系数的解析表达式，可以实时获得轴承运行过程中的油膜刚度系数，进而能够对缝隙节流液体静压轴承的运行进行有效监控。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

田助新，郭明慧，曹海印.

环形油腔液体静压推力轴承动态特性的影响因素研究

［J］. 工程设计学报， 2022， 29（4）： 456-464.