融合短时傅里叶变换和卷积神经网络的托辊故障诊断方法

doi:10.3785/j.issn.1006-754X.2024.03.203

融合短时傅里叶变换和卷积神经网络的托辊故障诊断方法

谢苗^,^,¹, 孟庆爽^,¹, 李博², 卢进南¹, 李玉岐¹, 杨志勇¹^,³

1.辽宁工程技术大学机械工程学院，辽宁阜新 123000

2.辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛 125000

3.新疆露天矿智能生产与管控重点实验室，新疆昌吉 831100

Idler fault diagnosis method fusing short-time Fourier transform and convolutional neural network

XIE Miao^,^,¹, MENG Qingshuang^,¹, LI Bo², LU Jinnan¹, LI Yuqi¹, YANG Zhiyong¹^,³

1.School of Mechanical Engineering, Liaoning Technical University, Fuxin 123000, China

2.Faculty of Electrical and Control Engineering, Liaoning Technical University, Huludao 125000, China

3.Xinjiang Open-pit Mine Intelligent Production and Control Key Laboratory, Changji 831100, China

通讯作者: 孟庆爽（1999—），女，硕士生，从事机械设计及理论研究，E-mail: 2724127290@qq.com

收稿日期: 2023-09-12 修回日期: 2023-11-06

基金资助:

国家自然科学基金面上项目. 51874158

First author contact: XIE M, MENG Q S, LI B, et al. Idler fault diagnosis method fusing short-time Fourier transform and convolutional neural network[J]. Chinese Journal of Engineering Design, 2024, 31(5): 565-574.

Received: 2023-09-12 Revised: 2023-11-06

作者简介 About authors

谢　苗（1980—），女，教授，博士，从事综掘、综采成套装备研究，E-mail:xiemiao1121@126.com，https://orcid.org/0000-0002-2980-0365 , E-mail：xiemiao1121@126.com

摘要

托辊故障已成为带式输送机运行中的常见问题。若不能及时诊断托辊故障，则将严重制约带式输送机的安全运行。为了解决上述问题，基于某矿带式输送机中间段托辊的实际运行工况，提出了一种融合短时傅里叶变换（short-time Fourier transform, STFT）和卷积神经网络（convolutional neural network, CNN）的托辊故障诊断方法。首先，以分布式光纤为基础，对托辊在正常、轴承损坏及筒皮断裂工况下运行时的振动信号进行采集并作STFT处理，得到对应的时频图样本集，并将其分为训练集和测试集。然后，将训练集输入CNN模型以进行诊断模型训练，在训练过程中不断更新不同工况下托辊的运行状态特征。最后，将训练好的CNN模型应用于测试集，并输出托辊运行状态的识别结果。结果表明，所构建的CNN模型的识别准确率高达99.6%。基于所提出的故障诊断方法，在某矿上开展现场实验，以进一步验证CNN模型的识别准确率。实验结果表明，CNN模型对带式输送机中间段托辊的运行状态有较高的识别准确率，可达96.5%，与测试集上的识别准确率仅相差3.1个百分点，说明所提出的故障诊断方法具有一定的可靠性。后续可通过不断增加不同工况下托辊的运行数据来提高该故障诊断方法的鲁棒性，这可为煤矿企业有效诊断托辊故障提供有力的理论基础。

关键词： 托辊 ; 故障诊断 ; 分布式光纤 ; 短时傅里叶变换 ; 卷积神经网络

Abstract

Idler fault has become a common problem in the operation of belt conveyors. If the idler fault cannot be diagnosed in time, it will seriously restrict the safe operation of belt conveyors. To solve the above problems, based on the actual operating conditions of idlers in the middle section of a certain mining belt conveyor, an idler fault diagnosis method fusing short-time Fourier transform (STFT) and convolutional neural network (CNN) is proposed. Firstly, based on distributed optical fiber, the vibration signals of the idler operating under normal, bearing damage and cylinder skin fracture conditions were collected and processed by STFT to obtain corresponding time-frequency image sample set, and the sample set was divided into training set and testing set. Then, the training set was input into the CNN model for diagnostic model training, and the operating state characteristics of idlers under different working conditions were constantly updated during the training process. Finally, the trained CNN model was applied to the testing set, and the recognition result of the idler operating state was output. The results showed that the recognition accuracy of the constructed CNN model was as high as 99.6%. Based on the proposed fault diagnosis method, field experiment were carried out in a certain mine to further verify the recognition accuracy of the CNN model. The experimental results showed that the CNN model had a high recognition accuracy of 96.5% for the operating state of idlers in the middle section of the belt conveyor, which was 3.1 percentage points lower than the recognition accuracy on the testing set, indicating that the proposed fault diagnosis method had a certain reliability. Subsequently, the robustness of the fault diagnosis method can be improved by continuously increasing the operation data of idlers under different working conditions, which can provide a powerful theoretical basis for the effective diagnosis of idler faults in coal mine enterprises.

Keywords： idler ; fault diagnosis ; distributed optical fiber ; short-time Fourier transform ; convolutional neural network

PDF (5856KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

谢苗, 孟庆爽, 李博, 卢进南, 李玉岐, 杨志勇. 融合短时傅里叶变换和卷积神经网络的托辊故障诊断方法[J]. 工程设计学报, 2024, 31(5): 565-574 doi:10.3785/j.issn.1006-754X.2024.03.203

XIE Miao, MENG Qingshuang, LI Bo, LU Jinnan, LI Yuqi, YANG Zhiyong. Idler fault diagnosis method fusing short-time Fourier transform and convolutional neural network[J]. Chinese Journal of Engineering Design, 2024, 31(5): 565-574 doi:10.3785/j.issn.1006-754X.2024.03.203

本文链接：https://www.zjujournals.com/gcsjxb/CN/10.3785/j.issn.1006-754X.2024.03.203

带式输送机是物料运输中最常用的设备之一，而托辊是带式输送机上数量最多且最关键的结构。托辊故障已成为带式输送机运行中的常见问题，若不能及时地诊断托辊故障，则将严重制约输送机的安全运行。目前，人工或机器人巡检都无法实时、准确地判断托辊故障，这会对带式输送机造成损坏，甚至可能会引发火灾^[1-2]。

针对托辊故障诊断，学者们不断通过采用不同的数据处理算法来提高故障诊断的准确率。在信号处理和特征提取方面，时频分析方法中的小波分析、经验模态分解和局部均值分解等的应用较为广泛^[3]，但这些方法只能对原始信号进行分解，而短时傅里叶变换（short-time Fourier transform, STFT）可同时得到信号的时域与频域信息^[4]。付忠广等^[5]利用STFT和移动视觉转换（mobile vision transformer, Mobile-VIT）网络模型对时频图进行特征提取，实现了旋转机械的故障诊断。隆军等^[6]利用希尔伯特-黄变换（Hilbert-Huang transform, HHT）和STFT方法对风力发电机轴承的故障信号进行特征提取，经对比发现，STFT具有较好的时频分辨率。李恒等^[7]利用STFT对滚动轴承的振动信号进行处理，并利用卷积神经网络（convolutional neural network, CNN）模型对轴承的故障类型进行了识别。金江涛等^[8]基于混沌理论对CNN模型进行不断完善，得到了一种适用于处理“大数据”的滚动轴承故障诊断方法。

CNN是一种重要的深度学习模型，被广泛应用于图像处理和语音识别等领域。近年来，越来越多的学者开始采用CNN模型来识别机械故障。刘慧斌等^[9]考虑到轴承故障来源复杂，分别通过CNN自动提取和人工提取方法来对轴承故障进行分析，结果表明，CNN能够有效地诊断轴承故障。Janssens等^[10]先利用快速傅里叶变换（fast Fourier transform, FFT）对轴承振动信号进行预处理，再利用CNN对轴承振动信号的特征进行识别，实现了轴承故障检测。董辛旻等^[11]提出了一种基于矢谱和L-M（Levenberg-Marquardt）神经网络的旋转机械故障诊断模型，并将模型预测的诊断结果与基于单通道的诊断结果进行对比，结果表明，矢谱融合技术可实现良好的诊断效果。

基于上述背景，本文提出了一种融合STFT和CNN的托辊故障诊断方法，将基于STFT得到的时频图输入CNN模型，以实现对托辊正常运行、轴承损坏和筒皮断裂等工况的识别。

1 托辊振动信号的采集方法

1.1　振动信号检测方法

托辊正常运行是保障带式输送机安全运行的关键^[12]。在正常运行的情况下，托辊可以减少输送带与物料之间的摩擦，从而避免输送带磨损或损坏。托辊一旦出现故障，就会增加输送带与托辊架之间的摩擦，导致轴承座与轴承发生不规则接触，从而产生不正常的振动信号，这与托辊正常运行时的振动信号存在较大差异，由此可判断托辊是否失效。不同运行状态的托辊如图1所示。为了保证托辊故障诊断的准确性和高效性，提出了一种分布式光纤检测法，即通过扎带将光纤固定在带式输送机两侧槽钢内部，以采集托辊的振动信号。考虑到带式输送机机头段和机尾段的干扰因素较多，本文以中间段托辊为研究对象。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 不同运行状态的托辊

Fig.1 Idlers in different operating states

本文提出的基于相位敏感光时域反射仪（phase sensitive optical time domain reflectometer, Φ-OTDR）的托辊振动信号采集方法如图2所示。由激光器产生一系列不间断的相干光，通过声光调制器将光信号转换为光脉冲信号，并利用光纤放大器对光脉冲信号进行放大处理，以使采集的信号更准确。随后，光脉冲信号依次经过隔离器和环形器并传输至光纤，光脉冲信号在经过光纤时会产生瑞利散射，后向瑞利散射光沿着光纤原路返回至环形器^[13]。利用滤波器对光脉冲信号进行去噪处理，以保证信号的准确性；过滤后的光脉冲信号由光电探测器转换为电信号，再利用数据采集卡对电信号进行实时检测，并在计算机中完成显示、处理与分析等，从而得到不同工况下托辊的振动信号。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 托辊振动信号采集方法

Fig.2 Acquisition method of idler vibration signal

1.2　基于Φ-OTDR技术的检测原理

Φ-OTDR技术是在传统瑞利散射原理的基础上进行了完善。建立图3所示的离散模型，以直观地描述分布式光纤中的后向瑞利散射干涉效应，从而清晰地理解Φ-OTDR技术的检测原理。将带式输送机中每一个托辊处的分布式光纤看作一个反射率与入射光相关的反射镜。假设布置在输送机机架上的长度为H的光纤由P个小段构成，则每一小段的长度 $Δ H = H / P$ 。分布式光纤中存在后向瑞利散射现象是因为入射光每传输到一个光纤小段时就会有一部分光被返回到入射光的光纤处。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 后向瑞利散射干涉效应的离散模型

Fig.3 Discrete model of backward Rayleigh scattering interference effect

假设图3中第d个反射镜为 $Δ H$ 光纤区域中的离散化中心，这一小段光纤中包含了N个离散化中心，则在分布式光纤上H_n 位置处多个后向瑞利散射光产生干涉现象，叠加后的电场可表示为：

E_{R B} (H_{n}) = E_{0} e^{- α (n - 1) Δ H} \sum_{r = 1}^{N} a_{n, r} e^{j φ_{n, r}}

(1)

式中：E₀为入射光的电场强度，α为光纤的衰减系数， $a_{n, r}$ 、 $φ_{n, r}$ 分别为第n部分中第r个离散化中心的振幅和相位。

由于光纤在传输中会产生双折射现象，单位长度 $Δ H$ 内的偏振态会沿着分布式光纤逐渐变化，因此检测到的后向瑞利散射光信号的形状为椭圆形。如图4所示，在外界环境干扰很小时，故障位置处振动前后会产生明显的幅值变化，而正常位置处振动前后的幅值几乎不变，因此通过振动前后的瑞利散射幅值曲线相减，即可实现对故障的定位。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 振动前后的瑞利散射时域曲线

Fig.4 Time-domain curve of Rayleigh scattering before and after vibration

2 托辊振动信号的处理方法

信号处理是故障诊断的关键环节，信号处理程度决定了故障的识别准确率。本文利用STFT和CNN对不同工况下托辊的振动信号进行处理，以提高对托辊运行状态的识别准确率。

2.1　STFT处理

STFT广泛应用于时变、非平稳信号的时频分析。STFT是先截取一定长度的时域信号作为窗函数，再对所截取的时域信号作FFT处理，即可得到时间段t上的频谱图。通过窗函数在检测时间段上的滑动，可得到每段频谱的集合。因此，STFT处理结果为关于时间和频率的二维函数^[14]，计算公式如下：

S_{f} (t, f) = \int_{- \infty}^{\infty} h (t) p (t - β) e^{- j ω t} d t

(2)

式中：f为频率； $h (t)$ 为时域信号； $p (t - β)$ 为以β为中心的窗函数，为了提高时频域的分辨率，本文选用Hamming窗函数；ω为角频率。

2.2　CNN模型构建

CNN是一种前反馈神经网络，可以准确地识别图像特征，实现大数据下的深度学习^[15]。自从Lecun等^[16]提出LeNet-5后，CNN的结构可以根据实际需求进行设计。CNN主要由卷积层、池化层和全连接层组成，如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 CNN的结构

Fig.5 Structure of CNN

利用CNN开展托辊故障诊断时，将经STFT处理得到的托辊振动信号时频图作为CNN模型的输入，将托辊运行状态作为CNN模型的输出。CNN模型对信号的处理过程分为前向传播和反向传播^[17]。

2.2.1　前向传播

CNN的前向传播过程包括卷积层、池化层和全连接层的操作^[18]。

1）卷积层。

卷积层是利用滤波器来提取输入信号的特征。每个滤波器通过在输入信号上滑动，来提取对应的特征图。通过多个卷积层的叠加，可提取更加全面的特征。最后，卷积层输出一组特征图，代表不同特征的响应。这些特征图传递至池化层，以进行进一步处理。卷积过程可表示为：

W_{p, j} = f (\sum_{i \in H_{j}} W_{p - 1, i} \cdot q_{p, i j} + k_{p, j})

(3)

式中： $W_{p, j}$ 为第p个卷积层的第j张特征图； $H_{j}$ 为第j张特征图对应的输入； $q_{p, i j}$ 为对应卷积层的权重；k_p_,_j 为对应卷积层的偏置项； $f (\cdot)$ 为激活函数，本文采用ReLU（rectified linear unit，修正线性单元）函数，具体表达式为 $f (x) = m a x (0, l g (1 + e^{x}))$ 。

2）池化层。

池化层通过将输入的特征图划分为不重叠的N₁×N₁个区域，并对每个区域进行汇聚操作，使得输出图像缩小N₁倍。这样可实现在缩小特征图的同时保留关键信息。池化层通过降低特征维度来提高计算效率，提升了CNN模型对平移和缩放变化的鲁棒性。最后，池化层输出经汇聚操作后的特征图。

3）全连接层。

输入的时频图经卷积层和池化层处理后到达全连接层，以进行特征识别。全连接层将输入的所有特征频谱展开为一维特征向量，对其进行加权求和与激活函数处理^[19]。全连接层的输出可表示为：

y_{m} = f (l_{m} x_{m - 1} + k_{m})

(4)

式中：y_m 为全连接层的输出；m为全连接层的序号； x_m_-1为展开的一维特征向量；l_m 为权重系数；k_m 为偏置项； $f (\cdot)$ 为激活函数，通常使用Softmax函数。

2.2.2　反向传播

CNN模型的训练目标是最小化网络的损失函数，故损失函数决定了CNN模型的识别准确率。本文选择交叉熵作为损失函数，具体表达式如下：

E = - \frac{1}{h} \sum_{u = 1}^{h} [Y_{u} l n w_{u} + (1 - Y_{u}) l n (1 - w_{u})]

(5)

式中：E为损失函数，h为样本数量，w_u 为预测值，Y_u 为真实值。

在训练过程中，通过求式(5)的一阶偏导来达到逐渐更新CNN参数的目的，具体计算公式如下：

l^{'} = l - η \frac{\partial E}{\partial l}

(6)

k^{'} = k - η \frac{\partial E}{\partial k}

(7)

式中： $l^{'}$ 、 $k^{'}$ 为更新后的权重系数和偏置；η为学习速率，若η值过大，则会导致局部最优，若η值过小，则会造成训练时间过长。

2.3　托辊故障诊断流程

基于STFT和CNN的托辊故障诊断方法是一种融合信号预处理、特征提取和分类的诊断方法，具体流程如图6所示。对分布式光纤采集的不同工况下的托辊振动信号进行STFT处理后，得到对应的时频图；将一部分时频图作为训练集并输入CNN模型，以实现诊断模型训练；当CNN模型的识别准确率达到要求后，将其应用于测试集并输出托辊的运行状态，以验证CNN模型的识别准确率。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 基于STFT和CNN的托辊故障诊断流程

Fig.6 Idler fault diagnosis process based on STFT and CNN

3 托辊故障诊断与分析

对带式输送机中间段托辊在正常运行和故障工况下的振动信号进行采集后，对振动信号进行STFT处理，得到振动信号的时频图，随后将得到的时频图作为CNN模型的输入，以对托辊运行状态进行识别，从而实现故障诊断。

3.1　基于STFT的振动信号处理

首先，对分布式光纤采集的托辊振动信号进行归一化处理。正常运行、筒皮断裂、轴承损坏工况下托辊振动信号的归一化处理结果如图7所示。由图7可以看出，托辊正常运行时的振幅较小，托辊发生轴承损坏和筒皮断裂时的振幅均较大，且均在[0, 1] mm内剧烈变化。因此，须对采集的振动信号进行进一步处理，以准确识别故障工况。

图7

新窗口打开| 下载原图ZIP| 生成PPT

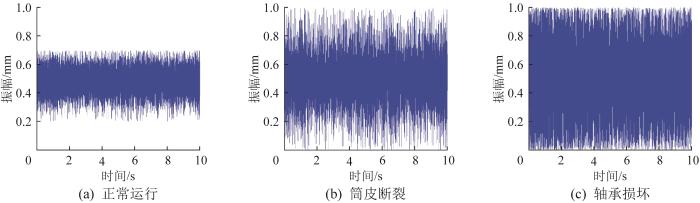
图7 不同工况下托辊的振幅—时间曲线

Fig.7 Amplitude-time curve of idler under different working conditions

对图7所示的归一化数据进行STFT处理，得到不同工况下托辊振动信号的时频图，如图8所示。由图8可知，在托辊正常运行工况下，托辊振动信号的频率很小，振幅均在0.12 mm以下；当托辊因筒皮断裂而失效时，托辊振动信号的频率分布在0~500 Hz范围内，频率为100 Hz时所对应的振幅最大，最大振幅为0.18 mm左右；当托辊因轴承损坏而失效时，托辊振动信号的频率较为分散，其中振动信号频率的极值主要集中在100 Hz附近，最大振幅达到0.27 mm左右。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同工况下托辊振动信号的时频图

Fig.8 Time-frequency diagram of idler vibration signal under different working conditions

3.2　基于CNN的故障诊断模型构建

通过上文分析可知，卷积层、池化层和全连接层的网络参数是影响CNN模型识别准确率的重要因素。利用MATLAB软件建立适用于带式输送机中间段托辊故障诊断的CNN模型，如图9所示，并对其结构参数进行设置，如表1所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 适用于托辊故障诊断的CNN模型

Fig.9 CNN model suitable for idler fault diagnosis

表1 CNN的结构参数

Table 1 Structural parameters of CNN

网络层	特征图数量/张	特征图大小/像素
输入层	1	64×64
池化层1	1	32×32
卷积层1	32	32×32
池化层2	32	16×16
卷积层2	64	16×16
池化层3	64	8×8
全连接层	1	2 048
输出层	1	1

新窗口打开| 下载CSV

将基于STFT处理得到的托辊振动信号时频图作为CNN模型的输入，特征图从输入到输出共经历了8层处理。输入CNN模型的时频图的像素为64×64，CNN模型的输出为托辊的3种运行状态。本文建立的CNN模型直接调用MATLAB软件中自带的imageDatastore函数。将不同工况下的3 000个样本（每种托辊工况对应1 000个）划分为训练集和测试集，其中训练集含2 250个样本，其余为测试集。在训练CNN模型时，对训练样本进行随机取样。对CNN模型进行4轮迭代，设置达到最大训练次数时停止迭代。

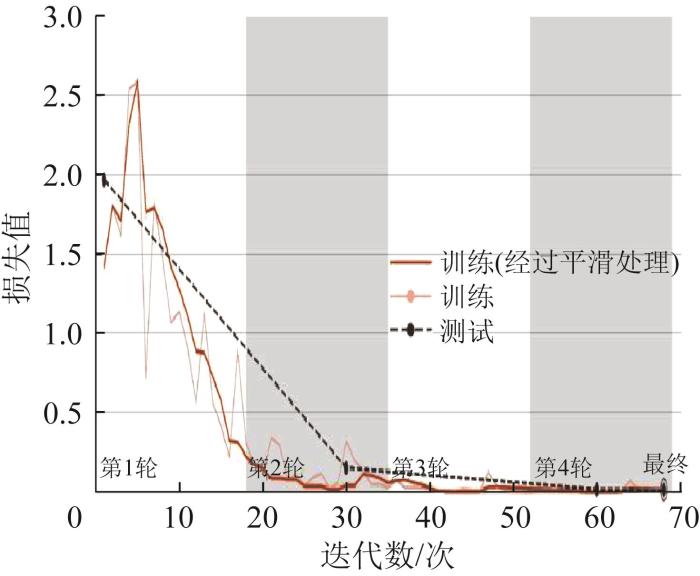
在CNN模型训练过程中采用“抓包”的形式，即将每轮训练好的CNN模型应用于测试集，并将识别的托辊运行状态与实际运行状态进行对比，得到所构建CNN模型的识别准确率和损失值，分别如图10和图11所示。由图10可知，在前2轮迭代过程中，CNN模型在训练集和测试集上的识别准确率均呈急剧增大趋势，一直增大至95%以上，在训练集上为迭代20次时趋于稳定，在测试集上为迭代30次时趋于稳定；随着迭代次数的增加，无论是在训练集还是在测试集上，CNN模型的识别准确率均在不断向极大值逼近。由图11可知，在开始迭代时，CNN模型在训练集和测试集上的损失值均在2.5附近，经过第1轮迭代后，CNN模型在训练集上的损失值降至0.2左右，而在测试集上的损失值降至0.8左右；经过30次迭代后，CNN模型在测试集上的损失值降至0.1左右；随着迭代次数的增加，CNN模型在训练集和测试集上的损失值均在不断向极小值逼近。最终，本文所构建的CNN模型的识别准确率达到99.6%，可实现对托辊故障的准确诊断。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 CNN模型在训练集和测试集上的识别准确率

Fig.10 Recognition accuracy of CNN model on training set and testing set

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 CNN模型在训练集和测试集上的损失值

Fig.11 Loss value of CNN model on training set and testing set

3.3　CNN模型的鲁棒性验证

鉴于上文的托辊振动信号是在带式输送机带速为4 m/s时采集的，考虑到实际工作环境和作业要求，采集输送机带速分别为3，5 m/s时托辊的振动信号并进行STFT处理，得到对应的时频图并形成新的样本集，以对上文训练得到的CNN模型进行鲁棒性验证。输送机带速为3 m/s和5 m/s时每种托辊工况均分别有1 000个样本，共计6 000个样本，分为10组，其他参数设置均与带速为4 m/s时相同。对3种带速下CNN模型识别托辊运行状态的准确率进行对比，结果如图12所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 不同带速下CNN模型的识别准确率对比

Fig.12 Comparison of recognition accuracy of CNN model under different belt speeds

由图12可知，基于输送机带速为4 m/s时运行数据所得到的CNN模型只能对该带速下托辊的运行状态进行准确识别，而对其他带速下托辊运行状态的识别准确率较低，说明目前的CNN模型并不具有广泛性。因此，须构造一个包含输送机不同带速下托辊运行状态的样本集，并重新对CNN模型进行训练，使其能实现对不同带速下托辊运行状态的准确识别。经过一段时间的托辊振动信号采集和对CNN模型的完善，利用新CNN模型对输送机带速为3，4，5 m/s时托辊的运行状态进行识别。设置9 000个样本，其中6 750个为训练集，其余2 250个为测试集。新CNN模型对输送机不同带速下托辊运行状态的识别准确率如图13所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 不同带速下新CNN模型的识别准确率对比

Fig.13 Comparison of recognition accuracy of new CNN model under different belt speeds

由图13可知，新CNN模型可以很好地识别输送机常用带速下托辊的运行状态。由此说明，CNN模型是一种基于数据集的识别方法，所采集的数据量越大，则其识别特征的能力越强大，即识别准确率越高。在本文中，由于经费以及现场条件的限制，仅考虑了带式输送机常用带速对托辊运行状态识别的影响。在后续的研究中，还应考虑输送机平均运量、噪音等因素对托辊运行状态识别的影响，以实现更为准确的故障诊断。

4 实验验证

为进一步验证本文所提出的托辊故障诊断方法的有效性，在某矿井下主暗斜井带式输送机（以4 m/s的带速运行）上开展实验。带式输送机运行现场如图14所示。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 带式输送机运行现场

Fig.14 Belt conveyor operation site

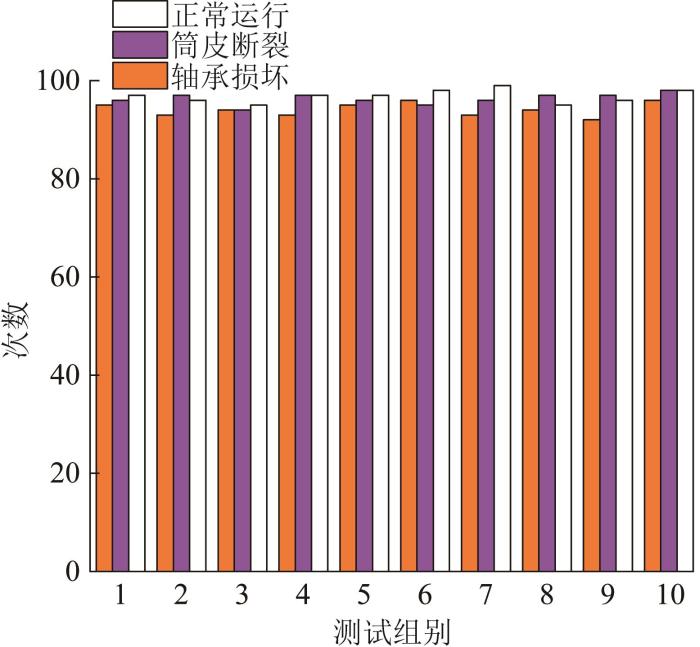
利用扎带将GYTS-4B1型铠装光缆固定在带式输送机两侧槽钢的内部，设传感距离为400 m，托辊振动信号的采样频率为16 kHz。对带式输送机中间段正常运行的托辊、发生轴承损坏和筒皮断裂的托辊进行监测并记录。经过一段时间的监测，对CNN模型诊断的1 000个故障样本（分为10组）进行验证。CNN模型诊断的故障次数与实际故障次数的对比如图15所示。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 CNN模型的故障诊断结果与实际故障结果对比

Fig.15 Comparison of fault diagnosis results of CNN model and actual fault results

由图15可知，在CNN模型诊断的1 000个故障样本中，978个为真故障，可能是托辊轴承损坏或筒皮断裂。经过工作人员核实，1 000次报警中仅有35次报错的情况，即与现场的实际故障不符。由此可知，CNN模型具有较高的识别准确率，可达96.5%。为了有针对性地提高CNN模型的识别准确率，继续进行验证，累计采集托辊正常运行、筒皮断裂和轴承损坏工况下的各1 000个样本，同样分成10组，并将CNN模型的识别结果与现场的实际托辊运行状态进行对比，结果如图16所示。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 CNN模型对不同托辊运行状态的识别结果

Fig.16 Recognition results of different idler operating states by CNN model

由图16可知，CNN模型对托辊正常运行、筒皮断裂、轴承损坏的识别准确率存在一定差距。其中，对托辊正常运行和筒皮断裂的识别准确率较高，可达96%左右（分别为96.8%和96.3%），而对托辊轴承损坏的识别准确率仅为94.1%左右。因此，需多采集托辊轴承损坏工况下的振动信号，以进一步完善CNN模型，从而实现对托辊轴承损坏这一故障的准确识别。

5 结论

本文针对带式输送机中间段托辊，提出了一种融合STFT和CNN的托辊故障诊断方法。对托辊振动信号进行预处理后，利用STFT实现了对托辊正常运行、轴承损坏和筒皮断裂工况下特征的提取与分类，并构建了一个识别准确率较高的CNN模型，在一定程度上实现了对托辊故障的准确诊断。所得结论如下：

1）基于STFT对托辊振动信号进行处理，通过得到的时频图已能够很好地判断托辊的运行状态；将时频图输入CNN模型并不断完善网络参数，即可取得更好的托辊故障诊断效果。

2）所构建的CNN模型在MATLAB软件中经过4轮迭代后的识别准确率高达99.6%，在现场验证中CNN模型的识别准确率为96.5%，两者仅相差3.1个百分点，由此说明CNN模型的识别精度较高。

3）在对CNN模型进行鲁棒性验证时，发现带式输送机、托辊的运行参数均会严重影响CNN模型的鲁棒性。本文仅考虑了带式输送机常用带速对CNN模型识别效果的影响，后续应不断增加不同工况下的数据，以进一步提高CNN模型对托辊运行状态的识别准确率。

4）实验结果表明，所构建的CNN模型对托辊正常运行、轴承损坏和筒皮断裂的识别准确率分别为96.8%，94.1%，96.3%，说明该模型对托辊轴承损坏这一故障的诊断效果还有待加强。在后续研究中，应增加托辊轴承损坏工况下振动信号的采集，以进一步提高CNN模型的整体识别准确率。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

齐庆杰，王欢，董子文，等.

矿井胶带运输巷火灾蔓延规律的数值模拟研究

［J］. 中国安全科学学报， 2016， 26（10）： 36-41. doi：10.16265/j.cnki.issn1003-3033.2016.10.007