基于子区间的雷达探测距离和测距精度分析

doi:10.3785/j.issn.1006-754X.2024.03.209

基于子区间的雷达探测距离和测距精度分析

欧阳衡^,^,¹^,², 高硕¹^,², 王世涛³, 马正琰¹^,², 张德权^,^,¹^,²

1.河北工业大学机械工程学院，天津 300401

2.河北工业大学省部共建电工装备可靠性与智能化国家重点实验室，天津 300401

3.31002部队，北京 100094

Analysis of radar detection distance and ranging accuracy based on subinterval

OUYANG Heng^,^,¹^,², GAO Shuo¹^,², WANG Shitao³, MA Zhengyan¹^,², ZHANG Dequan^,^,¹^,²

1.School of Mechanical Engineering, Hebei University of Technology, Tianjin 300401, China

2.State Key Lab of Reliability and Intelligence of Electrical Equipment, Hebei University of Technology, Tianjin 300401, China

3.No. 31002 Troops, Beijing 100094, China

通讯作者: 张德权（1990—），男，河北张家口人，教授，博士，从事装备不确定性量化与可靠性设计等研究，E-mail: dequan.zhang@hebut.edu.cn, https://orcid.org/0000-0003-3886-1546

收稿日期: 2023-10-20 修回日期: 2023-11-10

基金资助:

河北省博士后择优资助基金资助项目. 2021005004
省部共建电工装备可靠性与智能化国家重点实验室人才培育基金资助项目. EERIPD2021006

Received: 2023-10-20 Revised: 2023-11-10

作者简介 About authors

欧阳衡（1992—），男，湖南衡阳人，副教授，博士，从事复杂装备数字化与智能化设计等研究，E-mail:ouyangheng@hebut.edu.cn,https://orcid.org/0009-0009-9046-1604 , E-mail：ouyangheng@hebut.edu.cn

摘要

探测距离和测距精度是雷达的关键性能指标，在实际服役工况下受雷达系统内部信号传输损耗、外部信号干扰等不确定性因素的影响较大，提高其准确性已成为雷达研究领域的重要课题。为了评估上述不确定性因素对雷达性能的影响程度，开展了雷达探测距离和测距精度的不确定性分析。首先，建立了考虑信号传输损耗和信号干扰的雷达探测距离和测距精度模型；其次，采用区间模型量化不确定性参数，实现内外部参数统一框架下的不确定性度量；然后，构建准确的探测距离和测距精度响应面模型，并采用Sobol'全局敏感性分析方法实现多维参数对探测距离和测距精度影响的排序；最后，采用子区间分解分析方法获取了雷达探测距离和测距精度区间，并与通过蒙特卡洛模拟得到的结果进行对比，验证所提方法的有效性。将雷达探测距离和测距精度设定合理的容限与阈值，可提高雷达性能分析效率，降低性能分析成本。

关键词： 探测距离 ; 测距精度 ; 不确定性 ; 响应面 ; 子区间

Abstract

Detection range and ranging accuracy are the key performance indicators of radar. Under actual service conditions, they are greatly affected by uncertain factors such as internal signal transmission loss and external signal interference of radar system. Improving its accuracy has become an important topic in the field of radar research. In order to evaluate the influence of the above uncertain factors on the radar performance, the uncertainty analysis of radar detection range and ranging accuracy was carried out. Firstly, the radar detection range and ranging accuracy models considering signal transmission loss and signal interference were established; secondly, the interval model was used to quantify the uncertainty parameters to realize the uncertainty measurement under the unified framework of internal and external parameters; then, the accurate response surface models of detection range and ranging accuracy were constructed, and the influence of multi-dimensional parameters on detection range and ranging accuracy was sorted by using Sobol' global sensitivity analysis method; finally, the subinterval decomposition analysis method was used to obtain the radar detection range and ranging accuracy range, and the results were compared with those calculated by Monte Carlo simulation method to verify the effectiveness of the proposed method. Reasonable tolerance and threshold values are set for radar detection range and ranging accuracy, which can improve the efficiency of radar performance analysis and reduce the cost of performance analysis.

Keywords： detection distance ; ranging accuracy ; uncertainty ; response surface ; subinterval

PDF (1527KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

欧阳衡, 高硕, 王世涛, 马正琰, 张德权. 基于子区间的雷达探测距离和测距精度分析[J]. 工程设计学报, 2024, 31(3): 332-339 doi:10.3785/j.issn.1006-754X.2024.03.209

OUYANG Heng, GAO Shuo, WANG Shitao, MA Zhengyan, ZHANG Dequan. Analysis of radar detection distance and ranging accuracy based on subinterval[J]. Chinese Journal of Engineering Design, 2024, 31(3): 332-339 doi:10.3785/j.issn.1006-754X.2024.03.209

雷达是获取海陆空战场全天候、全天时战略和战术情报的重要设备，是自动化指挥系统的首要视觉传感器，被广泛应用于军事、航空航海及气象预报等领域^[1]。雷达性能直接决定了雷达系统所能完成任务的类型及完成效果^[2]。探测距离和测距精度是雷达性能的核心指标，其在雷达工作过程中会受到传输波动和杂波干扰等因素的影响，导致雷达的探测能力下降，无法准确捕捉目标信息^[3]。因此，开展雷达系统探测距离和测距精度的分析，对雷达技术的发展及工程应用具有重要意义^[4]。

近年来，有关雷达探测距离和测距精度提升的研究受到了国内外学者的广泛关注。刘育才等^[5]通过雷达方程获取了“本土链”雷达的探测距离，并提出了反干扰、抗摧毁等雷达未来发展方向；Dong等^[6]提出了一种基于泊松盘抽样和迭代软阈值算法的消除调频连续波雷达距离混叠的方法，在消除距离混叠的同时增大了探测距离，提高了雷达的多目标探测能力；曹丽等^[7]归纳了车载激光雷达探测距离的关键参数及决定因素，为雷达性能分析效率的提高奠定了基础；Chang等^[8]提出了一种超分辨率网络，在有限带宽下保证了最大可探测距离；李琴等^[9]采用地杂波动目标显示抑制技术，有效增大了低空小型无人机雷达的探测距离，为检测低小、较慢目标的地基雷达的设计提供了参考；Zhao等^[10]提出了一种远程目标探测距离模糊的解决方法，增强了雷达远距离探测能力；董云龙等^[11]根据海杂波对目标探测的影响，将一般雷达方程简化为信噪比方程，提高了探测距离的计算效率；汤华涛等^[12]在蒸发波导条件下建立了雷达组网探测范围的评估模型，扩大了在目标运动姿态未知情况下的探测范围；针对实际探测距离的计算须根据约束条件的变化不断调整的问题，陈超凡等^[13]提出了一种雷达实际探测威力快速生成算法，有效提高了探测距离的计算速度；马兰等^[14]通过高斯插值处理方法预估脉压波峰值出现的时间，减小了预估脉压波峰值与真实脉压波峰值之间的误差，有效提高了测距精度；Marom等^[15]提出了在测量坐标系中使用滤波器并将测量结果转换到笛卡尔坐标系的解决方案，提高了滤波后的测距精度；李鑫洋等^[16]引入频谱最大估值算法，减小了快速傅里叶变换计算的测距误差，提高了测距精度；Sim等^[17]通过比较包络检测后的采样数来区分每种频率的基带信号，提高了测距精度；Xu等^[18]基于相干谱模型提出了连续线性调频z变换算法，为雷达的精准探测提供了依据；罗韩君等^[19]采用统计原理与质心法建立了测距精度的理论模型，证明了回波强度和回波脉宽是测距精度的主要影响因素；李妍等^[20]建立了一种针对不确定性数据的雷达探测距离预测模型，有效降低了数据扰动对雷达探测性能的影响；邱志平等^[21]提出了一种非概率区间方法来近似估计雷达探测距离。

不确定性会导致雷达探测距离和测距精度的准确性降低，从而造成雷达模型不可靠。使用受不确定性影响的雷达模型进行雷达性能评估，可能会产生致使决策失误的严重后果。分析不确定性对雷达探测距离和测距精度的影响规律，可以使雷达性能分析的结果更加准确与合理，从而可提高雷达性能分析的可靠性。

本文考虑雷达系统内外部不确定性因素，深入分析不确定性对雷达关键性能指标的影响规律。通过子区间分解方法对雷达性能进行分析，并将计算结果与蒙特卡洛模拟（Monte Carlo simulation，MCS）结果进行比较，来验证本文所提方法的有效性，以期为雷达性能分析提供一种高效准确的方法。

1 雷达探测距离和测距精度模型

近年来，雷达技术发展迅速，对探测距离、自卫干扰距离、检测概率、测距精度、角精度等性能参数的要求更加严格。其中探测距离是雷达的重要性能指标，而测距精度是表征雷达探测距离准确度的关键指标。为了精确量化雷达探测距离和测距精度，利用雷达方程建立探测距离方程和测距精度方程。

1.1　探测距离方程

探测距离指雷达在不受干扰的情况下能探测到目标的最远距离，可以表示为^[4]：

R = {[\frac{P_{t} \cdot G_{t} \cdot G_{r} \cdot σ \cdot λ^{2} \cdot τ}{{(4 π)}^{3} \cdot k \cdot T_{0} \cdot F_{n} \cdot L}]}^{\frac{1}{4}}

(1)

式中：R为探测距离；P_t为雷达发射功率；G_t、G_r分别为发射增益和接收增益；σ为雷达截面积；λ为波长，其与天线增益和天线有效孔径有关；τ为脉冲宽度；k为玻尔兹曼常数，k= $1.380 650 5 \times 10^{- 23}$ ； $T_{0}$ 为噪声温度；F_n为噪声系数；L为综合损耗。

1.2　测距精度方程

测距精度指雷达探测距离的准确程度。对雷达探测距离的误差进行估计，可以表示为^[4]：

R_{r e s} = \frac{\sqrt[]{3} \cdot c}{2 π \cdot B_{n} \cdot \sqrt[]{2 \cdot R_{S N}}}

(2)

式中：R_res为测距精度；c为光速，取c= $3.0 \times 10^{8}$ m/s； $B_{n}$ 为信号带宽；R_SN为信噪比。

R_{S N} = \frac{P_{r} \cdot B_{n} \cdot τ \cdot n_{p}}{N_{i} + P_{j}}

(3)

式中：n_p为脉冲积累数； $P_{j}$ 为干扰功率；N_i为噪声功率， $N_{i} = F_{n} \cdot k \cdot T_{0} \cdot B_{n} \cdot G_{a}$ ，其中G_a为接收机增益，即接收天线的等效增益；P_r为回波功率。

P_{r} = \frac{P_{t} \cdot G_{t} \cdot G_{r} \cdot λ^{2} \cdot σ \cdot G_{a}}{{(4 π)}^{3} \cdot R^{4} \cdot L}

(4)

2 雷达系统参数

2.1　雷达参数和干扰参数

雷达主要由发射机、天线、接收机及信号处理机组成。其中发射机产生雷达信号，天线用于收发信号，接收机捕获反射信号，信号处理机用于分析数据。

由于杂波影响，雷达发射和接收的信号与初始信号存在一定误差，同时信号在雷达内部传递的过程中存在损耗，导致雷达参数在一定范围内波动。将雷达参数和干扰参数设为区间变量，如表1所示。在本文中，信号频率与干扰频率设置为相同数值。

表1 雷达参数和干扰参数

Table 1 Radar parameters and interference parameters

参数	单位	数值区间
信号频率	10⁸Hz	[3.0, 10.0]
信号带宽	10⁵Hz	[5.0, 10.0]
脉冲宽度	10^-3s	[1.0, 2.0]
脉冲积累数	个	[1, 10]
雷达发射功率	10⁵W	[1.0, 5.0]
发射增益	dB	[35.0, 40.0]
接收增益	dB	[35.0, 40.0]
综合损耗	dB	[40.0, 45.0]
方位波束宽度	(°)	[2.0, 3.0]
俯仰波束宽度	(°)	[2.0, 3.0]
测角误差斜率		[40.0, 70.0]
压制系数		[40.0, 70.0]
干扰频率	10⁸Hz	[3.0, 10.0]
干扰带宽	Hz	[3.0, 7.0]
干扰功率	10³W	[3.0, 7.0]
干扰发射增益	dB	[10.0, 20.0]

新窗口打开| 下载CSV

2.2　雷达系统参数筛选

2.2.1　雷达系统性能区间度量模型的建立

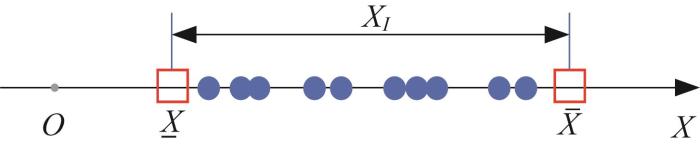
雷达系统存在雷达参数传输波动、信号干扰等不确定性因素，导致性能不稳定。已知雷达参数和干扰参数的数值区间，根据区间模型来度量雷达系统性能的不确定域。将影响雷达系统性能的不确定参数用区间进行量化，如图1所示，可以表示为^[22]：

X \in X_{I} = [\underset{̲}{X}, \bar{X}]

(5)

式中：I表示区间， $\underset{̲}{X}$ 表示区间下界， $\bar{X}$ 表示区间上界， $\underset{̲}{X} < \bar{X}$ 。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 影响雷达系统性能的不确定参数示意

Fig.1 Schematic of uncertain parameters affecting radar system performance

参数X的不确定性通过其区间上界 $\bar{X}$ 和下界 $\underset{̲}{X}$ 限定，所有可能值都包含于其构成的区间内。记X的中点和半径分别为X_c和X_r，可以表示为^[22]：

X_{c} = \frac{\bar{X} + \underset{̲}{X}}{2}

(6)

X_{r} = \frac{\bar{X} - \underset{̲}{X}}{2}

(7)

X_r反映了X的不确定性大小。X可记为： $X \in X_{I} = [X_{c} - X_{r}, X_{c} + X_{r}]$ 。

雷达系统的输入参数维度高，且部分参数间的数量级存在明显差异，若不进行处理会导致计算结果不准确，从而使雷达探测距离和测距精度产生较大误差。因此，为了提高雷达系统性能分析的精度，将雷达系统参数归一化，即把参数转化到[0, 1]区间内，降低参数数量级对性能分析的影响。

假设区间参数U的区间半径 $U_{r} = 0.5$ ，区间中点 $U_{c} = 0.5$ ，记为 $U \in U_{I} = [0, 1]$ 。可通过如下变换将参数从 X 空间转化为 U 空间，实现参数的归一化：

U = \frac{X - \underset{̲}{X}}{2 X_{r}}

(8)

2.2.2　雷达性能参数筛选

采用摄动法对雷达探测距离和测距精度进行局部敏感性分析，以单个参数引起的性能变化来分析上述不确定参数是否对雷达性能产生影响。将雷达参数区间均分为10份，计算各节点处的雷达探测距离和测距精度响应值，并获得雷达探测距离和测距精度的影响参数。

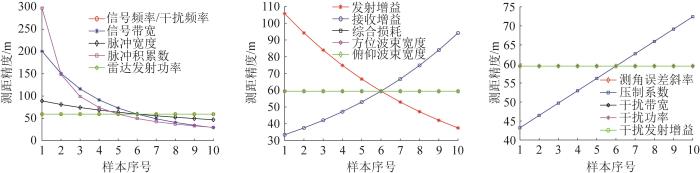
探测距离局部敏感性分析结果如图2所示。由图可知：雷达探测距离随着信号频率/干扰频率、脉冲宽度、雷达发射功率、发射增益、接收增益和综合损耗的变化而改变，说明上述参数是探测距离的影响因数；随着信号带宽、脉冲积累数、方位波束宽度、俯仰波束宽度、测角误差斜率、压制系数及各干扰参数的变化，探测距离并无变化，说明上述参数对探测距离没有影响。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 探测距离局部敏感性分析结果

Fig.2 Local sensitivity analysis results of detection distance

测距精度局部敏感性分析结果如图3所示。由图可知：测距精度随着信号带宽、脉冲宽度、脉冲积累数、发射增益、接收增益和压制系数的变化而变化，说明上述参数是测距精度的影响因素；随着信号频率/干扰频率、雷达发射功率、综合损耗、方位波束宽度、俯仰波束宽度、测角误差斜率及各干扰参数的变化，测距精度并无变化，说明上述参数对测距精度没有影响。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 测距精度局部敏感性分析结果

Fig.3 Local sensitivity analysis results of ranging accuracy

3 雷达性能参数全局敏感性分析

3.1　雷达性能响应面模型

随着雷达系统的复杂程度和性能要求的不断提高，其性能分析呈现变量多维、信息多源、分布多样等特点，导致基于高精度仿真模型的性能分析与计算的成本过高，难以应用。

多项式响应面模型具有收敛迅速的优点。将它应用于雷达性能分析中，可以有效提高性能分析的效率。其一般表达式为^[23]：

f (X) = \sum_{i = 1}^{n} a_{i} φ_{i} (X)

(9)

式中： $f (X)$ 为预测的雷达性能响应，n为多项式基函数 $φ_{i} (X)$ 的个数， $a_{i}$ 为待求解的系数。

不确定参数之间耦合性强，因此采用高阶多项式作为响应面模型，其表现形式为^[23]：

\begin{array}{l} f (X) = a_{0} + \sum_{i = 1}^{n} a_{i} X_{i} + \sum_{i = 1}^{n} a_{i i} X_{i}^{2} + \dots + \\ \sum_{i = 1}^{n} a_{\underset{n}{\underset{︸}{i \dots i}}} X_{i}^{m} + \sum_{i j (i < j)}^{n} a_{i j} X_{i} X_{j} \end{array}

(10)

式中： $X_{i}$ 为雷达系统的输入参数；m为多项式的阶数，在本文中取m=2； $a_{0}$ 、 $a_{i}$ 、 $a_{i j}$ 、a_ii 、 $a_{\underset{n}{\underset{︸}{i \dots i}}}$ 均为多项式的待定系数，所以对于该模型，至少需要进行[(n+1)(n+2)/2]+2n次计算。

通过观测值与模型预测值之间的复相关系数 $R^{2}$ 和均方根误差E_RMS^[24]来判断响应面模型在雷达性能分析中的准确性。

R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\tilde{y}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - {\bar{y}}_{i})}^{2}}

(11)

E_{R M S} = \frac{1}{n {\bar{y}}_{i}} \sqrt[]{\sum_{i = 1}^{n} {(y_{i} - {\tilde{y}}_{i})}^{2}}

(12)

式中： $y_{i}$ 为响应面模型的计算值， ${\tilde{y}}_{i}$ 和 ${\bar{y}}_{i}$ 分别为雷达性能模型的响应值及其平均值。

$R^{2}$ 值介于0与1之间，越接近于1，表明响应面模型的计算值与雷达性能模型响应值的误差越小。E_RMS的绝对值越小，表明响应面模型的拟合精度越高。

探测距离和测距精度响应面模型的精度验证结果如表2所示，可见响应面模型具有较高的精度。

表2 探测距离和测距精度响应面模型精度验证

Table 2 Accuracy verification of response surface model of detection distance and ranging accuracy

模型	R²	E_RMS
探测距离响应面模型	0.997 0	0.000 3
测距精度响应面模型	0.994 3	0.012 7

新窗口打开| 下载CSV

3.2　探测距离和探测距离全局敏感性分析

采用Sobol'全局敏感性分析方法获取雷达探测距离和测距精度影响参数的重要性排序。通过计算单个参数和参数组合的偏方差对总方差的影响来分析参数的重要程度。

假设雷达模型 $Y = g (X) = g (X_{1}, X_{2}, \dots, X_{n})$ ，其中 $X_{i}$ 在[0, 1]区间内服从均匀分布，则模型可以表示为^[25]：

\begin{array}{l} Y = g_{0} + \sum_{i = 1}^{n} g_{i} (X_{i}) + \sum_{1 \leq i \leq j \leq n}^{n} g_{i j} (X_{i}, X_{j}) + \dots + \\ g_{1, 2, \dots, n} (X_{1}, X_{2}, \dots, X_{n}) \end{array}

(13)

式中： $g_{0}$ 为常数； $X = (X_{1}, X_{2}, \dots, X_{n})$ 为n维相互独立的输入参数，所有子项两两正交。

总方差V为^[25]：

V = \int g^{2} (X) d X - g_{0}^{2}

(14)

单个参数的偏方差 $V_{i}$ 和参数组合的偏方差 $V_{i_{1}, \dots, i_{s}}$ 分别为^[25]：

V_{i} = \int g_{i}^{2} (X_{i}) d X_{i}

(15)

V_{i_{1}, \dots, i_{s}} = \int_{0}^{1} \dots \int_{0}^{1} g_{i_{1}, \dots, i_{s}}^{2} (X_{1}, \dots, X_{s}) d X_{i_{1}} \dots d X_{i_{s}}

(16)

式中：s=1, 2,…, n。

总方差V表示所有参数对系统输出的影响；偏方差 $V_{i}$ 表示单个参数对系统输出的影响， $V_{i_{1}, \dots, i_{s}}$ 表示多个输入参数间的交互效应对系统输出的影响。采用敏感性指标衡量参数的影响程度。敏感度 $S_{i_{1}, \dots, i_{s}}$ 定义为^[25]：

S_{i_{1}, \dots, i_{s}} = \frac{V_{i_{1}, \dots, i_{s}}}{V}

(17)

由上可知，各参数的敏感度之和为1，即^[26]：

\sum_{i = 1}^{n} S (i) + \sum_{i = 1}^{n} \sum_{j = i + 1}^{n} S (i, j) + \dots + S (1, 2, \dots, n) = 1

(18)

本文只考虑雷达系统模型的主效应指标，即单个参数对性能的影响程度，表示为^[26]：

S_{i} = \frac{V_{i}}{V}

(19)

探测距离和测距精度全局敏感性分析结果分别如表3和表4所示。

表3 探测距离全局敏感性分析结果

Table 3 Global sensitivity analysis results of detection range

影响参数	单位	数值区间	敏感度
信号频率/干扰频率	10⁸ Hz	[3.0, 10.0]	0.449 7
脉冲宽度	10^-3 s	[1.0, 2.0]	0.035 8
雷达发射功率	10⁵ W	[1.0, 5.0]	0.174 1
发射增益	dB	[35.0, 40.0]	0.104 3
接收增益	dB	[35.0, 40.0]	0.111 1
综合损耗	dB	[40.0, 45.0]	0.104 8

新窗口打开| 下载CSV

表4 测距精度全局敏感性分析结果

Table 4 Global sensitivity analysis results of ranging accuracy

影响参数	单位	数值区间	敏感度
信号带宽	10⁵ Hz	[5.0, 10.0]	0.242 3
脉冲宽度	10^-3 s	[1.0, 2.0]	0.020 6
脉冲积累数	个	[1, 10]	0.404 1
发射增益	dB	[35.0, 40.0]	0.070 4
接收增益	dB	[35.0, 40.0]	0.071 0
压制系数	dB	[40.0, 70.0]	0.013 0

新窗口打开| 下载CSV

由表3可知，参数对探测距离的影响程度从大到小依次为信号频率/干扰频率、雷达发射功率、接收增益、综合损耗、发射增益、脉冲宽度。

由表4可知，参数对测距精度的影响程度从大到小依次为脉冲积累数、信号带宽、接收增益、发射增益、脉冲宽度、压制系数。

4 雷达性能分析

经过雷达性能参数全局敏感性分析后，得到了雷达探测距离和测距精度的主要影响参数。对雷达探测距离和测距精度进行分析，获取其不确定域。分析流程如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 雷达探测距离和测距精度分析流程图

Fig.4 Analysis flowchart of radar detection distance and ranging accuracy

4.1　子区间分解分析方法

为了提高雷达性能分析效率，本文采用子区间分解分析方法，用响应面模型代替真实性能模型进行分析。子区间分解分析方法（subinterval decomposition analysis method，SDAM）^[27-28]将具有多维区间参数的原雷达系统分解为多个一维子系统，将每个子系统的不确定参数划分为几个不确定度较小的子区间，通过少数子区间的组合分析来近似计算雷达探测距离和测距精度的上界及下界。

将雷达探测距离和测距精度的响应面模型在区间中点处展开，可以得到^[27]：

f (X) = f (X_{c}) + G^{T} (X_{c}) δ X + \frac{1}{2} δ X^{T} H^{T} (X_{c}) δ X

(20)

式中： $G^{T}$ 和 $H^{T}$ 分别为梯度矩阵和Hessian矩阵。

G^{T} = [\frac{\partial f}{\partial X_{1}} \frac{\partial f}{\partial X_{2}} \dots \frac{\partial f}{\partial X_{n}}]

(21)

H^{T} = [\begin{matrix} \frac{\partial^{2} f}{\partial^{2} X_{1}} & \frac{\partial^{2} f}{\partial X_{1} \partial X_{2}} & \dots & \frac{\partial^{2} f}{\partial X_{1} \partial X_{n}} \\ \frac{\partial^{2} f}{\partial X_{2} \partial X_{1}} & \frac{\partial^{2} f}{\partial^{2} X_{2}} & \dots & \frac{\partial^{2} f}{\partial X_{2} \partial X_{n}} \\ ⋮ & ⋮ & ⋮ \\ \frac{\partial^{2} f}{\partial X_{n} \partial X_{1}} & \frac{\partial^{2} f}{\partial X_{n} \partial X_{2}} & \dots & \frac{\partial^{2} f}{\partial^{2} X_{n}} \end{matrix}]

(22)

将式(13)中的参数分别在每个参数 $X_{1},$ $X_{2}, \dots, X_{n}$ 处展开，其余参数用中点值代替，则根据式(20)可以求得雷达探测距离和测距精度的上界及下界，其数学模型可进一步表示为^[27]：

\begin{array}{l} f (X) = f (X_{1}, X_{c_{2}}, \dots, X_{c_{n}}) + f (X_{c_{1}}, X_{2}, \dots, X_{c_{n}}) + \\ \dots + f (X_{c_{1}}, X_{c_{2}}, \dots, X_{n}) - (n - 1) f (X_{c}) \end{array}

(23)

雷达探测距离和测距精度子区间分解分析的主要步骤如下。

步骤1：将探测距离和测距精度的主要影响参数的区间划分为N个子区间；

步骤2：将参数分别在其区间中点处展开，并代替初始的响应面模型；

步骤3：通过公式(23)计算每个子区间节点的探测距离和测距精度响应；

步骤4：将步骤3中获取的雷达探测距离和测距精度进行比较，取其中最大值为区间上界，最小值为区间下界，从而获得雷达探测距离和测距精度的数值区间，完成雷达性能不确定性分析。

取N=3，4，5，得到不同子区间下雷达探测距离和测距精度区间，如表5所示。通过MCS获取的雷达探测距离区间为[167 273, 725 512] m，测距精度区间为[4.91, 1 682.76] m，可见当N=3时通过SDAM算得的区间比MCS得到的大。当N=4与N=5时，得到的探测距离和测距精度区间相同，因此取N=4。

表5 不同子区间下雷达探测距离和测距精度区间 (m)

Table 5 Radar detection distance and ranging accuracy range under different subintervals

N	探测距离区间	测距精度区间
3	[71 200, 167 124]	[3.60, 1 660.35]
4	[167 385, 713 175]	[4.90,1 683.24]
5	[167 385, 713 175]	[4.90, 1 683.24 ]

新窗口打开| 下载CSV

4.2　雷达性能分析结果比较

考虑不确定性可以使雷达探测距离和测距精度的分析结果更加准确与合理，并且基于子区间的雷达性能分析可以实现系统性能与成本的最优平衡。采用MCS方法需要10万个样本，而采用本文方法仅需2 000个样本。不同方法下雷达性能不确定性分析结果如表6所示。表中，ε为误差， $ε = |f (X) - \tilde{f} (X) / \tilde{f} (X)| \times 100 %$ ，式中： $f (X)$ 、 $\tilde{f} (X)$ 分别为采用SDAM和MCS方法得到的雷达探测距离和测距精度的上下界。

表6 不同方法下雷达性能不确定性分析结果

Table 6 Uncertainty analysis results of radar performance under different methods

新窗口打开| 下载CSV

由表6可知，采用SDAM与MCS方法得到的探测距离区间之间的误差小于2%，测距精度区间之间的误差小于0.2%，表明本文方法可以有效计算雷达探测距离和测距精度的波动范围。

5 结论

本文考虑了影响雷达探测距离和测距精度的不确定性，采用基于子区间的性能分析方法探究了不确定性的影响机制。主要结论如下：

1）采用本文方法可以准确获得雷达探测距离和测距精度的区间上下界，提高了雷达探测的可靠性。

2）通过敏感性分析获得了雷达性能主要影响参数的敏感度。对探测距离影响最大的参数是信号频率/干扰频率，对测距精度影响最大的参数是脉冲积累数，这为降低雷达性能分析与计算成本提供了参考。

3）基于子区间的雷达性能分析方法相比于MCS方法，所需样本数减少了2个数量级，雷达性能分析效率得到提升。本研究为雷达性能不确定性分析提供了一种可行的研究思路。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

保铮

“雷达信号处理”专刊序言

［J］.电子与信息学报，2016，38（12）：2987. doi：10.3969/j.issn.1009-5896.2016.12.001

DOI:10.3969/j.issn.1009-5896.2016.12.001 [本文引用: 3]

BAO

. "

Radar signal processing" special issue preface

［J］. Journal of Electronics & Information Technology， 2016， 38（12）： 2987.

DOI:10.3969/j.issn.1009-5896.2016.12.001 [本文引用: 3]

[2]

王晓海

认知雷达系统技术发展综述

［J］.数字通信世界， 2018（）：40-43. doi：10.1109/icc.2018.8422762

DOI:10.1109/icc.2018.8422762 [本文引用: 1]

WANG

X H

Review on the development of cognitive radar systems

［J］. Digital Communication World， 2018 （）： 40-43.

DOI:10.1109/icc.2018.8422762 [本文引用: 1]

[3]

， ZHAO

A correction method for radar detection range analysis in interference environment

［C］//ITM Web of Conferences， León， Guanajuato， Oct. 5-7， 2022.

[本文引用: 1]

[4]

MAHAFZA

B R

. Radar systems analysis and design using matlab［M］. Boca Raton： CRC Press， 2021.

[本文引用: 3]

[5]

刘育才，马晓静，雷红.

“本土链”雷达主要性能分析及启示

［J］.火控雷达技术，2022，51（4）：47-52.

[本文引用: 1]

LIU

Y C

， MA

X J

， LEI

The main performance analysis and enlightenment of the CH radar

［J］. Fire Control Radar Technology， 2022， 51（4）： 47-52.

[本文引用: 1]

[6]

DONG

， LI

， WANG

， et al.

Range aliasing elimination for FMICW radar with uniform sampling bursts and poisson disk inter-burst delays

［J］. IEEE Sensors Journal， 2022， 22（2）： 1495-1508.

[本文引用: 1]

[7]

曹丽，宋梦洋，凌九红.

车载激光雷达关键性能参数及决定因素

［J］.汽车实用技术，2022，47（24）：196-199. doi：10.16638/j.cnki.1671-7988.2022.024.036

DOI:10.16638/j.cnki.1671-7988.2022.024.036 [本文引用: 1]

CAO

， SONG

M Y

， LING

J H

Key performance parameters and determinants of vehicle lidar

［J］. Automobile Applied Technology， 2022， 47（24）： 196-199.

DOI:10.16638/j.cnki.1671-7988.2022.024.036 [本文引用: 1]

[8]

CHANG

H Y

， CHEN

Y Y

， CHUNG

W H

RangeSRN： range super-resolution network using mmwave FMCW radar

［C］//2022 IEEE Global Communications Conference， Rio de Janeiro， Dec. 4-8， 2022.

[本文引用: 1]

[9]

李琴，黄卡玛.

低空小型无人机雷达探测距离仿真分析

［J］.无线电工程，2018，48（4）：303-307. doi：10.3969/j.issn.1003-3106.2018.04.11

DOI:10.3969/j.issn.1003-3106.2018.04.11 [本文引用: 1]

， HUANG

K M

Simulation analysis of radar detection range for small low-altitude UAV

［J］. Radio Engineering， 2018， 48（4）： 303-307.

DOI:10.3969/j.issn.1003-3106.2018.04.11 [本文引用: 1]

[10]

ZHAO

M X

， ZHANG

， YANG

， et al.

Using sky-wave echoes information to extend HFSWR's maximum detection range

［J］. Radio Science， 2018， 53（8）： 922-932.

[本文引用: 3]

[11]

董云龙，刘洋，刘宁波，等.

基于雷达方程修正的目标探测距离评估方法

［J］.信号处理，2022，38（10）：2102-2113.

[本文引用: 1]

DONG

Y L

， LIU

N B

， et al.

A method for evaluating target detection range based on radar range equation modification

［J］. Journal of Signal Processing， 2022， 38（10）： 2102-2113.

[本文引用: 1]

[12]

汤华涛，察豪，田斌，等.

微波超视距雷达组网探测范围研究

［J］.电波科学学报，2022，37（2）：274-278. doi：10.12265/j.cjors.2021114

DOI:10.12265/j.cjors.2021114 [本文引用: 1]

TANG

H T

， CHA H， TIAN

， et al.

Study on detection range of microwave over-the-horizon radar network

［J］. Chinese Journal of Radio Science， 2022， 37（2）： 274-278.

DOI:10.12265/j.cjors.2021114 [本文引用: 1]

[13]

陈超凡，江晶，李佳炜，等.

雷达实际探测威力快速生成算法研究

［J］.计算机仿真，2022，39（11）：7-10，183. doi：10.3969/j.issn.1006-9348.2022.11.002

DOI:10.3969/j.issn.1006-9348.2022.11.002 [本文引用: 1]

CHEN

C F

， JIANG

， LI

J W

， et al.

Research on a fast generation algorithm of radar detection power

［J］. Computer Simulation， 2022， 39（11）： 7-10， 183.

DOI:10.3969/j.issn.1006-9348.2022.11.002 [本文引用: 1]

[14]

马兰，李照照，杨雪林，等.

基于高斯插值提高雷达测距精度的研究

［J］.火控雷达技术，2021，50（1）：41-47.

[本文引用: 1]

， LI

Z Z

， YANG

X L

， et al.

Improving radar ranging accuracy based on Gaussian interpolation

［J］. Fire Control Radar Technology， 2021， 50（1）： 41-47.

[本文引用: 1]

[15]

MAROM

， BAR

S Y

， MILGROM

Bistatic radar tracking with significantly improved bistatic range accuracy

［J］. IEEE Transactions on Aerospace and Electronic Systems， 2023， 59（1）： 52-62.

[本文引用: 1]

[16]

李鑫洋，王洪源.

提高FMCW雷达测距精度的算法研究

［J］.中国新技术新产品，2016（19）：4-5. doi：10.3969/j.issn.1673-9957.2016.19.002

DOI:10.3969/j.issn.1673-9957.2016.19.002 [本文引用: 1]

X Y

， WANG

H Y

Research on algorithm to improve the ranging accuracy of FMCW radar

［J］. New Technology & New Products of China， 2016（19）： 4-5.

DOI:10.3969/j.issn.1673-9957.2016.19.002 [本文引用: 1]

[17]

SIM

J Y

， YANG

J R

Frequency discrimination method using asymmetric transmission time in FSK radar

［J］. Journal of Electromagnetic Engineering and Science， 2022， 22（4）： 496-501.

[本文引用: 1]

[18]

， QI

， ZHANG

A coherent CZT-based algorithm for high-accuracy ranging with FMCW radar

［J］. IEEE Transactions on Instrumentation and Measurement， 2023， 72： 1-11.

[本文引用: 1]

[19]

罗韩君，周仁龙，张禹涛.

光子雷达探测性能与测距精度的理论研究

［J］.激光技术，2014，38（3）：411-416. doi：10.7510/jgjs.issn.1001-3806.2014.03.028

DOI:10.7510/jgjs.issn.1001-3806.2014.03.028 [本文引用: 1]

LUO

H J

， ZHOU

R L

， ZHANG

Y T

Theoretical analysis of detection performance and range accuracy of photon ladar

［J］. Laser Technology， 2014， 38（3）： 411-416.

DOI:10.7510/jgjs.issn.1001-3806.2014.03.028 [本文引用: 1]

[20]

李妍，陈超，程光权，等.

面向不确定性数据的雷达预警建模方法研究

［J］.郑州大学学报（理学版），2022，54（5）： 37-42.

[本文引用: 1]

， CHEN

， CHENG

G Q

， et al.

Research on radar warning modelling methods for uncertainty-oriented data

［J］. Journal of Zhengzhou University （Natural Science Edition）， 2022， 54（5）： 37-42.

[本文引用: 1]

[21]

邱志平，陆强华.

雷达探测距离估计的非概率区间方法

［J］.国防科技，2008，29（2）：3-6. doi：10.3969/j.issn.1671-4547.2008.02.002

DOI:10.3969/j.issn.1671-4547.2008.02.002 [本文引用: 1]

QIU

Z P

， LU

Q H

Estimation for radar detection range using non-probabilistic interval method

［J］. National Defense Technology， 2008， 29（2）： 3-6.

DOI:10.3969/j.issn.1671-4547.2008.02.002 [本文引用: 1]

[22]

OUYANG

， LIU

， HAN

， et al.

Correlation propagation for uncertainty analysis of structures based on a non-probabilistic ellipsoidal model

［J］. Applied Mathematical Modelling， 2020， 88： 190-207.

[本文引用: 2]

[23]

季熠，李彦斌，杭晓晨，等.

基于响应面代理模型的雷达天线阵面风载分析

［J］.工程力学，2019，36（11）：222-229. doi：10.6052/j.issn.1000-4750.2018.12.0680

DOI:10.6052/j.issn.1000-4750.2018.12.0680 [本文引用: 2]

， LI

Y B

， HANG

X C

， et al.

Wind load analysis of radar antenna based on response surface model

［J］. Engineering Mechanics， 2019， 36（11）： 222-229.

DOI:10.6052/j.issn.1000-4750.2018.12.0680 [本文引用: 2]

[24]

胡长明，操卫忠，孙为民，等.

基于代理模型的车载雷达阵面风载疲劳分析

［J］.强度与环境，2020，47（4）：45-51.

[本文引用: 1]

C M

， CAO

W Z

， SUN

W M

， et al.

Fatigue analysis of vehicle radar under wind load based on surrogate models

［J］. Structure & Environment Engineering， 2020， 47（4）： 45-51.

[本文引用: 1]

[25]

SOBOL

I M

Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates

［J］. Mathematics and Computers in Simulation， 2001， 55（1/3）： 271-280.

[本文引用: 4]

[26]

张扬

多参数非线性系统全局敏感性分析与动态代理模型研究

［D］.长沙：湖南大学，2014.

[本文引用: 2]

ZHANG

The study on global sensitivity analysis and dynamic metamodel

［D］. Changsha： Hunan University， 2014.

[本文引用: 2]

[27]

OUYANG

， LIU

， HAN

， et al.

Non-probabilistic uncertain inverse problem method considering correlations for structural parameter identification

［J］. Structural and Multidisciplinary Optimization， 2021， 64（3）： 1327-1342.

[本文引用: 3]

[28]

C M

， CAO

L X

， TANG

J C

， et al.

A subinterval decomposition analysis method for uncertain structures with large uncertainty parameters

［J］. Computers & Structures， 2018， 197： 58-69.

[本文引用: 1]

“雷达信号处理”专刊序言

2016

... 雷达是获取海陆空战场全天候、全天时战略和战术情报的重要设备，是自动化指挥系统的首要视觉传感器，被广泛应用于军事、航空航海及气象预报等领域^[1].雷达性能直接决定了雷达系统所能完成任务的类型及完成效果^[2].探测距离和测距精度是雷达性能的核心指标，其在雷达工作过程中会受到传输波动和杂波干扰等因素的影响，导致雷达的探测能力下降，无法准确捕捉目标信息^[3].因此，开展雷达系统探测距离和测距精度的分析，对雷达技术的发展及工程应用具有重要意义^[4]. ...

... Radar parameters and interference parameters

Table 1

参数	单位	数值区间
信号频率	10⁸Hz	[3.0, 10.0]
信号带宽	10⁵Hz	[5.0, 10.0]
脉冲宽度	10^-3s	[1.0, 2.0]
脉冲积累数	个	[1, 10]
雷达发射功率	10⁵W	[1.0, 5.0]
发射增益	dB	[35.0, 40.0]
接收增益	dB	[35.0, 40.0]
综合损耗	dB	[40.0, 45.0]
方位波束宽度	(°)	[2.0, 3.0]
俯仰波束宽度	(°)	[2.0, 3.0]
测角误差斜率		[40.0, 70.0]
压制系数		[40.0, 70.0]
干扰频率	10⁸Hz	[3.0, 10.0]
干扰带宽	Hz	[3.0, 7.0]
干扰功率	10³W	[3.0, 7.0]
干扰发射增益	dB	[10.0, 20.0]

2.2　雷达系统参数筛选2.2.1　雷达系统性能区间度量模型的建立

雷达系统存在雷达参数传输波动、信号干扰等不确定性因素，导致性能不稳定.已知雷达参数和干扰参数的数值区间，根据区间模型来度量雷达系统性能的不确定域.将影响雷达系统性能的不确定参数用区间进行量化，如图1所示，可以表示为^[22]： ...

... Global sensitivity analysis results of ranging accuracy

Table 4

影响参数	单位	数值区间	敏感度
信号带宽	10⁵ Hz	[5.0, 10.0]	0.242 3
脉冲宽度	10^-3 s	[1.0, 2.0]	0.020 6
脉冲积累数	个	[1, 10]	0.404 1
发射增益	dB	[35.0, 40.0]	0.070 4
接收增益	dB	[35.0, 40.0]	0.071 0
压制系数	dB	[40.0, 70.0]	0.013 0

由表3可知，参数对探测距离的影响程度从大到小依次为信号频率/干扰频率、雷达发射功率、接收增益、综合损耗、发射增益、脉冲宽度. ...

“雷达信号处理”专刊序言

2016

... Radar parameters and interference parameters

Table 1

参数	单位	数值区间
信号频率	10⁸Hz	[3.0, 10.0]
信号带宽	10⁵Hz	[5.0, 10.0]
脉冲宽度	10^-3s	[1.0, 2.0]
脉冲积累数	个	[1, 10]
雷达发射功率	10⁵W	[1.0, 5.0]
发射增益	dB	[35.0, 40.0]
接收增益	dB	[35.0, 40.0]
综合损耗	dB	[40.0, 45.0]
方位波束宽度	(°)	[2.0, 3.0]
俯仰波束宽度	(°)	[2.0, 3.0]
测角误差斜率		[40.0, 70.0]
压制系数		[40.0, 70.0]
干扰频率	10⁸Hz	[3.0, 10.0]
干扰带宽	Hz	[3.0, 7.0]
干扰功率	10³W	[3.0, 7.0]
干扰发射增益	dB	[10.0, 20.0]

2.2　雷达系统参数筛选2.2.1　雷达系统性能区间度量模型的建立

... Global sensitivity analysis results of ranging accuracy

Table 4

影响参数	单位	数值区间	敏感度
信号带宽	10⁵ Hz	[5.0, 10.0]	0.242 3
脉冲宽度	10^-3 s	[1.0, 2.0]	0.020 6
脉冲积累数	个	[1, 10]	0.404 1
发射增益	dB	[35.0, 40.0]	0.070 4
接收增益	dB	[35.0, 40.0]	0.071 0
压制系数	dB	[40.0, 70.0]	0.013 0

由表3可知，参数对探测距离的影响程度从大到小依次为信号频率/干扰频率、雷达发射功率、接收增益、综合损耗、发射增益、脉冲宽度. ...

认知雷达系统技术发展综述

2018

认知雷达系统技术发展综述

2018

A correction method for radar detection range analysis in interference environment

2021

... 探测距离指雷达在不受干扰的情况下能探测到目标的最远距离，可以表示为^[4]： ...

... 测距精度指雷达探测距离的准确程度.对雷达探测距离的误差进行估计，可以表示为^[4]： ...

“本土链”雷达主要性能分析及启示

2022

... 近年来，有关雷达探测距离和测距精度提升的研究受到了国内外学者的广泛关注.刘育才等^[5]通过雷达方程获取了“本土链”雷达的探测距离，并提出了反干扰、抗摧毁等雷达未来发展方向；Dong等^[6]提出了一种基于泊松盘抽样和迭代软阈值算法的消除调频连续波雷达距离混叠的方法，在消除距离混叠的同时增大了探测距离，提高了雷达的多目标探测能力；曹丽等^[7]归纳了车载激光雷达探测距离的关键参数及决定因素，为雷达性能分析效率的提高奠定了基础；Chang等^[8]提出了一种超分辨率网络，在有限带宽下保证了最大可探测距离；李琴等^[9]采用地杂波动目标显示抑制技术，有效增大了低空小型无人机雷达的探测距离，为检测低小、较慢目标的地基雷达的设计提供了参考；Zhao等^[10]提出了一种远程目标探测距离模糊的解决方法，增强了雷达远距离探测能力；董云龙等^[11]根据海杂波对目标探测的影响，将一般雷达方程简化为信噪比方程，提高了探测距离的计算效率；汤华涛等^[12]在蒸发波导条件下建立了雷达组网探测范围的评估模型，扩大了在目标运动姿态未知情况下的探测范围；针对实际探测距离的计算须根据约束条件的变化不断调整的问题，陈超凡等^[13]提出了一种雷达实际探测威力快速生成算法，有效提高了探测距离的计算速度；马兰等^[14]通过高斯插值处理方法预估脉压波峰值出现的时间，减小了预估脉压波峰值与真实脉压波峰值之间的误差，有效提高了测距精度；Marom等^[15]提出了在测量坐标系中使用滤波器并将测量结果转换到笛卡尔坐标系的解决方案，提高了滤波后的测距精度；李鑫洋等^[16]引入频谱最大估值算法，减小了快速傅里叶变换计算的测距误差，提高了测距精度；Sim等^[17]通过比较包络检测后的采样数来区分每种频率的基带信号，提高了测距精度；Xu等^[18]基于相干谱模型提出了连续线性调频z变换算法，为雷达的精准探测提供了依据；罗韩君等^[19]采用统计原理与质心法建立了测距精度的理论模型，证明了回波强度和回波脉宽是测距精度的主要影响因素；李妍等^[20]建立了一种针对不确定性数据的雷达探测距离预测模型，有效降低了数据扰动对雷达探测性能的影响；邱志平等^[21]提出了一种非概率区间方法来近似估计雷达探测距离. ...

“本土链”雷达主要性能分析及启示

2022

Range aliasing elimination for FMICW radar with uniform sampling bursts and poisson disk inter-burst delays

2022

车载激光雷达关键性能参数及决定因素

2022

车载激光雷达关键性能参数及决定因素

2022

RangeSRN： range super-resolution network using mmwave FMCW radar

2022

低空小型无人机雷达探测距离仿真分析

2018

低空小型无人机雷达探测距离仿真分析

2018

Using sky-wave echoes information to extend HFSWR's maximum detection range

2018

... Radar parameters and interference parameters

Table 1

参数	单位	数值区间
信号频率	10⁸Hz	[3.0, 10.0]
信号带宽	10⁵Hz	[5.0, 10.0]
脉冲宽度	10^-3s	[1.0, 2.0]
脉冲积累数	个	[1, 10]
雷达发射功率	10⁵W	[1.0, 5.0]
发射增益	dB	[35.0, 40.0]
接收增益	dB	[35.0, 40.0]
综合损耗	dB	[40.0, 45.0]
方位波束宽度	(°)	[2.0, 3.0]
俯仰波束宽度	(°)	[2.0, 3.0]
测角误差斜率		[40.0, 70.0]
压制系数		[40.0, 70.0]
干扰频率	10⁸Hz	[3.0, 10.0]
干扰带宽	Hz	[3.0, 7.0]
干扰功率	10³W	[3.0, 7.0]
干扰发射增益	dB	[10.0, 20.0]

2.2　雷达系统参数筛选2.2.1　雷达系统性能区间度量模型的建立

... Global sensitivity analysis results of ranging accuracy

Table 4

影响参数	单位	数值区间	敏感度
信号带宽	10⁵ Hz	[5.0, 10.0]	0.242 3
脉冲宽度	10^-3 s	[1.0, 2.0]	0.020 6
脉冲积累数	个	[1, 10]	0.404 1
发射增益	dB	[35.0, 40.0]	0.070 4
接收增益	dB	[35.0, 40.0]	0.071 0
压制系数	dB	[40.0, 70.0]	0.013 0

由表3可知，参数对探测距离的影响程度从大到小依次为信号频率/干扰频率、雷达发射功率、接收增益、综合损耗、发射增益、脉冲宽度. ...

基于雷达方程修正的目标探测距离评估方法

2022

基于雷达方程修正的目标探测距离评估方法

2022

微波超视距雷达组网探测范围研究

2022

微波超视距雷达组网探测范围研究

2022

雷达实际探测威力快速生成算法研究

2022

雷达实际探测威力快速生成算法研究

2022

基于高斯插值提高雷达测距精度的研究

2021

基于高斯插值提高雷达测距精度的研究

2021

Bistatic radar tracking with significantly improved bistatic range accuracy

2023

提高FMCW雷达测距精度的算法研究

2016

提高FMCW雷达测距精度的算法研究

2016

Frequency discrimination method using asymmetric transmission time in FSK radar

2022

A coherent CZT-based algorithm for high-accuracy ranging with FMCW radar

2023

光子雷达探测性能与测距精度的理论研究

2014

光子雷达探测性能与测距精度的理论研究

2014

面向不确定性数据的雷达预警建模方法研究

2022

面向不确定性数据的雷达预警建模方法研究

2022

雷达探测距离估计的非概率区间方法

2008

雷达探测距离估计的非概率区间方法

2008

Correlation propagation for uncertainty analysis of structures based on a non-probabilistic ellipsoidal model

2020

... 雷达系统存在雷达参数传输波动、信号干扰等不确定性因素，导致性能不稳定.已知雷达参数和干扰参数的数值区间，根据区间模型来度量雷达系统性能的不确定域.将影响雷达系统性能的不确定参数用区间进行量化，如图1所示，可以表示为^[22]： ...

... 参数X的不确定性通过其区间上界

\bar{X}

和下界

\underset{̲}{X}

限定，所有可能值都包含于其构成的区间内.记X的中点和半径分别为X_c和X_r，可以表示为^[22]： ...

基于响应面代理模型的雷达天线阵面风载分析

2019

... 多项式响应面模型具有收敛迅速的优点.将它应用于雷达性能分析中，可以有效提高性能分析的效率.其一般表达式为^[23]： ...

... 不确定参数之间耦合性强，因此采用高阶多项式作为响应面模型，其表现形式为^[23]： ...

基于响应面代理模型的雷达天线阵面风载分析

2019

... 多项式响应面模型具有收敛迅速的优点.将它应用于雷达性能分析中，可以有效提高性能分析的效率.其一般表达式为^[23]： ...

... 不确定参数之间耦合性强，因此采用高阶多项式作为响应面模型，其表现形式为^[23]： ...

基于代理模型的车载雷达阵面风载疲劳分析

2020

... 通过观测值与模型预测值之间的复相关系数

R^{2}

和均方根误差E_RMS^[24]来判断响应面模型在雷达性能分析中的准确性. ...

基于代理模型的车载雷达阵面风载疲劳分析

2020

... 通过观测值与模型预测值之间的复相关系数

R^{2}

和均方根误差E_RMS^[24]来判断响应面模型在雷达性能分析中的准确性. ...

Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates

2001

... 假设雷达模型

Y = g (X) = g (X_{1}, X_{2}, \dots, X_{n})

，其中

X_{i}

在[0, 1]区间内服从均匀分布，则模型可以表示为^[25]： ...

... 总方差V为^[25]： ...

... 单个参数的偏方差

V_{i}

和参数组合的偏方差

V_{i_{1}, \dots, i_{s}}

分别为^[25]： ...

... 总方差V表示所有参数对系统输出的影响；偏方差

V_{i}

表示单个参数对系统输出的影响，

V_{i_{1}, \dots, i_{s}}

表示多个输入参数间的交互效应对系统输出的影响.采用敏感性指标衡量参数的影响程度.敏感度

S_{i_{1}, \dots, i_{s}}

定义为^[25]： ...

多参数非线性系统全局敏感性分析与动态代理模型研究

2014

... 由上可知，各参数的敏感度之和为1，即^[26]： ...

... 本文只考虑雷达系统模型的主效应指标，即单个参数对性能的影响程度，表示为^[26]： ...

多参数非线性系统全局敏感性分析与动态代理模型研究

2014

... 由上可知，各参数的敏感度之和为1，即^[26]： ...

... 本文只考虑雷达系统模型的主效应指标，即单个参数对性能的影响程度，表示为^[26]： ...

Non-probabilistic uncertain inverse problem method considering correlations for structural parameter identification

2021

... 为了提高雷达性能分析效率，本文采用子区间分解分析方法，用响应面模型代替真实性能模型进行分析.子区间分解分析方法（subinterval decomposition analysis method，SDAM）^[27-28]将具有多维区间参数的原雷达系统分解为多个一维子系统，将每个子系统的不确定参数划分为几个不确定度较小的子区间，通过少数子区间的组合分析来近似计算雷达探测距离和测距精度的上界及下界. ...

... 将雷达探测距离和测距精度的响应面模型在区间中点处展开，可以得到^[27]： ...

... 将式(13)中的参数分别在每个参数

X_{1},

X_{2}, \dots, X_{n}

处展开，其余参数用中点值代替，则根据式(20)可以求得雷达探测距离和测距精度的上界及下界，其数学模型可进一步表示为^[27]： ...

A subinterval decomposition analysis method for uncertain structures with large uncertainty parameters

2018

〈

〉