目前,翼型的几何表示方法主要包括B样条控制方法、参数化截面(parametric section, PARSEC)方法、Hicks-Henne方法和类别形状函数变换(class shape transformation, CST)方法等[8-9]。其中,CST方法具有鲁棒性强、参数相对较少和精度高等特点,其应用更加广泛[10]。利用CST方法拟合翼型时,需要控制的设计参数包括类函数中的2个参数、描述上下翼面形函数系数的a个参数以及翼型的后缘厚度。大量研究表明,为获得较为准确的翼型几何表示,考虑到翼型的上下表面,CST方法中的参数设置数量一般大于10[11]。尤其是对于前缘较钝的超临界翼型,如RAE5214翼型等,CST方法的拟合结果一直到12阶仍不理想。众所周知,翼型的拟合参数越多,则翼型的描述精度越高。同时,增加参数扰动后,所获取的翼型设计空间也更加多样化。但是,设计参数高维化会不可避免地增加计算流体力学预测成本,并增大优化算法的搜索难度。因此,如何克服设计参数高维化是翼型优化设计领域亟待解决的关键问题。为解决这一问题,部分学者采用本征正交分解(proper orthogonal decomposition, POD)对CST方法中的设计参数进行了降维处理,并证明了设计参数降维后仍能达到降维前的拟合效果[12]。此外,还有一些学者开始采用机器学习方法对翼型描述参数进行降维处理[1,13],但仍处于初级研究阶段。
随着人工智能的发展,以卷积神经网络(convolutional neural network, CNN)为代表的深度学习算法不仅能有效处理图像数据,而且能够实现数据降维,其已被广泛应用于各领域。基于此,笔者拟提出一种基于深度学习的翼型参数化建模方法,该方法可通过6个拟合参数来表征翼型。为了验证所提出方法对翼型表面曲线的表征能力,对该方法下典型翼型的拟合精度进行分析。最后,同步开发可视化翼型几何设计软件,以实现拟合参数的调整与修正,并分析各拟合参数对翼型形状的影响规律,旨在为新翼型的构造提供参考。
1 CNN的原理及结构
CNN是目前深度学习技术领域中最具代表性的神经网络之一,特别擅长处理图像数据,其在物体检测、人脸识别、自动驾驶及语音处理等领域得到了广泛应用[14-15]。CNN的主要架构通常由输入层、卷积层、池化层和全连接层组成。其中,卷积层用于提取输入数据的特征,卷积层叠加是指使用不同的过滤器对数据进行卷积操作,从而实现数据的多维特征提取,该过程不会增加数据量,可充分实现图像特征的分解和利用。池化层也称下采样层,其主要作用是利用池化函数将邻近的数据特征进行总体输出,同时减少网络参数,以减少过拟合现象和增强网络的泛化能力。全连接层通常在卷积、池化操作之后。全连接层中每一层的每个神经元均与上一层的每个神经元连接,用于将前层(卷积层、池化层等)计算得到的特征映射到样本标记空间。
为增强神经网络的表示能力和学习能力,通过在层与层之间加入激活函数来增加神经网络的非线性。目前,主要的激活函数有Sigmoid函数、Tanh函数和ReLU(rectified linear unit,修正线性单元)函数。其中,ReLU函数改善了Sigmoid函数及Tanh函数所存在的梯度消失问题,在深度神经网络中较为常用[16]。ReLU函数的表达式如下:
神经网络结合反向传播算法[17]进行训练,并利用优化算法加快训练速度,可实现神经网络的快速收敛。其中,反向传播算法的原理如下:数据输入神经网络后,先进行前向传播,到达输出层并输出结果;此时,输出结果与实际结果之间存在误差,计算两者的误差并反向传播到中间层、输入层;随后,神经网络根据反向传播的误差,利用梯度下降算法实时更新各神经元参数的值,以获得最优的训练效果。
优化算法主要包括BGD(batch gradient descent,批量梯度下降)算法、SGD(stochastic gradient descent,随机梯度下降)算法、AdaGrad(adaptive gradient,自适应梯度)算法、RMSProp(root mean square propagation,均方根传播)算法以及Adam(adaptive moment estimation,自适应矩估计)算法等。相比于BGD算法和SGD算法,RMSProp算法和AdaGrad算法在执行梯度下降算法时引入了动量(momentum)思想,且可以实现学习率的动态更新。其中,RMSProp算法是对AdaGrad算法的改进,通过引入指数加权平均算法来计算累积梯度,使得整体上对梯度的修正更加合理。Adam算法结合了RMSProp和动量思想,即兼顾了自适应学习率和动量这2个因素,属于目前最稳定、效果最理想的参数训练方法之一[18]。
完成训练后,需要对神经网络的训练结果进行评估,评估指标主要包括损失函数(loss function)和精准度(accuracy)。其中,损失函数用于衡量模型预测结果与真实结果的距离,损失函数值越小,表示模型的预测结果越好。常见的损失函数有MSE(mean squared error,均方误差)损失函数、L1损失函数以及交叉熵损失函数等。目前,最为常用的是MSE损失函数和交叉熵损失函数,其表达式分别如
式中:M表示MSE损失函数值,
式中:L表示交叉熵损失函数值,N表示样本数,K表示类别数,yjk 表示标签,pjk 表示标签yjk 的预测概率。
2 翼型参数化模型的建立
2.1 数据预处理
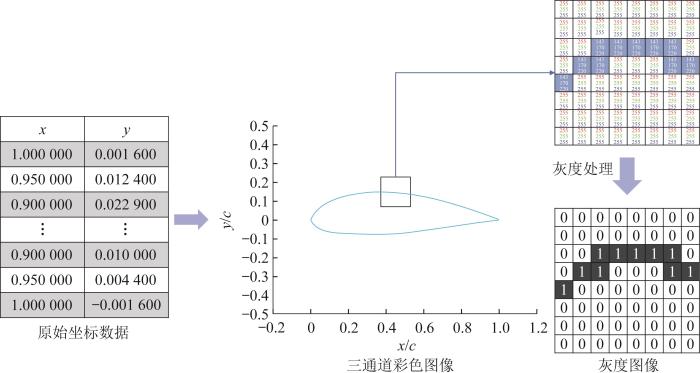
本文采用的翼型数据来自伊利诺伊大学厄巴纳-香槟分校(University of Illinois at Urbana-Champaign, UIUC)的开源翼型数据库,共含1 512个翼型数据。随机选取1 200个数据作为翼型参数化模型的训练集,剩余的312个数据作为模型的测试集。为使数据能够满足CNN的输入要求,对数据进行预处理。首先,考虑到数据集中包含的翼型种类不同以及各类翼型表面坐标点的数量不同,无法适配参数化模型,在保证源数据特征不变的情况下,根据CNN的结构对翼型表面坐标点数据进行适当取舍和添加,使得CNN训练所用的数据形式统一。其次,考虑到CNN在图像识别与处理方面的强大能力,为了更有效地提取翼型的几何特征,将数据库中翼型的点坐标数据转化为二维图像数据并进行灰度处理。具体处理方式如图1所示:从翼型的上下表面等距采样40个点,共计80个点;原始数据中未知的点坐标通过相邻已知的两点按比例进行计算。根据采样点,先使用Python中的matplotlib库将坐标数据转化为彩色的翼型几何图像,再使用PIL库将彩色的几何图像转化为(256
图1
2.2 参数化模型建立
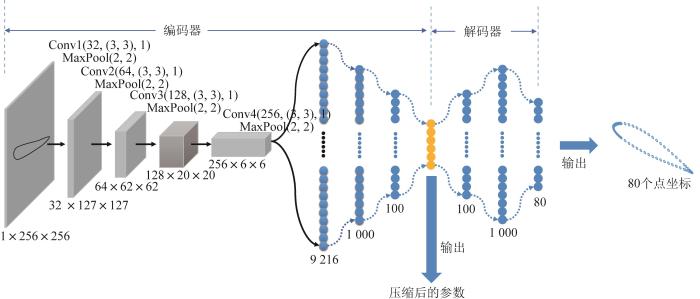
机器学习方法一般分为有监督学习和无监督学习。使用标记的输入进行神经网络训练属于有监督学习,而无监督学习则使用非标记输入。本文所研究的翼型参数化问题属于有监督的回归问题。基于CNN建立相应的翼型参数化模型,如图2所示。图中标注的Conv (32, (3, 3), 1)代表卷积核个数为32,卷积核大小为3×3,卷积步长为1,以此类推。首先,使用卷积运算对输入的翼型灰度图像数据进行几何特征提取;然后,通过多层感知机对所提取的几何特征进行分类和压缩,以将翼型形状压缩成若干个简化的拟合参数;最后,通过解码器恢复翼型图像并输出翼型上下表面各点的坐标以及压缩后的拟合参数。其中,参数化模型的前半部分与自动编码器类似,后半部分与解码器类似。输入的灰度图像先被编码器转化编码成参数,再通过解码器还原成翼型上各点的纵坐标y。为了提高翼型的拟合精度,在输出翼型的点坐标时,尽可能在翼型的前缘和尾缘位置处多布置一些点。
图2
图2
基于CNN的翼型参数化模型的结构及主要参数
Fig.2
Structure and main parameters of airfoil parametrized model based on CNN
2.3 参数化模型训练与测试
翼型参数化模型的训练与测试均使用Pytorch平台。训练时采用反向传播算法,并使用Adam优化器和一个自动调整学习率的调度器进行参数更新。设初始学习率为1
3 翼型参数化建模的结果与分析
3.1 拟合参数数量的影响
图3
图3
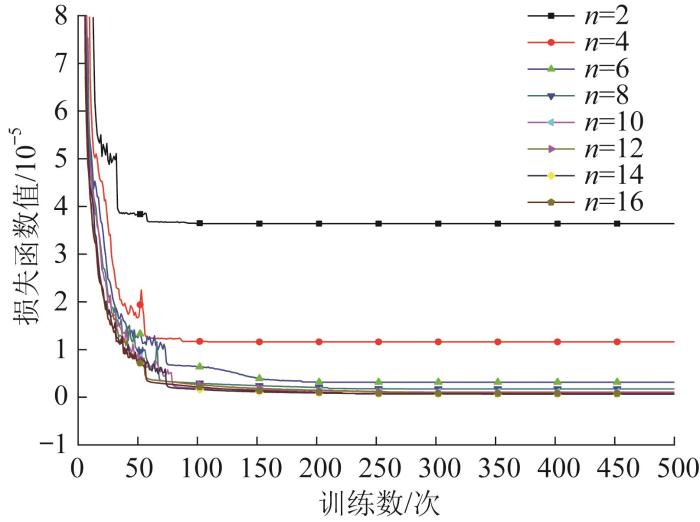
拟合参数数量对NACA0021翼型拟合精度的影响
Fig.3
Influence of number of fitting parameters on fitting accuracy of NACA0021 airfoil
为了在翼型优化设计时提供更大的设计空间,对拟合参数进行调整,以获取新的翼型形状。本文对比分析了不同拟合参数数量下拟合参数调整对翼型形状的影响(以NACA0021翼型和RAE2822翼型为例)。限于篇幅限制,仅展示典型情况下(n=6,10,14)对所有拟合参数施加相同幅度扰动后的翼型形状,结果如图4所示。结果表明,拟合参数调整均存在特定的范围,当拟合参数超过此范围后,翼型会出现畸形。同时还发现,在相同的参数调整幅度下,拟合参数设置越多,越易导致新翼型出现畸形,难以获得较为光滑的几何外形。通过对比可知,n=6时的参数化模型所生成的翼型最光滑且参数可调范围最大。
图4
图4
不同参数数量下拟合参数调整对翼型形状的影响
Fig.4
Influence of fitting parameter adjustment on airfoil shape under different number of parameters
综上所述,选用含6个拟合参数的CNN(下文简称CNN-6)模型作为翼型参数化模型,可在拟合精度损失较小的情况下,避免翼型拟合参数调整造成的畸形问题。同时,较少的拟合参数也大大缩减了构造新翼型的设计空间,可在后续翼型优化设计中实现参数降维。
3.2 CNN-6模型的拟合精度
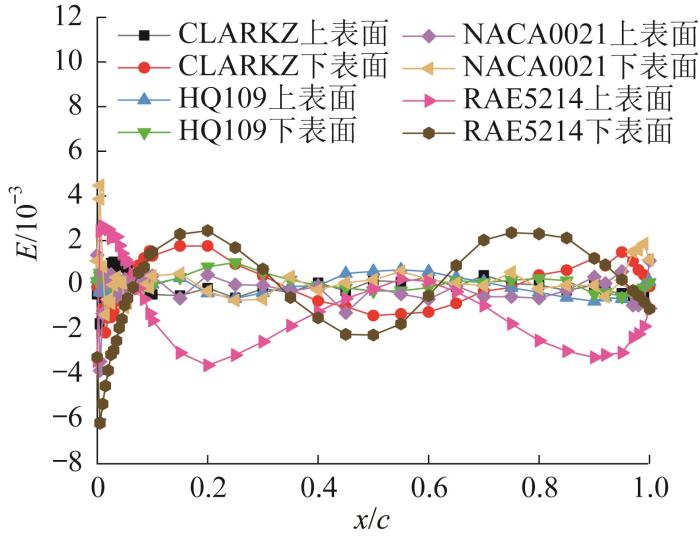
图5所示为CNN-6模型对4种不同翼型(包括普通翼型和超临界翼型,分别为CLARKZ、HQ109、NACA0021和RAE5214翼型)的拟合效果。从总体上来看,CNN-6模型可较好地拟合上述2类翼型。具体来说,对于CLARKZ、HQ109、NACA0021这3种普通翼型,CNN-6模型可实现翼型上下表面各个位置处的较好拟合;对于RAE5214等超临界翼型,CNN-6模型对其前缘附近较大宽度处和尾缘附近的拟合精度略有下降。
图5
图5
CNN-6模型对不同翼型的拟合效果
Fig.5
Fitting effect of different airfoils by CNN-6 model
图6
图6
不同翼型上下表面的拟合误差
Fig.6
Fitting error of upper and lower surfaces of different airfoils
图7
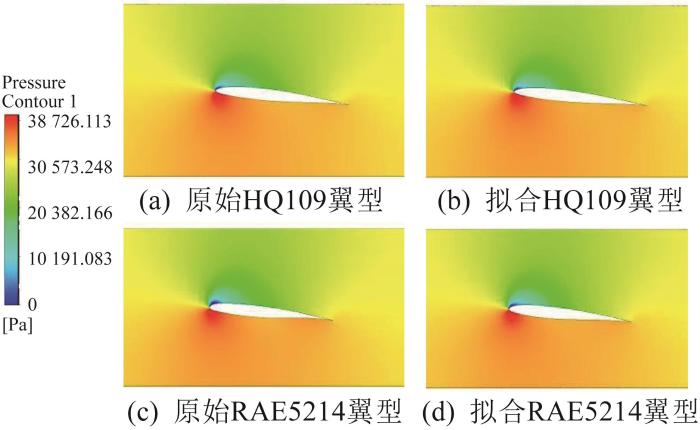
在仿真过程中,采用DES(detached eddy simulation,分离涡流模拟)湍流模型进行流场计算,获取的原始翼型与拟合翼型的压力云图如图8所示(以HQ109翼型和RAE5214翼型为例)。同时,监测了水翼绕流的关键参数(升力系数、阻力系数和表面压力系数),结果分别如表1和图9所示。结果表明:对于普通翼型(HQ109翼型),其原始翼型与拟合翼型的压力云图、升力系数、阻力系数以及表面压力系数的差异较小。对于超临界翼型RAE5214,其原始翼型与拟合翼型的压力云图仅在翼型吸力面前缘位置处略有不同,其他位置均无明显区别;通过对比该翼型的水翼绕流关键参数可知,升力系数的相对误差为2.78%,阻力系数的相对误差为5.56%,表面压力系数同样仅在前缘位置附近略有差异,在翼型后半部分的差异较小。由此说明,基于CNN-6的翼型参数化建模方法可以较准确地拟合不同翼型。
图8
图8
原始翼型与拟合翼型的压力云图对比
Fig.8
Comparison of pressure cloud map between original airfoil and fitted airfoil
表1 原始翼型与拟合翼型的升力系数、阻力系数对比
Table 1
| 参数 | HQ109翼型 | RAE5214翼型 | ||||
|---|---|---|---|---|---|---|
| 原始翼型 | 拟合翼型 | 相对误差/% | 原始翼型 | 拟合翼型 | 相对误差/% | |
| 升力系数 | 0.98 | 0.99 | 1.02 | 1.08 | 1.05 | 2.78 |
| 阻力系数 | 0.017 | 0.017 | 0 | 0.018 | 0.019 | 5.56 |
图9
图9
原始翼型与拟合翼型的表面压力系数对比
Fig.9
Comparison of surface pressure coefficient between original airfoil and fitted airfoil
3.3 新翼型的构造方法
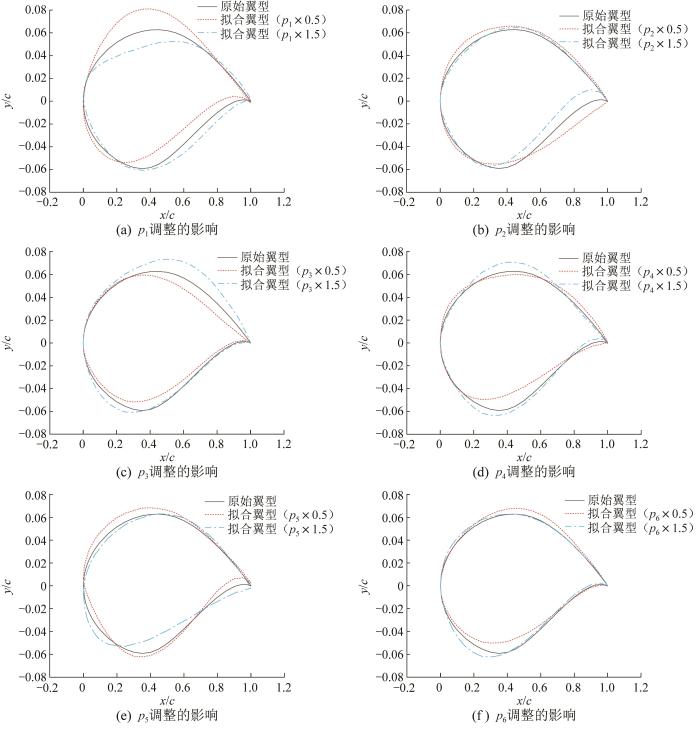
为探讨CNN-6模型中6个拟合参数(p1、p2、p3、p4、p5、p6)调整对翼型形状的影响规律,分别将6个拟合参数调整为原参数值的0.5和1.5倍并进行翼型拟合,拟合结果如图10所示(以RAE2822翼型为例)。结果表明,每个拟合参数均会对翼型形状产生全局影响。其中,p1会引起翼型形状的全局变化,包括前缘、尾缘及中间厚度较大的位置;p2主要影响翼型上表面靠近前缘和下表面靠近尾缘位置的形状;p3和p6主要影响翼型上表面靠近尾缘和下表面靠近前缘位置的形状,相比之下,p6的影响较小;p4主要影响翼型中间厚度最大位置处的形状;p5主要影响翼型下表面以及上表面靠近前缘位置的形状。
图10
图10
CNN-6模型中单个拟合参数调整对RAE2822翼型形状的影响
Fig.10
Influence of single fitting parameter adjustment in CNN-6 model on RAE2822 airfoil shape
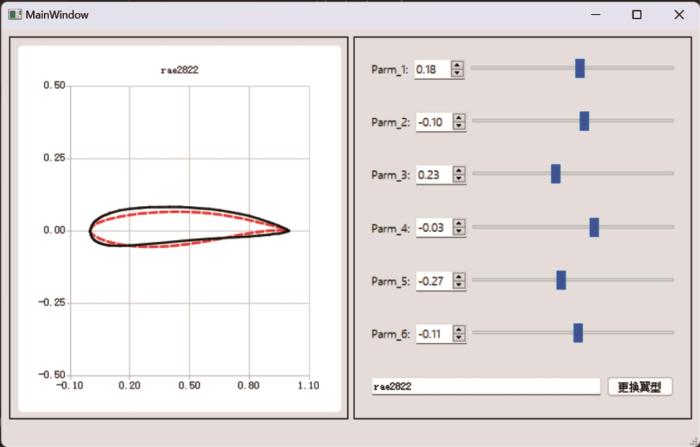
为方便新翼型的生成并适应其优化设计的需求,基于Python开发了可视化翼型几何设计软件,如图11所示。在该软件中,用户可以自行选定基础翼型,并对翼型进行相应调整,从而获取所需的设计空间。
图11
4 结 论
本文提出了一种基于深度学习的翼型参数化建模方法,并分析了各拟合参数对翼型形状的影响规律,同时开发了可视化翼型几何设计软件,这可为后续的翼型优化设计提供技术支持。主要结论如下:
1)确定了CNN-6模型结构,用于翼型的参数化建模。该模型能够在保证拟合精度的前提下,缩小翼型的设计空间,同时有效避免拟合参数过多造成的翼型畸形问题。
2)翼型绕流仿真结果验证了基于CNN-6的翼型参数化建模方法的拟合精度。结果表明,无论是普通翼型还是超临界翼型,CNN-6模型均可较为准确地拟合翼型。
3)CNN-6模型中的6个拟合参数均会对翼型形状产生全局影响,可通过单独或联合调节6个拟合参数来获得新的翼型设计空间,未来可用于翼型的优化设计。
参考文献
改进CST方法在翼型优化设计中的应用
[J].DOI:10.7682/j.issn.1673-1522.2017.05.002 [本文引用: 2]
Application of improved CST parametric method in airfoil design
[J].DOI:10.7682/j.issn.1673-1522.2017.05.002 [本文引用: 2]
Airfoil parameterization techniques: a review
[J].
Constrained design optimization using generative topographic mapping
[J].
Global aerodynamic design optimization based on data dimensionality reduction
[J].
Active subspaces of airfoil shape parameterizations
[J].
Deep generative model for efficient 3D airfoil parameterization and generation
[C]//
基于深度自动编码器神经网络的飞行器翼型参数降维与优化设计
[J].
Parameter dimensionality reduction and optimal design of aircraft airfoil based on deep autoencoder neural network
[J].
HicksHenne翼型参数化方法分析及改进
[J].DOI:10.3969/j.issn.1671-654X.2010.04.013 [本文引用: 1]
Analysis and improvement of HicksHenne airfoil parameterization method
[J].DOI:10.3969/j.issn.1671-654X.2010.04.013 [本文引用: 1]
带下表面射流的超临界翼型优化
[J/OL].
Optimization of supercritical airfoil with jet on the lower surface of trailing edge
[J/OL].
Gradient-based aerodynamic optimization of an airfoil with morphing leading and trailing edges
[J].
基于CST法的新能源无人机翼型优化设计
[J].
Optimization design of airfoil on new energy UAV based on CST method
[J].
Benchmark aerodynamic shape optimization with the POD-based CST airfoil parametric method
[J].
Fast flow field prediction over airfoils using deep learning approach
[J].
Face recognition in unconstrained environment with CNN
[J].
A review of convolutional neural network applied to fruit image processing
[J].
Dynamic ReLU
[C]//
Backpropagation and the brain
[J].
Adam: a method for stochastic optimization
[C]//
On the numerical simulations of vortical cavitating flows around various hydrofoils
[J].
Numerical simulation of cavitation around a hydrofoil and evaluation of a RNG κ-ε model
[J].