全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题。风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] 。在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] 。然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷。另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] 。因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要。基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] 。随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加。考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] 。
为此,笔者提出了一种基于超声导波的螺栓轴向应力测量方法。首先,分析超声导波的群速度频散特性,基于其传播规律提出风机在役螺栓轴向应力测量方案。然后,使用COMSOL软件对超声导波在螺栓内部的传播过程进行仿真分析,并针对超声导波多频多模态的特性以及实地测量存在较大噪声等问题,设计了超声导波回波信号模态分解算法,以实现对风机螺栓轴向应力的精确测量。
1 基于超声导波的螺栓轴向应力测量方法及仿真验证
1.1 基于超声导波的螺栓轴向应力测量模型
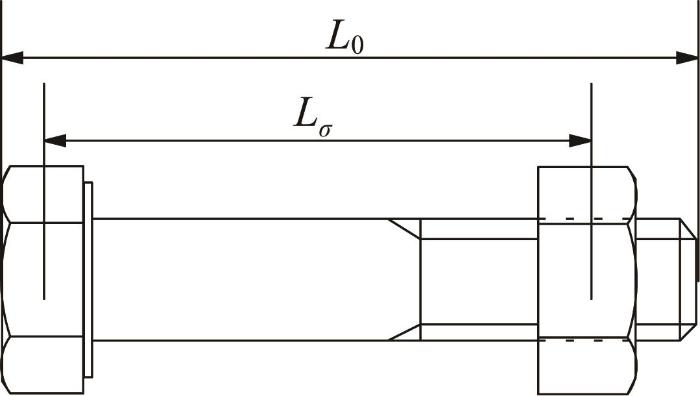
本文采用单波反射法对螺栓轴向应力进行测量。基于胡克定律和声弹性效应,推导并建立螺栓轴向应力与超声导波声时的数学模型。鉴于螺栓实际应用时的应力分布不均匀,对轴向受力时的螺栓模型进行简化,如图1 所示[10 ] 。
图1
图1
螺栓简化模型
Fig.1
Simplified bolt model
L 0 = L σ + L i (1)
式中:Lσ 为螺栓承受应力部分的长度,L i 为螺栓不承受应力部分的长度。
根据胡克定律,在螺栓的屈服极限内,螺栓所承受的应力σ 与螺栓长度变化量∆ Lσ 成正比关系,则可得:
Δ L σ = L σ σ E (2)
由超声导波的声弹性效应可知,螺栓中超声导波的声速与螺栓所受的应力有关。当螺栓只受到轴向压力或拉力时,超声导波在螺栓内部传播的速度与螺栓所受的轴向应力呈线性关系[11 ] ,由此可得:
v σ = v 0 ( 1 + A σ ) (3)
v 0 = 2 L 0 t 0
式中:v 0 、vσ 分别为螺栓所受轴向应力为0 Pa和σ 时的超声导波声速,m/s;t 0 为螺栓所受轴向应力为0 Pa时的超声导波声时,s;A 为螺栓材料的声弹性系数,Pa-1 。
联立式(1)至式(3),可得螺栓所受轴向应力为σ 时的超声导波声时tσ :
t σ = t 0 L σ ( E - 1 - A ) σ + L 0 ( 1 + A σ ) L 0 ( 1 + A σ ) (4)
t σ = t 0 L σ L 0 ( E - 1 - A ) σ + 1 (5)
σ = K ( t σ - t 0 ) (6)
由此可知,螺栓所受的轴向应力与超声导波的声时差近似呈线性关系,且常数K 仅与被测螺栓的材料特性有关。由于同一位置处螺栓受力部分的长度是固定的,因此只需测得超声导波在有无应力状态下的声时差,即可求得螺栓所受的轴向应力[12 ] 。在相同的螺栓预紧流程下,即螺栓受力长度相同时,只需标定其中一颗螺栓对应的K 值,就能实现该型号所有螺栓的轴向应力测量。
1.2 螺栓轴向应力测量模型仿真验证及分析
风机上的螺栓大多由12.9级合金钢制成,具有强度高、抗疲劳性强和耐腐蚀等优点。合金钢材料有多种类型,其材料性能无法准确获取。但本文基于超声导波的测量方法无需确定具体类型材料的性能。12.9级合金钢的一般材料性能参数如表1 所示。
为了准确模拟超声导波在螺栓内的传播过程,本文选择弹性波和时域显式物理场界面来模拟超声导波在线性弹性介质中的回波信号波形。采用间断有限元方法和显式时间积分格式来求解超声导波声时和有应力状态下的线弹性波动方程[13 -14 ] 。由于弹性波接口使用四阶函数,为获得适当的空间分辨率,定义最大网格单元尺寸h max 为:
h m a x = λ t 1.5 = v t 1.5 f t (7)
式中:λ t 为相速度极小值对应的超声导波波长,v t 为超声导波相速度极小值,f t 为超声导波的频率。
采用非一致性网格可减少模型中求解的自由度,本文在仿真分析时使用自由三角形网格对螺栓模型进行网格划分。
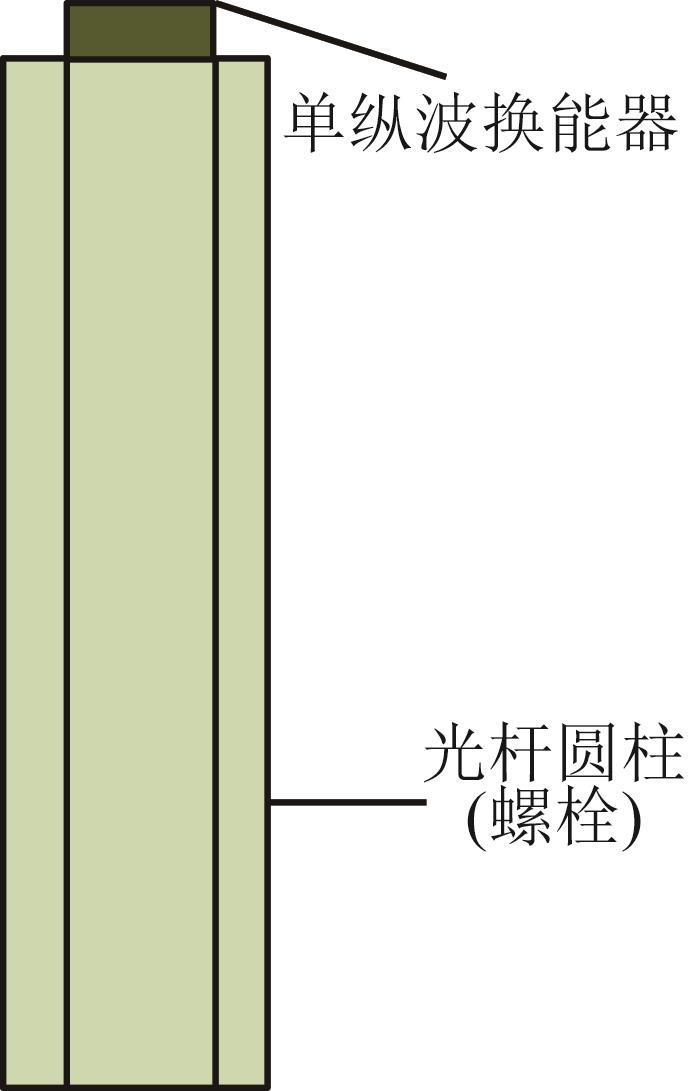
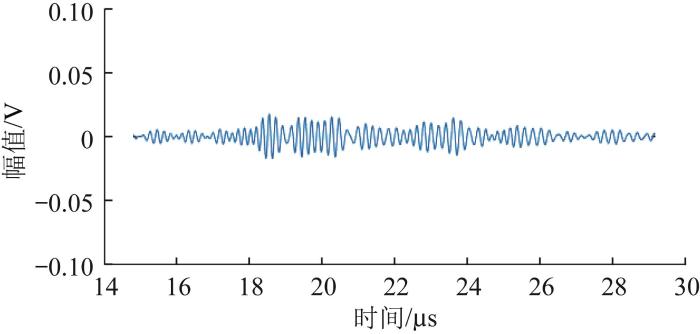
考虑到螺栓轴向应力的实际测量仅针对除螺纹、倒角之外的部分,故在仿真分析中忽略螺纹、倒角等结构的影响。利用COMSOL软件建立螺栓的超声导波应力测量仿真模型,如图2 所示,其中螺栓采用光杆圆柱模拟。同时,为了节约计算时间,设螺栓长度为30 mm,半径为4 mm。通过单纵波换能器激励出0.5 V的高斯脉冲信号,采用探针的方式获得超声导波的回波波形,如图3 所示。
图2
图2
螺栓的超声导波应力测量仿真模型
Fig.2
Ultrasonic guided wave stress measurement simulation model for bolt
图3
图3
超声导波回波波形
Fig.3
Ultrasonic guided wave echo waveform
由图3 可以看出,单纵波换能器在螺栓中可成功激励出超声导波回波,16—28 μs阶段对应的波形为超声导波的一次回波。此外,超声导波的回波信号中不仅包含纵波,还包含在时域内相互混叠的各模态导波。
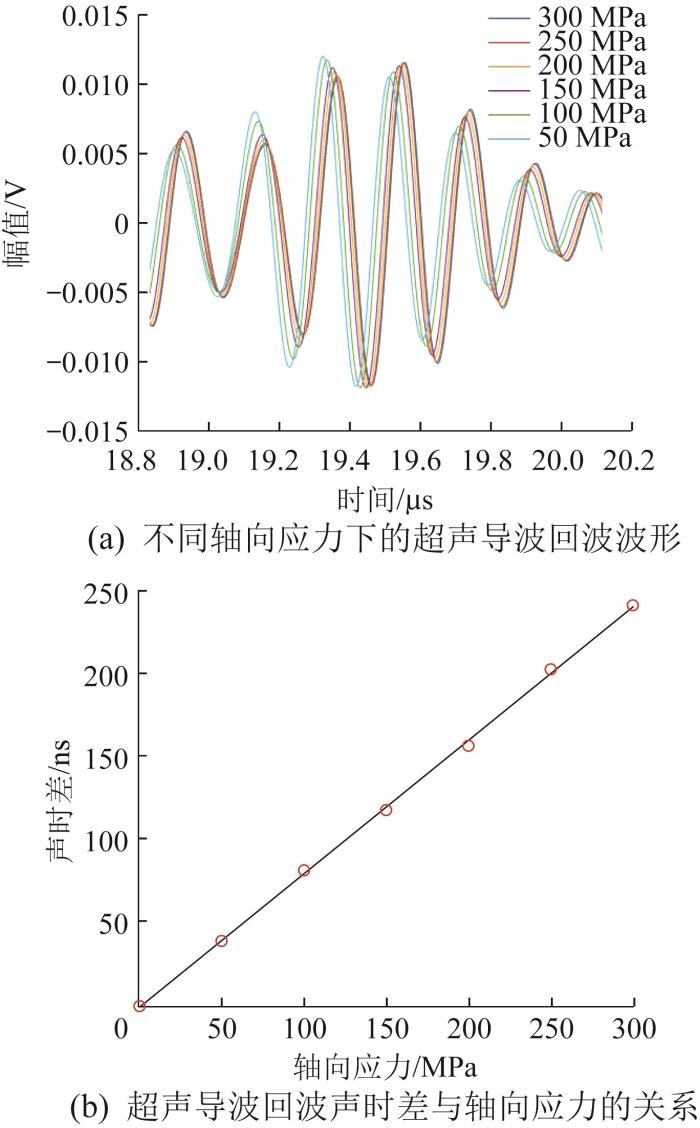
为研究螺栓轴向应力与超声导波声时差之间的定量关系,选择固体力学物理场,并使用瞬态求解器进行求解。在螺栓模型底部施加不同的轴向应力边界载荷(50,100,150,200,250,300 MPa),通过仿真得到应力作用下螺栓内部超声导波的传播情况。不同轴向应力下的超声导波回波波形仿真结果如图4 (a)所示。对不同轴向应力下的超声导波回波信号进行互相关处理,得到超声导波回波声时差随螺栓轴向应力的变化曲线,结果如图4 (b)所示。
图4
图4
不同轴向应力下的超声导波回波仿真结果
Fig.4
Simulation results of ultrasonic guided wave echo under different axial stress
由图4 (a)可以看出,随着螺栓所受的轴向应力增大,超声导波回波波形整体向右移动,且超声导波的声速降低,其回波的声时变大。由图4 (b)可以看出,超声导波回波的声时差与螺栓所受的轴向应力近似呈线性关系,这与理论分析结果相符。仿真结果表明,单纵波换能器可在圆柱螺栓内部激励出超声导波,且超声导波满足胡克定律和声弹性效应,即超声导波的声时随轴向应力的变化而变化并近似呈线性关系。仿真结果验证了上文所建立的基于超声导波的螺栓轴向应力测量模型的可行性。
2 超声导波回波信号处理算法
2.1 基于回波补偿的降噪处理
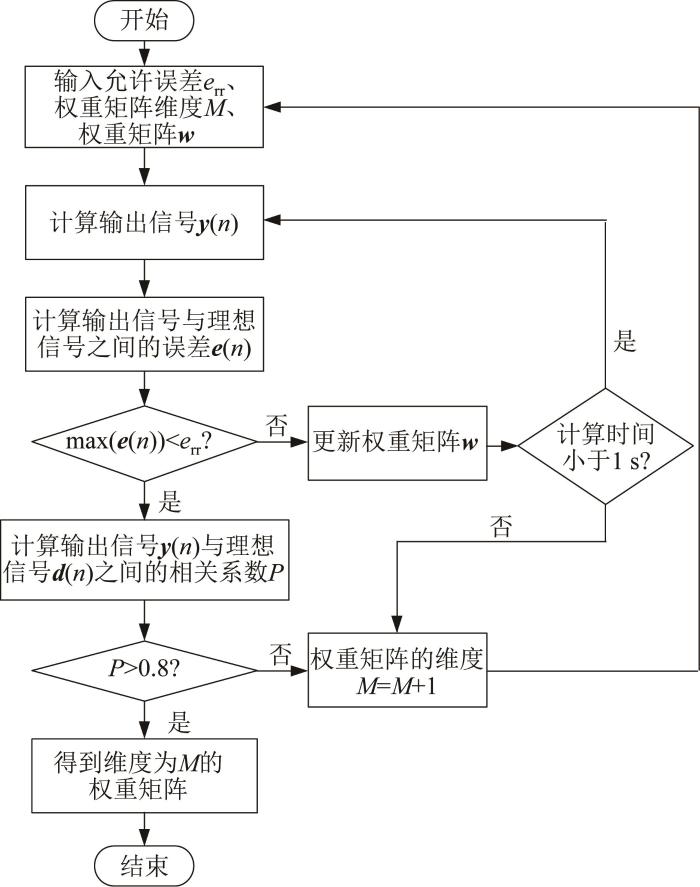
将在噪声较小的实验室环境下采集的螺栓(未安装,处于零应力状态)内部的超声导波回波信号记为理想信号d ( n ) d 1 d 2 … dn ],将在实际风力发电厂环境中采集的螺栓(已安装但未紧固)内部的超声导波回波信号记为x ( n ) x 1 x 2 … xn ],x ( n ) d ( n ) x ( n ) 图5 所示的流程对含噪信号x ( n )
图5
图5
超声导波回波信号的降噪处理流程
Fig.5
Noise reduction process of ultrasonic guided wave echo signal
首先,设定初始值,包括允许误差e rr 、迭代速度系数u 以及初始权重矩阵 w M 。此时,权重矩阵 w M 均是未知的,因此训练的目的是得到合适的维度以及具体的权重值。权重矩阵每进行一次更新后,均需根据式(8)计算基于该权重矩阵处理后的输出信号y ( n )
y ( n ) = X ⋅ w (8)
X = x 1 x 2 . . . x n - 1 x n x 2 x 3 . . . x n x 1 ⋮ ⋮ ⋮ ⋮ x M - 1 x M . . . x M - 3 x M - 2 x M x M + 1 . . . x M - 2 x M - 1 T
同时,计算输出信号y ( n ) d ( n ) e ( n )
e ( n ) = d ( n ) - y ( n ) = d ( n ) - X ⋅ w (9)
然后,通过对比计算得到的最大误差与设定的允许误差来判断是否需要更新权重矩阵。若该误差小于设定的允许误差,则可得到初步满足条件的权重矩阵的维度,但此时的权重矩阵不能作为最终的输出结果。这是因为此时迭代得到的权重矩阵的维度可能较小,基于较小维度权重矩阵计算得到的输出信号y ( n ) d ( n ) 式(10)求解初步满足误差设定条件的输出信号y ( n ) d ( n ) P :
P = ∑ i = 1 n ( y i - y ¯ ) ( d i - d ¯ ) ∑ i = 1 n ( y i - y ¯ ) 2 ∑ i = 1 n ( d i - d ¯ ) 2 (10)
式中:d ¯ y ¯
若Pearson相关系数P > 0.8 ,则说明输出信号与理想信号具有极强的相似性,这样可保证此时迭代得到的权重矩阵的维度以及权重值均满足加强超声导波回波信号以及有效滤除噪声的要求。
通过上述迭代训练得到未加载预紧力时螺栓内部的超声导波回波信号x ( n ) w w σ 条件下所采集的螺栓内部的超声导波回波信号x σ ( n ) = x σ, 1 x σ, 2 … x σ, n σ 下的含噪信号矩阵 X σ
X σ = x σ , 1 x σ , 2 ⋯ x σ , n - 1 x σ , n x σ , 2 x σ , 3 ⋯ x σ , n x σ , 1 ⋮ ⋮ ⋮ ⋮ x σ , M - 1 x σ , M ⋯ x σ , M - 3 x σ , M - 2 x σ , M x σ , M + 1 ⋯ x σ , M - 2 x σ , M - 1 T (11)
基于已知的权重矩阵 w X σ y σ ( n )
y σ ( n ) = X σ ⋅ w (12)
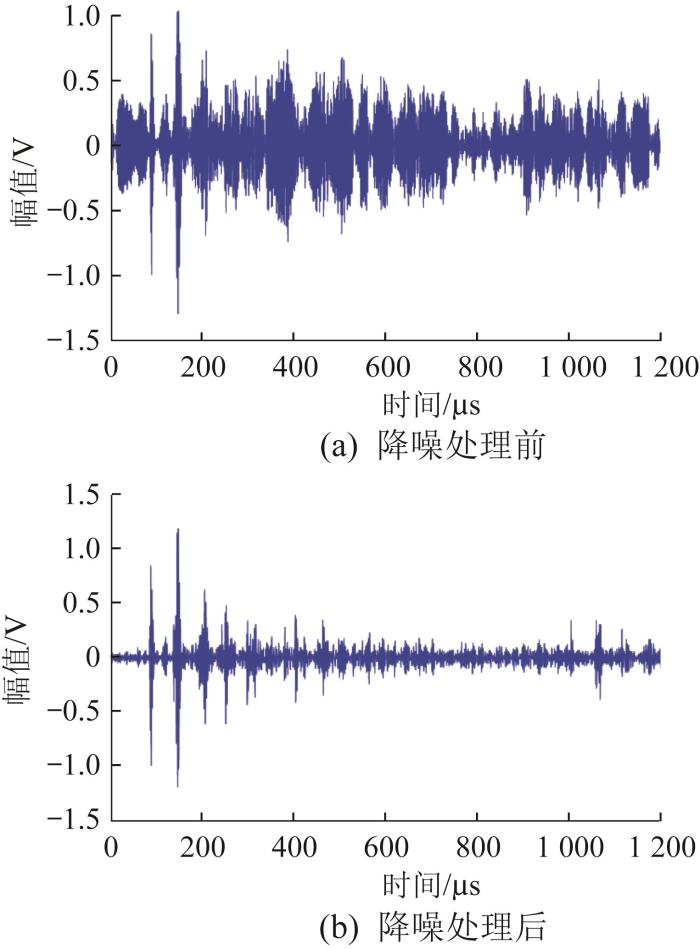
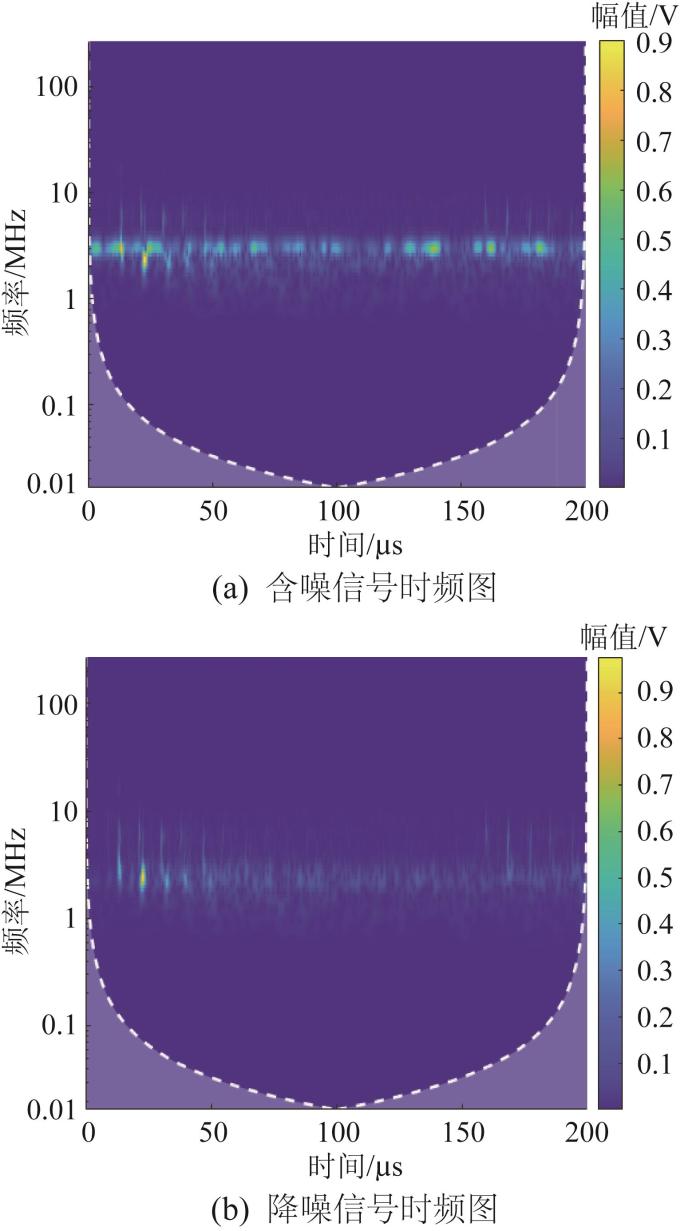
为验证上述基于回波补偿的降噪算法的可行性,对在复杂环境下采集的超声导波回波信号进行降噪处理,降噪效果如图6 所示。由图6 可以看出,降噪处理消除了大部分环境噪声,使得超声导波回波的包络更为明显。利用连续小波变换处理得到降噪处理前后超声导波回波信号在时频域中的能量分布情况,结果如图7 所示。从图7 中可以看出,降噪处理后超声导波回波信号的能量更集中,主要的回波包络可从连续的含噪信号中显示出来,各包络信号在时域上不再存在混叠现象。
图6
图6
降噪处理前后超声导波回波信号对比
Fig.6
Comparison of ultrasonic guided wave echo signals before and after noise reduction processing
图7
图7
降噪处理前后超声导波回波信号的时频分析结果对比
Fig.7
Comparison of time-frequency analysis result of ultrasonic guided wave echo signals before and after noise reduction processing
2.2 基于经验小波变换的模态分解
经验小波变换(empirical wavelet transform, EWT)算法是Gilles在传统模态分解算法的基础上提出的一种新型的自适应模态分解算法。由于EWT算法是在小波变换框架下建立的方法,其理论依据充分且计算量小,不会发生模态重叠的现象,更适合处理多频多模态信号[15 ] 。EWT算法的初始假设与经验模态分解(empirical mode decomposition, EMD)算法类似,即将初始信号f ( t ) R +1个不同的模态f r ( t )
f ( t ) = ∑ r = 0 R f r ( t ) (13)
f r ( t ) = F r ( t ) c o s ϕ r ( t ) (14)
式中:F r ( t ) ϕ r ( t ) f r ( t ) F r ( t ) > 0 ϕ r ' ( t ) > 0 Fr ( t ) ϕ r ' ( t ) ϕ r ( t )
假设在傅里叶频谱[0, π]范围内划分出R 个边界ωr ,ωr 选择为初始信号幅度谱中极大值点之间的中心,则初始信号的幅度谱Λ r
Λ r = [ ω r - 1 , ω r ] , r = 1 , 2 , ⋯ , R ∪ 1 R Λ r = [ 0 , π ] (15)
EWT算法的核心是构造自适应带通滤波器。本文以每个ωr 为中心点、宽度Tr =2τr 定义带通滤波器。其中,经验小波函数Ψ r ( ω ) φ r ( ω )
Ψ r ( ω ) = 1 , ω r + τ r ≤ ω ≤ ω r + 1 - τ r + 1 c o s π 2 β 1 2 τ r ω - ω r + 1 + τ r + 1 , ω r + 1 - τ r + 1 ≤ ω ≤ ω r + 1 + τ r + 1 s i n π 2 β 1 2 τ r ω - ω r + τ r , ω r - τ r ≤ ω ≤ ω r + τ r 0 , 其他 (16)
φ r ( ω ) = 1 , ω ≤ ω r - τ r c o s π 2 β 1 2 τ r ω - ω r + τ r , ω r - τ r ≤ ω ≤ ω r + τ r 0 , 其他 (17)
β ( x ) = x 4 ( 35 - 84 x + 70 x 2 - 20 x 3 )
τ r = γ ω r
γ < m i n r ω r + 1 - ω r ω r + 1 + ω r
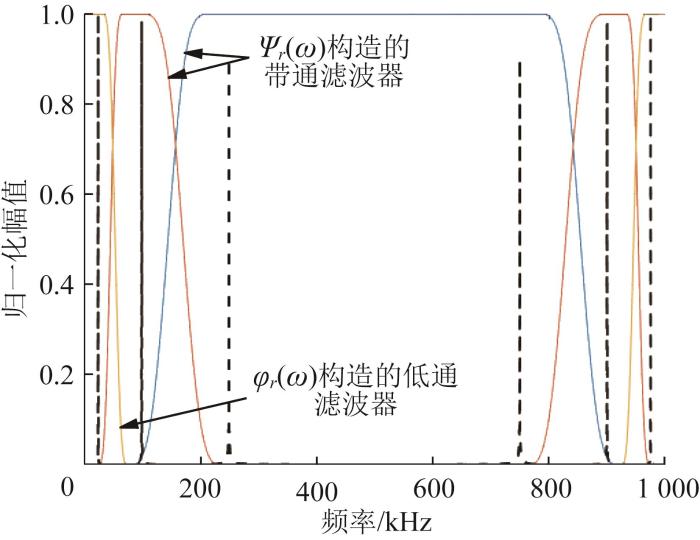
图8 所示为基于Ψ r ( ω ) φ r ( ω ) Ψ r ( ω ) φ r ( ω )
图8
图8
小波滤波器的频谱图
Fig.8
Spectrum diagram of wavelet filter
鉴于EWT与傅里叶变换的步骤相似,可根据傅里叶变换的数学原理来定义EWT的近似系数W f ε r , t r ≠
W f ε r , t = f ( t ) , Ψ r ( t ) (18)
当r =0时,近似系数W f ε 0 , t
W f ε 0 , t = f ( t ) , φ 1 ( t ) (19)
f ( t ) = W f ε 0 , t φ 1 ( t ) + ∑ r = 1 R W f ε r , t Ψ r ( t ) (20)
f 0 ( t ) = W f ε 0 , t φ 1 ( t ) f r ( t ) = W f ε r , t Ψ r ( t ) , r = 1 , 2 , ⋯ , R
通过EWT得到初始信号的分解模态后,对不同的模态进行小波逆变换,即可实现初始信号的重构。随后,对重构信号进行希尔伯特时频分析,即可得到其能量谱。
为检验基于EWT的模态分解算法的性能,选择一组超声导波回波信号进行模态分解。利用COMSOL软件得到一组不含噪声的超声导波回波信号,如图9 (a)所示。该信号主要由中心频率为0.95,1.25,1.50 MHz的高斯脉冲信号组成,这些高斯脉冲信号的声时相差不大,故其在时域上存在严重的模态混叠现象。为模拟实际环境中的噪声,在超声导波回波信号中添加5 dB的高斯噪声,如图9 (b)所示。由图可知,添加噪声后的超声导波回波信号发生了畸变,信号中的一些波峰已经完全无法辨认,几乎完全淹没在噪声中。
图9
图9
超声导波回波仿真信号
Fig.9
Ultrasonic guided wave echo simulation signal
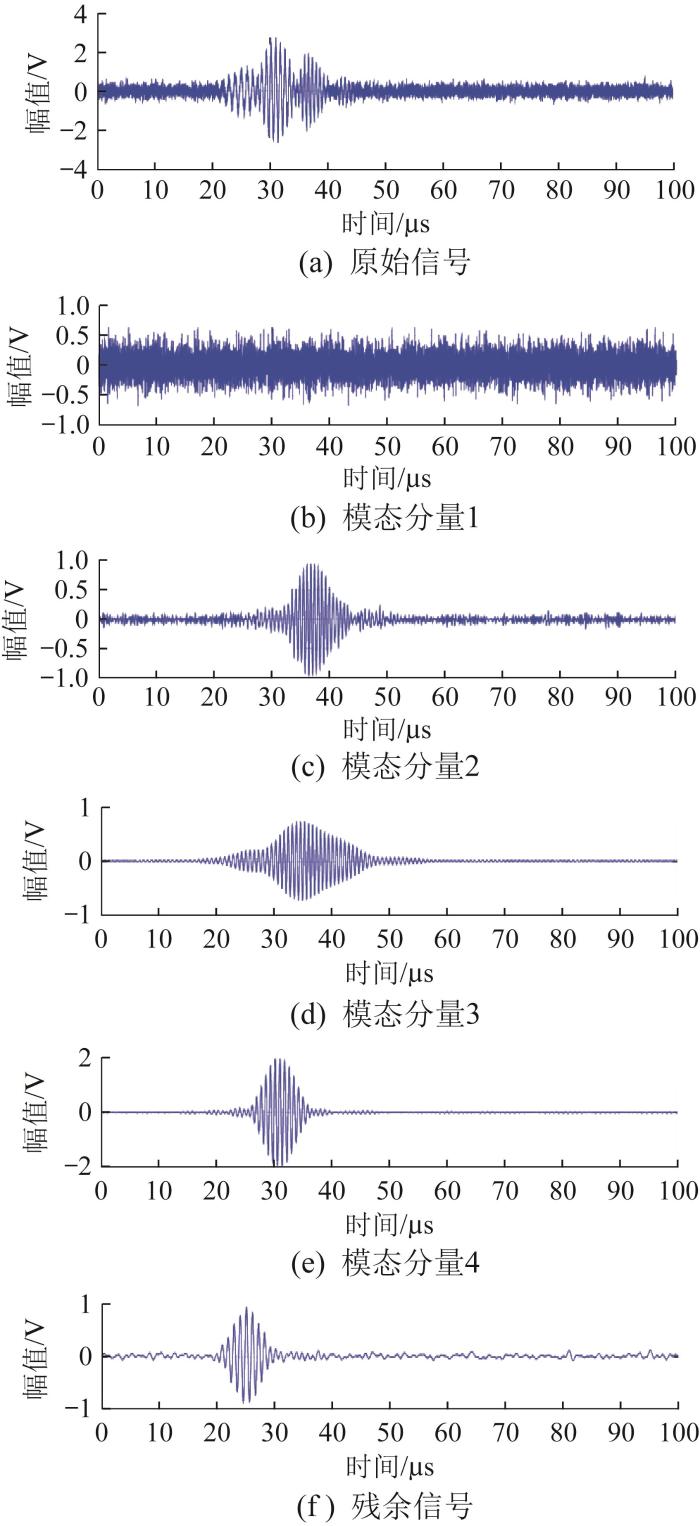
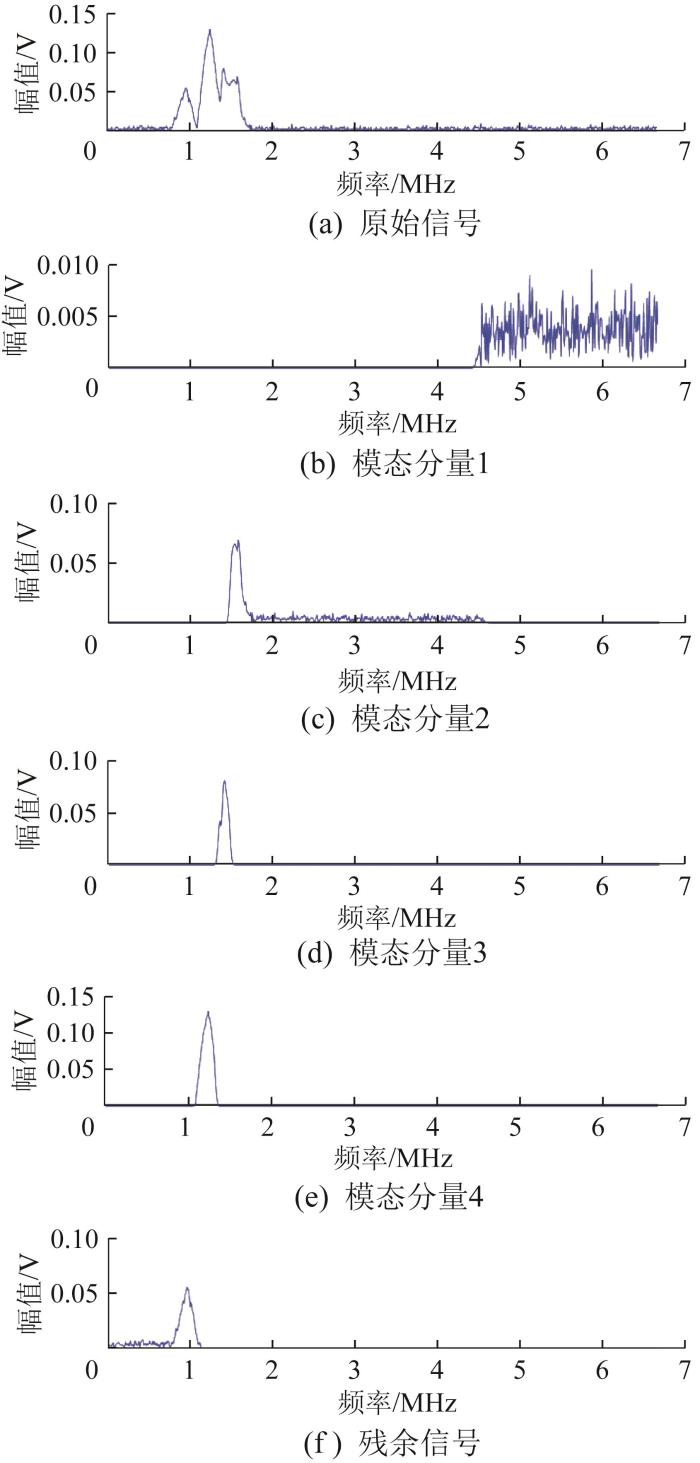
基于EWT对原始的超声导波回波信号进行模态分解,共得到4个模态,各个模态均包含不同的频率成分;同时,对分解得到的各个模态进行快速傅里叶变换(fast Fourier transform, FFT),得到各个模态的频谱,结果分别如图10 和图11 所示。从图中可以看出,模态分量1中主要包含高频噪声信号,模态分量2和模态分量3由混叠的1.50 MHz高斯脉冲信号分解得到,其中心频率分别为1.52 MHz和1.43 MHz;模态分量4被完全分解出来,该模态在时域和频域上均不包含其他模态的信息以及噪声;残余信号主要包含0.9 MHz的高斯脉冲信号和低频噪声。
图10
图10
基于EWT 的超声导波回波仿真信号模态分解结果
Fig.10
Modal decomposition results of ultrasonic guided wave echo simulation signal based on EWT
图11
图11
基于EWT 的超声导波回波仿真信号模态分量的频谱图
Fig.11
Spectrum diagram of modal component of ultrasonic guided wave echo simulation signal based on EWT
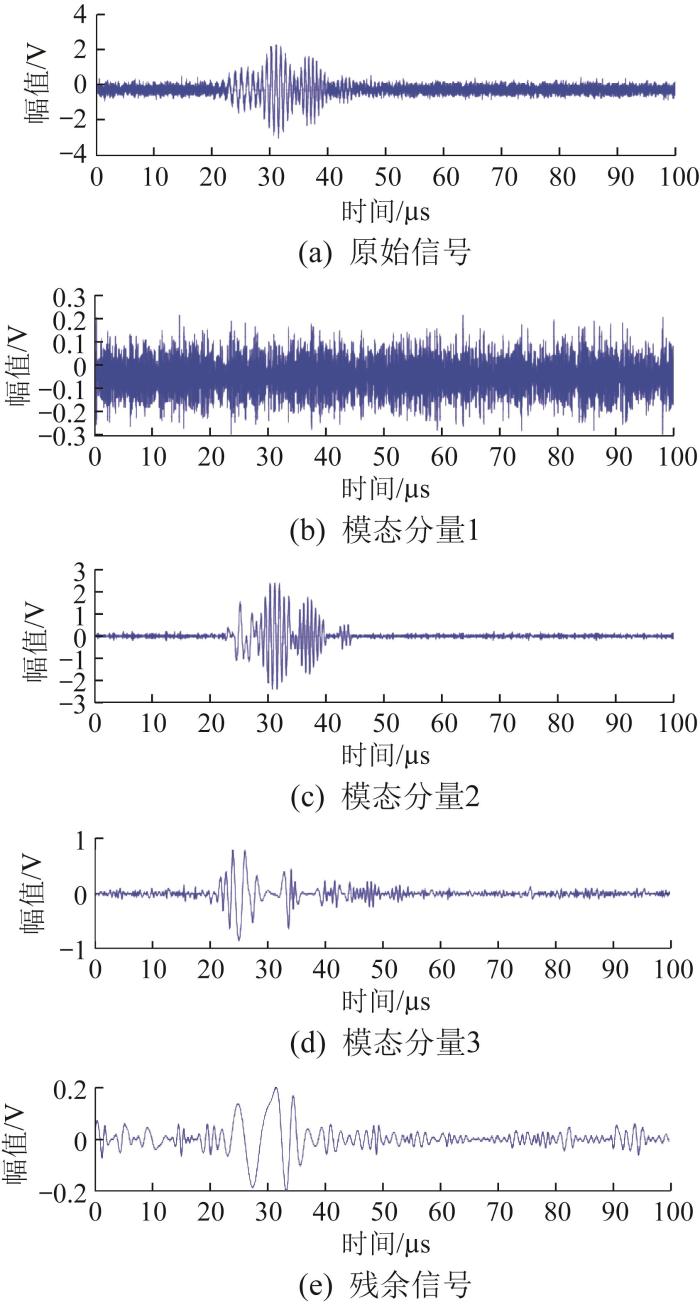
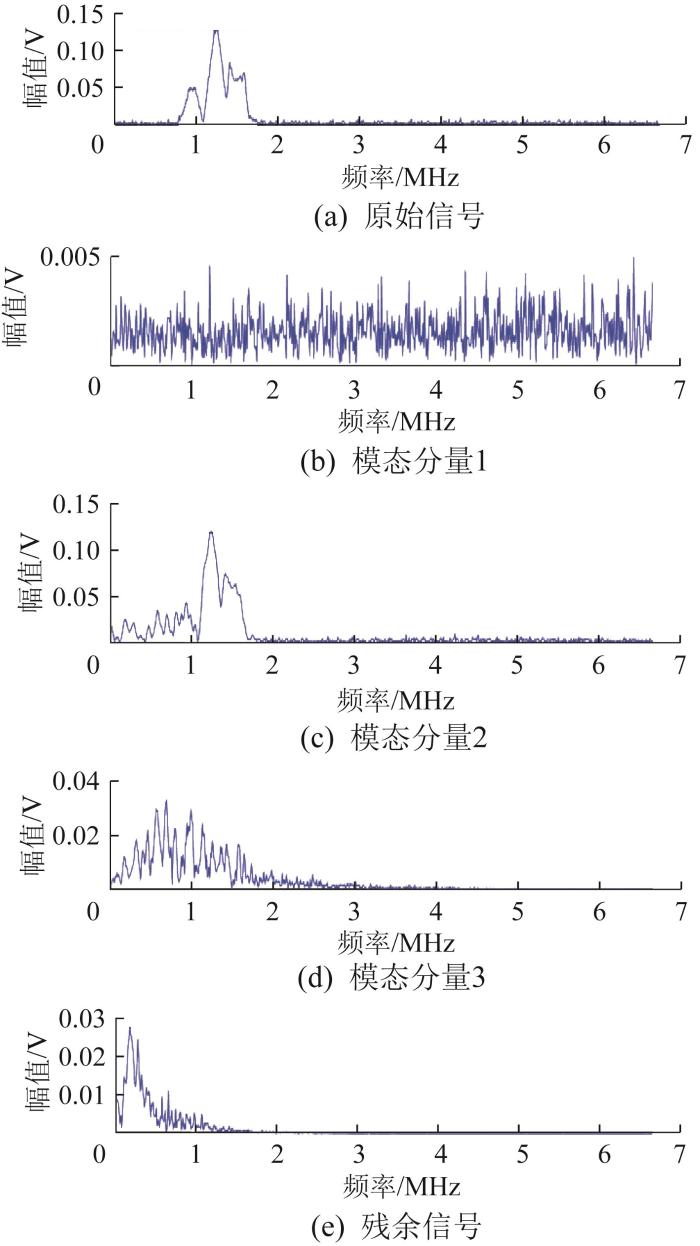
为了进一步验证基于EWT的模态分解算法的优越性,利用EMD算法对原始的超声导波回波信号进行模态分解并利用FFT对各模态分量进行处理,得到对应的时域图与频谱图,如图12 和图13 所示。通过对比发现,EMD算法难以实现超声导波回波信号的模态分解,只能分解出原始信号中的部分噪声信号,原始信号的能量主要分布在模态分量2中,且会产生虚假模态。由此可知,EMD算法并不具备分解中高频导波模态的能力[16 -18 ] ,而EWT算法十分适用于超声导波回波信号的模态分解,且各模态分量可被清晰地分解出来。
图12
图12
基于EMD 的超声导波回波仿真信号模态分解结果
Fig.12
Modal decomposition results of ultrasonic guided wave echo simulation signal based on EMD
图13
图13
基于EMD 的超声导波回波仿真信号模态分量的频谱图
Fig.13
Spectrum diagram of modal component of ultrasonic guided wave echo simulation signal based on EMD
2.3 超声导波回波信号的声时提取
声时提取是基于声弹性效应的应力测量的重要环节。目前,基于声弹性效应的应力测量精度不高的主要原因是由应力引起的声延时的计算不够准确。常用的声时计算方法包括峰值法、过零阈值法和互相关法等。其中:峰值法通过计算回波峰值的不同位置来计算时延,但该方法并未考虑应力对声波幅值的影响,因此精度不高;过零阈值法是以相邻回波第一次通过零点的时间差作为声时,该方法的弊端是当环境中存在与回波信号同频带的噪声时,极易引起过零阈值的误判;互相关法通过分析不同回波信号的相似性来计算声时差,不会因个别数据抖动和波形畸变而产生较大误差。因此,本文采用互相关法来提取超声导波回波信号的声时。令2个超声导波回波信号x 0 ( t ) x σ ( t ) R 0 σ ( τ )
R 0 σ ( τ ) = l i m T → ∞ 1 T ∫ - T 2 T 2 x 0 ( t ) x σ ( t - τ ) d t = l i m T → ∞ 1 T ∫ - T 2 T 2 x 0 ( t ) x 0 ( t - ( τ + D ) ) d t = R 00 ( τ + D ) (21)
式中:D 为声时差,R 00 ( τ ) x 0 ( t )
由式(6)可知,测量螺栓的轴向应力只需明确未知轴向应力σ 下超声导波回波信号相对于零应力状态下超声导波回波信号的声时差即可。因此,对零应力状态下的超声导波回波信号x 0 ( t ) σ 时的超声导波回波信号x σ ( t ) D 。根据自相关函数性质,可得:
R 00 ( 0 ) ≥ R 00 ( τ ) (22)
式(21)对于自相关函数恒成立,且自变量为零时取得最大值,即τ=-D 时自相关函数取得最大值。由此可知,R 00 ( τ ) D 的相反数。
3 实验验证
为验证基于超声导波的螺栓轴向应力测量方法的精度,设计了相应的测量系统,并选取M36×385等18种型号的螺栓(10.9级M36、M42、M48、M56、M64螺栓和双头螺柱)开展轴向应力测量实验,部分螺栓实物如图14 所示。实验地点位于湖南省常德市飞沃新能源科技股份有限公司,分别采用SHT-6206型微机控制电液伺服万能试验机和SAWL-6606型微机控制电液伺服卧式拉力试验机对螺栓进行拉伸试验。2台试验机的准确度等级均为0.5级,最大负荷分别为2 000 kN和6 000 kN。
图14
图14
部分螺栓的实物图
Fig.14
Physical drawing of some bolts
为实现螺栓的轴向应力测量,须先对不同型号的螺栓进行K 值标定实验。基于超声导波的螺栓轴向应力测量实验步骤如下:
1)利用超声波驱动器激励单纵波换能器,并调整示波器配置,直至获得清晰稳定的超声导波回波信号为止,并记录零应力状态下的超声导波回波信号。
2)控制万能试验机夹紧螺栓,从30%螺栓屈服强度开始,以5%螺栓屈服强度递进拉伸,每次拉伸完均保持2 min,以确保在应力稳定后记录超声导波回波信号,计算各轴向应力对应的声时差并进行曲线拟合。
3)完成K 值标定后,对所有型号螺栓在30%~90%屈服强度范围内的轴向应力进行测量。
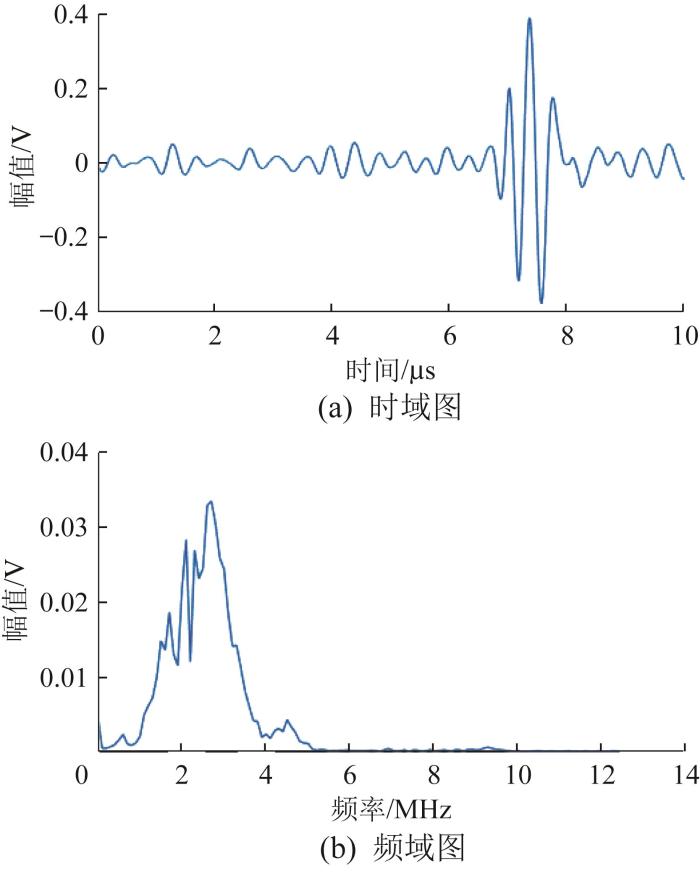
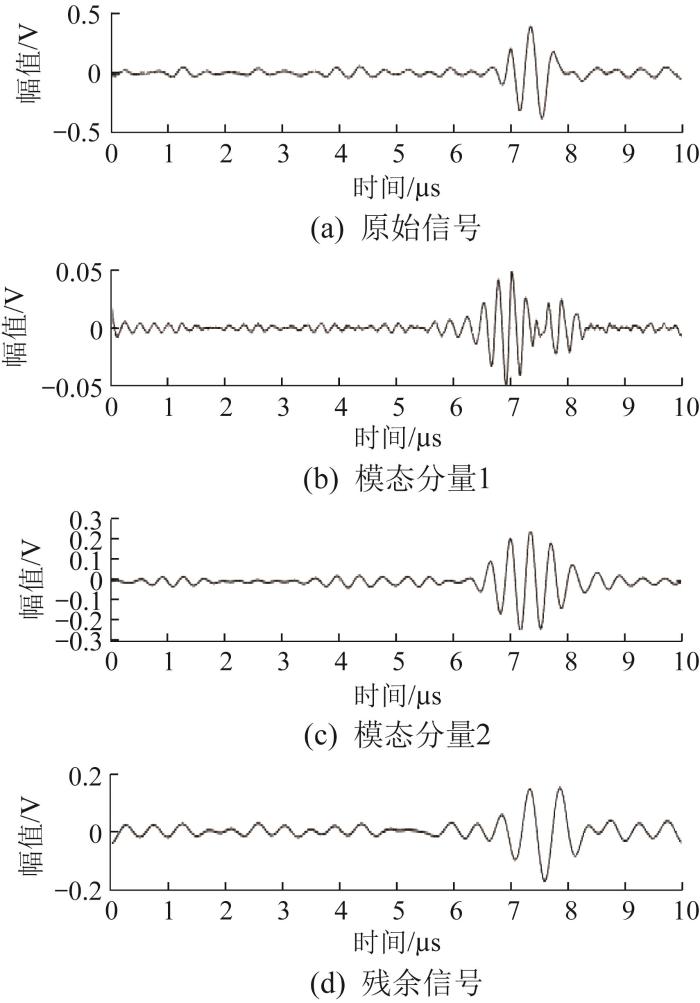
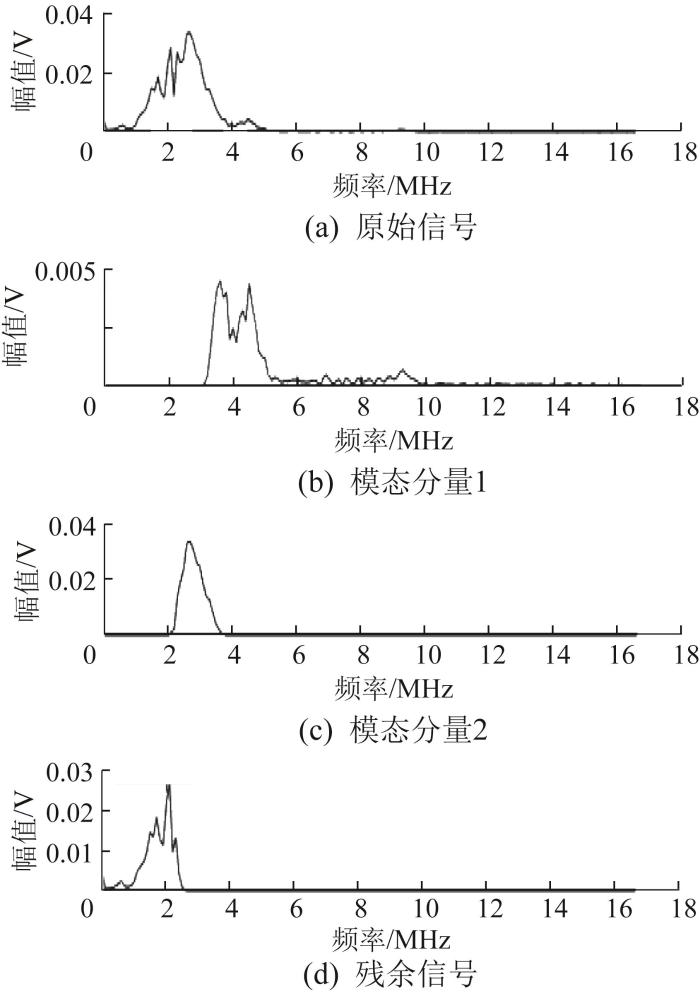
以M36×385螺栓为例,通过实验测得的超声导波回波信号如图15 所示。由图可知,该超声导波回波信号发生了畸变。这是因为单纵波换能器激励出的纵波具有一定带宽,导致超声导波回波信号的同一包络中可能包含多种模态。在高频状态下,各模态导波的群速度较为集中。由此可知,超声导波回波信号在实际情况下难以存在单一模态。不同超声导波回波信号的模态分量对应力的敏感程度不同,在对螺栓进行轴向应力加载后,不同模态会发生不同的时移。为了准确提取上述超声导波回波信号的声时,基于EWT对原始信号进行模态分解并进行FFT处理,原始信号的模态分解结果及其对应的频谱图分别如图16 和图17 所示。由图可知,原始超声导波回波信号的幅值谱明显包含多个能量水平相近的共振峰,其主要频率成分包括3.6,2.7,2.1 MHz;中心频率为2.7 MHz的模态分量2为本征模态。
图15
图15
超声导波回波实验信号(M36×385 螺栓)
Fig.15
Ultrasonic guided wave echo experimental signal (M36×385 bolt)
图16
图16
基于EWT 的超声导波回波实验信号的模态分解结果(M36×385 螺栓)
Fig.16
Modal decomposition results of ultrasonic guided wave echo experimental signal based on EWT (M36×385 bolt)
图17
图17
基于EWT 的超声导波回波实验信号模态分量的频谱图(M36×385 螺栓)
Fig.17
Spectrum diagram of modal component of ultrasonic guided wave echo experimental signal based on EWT (M36×385 bolt)
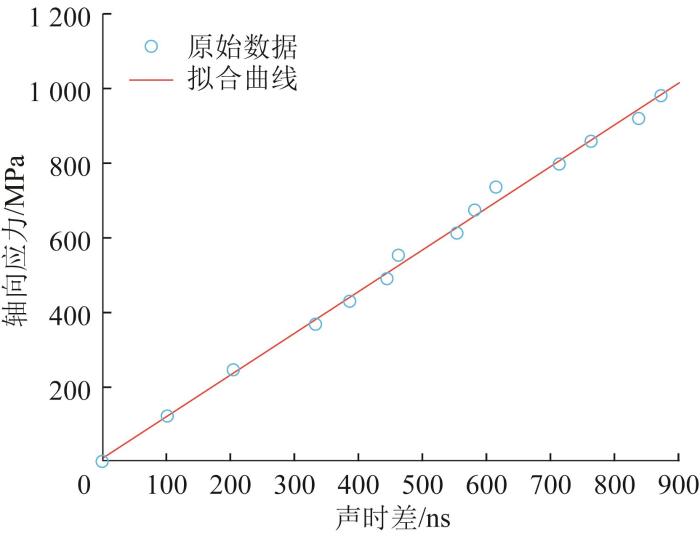
使用互相关法计算不同螺栓轴向应力下超声导波回波信号的声时差,从而得到M36×385螺栓的标定实验结果,如表2 所示。随后,对万能试验机上位机中记录的轴向应力值与超声导波回波信号的声时差进行线性拟合,结果如图18 所示。结果显示,M36×385螺栓的K 值为1.115。
图18
图18
M36×385 螺栓轴向应力与超声导波回波信号声时差的拟合曲线
Fig.18
Fitting curve between axial stress of M36×385 bolt and acoustic time difference of ultrasonic guided wave echo signal
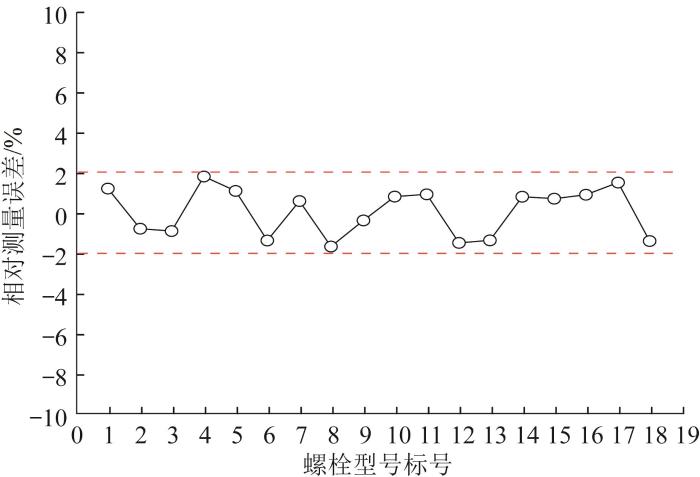
完成M36×385螺栓的标定实验后,对该型号螺栓在40%,50%,60%,70%,80%屈服强度下的轴向应力进行测量并计算对应的相对测量误差,结果如表3 所示。由表可知,相对测量误差均小于2%。其余17种型号螺栓的轴向应力测量步骤相同。18种型号螺栓的轴向应力的相对测量误差如图19 所示。经现场比对,本文基于超声导波的轴向应力测量方法的测量精度优于±2%。
图19
图19
18 种型号螺栓轴向应力的相对测量误差
Fig.19
Relative measurement error of axial stress of 18 types of bolts
4 总 结
本文针对风机在役螺栓的轴向应力测量,提出了一种基于超声导波的轴向应力测量方法。相对于传统的测量方法,本文提出的方法既简化了测量流程,又提高了测量精度。所做工作以及所得结论如下。
1)通过对超声导波在螺栓中的传播过程进行理论分析,结合超声导波的群速度频散曲线确定了使用中高频超声导波具有更高的轴向应力分辨率。然后,根据螺栓的受力情况,建立了基于超声导波的螺栓轴向应力测量模型。最后,在COMSOL软件中通过仿真验证了单纵波换能器实现超声导波应力测量的有效性。
2)针对实际测量中噪声对超声导波回波信号声时的影响,设计了基于回波补偿的降噪算法;针对超声导波回波信号多频多模态的特性,设计了基于EWT的模态分解算法,并基于超声导波回波仿真信号对比了EWT与EMD的模态分解性能,最后采用互相关法完成了超声导波回波信号声时的准确提取。
3)采用基于超声导波的轴向应力测量系统完成了18种不同型号螺栓的轴向应力测量。结果表明,相对测量误差均低于2%,证明了本文所提出的基于超声导波的轴向应力测量方法的精度较高。研究结果有助于改进螺栓装配工艺以及规范工人操作流程。
参考文献
View Option
[5]
徐春广 ,栗双怡 ,黄院生 ,等 基于扭矩法和超声法检测螺栓预紧力的误差分析
[J].电子机械工程 ,2023 ,39 (2 ):1 -4 .
[本文引用: 1]
XU C G LI S Y HUANG Y S et al Analysis of bolt preload measurement error with torque method and ultrasonic method
[J]. Elecro-Mechanical Engineering , 2023 , 39 (2 ): 1 -4 .
[本文引用: 1]
[7]
黄桥生 ,胡熠 ,刘世刚 ,等 在役风机螺栓超声检测新技术研究
[J].湖北电力 ,2022 ,46 (2 ):25 -29 .
HUANG Q S HU Y LIU S G et al Research on ultrasonic testing new technology for bolts of in-service wind turbines
[J]. Hubei Electric Power , 2022 , 46 (2 ): 25 -29 .
[9]
PAN Q X PAN R P SHAO C et al Research review of principles and methods for ultrasonic measurement of axial stress in bolts
[J]. Chinese Journal of Mechanical Engineering , 2020 , 33 : 11 .
[本文引用: 1]
[11]
DAMLJANOVIC V WEAVER R L Propagating and evanescent elastic waves in cylindrical waveguides of arbitrary cross section
[J]. Journal of the Acoustical Society of America , 2004 , 115 (4 ): 1572 -1581 .
[本文引用: 1]
[14]
DING X WU X J WANG Y G Bolt axial stress measurement based on a mode-converted ultrasound method using an electromagnetic acoustic transducer
[J]. Ultrasonics , 2014 , 54 (3 ): 914 -920 .
[本文引用: 1]
[15]
罗烨钶 ,陈永高 ,李升才 基于经验小波变换-噪声辅助分析的桥梁信号降噪方法
[J].振动与冲击 ,2022 ,41 (21 ):246 -256 .
[本文引用: 1]
LUO Y K CHEN Y G LI S C Adaptive denoising method of bridge vibration signal based on EWT-noise aided analysis theory
[J]. Journal of Vibration and Shock , 2022 , 41 (21 ): 246 -256 .
[本文引用: 1]
[16]
ERVIN B L REIS H BERNHARD J T et al Monitoring uniform and localized corrosion in reinforced mortar using high-frequency guided longitudinal wages
[C]//SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring . San Diego, Mar . 9 -13 , 2008 .
[本文引用: 1]
[17]
HUANG N E SHEN Z LONG S R et al The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis
[J]. Proceeding of the Royal Society A , 1998 , 454 (1971 ): 903 -995 .
[18]
张淑清 ,翟欣沛 ,董璇 ,等 EMD及Duffing振子在小电流系统故障选线方法中的应用
[J].中国电机工程学报 ,2013 ,33 (10 ):161 -167 .
[本文引用: 1]
ZHANG S Q ZHAI X P DONG X et al Application of EMD and Duffing oscillator to fault line detection in un-effectively grounded system
[J]. Proceedings of the CSEE , 2013 , 33 (10 ): 161 -167 .
[本文引用: 1]
风电产业发展现状及制约瓶颈
1
2018
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
风电产业发展现状及制约瓶颈
1
2018
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
风电叶片预埋型叶根连接螺栓抗疲劳优化设计研究
1
2021
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
风电叶片预埋型叶根连接螺栓抗疲劳优化设计研究
1
2021
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
风电叶片螺栓断裂失效分析
1
2015
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
风电叶片螺栓断裂失效分析
1
2015
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
在役螺栓轴力电磁超声测量系统的研制
1
2016
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
在役螺栓轴力电磁超声测量系统的研制
1
2016
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
基于扭矩法和超声法检测螺栓预紧力的误差分析
1
2023
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
基于扭矩法和超声法检测螺栓预紧力的误差分析
1
2023
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
纵横波测已紧固螺栓轴向应力
1
2000
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
纵横波测已紧固螺栓轴向应力
1
2000
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
螺栓横向剪力的超声检测
1
2022
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
螺栓横向剪力的超声检测
1
2022
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
Research review of principles and methods for ultrasonic measurement of axial stress in bolts
1
2020
... 全球化石能源不断减少,自然环境遭到破坏,如何实现经济发展与环境保护的双重目标成为目前亟须解决的问题.风能作为一种清洁的可再生能源,受到了世界各国的广泛关注[1 ] .在风力发电机组(下文简称风机)中,螺栓连接是最常见的装配方式,涉及轮毂、叶片、塔架与法兰等多个重要零部件,故螺栓自身的质量及其后续的定期检测是保障风机可靠运行的重要前提[2 -3 ] .然而,目前仍有很多风力发电厂长期使用落后的螺栓轴向应力测量方法,该方法的安全性、测量速度和准确性均存在严重缺陷.另外,由于螺栓结构复杂且型号繁多,传统的应力测量方法无法实现螺栓检测的工业化,这不仅增加了风电维稳的成本,还无法保证整体的检测效果[4 -5 ] .因此,使用简便可行的应力测量方法来判断螺栓是否处于合理的预紧区间显得尤为重要.基于超声波的无损检测方法因具有可检测范围广、对材料结构无损害、方便集成以及测量精度高等众多优势,获得了风电领域研究人员的青睐[6 -8 ] .随着国内风力发电厂的不断增多,螺栓的检测需求逐年增加.考虑到螺栓是风机核心零部件的连接结构以及传统应力测量方法的局限性,研究新的螺栓应力测量方法刻不容缓[9 ] . ...
超声柱面导波技术及其应用研究进展
1
2001
... 本文采用单波反射法对螺栓轴向应力进行测量.基于胡克定律和声弹性效应,推导并建立螺栓轴向应力与超声导波声时的数学模型.鉴于螺栓实际应用时的应力分布不均匀,对轴向受力时的螺栓模型进行简化,如图1 所示[10 ] . ...
超声柱面导波技术及其应用研究进展
1
2001
... 本文采用单波反射法对螺栓轴向应力进行测量.基于胡克定律和声弹性效应,推导并建立螺栓轴向应力与超声导波声时的数学模型.鉴于螺栓实际应用时的应力分布不均匀,对轴向受力时的螺栓模型进行简化,如图1 所示[10 ] . ...
Propagating and evanescent elastic waves in cylindrical waveguides of arbitrary cross section
1
2004
... 由超声导波的声弹性效应可知,螺栓中超声导波的声速与螺栓所受的应力有关.当螺栓只受到轴向压力或拉力时,超声导波在螺栓内部传播的速度与螺栓所受的轴向应力呈线性关系[11 ] ,由此可得: ...
螺栓拉应力超声无损检测方法
1
2014
... 由此可知,螺栓所受的轴向应力与超声导波的声时差近似呈线性关系,且常数K 仅与被测螺栓的材料特性有关.由于同一位置处螺栓受力部分的长度是固定的,因此只需测得超声导波在有无应力状态下的声时差,即可求得螺栓所受的轴向应力[12 ] .在相同的螺栓预紧流程下,即螺栓受力长度相同时,只需标定其中一颗螺栓对应的K 值,就能实现该型号所有螺栓的轴向应力测量. ...
螺栓拉应力超声无损检测方法
1
2014
... 由此可知,螺栓所受的轴向应力与超声导波的声时差近似呈线性关系,且常数K 仅与被测螺栓的材料特性有关.由于同一位置处螺栓受力部分的长度是固定的,因此只需测得超声导波在有无应力状态下的声时差,即可求得螺栓所受的轴向应力[12 ] .在相同的螺栓预紧流程下,即螺栓受力长度相同时,只需标定其中一颗螺栓对应的K 值,就能实现该型号所有螺栓的轴向应力测量. ...
风电螺栓超声导波检测技术仿真
1
2018
... 为了准确模拟超声导波在螺栓内的传播过程,本文选择弹性波和时域显式物理场界面来模拟超声导波在线性弹性介质中的回波信号波形.采用间断有限元方法和显式时间积分格式来求解超声导波声时和有应力状态下的线弹性波动方程[13 -14 ] .由于弹性波接口使用四阶函数,为获得适当的空间分辨率,定义最大网格单元尺寸h max 为: ...
风电螺栓超声导波检测技术仿真
1
2018
... 为了准确模拟超声导波在螺栓内的传播过程,本文选择弹性波和时域显式物理场界面来模拟超声导波在线性弹性介质中的回波信号波形.采用间断有限元方法和显式时间积分格式来求解超声导波声时和有应力状态下的线弹性波动方程[13 -14 ] .由于弹性波接口使用四阶函数,为获得适当的空间分辨率,定义最大网格单元尺寸h max 为: ...
Bolt axial stress measurement based on a mode-converted ultrasound method using an electromagnetic acoustic transducer
1
2014
... 为了准确模拟超声导波在螺栓内的传播过程,本文选择弹性波和时域显式物理场界面来模拟超声导波在线性弹性介质中的回波信号波形.采用间断有限元方法和显式时间积分格式来求解超声导波声时和有应力状态下的线弹性波动方程[13 -14 ] .由于弹性波接口使用四阶函数,为获得适当的空间分辨率,定义最大网格单元尺寸h max 为: ...
基于经验小波变换-噪声辅助分析的桥梁信号降噪方法
1
2022
... 经验小波变换(empirical wavelet transform, EWT)算法是Gilles在传统模态分解算法的基础上提出的一种新型的自适应模态分解算法.由于EWT算法是在小波变换框架下建立的方法,其理论依据充分且计算量小,不会发生模态重叠的现象,更适合处理多频多模态信号[15 ] .EWT算法的初始假设与经验模态分解(empirical mode decomposition, EMD)算法类似,即将初始信号f ( t ) R +1个不同的模态f r ( t )
基于经验小波变换-噪声辅助分析的桥梁信号降噪方法
1
2022
... 经验小波变换(empirical wavelet transform, EWT)算法是Gilles在传统模态分解算法的基础上提出的一种新型的自适应模态分解算法.由于EWT算法是在小波变换框架下建立的方法,其理论依据充分且计算量小,不会发生模态重叠的现象,更适合处理多频多模态信号[15 ] .EWT算法的初始假设与经验模态分解(empirical mode decomposition, EMD)算法类似,即将初始信号f ( t ) R +1个不同的模态f r ( t )
Monitoring uniform and localized corrosion in reinforced mortar using high-frequency guided longitudinal wages
1
2008
... 为了进一步验证基于EWT的模态分解算法的优越性,利用EMD算法对原始的超声导波回波信号进行模态分解并利用FFT对各模态分量进行处理,得到对应的时域图与频谱图,如图12 和图13 所示.通过对比发现,EMD算法难以实现超声导波回波信号的模态分解,只能分解出原始信号中的部分噪声信号,原始信号的能量主要分布在模态分量2中,且会产生虚假模态.由此可知,EMD算法并不具备分解中高频导波模态的能力[16 -18 ] ,而EWT算法十分适用于超声导波回波信号的模态分解,且各模态分量可被清晰地分解出来. ...
The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis
1998
EMD及Duffing振子在小电流系统故障选线方法中的应用
1
2013
... 为了进一步验证基于EWT的模态分解算法的优越性,利用EMD算法对原始的超声导波回波信号进行模态分解并利用FFT对各模态分量进行处理,得到对应的时域图与频谱图,如图12 和图13 所示.通过对比发现,EMD算法难以实现超声导波回波信号的模态分解,只能分解出原始信号中的部分噪声信号,原始信号的能量主要分布在模态分量2中,且会产生虚假模态.由此可知,EMD算法并不具备分解中高频导波模态的能力[16 -18 ] ,而EWT算法十分适用于超声导波回波信号的模态分解,且各模态分量可被清晰地分解出来. ...
EMD及Duffing振子在小电流系统故障选线方法中的应用
1
2013
... 为了进一步验证基于EWT的模态分解算法的优越性,利用EMD算法对原始的超声导波回波信号进行模态分解并利用FFT对各模态分量进行处理,得到对应的时域图与频谱图,如图12 和图13 所示.通过对比发现,EMD算法难以实现超声导波回波信号的模态分解,只能分解出原始信号中的部分噪声信号,原始信号的能量主要分布在模态分量2中,且会产生虚假模态.由此可知,EMD算法并不具备分解中高频导波模态的能力[16 -18 ] ,而EWT算法十分适用于超声导波回波信号的模态分解,且各模态分量可被清晰地分解出来. ...