考虑弹性误差的渐开线圆柱齿轮半解析接触模型与传动精度分析

doi:10.3785/j.issn.1006-754X.2024.03.309

考虑弹性误差的渐开线圆柱齿轮半解析接触模型与传动精度分析

肖康^,^,¹, 张楚², 董惠敏^,^,¹, 毛范海¹

1.大连理工大学机械工程学院，辽宁大连 116024

2.大连海事大学船舶与海洋工程学院，辽宁大连 116026

Semi-analytical contact model and transmission accuracy analysis of involute cylindrical gear considering elastic error

XIAO Kang^,^,¹, ZHANG Chu², DONG Huimin^,^,¹, MAO Fanhai¹

1.School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China

2.Naval Architecture and Ocean Engineering College, Dalian Maritime University, Dalian 116026, China

通讯作者: 董惠敏（1958—），女，辽宁大连人，教授，博士，从事齿轮传动系统精度特性和动力学性能分析与设计研究，E-mail: donghm@dlut.edu.cn，https://orcid.org/0009-0008-1051-7659

收稿日期: 2023-10-20 修回日期: 2023-12-11

基金资助:

国家自然科学基金资助项目. 52175045

Received: 2023-10-20 Revised: 2023-12-11

作者简介 About authors

肖康（1998—），男，辽宁葫芦岛人，硕士生，从事齿轮传动误差与振动研究，E-mail:xioakang@mail.dlut.edu.cn，https://orcid.org/0009-0005-2863-3074 , E-mail：xioakang@mail.dlut.edu.cn

摘要

在弹性和误差作用下，齿轮接触的高效、精准建模是研究齿轮传动精度的重要基础。为准确分析渐开线圆柱齿轮的弹性和误差对传动精度的影响，提出了一种考虑弹性误差的齿轮半解析接触模型。以渐开线斜齿圆柱齿轮为例，首先，结合齿轮的齿面方程与齿廓误差建立误差齿面模型，得到了误差齿面方程。然后，将解析法和有限元法相结合，建立了弹性误差作用下的齿轮半解析接触模型，并推导了其变形协调方程和力平衡方程。最后，建立齿轮的完整和局部有限元模型，通过提取接触齿面的柔度矩阵来计算齿轮的传动误差。应用所构建的半解析模型分析了齿廓误差和弹性变形对齿轮传动精度的影响规律，并与有限元仿真结果进行对比，验证了该半解析模型的高效性和精准性。研究结果可为渐开线圆柱齿轮在工程中的应用提供理论指导。

关键词： 渐开线圆柱齿轮 ; 弹性误差 ; 半解析模型 ; 传动误差

Abstract

Under the action of elasticity and errors, the efficient and precise modeling of gear contact is a crucial foundation for studying the transmission accuracy of gears. In order to accurately analyze the influence of elasticity and errors on the transmission accuracy of involute cylindrical gears, a semi-analytical contact model for gears considering elastic error is proposed. Taking the involute helical cylindrical gear as an example, firstly, the error tooth surface model of gear was established by combining the tooth surface equation and the tooth profile error, and the error tooth surface equation was obtained. Then, the semi-analytical contact model of gear under the action of elastic error was established by combining analytical method and finite element method, and the deformation coordination equation and force balance equation were derived. Finally, the complete and local finite element model of the gear was conducted, and the transmission error of the gear was calculated by extracting the compliance matrix of the contact tooth surface. The influence of the tooth profile error and elastic deformation on the transmission accuracy of gear was analyzed by using the semi-analytical model, and compared with the finite element simulation results, which verified the efficiency and accuracy of the semi-analytical model. The research results can provide theoretical guidance for the application of involute cylindrical gears in engineering.

Keywords： involute cylindrical gear ; elastic error ; semi-analytical model ; transmission error

PDF (1823KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

肖康, 张楚, 董惠敏, 毛范海. 考虑弹性误差的渐开线圆柱齿轮半解析接触模型与传动精度分析. 工程设计学报[J], 2024, 31(1): 91-97 doi:10.3785/j.issn.1006-754X.2024.03.309

XIAO Kang, ZHANG Chu, DONG Huimin, MAO Fanhai. Semi-analytical contact model and transmission accuracy analysis of involute cylindrical gear considering elastic error. Chinese Journal of Engineering Design[J], 2024, 31(1): 91-97 doi:10.3785/j.issn.1006-754X.2024.03.309

传动误差是影响齿轮传动精度和动力学特性的重要因素，对传动误差进行高效、精准的建模与分析是提升齿轮传动性能的重要基础。

目前，国内外学者针对齿轮传动误差的建模方法做了大量研究，常用的建模方法有解析法、有限元法及半解析法。例如：文献[1-6]采用有限元法对齿轮的传动误差进行了分析，该方法的求解精度较高，但由于建模复杂且网格划分密集，求解计算时间较长。为了提高求解效率，文献[7-12]采用解析法建立了齿轮传动误差的计算模型，极大地缩短了求解时间，但对齿轮的结构弹性问题考虑不足，导致求解精度受限。为了在缩短求解时间的同时保证准确性，现阶段很多学者开始研究半解析方法在齿轮传动精度分析中的应用，如Dong等^[13]采用半解析法建立了齿轮的传动模型，有效地提高了齿轮接触性能的求解效率。此外，在传动误差影响因素分析方面，Korta等^[1]在有限元建模的基础上探究了不同质量的材料对齿轮静态传动误差曲线的影响；邹帅东等^[7]在解析建模的基础上考虑了齿轮偏心的因素，研究了不同偏心程度对齿轮传动误差的影响；刘永平等^[3]分析了负载、转速及轴线误差等因素对齿轮传动误差的影响。

然而，上述针对齿轮传动误差的研究均未考虑弹性误差。为此，本文以渐开线圆柱齿轮为研究对象，在半解析方法的基础上建立考虑弹性误差的齿轮接触模型，并结合变形协调条件和力平衡方程，研究弹性误差对传动精度的影响规律，旨在为渐开线圆柱齿轮的工程应用提供指导。

1 渐开线圆柱齿轮的误差齿面模型

根据渐开线圆柱齿轮齿面的生成原理，将齿廓误差与齿面方程相结合，建立误差齿面模型，从而为齿轮传动误差的有限元求解提供理论基础。

1.1　齿轮的齿面方程

根据渐开线齿面的生成原理，当一条曲线在空间中沿螺旋线方向匀速拉伸变换时，所形成的表面即渐开线圆柱齿轮的齿面。如图1所示，以渐开线斜齿圆柱齿轮（后文简称斜齿轮）为例，推导其渐开线螺旋面方程^[14]，表示为：

\{\begin{array}{l} x = r_{b} s i n (u_{k} + θ) + r_{b} u_{k} c o s (u_{k} + θ) \\ y = r_{b} c o s (u_{k} + θ) - r_{b} u_{k} s i n (u_{k} + θ) \\ z = p θ \end{array}

(1)

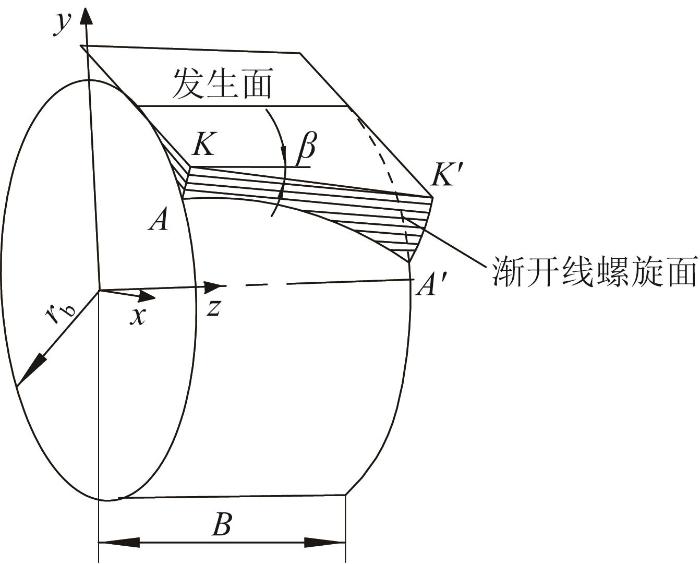
式中：r_b为齿轮的基圆半径，θ为母线绕轴线的旋转角度，p为螺旋线参数，u_k为渐开线发生角。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 渐开线螺旋面的生成

Fig.1 Generation of involute helical surface

设渐开线圆柱齿轮的直母线与圆柱在 $x$ 轴上的切点为 $s$ ，在该直母线上存在一个动点 $k$ ，令 $k$ 点到 $s$ 点的距离为 $l$ ，直母线与端截面的夹角为 $α$ ，则直母线的参数方程可表示为：

\{\begin{array}{l} x = r_{b} \\ y = l c o s α \\ z = l s i n α \end{array}

(2)

将直母线方程代入式(1)，得到渐开线圆柱齿轮的齿面方程：

\{\begin{array}{l} x = r_{b} c o s θ - l c o s α s i n θ \\ y = r_{b} s i n θ + l c o s α c o s θ \\ z = l s i n α + p θ \end{array}

(3)

1.2　齿轮的误差齿面方程

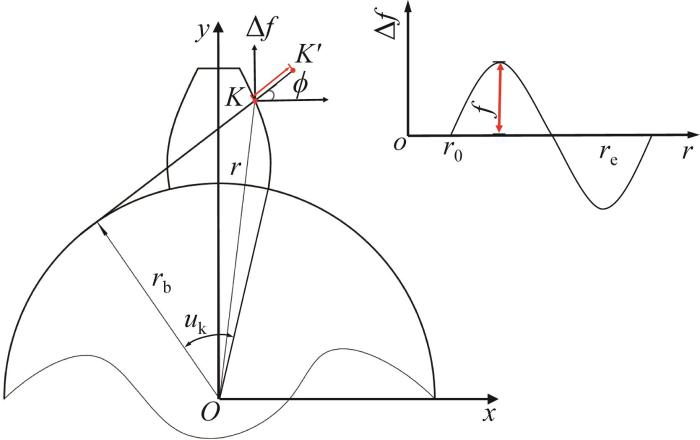
渐开线圆柱齿轮的齿廓误差具体值可通过查表确定^[15]。将渐开线圆柱齿轮的齿廓曲线离散成点，并计算得到齿廓上各点与齿轮中心的距离 $r$ 。以齿廓各点与齿轮中心的距离 $r$ 为横坐标，齿廓误差为纵坐标，构建考虑齿廓误差的齿廓曲线，如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 考虑齿廓误差的齿廓曲线

Fig.2 Tooth profile curve considering tooth profile error

根据图2，齿廓误差的表达式如下：

Δ f = f s i n [(r - r_{0}) w]

(4)

其中：

r = \sqrt[]{x_{K}^{2} + y_{K}^{2}}

w = 2 π / (r_{e} - r_{0})

式中： $Δ f$ 为齿廓离散点K的齿廓误差， $f$ 为齿廓误差最大值， $r_{0}$ 为齿廓上第1个离散点到齿轮中心的距离，r_e为齿廓上最后一个离散点到齿轮中心的距离， $(x_{K}, y_{K})$ 为齿廓上任意离散点K的坐标。

如图2所示，以对应点的齿廓误差作为偏移距离，将齿廓离散点沿法线方向进行偏移，得到新的齿廓离散点 $K^{'} (x_{K}^{'}, y_{K}^{'})$ 。将新的齿廓离散点沿着螺旋线方向分布，即可得到误差齿面。添加误差后的齿廓离散点 $K^{'} (x_{K}^{'}, y_{K}^{'})$ 的坐标可表示为：

\{\begin{array}{l} x_{K}^{'} = x_{K} + Δ f c o s ϕ \\ y_{K}^{'} = y_{K} + Δ f s i n ϕ \end{array}

(5)

式中： $ϕ$ 为齿廓离散点 $K$ 的法线方向与x轴的夹角。

2 考虑弹性误差的渐开线圆柱齿轮半解析接触模型

本文通过推导渐开线圆柱齿轮的变形协调方程、力平衡方程和提取柔度矩阵等来建立其半解析接触模型，以实现其传动误差的求解。

2.1　齿轮变形协调方程的推导

齿轮在传动过程中的接触可等效为弹性体的接触^[16]，则主、从动轮接触线上每一个点的变形协调方程可表示为：

Q_{i} = ε_{i} + σ_{i} - U_{i}

(6)

式中： $Q_{i}$ 为接触点i的间隙， $ε_{i}$ 为由误差引起的初始接触间隙，包括齿廓误差、修形量等， $U_{i}$ 为接触点i因齿轮齿体的刚性运动而产生的位移， $σ_{i}$ 为接触点i处产生的弹性变形量。

在载荷的作用下，齿轮接触点处产生的弹性变形包括整体变形和局部接触变形，其中整体变形是指弯曲-剪切变形。渐开线圆柱齿轮的弹性变形可表示为：

σ_{i} = σ_{h i} + σ_{b 1} + σ_{b 2}

(7)

式中： $σ_{h i}$ 为接触点 $i$ 处的接触变形， $σ_{b 1} 、 σ_{b 2}$ 分别为主、从动轮的弯曲-剪切变形。

渐开线圆柱齿轮在某一位置处的接触问题可看作2个圆柱体的接触问题。在接触过程中，主、从动轮在接触点处的法向曲率半径为圆柱体的半径。根据统计接触理论^[17]，在力作用下，接触点处的接触变形可表示为：

σ_{h i} = \frac{2 F_{i}}{π l_{i} E} (l n \frac{2 w_{i}}{B_{i}} + 0.148)

(8)

其中：

E = \frac{1}{(1 - μ_{1}^{2}) / E_{1} + (1 - μ_{2}^{2}) / E_{2}}

式中： $F_{i}$ 为接触点i处的载荷，N； $l_{i}$ 为接触点i所在接触线的分段距离，mm； $μ_{1} 、 μ_{2}$ 分别为主、从动轮的泊松比； $E_{1} 、 E_{2}$ 分别为主、从动轮的弹性模量，MPa； $w_{i}$ 为接触点i对应的齿轮厚度，mm； $B_{i}$ 为接触半宽，mm。

渐开线圆柱齿轮的柔度矩阵包括整体柔度矩阵和局部柔度矩阵。则完整的柔度矩阵可表示为：

λ_{w} = λ_{b 1} + λ_{b 2} + λ_{h}

(9)

式中： λ_w为齿轮副的完整柔度矩阵； λ_b1、 λ_b2分别为主、从动轮的弯曲-剪切柔度矩阵； λ_h为接触点的接触柔度矩阵。

渐开线圆柱齿轮的弹性变形量可表示为：

σ = λ_{w} F

(10)

式中： σ 为齿轮弹性变形量矩阵， F 为接触点法向力矩阵。

在渐开线圆柱齿轮的啮合过程中，由于受到齿轮六自由度运动的影响，使得接触线上的点产生了刚性位移。通过构建投影矩阵，将齿轮的刚性位移投影到接触线的法线方向上，则齿轮啮合过程中产生的刚性位移可表示为：

U = [G_{1} G_{2}] [\begin{array}{l} Φ_{1} \\ Φ_{2} \end{array}]

(11)

式中： U 为齿轮刚性位移在接触线法线方向上的投影量， $G_{1} 、 G_{2}$ 分别为主、从动轮的六自由度在接触线法线方向上的投影向量， $Φ_{1} 、 Φ_{2}$ 分别为主、从动轮的六自由度位移。

2.2　齿轮力平衡方程的推导

为了求解弹性变形影响下渐开线圆柱齿轮实际接触点的接触力，须建立主、从动轮的力和力矩的平衡方程。

当主动轮受到载荷作用时，需要主、从动轮之间的接触力和轴承支撑力来进行平衡。将主、从动轮之间的接触力投影到对应齿轮的坐标系下，则可得主动轮的受力平衡方程：

Τ_{1} = G_{1}^{T} F_{12} + K_{1} Φ_{1}

(12)

式中： $T_{1}$ 为主动轮的外部载荷矩阵， $F_{12}$ 为从动轮对主动轮的接触力， $K_{1}$ 为主动轮的支撑刚度矩阵。

同理，可得从动轮的受力平衡方程：

T_{2} = G_{2}^{T} F_{21} + K_{2} Φ_{2}

(13)

式中： T₂为从动轮的外部载荷矩阵， $F_{21}$ 为主动轮对从动轮的接触力， $K_{2}$ 为从动轮的支撑刚度矩阵。

将主、从动轮的受力平衡方程进行整合，可得到整体的受力平衡方程：

[\begin{matrix} T_{1} \\ T_{2} \end{matrix}] = [\begin{matrix} G_{1}^{T} & 0 \\ 0 & G_{2}^{T} \end{matrix}] [\begin{matrix} F_{12} \\ F_{21} \end{matrix}] + [\begin{matrix} K_{1} & 0 \\ 0 & K_{2} \end{matrix}] [\begin{matrix} Φ_{1} \\ Φ_{2} \end{matrix}]

(14)

2.3　齿轮柔度矩阵的提取

由于主、从动轮的参数相同，只需在ANSYS软件中建立主动轮的完整和局部有限元模型，即可获取主、从动轮的弯曲-剪切变形系数^[18]。以斜齿轮为例，其整体有限元模型采用五齿模型，如图3(a)所示。对齿轮中心孔处施加全约束，以获取整体柔度矩阵；轮体和齿体的弹性模量相同。斜齿轮局部有限元模型如图3(b)所示，对非接触齿面施加全约束，齿体弹性模量为齿面弹性模量的1 000倍，以确保接触齿面仅包含局部接触变形。主、从动轮接触齿面上的节点坐标和单元完全一致。

图3

新窗口打开| 下载原图ZIP| 生成PPT

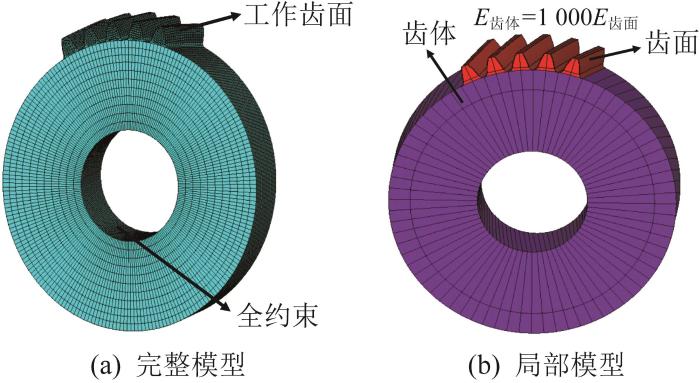
图3 斜齿轮的完整和局部有限元模型

Fig.3 Complete and local finite element model of helical gear

主、从动轮接触齿面上节点的弯曲-剪切柔度系数矩阵可表示为：

η_{b, f e}^{} = η_{t, f e}^{} - η_{l, f e}^{}

(15)

式中： η_{b, fe}为接触齿面节点的弯曲-剪切柔度系数矩阵， η_{t, fe}为完整有限元模型的弯曲-剪切柔度系数矩阵， η_{l, fe}为局部有限元模型的弯曲-剪切柔度系数矩阵。

完成齿轮完整有限元模型和局部有限元模型的构建后，采用ANSYS软件中自带的子结构法提取柔度系数矩阵^[19]。但采用子结构法时会涉及外部节点和内部节点，由于本文不考虑内部节点的自由度，则可使用凝聚的方法忽略内部节点。将各子结构组装成整体时仅包含外部节点，其方程维数比原模型的方程维数小得多。

采用形函数插值运算方法对所构建的柔度矩阵进行运算，获得齿面接触点的弯曲-剪切柔度矩阵。对于任意网格节点，在确定齿面接触点与网格节点的位置关系后，通过已知的柔度系数插值获得接触点的柔度系数。不同齿面上接触点的柔度矩阵可通过齿面接触点与完整有限元模型的网格节点位置关系求得。最后按照接触点顺序，重新组装成柔度矩阵^[20]。

2.4　考虑弹性误差的齿轮传动误差计算

基于上述建立的渐开线圆柱齿轮半解析接触模型，分析弹性误差对其传动精度的影响^[21]，并构建齿轮传动误差的计算流程，如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

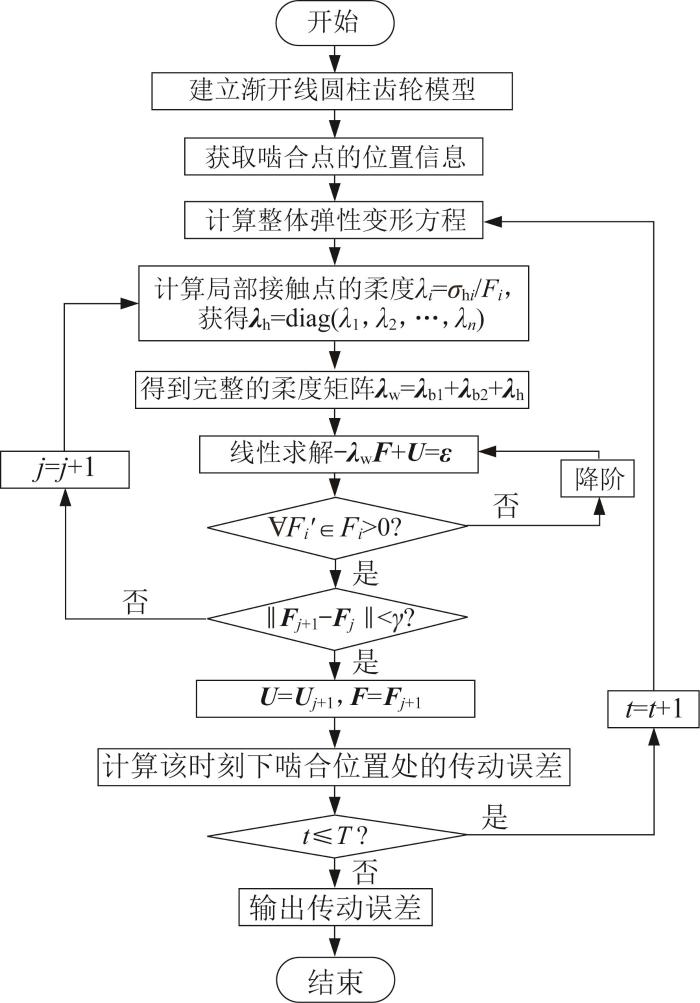
图4 考虑弹性误差的渐开线圆柱齿轮的传动误差计算流程

Fig.4 Calculation process for transmission error of involute cylindrical gear considering elastic error

考虑弹性误差的渐开线圆柱齿轮传动误差的计算步骤如下：

1）首先根据齿轮的基本参数，建立齿轮几何模型，以计算得到齿轮接触线的位置，并对齿轮接触线进行离散化处理，获得均匀分布的离散点并确定其位置坐标。

2）基于所获得的离散接触点的坐标，考虑齿廓误差，每个接触点对应的齿廓误差幅值由接触点到齿轮中心的距离来确定，将得到的齿廓误差幅值代入接触间隙，并结合初始离散接触点的坐标，得到新的接触点坐标。

3）假设初始载荷对所有潜在接触点的作用相同，从而获得各接触点处的位移以及整体柔度矩阵和局部接触柔度矩阵，进而整合得到齿轮副的完整柔度矩阵。

4）根据接触点的接触力，判断该接触点是否参与啮合： $F_{i} < 0$ N表示接触点不参与啮合， $F_{i} > 0$ N表示接触点参与啮合。通过迭代得到所有参与啮合的接触点，并更新柔度矩阵。

5）通过 $‖F_{j} + 1 - F_{j}‖ < γ$ （j为迭代次数，γ为收敛容差）来判断结果是否收敛，若不满足收敛条件，则进行第2次迭代，直至得到最终的方程解。

6）基于获得的方程解计算该时刻下齿轮的传动误差，并基于上述步骤计算下一时刻的传动误差，直到获得一个啮合周期T内的传动误差后计算结束，同时输出最终的传动误差结果。

3 基于半解析模型的渐开线圆柱齿轮传动精度分析

3.1　半解析模型验证

为验证上文所构建的渐开线圆柱齿轮半解析接触模型的准确性，根据表1所示的斜齿轮参数进行实例分析，并将基于半解析模型和有限元法的传动误差计算结果进行对比。

表1 斜齿轮的基本参数

Table 1 Basic parameters of helical gear

参数	主动轮	从动轮
齿数Z	36	36
模数m/mm	3	3
压力角α/（°）	20	20
齿宽B/mm	30	30
螺旋角β/（°）	15	15
变位系数g	0	0
顶隙系数c^*	0.25	0.25
弹性模量E/GPa	206	206
泊松比μ	0.3	0.3

新窗口打开| 下载CSV

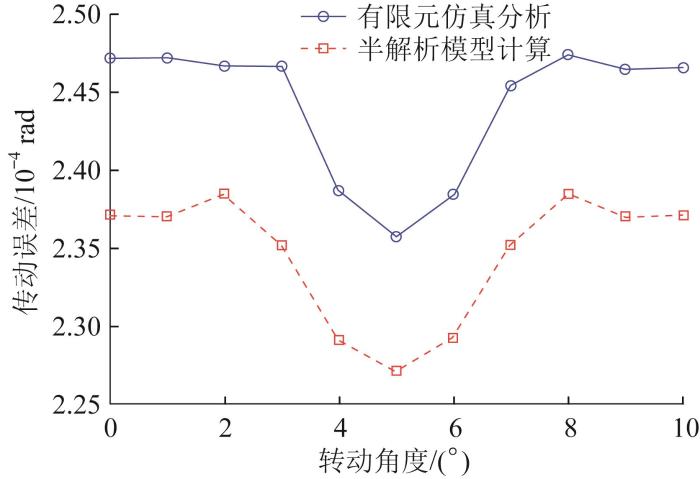
在ANSYS软件中建立一对斜齿轮的接触模型，2个齿轮在节点处刚好接触；在从动轮转动中心点处施加全约束，主动轮仅保留绕z轴方向的转动，在主动轮转动中心点处施加300 N∙m的转矩，求解结束后直接提取主动轮在1个啮合周期内的传动误差。同时，利用半解析模型计算该齿轮副在1个啮合周期内的传动误差，并与有限元仿真结果进行对比。基于不同方法的斜齿轮传动误差随转动角度的变化曲线如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 基于不同方法的斜齿轮传动误差对比

Fig.5 Comparison of transmission error of helical gear based on different methods

由图5可知，在1个啮合周期内，基于有限元仿真和半解析模型的斜齿轮传动误差的变化曲线基本一致。2种方法中斜齿轮模型在初始时刻下均处于同一个位置，同一时刻下齿轮传动误差的最大相对误差为5.8%，最小相对误差为3.2%，均在6%以内，验证了半解析建模方法的准确性。此外，半解析模型的求解时间为2.05 min，有限元仿真的求解时间为165 min，相比之下，半解析模型的求解速度提升了79.57倍，表明半解析方法在求解效率方面具有极大优势。

3.2　齿廓误差对齿轮传动精度的影响

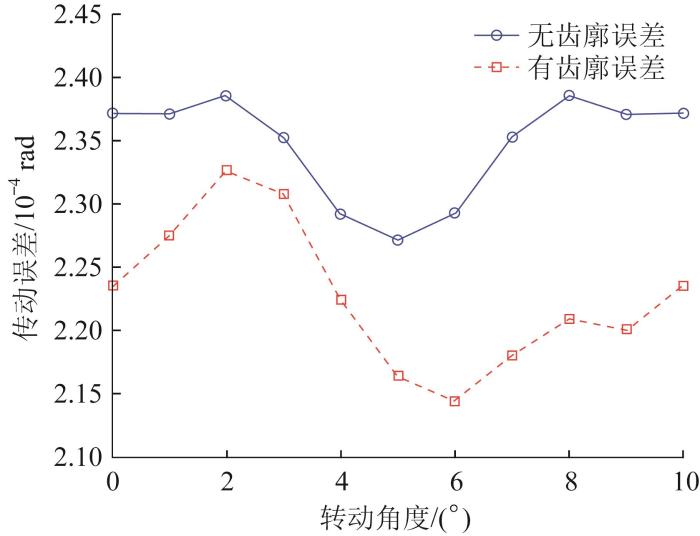
为分析齿廓误差对渐开线圆柱齿轮传动精度的影响规律，选用四级齿廓误差，在主动轮中心节点处施加300 N∙m的转矩，齿轮接触的初始位置为节点（齿廓接触点的公法线与连心线的交点）处，基于半解析模型计算有无齿廓误差情况下斜齿轮在1个啮合周期内的传动误差，结果如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 齿廓误差对斜齿轮传动误差的影响

Fig.6 Influence of tooth profile error on transmission error of helical gear

由图6可知，在无齿廓误差的情况下，斜齿轮的传动精度为1.133 0×10^-5 rad；在有四级齿廓误差的情况下，齿轮的传动精度为1.818 6×10^-5 rad。在有齿廓误差的情况下，斜齿轮的传动精度变大，由此可看出，齿廓误差会影响齿轮的传动精度。

3.3　载荷对齿轮传动精度的影响

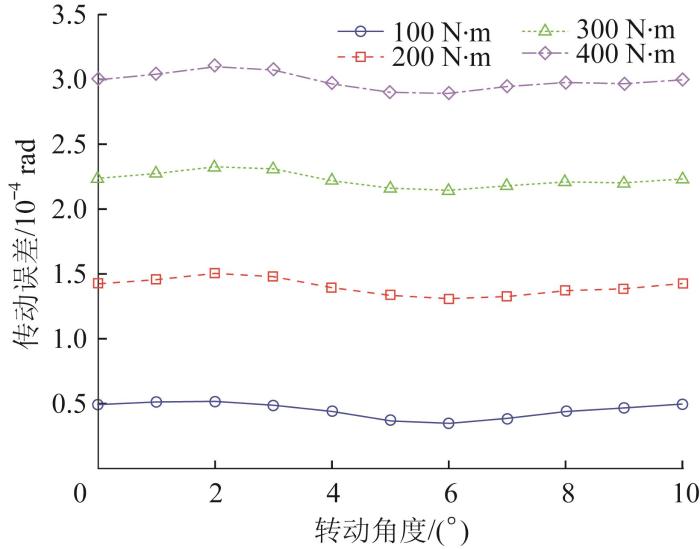
不同载荷下齿轮的传动精度也不同。为了研究载荷对渐开线圆柱齿轮传动精度的影响规律，在斜齿轮存在四级齿廓误差的基础上，分别施加100，200，300，400 N∙m的转矩，基于半解析模型计算不同载荷下斜齿轮的传动误差，结果如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 载荷对斜齿轮传动误差的影响

Fig.7 Influence of load on transmission error of helical gear

从图7中可以看出，在100，200，300，400 N∙m转矩的作用下，斜齿轮的传动精度分别为1.68×10^-5，1.95×10^-5，1.82×10^-5，2.05×10^-5 rad；随着载荷的增大，斜齿轮接触时的传动误差增大，且对应的传动精度也增大，说明载荷会对齿轮的传动性能产生较大的影响。

3.4　齿廓误差等级对齿轮传动精度的影响

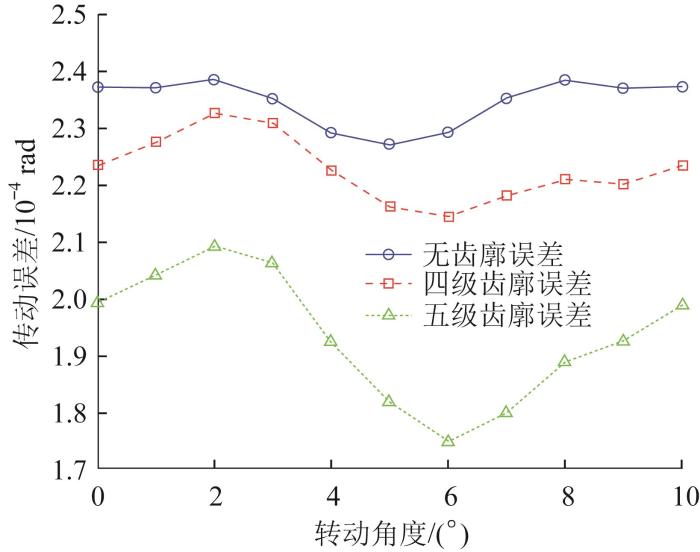
为探究不同等级齿廓误差对渐开线圆柱齿轮传动精度的影响规律，基于半解析模型分别对无齿廓误差、四级齿廓误差和五级齿廓误差情况下（主动轮中心节点处施加300 N∙m转矩）斜齿轮传动误差的变化情况进行分析，结果如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 齿廓误差等级对斜齿轮传动误差的影响

Fig.8 Influence of tooth profile error level on transmission error of helical gear

由图8可以看出，随着齿廓误差等级的变大，斜齿轮的传动精度也增大。在无齿廓误差的情况下，由于斜齿轮只受到载荷的影响，其传动精度的变化最小。当存在四级齿廓误差时，由于斜齿轮受到载荷和齿廓误差的综合影响，相对于无齿廓误差的情况下，其传动精度的变化较大。当存在五级齿廓误差时，由于斜齿轮的齿廓误差变大且同时受到载荷的作用，其传动精度的变化最大，且齿廓误差对齿轮的传动平稳性也有较大的影响。

4 结论

本文结合有限元法和解析法的优点，建立了考虑弹性误差的渐开线圆柱齿轮半解析接触模型，并通过与传统有限元法的结果进行对比，验证了所构建的半解析模型的正确性。结果表明，半解析方法可有效提高渐开线圆柱齿轮传动精度的求解效率，与传统有限元法相比，本文方法的求解速度提升了79.57倍，且求解准确性较高。同时，基于所构建的半解析模型分析了不同载荷和齿廓误差等级对渐开线圆柱齿轮传动精度的影响规律，为渐开线圆柱齿轮的工程应用提供了指导。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

KORTA

， MUNDO

， AMBROGIO

， et al.

Topology optimization and analysis of static transmission error in lightweight gears

［C］//Proceedings of the First International Conference of IFToMM Italy. Cham： Springer， 2017： 195-202.

[本文引用: 2]

[2]

马涛，周集祥，李泽文，等.

基于有限元法的直齿轮接触强度分析与优化

［J］.赤峰学院学报（自然科学版），2019，35（12）：97-99.

， ZHOU

J X

， LI

Z W

， et al.

Contact strength analysis and optimization of spur gears based on finite element method

［J］. Journal of Chifeng University （Natural Science Edition）， 2019， 35（12）： 97-99.

[3]

刘永平，任忠涛，魏永峭，等.

渐开线变齿厚直齿轮传动误差研究

［J］.机床与液压，2023，51（4）：1-6. doi：10.3969/j.issn.1001-3881.2023.04.001

[本文引用: 1]

LIU

Y P

， REN

Z T

， WEI

Y Q

， et al.

Research on transmission error of involute variable tooth thickness spur gears

［J］. Machine Tool & Hydraulics， 2023， 51（4）： 1-6.

DOI:10.3969/j.issn.1001-3881.2023.04.001 [本文引用: 1]

[4]

郭恒，刘卓婷，孙玉玖，等.

基于Workbench的齿轮稳态温度场和传动误差分析

［J］.机械传动，2023，47（5）：98-104.

GUO

， LIU

Z T

， SUN

Y J

， et al.

Analysis of gear bulk temperature field and transmission errors based on Workbench

［J］. Journal of Mechanical Transmission， 2023， 47（5）： 98-104.

[5]

WANG

J D

， HOWARD

I M

Error analysis on finite element modeling of involute spur gears

［J］. Journal of Mechanical Design， 2006， 128： 90-97.

[6]

潘毅，许妍妍，樊智敏.

双渐开线齿轮柔性多体动力学分析

［J］.机电工程，2022，39（8）：1088-1095. doi：10.3969/j.issn.1001-4551.2022.08.009

[本文引用: 1]

PAN

， XU

Y Y

， FAN

Z M

Flexible multi-body dynamics analysis of double involute gear

［J］. Journal of Mechanical & Electrical Engineering， 2022， 39（8）： 1088-1095.

DOI:10.3969/j.issn.1001-4551.2022.08.009 [本文引用: 1]

[7]

邹帅东，王光建.

双齿轮偏心的传动误差计算与研究

［J］.电子科技大学学报，2017，46（6）：955-960. doi：10.3969/j.issn.1001-0548.2017.06.027

[本文引用: 2]

ZOU

S D

， WANG

G J

Research on transmission error of dual-eccentric gears

［J］. Journal of University of Electronic Science and Technology of China， 2017， 46（6）： 955-960.

DOI:10.3969/j.issn.1001-0548.2017.06.027 [本文引用: 2]

[8]

DONG

， ZHANG

， BAI

， et al.

Modeling， analysis and testing of load distribution for planetary gear trains with 3D carrier pinhole position errors

［J］. International Journal of Precision Engineering and Manufacturing， 2019， 20： 1381-1394.

[9]

耿婷，韦玉庭，邓爱平，等.

行星线齿变速器基于装配误差的传动精度分析

［J］.机械传动，2021，45（3）：104-110.

GENG

， WEI

Y T

， DENG

A P

， et al.

Transmission precision analysis of planetary line gear transmission based on assembly error

［J］. Journal of Mechanical Transmission， 2021， 45（3）： 104-110.

[10]

汪训浪，范元勋.

齿轮传动误差主要影响因素分析与计算

［J］.组合机床与自动化加工技术，2018（2）：43-45.

WANG

X L

， FAN

Y X

Analysis of main influencing factors and calculation on gear transmission error

［J］. Modular Machine Tool & Automatic Manufacturing Technique， 2018（2）： 43-45.

[11]

林超，魏沛堂，朱才朝.

平行轴变齿厚斜齿轮传动接触分析

［J］.重庆大学学报，2012，35（12）：1-6. doi：10.11835/j.issn.1000-582X.2012.12.002

LIN

， WEI

P T

， ZHU

C Z

Tooth contact analysis of helical beveloid gear with parallel axis

［J］. Journal of Chongqing University， 2012， 35（12）： 1-6.

DOI:10.11835/j.issn.1000-582X.2012.12.002

[12]

文奇

具有误差特征的齿轮副空间解析理论及其力学特性研究

［D］.广州：华南理工大学，2019：22-33.

[本文引用: 1]

WEN

Research on space analytical theory and mechanical properties of gear pairs with error characteristics

［D］. Guangzhou： South China University of Technology， 2019： 22-33.

[本文引用: 1]

[13]

DONG

， TANG

， HU

， et al.

A semi-analytical method of time-varying mesh stiffness in concentric face gear split-torque transmission system

［J］. Journal of Mechanical Science and Technology， 2020， 34： 589-602.

[本文引用: 1]

[14]

梁世文

定轴圆柱齿轮传动系统的弹性误差建模与传动精度分析

［D］.大连：大连理工大学，2018：9-12.

[本文引用: 1]

LIANG

S W

Modeling and transmission accuracy analysis of fixed-axis cylindrical gear drive system with elasticity and errors

［D］. Dalian： Dalian University of Technology， 2018： 9-12.

[本文引用: 1]

[15]

闻邦椿

.机械设计手册.

第2卷：机械零部件设计（连接、紧固与传动）

［M］.5版.北京：机械工业出版社，2010：1202-1222.

[本文引用: 1]

WEN

B C

Machinery design manual

Volume 2： mechanical component design （connections， fasteners， and transmission）［M］. 5th ed. Beijing： China Machine Press， 2010： 1202-1222.

[本文引用: 1]

[16]

步鹏

斜齿圆柱齿轮传动的弹性误差建模及其精度分析

［D］.大连：大连理工大学，2019：10-14.

[本文引用: 1]

Modeling and transmission accuracy analysis of helical cylindrical gear drive with elasticity and errors

［D］. Dalian： Dalian University of Technology， 2019： 10-14.

[本文引用: 1]

[17]

GREENWOOD

， PUTIGNANO

， CIAVARELLA

A Greenwood and Williamson theory for line contact

［J］. Wear， 2011， 270（3/4）： 332-334.

[本文引用: 1]

[18]

常乐浩

平行轴齿轮传动系统动力学通用建模方法与动态激励影响规律研究

［D］.西安：西北工业大学，2014：19-28.

[本文引用: 1]

CHANG

L H

A generalized dynamic model for parallel shaft gear transmissions and the influences of dynamic excitations

［D］. Xi'an： Northwestern Polytechnical University， 2014： 19-28.

[本文引用: 1]

[19]

ZHANG

， DONG

， WANG

， et al.

A new effective mesh stiffness calculation method with accurate contact deformation model for spur and helical gear pairs

［J］. Mechanism and Machine Theory， 2022， 171： 104762.

[本文引用: 1]

[20]

KONG

， HU

， TANG

， et al.

Effects of gear flexibility on the dynamic characteristics of spur and helical gear system

［J］. Mechanical Systems and Signal Processing， 2023， 184： 109691.

[本文引用: 1]

[21]

李伟霞，张涛.

基于Transmission3D的轮齿啮合刚度求解方法

［J］.机械传动，2021，45（8）：105-109.

[本文引用: 1]

W X

， ZHANG

Solving method for the tooth mesh stiffness based on Transmission3D

［J］. Journal of Mechanical Transmission， 2021， 45（8）： 105-109.

[本文引用: 1]

Topology optimization and analysis of static transmission error in lightweight gears

2017

... 目前，国内外学者针对齿轮传动误差的建模方法做了大量研究，常用的建模方法有解析法、有限元法及半解析法.例如：文献[1-6]采用有限元法对齿轮的传动误差进行了分析，该方法的求解精度较高，但由于建模复杂且网格划分密集，求解计算时间较长.为了提高求解效率，文献[7-12]采用解析法建立了齿轮传动误差的计算模型，极大地缩短了求解时间，但对齿轮的结构弹性问题考虑不足，导致求解精度受限.为了在缩短求解时间的同时保证准确性，现阶段很多学者开始研究半解析方法在齿轮传动精度分析中的应用，如Dong等^[13]采用半解析法建立了齿轮的传动模型，有效地提高了齿轮接触性能的求解效率.此外，在传动误差影响因素分析方面，Korta等^[1]在有限元建模的基础上探究了不同质量的材料对齿轮静态传动误差曲线的影响；邹帅东等^[7]在解析建模的基础上考虑了齿轮偏心的因素，研究了不同偏心程度对齿轮传动误差的影响；刘永平等^[3]分析了负载、转速及轴线误差等因素对齿轮传动误差的影响. ...

... [1]在有限元建模的基础上探究了不同质量的材料对齿轮静态传动误差曲线的影响；邹帅东等^[7]在解析建模的基础上考虑了齿轮偏心的因素，研究了不同偏心程度对齿轮传动误差的影响；刘永平等^[3]分析了负载、转速及轴线误差等因素对齿轮传动误差的影响. ...

基于有限元法的直齿轮接触强度分析与优化

2019

基于有限元法的直齿轮接触强度分析与优化

2019

渐开线变齿厚直齿轮传动误差研究

2023

渐开线变齿厚直齿轮传动误差研究

2023

基于Workbench的齿轮稳态温度场和传动误差分析

2023

基于Workbench的齿轮稳态温度场和传动误差分析

2023

Error analysis on finite element modeling of involute spur gears

2006

双渐开线齿轮柔性多体动力学分析

2022

双渐开线齿轮柔性多体动力学分析

2022

双齿轮偏心的传动误差计算与研究

2017

... [7]在解析建模的基础上考虑了齿轮偏心的因素，研究了不同偏心程度对齿轮传动误差的影响；刘永平等^[3]分析了负载、转速及轴线误差等因素对齿轮传动误差的影响. ...

双齿轮偏心的传动误差计算与研究

2017

Modeling， analysis and testing of load distribution for planetary gear trains with 3D carrier pinhole position errors

2019

行星线齿变速器基于装配误差的传动精度分析

2021

行星线齿变速器基于装配误差的传动精度分析

2021

齿轮传动误差主要影响因素分析与计算

2018

齿轮传动误差主要影响因素分析与计算

2018

平行轴变齿厚斜齿轮传动接触分析

2012

平行轴变齿厚斜齿轮传动接触分析

2012

具有误差特征的齿轮副空间解析理论及其力学特性研究

2019

具有误差特征的齿轮副空间解析理论及其力学特性研究

2019

A semi-analytical method of time-varying mesh stiffness in concentric face gear split-torque transmission system

2020

定轴圆柱齿轮传动系统的弹性误差建模与传动精度分析

2018

... 根据渐开线齿面的生成原理，当一条曲线在空间中沿螺旋线方向匀速拉伸变换时，所形成的表面即渐开线圆柱齿轮的齿面.如图1所示，以渐开线斜齿圆柱齿轮（后文简称斜齿轮）为例，推导其渐开线螺旋面方程^[14]，表示为： ...

定轴圆柱齿轮传动系统的弹性误差建模与传动精度分析

2018

第2卷：机械零部件设计（连接、紧固与传动）

... 渐开线圆柱齿轮的齿廓误差具体值可通过查表确定^[15].将渐开线圆柱齿轮的齿廓曲线离散成点，并计算得到齿廓上各点与齿轮中心的距离

r

.以齿廓各点与齿轮中心的距离

r

为横坐标，齿廓误差为纵坐标，构建考虑齿廓误差的齿廓曲线，如图2所示. ...

第2卷：机械零部件设计（连接、紧固与传动）

... 渐开线圆柱齿轮的齿廓误差具体值可通过查表确定^[15].将渐开线圆柱齿轮的齿廓曲线离散成点，并计算得到齿廓上各点与齿轮中心的距离

r

.以齿廓各点与齿轮中心的距离

r

为横坐标，齿廓误差为纵坐标，构建考虑齿廓误差的齿廓曲线，如图2所示. ...

斜齿圆柱齿轮传动的弹性误差建模及其精度分析

2019

... 齿轮在传动过程中的接触可等效为弹性体的接触^[16]，则主、从动轮接触线上每一个点的变形协调方程可表示为： ...

斜齿圆柱齿轮传动的弹性误差建模及其精度分析

2019

... 齿轮在传动过程中的接触可等效为弹性体的接触^[16]，则主、从动轮接触线上每一个点的变形协调方程可表示为： ...

A Greenwood and Williamson theory for line contact

2011

... 渐开线圆柱齿轮在某一位置处的接触问题可看作2个圆柱体的接触问题.在接触过程中，主、从动轮在接触点处的法向曲率半径为圆柱体的半径.根据统计接触理论^[17]，在力作用下，接触点处的接触变形可表示为： ...

平行轴齿轮传动系统动力学通用建模方法与动态激励影响规律研究

2014

... 由于主、从动轮的参数相同，只需在ANSYS软件中建立主动轮的完整和局部有限元模型，即可获取主、从动轮的弯曲-剪切变形系数^[18].以斜齿轮为例，其整体有限元模型采用五齿模型，如图3(a)所示.对齿轮中心孔处施加全约束，以获取整体柔度矩阵；轮体和齿体的弹性模量相同.斜齿轮局部有限元模型如图3(b)所示，对非接触齿面施加全约束，齿体弹性模量为齿面弹性模量的1 000倍，以确保接触齿面仅包含局部接触变形.主、从动轮接触齿面上的节点坐标和单元完全一致. ...

平行轴齿轮传动系统动力学通用建模方法与动态激励影响规律研究

2014

A new effective mesh stiffness calculation method with accurate contact deformation model for spur and helical gear pairs

2022

... 完成齿轮完整有限元模型和局部有限元模型的构建后，采用ANSYS软件中自带的子结构法提取柔度系数矩阵^[19].但采用子结构法时会涉及外部节点和内部节点，由于本文不考虑内部节点的自由度，则可使用凝聚的方法忽略内部节点.将各子结构组装成整体时仅包含外部节点，其方程维数比原模型的方程维数小得多. ...

Effects of gear flexibility on the dynamic characteristics of spur and helical gear system

2023

... 采用形函数插值运算方法对所构建的柔度矩阵进行运算，获得齿面接触点的弯曲-剪切柔度矩阵.对于任意网格节点，在确定齿面接触点与网格节点的位置关系后，通过已知的柔度系数插值获得接触点的柔度系数.不同齿面上接触点的柔度矩阵可通过齿面接触点与完整有限元模型的网格节点位置关系求得.最后按照接触点顺序，重新组装成柔度矩阵^[20]. ...

基于Transmission3D的轮齿啮合刚度求解方法

2021

... 基于上述建立的渐开线圆柱齿轮半解析接触模型，分析弹性误差对其传动精度的影响^[21]，并构建齿轮传动误差的计算流程，如图4所示. ...

基于Transmission3D的轮齿啮合刚度求解方法

2021

... 基于上述建立的渐开线圆柱齿轮半解析接触模型，分析弹性误差对其传动精度的影响^[21]，并构建齿轮传动误差的计算流程，如图4所示. ...

〈

〉