滚动轴承径向游隙可靠性设计

doi:10.3785/j.issn.1006-754X.2023.03.164

滚动轴承径向游隙可靠性设计

李军星^,^,¹^,², 宁世杰¹, 邱明¹

1.河南科技大学机电工程学院，河南洛阳 471003

2.高端轴承河南省协同创新中心，河南洛阳 471003

Reliability design of radial clearance of rolling bearing

LI Junxing^,^,¹^,², NING Shijie¹, QIU Ming¹

1.School of Mechatronical Engineering, Henan University of Science and Technology, Luoyang 471003, China

2.Henan Provincial Collaborative Innovation Center for High-end Bearings, Luoyang 471003, China

收稿日期: 2023-05-12 修回日期: 2023-06-12

基金资助:

国家自然科学基金资助项目.  52005159
河南省高校青年骨干教师培养计划资助项目.  2021GGJS048
河南省青年人才托举工程项目.  2023HYTP050
河南省科技研发计划联合基金资助项目.  225200810073.  232103810043

Received: 2023-05-12 Revised: 2023-06-12

作者简介 About authors

李军星（1990—），男，河南驻马店人，副教授，博士，从事可靠性设计与评估研究，E-mail:lijun-xing2008@163.com,https://orcid.org/0000-0001-9417-5343 , E-mail：lijun-xing2008@163.com

摘要

游隙是评价滚动轴承精度和质量的关键因素之一。科学合理地选择游隙有利于延长轴承寿命，而传统基于工程经验的游隙确定方法往往缺乏理论依据和可靠性。由此，提出了基于应力-强度干涉模型的滚动轴承径向游隙可靠性设计方法。首先，将轴承原始径向游隙和失效径向游隙看作随机变量，构建轴承二维随机干涉模型；其次，针对工程中常用的服从正态分布、对数正态分布、指数分布和Weibull分布的轴承原始径向游隙和失效径向游隙，推导了求解滚动轴承可靠性的解析式以及在给定可靠度下轴承径向游隙置信区间；最后，将求得的16004深沟球轴承径向游隙置信区间与现行国家标准对比，结果验证了所提出方法的有效性和适用性。研究表明：采用所提出方法设计的滚动轴承径向游隙置信区间符合国家标准，且更加合理可靠；可以设计出任意可靠度下的轴承径向游隙置信区间，为滚动轴承的设计和优化提供了理论支撑。

关键词： 滚动轴承 ; 径向游隙设计 ; 应力-强度干涉模型 ; 正态分布 ; Weibull分布

Abstract

Clearance is one of the key factors in evaluating the accuracy and quality of rolling bearings. Scientific and reasonable selection of clearance is conducive to increasing bearing life, while traditional methods for determining clearance based on engineering experience often lack theoretical basis and reliability. Therefore, a reliability design method for radial clearance of rolling bearing based on stress-strength interference model was proposed. Firstly, the original radial clearance and failed radial clearance of the bearing were regarded as random variables, and a two-dimensional random interference model of the bearing was constructed; secondly, according to the original radial clearance and failed radial clearance of bearing with normal, lognormal, exponential and Weibull distributions commonly used in engineering, the analytical formula for solving the reliability of rolling bearing and the confidence interval of bearing radial clearance under given reliability were derived; finally, the obtained confidence interval of 16004 deep groove ball bearing radial clearance was compared with that of the current national standard, and the effectiveness and applicability of the proposed method were verified. The results showed that the confidence interval of radial clearance of rolling bearing designed by the proposed method met the national standard and was more reasonable and reliable. The confidence interval of radial clearance under any reliability could be designed, which provided theoretical support for the design and optimization of rolling bearings.

Keywords： rolling bearing ; radial clearance design ; stress-intensity interference model ; normal distribution ; Weibull distribution

PDF (1178KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李军星, 宁世杰, 邱明. 滚动轴承径向游隙可靠性设计. 工程设计学报[J], 2023, 30(6): 738-745 doi:10.3785/j.issn.1006-754X.2023.03.164

LI Junxing, NING Shijie, QIU Ming. Reliability design of radial clearance of rolling bearing. Chinese Journal of Engineering Design[J], 2023, 30(6): 738-745 doi:10.3785/j.issn.1006-754X.2023.03.164

滚动轴承是一种精密机械元件，在机械行业应用广泛。其性能和可靠性会直接影响机械设备的工作性能、寿命及运行安全。影响滚动轴承寿命和可靠性的一个关键因素是其径向游隙：若径向游隙过小，会使轴承的摩擦力矩增大，进而产生摩擦热，易引发轴承发热而损坏；若径向游隙过大，则会造成设备在运行过程中振动较大，从而导致轴承的使用寿命缩短。以往大多是根据轴承径向游隙公差带或者工程经验来确定轴承径向游隙的合理区间，导致误差非常大。因此，滚动轴承径向游隙的可靠性设计一直是机械设计领域研究的重点和难点。

已有很多学者开展了滚动轴承径向游隙优化设计研究。如：李皓川等^[1]在极变换的基础上提出了一种选点的方法，结合稀疏响应面，对滚动轴承工作游隙极限状态函数进行拟合，并基于有限元方法计算出工作游隙；郑牧等^[2]对轴承安装后的径向游隙减小量进行了分析和计算，推导了轴承的原始径向游隙；邱明等^[3-4]分析了轴承径向游隙的变化对轴承刚度及疲劳寿命的影响，指出径向游隙是影响轴承力学性能的关键指标；沈宇涵等^[5]分析了圆柱滚子轴承径向游隙对径向刚度的影响；胡北等^[6]考虑了轴承温升、径向载荷等因素的影响，分析并计算了轴承径向游隙。然而，以上研究大多是通过修正经验公式或仿真分析来确定滚动轴承径向游隙的合理范围，缺乏对滚动轴承整个部件可靠性的考虑。

针对产品的可靠性设计，应力-强度干涉模型在工程实际中已得到广泛应用。如：Zhang等^[7]研究了应力分布与强度分布之间的关系，引入条件可靠度的概念，建立了在单应力和多应力作用下的系统可靠性模型；Ali等^[8]讨论了形状参数不同时应力和强度分别服从广义Weibull分布以及对数正态分布时的应力-强度干涉模型，并对系统可靠性进行了评估；Wang等^[9]建立了在应力和强度服从一定分布时可靠度的极大似然估计模型，并确定了可靠度置信区间；杨晓蔚^[10]运用应力-强度干涉理论，在轴承寿命分布为Weibull分布的前提下，建立了评估可靠寿命的Weibull失效概率密度函数表达式和可靠度函数表达式；张先超等^[11]推导了基于应力-强度干涉理论的可靠度计算公式，并提出了当应力和强度分别同时服从单参数和双参数指数分布时的可靠度估计方法；伊枭剑等^[12]提出了基于应力-强度干涉模型的可靠性设计方法，将火工品感度参数和外界刺激参数引入应力-强度干涉模型，来评估火工品的可靠性。

本文提出了一种基于应力-强度干涉模型的滚动轴承可靠性设计方法。首先，将轴承原始径向游隙和失效径向游隙看作随机变量，构建轴承二维随机干涉模型；其次，针对工程中常用的轴承原始径向游隙和失效径向游隙分布模型，推导了滚动轴承可靠性评估解析式和径向游隙置信区间；最后，结合工程实例及现行国家标准，验证本文方法的有效性和适用性。

1 滚动轴承径向游隙可靠性设计模型

研究发现，滚动轴承游隙与轴承的多种失效模式密切相关，是影响轴承可靠性的重要因素^[13]。根据大量试验可知，由于在生产过程中加工、装配等因素的影响，轴承原始径向游隙呈随机分布，而造成轴承失效的失效径向游隙也因工作环境的影响而呈随机分布。因此，本文引入应力-强度干涉模型。此处应力和强度的概念是广义的，应力指影响零件性能和功能的各种环境因素，强度指零件抵抗应力的因素。轴承的原始径向游隙会影响轴承所受应力的分布，而失效径向游隙是轴承抵抗应力所导致的，因而，将原始径向游隙 $X$ 看作应力因素，失效径向游隙 $Y$ 看作强度因素，则轴承的可靠度 $R$ 可以定义为^[14]：

R = P (Y > X) = \int_{- \infty}^{+ \infty} f (x) [\int_{x}^{+ \infty} g (y) d y] d x

式中： $P$ 为概率值， $f (x)$ 为应力的概率密度函数， $g (y)$ 为强度的概率密度函数。

在给定轴承径向游隙X时，可通过式(1)对轴承进行可靠性评估。

此外，由于工程中更关注轴承原始径向游隙的设计，则根据式(1)，可以设计出在给定可靠度 $R$ 下轴承原始径向游隙 $X_{R}$ ：

X_{R} = R^{- 1} (X | Y)

同时，考虑到轴承原始径向游隙的估计精确程度取决于样本容量的大小，仅用点估计是不够的，因此给出轴承原始径向游隙的置信区间：

[X_{R l}, X_{R u}] = [R_{l}^{- 1} (X | Y), R_{u}^{- 1} (X | Y)]

式中：下标l和u分别表示各参数值的下限与上限。

由此，可以对轴承的原始径向游隙进行设计,使得该轴承的可靠性达到要求。

2 滚动轴承径向游隙可靠性设计方法

轴承原始径向游隙和失效径向游隙都是服从一定分布的随机变量，可以通过试验数据拟合得到，一般服从正态分布和对数正态分布的较多。本文分别讨论轴承原始径向游隙和失效径向游隙同时服从正态分布、对数正态分布、指数分布和Weibull分布（分别表示为正态分布-正态分布、对数正态分布-对数正态分布、指数分布-指数分布、Weibull分布-Weibull分布）时滚动轴承可靠性设计方法。

2.1　正态分布-正态分布

假设原始径向游隙 $X$ 服从正态分布 $N (μ_{x}, σ_{x}^{2})$ ，失效径向游隙 $Y$ 服从正态分布 $N (μ_{y}, σ_{y}^{2})$ ，其中 $μ_{x}$ 、 $σ_{x}$ 分别为 $X$ 的均值和标准差， $μ_{y}$ 、 $σ_{y}^{}$ 分别为Y的均值和标准差，则 $X$ 、 $Y$ 的概率密度函数分别为：

f (x) = \frac{1}{σ_{x} \sqrt[]{2 π}} e^{- \frac{(x - μ_{x})^{2}}{2 {σ_{x}}^{2}}}

(4)

g (y) = \frac{1}{σ_{y} \sqrt[]{2 π}} e^{- \frac{(y - μ_{y})^{2}}{2 {σ_{y}}^{2}}}

(5)

令 $Z = Y - X$ ，根据正态分布的加法定理可知， $Z$ 服从正态分布 $N (μ_{z}, σ_{z}^{2})$ ，且：

\{\begin{array}{l} μ_{z} = μ_{y} - μ_{x} \\ σ_{z} = \sqrt[]{σ_{y}^{2} + σ_{x}^{2}} \end{array}

则式(1)可变换为：

\begin{array}{l} R = P (Z > 0) = \int_{0}^{+ \infty} \frac{1}{σ_{z} \sqrt[]{2 π}} e^{- \frac{(z - μ_{z})^{2}}{2 {σ_{z}}^{2}}} d z, - \infty < z < + \infty \end{array}

(6)

令 $u = (z - μ_{z}) / σ_{z}$ ，得到原始径向游隙和失效径向游隙均服从正态分布时轴承的可靠度为：

R = \int_{- \frac{μ_{z}}{σ_{z}}}^{+ \infty} \frac{1}{\sqrt[]{2 π}} e^{- \frac{u^{2}}{2}} d u = Φ (\frac{μ_{z}}{σ_{z}}) = Φ (\frac{μ_{y} - μ_{x}}{\sqrt[]{σ_{y}^{2} + σ_{x}^{2}}})

(7)

式中： $Φ (•)$ 为标准正态分布函数。

根据式(1)可以得到在给定可靠度 $R$ 下轴承的可靠度指标为：

Φ^{- 1} (R) = \frac{μ_{y} - μ_{x}}{\sqrt[]{σ_{y}^{2} + σ_{x}^{2}}}

(8)

因此，当轴承可靠度为 $R$ 时可以设计出轴承原始径向游隙：

μ_{x} = μ_{y} - Φ^{- 1} (R) \sqrt[]{σ_{y}^{2} + σ_{x}^{2}}

(9)

在实际中，均值和方差是通过样本统计分析获得的，其精度由样本容量决定，且仅用点估计是不够的，因此进一步设计轴承原始径向游隙的置信区间。

由于 $μ_{x}$ 、 $μ_{y}$ 、 $σ_{x}$ 、 $σ_{y}$ 也是随机变量，根据随机变量参数区间估计理论和区间数扩张原理，考虑了随机变量参数估计区间后，式(8)可改写为^[15]：

[Z_{R l}, Z_{R u}] = [\frac{\underset{̲}{(μ_{y} - μ_{x})}}{\bar{\sqrt[]{σ_{x}^{2} + σ_{y}^{2}}}}, \frac{\bar{(μ_{y} - μ_{x})}}{\underset{̲}{\sqrt[]{σ_{x}^{2} + σ_{y}^{2}}}}]

(10)

式中： $\bar{(μ_{y} - μ_{x})}$ 、 $\underset{̲}{(μ_{y} - μ_{x})}$ 、 $\bar{\sqrt[]{σ_{x}^{2} + σ_{y}^{2}}}$ 、 $\underset{̲}{\sqrt[]{σ_{x}^{2} + σ_{y}^{2}}}$ 分别为 $(μ_{y} - μ_{x})$ 和 $\sqrt[]{σ_{x}^{2} + σ_{y}^{2}}$ 在给定置信度下的上限和下限。

进而可靠度 $R$ 的区间为：

[R_{l}, R_{u}] = [Φ (Z_{R l}), Φ (Z_{R u})]

(11)

由数理统计理论可知：

\frac{({\hat{μ}}_{y} - {\hat{μ}}_{x}) - (μ_{y} - μ_{x})}{\sqrt[]{\frac{σ_{x}^{2}}{n_{x}} + \frac{σ_{y}^{2}}{n_{y}}}} \sim N (0, 1)

(12)

式中： ${\hat{μ}}_{x}$ 、 $n_{x}$ 分别为 $X$ 的样本均值和容量， ${\hat{μ}}_{y}$ 、 $n_{y}$ 分别为Y的样本均值和容量。

则在置信度为 $1 - α$ 下， $μ_{x}$ 的下限和上限为：

\{\begin{array}{l} μ_{x l} = μ_{y} + {\hat{μ}}_{x} - {\hat{μ}}_{y} - Z_{α / 2} \sqrt[]{\frac{σ_{x}^{2}}{n_{x}} + \frac{σ_{y}^{2}}{n_{y}}} \\ μ_{x u} = μ_{y} + {\hat{μ}}_{x} - {\hat{μ}}_{y} + Z_{α / 2} \sqrt[]{\frac{σ_{x}^{2}}{n_{x}} + \frac{σ_{y}^{2}}{n_{y}}} \end{array}

(13)

式中： $Z_{α / 2}$ 为标准正态分布的百分位点。

将式(13)代入式(8)，可得：

\{\begin{array}{l} Z_{R l} = \frac{{\hat{μ}}_{y} - {\hat{μ}}_{x} - Z_{α / 2} \sqrt[]{\frac{σ_{x}^{2}}{n_{x}} + \frac{σ_{y}^{2}}{n_{y}}}}{\sqrt[]{σ_{x}^{2} + σ_{y}^{2}}} \\ Z_{R u} = \frac{{\hat{μ}}_{y} - {\hat{μ}}_{x} + Z_{α / 2} \sqrt[]{\frac{σ_{x}^{2}}{n_{x}} + \frac{σ_{y}^{2}}{n_{y}}}}{\sqrt[]{σ_{x}^{2} + σ_{y}^{2}}} \end{array}

(14)

当样本数量 $n_{x}$ 、 $n_{y}$ 足够大时，可近似认为 $σ_{x} = S_{x}$ , $σ_{y} = S_{y}$ ，其中 $S_{x}$ 、 $S_{y}$ 分别为 $X$ 、 $Y$ 的样本标准差。将 $S_{x}$ 、 $S_{y}$ 代入式(13)，可得轴承可靠度指标 $Z_{R}$ 的区间。

当样本数量 $n_{x}$ 、 $n_{y}$ 不是很大时， $(μ_{y} - μ_{x})$ 的下限和上限为：

\{\begin{array}{l} \underset{̲}{(μ_{y} - μ_{x})} = {\hat{μ}}_{y} - {\hat{μ}}_{x} - t_{α^{'} / 2} (v) \sqrt[]{\frac{S_{x}^{2}}{n_{x}} + \frac{S_{y}^{2}}{n_{y}}} \\ \bar{(μ_{y} - μ_{x})} = {\hat{μ}}_{y} - {\hat{μ}}_{x} + t_{α^{'} / 2} (v) \sqrt[]{\frac{S_{x}^{2}}{n_{x}} + \frac{S_{y}^{2}}{n_{y}}} \end{array}

(15)

式中：v为自由度。

v = \frac{{(\frac{S_{x}^{2}}{n_{x}} + \frac{S_{y}^{2}}{n_{y}})}^{2}}{{(\frac{S_{y}^{2}}{n_{y}})}^{2} / (n_{y} - 1) + {(\frac{S_{x}^{2}}{n_{x}})}^{2} / (n_{x} - 1)}

(16)

取 $v$ 为整数，则风险系数α′^[15]为：

α^{'} = \sqrt[]{\frac{8 α}{2 + π}}

(17)

根据概率论与数理统计，可得：

\frac{(n - 1) S^{2}}{σ^{2}} \sim χ^{2} (n - 1)

(18)

进而可得：

\{\begin{array}{l} \underset{̲}{\sqrt[]{σ_{x}^{2} + σ_{y}^{2}}} = \sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{α^{'} / 2}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{α^{'} / 2}^{2} (n_{x} - 1)}} \\ \bar{\sqrt[]{σ_{x}^{2} + σ_{y}^{2}}} = \sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{x} - 1)}} \end{array}

(19)

将式(15)和(19)代入式(8)^[15]，可得 $Z_{R}$ 的下限和上限为：

\{\begin{array}{l} Z_{R l} = \frac{{\hat{μ}}_{y} - {\hat{μ}}_{x} - t_{α^{'} / 2} (v) \sqrt[]{\frac{S_{x}^{2}}{n_{x}} + \frac{S_{y}^{2}}{n_{y}}}}{\sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{x} - 1)}}} \\ Z_{R u} = \frac{{\hat{μ}}_{y} - {\hat{μ}}_{x} + t_{α^{'} / 2} (v) \sqrt[]{\frac{S_{x}^{2}}{n_{x}} + \frac{S_{y}^{2}}{n_{y}}}}{\sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{α^{'} / 2}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{α^{'} / 2}^{2} (n_{x} - 1)}}} \end{array}

(20)

由式(9)、(11)、(20)可得当可靠度为 $R$ 时 $μ_{x}$ 的下限和上限为：

\{\begin{array}{l} μ_{x l} = {\hat{μ}}_{y} - [{\hat{μ}}_{y} - {\hat{μ}}_{x} + t_{α^{'} / 2} (v) \sqrt[]{\frac{S_{x}^{2}}{n_{x}} + \frac{S_{y}^{2}}{n_{y}}}] \times \\ \frac{\sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{x} - 1)}}}{\sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{α^{'} / 2}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{α^{'} / 2}^{2} (n_{x} - 1)}}} \\ μ_{x u} = {\hat{μ}}_{y} - [{\hat{μ}}_{y} - {\hat{μ}}_{x} - t_{α^{'} / 2} (v) \sqrt[]{\frac{S_{x}^{2}}{n_{x}} + \frac{S_{y}^{2}}{n_{y}}}] \times \\ \frac{\sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{α^{'} / 2}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{α^{'} / 2}^{2} (n_{x} - 1)}}}{\sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{x} - 1)}}} \end{array}

(21)

2.2　对数正态分布-对数正态分布

假设原始径向游隙 $X$ 服从对数正态分布 $l n (μ_{x}, σ_{x}^{2})$ ，失效径向游隙 $Y$ 服从对数正态分布 $l n (μ_{y}, σ_{y}^{2})$ ，其中 $μ_{x}$ 、 $σ_{x}$ 分别为 $X$ 的对数均值和对数标准差， $μ_{y}$ 、 $σ_{y}$ 分别为Y的对数均值和对数标准差，则 $X$ 、 $Y$ 的概率密度函数分别为：

f (x, μ_{x}, σ_{x}) = \{\begin{matrix} \frac{1}{x \sqrt[]{2 π} σ_{x}} e^{- \frac{l n x - μ_{x}}{2 {σ_{x}}^{2}}}, x > 0 \\ 0, x \leq 0 \end{matrix}

(22)

g (y, μ_{y}, σ_{y}) = \{\begin{matrix} \frac{1}{y \sqrt[]{2 π} σ_{y}} e^{- \frac{l n y - μ_{y}}{2 {σ_{y}}^{2}}}, y > 0 \\ 0, y \leq 0 \end{matrix}

(23)

根据式(1)可得：

R = P (Y > X) = P (l n Y > l n X) = P (Z > 0)

(24)

式中： $Z = l n Y - l n X$ 。

根据正态分布的加法定理可知， $Z$ 服从对数正态分布 $N (σ_{z}, σ_{z}^{2})$ ，且：

\{\begin{array}{l} μ_{z} = μ_{y} - μ_{x} \\ σ_{z} = \sqrt[]{σ_{y}^{2} + σ_{x}^{2}} \end{array}

根据上节内容可知，可根据标准正态分位数 $Z_{R} = (μ_{y} - μ_{x}) / \sqrt[]{σ_{y}^{2} + σ_{x}^{2}}$ 在标准正态分布表中查得可靠度 $R$ 的数值。

由于 $X$ 和 $Y$ 均服从对数正态分布，其对数形式服从正态分布，推导过程与2.1节一致，这里不再赘述，只给出最终的原始径向游隙估计区间。

由(21)式易知，当可靠度为 $R$ 时 $μ_{x}$ 的下限和上限为：

\{\begin{array}{l} μ_{x l} = e x p \{{\hat{μ}}_{y} - [{\hat{μ}}_{y} - {\hat{μ}}_{x} + t_{α^{'} / 2} (v) \sqrt[]{\frac{S_{x}^{2}}{n_{x}} + \frac{S_{y}^{2}}{n_{y}}}] \times \\ \frac{\sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{x} - 1)}}}{\sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{α^{'} / 2}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{α^{'} / 2}^{2} (n_{x} - 1)}}} \overset{}{\underset{}{\overset{}{\underset{}{\overset{}{\underset{}{}}}}}}\} \\ μ_{x u} = e x p \{{\hat{μ}}_{y} - [{\hat{μ}}_{y} - {\hat{μ}}_{x} - t_{α^{'} / 2} (v) \sqrt[]{\frac{S_{x}^{2}}{n_{x}} + \frac{S_{y}^{2}}{n_{y}}}] \times \\ \frac{\sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{α^{'} / 2}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{α^{'} / 2}^{2} (n_{x} - 1)}}}{\sqrt[]{\frac{(n_{y} - 1) S_{y}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{y} - 1)} + \frac{(n_{x} - 1) S_{x}^{2}}{χ_{(1 - α^{'} / 2)}^{2} (n_{x} - 1)}}} \overset{}{\underset{}{\overset{}{\underset{}{\overset{}{\underset{}{}}}}}}\} \end{array}

(25)

2.3　指数分布-指数分布

假设原始径向游隙 $X$ 服从指数分布 $E (μ_{x})$ ，失效径向游隙 $Y$ 服从指数分布 $E (μ_{y})$ ，其中 $μ_{x}$ 、 $μ_{y}$ 均为服从指数分布的一个参数，则 $X$ 、 $Y$ 的概率密度函数分别为：

f (x) = \{\begin{matrix} μ_{x} e^{- μ_{x} x}, x > 0 \\ 0, x \leq 0 \end{matrix}

(26)

g (y) = \{\begin{matrix} μ_{y} e^{- μ_{y} y}, y > 0 \\ 0, y \leq 0 \end{matrix}

(27)

在没有给出 $μ_{x}$ 和 $μ_{y}$ 确切数值的情况下，需要根据样本数据对 $R$ 进行估计，这里采取极大似然估计法。根据极大似然估计的不变性^[16]，可以得到 $μ_{x}$ 、 $μ_{y}$ 的估计值 ${\hat{μ}}_{x}$ 、 ${\hat{μ}}_{y}$ ，则可靠度 $R$ 的估计值 $\hat{R}$ 为：

\hat{R} = R ({\hat{μ}}_{x}, {\hat{μ}}_{y})

(28)

根据式(1)可得^[10]：

\begin{array}{l} R = \int_{- \infty}^{+ \infty} [1 - \int_{- \infty}^{x} g (y) d y] f (x) d x = \int_{- \infty}^{+ \infty} e^{- μ_{y} x} μ_{x} e^{- μ_{x} x} d x = \\ \frac{μ_{x}}{μ_{x} + μ_{y}} \end{array}

(29)

则：

\hat{R} = \frac{{\hat{μ}}_{x}}{{\hat{μ}}_{x} + {\hat{μ}}_{y}}

(30)

设 $x_{1}, x_{1}, \dots, x_{m}$ 和 $y_{1}, y_{2}, \dots, y_{n}$ 分别来自样本总体 $X$ 和 $Y$ ，则 $μ_{x}$ 和 $μ_{y}$ 的函数分别为：

L (μ_{x}) = \prod_{i = 1}^{m} f (x_{i})

(31)

L (μ_{y}) = \prod_{j = 1}^{n} g (y_{j})

(32)

由文献[17]可得 $μ_{x}$ 和 $μ_{y}$ 的极大似然估计分别为：

{\hat{μ}}_{x} = 1 / \bar{x}

(33)

{\hat{μ}}_{y} = 1 / \bar{y}

(34)

式中： $\bar{x}$ 和 $\bar{y}$ 分别为样本 $X$ 和 $Y$ 的平均值。

则：

\hat{R} = \frac{{\hat{μ}}_{x}}{{\hat{μ}}_{x} + {\hat{μ}}_{y}} = \frac{1 / \bar{x}}{1 / \bar{x} + 1 / \bar{y}} = \frac{1}{1 + \bar{x} / \bar{y}}

(35)

对式(35)作变换，可以得到原始径向游隙和失效径向游隙均服从指数分布时轴承的可靠性设计方法，表示为：

μ_{x} = \frac{μ_{y}}{1 / R - 1}

(36)

而对于服从指数分布参数的区间估计，可参考文献[18]进行。

2.4　Weibull分布-Weibull分布

假设原始径向游隙 $X$ 服从Weibull分布 $W (η_{x}, m_{x})$ ，失效径向游隙 $Y$ 服从Weibull分布 $W (η_{y}, m_{y})$ ，其中 $η_{x}$ 、 $η_{y}$ 、 $m_{x}$ 、 $m_{y}$ 分别为分布的比例参数和形状参数，则 $X$ 、 $Y$ 的概率密度函数分别为：

f (x, η_{x}, m_{x}) = \{\begin{matrix} \frac{m_{x}}{η_{x}} {(\frac{x}{η_{x}})}^{m_{x} - 1} e^{- (x / η_{x})^{m_{x}}}, x \geq 0 \\ 0, x < 0 \end{matrix}

(37)

g (y, η_{y}, m_{y}) = \{\begin{matrix} \frac{m_{y}}{η_{y}} {(\frac{x}{η_{y}})}^{m_{y} - 1} e^{- (y / η_{y})^{m_{y}}}, y \geq 0 \\ 0, y < 0 \end{matrix}

(38)

在式(37)中，令 $r = x^{m_{x}}$ ，则根据分布类型变换的数学理论^[11]，有：

h (r) = μ_{x} e^{- μ_{x} r}, \begin{matrix}  \end{matrix} r > 0

(39)

式中：

μ_{x} = η_{x}^{- m_{x}}

(40)

同理，令 $s = y^{m_{y}}$ ，则有：

h (s) = μ_{y} e^{- μ_{y} s} \begin{matrix} , \end{matrix} s > 0

(41)

式中：

μ_{y} = η_{y}^{- m_{y}}

(42)

因此，可靠度的估计值 $\hat{R}$ 为：

\hat{R} = \frac{{\hat{μ}}_{x}}{{\hat{μ}}_{x} + {\hat{μ}}_{y}} = \frac{1 / \bar{r}}{1 / \bar{r} + 1 / \bar{s}} = \frac{1}{1 + \bar{r} / \bar{s}}

(43)

将式(43)变换为：

μ_{x} = \frac{μ_{y}}{1 / R - 1}

(44)

将式(40)、(42)代入式(44)，可得到原始径向游隙和失效径向游隙均服从Weibull分布时轴承的可靠性设计方法，表示为：

η_{x} = {(\frac{η_{y}^{- m_{y}}}{1 / R - 1})}^{m_{x}}

(45)

可以将Weibull分布与指数分布进行变换，因此，对于服从Weibull分布参数的区间估计与指数分布类似，但前者更复杂，也可参考文献[18]进行。

3 工程实例

为了验证本文方法的有效性和适用性，以16004深沟球轴承为例，进行其可靠性分析。轴承内圈直径 $d = 20 m m$ ，外圈直径 $D = 42 m m$ ，宽度 $w = 8 m m$ 。

采用轴承径向游隙测量仪测试滚动轴承的径向游隙。共采集10组，每组测试3次后取平均值。测试现场如图1所示，测试结果如表1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 滚动轴承径向游隙测试现场

Fig.1 Test site of radial clearance of rolling bearing

表1 滚动轴承径向游隙测试结果 (μm)

Table 1 Test results of radial clearance of rolling bearing

组号	原始径向游隙测试值	失效径向游隙测试值
1	19.0	23.0
2	15.8	18.5
3	18.0	20.3
4	18.5	21.3
5	14.5	17.7
6	16.2	19.8
7	16.2	19.3
8	20.0	25.0
9	16.8	20.3
10	17.2	21.7

新窗口打开| 下载CSV

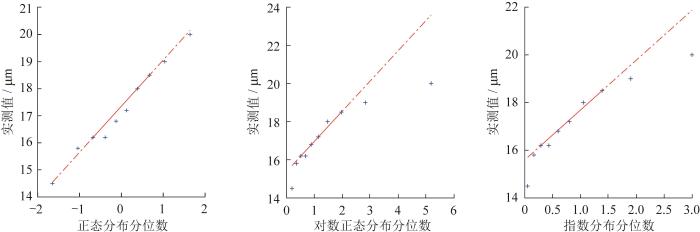
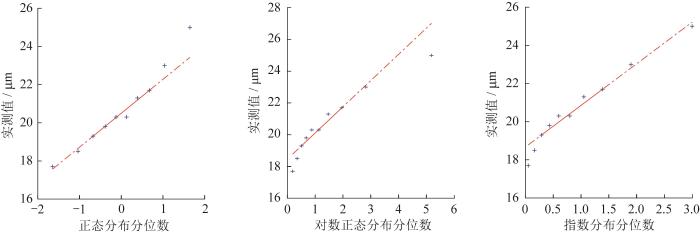
当样本数据服从Weibull分布时，参数估计的精度受样本数量的影响较大。一般来说，当样本数量较少时，参数估计很可能不准确，故分别做出原始径向游隙和失效径向游隙服从正态分布、对数正态分布、指数分布时的 $Q - Q$ 图，进行定性检验。原始径向游隙和失效径向游隙的 $Q - Q$ 图分别如图2和图3所示。由图可知，原始径向游隙和失效径向游隙的数据同时服从正态分布时的拟合效果比其他分布的效果好。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 滚动轴承原始径向游隙的 $Q$ $- Q$ 图

Fig.2 $Q$ $- Q$ diagram of original radial clearance of rolling bearing

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 滚动轴承失效径向游隙的 $Q$ $- Q$ 图

Fig.3 $Q$ $- Q$ diagram of failed radial clearance of rolling bearing

接下来采用非参数检验（单样本柯尔莫戈洛夫-斯米诺夫检验）进行定量检验。假设样本数据服从原假设，显著性水平为0.05，当样本呈显著性即 $p$ >0.05时，认为原假设成立。检验结果如表2所示。

表2 滚动轴承径向游隙非参数检验结果

Table 2 Non-parametric test results of radial clearance of rolling bearing

原假设	自由度	p	决策
原始径向游隙服从正态分布	10	0.200^①	保留原假设
失效径向游隙服从正态分布	10	0.200^①	保留原假设
原始径向游隙服从对数正态分布	10	0.200^①	保留原假设
失效径向游隙服从对数正态分布	10	0.200^①	保留原假设
原始径向游隙服从指数分布	10	0.003	拒绝原假设
失效径向游隙服从指数分布	10	0.003	拒绝原假设

注：显著性水平为0.05。

①为经过里利氏显著性修正后真显著性的下限。

新窗口打开| 下载CSV

由表2可知，原假设为正态分布和对数正态分布时，原始径向游隙和失效径向游隙样本数据的 $p$ 值均大于0.05，故接受原假设，认为原始径向游隙和失效径向游隙均服从正态分布和对数正态分布。

当样本数据均服从正态分布时，结合试验数据，计算后可得：

R = Φ (\frac{μ_{y} - μ_{x}}{\sqrt[]{σ_{y}^{2} + σ_{x}^{2}}}) = 0.898 5

进一步进行轴承径向游隙可靠性设计。分别选取工程中常用的可靠度 $0.95$ 和 $0.999$ ，对轴承原始径向游隙置信区间进行设计。

通过式(16)计算可得 $t$ 分布中自由度 $v = \begin{matrix} 16.877 \end{matrix}$ ，取整后 $v = 16$ 。

当 $R = 0.95$ 时，由式(17)可得 $α^{'} = \begin{matrix} 0.394 5 \end{matrix}$ 。查表得 $t_{\begin{matrix} α / 2 \end{matrix}} (16) = \begin{matrix} \begin{matrix} 0.917 6 \end{matrix} \end{matrix}$ 。

同理，有：

χ_{α / 2}^{2} (9) = 12.548 2

χ_{\begin{matrix} 1 - α / 2 \end{matrix}}^{2} (9) = \begin{matrix} \begin{matrix} \begin{matrix} 5.290 0 \end{matrix} \end{matrix} \end{matrix}

将上述数据代入式(21)，可得 $R = 0.95$ 时轴承原始径向游隙的置信区间为：

[μ_{x l}, μ_{x u}] = [14.127 3, \begin{matrix} 18.950 6 \end{matrix}] μ m

当 $R = 0.999$ 时，由式(17)可得 $α^{'} = 0.055 78$ ，查表得 $t_{\begin{matrix} α^{'} / 2 \end{matrix}} (16) = 1.926 8$ 。

同理，有：

χ_{α^{'} / 2}^{2} (9) = 17.907 2

χ_{\begin{matrix} 1 - α^{'} / 2 \end{matrix}}^{2} (9) = 2.952 3

将上述数据代入式(21)，可得 $R = 0.999$ 时轴承原始径向游隙的置信区间为：

[μ_{x l}, μ_{x u}] = [8.053 1, \begin{matrix} \begin{matrix} 19.955 5 \end{matrix} \end{matrix}] μ m

当样本数据均服从对数正态分布时，计算步骤与正态分布类似，计算过程不再赘述。

轴承可靠度为：

R = Φ (\frac{μ_{y} - μ_{x}}{\sqrt[]{σ_{y}^{2} + σ_{x}^{2}}}) = 0.903 2

$R = 0.95$ 时轴承原始径向游隙的置信区间为：

[μ_{x l}, μ_{x u}] = [14.588 3, \begin{matrix} 18.775 2 \end{matrix}] μ m

$R = 0.999$ 时轴承原始径向游隙的置信区间为：

[μ_{x l}, μ_{x u}] = [10.630 3, \begin{matrix} \begin{matrix} 19.791 9 \end{matrix} \end{matrix}] μ m

综上可知：当样本数据服从正态分布时，滚动轴承的可靠度为0.898 5；当样本数据服从对数正态分布时，可靠度为0.903 2。不同分布下原始径向游隙置信区间如表3所示。由图2可知，样本数据服从正态分布的拟合效果比对数正态分布好，结合表3可知样本数据服从正态分布时算得的游隙置信区间更为可靠。

表3 不同样本数据分布下滚动轴承原始径向游隙置信区间

Table 3 Confidence interval of original radial clearance of rolling bearing under different distributions of sample data

可靠度	原始径向游隙置信区间
可靠度	正态分布	对数正态分布
0.95	[14.127 3, 18.950 6] μm	[14.588 3, 18.775 2] μm
0.999	[8.0531, 19.955 5] μm	[10.630 3, 19.791 9] μm

新窗口打开| 下载CSV

根据GB/T 4604—2006可知^[19]，16004深沟球轴承径向游隙的参考范围为[5，20] μm，由此可知算得的径向游隙符合国家标准。此外，采用本文方法可以设计出任意可靠度下的滚动轴承径向游隙置信区间，且结果更加合理可靠。

4 结论

1）提出了一种基于应力-强度干涉模型的轴承径向游隙可靠性设计方法。将轴承原始径向游隙和失效径向游隙看作随机变量，构建了轴承二维随机干涉模型，从而实现了滚动轴承径向游隙的可靠设计。

2）针对工程中常用的服从正态分布、对数正态分布、指数分布和Weibull分布的径向游隙样本数据，分别推导了求解滚动轴承可靠性和径向游隙置信区间的解析式，为滚动轴承可靠性设计和评估提供了理论依据。

3）将所求得的16004深沟球轴承径向游隙置信区间与现行国家标准对比，结果验证了本文方法的有效性和适用性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李皓川，孙志礼，冯吉路，等.

基于极变换与稀疏响应面的滚动轴承游隙可靠性分析

［J］.东北大学学报（自然科学版），2017，38（11）：1579-1583. doi：10.12068/j.issn.1005-3026.2017.11.013

[本文引用: 1]

H C

， SUN

Z L

， FENG

J L

， et al.

Reliability analysis of rolling bearing clearance based on sparse response surface and polar transformation

［J］. Journal of Northeast University （Natural Science）， 2017， 38（11）： 1579-1583.

DOI:10.12068/j.issn.1005-3026.2017.11.013 [本文引用: 1]

[2]

郑牧，牛建平.

双列球轴承原始径向游隙与压出力设计计算

［J］.轴承，2018（2）：7-10.

[本文引用: 1]

ZHENG

， NIU

J P

Design calculation of original radial clearance and extrusion pressure of double row ball bearings

［J］. Bearing， 2018（2）： 7-10.

[本文引用: 1]

[3]

邱明，牛振华，杜辉，等.

薄壁交叉圆柱滚子轴承最佳径向工作游隙

［J］.航空动力学报，2018， 33（7）：1725-1735.

[本文引用: 1]

QIU

， NIU

Z H

， DU

， et al.

Optimum radial working clearance of thin-walled crossed cylindrical roller bearings

［J］. Journal of Aerospace Power， 2018， 33（7）： 1725-1735.

[本文引用: 1]

[4]

刘璐，邱明，邹春生，等.

游隙对铁路客车轴箱轴承性能的影响分析

［J］.现代制造工程，2019（10）：140-147.

[本文引用: 1]

LIU

， QIU

， ZOU

C S

， et al.

Analysis of the influence of clearance on the performance of rail-way passenger car axle box bearings

［J］. Modern Manufacturing Engineering， 2019（10）： 140-147.

[本文引用: 1]

[5]

沈宇涵，宋爱平，彭云，等.

径向游隙对圆柱滚子轴承径向刚度的影响

［J］.轴承，2017（6）：14-16. doi：10.19533/j.issn1000-3762.2017.06.003

[本文引用: 1]

SHEN

Y H

， SONG

A P

， PENG

， et al.

Influence of radial clearance on radial stiffness of cylindrical roller bearings

［J］. Bearing， 2017（6）： 14-16.

DOI:10.19533/j.issn1000-3762.2017.06.003 [本文引用: 1]

[6]

胡北，公平，于庆杰，等.

中介轴承套圈过盈量及径向游隙计算

［J］.轴承，2022（5）： 21-23.

[本文引用: 1]

， GONG

， YU

Q J

， et al.

Calculation of interference and radial clearance of intermediate bearing rings

［J］. Bearing， 2022（5）： 21-23.

[本文引用: 1]

[7]

ZHANG

， LÜ

R N

， SI

S B

， et al.

Reliability analysis of systems with common cause failure based on stress-strength interference model

［J］. Journal of Shanghai Jiaotong University （Science）， 2018， 23（5）： 707-710.

[本文引用: 1]

[8]

ALI

S S

， KANNAN

A diagnostic approach to Weibull-Weibull stress-strength model and its generalization

［J］. International Journal of Quality & Reliability Management， 2011， 28（4/5）： 451-463.

[本文引用: 1]

[9]

WANG

， DEY

， TRIPATHI

Y M

， et al.

Reliability inference for a multicomponent stress-strength model based on Kumaraswamy distribution

［J］. Journal of Computational and Applied Mathematics， 2020， 376： 112823.

[本文引用: 1]

[10]

杨晓蔚

滚动轴承的可靠性设计

［J］.轴承，2013（12）：1-5. doi：10.3969/j.issn.1000-3762.2013.12.001

[本文引用: 2]

YANG

X W

Reliability design of rolling bearings

［J］. Bearing， 2013（12）： 1-5.

DOI:10.3969/j.issn.1000-3762.2013.12.001 [本文引用: 2]

[11]

张先超，李传日，李君.

基于应力-强度干涉理论的可靠度点估计研究

［J］.装备环境工程，2010，7（1）：18-21，25. doi：10.3969/j.issn.1672-9242.2010.01.005

[本文引用: 2]

ZHANG

X C

， LI

C R

， LI

Point estimation of reliability based on stress-strength interference

［J］. Equipment Environmental Engineering， 2010， 7 （1）： 18-21， 25.

DOI:10.3969/j.issn.1672-9242.2010.01.005 [本文引用: 2]

[12]

伊枭剑，董海平，翟志强，等.

基于应力-强度干涉模型的火工品可靠性设计方法

［J］.北京理工大学学报，2014，34（10）：1007-1011.

[本文引用: 1]

X J

， DONG

H P

， ZHAI

Z Q

， et al.

Reliability design for initiating devices based on stress-strength interference model

［J］. Transactions of Beijing Institute of Technology， 2014， 34（10）： 1007-1011.

[本文引用: 1]

[13]

李皓川

航空发动机主轴轴承游隙的可靠性保障理论研究

［D］.沈阳：东北大学，2013：1-79.

[本文引用: 1]

H C

Reliability guarantee theory research of clearance of aeroengine main shaft bearings

［D］. Shenyang： Northeastern University， 2013： 1-79.

[本文引用: 1]

[14]

张洪才

应力-强度干涉模型的可靠度计算方法的研究

［J］.机械设计，2001（6）：45-47. doi：10.3969/j.issn.1001-2354.2001.06.019

[本文引用: 1]

ZHANG

H C

Research on the reliability calculation method of stress-strength interference model

［J］. Mechanical Design， 2001（6）： 45-47.

DOI:10.3969/j.issn.1001-2354.2001.06.019 [本文引用: 1]

[15]

包洪兵，姚卫星.

基于参数估计区间的应力-强度干涉模型

［J］.机械科学与技术，2010，29（2）：239-243.

[本文引用: 3]

BAO

H B

， YAO

W X

A stress-strength interference model based on parameter estimation interval

［J］. Mechanical Science and Technology for Aerospace Engineering， 2010， 29（2）： 239-243.

[本文引用: 3]

[16]

DE VAN VIJVER

F J R

， AVVISATI

， DAVIDOV

， et al.

Invariance analyses in large-scale studies

［J/OL］//OECD Education Working Papers. （2019-05-03）［2023-05-07］. .

URL [本文引用: 1]

[17]

同济大学数学系

.概率论与数理统计［M］.北京：人民邮电出版社，2017：1-252.

[本文引用: 1]

Mathematics Department of Tongji University. Probability and statistics［M］. Beijing： Posts and Telecom Press， 2017： 1-252.

[本文引用: 1]

[18]

COHEN

A C

， WHITTEN

B J

. Parameter estimation in reliability and life span models［M］. Florida： CRC Press， 2020： 1-312.

[本文引用: 2]

[19]

中国机械工业联合会. 滚动轴承径向游隙：［S］.北京：中国标准出版社，2006：1-10.

[本文引用: 1]

China Machinery Industry Federation. Rolling bearings-radial internal clearance：［S］. Beijing： Standards Press of China， 2006： 1-10.

[本文引用: 1]

基于极变换与稀疏响应面的滚动轴承游隙可靠性分析

2017

... 已有很多学者开展了滚动轴承径向游隙优化设计研究.如：李皓川等^[1]在极变换的基础上提出了一种选点的方法，结合稀疏响应面，对滚动轴承工作游隙极限状态函数进行拟合，并基于有限元方法计算出工作游隙；郑牧等^[2]对轴承安装后的径向游隙减小量进行了分析和计算，推导了轴承的原始径向游隙；邱明等^[3-4]分析了轴承径向游隙的变化对轴承刚度及疲劳寿命的影响，指出径向游隙是影响轴承力学性能的关键指标；沈宇涵等^[5]分析了圆柱滚子轴承径向游隙对径向刚度的影响；胡北等^[6]考虑了轴承温升、径向载荷等因素的影响，分析并计算了轴承径向游隙.然而，以上研究大多是通过修正经验公式或仿真分析来确定滚动轴承径向游隙的合理范围，缺乏对滚动轴承整个部件可靠性的考虑. ...

基于极变换与稀疏响应面的滚动轴承游隙可靠性分析

2017

双列球轴承原始径向游隙与压出力设计计算

2018

双列球轴承原始径向游隙与压出力设计计算

2018

薄壁交叉圆柱滚子轴承最佳径向工作游隙

2018

薄壁交叉圆柱滚子轴承最佳径向工作游隙

2018

游隙对铁路客车轴箱轴承性能的影响分析

2019

游隙对铁路客车轴箱轴承性能的影响分析

2019

径向游隙对圆柱滚子轴承径向刚度的影响

2017

径向游隙对圆柱滚子轴承径向刚度的影响

2017

中介轴承套圈过盈量及径向游隙计算

2022

中介轴承套圈过盈量及径向游隙计算

2022

Reliability analysis of systems with common cause failure based on stress-strength interference model

2018

... 针对产品的可靠性设计，应力-强度干涉模型在工程实际中已得到广泛应用.如：Zhang等^[7]研究了应力分布与强度分布之间的关系，引入条件可靠度的概念，建立了在单应力和多应力作用下的系统可靠性模型；Ali等^[8]讨论了形状参数不同时应力和强度分别服从广义Weibull分布以及对数正态分布时的应力-强度干涉模型，并对系统可靠性进行了评估；Wang等^[9]建立了在应力和强度服从一定分布时可靠度的极大似然估计模型，并确定了可靠度置信区间；杨晓蔚^[10]运用应力-强度干涉理论，在轴承寿命分布为Weibull分布的前提下，建立了评估可靠寿命的Weibull失效概率密度函数表达式和可靠度函数表达式；张先超等^[11]推导了基于应力-强度干涉理论的可靠度计算公式，并提出了当应力和强度分别同时服从单参数和双参数指数分布时的可靠度估计方法；伊枭剑等^[12]提出了基于应力-强度干涉模型的可靠性设计方法，将火工品感度参数和外界刺激参数引入应力-强度干涉模型，来评估火工品的可靠性. ...

A diagnostic approach to Weibull-Weibull stress-strength model and its generalization

2011

Reliability inference for a multicomponent stress-strength model based on Kumaraswamy distribution

2020

滚动轴承的可靠性设计

2013

... 根据式(1)可得^[10]： ...

滚动轴承的可靠性设计

2013

... 根据式(1)可得^[10]： ...

基于应力-强度干涉理论的可靠度点估计研究

2010

... 在式(37)中，令

r = x^{m_{x}}

，则根据分布类型变换的数学理论^[11]，有： ...

基于应力-强度干涉理论的可靠度点估计研究

2010

... 在式(37)中，令

r = x^{m_{x}}

，则根据分布类型变换的数学理论^[11]，有： ...

基于应力-强度干涉模型的火工品可靠性设计方法

2014

基于应力-强度干涉模型的火工品可靠性设计方法

2014

航空发动机主轴轴承游隙的可靠性保障理论研究

2013

... 研究发现，滚动轴承游隙与轴承的多种失效模式密切相关，是影响轴承可靠性的重要因素^[13].根据大量试验可知，由于在生产过程中加工、装配等因素的影响，轴承原始径向游隙呈随机分布，而造成轴承失效的失效径向游隙也因工作环境的影响而呈随机分布.因此，本文引入应力-强度干涉模型.此处应力和强度的概念是广义的，应力指影响零件性能和功能的各种环境因素，强度指零件抵抗应力的因素.轴承的原始径向游隙会影响轴承所受应力的分布，而失效径向游隙是轴承抵抗应力所导致的，因而，将原始径向游隙

X

看作应力因素，失效径向游隙

Y

看作强度因素，则轴承的可靠度

R

可以定义为^[14]： ...

航空发动机主轴轴承游隙的可靠性保障理论研究

2013

X

看作应力因素，失效径向游隙

Y

看作强度因素，则轴承的可靠度

R

可以定义为^[14]： ...

应力-强度干涉模型的可靠度计算方法的研究

2001

X

看作应力因素，失效径向游隙

Y

看作强度因素，则轴承的可靠度

R

可以定义为^[14]： ...

应力-强度干涉模型的可靠度计算方法的研究

2001

X

看作应力因素，失效径向游隙

Y

看作强度因素，则轴承的可靠度

R

可以定义为^[14]： ...

基于参数估计区间的应力-强度干涉模型

2010

... 由于

μ_{x}

、

μ_{y}

、

σ_{x}

、

σ_{y}

也是随机变量，根据随机变量参数区间估计理论和区间数扩张原理，考虑了随机变量参数估计区间后，式(8)可改写为^[15]： ...

... 取

v

为整数，则风险系数α′^[15]为： ...

... 将式(15)和(19)代入式(8)^[15]，可得

Z_{R}

的下限和上限为： ...

基于参数估计区间的应力-强度干涉模型

2010

... 由于

μ_{x}

、

μ_{y}

、

σ_{x}

、

σ_{y}

也是随机变量，根据随机变量参数区间估计理论和区间数扩张原理，考虑了随机变量参数估计区间后，式(8)可改写为^[15]： ...

... 取

v

为整数，则风险系数α′^[15]为： ...

... 将式(15)和(19)代入式(8)^[15]，可得

Z_{R}

的下限和上限为： ...

Invariance analyses in large-scale studies

... 在没有给出

μ_{x}

和

μ_{y}

确切数值的情况下，需要根据样本数据对

R

进行估计，这里采取极大似然估计法.根据极大似然估计的不变性^[16]，可以得到

μ_{x}

、

μ_{y}

的估计值

{\hat{μ}}_{x}

、

{\hat{μ}}_{y}

，则可靠度

R

的估计值

\hat{R}

为： ...

2017

... 由文献[17]可得

μ_{x}

和

μ_{y}

的极大似然估计分别为： ...

2017

... 由文献[17]可得

μ_{x}

和

μ_{y}

的极大似然估计分别为： ...

2020

... 而对于服从指数分布参数的区间估计，可参考文献[18]进行. ...

... 可以将Weibull分布与指数分布进行变换，因此，对于服从Weibull分布参数的区间估计与指数分布类似，但前者更复杂，也可参考文献[18]进行. ...

2006

... 根据GB/T 4604—2006可知^[19]，16004深沟球轴承径向游隙的参考范围为[5，20] μm，由此可知算得的径向游隙符合国家标准.此外，采用本文方法可以设计出任意可靠度下的滚动轴承径向游隙置信区间，且结果更加合理可靠. ...

2006

〈

〉