对辊破碎机对钨矿石的层压破碎特性研究

doi:10.3785/j.issn.1006-754X.2023.00.012

对辊破碎机对钨矿石的层压破碎特性研究

李洋波^,^,¹^,²^,³, 蔡改贫^,³^,⁴, 阮辽³

1.矿冶科技集团有限公司矿物加工科学与技术国家重点实验室，北京 100160

2.北矿机电科技有限责任公司，北京 100160

3.江西理工大学机电工程学院，江西赣州 341000

4.江西省矿冶机电工程技术研究中心，江西赣州 341000

Study on laminated crushing characteristics of W-ore with dual-roller crusher

LI Yangbo^,^,¹^,²^,³, CAI Gaipin^,³^,⁴, RUAN Liao³

1.State Key Laboratory of Mineral Processing, BGRIMM Technology Group, Beijing 100160, China

2.BGRIMM Machinery & Automation Technology Co. , Ltd. , Beijing 100160, China

3.School of Mechanical and Electrical Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China

4.Jiangxi Province Engineering Research Center for Mechanical and Electrical of Mining and Metallurgy, Ganzhou 341000, China

通讯作者: 蔡改贫（1964—），男，江西赣州人，教授，博士生导师，博士，从事矿山机械散体系统研究，E-mail: cgp4821@163.com

收稿日期: 2022-06-20 修回日期: 2022-08-26

基金资助:

国家自然科学基金资助项目. 51464017
江西省重点研发计划项目. 20181ACE50034

Received: 2022-06-20 Revised: 2022-08-26

作者简介 About authors

李洋波（1996—），男，安徽合肥人，助理工程师，硕士，从事岩石碎磨机理研究，E-mail:2827648047@qq.com,https://orcid.org/0000-0001-9625-6833 , E-mail：2827648047@qq.com

摘要

针对岩石破碎过程的复杂性以及传统仿真模型的局限性——反映替换颗粒群信息少且无法定位替换颗粒群中某一颗粒，使得所模拟的颗粒无法被连续破碎，导致仿真精度较低等问题，提出了通过离散元应用编程接口开发的改进破碎模型——多次替换的颗粒黏结模型（bonded particle model, BPM）。该方法能实现颗粒在破碎过程中的多次连续替换，更加贴近实际破碎过程，可提升仿真精度。基于对辊破碎机的三维模型与参数标定后的钨矿石颗粒群，对破碎机内的钨矿石颗粒群进行层压破碎可视化仿真分析，并结合室内试验研究了对辊破碎机的层压破碎特性，以验证数值仿真的有效性。结果表明：通过仿真得到的钨矿石颗粒受力与破碎速率的关系说明对辊破碎机可实现层压破碎；钨矿石碎后粒径分布误差为0.889~1.940 mm，且碎后粒径分布满足正态分布，说明仿真分析准确且有效。不同粒径配比下的钨矿石层压破碎试验结果表明，颗粒间相互作用力对破碎效率的影响程度大于颗粒低孔隙率。研究结果为进一步提高对辊破碎机的生产效率提供了依据，且所提出的改进破碎模型为物料的破碎研究提供了一种新方法。

关键词： 改进破碎模型 ; 颗粒黏结模型 ; 对辊破碎机 ; 可视化仿真 ; 层压破碎试验

Abstract

Aiming at the complexity of rock crushing process and the limitations of traditional simulation models, which reflects the little information about the replacement particle groups and can not locate a particle in the replacement particle groups, resulting in the simulated particles can not be broken continuously and the simulation accuracy is low, an improved crushing model developed by the discrete element application program interface is proposed, which is the bonded particle model (BPM) with multiple replacements. This method realizes the multiple continuous replacements of particles during the crushing process, which is closer to the actual crushing process and can improve the simulation accuracy. Based on the three-dimensional model of dual-roller crusher and the W-ore particle groups after parameter calibration, the visual simulation analysis of laminated crushing of W-ore particle groups in crusher was carried out, and the laminated crushing characteristics of the dual-roller crusher were studied through indoor tests to verify the effectiveness of numerical simulation. The results showed that: the relationship between the force on W-ore particles and the crushing rate obtained through simulation indicated that the dual-roller crusher could achieve laminated crushing; the error of particle size distribution after crushing was 0.889‒1.940 mm, and the particle size distribution after crushing met the normal distribution, which verified the simulation analysis was accurate and effective. The laminating crushing test results of W-ore with different particle size ratios showed that the influence of particle interaction on crushing efficiency was greater than that of particle low porosity. The research results provide a basis for improving the production efficiency of dual-roller crusher, and the proposed improved crushing model also provides a new method for the study of material crushing.

Keywords： improved crushing model ; bonded particle model ; dual-roller crusher ; visual simulation ; lamination crushing test

PDF (6231KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李洋波, 蔡改贫, 阮辽. 对辊破碎机对钨矿石的层压破碎特性研究. 工程设计学报[J], 2023, 30(2): 212-225 doi:10.3785/j.issn.1006-754X.2023.00.012

LI Yangbo, CAI Gaipin, RUAN Liao. Study on laminated crushing characteristics of W-ore with dual-roller crusher. Chinese Journal of Engineering Design[J], 2023, 30(2): 212-225 doi:10.3785/j.issn.1006-754X.2023.00.012

破碎机作为一种物料破碎设备，被广泛应用于矿产、冶金和建筑等行业，具有重要的研究价值。面对资源紧缺等问题，Schwindig^[1]在20世纪60年代首次提出了层压破碎（料层破碎）理论。经验证该方法可显著提高物料的破碎效率。因此，研究破碎机的层压破碎特性以提高其工作效率，成为当前关注的主要问题。钨矿石的价格为普通煤的40倍、铁矿石的200倍，且钨矿石的普氏硬度系数为14~18，而煤矿石与铁矿石的普氏硬度系数分别为1.8与6~10。因此，矿石破碎初选环节的成本差异较大^[2]。本文将以钨矿石为对象，开展破碎机的层压破碎特性研究。

目前，许多学者针对层压破碎理论的工程应用展开了研究，并取得了一定的成果。徐长锋等^[3]基于层压破碎理论，通过分离式霍普金森压杆对海泡石的破碎状态进行了描述；Schoenert教授^[4]通过分析得出单颗粒破碎能耗与挤压载荷成正比，即挤压载荷越低，能耗越低的结论；Rashidi等^[5]进一步通过层压破碎试验证明了料层破碎能耗远小于单颗粒破碎；Fuerstenau等^[6]对高压辊磨机的破碎机理进行了探究。

在岩土工程仿真中，离散元法的研究和应用已长达30年^[7-8]，现已被众多学者用于对物料散体系统的模拟研究。Gobbin等^[9]基于离散元法开发建立了静力弹塑性（Pushover）曲线程序，用于描述较复杂的物体坍塌现象；陈兵等^[10]通过离散元模型开展了多组物料筛分正交试验，分析了不同振动参数对筛分效率、颗粒分布与物料运输速度的影响规律，并通过实验加以验证且优化了振动参数。

颗粒破碎模型的构建方法主要有以下2种。

1）颗粒黏结模型（bonded particle model，BPM）。

BPM于2004年由Potyondy和Cundall等^[11]首次提出。该模型通过颗粒间黏结键断裂来表征颗粒的破碎过程，适用于对单颗粒以及小规模颗粒群的破碎研究，可有效反映颗粒外观、尺寸及力学关系等信息。

2）碎片代替模型（fragment replacement model，FRM）。

FRM是一种采用小颗粒代替破碎颗粒的模拟方法，适用于大规模颗粒群的破碎研究，可有效反映颗粒群的破碎过程、力学关系等信息，但建模方式复杂，有待改进^[12]。

验证仿真模拟的方法分为直接验证与间接验证两种。方继松等^[13]通过采用直接验证方法——对比石英玻璃球撞击刚性壁时破碎形态的仿真结果和实验结果，验证了仿真分析的有效性；江汇^[14]、池昌江^[15]、邵一哲等^[16]通过采用间接验证方法——对比颗粒碎后粒径分布的仿真结果和实验结果，验证了仿真分析的有效性。

综上所述，目前学者在利用离散元法研究物料的层压破碎时，构建的颗粒破碎模型较为简单，所能获取的破碎过程及碎后颗粒信息少，局限性较大，与试验结果的误差较大。此外，基于层压破碎理论研发的破碎机具有受破碎环境限制以及产品投入成本高等劣势^[17]。为此，通过改进物料颗粒破碎模型，进一步探究破碎机的层压破碎特性尤为重要。对辊破碎机具有结构简单、破碎能耗低和处理量大等优势^[18]，可有效降低产品前期投入成本，且破碎壁为弧状曲面，主要破碎方式为挤压与磨削^[19]，故在理论上其存在层压破碎——辊面与颗粒、颗粒与颗粒之间的相互作用力使物料破碎，但目前缺乏对其的深入研究，且杨松荣等^[20]认为对辊破碎机中矿石颗粒的破碎仅依靠辊面与颗粒间的作用，即只发生传统的单颗粒破碎。此外，经对辊破碎机破碎后矿石颗粒的粒径范围分布较广，针片率较高。因此，本文基于钨矿石的本征特征，建立符合实际破碎状态的钨矿石外观简化模型，并基于离散元应用编程接口（application program interface, API）进行二次开发，以建立改进的颗粒群破碎模型；然后，通过单轴压缩试验来标定颗粒模型的参数，并建立对辊破碎机的三维模型，对已完成参数标定的颗粒进行层压破碎可视化仿真；最后，通过试验分析对辊破碎机的层压破碎特性，旨在为提高其工作效率提供一定的理论依据。

1 颗粒群破碎模型的建立及其参数标定

1.1　颗粒模型参数标定

在离散元软件中标定准确的颗粒模型参数是有效模拟矿石实际破碎效果的前提。颗粒模型参数标定包括材料本征参数标定和物料接触参数标定。

1）材料本征参数标定。

矿石与破碎设备材料的种类繁多，不同材料的本征参数各异，其为材料的固有属性，与外部条件无关。材料本征参数主要包括泊松比、剪切模量和密度。本文所研究的对辊破碎机的材质为钢，破碎矿石的类型为钨矿石，其材料本征参数如表1所示^[21]。

表1 钢和钨矿石的材料本征参数

Table 1 Material intrinsic parameters of steel and W-ore

材料	泊松比	剪切模量/GPa	密度/(kg/m³)
钢	0.31	212	7 850
钨矿石	0.35	25	2 830

新窗口打开| 下载CSV

2）物料接触参数标定。

物料接触参数用于描述颗粒与颗粒、颗粒与几何体之间的弹性恢复系数、静摩擦因数和滚动摩擦因数。为获取准确的物料接触参数值，开展物料堆积试验^[22]，通过比较堆积角的仿真值与实测值来获取最佳接触参数值。

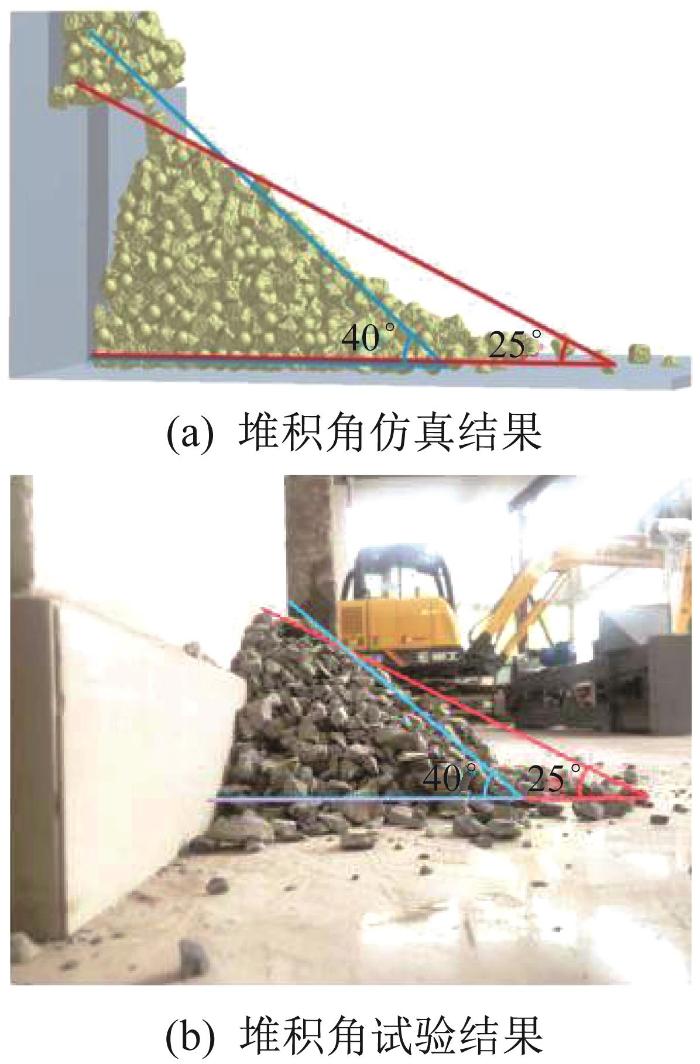
在本文的钨矿石颗粒堆积仿真分析中，采用类L形板模拟实际堆积面（靠墙面），材料的本征参数和尺寸与试验一致。其中：外墙高200 mm，内墙到外墙的距离为20 mm。由于钨矿石形状各异，为方便堆积模拟，按接触方式分成以下3类形式：球状（点-点接触）颗粒、锥状（点-面接触）颗粒和柱状（面-面接触）颗粒。颗粒运动停止后测量堆积角，并与实测堆积角进行比较，结果如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 钨矿石颗粒堆积角仿真结果与试验结果对比

Fig.1 Comparison between simulation results and experimental results of stacking angle of W-ore particles

由图1可知，钨矿石颗粒外堆积角的仿真值和实测值均为 $25$ °，内堆积角的仿真值和实测值均为 $40$ °。由此说明，仿真时设置的接触参数符合实际工况。记录此时的接触参数值，作为最佳接触参数，具体数值如表2所示。

表2 钨矿石的接触参数

Table 2 Contact parameters of W-ore

接触参数	钨矿-钨矿	钨矿-钢
弹性恢复系数	0.45	0.45
静摩擦因数	0.48	0.48
滚动摩擦因数	0.30	0.35

新窗口打开| 下载CSV

1.2　颗粒群破碎模型的实现

为进一步观察钨矿石在受挤压时的破碎特性，为替换颗粒分布选取提供一定的参考，开展挤压试验。试验设备由上压头、外筒壁和下底板组成，如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 挤压试验设备

Fig.2 Extrusion test instrument

将待破碎的钨矿石放在外筒壁与下底板中，然后将上压头插入，通过万能材料试验机挤压上压头，直至钨矿石发生破碎，结果如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 钨矿石挤压破碎结果

Fig.3 Crushing results of W ore by compression

由图3可知，钨矿石被挤压破碎成两大块（有时为一大块）与若干小块，此过程记为一次破碎。在实际对锟破碎机的破碎腔中，矿石的破碎过程是反复进行的，而传统的颗粒群破碎模型仅进行一次破碎替换，无法较好地反映反复的破碎过程，且包含的颗粒信息少，误差较大，不利于分析实际破碎工况。为此，本文通过离散元API二次开发编写DLL（dynamic link library，动态链接库）插件来实现基于应力破碎的钨矿石颗粒群的连续破碎模型——多次替换的BPM，如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

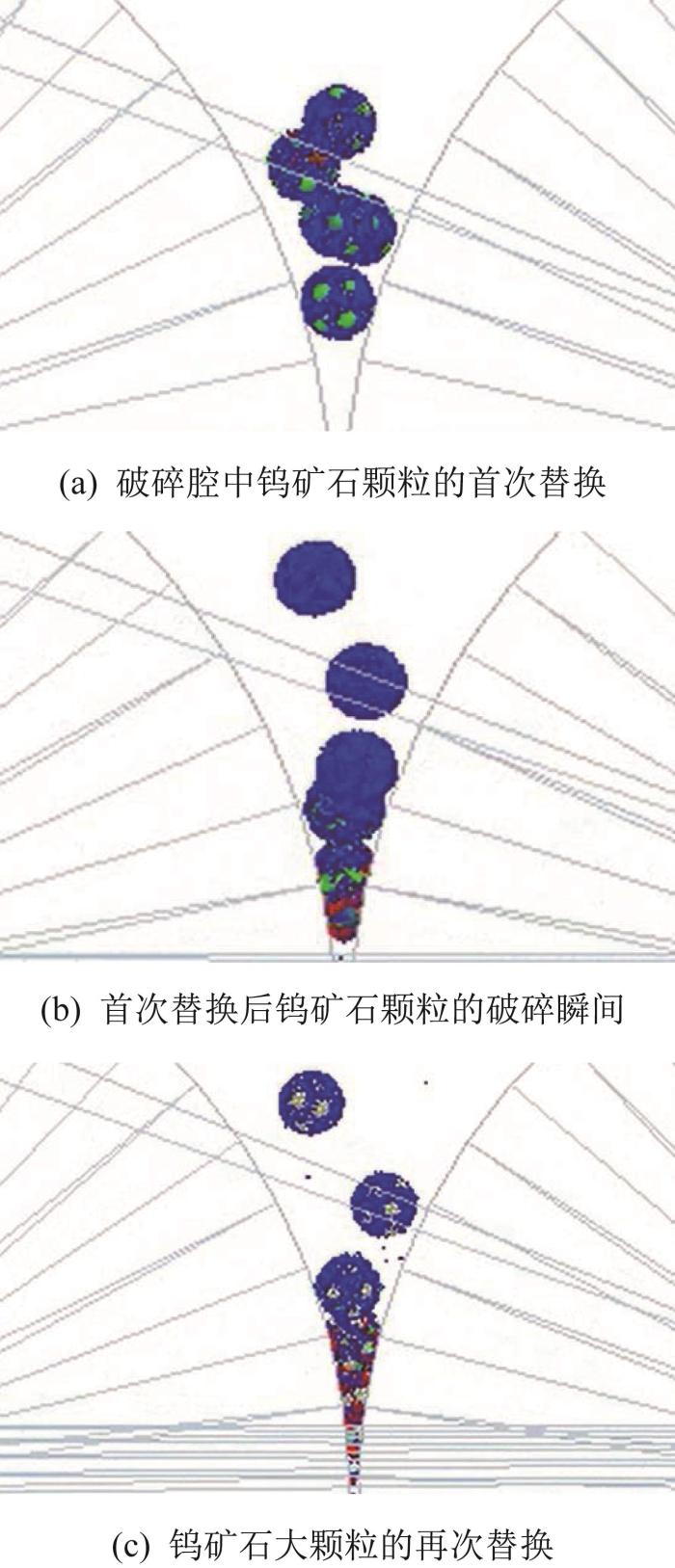
图4 多形状钨矿石颗粒的连续破碎模型

Fig.4 Continuous crushing model of multi-shape W-ore particles

根据图4，实现连续破碎模型的具体步骤如下：

1）在颗粒工厂中建立3种不同形状的待破碎钨矿石颗粒模型，如图4(a)所示。

2）根据图3所示的破碎试验结果，记第1次破碎为两大块与若干小块，替换小颗粒的粒径d_n （n=1, 2）与质量 $m_{n}$ 的关系为：

\{\begin{array}{l} m_{1} = \frac{A_{1}}{\sqrt[]{2 π} h_{1}} e^{- \frac{(d_{1} - {\bar{d}}_{1})^{2}}{2 h_{1}^{2}}} \\ m_{2} = \frac{A_{2}}{\sqrt[]{2 π} h_{2}} e^{- \frac{(d_{2} - {\bar{d}}_{2})^{2}}{2 h_{2}^{2}}} \\ M = \int_{d_{0}}^{\frac{d_{0} + d_{3}}{2}} m_{1} d d_{1} + \int_{d_{0}}^{\frac{d_{0} + d_{3}}{2}} m_{2} d d_{2} \\ d_{0} \leq d_{1} \leq \frac{d_{0} + d_{3}}{2}; \frac{d_{0} + d_{3}}{2} < d_{2} \leq d_{3} \end{array}

(1)

式中：A_n 为修正系数；d_n 为碎后颗粒质量分数占比最大的粒径区间中值，mm；h_n 为首次碎后的粒径分布标准差，mm； $d_{0}$ 为碎后颗粒最小粒径，mm； $d_{3}$ 为碎后颗粒最大粒径，mm； $M$ 为颗粒的总质量，g； $m_{1}$ 为碎后各小块的质量； $m_{2}$ 为碎后各大块的质量。

破碎后的两大块与若干小块钨矿石颗粒的首次替换过程如图4(b)所示。

3）为相对简化颗粒破碎过程，假定第1次碎后的小块颗粒不再破碎，大块颗粒在一定外力作用下再次破碎（即二次破碎），破碎过程的建模方法与步骤2）一致。根据式(1)，二次替换颗粒的粒径与质量的关系如式(2)所示，替换过程如图4(c)所示。

\{\begin{array}{l} m_{1} = \frac{A_{1}}{\sqrt[]{2 π} h_{1}} e^{- \frac{(d_{1} - {\bar{d}}_{1})^{2}}{2 h_{1}^{2}}} \\ m_{2 i} = \frac{A_{2 i}}{\sqrt[]{2 π} h_{2 i}} e^{- \frac{(d_{2 i} - {\bar{d}}_{2 i})^{2}}{2 h_{2 i}^{2}}} \\ M = \int_{d_{0}}^{\frac{d_{0} + d_{3}}{2}} m_{1} d d_{1} + \sum_{i = 1}^{g} \int_{d_{0}}^{d_{2 i, m}} m_{2 i} d d_{2 i} \\ d_{0} \leq d_{1} \leq \frac{d_{0} + d_{3}}{2}; d_{0} \leq d_{2 i} \leq d_{2 i, m} \leq d_{3} \end{array}

(2)

式中：A₂_i 为二次替换的修正系数；d₂_i 为二次替换颗粒的粒径，mm；m₂_i 为二次替换颗粒的质量，g；d₂_i_{, m}为二次替换颗粒的最大粒径，mm；d₂_i 为大块颗粒再次碎后颗粒质量分数占比最大的粒径区间中值，mm；h₂_i 为再次碎后的粒径分布标准差，mm；g为需替换的颗粒个数。

4）重复上述步骤，直至所有颗粒被最小粒级小颗粒替换，如图4(d)所示。

通过总结钨矿石挤压试验结果可得，粒径d<16 mm的颗粒一次碎后的粒径分布如表3所示。由表可知：粒径d<4 mm的颗粒破碎后有超过50%的颗粒的粒径d<1 mm。因此，假定粒径d<4 mm的颗粒为最小粒级颗粒，即碎后颗粒被d<4 mm颗粒替换后不再被更小粒级的颗粒替换。例如：模拟破碎d=10 mm的颗粒，先建立10 mm颗粒的外观特征，然后使用d=8~<12 mm对应的小颗粒进行填充，并读取d>4 mm的颗粒粒径信息；根据获得的粒径，按表3中对应数据进行二次替换，重复上述步骤，直至颗粒完全被d<4 mm的颗粒替换。

表3 钨矿石挤压破碎后的粒径分布 (mm)

Table 3 Particle size distribution of W-ore after compression crushing

原始粒径	碎后粒径
原始粒径	平均值	标准差	下限	上限
0~<4	0.7	0.700	0.1	4
4~<8	0.8	2.250	0.3	8
8~<12	1.0	3.875	0.5	12
12~16	2.0	4.785	0.8	16

新窗口打开| 下载CSV

1.3　物料破碎过程分析

BPM通过Hertz-Mindlin接触模型来模拟颗粒内部的黏结键，用于计算和表示物料的实际破碎效果。图5所示为离散元Hertz-Mindlin接触模型，其能准确计算不同时刻下颗粒-颗粒、颗粒-结构体之间力的变化。其中：法向力源自Hertz接触理论^[23]，切向力源自Mindlin理论^[24]。

图5

新窗口打开| 下载原图ZIP| 生成PPT

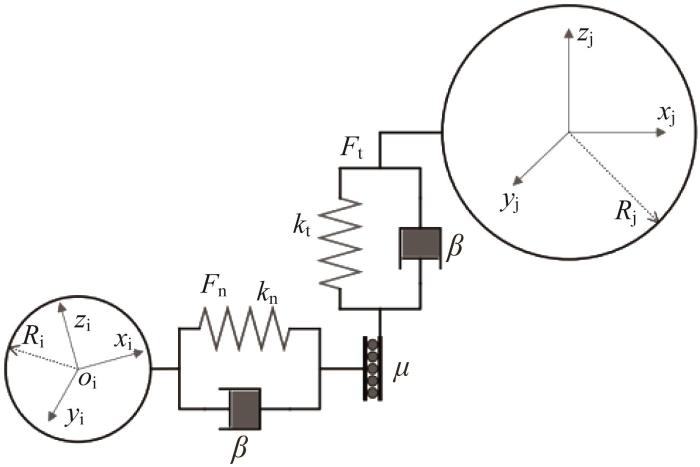
图5 离散元Hertz-Mindlin接触模型示意

Fig.5 Schematic of discrete element Hertz-Mindlin contact model

在图5中，将阻尼系数添加到法向力与切向力中。根据图5，法向力F_n可表示为：

F_{n} = \frac{4}{3} \sqrt[]{R} E U_{n}^{\frac{3}{2}}

(3)

其中：

\frac{1}{R} = \frac{1}{R_{i}} + \frac{1}{R_{j}}

\frac{1}{E} = \frac{1 - v_{i}^{2}}{E_{i}} + \frac{1 - v_{j}^{2}}{E_{j}}

式中：R为等效半径，m；E为等效杨氏模量，Pa；U_n为接触颗粒的法向重叠面积，m²；E_i、E_j为接触颗粒的杨氏模量，Pa；υ_i、υ_j为接触颗粒的泊松比；R_i、R_j为接触颗粒的半径，m。

法向阻尼力F_nd可表示为：

F_{n d} = - 2 \sqrt[]{\frac{5}{6}} β \sqrt[]{k_{n} m} v_{n}

(4)

其中：

m = {(\frac{1}{m_{i}} + \frac{1}{m_{j}})}^{- 1}

β = \frac{l n η}{\sqrt[]{l n^{2} η + π^{2}}}

k_{n} = 2 E \sqrt[]{R U_{n}}

式中： $β$ 为阻尼系数；k_n为法向刚度系数，N/m²；m为等效质量，kg；m_i、m_j为接触颗粒的质量，kg；v_n为相对速度的法向分量，m/s； $η$ 为弹性恢复系数。

切向力F_t可表示为：

F_{t} = - k_{t} U_{t}

(5)

其中：

k_{t} = 8 G \sqrt[]{R U_{n}}

式中：k_t为切向刚度系数，N/m²；U_t为接触颗粒的切向重叠面积，m²；G为当量剪切模量，Pa。

切向阻尼力F_td可表示为：

F_{t d} = - 2 \sqrt[]{\frac{5}{6}} β \sqrt[]{k_{t} m} v_{t}

(6)

式中：v_t为相对速度的切向分量，m/s。

1.4　破碎参数试验标定

离散元软件中的Hertz-Mindlin with Bonding模型有 5 个基本黏结参数需要设置，即单位面积法向刚度K_nA、单位面积切向刚度K_tA、法向极限应力σ_{n, max}、切向极限应力σ_{t, max}和等效黏结半径R。

在不同载荷下，颗粒的断裂形式不同^[25]，这对物料破碎结果的影响很大；此外，现有参数较为模型化，难以与实际的物料特性直接换算^[19]。因此，目前常采用模型参数匹配法进行参数设置。具体过程为：根据矿石自身的力学特性，利用式(7)^[26]计算5个黏结参数，再以计算值为参考，选定Hertz-Mindlin模型中各参数的标定范围，通过破碎正交试验校核选定范围内的黏结参数值，对比计算结果与试验结果后获得一组最佳的黏结参数。

\{\begin{array}{l} K_{n A} = \frac{π R^{2} E_{c}}{L} \\ K_{t A} = \frac{3 π R^{4} E_{c}}{L^{3}} \\ \frac{σ_{n, m a x}}{σ_{t, m a x}} = 2.11 + 0.38 l n μ - 0.63 l n \frac{σ_{t, m a x}}{σ_{n, m a x}} - 0.22 l n μ \frac{σ_{t, m a x}}{σ_{n, m a x}} \\ \frac{E}{E_{c}} = 0.78 + 0.14 l n \frac{L}{R} - 0.34 l n \frac{K_{n A}}{K_{t A}} \\ R = \frac{R_{i} + R_{j}}{2} \end{array}

(7)

式中：E_c为接触颗粒的弹性模量，Pa；L为接触颗粒间黏结键的长度（即颗粒的中心距离），m；μ为接触颗粒间的摩擦系数。

此处参考澳大利亚标准AS 4133.4.3.1—2009，设计搭建单轴压缩试验平台。通过万能材料试验机与位移传感器获取单块钨矿石在单轴压缩破碎过程中的应力—应变曲线。准备2组规格为⌀100 mm×250 mm的柱状钨矿石试样，依次通过夹具固定在万能材料试验机上，而后试验机的上压头在控制台中液压油的作用下保持向下匀速缓慢运动，速度约为0.05 mm/s；与上压头连接的力学传感器用于记录各时刻下钨矿石的受压情况，直至钨矿石破碎。单轴压缩试验平台及试验结果如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 钨矿石单轴压缩试验结果

Fig.6 Uniaxial compression test results of W-ore

由图6可知，钨矿石试样按轴线方向呈一定倾斜角破碎成大小不等的几块。根据钨矿石单轴压缩试验结果，在离散元软件中设置与试验条件一致的环境参数，并开展柱状钨矿石单轴压缩仿真分析，压缩过程中钨矿石的力链变化情况如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 单轴压缩仿真过程中钨矿石力链的变化情况

Fig.7 Changes of force chain of W-ore during uniaxial compression simulation

由图7可知，基于改进破碎模型的钨矿石单轴压缩仿真结果与试验结果吻合。为获得最佳的黏结参数，通过仿真得到8组不同黏结参数下钨矿石在单轴压缩过程中的应力—应变曲线，其中黏结参数的设置如表4所示。

表4 钨矿石颗粒黏结参数设置

Table 4 Setting of bonding parameters for W-ore particles

组别	K_nA/(N/m³)	K_tA/(N/m³)	σ_{n, max}/Pa	σ_{t, max}/Pa	R/mm
1	5.0×10¹⁰	1.0×10¹⁰	7.5×10⁷	2.5×10⁷	1.2
2	7.5×10¹¹	2.5×10¹¹	5.0×10⁸	1.0×10⁸	1.2
3	7.5×10¹⁰	2.5×10¹⁰	5.0×10⁸	1.0×10⁸	1.2
4	7.5×10¹¹	5.5×10¹¹	2.5×10⁸	1.0×10⁸	0.5
5	7.5×10¹²	5.5×10¹²	2.5×10⁹	1.0×10⁹	0.5
6	9.5×10¹²	7.5×10¹²	5.0×10⁹	2.5×10⁹	0.5
7	2.5×10¹³	9.5×10¹²	7.5×10⁹	5.0×10⁹	0.5
8	5.0×10¹³	2.5×10¹³	1.0×10¹⁰	7.5×10⁹	0.5

新窗口打开| 下载CSV

记录2次单轴压缩试验中钨矿石的平均应力—应变曲线。按表4中的黏结参数开展钨矿石单轴压缩仿真分析，并与试验曲线对比，结果如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

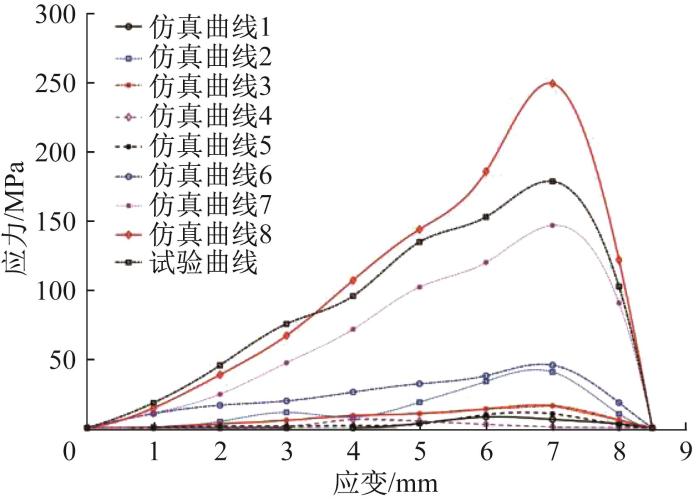
图8 钨矿石单轴压缩过程中的应力—应变曲线对比

Fig.8 Comparison of stress-strain curves of W-ore during uniaxial compression

由图8可知，钨矿石的极限应力为178 MPa，其在压密阶段的临界应力为17.8 MPa，弹性阶段的临界应力为72 MPa。根据AS 4133.4.3.1—2009，岩石抗压强度应大于50 MPa，说明仿真结果合理且有效。采用标准差公式计算钨矿石应力仿真结果与试验结果的误差。

e = \sqrt[]{\frac{1}{J} \sum_{j = 1}^{J} (σ_{j} - σ_{0 j})^{2}}

(8)

式中：σ_j 为第j个应力仿真值，MPa；σ₀_j 为第j个应力试验值，MPa；J为应力取值个数。

8组黏结参数下钨矿石应力仿真值与试验值的误差如表5所示。

表5 不同黏结参数下钨矿石应力仿真值与试验值的误差

Table 5 Error between simulation and experimental values of stress of W-ore under different bonding parameters

组别	误差/MPa
1	97.210
2	82.814
3	91.932
4	98.416
5	96.071
6	75.523
7	24.852
8	29.212

新窗口打开| 下载CSV

由表5可知，在第7组黏结参数下，钨矿石应力仿真值与试验值的误差最小，其标准差为24.852 MPa，两者的相对误差为3.11%。因此，选择第7组黏结参数作为对辊破碎机层压破碎仿真分析中钨矿石的破碎参数。

2 对辊破碎机层压破碎仿真分析

在对辊破碎机层压破碎仿真分析中，钨矿石颗粒的连续替换过程如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 钨矿石颗粒在对辊破碎机破碎腔中的连续替换过程

Fig.9 Continuous replacement process of W-ore particles in the crushing chamber of dual-roller crusher

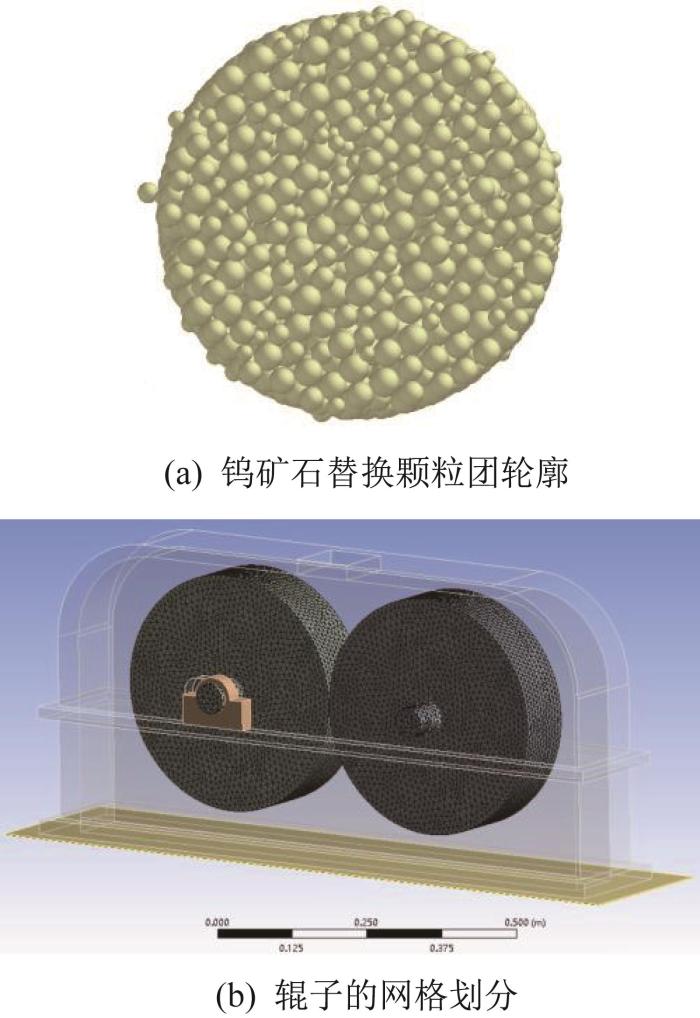
如图9(a)所示，钨矿石颗粒首次替换后按多峰分布生成2类颗粒：大颗粒和小颗粒1（图中的绿色大颗粒与蓝色小颗粒），同时生成3种不同的黏结键：大颗粒—大颗粒；大颗粒—小颗粒1；小颗粒1—小颗粒1。颗粒受挤压再次破碎，如图9(b)所示，将首次替换的大颗粒继续替换为小颗粒2（图中黄色小颗粒），如图9(c)所示，此时亦生成3种不同的黏结键：小颗粒1—小颗粒1；小颗粒1—小颗粒2；小颗粒2—小颗粒2。

基于图9，建立对辊破碎机的层压破碎仿真模型。为提高仿真效率，利用三维建模软件建立2PG400×250型对辊破碎机的简化三维模型，其中辊子直径与实物一致，辊子长度减小至 100 mm，去除电机、皮带等不影响破碎可视化仿真结果的零部件，以便观察。此外，在仿真过程中不考虑对辊破碎机自身的磨损情况。

每个替换小颗粒均可视作1个独立体，因此钨矿石颗粒的网格数量即为替换颗粒簇剖面的层数^[14]。根据Moes理论^[27]，颗粒断裂网格层数应大于10层，如图10(a)所示，本文中钨矿石颗粒断裂网格层数为19层。由于被碾压后的物质多为粉末或黏结成型，参考圆锥破碎机的几何建模理论^[28]，将对辊破碎机的辊子定义为刚性体元件，并利用有限元mesh网格功能进行划分，如图10(b)所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 钨矿石颗粒团和对辊破碎机辊子的网格划分

Fig.10 W-ore particle clusters and grid division of rollers in dual-roller crusher

为使仿真更贴近真实情况，将待破碎钨矿石颗粒按点-点接触、点-面接触、面-面接触在颗粒工厂生成3类不同形状的颗粒。对不同钨矿石入料粒径配比下的对辊破碎机层压破碎过程进行3组仿真分析，其中钨矿石的粒径和质量设置如表6所示。

表6 仿真分析中钨矿石颗粒的粒径和质量设置

Table 6 Setting of particle size and mass of W-ore particles in simulation analysis

粒径/mm	质量/g
粒径/mm	第1组	第2组	第3组
8	100	16.67	20
9	100	16.67	20
10	100	16.67	20
11	75	25	30
12	75	25	30
13	30	25	60
14	30	25	60
15	15	25	30
16	15	25	30
17	30	25	150
18	30	25	150

新窗口打开| 下载CSV

按表1、2以及表4中第7组参数对对辊破碎机层压破碎仿真模型的参数进行设定，其中辊子转速设为±135 r/min（2个锟子的转动方向相反）。钨矿石的破碎过程按破碎的不同时期——生成破碎颗粒、料层密实阶段、破碎阶段、排料阶段^[29]进行可视化仿真分析，如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

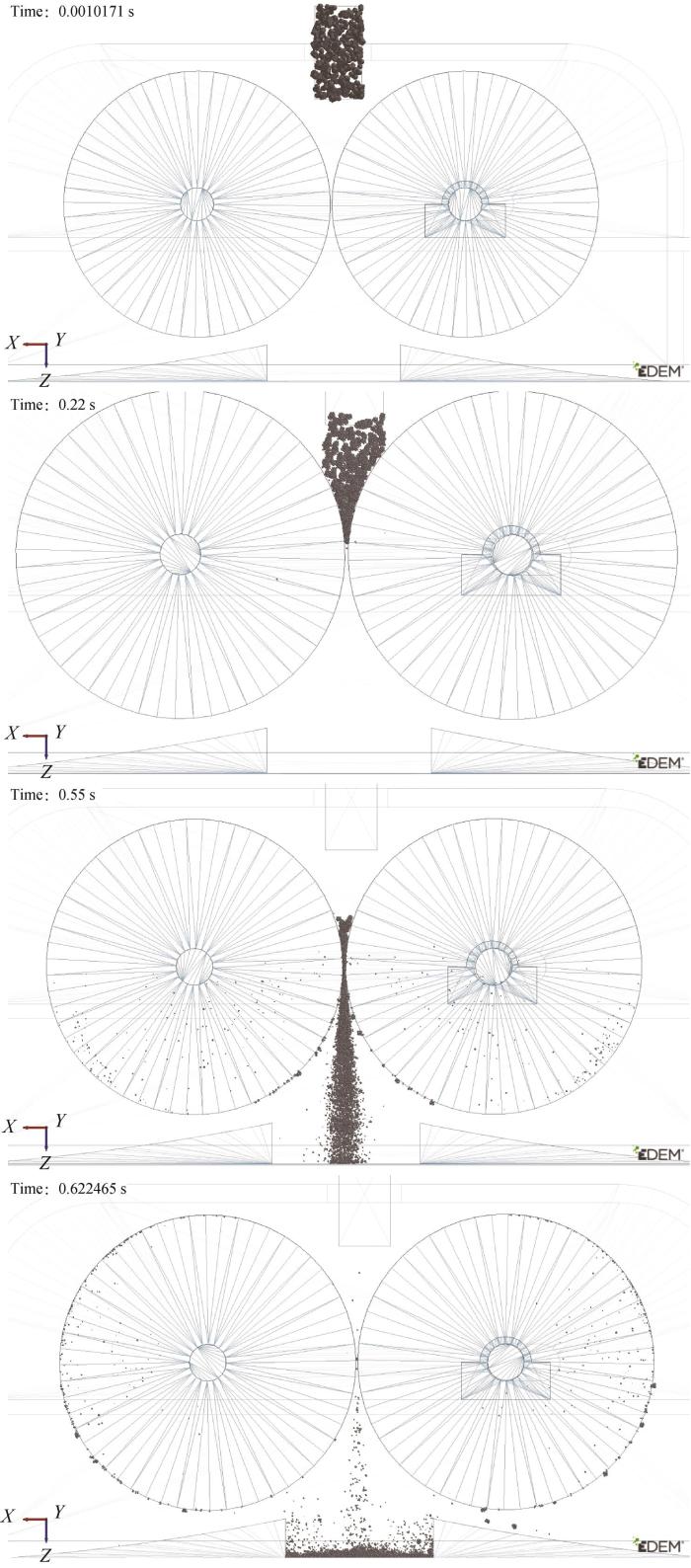
图11 钨矿石颗粒破碎过程可视化仿真

Fig.11 Visual simulation of W-ore particles crushing process

如图11所示，在t=0.001 s时，所有颗粒在颗粒工厂中生成；在t=0.220 s时，部分颗粒完成破碎并从出料口排出；在t=0.622 s时，完成破碎。

通过后处理，进一步研究钨矿石颗粒在破碎过程中颗粒与颗粒、颗粒与辊子间受力的变化情况以及颗粒数量随破碎时间的变化情况，结果如图12所示。

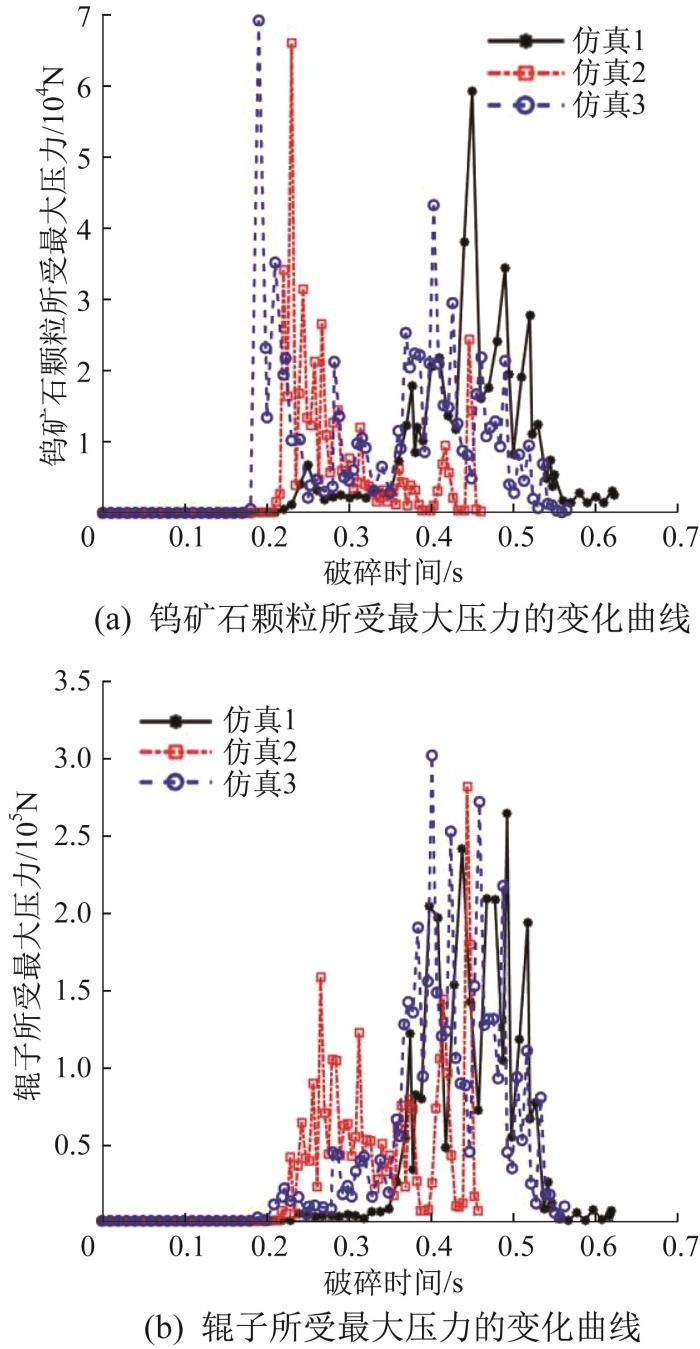
图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 破碎过程中钨矿石颗粒和辊子所受最大压力的变化曲线

Fig.12 Variation curves of maximum pressure on W-ore particles and rollers during crushing process

通过仿真可知，由于第3组仿真中大颗粒占比高，而第1组仿真中小颗粒占比高，第3组仿真中钨矿石颗粒率先接触辊子。此外，从图12中还可以看出，钨矿石在破碎期间所受的最大压力呈振荡波动变化，说明破碎过程中颗粒运动具有复杂性。在3组仿真中，钨矿石颗粒所受的最大压力为7.0×10⁴ N，辊子所受的最大压力为3.0×10⁵ N。

为进一步验证将辊子视为刚性体的合理性，对辊子工作时辊面的最大弹性形变量进行分析。弹性形变量δ的计算式如下：

δ = \frac{F_{r} l}{E_{r} S}

式中： $F_{r}$ 为辊子所受的最大压力，N； $l$ 为辊子的长度，m，本文取 $l$ =0.1 m；E_r为辊子的弹性模量，Pa；S为接触面积，m²，由于接触面积较难直接获取，利用S=F_r/P计算得到，其中P为辊子所受的压强，Pa。

将仿真得到的后处理数据代入式(9)，得出辊子的最大弹性形变量为0.09 mm，形变量较小，因此可将辊子视为刚性体。

为准确直观地解释对辊破碎机的层压破碎特性，提取第3组仿真中某段时间内的数据，并利用插值拟合法进行处理，结果如图13所示（每个时间步长为0.005 s）。其中：图13(a)所示为某段时间内钨矿石颗粒间的最大相互作用力与辊子的最大作用力的差值（下文简称为净作用力），该值越大，说明颗粒间相互作用力在颗粒破碎中的主导作用越显著；图13(b)所示为该段时间内钨矿石颗粒破碎后的数量变化。

图13

新窗口打开| 下载原图ZIP| 生成PPT

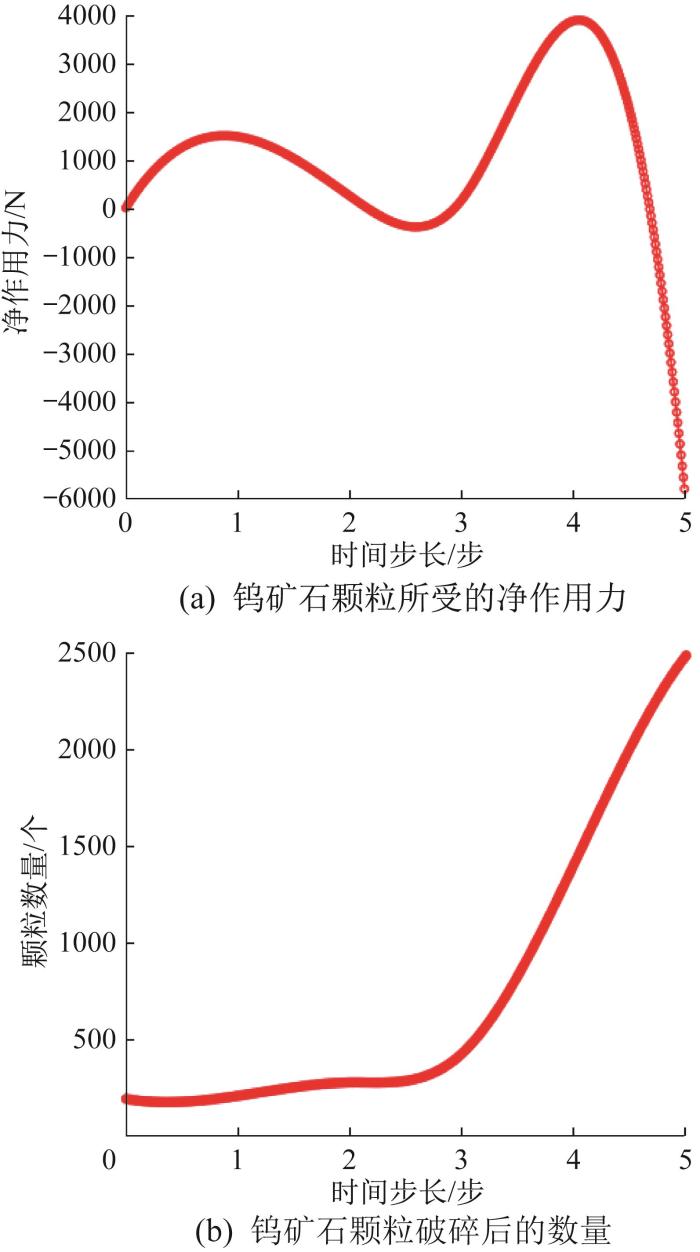
图13 某段时间内钨矿石颗粒的破碎信息

Fig.13 Crushing information of W-ore particles within a certain time

由图13可知，时间步长为0时钨矿石颗粒群所受的颗粒间相互作用力与辊子的作用力一致，且颗粒破碎速率较小，说明此时刚进入破碎阶段。随着破碎时间的增加，在时间步长为0~2时，钨矿石颗粒所受的颗粒间相互作用力比辊子的作用力大，颗粒破碎速率有所增大，但净作用力的最大值约为1 600 N，无法有力说明此时颗粒破碎主要受颗粒间相互作用力的影响。在约第4个时间步长处，净作用力达到最大，而后不断减小，但钨矿石颗粒所受的颗粒间相互作用力和锟子作用力的合力变化较小，因此破碎速率并无明显变化。在第5个时间步长处，净作用力为-6 000 N，说明此时颗粒破碎主要受辊子作用力的影响。

利用式(10)对图13(a)中的数据进行拟合，结果如表7所示。

Δ F = \sum_{s = 0}^{W} q_{s} t_{f}^{s}

式中：ΔF为某段时间内钨矿石颗粒所受的净作用力；q_s 为拟合参数；t_f为时间步长。

表7 钨矿石颗粒所受的净作用力与时间的拟合参数取值

Table 7 Fitting parameter values of net force on W-ore particles and time

参数	数值
$q_{0}$	73.68
$q_{1}$	2 752
$q_{2}$	193.4
$q_{3}$	-2 316
$q_{4}$	997.6
$q_{5}$	-114.9

新窗口打开| 下载CSV

根据表7结果，计算得到上述拟合函数的相关系数r²=0.989 8，说明该函数可用于描述该时间段内钨矿石颗粒的受力情况。

同样，利用式(11)对图13(b)中的数据进行拟合，拟合结果如表8所示。

N = c_{1} + \sum_{s = 0}^{W} a_{s} e^{b_{s} t_{f}}

式中：N为钨矿石颗粒的数量；a_s 、b_s 、c₁为拟合参数。

表8 钨矿石颗粒数量与时间的拟合参数取值

Table 8 Fitting parameter values of W-ore particle quantity and time

参数	数值
$a_{0}$	3.415
$a_{1}$	5.029×10⁴
$b_{0}$	1.245
$b_{1}$	0.003 16
c₁	-5.028×10⁴

新窗口打开| 下载CSV

根据表8结果，计算得到该拟合函数的相关系数r²=0.964 8，说明该函数可用于描述该时间段内钨矿石颗粒数量的变化情况。

求式(10)关于时间步长的一阶与二阶导数，计算得到钨矿石颗粒所受的净作用力最大时对应的时间步长t_f=4.116（即开始计时0.020 6 s后），此时最大净作用力为3 767.85 N（颗粒间最大相互作用力为辊子最大作用力的2倍）。求式(11)关于时间步长的一阶导数，代入t_f=4.116，计算得到该时刻下钨矿石颗粒的破碎速率v_f=875.60 颗/时间步长，即破碎后其数量以875.0颗/时间步长的速度增加。由此可知，对辊破碎机在一定程度上可实现层压破碎。

3 对辊破碎机层压破碎试验

为验证钨矿石颗粒破碎仿真分析的正确性和探究对辊破碎机的层压破碎特性，利用2PG400×250型对辊破碎机开展钨矿石破碎试验，试验平台以及相应工具如图14所示。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 钨矿石破碎试验平台及相应工具

Fig.14 W-ore crushing test platform and corresponding tools

根据表6的入料粒径配比，开展对应的钨矿石破碎试验（每组配比下均开展3次重复试验，记为A、B、C）。鉴于VC++软件的运算速度快，精度高，利用VC++编写整理仿真后处理数据的程序，并将所得结果与试验结果进行对比。钨矿石碎后不同粒径颗粒的占比（用质量分数表示）和质量的对比如图15所示。

图15

新窗口打开| 下载原图ZIP| 生成PPT

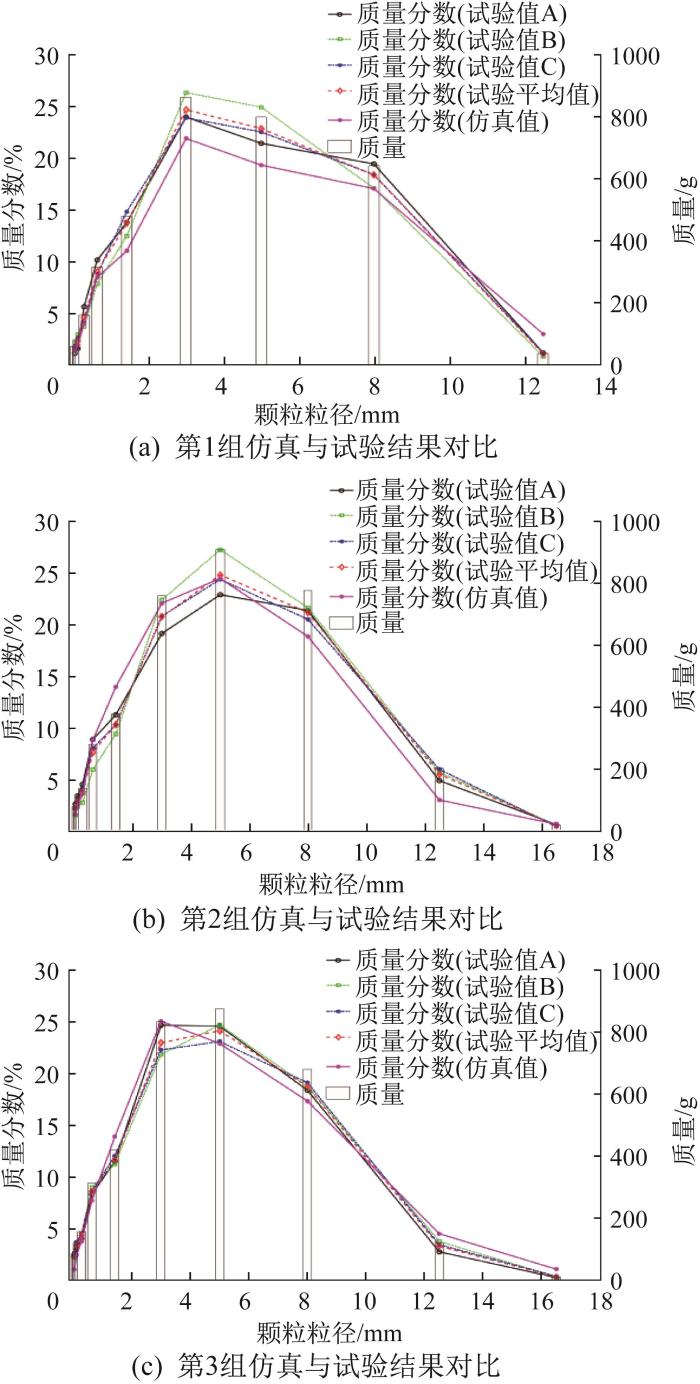
图15 钨矿石碎后不同粒径颗粒的占比及质量对比

Fig.15 Comparison of proportion and quality of particles with different sizes of W-ore after crushing

利用式(12)对钨矿石碎后粒径分布仿真结果进行拟合，拟合结果如表9所示。

y = a e^{- {(\frac{d - b}{c})}^{2}}

式中：y为质量分数；a、b、c为拟合参数。

表9 钨矿石碎后粒径分布拟合参数取值

Table 9 Fitting parameters values of particle size distribution of W-ore after crushing

组别	拟合参数
组别	a	b	c
1	23.42	5.415	4.319
2	27.16	5.395	4.143
3	26.88	5.169	3.992

新窗口打开| 下载CSV

上述3组仿真结果拟合函数的相关系数r²=0.906 8，0.928 4，0.914 4，由此说明钨矿石碎后粒径分布满足正态分布。

根据图15，计算钨矿石碎后颗粒质量分数的仿真结果与试验结果的误差，计算方式如下：1）选取与仿真结果接近的试验数据进行计算（记为方案1）；2）利用试验数据平均值进行计算（记为方案2）。钨矿石碎后质量分数仿真结果与试验结果的误差如表10所示。

表10 钨矿石碎后质量分数仿真结果与试验结果的误差

Table 10 Error between simulation results and experimental results of mass fraction of W-ore after crushing

组别	误差/%
组别	方案1	方案2
1	1.257	1.940
2	1.183	1.689
3	0.889	1.369

新窗口打开| 下载CSV

由图15可以看出，钨矿石颗粒碎后粒径呈正态分布，其中d=2~6 mm的颗粒最多，其质量达到近1 700 g；d<2 mm与d>10 mm的颗粒的占比均不足15%，仅有1种粒径的颗粒超过了25%。此外，入料粒径越大，破碎时钨矿石对辊子的压力越大，导致辊缝越大，从而导致最终占比高的颗粒粒径越大。由表10可知，钨矿石颗粒碎后粒径分布的仿真结果与试验结果的误差较小。对于方案1，其误差为0.889%~1.257%；对于方案2，其误差为1.369%~1.940%。由此可知，仿真分析可近似描述对锟破碎机的实际破碎情况，对实际生产有一定指导意义。

为进一步研究对辊破碎机真实的层压破碎特性，在辊隙为2 mm、频率为50 Hz的条件下，选取8种不同的钨矿石入料粒径配比，开展钨矿石层压破碎试验。具体方案如下：

1）取粒径分别为8~<10，10~<12，12~<14，14~<16，16~18 mm（定义为5个粒径等级，即等级1，2，3，4，5）的钨矿石颗粒，按表11配比将其混合均匀，每次试验中钨矿石颗粒的总质量为8 kg，总计728 kg。经计算，5个粒径等级的钨矿石颗粒分别需要191.1，127.4，136.5，136.5，136.5 kg。

表11 钨矿石入料粒径配比（质量分数)

Table 11 Feed particle size ratio of W-ore (mass fraction) %

编号	粒径/mm
编号	8~<10	10~<12	12~<14	14~<16	16~18
1	50	20	10	10	10
2	50	10	20	10	10
3	20	40	20	10	10
4	40	20	20	10	10
5	20	20	20	20	20
6	10	10	20	30	30
7	10	10	20	20	40
8	10	10	20	40	20

新窗口打开| 下载CSV

2）调节对锟破碎机出料口的间隙（即锟隙）为2 mm以及频率为50 Hz。启动破碎机，待其空载运行平稳后，一次性快速地将混合均匀的钨矿石颗粒倒入破碎腔，并使其在破碎腔中平铺，以满足层压破碎的条件，然后开始破碎试验。为减小误差，对每组配比下的钨矿石颗粒重复进行3次破碎试验。

3）将碎后的钨矿石颗粒进行缩分取样，按50%（约4 kg）进行统计。将碎后的钨矿石颗粒倒入分选筛进行筛分，并用电子秤测量各粒级钨矿石颗粒的质量，用于分析对锟破碎机的层压破碎特性。

层压破碎试验用钨矿石颗粒原料与破碎后的钨矿石颗粒如图16所示。图中1~8对应表11中入料粒径配比的编号。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 层压破碎试验用钨矿石原料及其碎后颗粒

Fig.16 W-ore raw materials for laminated crushing test and their crushed particles

统计碎后不同粒径钨矿石颗粒的质量分数，结果如图17所示。

图17

新窗口打开| 下载原图ZIP| 生成PPT

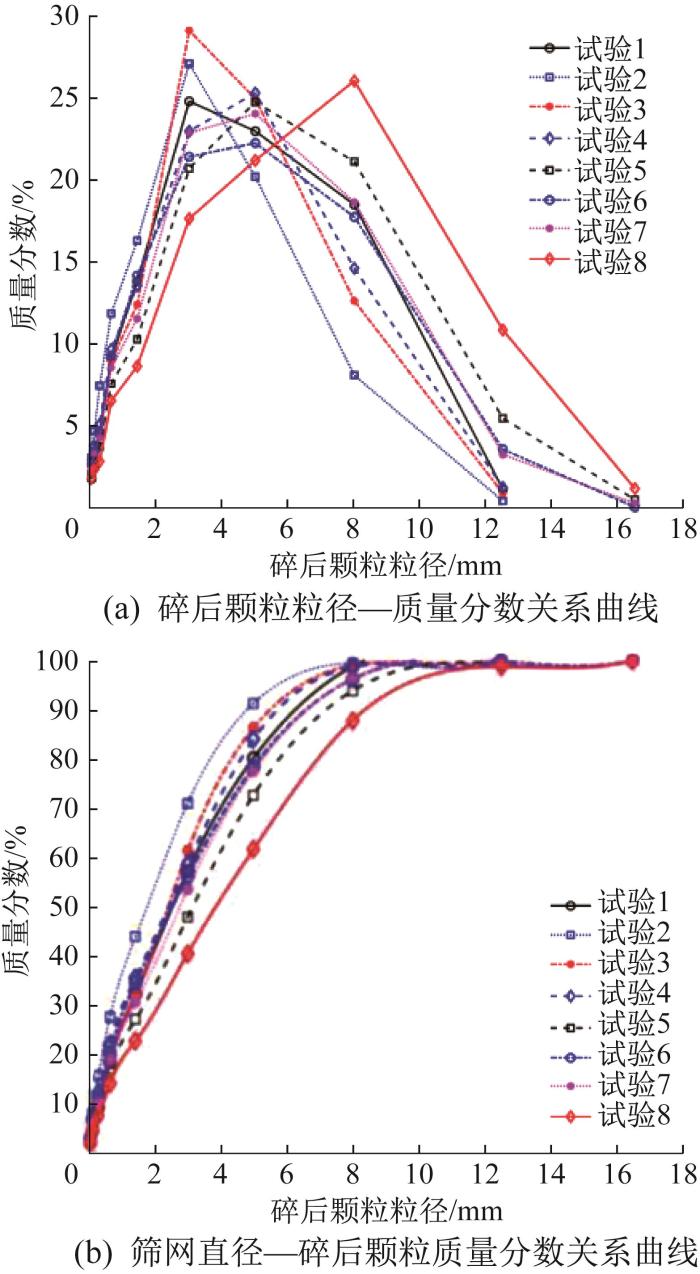
图17 不同入料粒径配比下钨矿石碎后的粒度分布

Fig.17 Particles size distribution of W-ore after crushing under different feed particle size ratios

通过查阅文献[30]与孔隙率试验，选取不同的钨矿石混合颗粒，开展10组注水试验以计算其孔隙率，结果如表12所示。结果表明，入料粒径越小，试样孔隙率越小，即试样越密实。

表12 钨矿石入料粒径配比与对应孔隙率

Table 12 Feed particle size ratio of W-ore and corresponding porosity

试验编号	颗粒1		颗粒2		颗粒3		孔隙率/%
试验编号	粒径/mm	质量/kg	粒径/mm	质量/kg	粒径/mm	质量/kg	孔隙率/%
1	4~6	10					34.16
2	8~10	10					48.54
3	0~0.15	4	8~10	10			29.85
4	0~0.15	6	8~10	10			19.36
5	4~6	5	8~10	5			41.44
6	4~6	3	8~10	6			45.92
7	6~<8	5	8~10	5			37.30
8	8~<10	5	10~12	5			33.75
9	8~<10	6	10~12	3			32.02
10	2~<4	0.9	4~<6	7.2	6~8	1.8	33.30

新窗口打开| 下载CSV

由图17(a)可知，钨矿石颗粒碎后粒径与对应质量分数的关系：当入料粒径d=8~<12 mm颗粒（小颗粒）的占比超过50%时，碎后粒径分布在0~15 mm；当其占比不超过50%时，碎后粒径分布在0~18 mm。由图17(b)可知，试验2对应的曲线斜率最大，说明碎后小颗粒的占比最高，其中试验1~4中小颗粒的占比高于试验5~8，且试验1~4中小颗粒的占比从高到低依次为：试验2、试验3、试验4、试验1。

试验2，3的结果对比说明，在入料大粒径（等级3~5）颗粒一定的条件下，等级1的颗粒占比足够高（等级1颗粒与等级2颗粒的占比为5∶1）时的破碎效果较好，试验2中碎后粒径d<6 mm的颗粒比试验3多出5.02%。试验3，4的结果对比说明，在入料大粒径（等级3~5）颗粒占比一定的条件下，等级2颗粒的占比略高于等级1颗粒（2∶1）时的破碎效果较好，试验3中碎后粒径d<6 mm的颗粒比试验4多出2.33%。究其原因，孔隙率与颗粒间相互作用力共同影响层压破碎效果。试验5结果说明，不同粒径颗粒均匀混合（1∶1∶1∶1∶1）时的破碎效果差，其破碎效果不及试验6，7（等级3~5颗粒的占比为80%），试验5中碎后粒径d<6 mm的颗粒比试验6，7分别少5.74%，4.92%。试验7，8的结果解释了颗粒间相互作用力有时比低孔隙率更能影响层压破碎效果。

4 结论

为研究对辊破碎机的层压破碎特性，以钨矿石为对象，对其层压破碎过程进行仿真和试验分析，得出以下结论：

1）通过堆积试验获得了准确的钨矿石本征参数与接触参数；利用离散元API设计了一种改进破碎模型（改进的BPM），实现了颗粒的连续多次替换；通过单轴压缩试验采集了钨矿石的应力—应变数据，并应用于模型的参数标定。

2）通过离散元软件对对辊破碎机的层压破碎过程进行可视化仿真分析，说明了钨矿石在对辊破碎机中连续多次替换的实现过程，并开展3组不同入料粒径配比下的钨矿石层压破碎仿真分析，通过对破碎过程中某时间段内钨矿石颗粒的受力情况及其碎后数量的定量分析，验证了对辊破碎机可实现层压破碎。

3）开展对辊破碎机层压破碎试验，统计钨矿石碎后粒径分布情况。结果表明，碎后粒径分布满足正态分布，并验证了仿真分析的有效性；通过不同入料粒径配比下的层压破碎试验得出，颗粒间相互作用力与颗粒孔隙率共同影响破碎效果，且颗粒间相互作用力的影响程度大于颗粒低孔隙率。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

SCHWINDIG

Versuche und Betrachtungen zur Ueberwalzzerkleine rung eines Mahlbettes

［J］. Aufbereitungstechnik， 1966， 8： 489-492.