滚动轴承具有精度高、负载大、磨损小和使用寿命长等优点，被广泛用作旋转机械中重要的基础零部件。据统计，30%的旋转机械故障和44%的大型异步电机故障均是由轴承故障引起的^[1]。轴承的运行状态直接影响机械的使用，轴承故障会造成经济损失甚至危害人身安全。因此，开展轴承动力学建模并对其内部动态特性进行研究，对轴承故障识别有十分重要的现实意义，同时也能为轴承监测系统的研发提供有效帮助。

随着计算机技术和弹性接触理论的发展，很多学者开始利用有限元法来求解滚动轴承的振动特性及动态特性。针对正常轴承，林腾蛟等^[2]利用有限元仿真软件建立了深沟球轴承多体动力学模型，研究了不同转速下其滚动体与各元件动态应力及接触力的变化。姚灿江等^[3]通过对RV（rotary vector，旋转矢量）减速器中的滚动轴承进行有限元仿真，分析了该轴承在实际工作中的接触应力和接触变形。针对单一故障轴承，不少学者对其内部动态特性展开了研究。汤武初等^[4]建立了正常和滚动体表面剥落情况下圆锥滚子轴承的有限元模型，研究了滚动体故障时该轴承的等效应力集中位置。He等^[5]采用有限元法建立了存在滚子剥落缺陷的圆柱滚子轴承动力学模型，分析了缺陷滚子和轴承的振动响应以及滚子与保持架的接触力。陈培红^[6]建立了在滚动体破裂、剥落和出现麻点等故障状态下滚动轴承的有限元模型，并与无故障滚动轴承的动态应力和接触力进行了对比分析。Gao等^[7]建立了6206深沟球轴承的动力学模型，模拟了该轴承在滚动体断裂、滚动体剥落和轴承点蚀状态下的有效应力和接触力，并与正常深沟球轴承的接触特性进行了比较。江泽鹏等^[8]建立了盾构主推力滚子轴承有限元模型，研究了转速和轴向载荷对该轴承动态应力的影响。然而，上述学者大多是针对滚动体故障，研究了转速及载荷对滚动轴承动态应力的影响，但忽略了外圈故障对其动态特性的影响。

为此，李国超等^[9]建立了滚动轴承外圈裂纹故障有限元模型，分析了外圈故障时轴承各元件的应力。Singh等^[10]利用ANSYS/LS-DYNA软件建立了外圈故障时滚动轴承的有限元模型，针对滚动体进入和离开故障区域阶段进行了时域和频域处理。Zhang等^[11]运用显式动力学方法模拟了滚动体经过缺陷时滚动轴承缺陷区域的最大Mises应力和最大接触压力，并研究了径向载荷、转速和初始缺陷尺寸对应力的影响。Tang等^[12]建立了缺陷圆柱滚子轴承的有限元模型，计算了缺陷周围的应力分布，得出：随着转子转速的增大，滚子离开缺陷区域时所受的应力增大；径向载荷或缺陷长度的增大会导致所有阶段的应力增大。张志伟^[13]利用ANSYS/LS-DYNA软件对正常和外圈剥落的滚动轴承进行显式动力学求解，分析了正常和外圈剥落时轴承的等效应力云图和切片应力云图。谢向宇等^[14]建立了内圈损伤和正常轴承的有限元模型，并对内圈损伤轴承的应力和位移等动态特性进行了分析。马辉等^[15]建立了圆柱滚子轴承的二维有限元模型，对故障区域单元的等效应力及滚子经过内、外圈局部缺陷区域的过程进行了研究。综上所述，学者们对滚动轴承的仿真主要集中在研究单一故障下故障尺寸、转速及载荷对轴承内部动态特性的影响，而对不同元件在相同条件下出现故障时轴承动态特性之间的差异性和相似性的研究较少。

基于此，笔者以NU306圆柱滚子轴承为研究对象，利用ANSYS/LS-DYNA软件建立其有限元模型，并利用显式动力学方法对正常轴承以及具有外圈、内圈和滚动体单一故障的轴承的应力特性、振动特性和运动特性进行动态模拟，以揭示不同元件出现故障时轴承内部动态特性之间的差异性及相似性，旨在为滚动轴承的故障预测及动态性能评估提供理论依据。

以NU306圆柱滚子轴承为研究对象，其主要的几何参数如表1所示。在该滚动轴承外圈、滚动体及内圈上分别设立1 mm×1 mm的贯穿缺陷，分别建立正常和故障轴承的有限元模型。

在实际工作中，滚动轴承主要承受径向载荷，其所受的轴向作用力较小^[16]。在滚动轴承有限元分析过程中，将模型离散为节点和单元是一个重要步骤。基于体单元的三维有限元模型虽可以精确地描述滚动轴承的振动状态，但其需要的计算内存和时间较多。而基于壳单元的二维有限元模型同样可以精确描述滚动轴承的振动状态，且其单元数和节点数少，只需要较少的计算内存和时间^[17]。基于此，本文采用ANSYS/LS-DYNA软件建立NU306圆柱滚子轴承的二维有限元模型，模型中所有元件均选用Shell 163壳单元进行网格划分，这是因为高质量的四边形单元可以提高模型的精度并缩短求解时间^[5]。而对内、外圈和滚动体的接触区域则采用较密的网格进行划分，这是因为滚动体需要与内、外圈保持连续滚动接触，以便滚道之间传递负载。有限元仿真分析结果的准确性取决于网格划分质量，故需通过不断调整网格尺寸，并观察仿真结果是否满足以下3个条件来确定最佳的网格尺寸：1）在仿真过程中，滚动体与滚道保持连续接触；2）计算精度达到要求；3）因网格划分而产生的振动噪声尽量小。

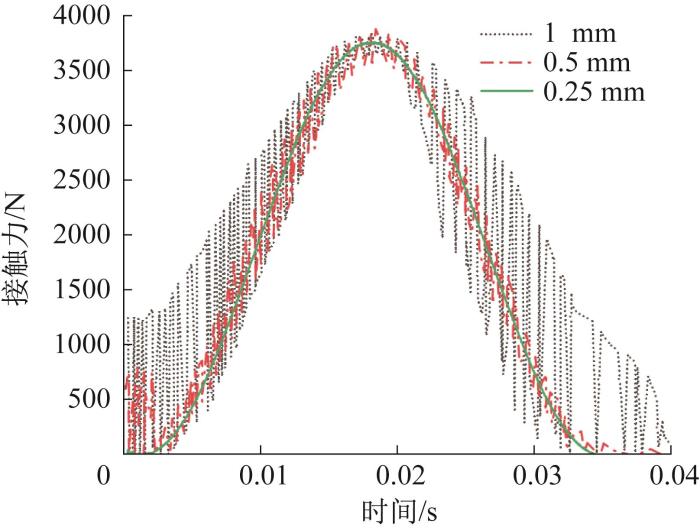
为综合满足上述3个条件，本文选取网格尺寸为1，0.5，0.25 mm进行试算，并对比不同网格尺寸下NU306圆柱滚子轴承滚动体与外圈的接触力，结果如图1所示。

从图1中可以看出，网格尺寸较大时接触力曲线不连续，而当网格尺寸小到一定程度（0.25 mm）时，接触力曲线较为光滑，说明此时滚动体与内、外圈可保持连续接触。因此，本文采用0.25 mm的网格对模型进行离散化。

为获得准确的动态响应，通常要求在波传播过程中波长大于网格尺寸的20倍。在进行瞬态结构动力学分析时，将滚动轴承的外圈视作一个薄板，其弯曲波速C_b可表示为^[10]：

式中：ω为角速度；E、ρ、ν分别为材料的弹性模量、密度和泊松比；T为薄板厚度。

已知薄板的角速度为220 rad/s、频率为40 kHz、厚度为19 mm以及各材料参数，将各参数代入式(1)计算得到外圈的弯曲波速为2 722.50 m/s，对应的波长为0.067 9 m，相当于0.25 mm网格的271倍，远大于20倍，可确保外圈与滚动体连续接触，使得滚动体接触应力的变化控制在5%以内^[18]。

最终的NU306圆柱滚子轴承二维有限元模型如图2所示，共含66 556个单元，69 227个节点。

本文主要研究滚动轴承内部的动态应力，故其内部元件采用线弹性材料模型。轴承的内、外圈及滚动体选用GCr15钢，其密度ρ₁=7 830 kg/m³，弹性模量E₁=206 GPa，泊松比v₁=0.3；保持架材料为黄铜，其密度ρ₂=8 500 kg/m³，弹性模量E₂=105 GPa，泊松比v₂=0.324。

由结构动力学可知，物体在冲击下会产生振动，而结构阻尼的存在会使振动逐渐减缓。因此，在滚动轴承非线性有限元分析中，考虑采用施加阻尼的方法来减缓振动。本文通过关键字来抑制低频的结构振动模式，同时为抑制刚体模式的效应以及高频振动和数值振荡，施加质量比例系统阻尼。施加阻尼前后NU306圆柱滚子轴承有限元模型网格单元的位移如图3所示。

从图3中可以看出，当模型未施加阻尼时，网格单元中心位移会出现明显的数值振荡现象，经较长时间后才会收敛，最终收敛时间为0.1 s（一般有限元计算时间为0.02 s），与施加阻尼后的计算时间相比延长了几倍；而当模型施加阻尼后，数值振荡的频率和幅度明显减小且计算时间明显缩短，有效地提高了计算效率。

为利用有限元模型模拟真实滚动轴承运转过程中的实际工况，在建模过程中施加与实际工况一致的载荷、转速及边界约束。滚动轴承在工作时多安装于轴承座中，其外圈与轴承座过盈配合，故对外圈施加全约束；在内圈内表面节点上施加一个恒定的转速（n=2 100 r/min），使内圈逆时针旋转，同时在内圈内表面上施加恒定的径向载荷（F=3 000 N，沿Y轴正向）。

在定义滚动体内部接触状态时，应尽量避免其节点在初始状态下产生接触。本文通过采用接触力罚函数来避免从面穿透主面。在定义滚动体与内、外圈的接触时，本文选择二维自动面-面接触，滚动体外表面为接触面，内、外圈内表面及保持架表面为目标面，分别建立了内、外圈和保持架与12个滚动体的接触对。滚动体与内、外圈及保持架兜孔的静摩擦因数为0.01，动摩擦因数为0.005^[19]。

为了验证所构建的有限元模型的有效性，搭建了NU306圆柱滚子轴承实验台。其主要由伺服电机、径向加载装置、JL1086型力显示器、加速度传感器、伺服电机控制器和KSI-8904N型采集卡以及实验轴承、加载轴承和支撑轴承等组成，如图4所示。利用径向加载装置将径向载荷施加到加载轴承上，通过杠杆原理将一半的载荷传递至故障轴承内圈。故障轴承过盈安装在轴承座内，其内圈随电机主轴旋转。加速度传感器安装在轴承座表面上，通过数据采集卡采集轴承的振动信号，经LabVIEW图形转换后在个人计算机上显示，以便观察。

图5和图6所示分别为内、外圈故障时NU306圆柱滚子轴承滚动体振动加速度的仿真与实验结果的对比。由图可知，当轴承发生故障时，滚动体会产生周期性的冲击信号，仿真结果更为显著，这是因为在实验过程中存在一定的噪声干扰。此外，仿真与实验所得的振动加速度幅值接近，较好地验证了有限元模型的有效性。振动加速度仿真值略大于实验值，这是因为：1）在建立有限元模型时将滚动体与内、外圈的圆弧接触面划分成四边形网格，多边形效应导致振动幅值略有增大；2）仿真时提取距离故障较近的轴承内部的振动信号，实验时提取轴承座的振动信号。

为进一步验证有限元模型的有效性，对NU306圆柱滚子轴承故障特征频率的仿真和实验结果进行比较。轴承内、外圈故障特征频率f_ic、f_oc分别为：

式中：α为接触角，本文NU306圆柱滚子轴承的接触角为0º。

根据表1所示参数以及接触角和内圈转速，利用式(2)和式(3)计算得到该轴承的内圈故障特征频率为254.85 Hz、外圈故障特征频率为165.1 Hz。

对仿真和实验中采集到的振动加速度信号进行包络分析，得到NU306圆柱滚子轴承的故障特征频率，结果如表2所示。由表可知，外圈故障时实验特征频率为164.1 Hz，仿真特征频率为166.0 Hz，两者之间的相对误差为1.15%；内圈故障时实验特征频率为255.2 Hz，仿真特征频率为256.4 Hz，两者之间的相对误差为0.5%。故障特征频率的仿真值和实验值均接近理论值，但仿真值比实验值大，这是因为在实验过程中人为地加入了阻尼，使得实验转速比仿真转速低，从而导致实验特征频率小于仿真特征频率。综上所述，内、外圈故障时仿真结果与实验结果均吻合良好，验证了所构建的有限元模型的有效性。

当滚动轴承内部某一元件发生故障时，各元件的应力特性除了受故障的影响外，还会受元件位置的影响。将滚动体与内、外圈先接触的位置称为前端，后接触的位置称为后端。为研究滚动轴承各元件故障前后端等效应力的变化情况，对滚动体与内、外圈接触前后的动态应力进行分析。在不同元件的故障前后端选取对应单元，同时在正常轴承的相同位置处选择对应单元。不同故障位置前后端对应的单元编号如图7所示。

图8所示为不同故障状态下外圈故障前后端的等效应力。由图可知，不同故障状态下，外圈故障前端的应力均比正常轴承的应力滞后，而后端的应力均比正常轴承的提前，其中外圈故障时最为显著。这是因为在正常滚道中，滚动体在未到达外圈故障前端附近时就会形成应力集中区；而在滚道发生故障时，当滚动体到达外圈故障前端一侧时，故障区域会形成一定的应力积累缓冲。

不同故障状态下外圈故障前后端的平均等效应力如表3所示。由表可知，当外圈故障时，外圈故障前后端的平均等效应力远大于正常轴承。这是因为滚动体经过故障区域时发生了应力集中，故障区域产生了塑性变形。当内圈故障时，外圈故障前端的平均等效应力大于后端；当滚动体故障时，外圈故障后端的平均等效应力大于前端。通过对比不同故障状态下外圈故障前后端的平均等效应力可知，对于前端，外圈故障时平均等效应力的增长幅度最大，内圈故障时居中，滚动体故障时最小；对于后端，外圈故障时平均等效应力的增长幅度最大，滚动体故障时居中，内圈故障时最小。

图9所示为不同故障状态下内圈故障前后端的等效应力。由图可知，在不同故障状态下，内圈故障前端的应力均比正常轴承的应力滞后，而后端的应力均比正常轴承的提前，其中内圈故障时最为显著。这是因为内圈与滚动体的运动方向相反，当内圈故障时，滚动体在进入故障区域前因滚道接触刚度变化而导致故障前端的应力滞后，而滚动体从故障内圈离开时，故障前端的推力使得应力提前。

表4所示为不同故障状态下内圈故障前后端的平均等效应力。由表可知，不同故障状态下内圈故障前后端应力的变化趋势相似，内圈故障时的增长幅度最大，外圈故障时居中，滚动体故障时最小。

图10所示为不同故障状态下滚动体故障前后端的等效应力。由图可知，当滚动体故障时，滚动体故障前端的应力比正常轴承的应力滞后，而后端的应力比正常轴承的提前；而当内圈和外圈故障时，滚动体故障前端的应力比正常轴承的应力提前，后端的应力比正常轴承的滞后。

表5所示为不同故障状态下滚动体故障前后端的平均等效应力。由表可知，对于滚动体故障前后端的平均等效应力，滚动体故障时远大于内、外圈故障时，且滚动体故障时后端的应力大于前端；滚动体故障时应力的增长幅度最大，内圈故障时居中，外圈故障时最小。

综上所述，当滚动轴承内部元件发生故障时，相应故障后端的等效应力大于故障前端。这是因为除了滚动体边缘在通过连接滚动体和滚道的中心线时产生冲量外，滚动体缺陷与滚道之间也会产生冲量^[20]。当不同元件发生故障时，故障前端应力均会滞后，后端应力均会提前。外圈故障时滚道的塑性变形最大，故应力变化最大。

为研究在不同元件（外圈、内圈、滚动体）发生故障的状态下，滚动体进入、离开故障区域时滚动轴承的振动特性，对相同工况下不同元件故障时滚动体的振动加速度进行分析。将滚动体与外圈的接触点经过故障区域的整个过程分为3个阶段：进入故障区域前（滚动体接触刚度因故障而变化起至接触点到故障前端）、过故障区域期间（接触点从故障前端到故障后端）和离开故障区域后（接触点从故障后端到滚动体接触刚度恢复正常）。为方便表述，下文将这3个阶段简称为进入故障前、过故障期间和离开故障后。

图11所示为外圈故障时滚动体的振动加速度信号。当外圈故障时，在进入故障前，滚动体的振动加速度增大；在过故障期间，滚动体的振动加速度先减小后增大；在离开故障后，滚动体的振动加速度先减小后增大。这是因为外圈在发生故障后接触刚度减小，使得滚动体与外圈滚道的接触力减小；离开故障后，滚动体与外圈滚道逐渐恢复正常接触，产生应力后滚动体的振动加速度增大。

图12所示为内圈故障时滚动体的振动加速度信号。在经过内圈故障区域的整个过程中，滚动体振动加速度的波动较小。在进入故障前，滚动体的振动加速度逐渐减小；在过故障期间，滚动体的振动加速度处于小幅度波动式上升状态。这是因为当内圈故障时，滚动体在进入故障前与内圈的间隙逐渐增大，两者的接触力逐渐减小，从而导致振动加速度减小，而滚动体在过故障期间因自身重力作用而导致在到达故障区域中间时振动加速度增大。在离开故障后，滚动体的惯性力和故障后端的推力使滚动体的振动加速度在小范围内波动变化。

图13所示为滚动体自身故障时与内、外圈接触处的振动加速度信号。在进入故障前和离开故障后，滚动体的振动加速度减小；在过故障期间，滚动体的振动加速度增大。这是因为当滚动体故障时，在进入故障前和离开故障后，滚动体的运转方向与内圈相反，滚动体除了受到内圈的推力外，还会因自身的逆时针运转而削弱振动加速度；而在过故障期间，滚动体在原有推力的基础上还受到自身重力的作用，故振动加速度增大。

为了进一步定量描述经过故障区域期间滚动体振动信号的差异性，选取不同故障状态下滚动体振动信号的时域指标进行对比。各时域指标的计算式如下。

峰峰值P_k为：

峭度值K_u为：

式中：N为振动信号个数；μ、σ分别为振动信号的均值和标准差。

均方根值R_MS为：

脉冲指标I为：

不同故障状态下滚动体振动加速度的时域指标如表6所示。通过分析可知，在相同工况下，内圈故障时滚动体的振动信号更为平缓，这与图12所示结果相吻合；外圈故障时振动信号的峭度值最大，即较内圈和滚动体故障时的振动信号明显；滚动体故障时振动信号的均方根最大，即振动信号的冲击幅值变化最明显。

综上所述，当内圈故障时，滚动体的振动加速度最小；当外圈故障时，在进入故障前滚动体的振动加速度增大，在过故障期间和离开故障后均是先减小后增大；当滚动体故障时，在进入故障前和离开故障后滚动体的振动加速度减小，在过故障期间增大。

滚动体的公转转速是指内圈带动滚动体绕轴心运动时的转速。观察过故障期间滚动体公转转速之间的差异性，可为轴承故障的诊断提供依据。正常轴承滚动体的公转转速n_m可表示为：

滚动体公转转速n_m与公转角速度Ω的转换关系为：

将所有参数代入式(8)和式(9)，得到正常轴承滚动体的公转角速度Ω=86.7 rad/s。

图14所示为不同故障状态下滚动体经过故障区域期间的公转角速度。通过分析图14数据可知，当外圈故障时，滚动体在进入故障前的公转转速在理论公转转速附近波动；在过故障期间，滚动体的公转转速降低；在离开故障后，滚动体的公转转速升高并在理论公转转速附近波动。这是因为在过故障期间滚动体与滚道失去部分接触，两者之间的接触力减小，内圈对滚动体的驱动力也减小，导致公转转速降低；而离开故障后，滚动体与滚道恢复正常接触，两者之间的接触力增大，内圈对滚动体的驱动力也增大，故公转转速升高。

当内圈故障时，在进入故障前，滚动体的公转转速比理论公转转速小，这是因为在进入故障前滚道的接触刚度因故障存在而发生变化，使得滚动体与滚道间的变形增大。在过故障期间，滚动体的公转转速比理论公转转速大，这是因为滚动体在经过内圈故障区域时，除了受到摩擦力外，内圈还会产生推力来带动滚动体随保持架旋转。在离开故障后，滚动体的公转转速在理论公转转速附近波动。在进入故障前和离开故障后，滚动体的公转转速均减小；在过故障期间，公转转速增大。这是因为过故障期间滚动体与内圈的接触间隙增大，使得摩擦力减小，从而导致公转转速增大。

当滚动体故障时，滚动体的公转转速与外圈故障时类似：在进入故障前和离开故障后，滚动体的公转转速在理论公转转速附近波动；在过故障期间，滚动体的公转转速先减小后增大，这是因为故障滚动体在与一个滚道接触时会与另一个滚道失去接触，则未接触滚道对滚动体的驱动力减小，导致公转转速减小。当离开故障后，滚动体与滚道的接触开始恢复正常，滚道对滚动体的驱动力增大，使得公转转速增大。当滚动体故障时，滚动体的公转转速在过故障期间的波动幅度比外圈故障时大，这是因为滚动体自身故障后因质量减小而导致加速度增大，使得公转转速的变化较大。

本文以NU306圆柱滚子轴承为研究对象，构建了其线弹性有限元模型，并对比分析了故障轴承（外圈故障、内圈故障及滚动体故障）与正常轴承的应力特性、振动特性和运动特性，主要结论如下。

1）当轴承内部元件发生故障后，故障前端应力均会滞后，后端应力均会提前，其中外圈故障时应力的增长幅度最大。

2）在经过故障区域期间，外圈故障时滚动体的振动加速度先减小后增大，内圈故障和滚动体故障时振动加速度先增大后减小，且内圈故障时振动加速度的变化幅度最小，外圈故障时变化幅度最大。

3）当外圈和滚动体故障时，滚动体经过故障区域期间的公转转速均比理论公转转速小，其中滚动体故障时的波动幅度比外圈故障时大；当内圈故障时，滚动体经过故障区域期间的公转转速比理论公转转速大。