工程设计学报

工程设计学报, 2023, 30(1): 102-108 doi: 10.3785/j.issn.1006-754X.2023.00.015

建模、仿真、分析与决策

双频激振下带V形缺口轴的疲劳寿命研究

化春键,,1,2, 李冬冬1,2, 蒋毅1,2, 俞建峰1,2, 陈莹3

1.江南大学 机械工程学院，江苏 无锡 214122

2.江南大学 江苏省食品先进制造装备技术重点实验室, 江苏 无锡 214122

3.江南大学 物联网工程学院，江苏 无锡 214122

Study on fatigue life of shaft with V-notch under dual-frequency excitation

HUA Chun-jian,,1,2, LI Dong-dong1,2, JIANG Yi1,2, YU Jian-feng1,2, CHEN Ying3

1.School of Mechanical Engineering, Jiangnan University, Wuxi 214122, China

2.Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment & Technology, Jiangnan University, Wuxi 214122, China

3.School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China

收稿日期: 2022-07-16   修回日期: 2022-08-02  

基金资助: 国家自然科学基金资助项目.  61573168

Received: 2022-07-16   Revised: 2022-08-02  

作者简介 About authors

化春键（1975—），男，北京人，副教授，博士，从事金属棒料、管材分离方法及机器视觉等研究，E-mail:cjhua@jiangnan.edu.cn,https://orcid.org/0000-0001-5397-2688 , E-mail：cjhua@jiangnan.edu.cn

摘要

针对金属轴类零件在实际复杂工况下易产生应力集中而发生疲劳破坏的问题，利用双频激振系统，研究带V形缺口轴的疲劳寿命随缺口几何参数的变化规律。首先，提出了促进轴疲劳裂纹萌生的激振频率控制曲线，同时采用响应曲面法中的Box-Behnken设计法对V形缺口的夹角、圆角半径和深度进行三因素三水平的实验设计；其次，建立了疲劳寿命多元回归预测模型，并采用方差分析法对模型进行可靠性评价；最后，利用响应曲面和等高线图分析了缺口的夹角、圆角半径和深度对轴疲劳寿命的影响规律，并进行了预测模型的应用。研究结果表明：疲劳寿命预测值与实测值之间的误差在4.2%以内，预测精度较高，预测模型可靠；缺口几何参数对疲劳寿命从大到小的影响次序是缺口深度、缺口圆角半径、缺口夹角，以圆角半径和深度的交互作用对轴疲劳寿命的影响最为显著。研究结果可为金属轴类零件的抗疲劳设计提供重要参考。

关键词： 双频激振 ; V形缺口 ; 疲劳寿命 ; 响应曲面法 ; 预测模型

Abstract

In view of the problem that metal shaft parts are prone to stress concentration and fatigue failure under actual complex working conditions, the variation of fatigue life of shaft with V-notch with notch geometric parameters was studied by using dual-frequency excitation system. Firstly, the excitation frequency control curve to promote the initiation of shaft fatigue crack was proposed. At the same time, the Box-Behnken design method in response surface method was used to carry out the experimental design of three factors and three levels of angle, fillet radius and depth of V-notch; secondly, a multiple regression prediction model of fatigue life was established, and the reliability of the model was evaluated by variance analysis; finally, the influence of the angle, fillet radius and depth of the notch on the fatigue life of the shaft was analyzed by using the response surface and contour map, and the prediction model was applied. The results showed that the error between the predicted and experimental values of fatigue life was within 4.2%, the prediction accuracy was higher, and the prediction model was reliable; the influence of the geometric parameters of the notch on the fatigue life from large to small was the depth, fillet radius, and the angle of notch. The interaction of fillet radius and depth had the most significant impact on the fatigue life of shaft. The research results can provide an important reference for the anti-fatigue design of metal shaft parts.

Keywords： dual-frequency excitation ; V-notch ; fatigue life ; response surface method ; prediction model

PDF (4058KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

化春键, 李冬冬, 蒋毅, 俞建峰, 陈莹. 双频激振下带V形缺口轴的疲劳寿命研究. 工程设计学报[J], 2023, 30(1): 102-108 doi:10.3785/j.issn.1006-754X.2023.00.015

HUA Chun-jian, LI Dong-dong, JIANG Yi, YU Jian-feng, CHEN Ying. Study on fatigue life of shaft with V-notch under dual-frequency excitation. Chinese Journal of Engineering Design[J], 2023, 30(1): 102-108 doi:10.3785/j.issn.1006-754X.2023.00.015

随着中国制造业的高速发展，金属轴类零件的需求量逐年增多，且对其质量要求越来越高[1]。轴类零件在服役过程中主要承受扭矩、弯曲应力以及冲击载荷的作用，容易引发疲劳问题[2-4]，严重时其内部会萌生疲劳裂纹甚至发生疲劳断裂，进而造成工业事故。据统计，高达60%以上的金属轴类零件的失效源于疲劳破坏[5]。因此，许多学者对金属轴类零件的疲劳问题展开了理论和实验研究。李有堂等[6]采用有限元软件分析了U形切口轴在扭转载荷作用下的疲劳寿命；张立军等[7]利用应力集中系数公式提出了在横幅载荷作用下棒料V形槽尖端裂纹寿命的数学表达式；李德勇等[8]采用名义应力法进行了缺口件振动疲劳寿命的分析与预测；赵升吨等[9]应用低应力疲劳裂纹可控式精密分离技术对金属棒、管材进行精密下料；Zhang等[10]提出了对棒料裂纹萌生和扩展阶段进行分段处理的方法，获得了高质量的断面变频加载曲线；胡海涛等[11]在不同激振频率下对2024铝合金悬臂梁进行了振动疲劳寿命的测试。

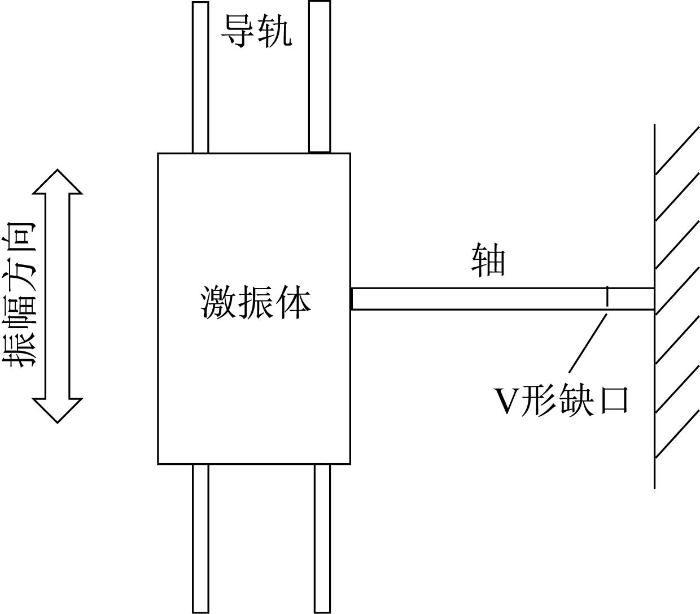
可以看到，目前已有的研究大多是对金属轴类零件施加单频载荷来探究其对金属轴疲劳裂纹产生及寿命的影响。然而，金属轴类零件实际的工作环境是复杂多样的，仅采用单一类型的载荷进行实验不能真实反映金属轴在实际服役载荷环境中的疲劳过程[12]，也不能准确预测轴类零件的疲劳寿命。因此，作者基于响应曲面法[13]，利用双频激振系统[14]进行实验设计，研究7A09铝合金轴V形缺口的几何参数对其疲劳寿命的影响规律；建立7A09铝合金轴疲劳寿命与V形缺口几何参数之间的二阶回归模型，并检验模型的准确性。

1 双频激振系统的工作原理

作者自主研发了双频激振系统，如图1所示。双频激振载荷由大、小变频电机带动2组偏心机构产生，每组偏心机构中偏心机构的运转情况相同，使得产生的2组激振力在竖直方向均完全抵消，在水平方向叠加而产生双频激振力[15]。被夹具夹持的轴在双频激振力作用下，由于应力集中[16]，在缺口底部萌生、扩展疲劳裂纹，进而发生疲劳断裂现象。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   双频激振系统

Fig.1   Dual-frequency excitation system


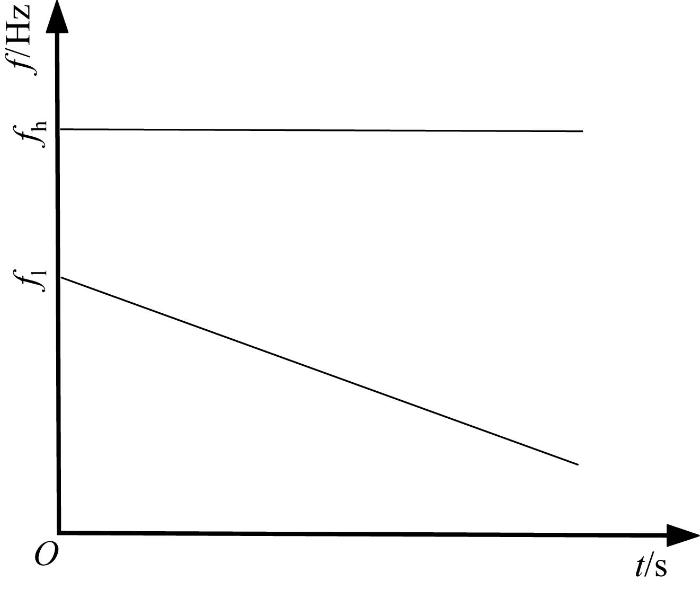
带V形缺口轴的双频激振模型如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   带V形缺口轴的双频激振模型

Fig.2   Double-frequency excitation model of shaft with V-notch


2 疲劳破坏实验设计

选用在工业领域广泛使用的7A09铝合金作为带V形缺口轴的材料，对其预制了若干不同几何参数的V形缺口。其几何参数如图3所示。图中：b为轴的半径；θ为缺口夹角；r为缺口圆角半径；d为缺口深度。已有研究表明，同时施加恒频的高频载荷和递减的低频载荷会加快带V形缺口轴表面裂纹的萌生[17]。采用的激振频率控制曲线如图4所示。实验中，取高频振动频率fh=25 Hz，低振动频率fl=0~12 Hz。在双频加载过程中，轴的振幅由加速度传感器、压电传感器实时采集，并通过LMS SCADAS多功能数据采集系统输出。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   带V形缺口轴几何参数示意

Fig.3   Schematic of geometric parameters of shaft with V-notch


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   激振频率控制曲线

Fig.4   Excitation frequency control curve


采用响应曲面法中的Box-Behnken Design（BBD）设计法进行疲劳破坏实验三因素三水平设计。疲劳破坏实验三因素三水平设置如表1所示。

表1   疲劳破坏实验三因素三水平设置

Table 1  Setting of three factors and three levels of fatigue failure experiment

水平因素
θ/(°)r/mmd/mm
-1600.21
0900.32
11200.43

新窗口打开| 下载CSV


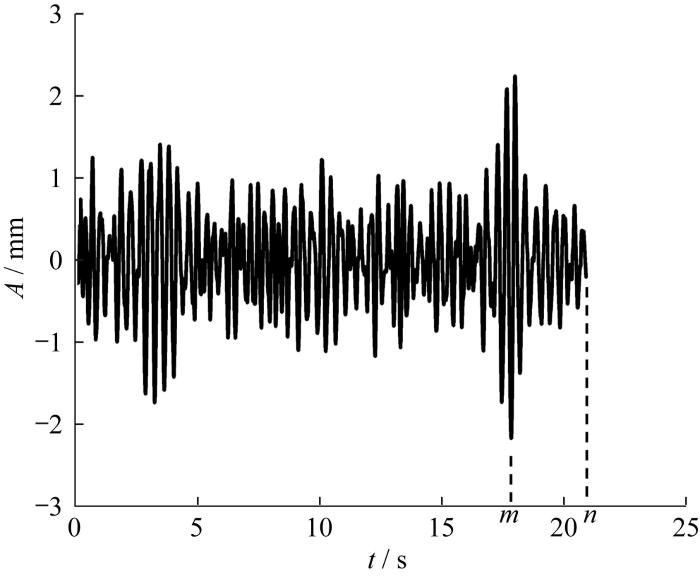
缺口轴的疲劳寿命可通过其激振过程中的振幅历程得到。缺口轴的振幅历程如图5所示。缺口轴的振幅A在电机启动过程中逐渐增大，在达到某一极值后开始在一定范围内波动，随后在m时刻振幅达到最大值，最终在n时刻出现疲劳断裂的现象。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   缺口轴的振幅历程

Fig.5   Amplitude history of notch axis


为了减小实验随机误差，以3次测量结果的平均值作为该组参数下的疲劳寿命。疲劳破坏实验结果如表2所示。表中y为疲劳寿命。

表2   带V形缺口轴疲劳破坏实验结果

Table 2  Experimental results of fatigue failure of shaft with V-notch

序号θ/(°)r/mmd/mmy/s
11200.2224.2
2900.2313.5
3900.3221.4
4900.4126.2
5600.2221.3
61200.3124.9
7900.3221.2
8600.3316.3
9900.2121.8
10900.4320.1
111200.4227.0
12900.3221.4
13900.3221.2
14600.4226.8
15900.3220.8
16600.3123.4
171200.3317.9

新窗口打开| 下载CSV


3 疲劳寿命预测模型的建立及分析

3.1　回归模型建立

为了得到V形缺口的几何参数对轴疲劳寿命的影响规律，构建曲面响应法中目标函数与影响因子之间的二阶数学预测模型[18]，如式(1)所示。

Yx=a0+∑i=13aixi+∑i=13∑j=i+13aijxixj+∑i=13aixi2+e

式中：Yx为疲劳寿命预测值；x1、x2、x3分别为θ、r、d；a0、ai 、aij 、aii 均为模型系数；e为误差。

采用Design-Expert 12分析软件对实验数据进行非线性回归拟合，得到带V形缺口轴在双频激振下疲劳寿命多元二阶预测模型，如式(2)所示。

Yx=21.2+0.775x1+2.41x2-3.56x3-              0.675x1x2+0.025x1x3+0.55x2x3+1.92x12+              1.7x22-2.5x32

3.2　疲劳寿命预测模型的方差分析

对疲劳寿命预测模型进行方差分析，结果如表3所示。其中p代表回归方程的显著性水平。选择置信度为95%，p<0.01表示该因素的影响极显著，p<0.05表示该因素的影响显著，p>0.05表示该因素的影响不显著。F为统计特征量，其值越大，表示所对应的影响因子对响应值的影响越显著。由表可知：预测模型的p<0.000 1，表示该模型极显著；用来评估预测模型可靠性的失拟项的p=0.074 2>0.05，表示失拟不显著，预测模型可靠；用来表征预测模型预测值和实验值吻合程度的多元相关系数R2=0.994 4，修正后的多元相关系数R2adj=0.987 3，R2与R2adj十分接近，说明模型预测值和实验值吻合程度较高[19]；表征实验可信度的变异系数Cv=1.88%，较小，表示实验结果是可信的[20]。同时，θ、r和d所对应的p值均小于0.05，说明它们对响应值的影响显著，其中r和d的所对应的p值都不大于0.000 1，说明r和d对疲劳寿命的影响极显著。θ、r和d所对应的F值依次增大，可以判断对目标函数影响的显著性从大到小依次为d、r、θ。

表3   疲劳寿命预测模型方差分析结果

Table 3  Variance analysis results of fatigue life prediction model

来源平方和自由度均方差F值p值
R2=0.994 4， R2adj=0.987 3， Cv=1.88%
预测模型207.61923.07138.9<0.000 1
x14.8114.8128.930.001
x246.56146.56280.370.000 1
x3101.531101.53611.37<0.000 1
x1x21.8211.8210.970.012 9
x1x30.002 510.002 50.015 10.905 8
x2 x31.2111.217.290.030 7
x1215.6115.693.95<0.000 1
x2212.17112.1773.27<0.000 1
x3226.32126.32158.46<0.000 1
残差1.1670.166 1
失拟项0.922 530.307 55.130.074 2
纯误差0.2440.06
总和208.7816

新窗口打开| 下载CSV


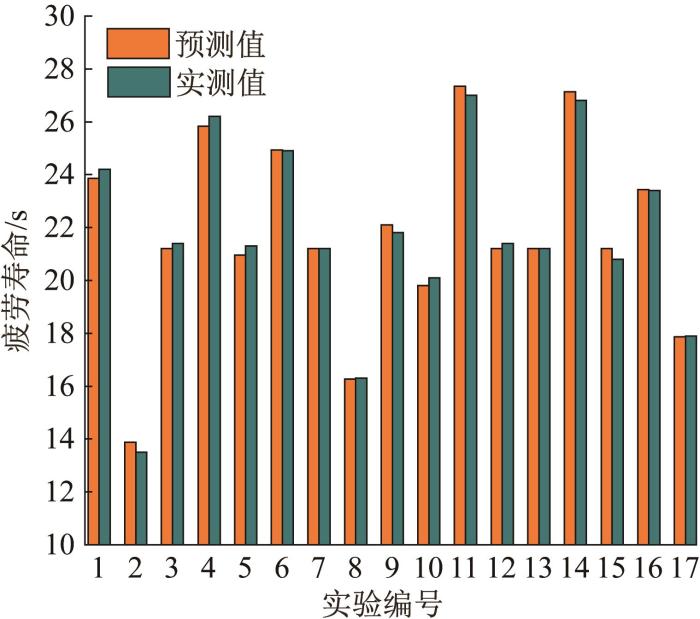
预测在实验设置的17组V形缺口几何参数值下的轴疲劳寿命。疲劳寿命预测值与实测值的对比如图6所示。由图可知，预测值与实测值较接近，误差均在4.2%以内。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   带V形缺口轴疲劳寿命预测值与实测值的对比

Fig.6   Comparison between predicted and experimental values of fatigue life of shaft with V-notch


综上所述，基于响应曲面法得到的二阶回归模型可以预测双频激振下带V形缺口轴的疲劳寿命，且预测精度较高。

3.3　V形缺口几何参数对疲劳寿命的影响

V形缺口几何参数对疲劳寿命的影响规律如图7所示。应力集中是造成缺口类零件疲劳强度下降的重要因素[21]。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   V形缺口几何参数对疲劳寿命的影响规律

Fig.7   Influence rule of V-notch geometric parameters on fatigue life


由图7(a)和(b)可知，当缺口夹角在60°~120°范围内变化时，疲劳寿命幅值变化较小，这是因为缺口夹角对缺口尖端应力集中的影响不明显，缺口尖端的应力集中因子变化较小[22]，疲劳强度也无明显变化，故疲劳寿命幅值只有小范围的波动。

由图7(a)和(c)可知，当缺口圆角半径在0.2~0.4 mm范围内变化时，疲劳寿命幅值变化较大，这是因为缺口圆角半径对缺口尖端应力集中的影响较明显。当缺口圆角半径较小时，缺口尖端的应力集中因子较大，疲劳强度较小，疲劳寿命幅值较小；当圆角半径增大至大于临界缺口半径（约为0.3 mm）时[23]，缺口尖端的应力集中因子减小，疲劳强度增大，进而导致疲劳寿命幅值增大。

由图7(b)和(c)可知，当缺口深度在1~3 mm范围内变化时，疲劳寿命幅值变化最大，这是因为缺口深度对缺口尖端应力集中的影响很明显。当缺口深度较小时，缺口尖端的应力集中因子较小，疲劳强度较高，疲劳寿命幅值则较大；当缺口深度增大至2 mm左右时，缺口尖端的应力集中因子明显增大，疲劳强度降低迅速，进而导致疲劳寿命幅值大幅减小。

通过以上分析可知，在V形缺口几何参数中，深度对疲劳寿命的影响最为显著，圆角半径次之，夹角的影响最小。

进一步观察图7可以发现：疲劳寿命最大值为图(a)中的最高点27 s，和图(c)中的最高点26.2 s较为接近；最小值为图(c)中的最低点13.5 s，明显低于图(a)、(b)的极小值；在图(c)中响应曲面的倾斜角度最大，且等高线的曲率半径最大，表明r和d的交互作用对轴疲劳寿命的影响最为显著。

4 疲劳寿命预测模型的应用

选取θ=90°，r=0.2 mm，以极显著影响因素d为变量，分别取为1.5、1.8和2.4 mm，双频激振频率的设置同第2节，采用疲劳寿命预测模型对缺口轴疲劳寿命进行预测，并将预测值与实测值进行对比，结果如表4所示。由表可知，疲劳寿命的预测值与实测值之间无明显差异，误差在合理范围内，表明预测模型的预测能力较好。

表4   疲劳寿命预测模型的应用方案及结果

Table 4  Application scheme and result of fatigue life prediction model

序号θ/(°)r/mmd/mm预测值/s实测值/s实测平均值/s

误差/

%

1900.21.522.022.322.73.1
222.6
323.2
41.821.220.420.43.9
520.0
620.8
72.418.418.618.82.1
819.2
918.6

新窗口打开| 下载CSV


5 结 论

1）利用Design-Expert 12分析软件建立了基于响应曲面法的7A09铝合金带V形缺口轴在双频激振下疲劳寿命二阶预测模型。理论分析及实验结果表明，该预测模型可靠，预测精度较高。

2）根据疲劳损伤机理分析和疲劳寿命测试结果得出，V形缺口几何参数对疲劳寿命从大到小的影响次序是缺口深度、缺口圆角半径、缺口夹角。利用响应曲面和等高线评价了影响因子的交互作用，其中以圆角半径和深度的交互作用对轴疲劳寿命的影响最为显著。研究结果可为金属轴类零件的抗疲劳设计提供重要参考。

参考文献

李泳峄，赵升吨，孙振宇，等.

花键轴高效精密批量化生产工艺的合理性探讨

［J］.锻压技术，2012，37（3）：1-6. doi：10.3969/j.issn.1000-3940.2012.03.001

[本文引用: 1]

LI Yong-yi， ZHAO Sheng-dun， SUN Zhen-yu， et al.

Discussion on the rationality of the efficient and precise mass production process of spline shafts

［J］. Forging Technology， 2012， 37（3）： 1-6.

DOI:10.3969/j.issn.1000-3940.2012.03.001      [本文引用: 1]

毕艳茹，王志勃，姜亚南.

典型轴零件的综合机械性能分析

［J］.装备制造技术，2013（11）：143-144，156. doi：10.3969/j.issn.1672-545X.2013.11.053

[本文引用: 1]

BI Yan-ru， WANG Zhi-bo， JIANG Ya-nan.

Comprehensive mechanical properties analysis of typical shaft parts

［J］. Equipment Manufacturing Technology， 2013（11）： 143-144， 156.

DOI:10.3969/j.issn.1672-545X.2013.11.053      [本文引用: 1]

刘龙杰，赵礼辉，史成淼，等.

基于响应面法传动直轴疲劳寿命优化

［J］.机械强度，2022， 44：215-224.

LIU Long-jie， ZHAO Li-hui， SHI Cheng-miao， et al.

Fatigue life optimization of transmission straight shaft based on response surface method

［J］. Mechanical Strength， 2022， 44（1）： 215-224.

陈伟军，黄德杰，汪峰，等.

乘用车轮毂轴颈承载能力研究

［J］.机电工程，2022，39（5）：668-673. doi：10.3969/j.issn.1001-4551.2022.05.014

[本文引用: 1]

CHEN Wei-jun， HUANG De-jie， WANG Feng， et al.

Research on bearing capacity of pass-enger wheel hub journals

［J］. Mechanical and Electrical Engineering， 2022， 39（5）： 668-673.

DOI:10.3969/j.issn.1001-4551.2022.05.014      [本文引用: 1]

任皓靖.

复合频率激振下轴类构件的断裂行为研究

［D］.无锡：江南大学，2019：1-7.

[本文引用: 1]

REN Hao-jing.

Research on fracture behavior of shaft members under compound frequency excitation

［D］. Wuxi： Jiangnan University， 2019： 1-7.

[本文引用: 1]

李有堂，李全宝.

U形切口中缺口参数对轴类件疲劳寿命的影响

［J］.甘肃科学学报，2010，22（3）：84-87. doi：10.3969/j.issn.1004-0366.2010.03.021

[本文引用: 1]

LI You-tang， LI Quan-bao.

Influence of notch parameters in U-shaped notches on fatigue life of shaft parts

［J］. Gansu Science Journal， 2010， 22（3）： 84-87.

DOI:10.3969/j.issn.1004-0366.2010.03.021      [本文引用: 1]

张立军，赵升吨.

恒幅载荷下棒料V形槽尖端裂纹起始寿命的估算

［J］.塑性工程学报，2008（5）：73-77.

[本文引用: 1]

ZHANG Li-jun， ZHAO Sheng-dun.

Estimation of crack initiation life at the tip of bar V-groove under constant amplitude load

［J］.Chinese Journal of Plastic Engineering， 2008（5）： 73-77.

[本文引用: 1]

李德勇，姚卫星.

缺口件振动疲劳寿命分析的名义应力法

［J］.航空学报，2011，32（11）： 2036-2041.

[本文引用: 1]

LI De-yong， YAO Wei-xing.

Nominal stress method for vibration fatigue life analysis of notched parts

［J］. Chinese Journal of Aeronautics and Astronautics， 2011， 32（11）： 2036-2041.

[本文引用: 1]

赵升吨，任芋见，杨昌群，等.

低应力疲劳裂纹可控式精密分离技术

［J］.塑性工程学报，2020， 27（12）：1-8. doi：10.3969/j.issn.1007-2012.2020.12.001

[本文引用: 1]

ZHAO Sheng-tun， REN Yu-jian， YANG Chang-qun， et al.

Controllable precision separation technology for low stress fatigue cracks

［J］. Chinese Journal of Plastic Engineering， 2020， 27（12）： 1-8.

DOI:10.3969/j.issn.1007-2012.2020.12.001      [本文引用: 1]

ZHANG Li-jun， ZHANG De-pei， WANG Han-xiang， et al.

Research on variable frequency-loading curve in precision cropping system with high-speed and centrifugal action

［J］. The International Journal of Advanced Manufacturing Technology， 2018， 97（5/8）： 2969-2978.

[本文引用: 1]

胡海涛，李玉龙，索涛，等.

2024铝合金振动疲劳特性及断口分析

［J］.航空材料学报，2013，33（4）：78-83.

[本文引用: 1]

HU Hai-tao， LI Yu-long， SUO Tao， et al.

2024 aluminum alloy vibration fatigue characteristics and fracture analysis

［J］. Journal of Aeronautical Materials， 2013， 33（4）： 78-83.

[本文引用: 1]

化春键，王超凡，陆云健.

基于高低频复合振动的金属管材断裂行为研究

［J］.工程设计学报，2019，26（2）：223-229. doi：10.3785/j.issn.1006-754X.2019.02.014

[本文引用: 1]

HUA Chun-jian， WANG Chao-fan， LU Yun-jian.

Study on fracture behavior of metal pipes based on high and low frequency composite vibration

［J］. Chinese Journal of Engineering Design， 2019， 26（2）： 223-229.

DOI:10.3785/j.issn.1006-754X.2019.02.014      [本文引用: 1]

WEI Ke， ZHAN Mei， FAN Xiao-guang， et al.

Unequal-thickness billet optimization in transitional region during isothermal local loading forming of Ti-alloy rib-web component using response surface method

［J］. Chinese Journal of Aeronautics and Astronautics， 2018， 31（4）： 845-859.

[本文引用: 1]

化春键，任皓靖，陆云健.

双频激振系统下带V形槽棒料下料寿命模型

［J］. 锻压技术，2019，44（7）：177-183.

[本文引用: 1]

HUA Chun-jian， REN Hao-jing， LU Yun-jian.

The blanking life model of bar with V-groove under dual-frequency excitation system

［J］. Forging Technology， 2019， 44（7）： 177-183.

[本文引用: 1]

化春键，王超凡，陆云健.

双频振动金属管材分离过程可控性研究

［J］.塑性工程学报，2019，26（5）：190-196. doi：10.3969/j.issn.1007-2012.2019.05.028

[本文引用: 1]

HUA Chun-jian， WANG Chao-fan， LU Yun-jian.

Study on the controllability of the separation process of metal pipes with dual-frequency vibration

［J］. Chinese Journal of Plastic Engineering， 2019， 26（5）： 190-196.

DOI:10.3969/j.issn.1007-2012.2019.05.028      [本文引用: 1]

YU Hai-bing， CHEN Tie-feng， QIU Yan-jie.

Optimal location and shape definition of elliptical ventilation openings on aero engine turbine rotors with stress concentration effect

［J］. Chinese Journal of Aeronautics and Astronautics， 2022， 35（1）： 388-397.

[本文引用: 1]

化春键，陆云健，袁浩.

双频振动载荷下带V形槽铝合金棒料的断裂行为

［J］.中国机械工程，2017，28（14）：1753-1758. doi：10.3969/j.issn.1004-132X.2017.14.020

[本文引用: 1]

HUA Chun-jian， LU Yun-jian， YUAN Hao.

Fracture behavior of aluminum alloy bars with V-groove under dual-frequency vibration load

［J］. China Mechanical Engineering， 2017， 28（14）： 1753-1758.

DOI:10.3969/j.issn.1004-132X.2017.14.020      [本文引用: 1]

史丽晨，贾永康，张军锋.

车削去除钛合金棒材表面氧化皮工艺参数试验研究

［J］.表面技术，2021，50（5）：372-379.

[本文引用: 1]

SHI Li-chen， JIA Yong-kang， ZHANG Jun-feng.

Experimental research on process parameters of removing oxide scale from titanium alloy bars by turning

［J］. Surface Technology， 2021， 50（5）： 372-379.

[本文引用: 1]

佘文韬，樊文欣，史永鹏，等.

基于响应曲面法的连杆衬套表面粗糙度预测模型和优化

［J］.塑性工程学报，2017，24（6）：172-176.

[本文引用: 1]

SHE Wen-tao， FAN Wen-xin， SHI Yong-peng， et al.

Prediction model and optimization of connecting rod bushing surface roughness based on response surface method

［J］. Chinese Journal of Plastic Engineering， 2017， 24（6）： 172-176.

[本文引用: 1]

徐勇，尹阔，夏亮亮，等.

面向航空铝合金薄壁深腔构件的冲击液压成形工艺优化

［J］.航空学报，2021，42（10）：358-369.

[本文引用: 1]

XU Yong， YIN Kuo， XIA Liang-liang， et al.

Optimization of impact hydroforming process for aerospace aluminum alloy thin-walled deep cavity components

［J］. Journal of Aeronautics and Astronautics， 2021， 42（10）： 358-369.

[本文引用: 1]

陈涛，刘攀，徐晓.

疲劳强度减弱系数与应力集中系数在螺纹疲劳分析中的应用研究

［J］.核动力工程，2018，39（3）：62-66.

[本文引用: 1]

CHEN Tao， LIU Pan， XU Xiao.

Application of fatigue strength reduction factor and stress concentration factor in thread fatigue analysis

［J］. Nuclear Power Engineering， 2018， 39（3）： 62-66.

[本文引用: 1]

赵仁峰，杨明顺，肖旭东，等.

管材表面环状V形缺口几何参数对应力集中效应的影响

［J］.塑性工程学报，2020，27（12）：106-112.

[本文引用: 1]

ZHAO Ren-feng， YANG Ming-shun， XIAO Xu-dong， et al.

Influence of geometrical parameters of annular V-notch on pipe surface on stress concentration effect

［J］. Chinese Journal of Plastic Engineering， 2020， 27（12）： 106-112.

[本文引用: 1]

靖雅，钟飞，苑光健，等.

基于晶体塑性理论的GH4169合金缺口效应研究

［J］.机械工程材料，2021，45（5）：84-90，95. doi：10.11973/jxgccl202105015

[本文引用: 1]

JING Ya， ZHONG Fei， YUAN Guang-jian， et al.

Research on notch effect of GH4169 alloy based on crystal plasticity theory

［J］. Mechanical Engineering Materials， 2021， 45（5）： 84-90， 95.

DOI:10.11973/jxgccl202105015      [本文引用: 1]

/

〈 〉