混凝土湿喷机摆动系统工作特性研究

doi:10.3785/j.issn.1006-754X.2022.00.050

混凝土湿喷机摆动系统工作特性研究

李科军^,^,¹^,², 邓旻涯¹, 黄文静¹, 张宇¹, 曾家旺¹, 陈淼林²

1.中南林业科技大学材料科学与工程学院，湖南长沙 410000

2.湖南长院悦诚装备有限公司，湖南长沙 410000

Study on working characteristics of swing system of concrete wet spraying machine

LI Ke-jun^,^,¹^,², DENG Min-ya¹, HUANG Wen-jing¹, ZHANG Yu¹, ZENG Jia-wang¹, CHEN Miao-lin²

1.School of Materials Science and Engineering, Central South University of Forestry and Technology, Changsha 410000, China

2.Hunan Changyuan Yuecheng Machinery Co. , Ltd. , Changsha 410000, China

收稿日期: 2021-06-02 修回日期: 2021-07-16

基金资助:

国家自然科学基金资助项目. 51805555

Received: 2021-06-02 Revised: 2021-07-16

作者简介 About authors

李科军（1984—），男，湖南邵东人，讲师，博士，从事隧道工程装备的设计、分析与优化研究，E-mail：likejuncsu@126.com，https：//orcid.org/0000-0001-8761-1434 , E-mail：likejuncsu@126.com

摘要

为了深入了解混凝土湿喷机摆动系统的工作特性，根据摆动系统的结构及工作原理，考虑液压元件内部阀芯等零部件的运动响应时间等因素，建立了摆动系统的键合图模型和动力学方程，仿真分析了在摆臂摆动过程中恒压泵、蓄能器和电液换向阀等液压元件的工作特性，并搭建了摆臂摆动测试平台进行实验验证。研究结果表明：在摆臂运动达到稳定状态之前，恒压泵斜盘处于最大倾角状态，泵出高压油液用于左右摆动缸的运动和蓄能器充液，蓄能器气室压力随着摆臂摆动次数的增加而逐渐升高，并最终稳定在14 MPa；在摆臂运动达到稳定状态之后，恒压泵斜盘倾角在0°~19°之间周期性变化，蓄能器放液最大瞬时流量达到322.5 L/min，可实现S形分配阀在0.24 s内完成换向；摆动缸无杆腔工作压力的测试结果与仿真结果基本一致，验证了所建模型的准确性。研究结果为进一步优化混凝土湿喷机摆动系统提供了参考。

关键词： 混凝土湿喷机 ; 摆动系统 ; 键合图 ; 动力学建模 ; 仿真

Abstract

In order to deeply understand the working characteristics of the swing system of concrete wet spraying machine, according to the structure and working principle of the swing system, the bond graph model and dynamic equation of the swing system were established by taking into account the motion response time of components such as the internal valve core of hydraulic element. The working characteristics of hydraulic components such as constant pressure pump, accumulator and electro-hydraulic directional valve were simulated and analyzed in the process of swing arm movement, and a swing arm swing test platform was built for experimental verification. The research results showed that the swash plate of constant pressure pump was in a maximum inclination angle state before swing arm movement reached a stable state. The high-pressure oil pumped out was used for the movement of left and right swing cylinders and the charging of the accumulator. The pressure of the accumulator gas chamber gradually increased with the increase of swing times of swing arm and finally stabilized at 14 MPa; after the swing arm movement reached a stable state, the inclination angle of the swash plate of the constant pressure pump changed periodically at 0°-19°, and the maximum instantaneous flow of the accumulator discharge reached 322.5 L/min, and the S-shaped distribution valve could realize the reversing within 0.24 s; the test results of the working pressure of the rodless cavity of swing cylinder were basically consistent with the simulation results, which verified the accuracy of the established model. The research results provide a reference for the further optimization of the swing system of wet shotcrete machine.

Keywords： concrete wet spraying machine ; swing system ; bond graph ; dynamic modeling ; simulation

PDF (2899KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李科军, 邓旻涯, 黄文静, 张宇, 曾家旺, 陈淼林. 混凝土湿喷机摆动系统工作特性研究. 工程设计学报[J], 2022, 29(4): 519-526 doi:10.3785/j.issn.1006-754X.2022.00.050

LI Ke-jun, DENG Min-ya, HUANG Wen-jing, ZHANG Yu, ZENG Jia-wang, CHEN Miao-lin. Study on working characteristics of swing system of concrete wet spraying machine. Chinese Journal of Engineering Design[J], 2022, 29(4): 519-526 doi:10.3785/j.issn.1006-754X.2022.00.050

目前，国内大力开展中西部铁路、公路等基础设施建设，其中隧道建设里程占比较大。混凝土喷射是隧道修筑中的一项关键技术：借助机械，将速凝混凝土喷向岩石或结构物表面，使岩石或结构物得到加强和保护^［1］。湿喷机用于输送和喷射混凝土，是隧道施工中不可缺少的关键设备。湿喷机摆动系统设计在料斗后方，2个摆动缸在高压油液的作用下驱动摆臂左右摆动，实现S形分配阀迅速换向，配合泵送系统将混凝土通过管路输送到喷嘴处进行喷射。摆动系统的换向特性直接关系着湿喷机的泵送效率和喷射质量，因此有必要对摆动系统的工作性能进行深入研究。靖保平等^［2-3］建立了湿喷机摆动系统的AMESim模型，分析了S形分配阀快速换向及其引起系统冲击的原因，但将恒压泵简化成定量泵，不能非常准确地反映摆动系统的工作特性。胡军科等^［4］提出了在变量缸敏感腔进油口设置比例节流阀以控制阀口开度的方法，对变量缸的流量及运动速度进行调节，较好地解决了摆动系统的恒压泵瞬时吸空的问题。为了提高湿喷机的喷射效率和施工安全，刘在政等^［5］研发了喷射机械手的智能化控制系统，采用全站型电子速测仪、三维激光扫描仪获取湿喷机和待喷面的坐标，基于喷头的运动学模型对湿喷机臂架关节的位姿进行规划，实现了混凝土喷射的自动化和智能化。刘蕾等^［6］利用功率键合图法建立了混凝土泵车泵送系统的动力学模型，得出了泵送油缸缓冲阻尼孔的孔径对泵送液压冲击和振动的影响规律；黄毅等^［7］对混凝土泵车臂架的动态特性和振动响应进行预测分析，为臂架减振研究提供了理论依据；胡仕成等^［8］采用解析几何法和拉格朗日方程建立了湿喷机臂架系统的动力学模型，分析了驱动油缸铰点位置变化对油缸最大驱动力的影响规律；卢志学等^［9］运用Fluent软件对泵车无杆腔联通阀组的内部流道进行优化设计，以减小压损，降低能耗。可见，现有研究主要集中在泵车结构强度、泵送系统动态特性、喷射头轨迹规划、臂架动力学建模和振动控制等方面，对摆动系统的研究较少。本文通过分析湿喷机摆动系统的结构及工作原理，建立摆动系统在摆动过程中的动力学模型，仿真分析摆动系统的工作特性，并搭建实验平台进行实验验证，以期为摆动系统的动力学优化提供依据。

1 湿喷机摆动系统的结构及工作原理

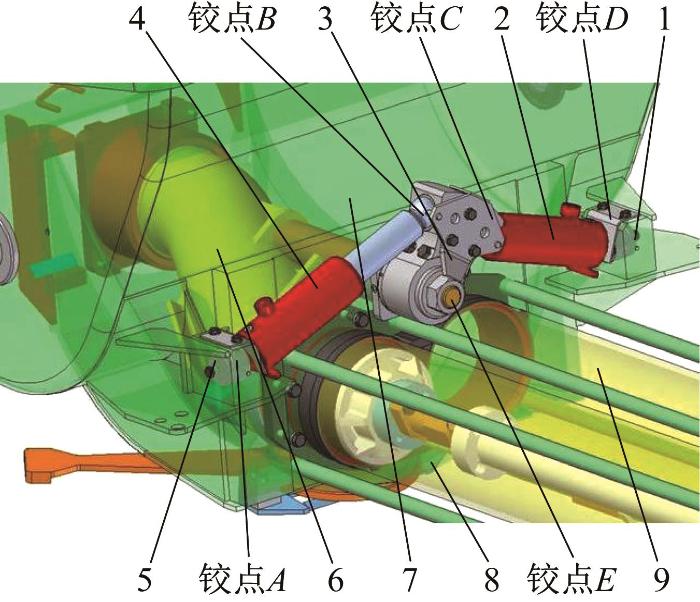
湿喷机摆动系统的结构如图1所示。摆动机构是摆动系统的执行机构，主要由左右固定支座、左右摆动缸、摆臂和S形分配阀组成。2个摆动缸对称分布于摆臂的两侧，摆臂活塞杆与摆臂铰接，摆动缸缸筒与固定支座铰接，由此形成曲柄滑块机构。摆臂与S形分配阀固结在一起，摆动缸驱动摆臂转动，实现S形分配阀换向。两摆动缸无杆腔轮流进油，当左摆动缸活塞杆伸出时，右摆动缸活塞杆缩回，同时驱动摆臂，使S形分配阀完成换向，配合左泵缸压出混凝土，右泵缸吸入混凝土；当左泵缸伸出至极限位置时，右摆动缸活塞杆伸出，左摆动缸活塞杆缩回，S形分配阀与右泵缸接通压出混凝土，左泵缸吸入混凝土。两摆动缸交替动作，使S形分配阀左右摆动，从而实现混凝土的连续泵送与喷射。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 湿喷机摆动系统的结构

1—右固定支座；2—右摆动缸；3—摆臂；4—左摆动缸；5—左固定支座；6—S形分配阀；7—料斗；8—左泵缸；9—右泵缸。

Fig.1 Structure of swing system of wet spraying machine

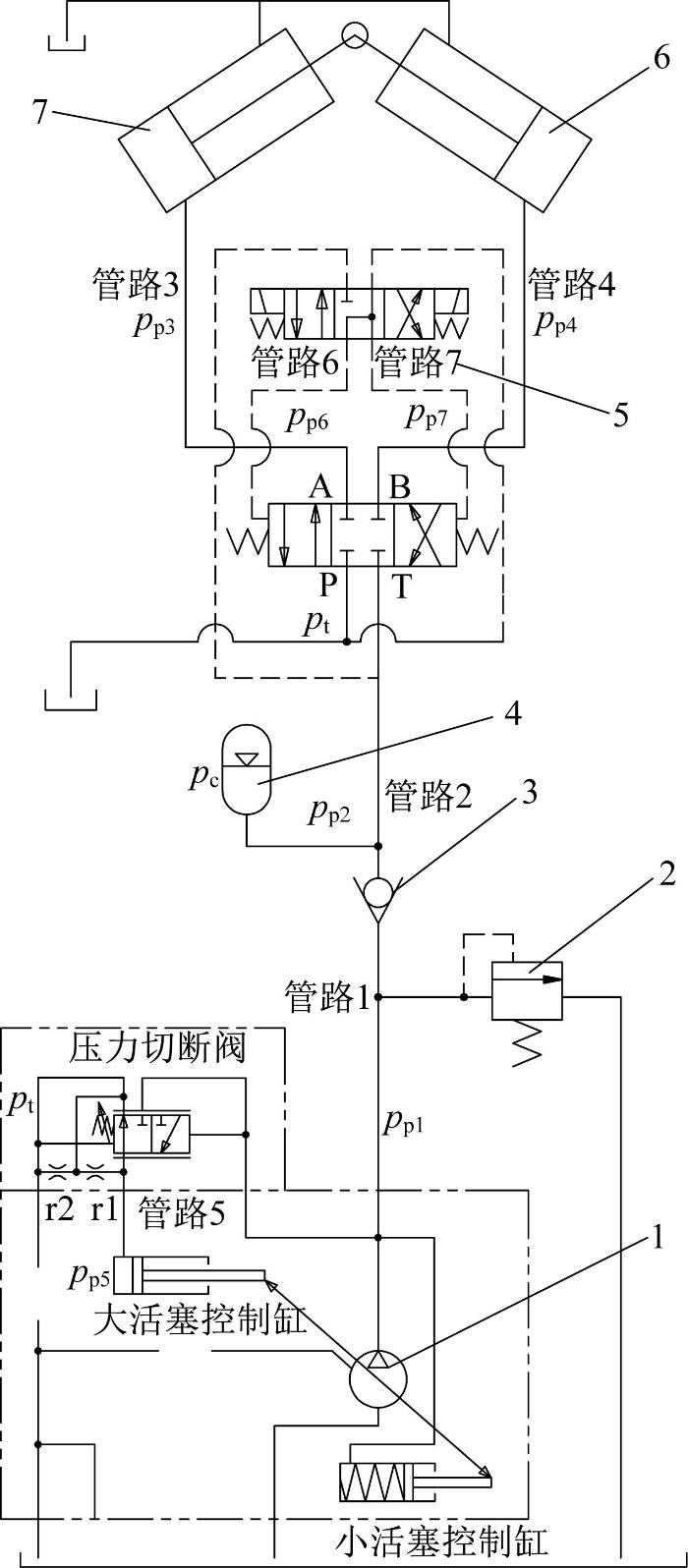
湿喷机摆动液压系统如图2所示。其主要由恒压泵、溢流阀、单向阀、蓄能器、电液换向阀和左右摆动缸组成。恒压泵作为压力油源向系统供油。当电液换向阀处于中位时，高压油液首先通过单向阀进入蓄能器，为蓄能器充液。当蓄能器中气体压力上升至变量泵压力切断阀的设定压力14 MPa时，压力切断阀工作，恒压泵开始高压待命，输出流量仅为系统泄漏流量，以降低系统的功率损耗和发热，提高系统的效率。当左泵缸（或右泵缸）伸出至极限位置时，电液换向阀右位（或左位）得电，蓄能器的压力油与恒压泵输出的压力油共同经过电液换向阀快速向右摆动缸（或左摆动缸）充油，驱动S形分配阀与右泵缸（或左泵缸）连通，实现泵送系统持续输送混凝土。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 湿喷机摆动液压系统示意

1—恒压泵；2—溢流阀；3—单向阀；4—蓄能器；

5—电液换向阀；6—右摆动缸；7—左摆动缸。

Fig.2 Schematic of swing hydraulic system of wet spraying machine

2 湿喷机摆动系统数学建模

根据湿喷机摆动系统的结构及工作原理，建立在S形分配阀摆动过程中摆动系统的键合图模型和动力学方程。在建模前，作如下简化：

1）忽略变量泵和换向阀等液压元件的内部泄漏；

2）电机输入转速恒定，不考虑油源流量的脉动；

3）蓄能器为S形分配阀提供压力油的过程很短，视该过程为绝热过程；

4）不考虑油液体积弹性模量等工作特性参数随温度和压力的变化；

5）两摆动缸有杆腔直接连油箱，视其压力为0 MPa。

2.1　摆动系统键合图模型

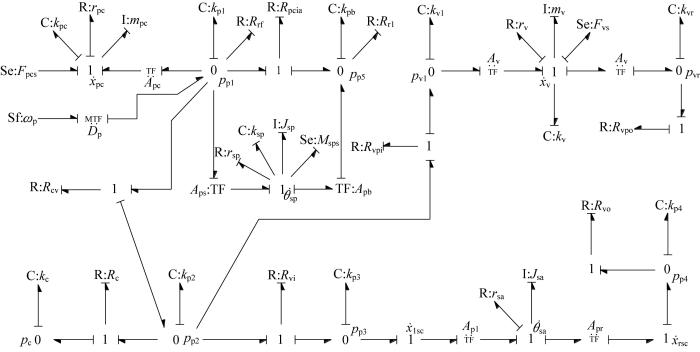
建立的湿喷机摆动系统键合图模型如图3所示。图中： $ω_{p}$ 为电机输入转速； $D_{p}$ 为变量泵的排量，由负载压力决定； $R_{r f}$ 为泵出口溢流阀的溢流液阻； $m_{p c}$ 、 ${\dot{x}}_{p c}$ 、 $r_{p c}$ 、 $k_{p c}$ 、 $F_{p c s}$ 、 $A_{p c}$ 分别为压力切断阀阀芯的质量、运动速度、运动黏性阻尼系数、弹簧刚度系数、稳态液动力和有效作用面积； $R_{p c i}$ 为泵出口到大活塞控制缸无杆腔的等效液阻； $R_{r 1}$ 为阻尼孔r1的等效液阻； $A_{p b}$ 、 $A_{p s}$ 分别为大、小活塞控制缸活塞杆的运动速度与斜盘转动速度的比值； $J_{s p}$ 、 ${\dot{θ}}_{s p}$ 、 $r_{s p}$ 、 $k_{s p}$ 、 $M_{s p s}$ 分别为斜盘的转动惯量、转动速度、转动黏性阻尼系数、小活塞控制缸弹簧等效扭转刚度系数和弹簧预紧力等效力矩； $R_{c v}$ 为单向阀等效液阻； $R_{c} 、 k_{c}$ 分别为蓄能器入口的等效液阻和等效液压刚度； $R_{v i}$ 、 $R_{v o}$ 分别为电液换向阀主阀进、出口的等效液阻； $A_{p l}$ 、 $A_{p r}$ 分别为左、右摆动缸活塞杆运动速度与摆臂转动速度的比值； $J_{s a}$ 、 ${\dot{θ}}_{s a}$ 、 $r_{s a}$ 分别为摆臂的转动惯量、转动速度和转动黏性阻尼系数； $R_{v p i}$ 、 $R_{v p o}$ 分别为电液换向阀电磁阀进、出口的等效液阻； $m_{v}$ 、 ${\dot{x}}_{v}$ 、 $r_{v}$ 、 $k_{v}$ 、 $F_{v s}$ 、 $A_{v}$ 分别为电液换向阀主阀阀芯的质量、运动速度、运动黏性阻尼系数、弹簧刚度系数、稳态液动力和两端作用面积； $p_{p 1}$ 、 $p_{p 2}$ 、p_p3、p_p4、p_p5分别为管路1，2，3，4，5的工作容腔压力，k_p1、k_p2、k_p3、k_p4、k_p5分别为其工作容腔油液的等效液压刚度； $p_{c}$ 为蓄能器的实时工作压力；x_lsc、x_rsc分别为左、右摆动缸的位移； $k_{v l}$ 、 $p_{v l}$ 分别为电液换向阀主阀左工作腔的等效液压刚度和工作压力； $k_{v r}$ 、 $p_{v r}$ 分别为电液换向阀主阀右工作腔的等效液压刚度和工作压力。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 湿喷机摆动系统键合图模型

Fig.3 Bond graph model of swing system of wet spraying machine

2.2　摆动系统动力学模型

根据湿喷机摆动系统键合图模型状态方程生成规则，可以快速方便地得到其动力学模型^［10-14］。

管路1工作容腔的流量连续性方程为^［15］：

{\dot{V}}_{p 1} = ω_{p} D_{p} - {\dot{V}}_{r f} - {\dot{V}}_{p c i} - A_{p c} {\dot{x}}_{p c} - {\dot{V}}_{c v} - A_{p s} {\dot{θ}}_{s p}

（1）

D_{p} = \frac{θ_{s p}}{18} D_{p m a x}

（2）

{\dot{V}}_{r f} = C_{r f} A_{r f} \sqrt[]{\frac{2 p_{p 1}}{ρ}}

（3）

{\dot{V}}_{p c i} = C_{p c i} A_{p c} \sqrt[]{\frac{2 (p_{p 1} - p_{p 5})}{ρ}}

（4）

{\dot{V}}_{c v} = C_{c v} A_{c v} \sqrt[]{\frac{2 (p_{p 1} - p_{p 2})}{ρ}}

（5）

式中： ${\dot{V}}_{p 1}$ 为管路1工作容腔的流量； ${\dot{V}}_{r f}$ 为通过溢流阀的流量； ${\dot{V}}_{p c i}$ 为泵出口到大活塞控制缸无杆腔的的流量； ${\dot{V}}_{c v}$ 为通过单向阀的流量； $D_{p m a x}$ 为柱塞泵斜盘达到最大倾角19°时变量泵的排量； $C_{r f}$ 、 $A_{r f}$ 分别为溢流阀阀口的流量特性系数和开口面积； $C_{p c i}$ 为压力切断阀阀口的流量特性系数^［14］； $C_{c v}$ 、 $A_{c v}$ 分别为单向阀阀口的流量特性系数和开口面积； $ρ$ 为液压油密度。

管路2工作容腔的流量连续性方程为：

{\dot{V}}_{p 2} = {\dot{V}}_{c v} - {\dot{V}}_{c} - {\dot{V}}_{v i} - {\dot{V}}_{v p i}

（6）

{\dot{V}}_{v i} = C_{v i} A_{v i} \sqrt[]{\frac{2 (p_{p 2} - p_{p 3})}{ρ}}

（7）

{\dot{V}}_{v p i} = C_{v p i} A_{v p i} \sqrt[]{\frac{2 (p_{p 2} - p_{v l})}{ρ}}

（8）

式中： ${\dot{V}}_{p 2}$ 为管路2工作容腔的流量； ${\dot{V}}_{c}$ 为通过蓄能器入口的的流量； ${\dot{V}}_{v i}$ 为通过电液换向阀主阀进口的流量； ${\dot{V}}_{v p i}$ 为通过电液换向阀电磁阀进口的流量； $C_{p c i}$ 为电液换向阀主阀的进口流量特性系数； $C_{v i}$ 、 $A_{v i}$ 分别为电液换向阀主阀的进口流量特性系数和开口面积； $C_{v p i}$ 、 $A_{v p i}$ 分别为电液换向阀电磁阀的进口流量特性系数和开口面积。

管路3工作容腔的流量连续性方程为：

{\dot{V}}_{p 3} = {\dot{V}}_{v i} - A_{p l} {\dot{θ}}_{s a}

（9）

式中： ${\dot{V}}_{p 3}$ 为管路3工作容腔的流量。

管路4工作容腔的流量连续性方程为：

{\dot{V}}_{p 4} = A_{p r} {\dot{θ}}_{s a} - {\dot{V}}_{v o}

（10）

{\dot{V}}_{v o} = C_{v o} A_{v o} \sqrt[]{\frac{2 p_{p 4}}{ρ}}

（11）

式中： ${\dot{V}}_{p 4}$ 为管路4工作容腔的流量； ${\dot{V}}_{v o}$ 为通过电液换向阀主阀出口的流量； $C_{v o}$ 、 $A_{v o}$ 分别为电液换向阀主阀的出口流量特性系数和开口面积。

管路5工作容腔的流量连续性方程为：

{\dot{V}}_{p 5} = {\dot{V}}_{p c i} + A_{p b} {\dot{θ}}_{s p} - {\dot{V}}_{r 1}

（12）

{\dot{V}}_{r 1} = C_{r 1} A_{r 1} \sqrt[]{\frac{2 p_{p 5}}{ρ}}

（13）

式中： ${\dot{V}}_{p 5}$ 为管路5工作容腔的流量； ${\dot{V}}_{r 1}$ 、 $C_{r 1}$ 、 $A_{r 1}$ 分别为阻尼孔r1的流量、流量特性系数和过流面积。

管路6工作容腔的流量连续性方程为：

{\dot{V}}_{p 6} = {\dot{V}}_{v p i} - A_{v} {\dot{x}}_{v}

（14）

式中： ${\dot{V}}_{p 6}$ 为管路6工作容腔的流量。

管路7工作容腔的流量连续性方程为：

{\dot{V}}_{p 7} = A_{v} {\dot{x}}_{v} - {\dot{V}}_{v p o}

（15）

{\dot{V}}_{v p o} = C_{v p o} A_{v p o} \sqrt[]{\frac{2 p_{p 7}}{ρ}}

（16）

式中： ${\dot{V}}_{p 7}$ 为管路7工作容腔的流量； ${\dot{V}}_{v p o}$ 为通过电液换向阀电磁阀出口的流量； $C_{v p o}$ 、 $A_{v p o}$ 分别为电液换向阀电磁阀的出口流量特性系数和开口面积； $p_{p 7}$ 为管路7的工作容腔压力。

各管路工作容器的压力计算方程为：

p_{p i} = k_{p i} V_{i}

（

i = 1, 2, \dots, 7

）（17）

式中： $k_{p i}$ 、 $V_{i}$ 分别为各管路工作容腔油液的等效液压刚度和变化体积。

蓄能器工作压力计算方程为：

p_{c} = \frac{1.4 p_{c 0}}{V_{c 0}} V_{c}

（18）

V_{c} = V_{c 0} - V_{c t}

（19）

式中： $p_{c 0}$ 、 $V_{c 0}$ 分别为蓄能器的初始充气压力和初始工作容积； $V_{c t}$ 为蓄能器工作容积。

恒压泵斜盘转动的动力学方程为：

{\dot{P}}_{s p} = p_{p 1} A_{p s} - p_{p 5} A_{p b} - r_{s p} {\dot{θ}}_{s p} - M_{s p s} - k_{s p} θ_{s p}

（20）

式中： $P_{s p}$ 为恒压泵斜盘的角动量。

恒压泵斜盘转动速度为：

{\dot{θ}}_{s p} = \frac{P_{s p}}{J_{s p}}

（21）

压力切断阀阀芯的动力学方程为^［16］：

{\dot{P}}_{p c} = A_{p c} p_{p 1} - F_{p c p} - k_{p c} x_{p c} - r_{p c} {\dot{x}}_{p c} - F_{p c s}

（22）

F_{p c s} = 2 C_{p c} A_{p c} c o s θ_{p c} (p_{p 1} - p_{p 5})

（23）

式中： $P_{p c}$ 、 $F_{p c s}$ 分别为压力切断阀阀芯的动量和弹簧预紧力； $C_{p c}$ 、 $θ_{p c}$ 分别为压力切断阀阀口的流量特性系数和油液速度方向角。

压力切断阀阀芯的运动速度为：

{\dot{x}}_{p c} = \frac{P_{p c}}{m_{p c}}

（24）

电液换向阀主阀阀芯的动力学方程为：

{\dot{P}}_{v} = A_{v} (p_{p 6} - p_{p 7}) - F_{v p} - k_{v} x_{v} - r_{v} {\dot{x}}_{v} - F_{v s}

（25）

F_{v s} = 2 C_{v i} A_{v i} c o s θ_{v i} (p_{p 1} - p_{p 3}) + 2 C_{v o} A_{v o} c o s θ_{v o} p_{p 4}

（26）

式中： $P_{v}$ 为电液换向阀主阀阀芯的动量；p_p6为管路6的工作容腔压力； $θ_{v i}$ 、 $θ_{v o}$ 分别为主阀进、出口油液速度方向角。

电液换向阀主阀阀芯的运动速度为：

{\dot{x}}_{v} = \frac{P_{v}}{m_{v}}

（27）

摆臂转动的动力学方程为：

{\dot{P}}_{s a} = p_{p 3} A_{p l} - p_{p 4} A_{p r} - {\dot{θ}}_{s a} r_{s a}

（28）

式中： $P_{s a}$ 为摆臂的角动量。

摆臂的转动速度为：

{\dot{θ}}_{s a} = \frac{P_{s a}}{J_{s a}}

（29）

左摆动缸的运动速度为：

{\dot{x}}_{l s c} = \frac{{\dot{θ}}_{s a}}{A_{p l}}

（30）

右摆动缸的运动速度为：

{\dot{x}}_{r s c} = \frac{{\dot{θ}}_{s a}}{A_{p r}}

（31）

3 湿喷机摆臂摆动仿真分析

进行湿喷机摆臂摆动仿真分析。设置主要仿真参数如下：摆动缸的缸筒内径、活塞杆直径和工作行程分别为90，60和200 mm；摆臂的质量为72 kg，转动惯量为43.5 kgm²，摆臂半径为165 mm；铰点A与铰点D的距离为1 024 mm，铰点A与铰点E的距离为514 mm；恒压泵排量为40 mL/r；压力切断阀控制压力设定值为14 MPa；蓄能器的容积为10 L，初始充气压力为7 MPa；溢流阀设定压力为16 MPa；电液换向阀主阀阀芯的直径为25 mm，主阀弹簧预紧力为102 N；电机转速为1 500 r/min。

基于MATLAB仿真平台对所建立的湿喷机摆动系统的数学模型进行仿真分析，采用四阶‒龙格库塔算法进行数值模拟，仿真时间为20 s，仿真步长为0.01 s。摆臂最大摆动频率为30 次/min，设置电液换向阀的换向频率为0.5 Hz。由于混凝土的搅拌阻力复杂多变，为简化仿真，只分析料斗中无混凝土的工况。开始时，左、右摆动缸伸出的长度相等，即摆臂处于中心位置，此时S形分配阀既不与左泵缸连通，也不与右泵缸连通。启动时（即t=0 s），先给电磁阀左位通电并保持，左摆动缸无杆腔进压力油，驱动摆臂顺时针转动，使得S形分配阀与左泵缸连通；2 s后，电磁阀右位得电并保持，右摆动缸无杆腔进压力油，驱动摆臂逆时针转动，使得S形分配阀与右泵缸连通。如此，循环动作。

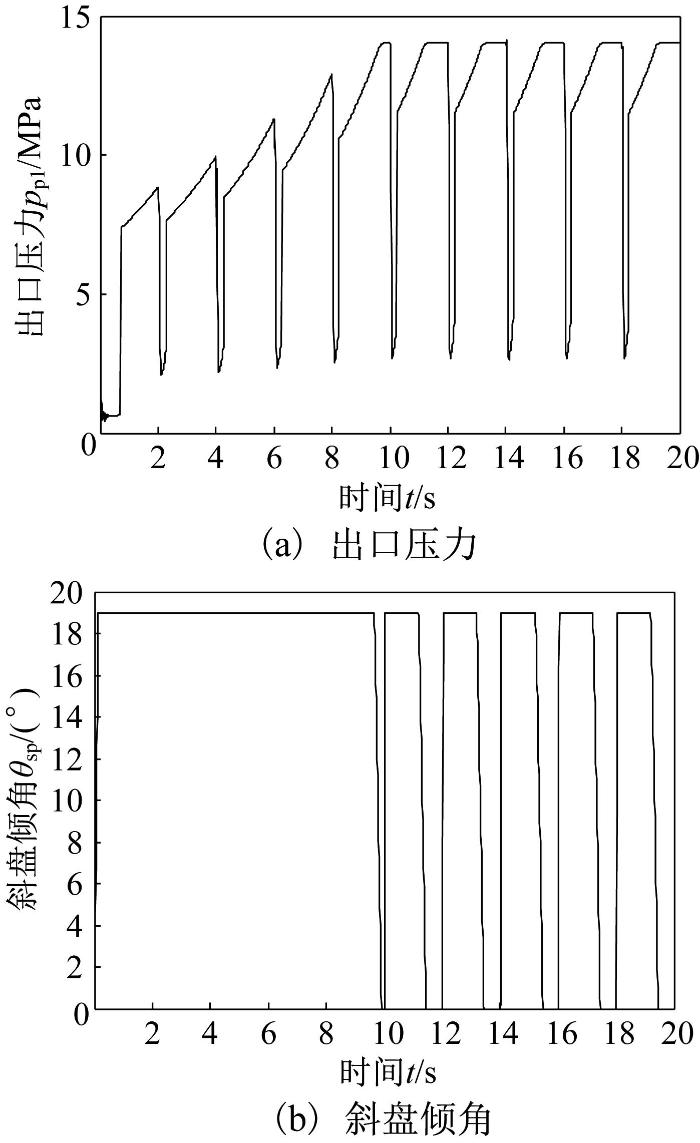
在摆臂摆动过程中恒压泵的响应曲线如图4所示。由图4（a）可知：在摆臂前5次摆动过程中，斜盘一直处于最大倾角状态，这是因为在摆臂摆动过程中恒压泵一方面给摆动缸供油，另一方面在摆臂达到极限位置后须给蓄能器充液，直至蓄能器压力达到恒压泵压力切断阀的设定压力14 MPa；在摆臂第1次摆动时，恒压泵出口压力仅为0.6 MPa，这是因为摆臂处于空载状态，仅克服摆臂转动阻力和右摆动缸无杆腔回油阻力，无法给蓄能器充液，直至摆臂顺时针运动到极限位置；随着摆臂摆动次数的增加，摆臂运动至极限位置时的泵出口压力逐渐升高，在第5次摆动到极限位置时，泵出口压力达到系统最大工作压力；此后，在摆臂摆动过程中，泵出口压力先在0.24 s内由14 MPa下降至2.6 MPa，与蓄能器一起给摆动缸供油，紧接着在0.41 s内升高至11.6 MPa而给蓄能器充液，再缓慢升高至14 MPa完成对蓄能器充液。由图4（b）可知，斜盘倾角随之呈0°~19°的周期性变化。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 恒压泵响应曲线

Fig.4 Response curve of constant pressure pump

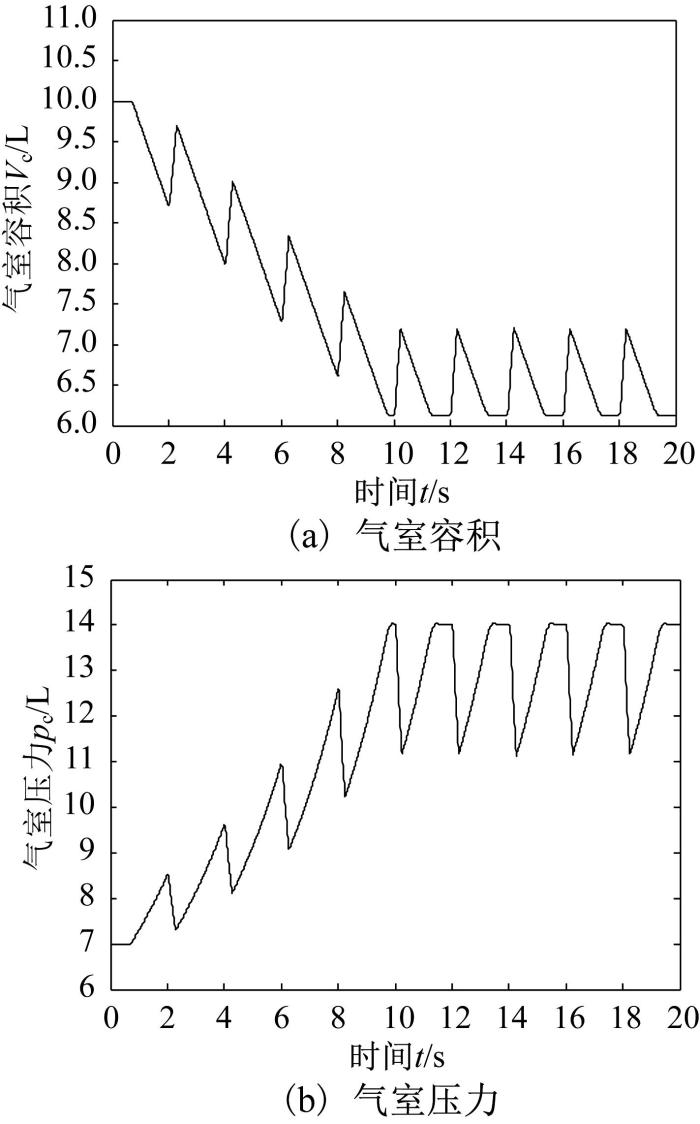
在摆臂摆动过程中蓄能器的响应曲线图5所示。由图可知：在摆臂开始第1次摆动时，蓄能器气室压力高于恒压泵出口压力，恒压泵出口油液全部供给摆动缸，当摆动缸运动至极限位置时，蓄能器开始充液，当压力达到8.5 MPa时，摆臂开始第2次摆动，此时蓄能器和恒压泵一起给摆动缸供油，在摆臂运动至极限位置时，蓄能器又开始充液，当压力达到9.6 MPa时，摆臂开始第3次摆动，如此循环反复，在摆臂完成第5次摆动时，蓄能器气室压力达到14 MPa。此后，蓄能器气室压力在11.2~14 MPa之间变化，相应的气室容积在6.1~7.1 L之间变化，不断进行充液与放液。在每次换向过程中供给摆动缸的油液流量约为50.5 L/min。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 蓄能器响应曲线

Fig.5 Response curve of accumulator

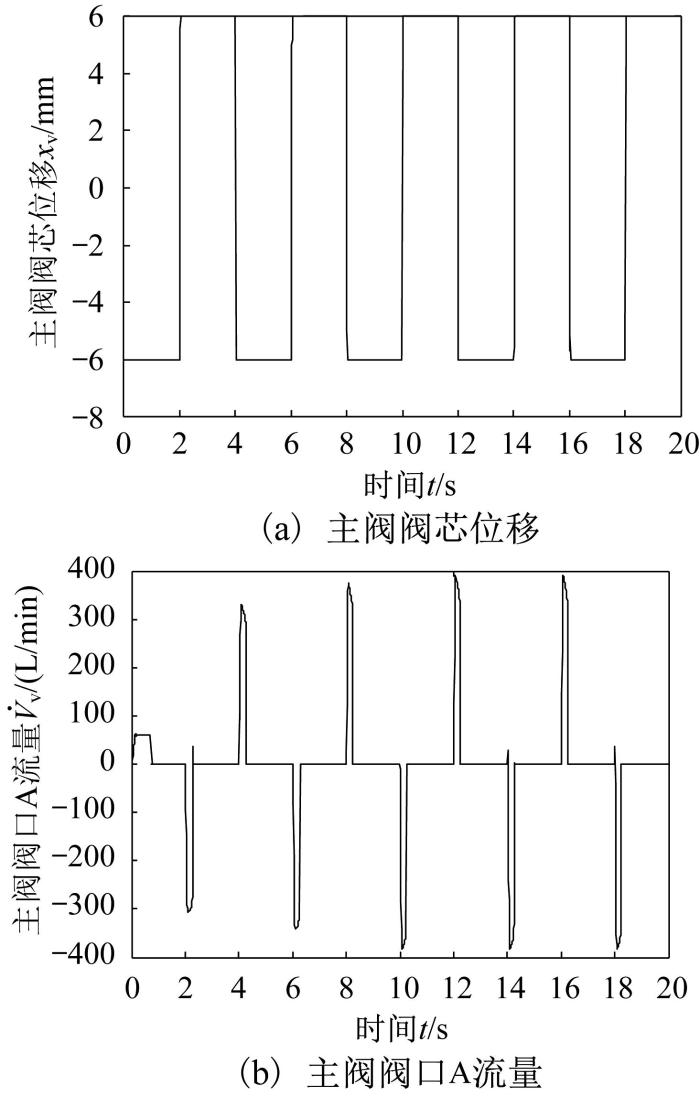
在摆臂摆动过程中电液换向阀主阀的响应曲线如图6所示。其中主阀阀口A流量为正表示油液流入左摆动缸无杆腔，为负表示油液流出左摆动缸无杆腔。由图6（a）可知：主阀阀芯左右方向的运动行程很短，只有6 mm，兼之左右回位弹簧预紧力较小，左右控制腔较小的油压就可以驱动主阀阀芯运动，在3 ms内完成换向，不受蓄能器充液压力的影响。由图6（b）可知：在摆臂开始第1次摆动时，主阀阀口A的最大流量只有60 L/min，这是因为蓄能器气室压力高于泵出口压力，还无法充液，摆动缸的运动完全由恒压泵供油，当摆动缸运动至极限位置时，恒压泵才给蓄能器充液；在摆臂开始第2次摆动时，主阀阀口A的最大流量增至305 L/min，这是因为蓄能器与恒压泵一起给摆动缸供油；随着摆动次数的增加，系统达到稳定状态，主阀阀口A的最大流量稳定在382.5 L/min，而泵出口最大流量仅为60 L/mim，说明蓄能器短时间内大流量放液是引起S形分配阀快速换向的主要原因。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 电液换向阀主阀响应曲线

Fig.6 Response curve of main valve of electro hydraulic directional valve

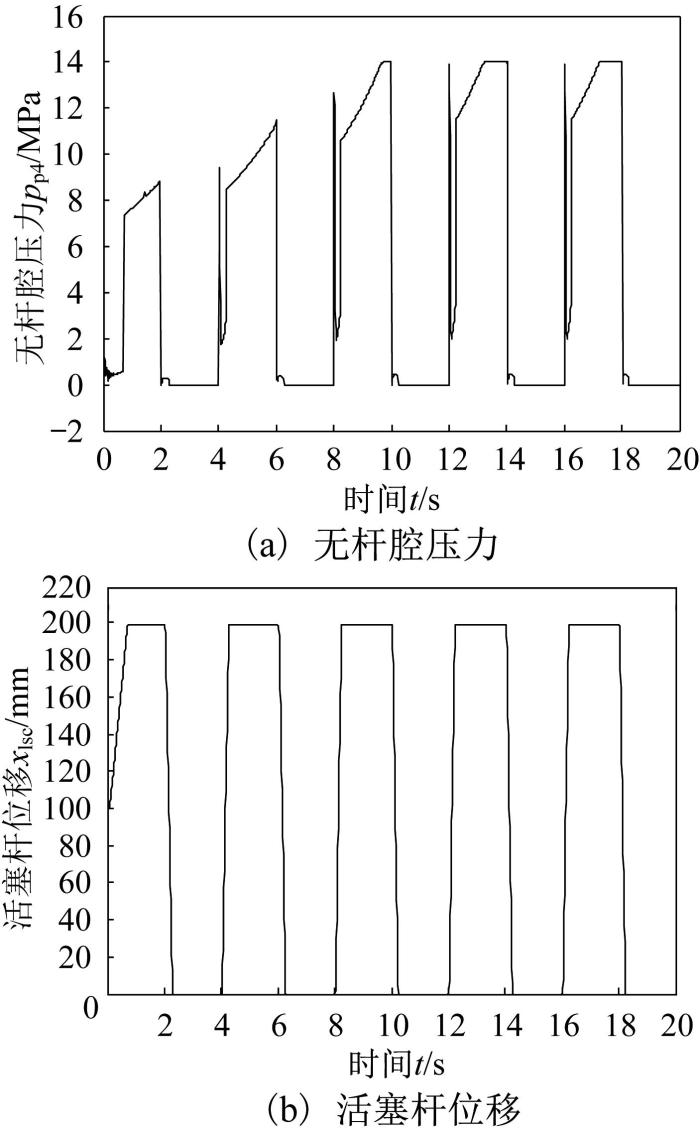
在摆臂摆动过程中左摆动缸响应曲线如图7所示。由图可知：左摆动缸的运动可以分为4个状态：状态1，伸出运动；状态2，伸出至极限位置保持不动；状态3，缩回运动；状态4，缩回至极限位置保持不动。在系统未达到稳定状态之前，左摆动缸处于状态1时，无杆腔油液压力出现峰值，并随着摆动次数的增加逐渐升高至14 MPa，但压力峰值的维持时间很短，然后急速下降至2 MPa，活塞杆的伸缩（位移由0 mm至200 mm，或由200 mm 至0 mm）时间也由0.72 s减小至0.24 s，这是因为系统高压待命，但负载较小，压力短时间出现峰值后急速降低，但蓄能器的放液作用使得S形分配阀快速完成换向；当左摆动缸处于状态2时，恒压泵开始给蓄能器充液，无杆腔油液压力和蓄能器充液压力变化一致，且随着摆动次数的增加充液压力逐渐升高，最终稳定在14 MPa；当左摆动缸处于状态3时，无杆腔油液压力在较短时间内维持0.4 MPa的回油阻力，随着摆动次数的增加活塞杆缩回时间稳定在0.24 s；当左摆动缸处于状态4时，摆动缸无杆腔直接与油箱相连，油液压力为0 MPa。右摆动缸的运动规律与左摆动缸类似，不再赘述。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 左摆动缸响应曲线

Fig.7 Response curve of left swing cylinder

4 湿喷机摆臂摆动实验

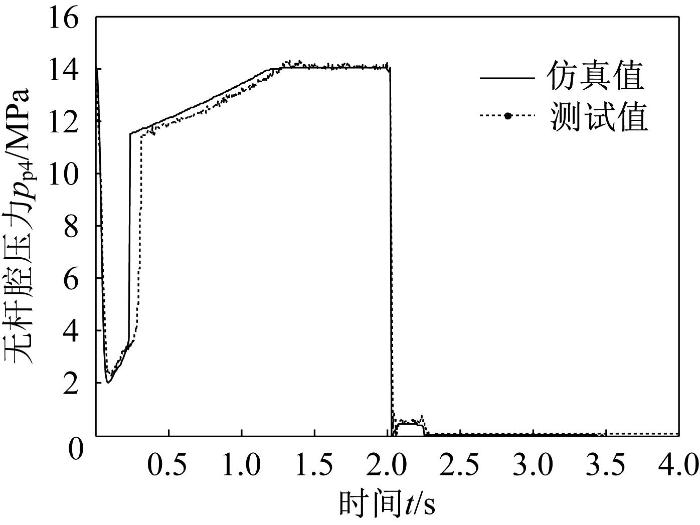
在混凝土湿喷机上搭建摆臂摆动测试平台，如图8所示。将压力传感器安装在左摆动缸无杆腔进油口处以采集油液工作压力，设置传感器的采样周期为0.01 s。启动电机，电液换向阀的换向周期为2 s，摆臂在空载情况下运动2 min至稳定状态，然后通过手持式液压测试仪采集左摆动缸无杆腔的压力，并将压力数据导入电脑。左摆动缸无杆腔压力测试结果与仿真结果的对比如图9所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 混凝土湿喷机摆臂摆动测试平台

Fig.8 Swing test platform of swing arm of concrete wet spraying machine

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 左摆动缸无杆腔压力测试结果与仿真结果的对比

Fig.9 Comparison of pressure test results and simulation results of rodless cavity of left swing cylinder

由图9可知：左摆动缸活塞杆完成伸缩和蓄能器完成充液的时间分别为0.31 s和1.06 s，比仿真所得的时间略有增加，且压力有一定的波动。这是因为在摆臂实际摆动过程中恒压泵输出油液具有脉动性，且仿真变量与实际参数的取值有差异，也受到了传感器测量精度的影响，加之没有考虑恒压泵等液压元件的泄漏。但左摆动缸无杆腔工作压力测试结果与仿真结果的峰值和稳态值基本相等，且变化趋势基本一致，验证了所建摆动系统动力学模型的准确性。

5 结论

根据混凝土湿喷机摆动系统的结构及工作原理，考虑液压元件内部阀芯等零部件的运动响应时间等因素，基于键合图理论建立了摆动系统的动力学模型，并进行仿真分析和实验测试，得出如下结论：

1）在摆臂运动达到稳定状态之前，恒压泵一直处于全排量供油状态，蓄能器反复充液与放液，且充液压力随摆臂摆动次数的增加而逐渐升高，最终稳定在14 MPa；S形分配阀换向时间随摆臂摆动次数的增加而逐渐减少，最终稳定在0.24 s。

2）在摆臂运动达到稳定状态之后，恒压泵斜盘摆角在0°~19°之间交替变化，蓄能器充液与放液体积稳定在1.1 L左右，使得电液换向阀最大瞬间流量可以达到382.5 L/min，满足S形分配阀快速换向的要求。

3）电液换向阀主阀弹簧预紧力较小，且运动行程较短，而阀芯端面作用面积较大，较低的油压就可以驱动阀芯完成换向，其换向时间不受蓄能器工作压力的影响，但最大换向瞬时流量由蓄能器放液流量决定。

4）摆动缸无杆腔工作压力的测试结果与仿真结果基本一致，验证了所建模型的准确性，为进一步分析和优化摆动系统的动力学性能提供了参考。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

袁定辉，林春，叶水标，等.

大断面公路隧道湿喷混凝土施工关键技术研究

［J］.现代隧道技术，2018，55（S2）：232-235.

[本文引用: 1]

YUAN

Ding-hui

， LIN

Chun

， YE

Shui-biao

， et al.

Key techniques for wet sprayed concrete construction in large cross-section highway tunnels

［J］. Modern Tunnelling Technology， 2018， 55（S2）： 232-235.

[本文引用: 1]

[2]

靖保平，傅连东，邓江洪，等.

混凝土泵车摆动系统的动态特性研究

［J］.机械设计与制造，2015（11）：163-166，170. doi：10.3969/j.issn.1001-3997.2015.11.041

[本文引用: 1]

JING

Bao-ping

， FU

Lian-dong

， DENG

Jiang-hong

， et al.

Dynamic characteristics research of concrete pump truck swing system

［J］. Machinery Design & Manufacture， 2015（11）： 163-166， 170.

DOI:10.3969/j.issn.1001-3997.2015.11.041 [本文引用: 1]

[3]

王超，曾发林，刘蕾.

基于AMESim的混凝土泵车摆动系统仿真与研究

［J］.机床与液压，2011，39（21）：142-144，148. doi：10.3969/j.issn.1001-3881.2011.21.041

[本文引用: 1]

WANG

Chao

， ZENG

Fa-lin

， LIU

Lei

Simulation study of the swing hydraulic system of concrete pumping truck based on AMESim

［J］. Machine Tool & Hydraulics， 2011， 39（21）： 142-144， 148.

DOI:10.3969/j.issn.1001-3881.2011.21.041 [本文引用: 1]

[4]

胡军科，赵斌，蒋亚军，等.

摆动系统恒压变量泵瞬时吸空问题

［J］.长安大学学报（自然科学版），2016，36（5）：118-126.

[本文引用: 1]

Jun-ke

， ZHAO

Bin

， JIANG

Ya-jun

， et al.

Instantaneous air suction of constant pressure variable displacement pump of swing system

［J］. Journal of Chang'an University （Natural Science Edition）， 2016， 36（5）： 118-126.

[本文引用: 1]

[5]

刘在政，秦念稳，邹今检，等.

喷射机械手智能控制系统与喷射路径规划设计研究

［J］.隧道建设，2018，38（8）：1391-1396.

[本文引用: 1]

LIU

Zai-zheng

， QIN

Nian-wen

， ZOU

Jin-jian

， et al.

Research on intelligent control system and path planning of spraying manipulator

［J］. Tunnel Construction， 2018， 38（8）： 1391-1396.

[本文引用: 1]

[6]

刘蕾，曾发林，王超，等.

混凝土泵车泵送系统缓冲效果仿真研究

［J］.机床与液压，2011，39（13）：110-113. doi：10.3969/j.issn.1001-3881.2011.13.033

[本文引用: 1]

LIU

Lei

， ZENG

Fa-lin

， WANG

Chao

， et al.

Simulation analysis of the buffer effect of the pumping hydraulic system in concrete pumping truck

［J］. Machine Tool & Hydraulics， 2011， 39（13）： 110-113.

DOI:10.3969/j.issn.1001-3881.2011.13.033 [本文引用: 1]

[7]

黄毅，郭岗，邝昊，等.

混凝土泵车臂架回转系统动力学分析及预测

［J］.机械强度，2014，36（2）：300-304.

[本文引用: 1]

HUANG

， GUO

Gang

， KUANG

Hao

， et al.

Dynamics analysis and prediction on boom slewing system of the concrete pump truck

［J］. Journal of Mechanical Strength， 2014， 36（2）： 300-304.

[本文引用: 1]

[8]

胡仕成，宋晶晶，王祥军.

混凝土湿喷机臂架系统的动力学建模与分析

［J］.工程设计学报，2014，21（3）：227-234. doi：10.3785/j.issn.1006-754X.2014.03.005

[本文引用: 1]

Shi-cheng

， SONG

Jing-jing

， WANG

Xiang-jun

Dynamics modeling and analysis on boom system of wet spraying machine

［J］. Chinese Journal of Engineering Design， 2014， 36（2）： 300-304.

DOI:10.3785/j.issn.1006-754X.2014.03.005 [本文引用: 1]

[9]

卢志学，贺电，徐周.

基于Fluent的混凝土泵车联通阀组流道仿真分析与试验研究

［J］.液压与气动，2020（10）：127-131.

[本文引用: 1]

Zhi-xue

， HE

Dian

， XU

Zhou

Analysis and experimental study on flow channel of connecting valve group of concrete pump truck based on Fluent

［J］. Chinese Hydraulics & Pneumatics， 2020（10）： 127-131.

[本文引用: 1]

[10]

罗艳蕾，屠松庭，石立明，等.

基于负载敏感系统的山地液压割草机工作回路研究

［J］.液压与气动，2020（2）：71-77.

[本文引用: 1]

LUO

Yan-lei

， TU

Song-ting

， SHI

Li-ming

， et al.

Research on working circuit of mountain hydraulic lawn mower based on load sensitive system

［J］. Chinese Hydraulics & Pneumatics， 2020（2）： 71-77.

[本文引用: 1]

[11]

陈素丽，樊岩松，王威，等.

基于键合图理论的轨道钳升降系统建模与仿真

［J］.机械传动，2016，40（7）：83-86.

CHEN

Su-li

， FAN

Yan-song

， WANG

Wei

， et al.

Modeling and simulation of track clamp jacking system based on bond graph theory

［J］. Journal of Mechanical Transmission， 2016， 40（7）： 83-86.

[12]

胡均平，李科军.

螺旋钻机变幅时机液耦合动力学的键合图建模

［J］.中南大学学报（自然科学版），2016，47（2）：495-502.

Jun-ping

， LI

Ke-jun

Dynamics model of mechanical-hydraulic coupling of auger driller during luffing motion by bond graph

［J］. Journal of Central South University （Science and Technology）， 2016， 47（2）： 495-502.

[13]

张寒冰，楫骏，杨玉虎，等.

TBM推进系统键合图建模与动态仿真

［J］.机械设计，2018，35（1）：7-13.

ZHANG

Han-bing

， JI

Jun

， YANG

Yu-hu

， et al.

Bond graph modeling and dynamic simulation of tunnel boring machine propulsion system

［J］. Journal of Machine Design， 2018， 35（1）： 7-13.

[14]

刘志双，李科军，施发永，等.

核岛内环吊拱架安装车臂架伸缩臂液压系统建模分析

［J］.现代制造工程，2021（10）：125-131.

[本文引用: 2]

LIU

Zhi-shuang

， LI

Ke-jun

， SHI

Fa-yong

， et al.

Modeling and analysis of the telescopic hydraulic system of the boom of the ring crane arch frame installation vehicle on the nuclear island

［J］. Modern Manufacturing Engineering， 2021（10）：125-131.

[本文引用: 2]

[15]

杨曙东，何存兴.液压传动与气压传动［M］.3版.武汉：华中科技大学出版社，2008：112-120.

[本文引用: 1]

YANG

Shu-dong

， HE

Cun-xing

. Hydraulic transmission and pneumatic transmission［M］. 3th ed. Wuhan： Huazhong University of Science and Technology Press， 2008： 112-120.

[本文引用: 1]

大断面公路隧道湿喷混凝土施工关键技术研究

2018

... 目前，国内大力开展中西部铁路、公路等基础设施建设，其中隧道建设里程占比较大.混凝土喷射是隧道修筑中的一项关键技术：借助机械，将速凝混凝土喷向岩石或结构物表面，使岩石或结构物得到加强和保护^［1］.湿喷机用于输送和喷射混凝土，是隧道施工中不可缺少的关键设备.湿喷机摆动系统设计在料斗后方，2个摆动缸在高压油液的作用下驱动摆臂左右摆动，实现S形分配阀迅速换向，配合泵送系统将混凝土通过管路输送到喷嘴处进行喷射.摆动系统的换向特性直接关系着湿喷机的泵送效率和喷射质量，因此有必要对摆动系统的工作性能进行深入研究.靖保平等^［2-3］建立了湿喷机摆动系统的AMESim模型，分析了S形分配阀快速换向及其引起系统冲击的原因，但将恒压泵简化成定量泵，不能非常准确地反映摆动系统的工作特性.胡军科等^［4］提出了在变量缸敏感腔进油口设置比例节流阀以控制阀口开度的方法，对变量缸的流量及运动速度进行调节，较好地解决了摆动系统的恒压泵瞬时吸空的问题.为了提高湿喷机的喷射效率和施工安全，刘在政等^［5］研发了喷射机械手的智能化控制系统，采用全站型电子速测仪、三维激光扫描仪获取湿喷机和待喷面的坐标，基于喷头的运动学模型对湿喷机臂架关节的位姿进行规划，实现了混凝土喷射的自动化和智能化.刘蕾等^［6］利用功率键合图法建立了混凝土泵车泵送系统的动力学模型，得出了泵送油缸缓冲阻尼孔的孔径对泵送液压冲击和振动的影响规律；黄毅等^［7］对混凝土泵车臂架的动态特性和振动响应进行预测分析，为臂架减振研究提供了理论依据；胡仕成等^［8］采用解析几何法和拉格朗日方程建立了湿喷机臂架系统的动力学模型，分析了驱动油缸铰点位置变化对油缸最大驱动力的影响规律；卢志学等^［9］运用Fluent软件对泵车无杆腔联通阀组的内部流道进行优化设计，以减小压损，降低能耗.可见，现有研究主要集中在泵车结构强度、泵送系统动态特性、喷射头轨迹规划、臂架动力学建模和振动控制等方面，对摆动系统的研究较少.本文通过分析湿喷机摆动系统的结构及工作原理，建立摆动系统在摆动过程中的动力学模型，仿真分析摆动系统的工作特性，并搭建实验平台进行实验验证，以期为摆动系统的动力学优化提供依据. ...

大断面公路隧道湿喷混凝土施工关键技术研究

2018

混凝土泵车摆动系统的动态特性研究

2015

混凝土泵车摆动系统的动态特性研究

2015

基于AMESim的混凝土泵车摆动系统仿真与研究

2011

基于AMESim的混凝土泵车摆动系统仿真与研究

2011

摆动系统恒压变量泵瞬时吸空问题

2016

摆动系统恒压变量泵瞬时吸空问题

2016

喷射机械手智能控制系统与喷射路径规划设计研究

2018

喷射机械手智能控制系统与喷射路径规划设计研究

2018

混凝土泵车泵送系统缓冲效果仿真研究

2011

混凝土泵车泵送系统缓冲效果仿真研究

2011

混凝土泵车臂架回转系统动力学分析及预测

2014

混凝土泵车臂架回转系统动力学分析及预测

2014

混凝土湿喷机臂架系统的动力学建模与分析

2014

混凝土湿喷机臂架系统的动力学建模与分析

2014

基于Fluent的混凝土泵车联通阀组流道仿真分析与试验研究

2020

基于Fluent的混凝土泵车联通阀组流道仿真分析与试验研究

2020

基于负载敏感系统的山地液压割草机工作回路研究

2020

... 根据湿喷机摆动系统键合图模型状态方程生成规则，可以快速方便地得到其动力学模型^［10-14］. ...

基于负载敏感系统的山地液压割草机工作回路研究

2020

... 根据湿喷机摆动系统键合图模型状态方程生成规则，可以快速方便地得到其动力学模型^［10-14］. ...

基于键合图理论的轨道钳升降系统建模与仿真

2016

基于键合图理论的轨道钳升降系统建模与仿真

2016

螺旋钻机变幅时机液耦合动力学的键合图建模

2016

螺旋钻机变幅时机液耦合动力学的键合图建模

2016

TBM推进系统键合图建模与动态仿真

2018

TBM推进系统键合图建模与动态仿真

2018

核岛内环吊拱架安装车臂架伸缩臂液压系统建模分析

2021

... 根据湿喷机摆动系统键合图模型状态方程生成规则，可以快速方便地得到其动力学模型^［10-14］. ...

... 式中：

{\dot{V}}_{p 1}

为管路1工作容腔的流量；

{\dot{V}}_{r f}

为通过溢流阀的流量；

{\dot{V}}_{p c i}

为泵出口到大活塞控制缸无杆腔的的流量；

{\dot{V}}_{c v}

为通过单向阀的流量；

D_{p m a x}

为柱塞泵斜盘达到最大倾角19°时变量泵的排量；

C_{r f}

、

A_{r f}

分别为溢流阀阀口的流量特性系数和开口面积；

C_{p c i}

为压力切断阀阀口的流量特性系数^［14］；

C_{c v}

、

A_{c v}

分别为单向阀阀口的流量特性系数和开口面积；

ρ

为液压油密度. ...

核岛内环吊拱架安装车臂架伸缩臂液压系统建模分析

2021

... 根据湿喷机摆动系统键合图模型状态方程生成规则，可以快速方便地得到其动力学模型^［10-14］. ...

... 式中：

{\dot{V}}_{p 1}

为管路1工作容腔的流量；

{\dot{V}}_{r f}

为通过溢流阀的流量；

{\dot{V}}_{p c i}

为泵出口到大活塞控制缸无杆腔的的流量；

{\dot{V}}_{c v}

为通过单向阀的流量；

D_{p m a x}

为柱塞泵斜盘达到最大倾角19°时变量泵的排量；

C_{r f}

、

A_{r f}

分别为溢流阀阀口的流量特性系数和开口面积；

C_{p c i}

为压力切断阀阀口的流量特性系数^［14］；

C_{c v}

、

A_{c v}

分别为单向阀阀口的流量特性系数和开口面积；

ρ

为液压油密度. ...

2008

... 管路1工作容腔的流量连续性方程为^［15］： ...

2008

... 管路1工作容腔的流量连续性方程为^［15］： ...

〈

〉