环形油腔液体静压推力轴承动态特性的影响因素研究

doi:10.3785/j.issn.1006-754X.2022.00.060

环形油腔液体静压推力轴承动态特性的影响因素研究

田助新^,^,¹^,², 郭明慧², 曹海印²

1.三峡大学机械与动力学院，湖北宜昌 443002

2.华中科技大学机械科学与工程学院，湖北武汉 430074

Study on influencing factors of dynamic characteristics of annular recess hydrostatic thrust bearing

TIAN Zhu-xin^,^,¹^,², GUO Ming-hui², CAO Hai-yin²

1.School of Mechanical and Power Engineering, China Three Gorges University, Yichang 443002, China

2.School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China

收稿日期: 2021-11-29 修回日期: 2022-01-12

基金资助:

国家自然科学基金面上项目. 51875223
科学挑战计划专题项目. TZ2018006-0102-03

Received: 2021-11-29 Revised: 2022-01-12

作者简介 About authors

田助新（1987—），男，湖北潜江人，讲师，博士，从事流体静压及动压支承系统研究，E-mail：zhuxintian1987@sina.com，https：//orcid.org/0000-0002-5286-5714 , E-mail：zhuxintian1987@sina.com

摘要

液体静压推力轴承的动态特性直接决定了其运行状态的稳定性，而油腔结构和节流方式是影响其动态特性的重要因素。为此，基于小扰动法将环形油腔液体静压推力轴承的Reynolds方程分解成动态方程和静态方程，分别求解得到小孔和毛细管节流方式下其油膜刚度和阻尼系数的解析表达式。同时，通过开展油膜刚度测量实验来验证理论计算结果的正确性，两者之间的相对误差小于15%。理论计算结果显示：对于液体静压推力轴承，环形油腔优于圆形油腔，小孔节流优于毛细管节流。通过分析油腔面积和油腔位置对小孔节流环形油腔液体静压推力轴承油膜刚度和阻尼系数的影响规律发现，当内、外径等基本结构参数确定时，调整油腔的面积和位置可以有效优化该轴承的动态特性系数。研究结果有助于以动态特性为目标的液体静压推力轴承的结构优化设计。

关键词： 液体静压推力轴承 ; 环形油腔 ; 动态特性 ; 小扰动法

Abstract

The dynamic characteristics of hydrostatic thrust bearing directly determine the stability of its operating state, and the recess structure and throttling pattern are important factors affecting its dynamic characteristics. Therefore, based on the small perturbation method, the Reynolds equation of annular recess hydrostatic thrust bearing was decomposed into dynamic equation and static equation, and then the analytical expressions of its oil film stiffness and damping coefficient under the throttling patterns of orifice and capillary were obtained. At the same time, the correctness of theoretical calculation results was verified by oil film stiffness measurement experiment, which showed that the relative error was less than 15%. The theoretical calculation results showed that： for the hydrostatic thrust bearing, the annular recess was better than the circular recess, and the orifice throttling was better than the capillary throttling. By analyzing the influence of the area and position of recess on the oil film stiffness and damping coefficient of annular recess hydrostatic thrust bearing with orifice throttling, it was found that when the internal and external diameters and other basic structural parameters were determined, the dynamic characteristic coefficients of this bearing could be effectively optimized by adjusting the area and position of recess. The research results were conducive to the structural optimization design of hydrostatic thrust bearings with dynamic characteristics as target.

Keywords： hydrostatic thrust bearing ; annular recess ; dynamic characteristics ; small perturbation method

PDF (3921KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

田助新, 郭明慧, 曹海印. 环形油腔液体静压推力轴承动态特性的影响因素研究. 工程设计学报[J], 2022, 29(4): 456-464 doi:10.3785/j.issn.1006-754X.2022.00.060

TIAN Zhu-xin, GUO Ming-hui, CAO Hai-yin. Study on influencing factors of dynamic characteristics of annular recess hydrostatic thrust bearing. Chinese Journal of Engineering Design[J], 2022, 29(4): 456-464 doi:10.3785/j.issn.1006-754X.2022.00.060

近年来，随着液体静压技术的发展，液体静压推力轴承已被应用于许多大型设备^［1-2］。其工作原理是：通过液压泵将压力油导入油腔，以隔开转动部件与支承部件，从而减小转动副运动过程中的摩擦。因具有油膜刚度大、吸振性好和启动功率低等优点，液体静压推力轴承在车床、磨床等承载力大且载荷波动剧烈的机床上得到了广泛应用^［3-5］。

Dowson^［6］在研究圆形油腔液体静压推力轴承的过程中引入了油膜惯性效应，并给出了其静态特性的解析求解方法。随后，为了验证这一理论研究结果，Coombs等人^［7］设计了相关实验，发现当圆形油腔液体静压推力轴承转速较小时，其静态特性的理论计算结果与实验结果吻合；而当转速较大时，两者之间的误差较为明显。他们认为该误差是由油膜温升导致的润滑油黏度改变所引起的。而Tian等人^［8］则认为这一误差产生的原因是在理论分析过程中未考虑供油孔区域油膜的惯性效应，并在考虑供油孔区域油膜惯性效应的基础上，提出了一种计算圆形油腔液体静压推力轴承静态特性的新方法，其计算结果更符合实验结果。张艳芹等人^［9-10］对矩形油腔液体静压推力轴承的内部流场和润滑特性进行了分析。于晓东等人^［11］讨论了矩形油腔液体静压推力轴承在瞬态冲击载荷作用下的动态特性。Chow等人^［12］讨论了环形油腔液体静压推力轴承的静态特性并给出了其理论计算方法。在此基础上，其他学者还分析了轴承结构^［13］、润滑剂的非牛顿性^［14］以及轴承表面纹理^［15］等因素对环形油腔液体静压推力轴承静态特性的影响。关于扇形油腔液体静压推力轴承，其相关研究主要集中在承载力^［16］、润滑特性^［17-18］等静态特性方面。此外，学者们也讨论了一些其他因素对液体静压推力轴承静、动态特性的影响，如：Shen等人^［19］对比分析了油腔结构不同的液体静压推力轴承的静态特性；Lin等人^［20］讨论了润滑剂的非牛顿性对圆形油腔液体静压推力轴承动态特性的影响。

综上可知，上述文献主要讨论了油腔形状不同的液体静压推力轴承的静态特性以及圆形油腔液体静压推力轴承的动态特性，尚缺乏对环形油腔液体静压推力轴承动态特性的研究。为此，笔者拟基于小扰动法来求解环形油腔液体静压推力轴承的Reynolds方程，以得到其油膜刚度和阻尼系数的解析表达式，并搭建相应的实验台开展油膜刚度测量实验，以对理论计算结果进行验证。同时，对圆形油腔和环形油腔液体静压推力轴承在小孔和毛细管节流方式下的油膜刚度和阻尼系数进行对比。最后，以小孔节流环形油腔液体静压推力轴承为对象，讨论油腔面积和油腔位置对其动态特性的影响规律。

1 环形油腔液体静压推力轴承的动、静态特性理论分析

1.1　动、静态方程建立

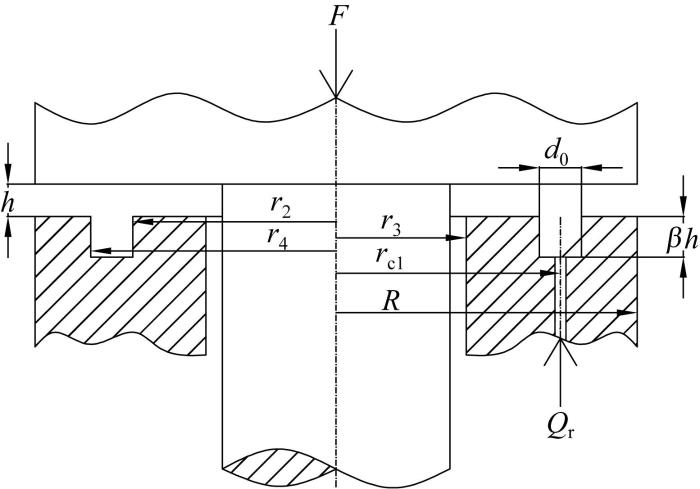
环形油腔液体静压推力轴承的结构如图1所示，在实际工况下该轴承主轴以角速度ω转动。图中：R为轴承外径，r₃为轴承内径；r₄为油腔内径，r_c1为油腔中径，r₂为油腔外径，d₀为油腔宽度。在该轴承运行过程中，其轴向负载为F，流量为Q_r；封油边处油膜厚度为h，油腔区域油膜厚度为βh（β为油腔深度与封油边油膜厚度之比）；供油压力为P_s，油腔压力为P_r；润滑剂为牛顿流体。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 环形油腔液体静压推力轴承结构示意

Fig.1 Structure diagram of annular recess hydrostatic thrust bearing

考虑到环形油腔液体静压推力轴承结构的轴对称性，以其表面圆心为原点建立柱坐标系，则油膜运动方程可表示为：

- \frac{\partial P}{\partial r} + η \frac{\partial^{2} u}{\partial z^{2}} = - ρ \frac{v^{2}}{r}

（1）

η \frac{\partial^{2} v}{\partial z^{2}} = 0

（2）

\frac{\partial P}{\partial z} = 0

（3）

式中：P为油膜压力；r、z分别为径向和竖直方向的位置；u、v分别为油膜沿径向和周向的速度；ρ、η分别为润滑油的密度和黏度。

根据边界条件 $u |_{z = 0} = u |_{z = h} = 0, v |_{z = 0} = 0, v |_{z = h} = r ω$ ，求解油膜运动方程，可得油膜沿径向和周向的速度u、v分别为：

u = \frac{\partial P}{\partial r} \frac{z^{2} - h z}{2 η} - \frac{ρ}{η} \frac{r ω^{2}}{h^{2}} \frac{z^{4} - h^{3} z}{12}

（4）

v = \frac{r ω}{h} z

（5）

由此可得，环形油腔液体静压推力轴承的流量Q_r为：

Q_{r} = 2 π r \int_{0}^{h} u d z = \frac{1}{20} \frac{π ρ r^{2} ω^{2} β^{3} h^{3}}{η} - \frac{π β^{3} h^{3} r}{6 η} \frac{\partial P}{\partial r}

（6）

基于式（6）可得：

\frac{\partial P}{\partial r} = - \frac{6 μ Q_{r}}{π h^{3} r} + \frac{3}{10} ρ r ω^{2}

（7）

由于油膜厚度的单位为μm，而轴承结构参数的单位为mm，为防止计算过程中产生精度损失以及简化公式，引入以下无量纲量：

\begin{matrix} r^{*} = \frac{r}{R}, h^{*} = \frac{h}{h_{0}}, P^{*} = \frac{P}{P_{s}}, t^{*} = μ t \\ S = \frac{3}{20} \frac{ρ ω^{2} R^{2}}{P_{s}}, σ = \frac{12 η μ R^{2}}{P_{s} h_{0}^{2}}, Q_{r}^{*} = \frac{6 η Q_{r}}{π P_{s} h_{0}^{3}} \end{matrix}

式中：h₀为静态油膜厚度；μ为扰动频率；S为惯性参数。

则式（7）可转换为：

\frac{\partial P^{*}}{\partial r^{*}} = - \frac{Q_{r}^{*}}{h^{* 3} r^{*}} + 2 S r^{*}

（8）

在外封油面处引入边界条件 $P^{*} |_{r^{*} = r_{2}^{*}} = P_{r}^{*}, P^{*} |_{r^{*} = 1} = 0$ ，求解式（8）可得：

Q_{1}^{*} = \frac{h^{* 3}}{l n r_{2}^{*}} [P_{r}^{*} - S (r_{2}^{* 2} - 1)]

（9）

在内封油面处引入边界条件 $P^{*} |_{r^{*} = r_{4}^{*}} = P_{r}^{*}, P^{*} |_{r^{*} = r_{3}^{*}} = 0$ ，求解式（8）可得：

Q_{2}^{*} = \frac{h^{* 3}}{l n r_{3}^{*} - l n r_{4}^{*}} [P_{r}^{*} - S (r_{4}^{* 2} - r_{3}^{* 2})]

（10）

环形油腔液体静压推力轴承的总流量为内、外封油面处的流量之和，即有：

\begin{array}{l} Q_{r}^{*} = Q_{1}^{*} + Q_{2}^{*} = [- \frac{P_{r}^{*} - S (r_{2}^{* 2} - 1)}{l n r_{2}^{*}} + \\ \frac{P_{r}^{*} - S (r_{4}^{* 2} - r_{3}^{* 2})}{l n r_{3}^{*} - l n r_{4}^{*}}] h^{* 3} \end{array}

（11）

为求解环形油腔液体静压推力轴承的油膜压力，建立其Reynolds方程^［13］：

\frac{h^{* 3}}{r^{*}} \frac{\partial}{\partial r^{*}} (r^{*} \frac{\partial P^{*}}{\partial r^{*}}) = 4 S h^{* 3} + σ \frac{\partial h^{*}}{\partial t^{*}}

（12）

设此时该轴承在z方向受到小扰动，则其油膜厚度和油膜压力分别为：

\{\begin{array}{l} h^{*} = 1 + ε e^{i t^{*}} \\ P^{*} = P_{0}^{*} + ε e^{i t^{*}} P_{1}^{*} \end{array}

（13）

式中： $P_{0}^{*}$ 为无量纲静态油膜压力； $P_{1}^{*}$ 为小扰动作用下的无量纲动态油膜压力；i为虚数单位；ε为小扰动量。

联立式（12）和式（13），并忽略小扰动ε的高阶项，同时在等式两边分别对常数项和ε的一阶项待定系数，则可得环形油腔液体静压推力轴承的静态方程和动态方程，分别为：

\frac{1}{r^{*}} \frac{\partial}{\partial r^{*}} (r^{*} \frac{\partial P_{0}^{*}}{\partial r^{*}}) = 4 S

（14）

\frac{1}{r^{*}} \frac{\partial}{\partial r^{*}} (r^{*} \frac{\partial P_{1}^{*}}{\partial r^{*}}) = i σ

（15）

1.2　动、静态方程求解

1.2.1　静态方程求解

设油腔区域的静态油膜压力 $P_{0}^{*}$ 等于静态油腔压力 $P_{r 0}^{*}$ ，外部大气压为0 Pa，则对于外封油面区域（r₂，R），可得如下边界条件：

\{\begin{array}{l} P_{0}^{*} |_{r^{*} = r_{2}^{*}} = P_{r 0}^{*} \\ P_{0}^{*} |_{r^{*} = 1} = 0 \end{array}

（16）

将边界条件（16）代入静态方程（14），通过求解可得外封油面区域的静态油膜压力 $P_{0}^{*}$ ：

P_{0}^{*} = S (r^{* 2} - 1) + [P_{r 0}^{*} - S (r_{2}^{* 2} - 1)] \frac{l n r^{*}}{l n r_{2}^{*}}

（17）

则外封油面处的静态流量为：

Q_{r 01}^{*} = \frac{P_{r 0}^{*} - S (r_{2}^{* 2} - 1)}{l n r_{2}^{*}}

（18）

对于内封油面区域（r₄，r₃），采用与外封油面区域类似的边界条件：

\{\begin{array}{l} P_{0}^{*} |_{r^{*} = r_{4}^{*}} = P_{r 0}^{*} \\ P_{0}^{*} |_{r^{*} = r_{3}^{*}} = 0 \end{array}

（19）

同理求解得到内封油面区域的静态油膜压力和静态流量，分别为：

P_{0}^{*} = S (r^{* 2} - r_{3}^{* 2}) + [P_{r 0}^{*} - S (r_{4}^{* 2} - r_{3}^{* 2})] \frac{l n r^{*} - l n r_{3}^{*}}{l n r_{4}^{*} - l n r_{3}^{*}}

（20）

Q_{r 02}^{*} = \frac{P_{r 0}^{*} - S (r_{4}^{* 2} - r_{3}^{* 2})}{l n r_{4}^{*} - l n r_{3}^{*}}

（21）

由此可得，环形油腔液体静压推力轴承的总静态流量为：

Q_{r 0}^{*} = Q_{r 01}^{*} + Q_{r 02}^{*} = - \frac{P_{r 0}^{*} - S (r_{2}^{* 2} - 1)}{l n r_{2}^{*}} + \frac{P_{r 0}^{*} - S (r_{4}^{* 2} - r_{3}^{* 2})}{l n r_{4}^{*} - l n r_{3}^{*}}

（22）

对静态油膜压力关于其分布区域面积进行积分，可得静态承载力 $W_{0}^{*}$ ：

W_{0}^{*} = P_{r 0}^{*} C_{1} + S C_{2}

（23）

其中：

C_{1} = \frac{r_{2}^{* 2} - 1}{2 l n r_{2}^{*}} + \frac{(r_{3}^{* 2} - r_{4}^{* 2}) (l n r_{3}^{*} - 1)}{2 (l n r_{4}^{*} - l n r_{3}^{*})} - r_{4}^{* 2} - r_{3}^{* 2}

（24）

\begin{array}{l} C_{2} = \frac{r_{2}^{* 4} + r_{3}^{* 2} - r_{4}^{* 2} - 1}{2} - \frac{{(r_{2}^{* 2} - 1)}^{2}}{2 l n r_{2}^{*}} - \\ {(r_{3}^{* 2} - r_{4}^{* 2})}^{2} [\frac{(l n r_{3}^{*} - 1)}{2 (l n r_{4}^{*} - l n r_{3}^{*})} + 1] \end{array}

（25）

式中：C₁和C₂为环形油腔液体静压推力轴承的结构系数。

1.2.2　动态方程求解

设油腔区域的动态油膜压力 $P_{1}^{*}$ 等于动态油腔压力 $P_{r 1}^{*}$ ，外部大气压为0 Pa，则对于外封油面区域（r₂，R），可得如下边界条件：

\{\begin{array}{l} P_{1}^{*} |_{r^{*} = r_{2}^{*}} = P_{r 1}^{*} \\ P_{1}^{*} |_{r^{*} = 1} = 0 \end{array}

（26）

将边界条件（26）代入动态方程（15），通过求解可得外封油面区域的动态油膜压力 $P_{1}^{*}$ ：

P_{1}^{*} = \frac{i σ}{4} (r^{* 2} - 1) + [P_{r 1}^{*} - \frac{i σ}{4} (r_{2}^{* 2} - 1)] \frac{l n r^{*}}{l n r_{2}^{*}}

（27）

同理可得，内封油面区域的动态油膜压力 $P_{1}^{*}$ 为：

P_{1}^{*} = \frac{i σ}{4} (r^{* 2} - r_{3}^{* 2}) + [P_{r 1}^{*} - \frac{i σ}{4} (r^{* 2} - r_{3}^{* 2})] \times

\frac{l n r^{*} - l n r_{3}^{*}}{l n r_{4}^{*} - l n r_{3}^{*}}

（28）

则动态承载力 $W_{1}^{*}$ 为：

W_{1}^{*} = P_{r 1}^{*} C_{1} + \frac{i σ}{4} C_{2}

（29）

由此可得，环形油腔液体静压推力轴承的无量纲油膜刚度 $K_{d}^{*}$ 和阻尼系数 $D_{d}^{*}$ 分别为：

\{\begin{array}{l} K_{d}^{*} = - R e (W_{1}^{*}) \\ D_{d}^{*} = - \frac{I m (W_{1}^{*})}{σ} \end{array}

（30）

式中：Re（）、Im（）分别表示复数的实部和虚部。

1.3　动、静态油腔压力求解

静态油腔压力 $P_{r 0}^{*}$ 和动态油腔压力 $P_{r 1}^{*}$ 是基于节流器特性进行求解的。考虑到油腔内流体的压缩性，小孔节流器和毛细管节流器的节流方程可分别表示为：

\frac{π d_{c}^{4}}{128 η L_{c}} (P_{s} - P_{r}) = Q_{r} + A \frac{\partial h}{\partial t} + \frac{1}{ρ} \frac{\partial}{\partial t} (ρ V_{0})

（31）

\frac{α π d_{o}^{2}}{4} \sqrt[]{\frac{2 (P_{s} - P_{r})}{ρ}} = Q_{r} + A \frac{\partial h}{\partial t} + \frac{1}{ρ} \frac{\partial}{\partial t} (ρ V_{0})

（32）

式中：d_c、L_c分别为毛细管的截面直径和长度；d_o为小孔的截面直径；V₀为油腔体积；A为油腔面积；δ_c为毛细管节流参数， $δ_{c} = \frac{3 d_{c}^{4}}{32 h_{0}^{3} L_{c}}$ ；δ_o为小孔节流参数， $δ_{o} = \frac{3 π C_{k} d_{o}^{2}}{{(ρ P_{s})}^{\frac{1}{2}} h_{0}^{3}}$ ，其中C_k为小孔节流修正参数，C_k= $\sqrt[]{2} α$ 。

对式（31）和式（32）进行无量纲化处理，则小孔节流器和毛细管节流器的节流方程可分别转换为：

δ_{c} (1 - P_{r}^{*}) = Q_{r}^{*} P_{r}^{*} + σ r_{1}^{* 2} \frac{\partial h^{*}}{\partial t^{*}} + σ r_{1}^{* 2} γ \frac{\partial P_{r}^{*}}{\partial t^{*}}

（33）

δ_{o} {(1 - P_{r}^{*})}^{1 / 2} = Q_{r}^{*} P_{r}^{*} + σ r_{1}^{* 2} \frac{\partial h^{*}}{\partial t^{*}} + σ r_{1}^{* 2} γ \frac{\partial P_{r}^{*}}{\partial t^{*}}

（34）

式中：γ为油腔体积参数， $γ = \frac{P_{s} β_{l} V_{0}}{π R^{2} h_{0}}$ ；β_l为润滑剂的压缩率； $r_{1}^{* 2} = r_{2}^{* 2} - r_{3}^{* 2}$ 。

利用小扰动法引入如下无量纲量：

h^{*} = 1 + ε e^{i t^{*}}, P_{r}^{*} = P_{r 0}^{*} + ε e^{i t^{*}} P_{r 1}^{*}, Q_{r}^{*} = Q_{r 0}^{*} + ε e^{i t^{*}} Q_{r 1}^{*}

（35）

式中： $Q_{r 1}^{*}$ 为无量纲动态流量。

对于毛细管节流环形油腔液体静压推力轴承，将式（35）代入式（33），忽略小扰动ε的高阶项，并分别对常数项和ε的一次项待定系数，可得其静、动态油腔压力，分别为：

P_{r 0}^{*} = \frac{δ_{c}}{λ_{c}}

（36）

P_{r 1}^{*} = - \frac{Q_{r 1}^{*} P_{r 0}^{*} + i σ r_{1}^{* 2}}{λ_{c}}

（37）

其中：

\{\begin{array}{l} λ_{c} = Q_{r 0}^{*} + δ_{c} \\ Q_{r 1}^{*} = \frac{\partial Q_{r}^{*}}{\partial h^{*}} |_{h^{*} = 1} = 3 Q_{r 0}^{*} + C_{3} P_{r 1}^{*} \end{array}

（38）

式中：C₃为环形油腔推力轴承的结构系数， $C_{3} = - \frac{1}{l n r_{2}^{*}} + \frac{1}{l n r_{3}^{*} - l n r_{1}^{*}}$ 。

将式（38）代入式（37），可得：

P_{r 1}^{*} = - \frac{3 Q_{r 0}^{*} P_{r 0}^{*} + i σ r_{1}^{* 2}}{λ_{c} + C_{3} P_{r 0}^{*}}

（39）

将式（39）代入式（29），可得：

W_{1}^{*} = - \frac{3 Q_{r 0}^{*} P_{r 0}^{*}}{λ_{c} + P_{r 0}^{*} C_{3}} C_{1} + i σ (- \frac{C_{1} r_{1}^{* 2}}{λ_{c} + C_{3} P_{r 0}^{*}} + \frac{C_{2}}{4})

（40）

由此可得，毛细管节流环形油腔液体静压推力轴承的油膜刚度和阻尼系数分别为：

K_{d}^{*} = - R e (W_{1}^{*}) = - \frac{3 Q_{r 0}^{*} P_{r 0}^{*}}{λ_{c} + P_{r 0}^{*} C_{3}} C_{1}

（41）

D_{d}^{*} = - \frac{I m (W_{1}^{*})}{σ} = - \frac{C_{1} r_{1}^{* 2}}{λ_{c} + C_{3} P_{r 0}^{*}} + \frac{C_{2}}{4}

（42）

对于小孔节流环形油腔液体静压推力轴承，不考虑流体可压缩性，将式（35）代入式（34），忽略小扰动ε的高阶项，并分别对常数项和ε的一次项待定系数，可得其静、动态油腔压力，分别为：

P_{r 0}^{*} = \frac{\sqrt[]{δ_{o}^{4} + 4 Q_{r 0}^{* 2} δ_{o}^{2}} - δ_{o}^{2}}{2 Q_{r 0}^{* 2}}

（43）

P_{r 1}^{*} = - \frac{Q_{r 1}^{*} P_{r 0}^{*} + i σ r_{1}^{* 2}}{λ_{o}}

（44）

其中：

\{\begin{array}{l} λ_{o} = \frac{δ_{o}^{2} + 2 Q_{r 0}^{* 2} P_{r 0}^{*}}{2 P_{r 0}^{*} Q_{r 0}^{*}} \\ Q_{r 1}^{*} = \frac{\partial Q_{r}^{*}}{\partial h^{*}} |_{h^{*} = 1} = 3 Q_{r 0}^{*} + C_{3} P_{r 1}^{*} \end{array}

（45）

将式（45）代入式（44），可得：

P_{r 1}^{*} = - \frac{3 Q_{r 0}^{*} P_{r 0}^{*} + i σ r_{1}^{* 2}}{λ_{o} + C_{3} P_{r 0}^{*}}

（46）

将式（46）代入式（29），可得：

W_{1}^{*} = - \frac{3 Q_{r 0}^{*} P_{r 0}^{*}}{λ_{o} + C_{3} P_{r 0}^{*}} C_{1} + i σ (- \frac{C_{1} r_{1}^{* 2}}{λ_{o} + C_{3} P_{r 0}^{*}} + \frac{C_{2}}{4})

（47）

由此可得，小孔节流环形油腔液体静压推力轴承的油膜刚度和阻尼系数分别为：

K_{d}^{*} = - R e (W_{1}^{*}) = \frac{3 Q_{r 0}^{*} P_{r 0}^{*}}{λ_{o} + C_{3} P_{r 0}^{*}} C_{1}

（48）

D_{d}^{*} = - \frac{I m (W_{1}^{*})}{σ} = \frac{C_{1} r_{1}^{* 2}}{λ_{o} + C_{3} P_{r 0}^{*}} - \frac{C_{2}}{4}

（49）

2 环形油腔液体静压推力轴承油膜刚度测量实验

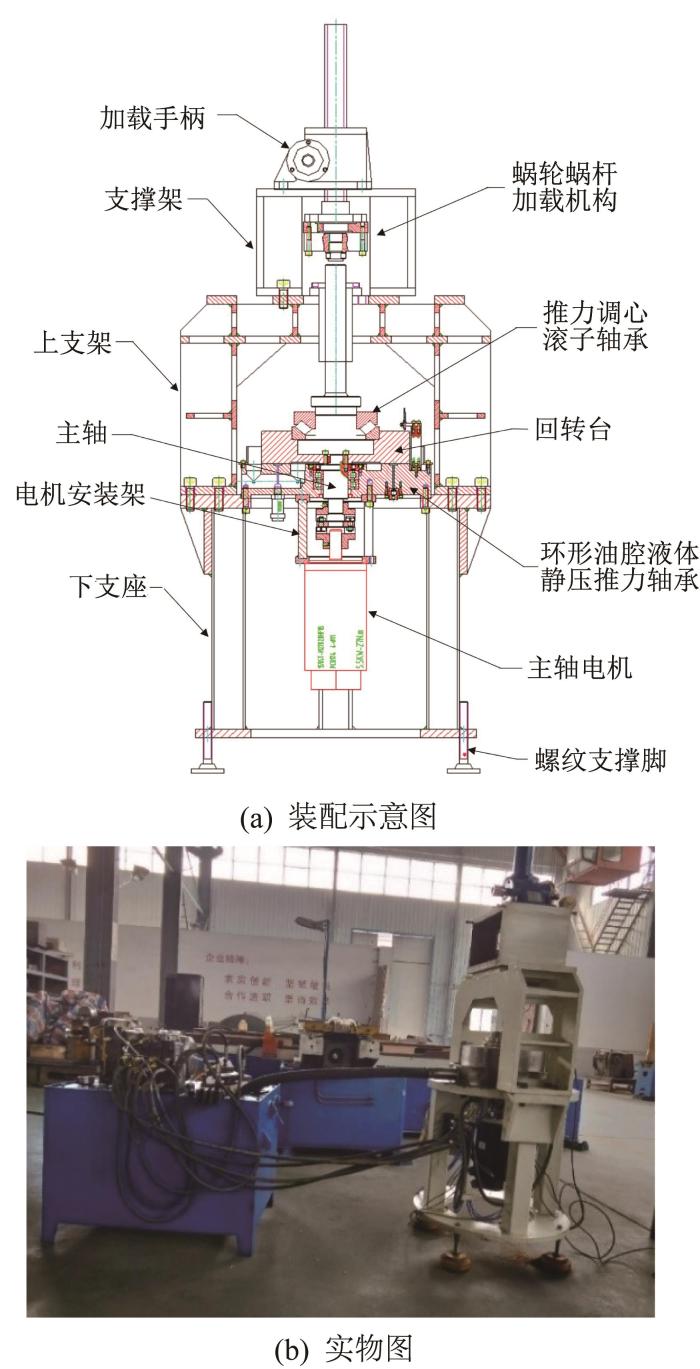
为了验证上述理论分析的正确性，以小孔节流环形油腔液体静压推力轴承为例，在实验台（见图2）上开展油膜刚度测量实验（轴承静止）。具体测量过程如下：首先，设供油压力为2 MPa，待油膜厚度达到稳定状态后，记录静态油膜厚度h₀；然后，通过加载手柄给轴承施加载荷W₁，待油膜厚度达到稳定状态后，记录此时的油膜厚度h₁；最后，继续增大载荷至W₂，待油膜厚度达到稳定状态后，记录此时的油膜厚度h₂。通过计算可得到该轴承的平均油膜刚度K_d=（W₂ $-$ W₁）/（h₂ $-$ h₁）。在实验过程中，保证ΔW=W₁ $-$ W₂=500 N，并以ΔW为增量持续递增加载，由此可以测量得到油膜刚度与油腔压力之间的关系。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 环形油腔液体静压推力轴承实验台

Fig.2 Experimental platform of annular recess hydrostatic thrust bearing

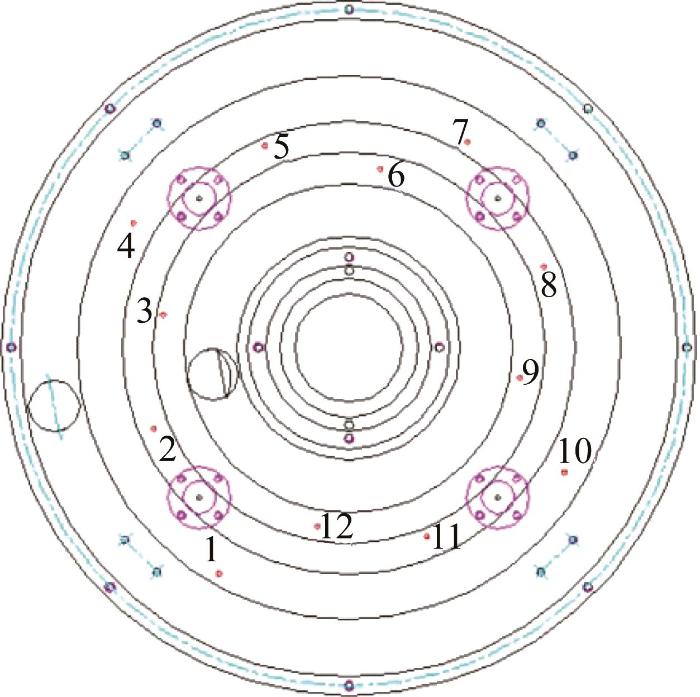
测量用小孔节流环形油腔液体静压推力轴承的实物如图3所示，其结构参数如表1所示。在该轴承上布置12个压力传感器，以测量不同位置的油膜压力。压力传感器的量程为10 MPa，分辨率为0.001 MPa，其位置分布如图4所示。油膜厚度由电涡流位移传感器测量，其量程为0~0.5 mm，精度为0.04 μm，安装情况如图5所示，其前端探头与回转台表面之间的安装距离为350 μm。考虑到轴承在加载过程中可能会倾斜，通过间隔90^o的方式在回转台上方安装了4个位移传感器。轴承的加载力通过称重传感器（见图6）测量，其安装在蜗轮蜗杆加载机构上，最大量程为10 t，测量精度为1 kg。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 小孔节流环形油腔液体静压推力轴承实物

Fig.3 Physical object of annular recess hydrostatic thrust bearing with orifice throttling

表1 小孔节流环形油腔液体静压推力轴承几何参数 (mm)

Table 1 Geometric parameters of annular recess hydrostatic thrust bearing with orifice throttling

参数	数值
轴承外径R	180
轴承内径r₂	109
油腔外径r₄	150
油腔内径r₃	130

新窗口打开| 下载CSV

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 压力传感器分布情况

Fig.4 Distribution diagram of pressure sensors

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 位移传感器安装情况

Fig.5 Installation diagram of displacement sensors

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 称重传感器实物

Fig.6 Physical object of weighing sensor

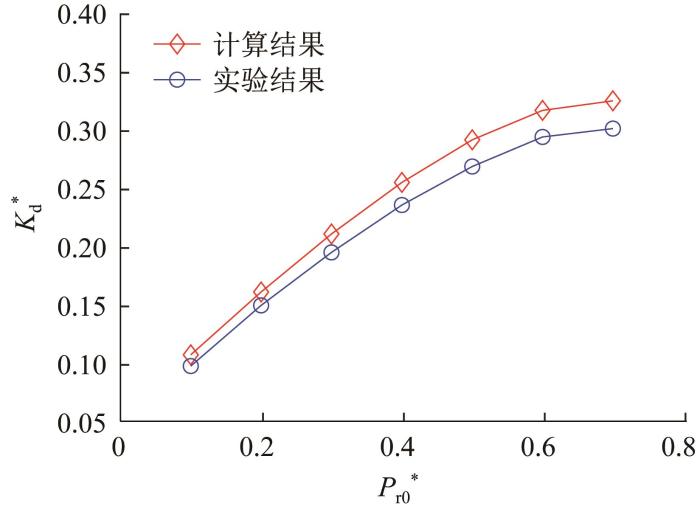
通过实验测量得到小孔节流环形油腔液体静压推力轴承在静止情况下（即惯性参数S = 0）的油膜刚度，并与其理论计算结果进行对比，结果如图7所示。通过对比发现：该轴承油膜刚度的理论计算值与实验测量值的变化趋势基本一致，且两者之间的相对误差不超过15%，由此可认为本文的理论分析结果是正确的。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 小孔节流环形油腔液体静压推力轴承油膜刚度对比

Fig.7 Comparison of oil film stiffness of annular recess hydrostatic thrust bearing with orifice throttling

3 液体静压推力轴承动态特性变化规律分析

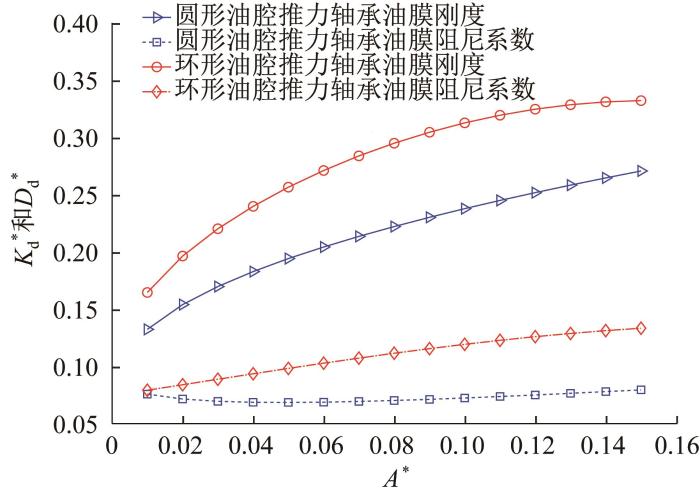
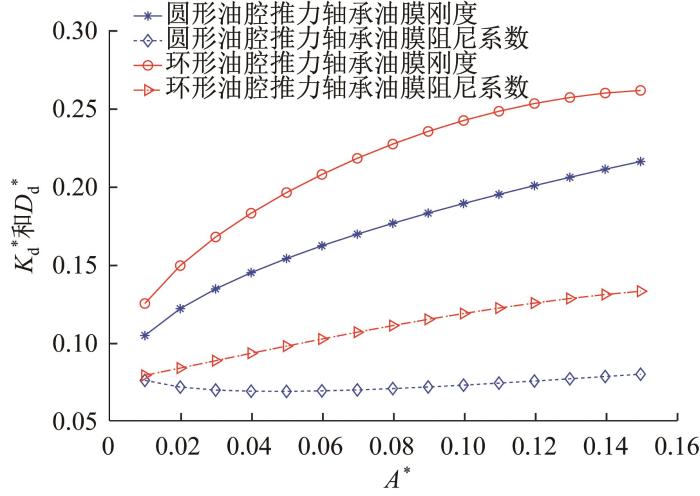
为了探究油腔形状和节流方式对液体静压推力轴承油膜刚度和阻尼系数的影响，对圆形油腔和环形油腔液体静压推力轴承在小孔和毛细管节流方式下的油膜刚度和阻尼系数进行对比分析。设定上述2种轴承的运行工况相同，具体为：静态油腔压力 $P_{r 0}^{*}$ =0.4，惯性参数S=0.1，油腔面积A^*=0.01~0.15（A^*= A/πR²）。图8和图9所示分别为小孔和毛细管节流方式下圆形油腔和环形油腔液体静压推力轴承的动态特性对比。通过图8和图9可以看出，在相同工况下，相比于环形油腔液体静压推力轴承，圆形油腔液体静压推力轴承的油膜刚度和阻尼系数明显要小。由此说明，对于相同工况，环形油腔液体静压推力轴承的动态特性较优；同时还可以看出，在相同工况下，小孔节流液体静压推力轴承的动态特性优于毛细管节流液体静压推力轴承。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 小孔节流方式下圆形油腔和环形油腔液体静压推力轴承的动态特性对比

Fig.8 Comparison of dynamic characteristics of circular recess and annular recess hydrostatic thrust bearing under orifice throttling

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 毛细管节流方式下圆形油腔和环形油腔液体静压推力轴承的动态特性对比

Fig.9 Comparison of dynamic characteristics of circular recess and annular recess hydrostatic thrust bearing under capillary throttling

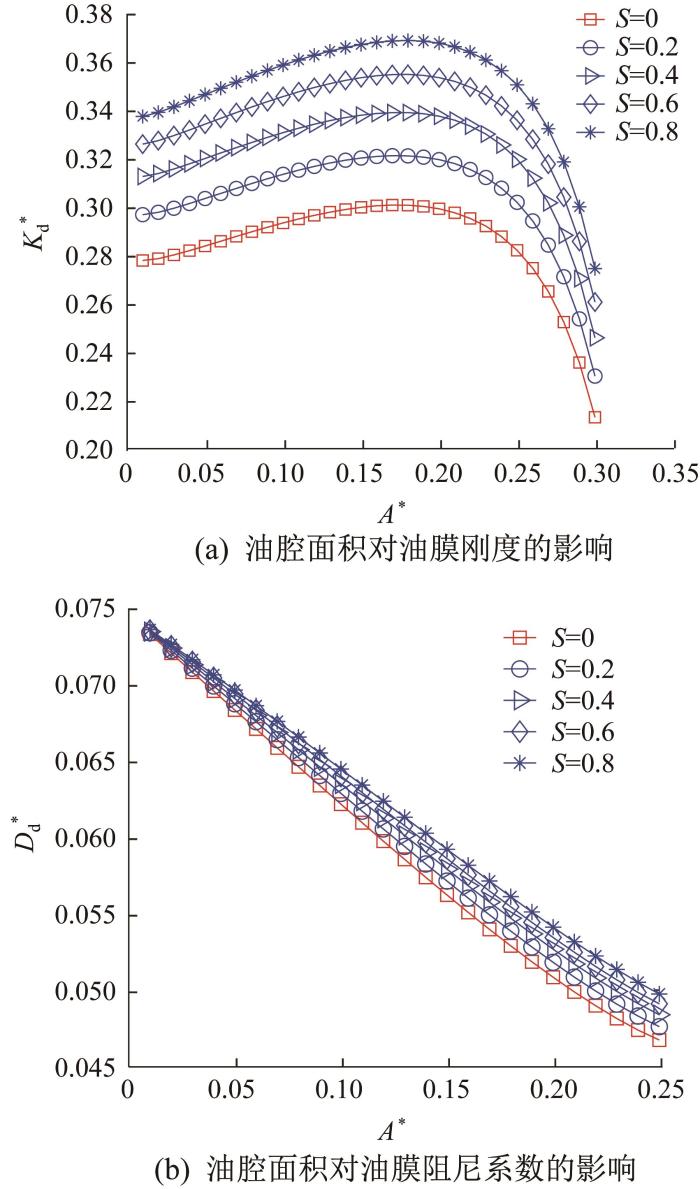
综上所述，在相同工况下，小孔节流环形油腔液体静压推力轴承的动态特性最优。为了讨论油腔结构参数（面积和位置）对小孔节流环形油腔液体静压推力轴承动态特性的影响，选取不同惯性参数（S = 0，0.2，0.4，0.6和0.8），分析油腔结构参数对该轴承动态特性的影响规律。

图10所示为油腔面积对小孔节流环形油腔液体静压推力轴承动态特性的影响规律：图10（a）为油腔面积与油膜刚度的关系，图10（b）为油腔面积与油膜阻尼系数的关系。此处轴承的基本结构参数为：外径为R，内径r₃=0.4R，油腔中径r_c1=0.7R，通过改变油腔的内、外径来改变油腔面积。由图10（a）可以看出：当油腔面积逐渐变大时，油膜刚度先增大再减小；而油膜刚度与惯性参数S呈正相关，但惯性参数的变化不会影响最大油膜刚度对应的油腔面积A^*=0.175。由此可知，对于小孔节流环形油腔液体静压推力轴承，为保证其油膜刚度最大，可取油腔内径r₄=0.638R，油腔外径r₂=0.763R。由图10（b）可以看出：油膜阻尼系数与油腔面积呈负相关，而油膜阻尼系数与惯性参数呈正相关，且油腔面积的增大能强化惯性参数对油膜阻尼系数的影响。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 油腔面积对小孔节流环形油腔液体静压推力轴承动态特性的影响

Fig.10 Effect of recess area on dynamic characteristics of annular recess hydrostatic thrust bearing with orifice throttling

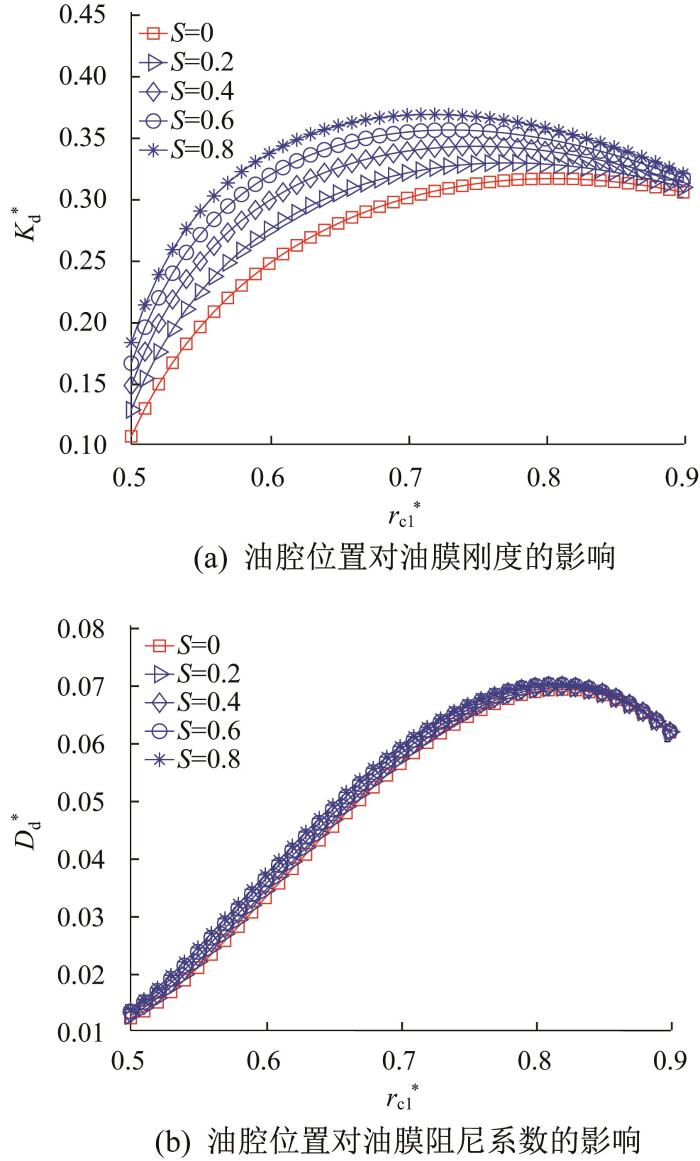
图11所示为油腔位置对小孔节流环形油腔液体静压推力轴承动态特性的影响规律：图11（a）为油腔位置与油膜刚度的关系，图11（b）为油腔位置与油膜阻尼系数的关系。此处轴承的基本结构为：外径为R，内径r₃=0.4R，油腔面积A^*=0.15。通过无量纲油腔中径r $_{c 1}^{*}$ 来标定油腔位置，其取值为0.5~0.9。由图11（a）可以看到：随着油腔中径的变大，油膜刚度先增大后减小；当惯性参数S变大时，油膜刚度也随之变大。此外，当惯性参数不同时，最大油膜刚度对应的油腔位置也不同：当S=0时，最大油膜刚度对应的油腔中径r_c1=0.805R；当S=0.2时，最大油膜刚度对应的油腔中径r_c1=0.770R；当S=0.4时，最大油膜刚度对应的油腔中径r_c1=0.750R；当S=0.6时，最大油膜刚度对应的油腔中径r_c1=0.731R；当S=0.8时，最大油膜刚度对应的油腔中径r_c1=0.725R。由图11（b）中油腔位置与油膜阻尼系数之间的关系可以得到：随着油腔中径的变大，油膜阻尼系数先增大再减小；当惯性参数S变大时，油膜阻尼系数也随之变大，但是惯性参数S对油膜阻尼系数的影响较小。此外，当惯性参数S变化时，最大油膜阻尼系数对应的油腔位置几乎不变，即油腔中径r_c1=0.815R。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 油腔位置对小孔节流环形油腔液体静压推力轴承动态特性的影响

Fig.11 Effect of recess position on dynamic characteristics of annular recess hydrostatic thrust bearing with orifice throttling

4 结论

1）基于小扰动法，将环形油腔液体静压推力轴承的Reynolds方程分解成静态方程和动态方程，并求解得到其油膜刚度和阻尼系数的解析表达式，同时通过实验验证了理论计算结果的正确性。

2）对比分析了环形油腔和圆形油腔液体静压推力轴承在小孔和毛细管节流方式下的动态特性。理论计算结果表明，在相同工况下，小孔节流环形油腔液体静压推力轴承的动态特性最优。

3）以小孔节流环形油腔液体静压推力轴承为对象，讨论了油腔的结构参数对其动态特性的影响规律。结果显示，油腔面积和油腔位置对该轴承动态特性的影响明显；可通过选择合适的油腔面积和油腔位置来使油膜具有最大刚度；油膜阻尼系数与油腔面积呈明显负相关，可通过调整油腔位置来使油膜具有最大阻尼系数。

研究结果可为液体静压推力轴承的设计提供参考，有助于以动态特性为目标的轴承结构优化设计。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘小军，陶邵佳，张亚宾，等.

核主泵轴承重载惰转停机承载性能研究

［J］.流体机械，2019，47（10）：51-54，88. doi：10.3969/j.issn.1005-0329.2019.10.010