基于数论网格法与Morris法的翼型气动特性敏感性分析

doi:10.3785/j.issn.1006-754X.2022.00.055

基于数论网格法与Morris法的翼型气动特性敏感性分析

文泽军^,^,, 孟祥恒^,^,, 肖钊, 张帆

湖南科技大学机电工程学院，湖南湘潭 411201

Sensitivity analysis of airfoil aerodynamic characteristics based on NT-net method and Morris method

WEN Ze-jun^,^,, MENG Xiang-heng^,^,, XIAO Zhao, ZHANG Fan

School of Mechanical and Electrical Engineering, Hunan University of Science and Technology, Xiangtan 411201, China

通讯作者: 孟祥恒（1995—），男，山东临沂人，硕士生，从事风力机翼型不确定性分析与优化研究，E-mail：meng372021@163.com，https：//orcid.org/0000-0002-3203-9490孟祥恒（1995—），男，山东临沂人，硕士生，从事风力机翼型不确定性分析与优化研究，E-mail：meng372021@163.com，https：//orcid.org/0000-0002-3203-9490

收稿日期: 2021-10-08 修回日期: 2021-11-19

基金资助:

国家自然科学基金资助项目. 51905165
国家重点研发计划资助项目. 2016YFF0203400

Received: 2021-10-08 Revised: 2021-11-19

作者简介 About authors

文泽军（1966—），男，湖南湘乡人，教授，博士生导师，博士，从事风电装备服役质量设计研究，E-mail：zjwen732@163.com，https：//orcid.org/0000-0003-1576-222X , E-mail：zjwen732@163.com

摘要

针对在风力机翼型气动特性敏感性分析中计算效率较低的问题，提出了一种基于数论网格（number theoretic net，NT-net）法与Morris法的翼型气动特性敏感性分析方法。首先，构建了拟合精度较高的翼型参数化模型；其次，阐述了NT-net法的计算原理，采用NT-net法对翼型参数化模型的多项式系数进行抽样；然后，以风力机翼型S832为研究对象，采用Morris法进行翼型气动特性的全局敏感性分析；最后，进一步分析在特定工况下风力机翼型参数化模型的多项式系数对翼型外形及气动特性的影响。结果表明：影响翼型气动特性的主要因素依次为翼型的最大相对厚度和最大相对弯度、前缘半径和后缘厚度；当来流攻角较小时，最大相对厚度和最大相对弯度取适当的较小值、前缘半径取适当的较大值可有效增强该工况下风力机翼型的气动特性，同时也验证了NT-net法的计算效率更高。研究结果为风力机翼型气动设计提供了理论参考。

关键词： 数论网格法 ; 敏感性分析 ; 气动特性 ; 风力机翼型

Abstract

Aiming at the problem of lower computational efficiency in the sensitivity analysis of aerodynamic characteristics of wind turbine airfoil, a sensitivity analysis method of airfoil aerodynamic characteristics based on number theoretical net (NT-net) method and Morris method was proposed. Firstly, a airfoil parameterized model with higher fitting accuracy was constructed; secondly, the calculation principle of NT-net method was described and the method was used to sample polynomial coefficients of airfoil parameterized model; then, taking wind turbine airfoil S832 as research object, global sensitivity analysis of airfoil aerodynamic characteristics was carried out by Morris method; finally, the influence of polynomial coefficients of parameterized model of wind turbine airfoil on airfoil profile and aerodynamic characteristics under specific conditions was further analyzed. The results showed that main factors affecting airfoil aerodynamic characteristics were maximum relative thickness, maximum relative camber, leading edge radius and trailing edge thickness of airfoil. When the angle of attack of the incoming flow was smaller, taking the appropriate smaller value of the maximum relative thickness and the maximum relative camber, and taking the appropriate larger value of the leading edge radius could effectively improve the aerodynamic characteristics of wind turbine airfoil under that working condition, and also verified that the calculation efficiency of NT-net method was higher. The research results provide a theoretical reference for the aerodynamic design of wind turbine airfoil.

Keywords： number theoretic net (NT-net) method ; sensitivity analysis ; aerodynamic characteristics ; wind turbine airfoil

PDF (1101KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

文泽军, 孟祥恒, 肖钊, 张帆. 基于数论网格法与Morris法的翼型气动特性敏感性分析. 工程设计学报[J], 2022, 29(4): 438-445 doi:10.3785/j.issn.1006-754X.2022.00.055

WEN Ze-jun, MENG Xiang-heng, XIAO Zhao, ZHANG Fan. Sensitivity analysis of airfoil aerodynamic characteristics based on NT-net method and Morris method. Chinese Journal of Engineering Design[J], 2022, 29(4): 438-445 doi:10.3785/j.issn.1006-754X.2022.00.055

翼型气动特性是风力机设计的决定性因素^［1］。通过改变翼型的厚度、弯度和前缘半径等设计变量，可以设计出不同几何外形和气动性能的风力机翼型^［2］。目前，CST（class function/shape function transformation，类型函数/形状函数转换）方法被广泛应用于风力机翼型设计中，提高了翼型设计的效率^［3］。在CST方法的应用过程中，参数化模型的设计变量通常在一定区间内变化，且变化带有一定的随机性，常被认为是服从正态分布的随机变量^［4］。该随机变量会导致所设计的风力机翼型出现几何偏差，从而可能导致风力机翼型的气动性能不能满足设计要求^［5］。如Campobasso等^［6］指出风力机翼型在设计及制造时随机产生的几何误差会对风力机的功率特性造成一定影响。因此，在风力机翼型气动设计中须考虑几何不确定性的影响。国内外学者围绕翼型气动特性开展了大量研究。如：Ju等^［7］基于蒙特卡洛模拟（Monte Carlo simulation，MCS）研究了风力机翼型气动特性对翼型前缘的敏感性，但MCS法的样本收敛性易受到模拟次数及样本数的限制；Ernst等^［8］采用拉丁超立方法研究了风力机翼型的相对厚度和相对弯度等几何结构参数对气动特性的影响，但拉丁超立方法存在样本空间收敛性不足、不适用于高维运算等问题；王晓东等^［9-10］研究了多项式混沌方法在随机方腔流动模拟中的应用；姜昌伟等^［11］采用嵌入式多项式混沌展开法研究了在随机边界下流动与传热问题的不确定性，但由于须对系统内部方程进行扩维处理，容易引入数值误差；刘全等^［12］研究了非嵌入式多项式混沌方法在拉氏计算中的应用，但在正交多项式基的构建中易出现矩匹配方程的奇异解，难以保证计算精度；为了较好地求解圆筒实验模型，梁霄等^［13］提出了一种多元非嵌入多项式混沌方法，但在预测非嵌入样本点处的响应值时，样本点的数量和位置都不是任意的，求解展开式系数时主观性较大，容易引入近似误差；邬晓敬等^［14］采用非嵌入多项式混沌方法开展翼型气动特性全局敏感性分析，但因易受多项式模型的阶数影响，近似解计算的主观性较大；祝宏宇等^［15］采用Sobol全局敏感性分析方法研究翼型气动特性的敏感性，但该方法在求解高维运算问题时时间成本过高；Wang等^［16］采用多点泰勒展开的近似伴随方法分析翼型几何的设计变量对气动特性的影响，但近似伴随方法依然易受到多点泰勒展开式项数的影响，导致样本空间的计算精度不高；Peter等^［17］对翼型气动设计中的敏感性分析方法进行了总结。综上可知，目前的研究方法存在计算效率低、样本收敛性差及不适用于高维运算等不足，因此须对翼型气动特性的敏感性作进一步研究。

近年来，数论网格（number theoretic net，NT-net）法被广泛应用于工程统计分析领域。方开泰等^［18］阐述了NT-net法在统计中的应用；刘飞等^［19］阐述了NT-net法在极大似然估计中的应用，指出NT-net法具有较高的采样效率和计算精度；赖斌等^［20］阐述了NT-net法在流体随机模拟中的应用，指出NT-net法可适用于高维随机模拟。目前，将NT-net法应用于风力机翼型气动特性敏感性分析的研究还不多见。

因此，本文以风力机翼型S832（以下简称翼型）为研究对象，基于CST方法构建翼型参数化模型，并提出一种基于NT-net法与Morris法的翼型气动特性敏感性分析方法。首先，基于CST方法建立精度较高的翼型参数化模型；其次，应用NT-net法对参数化模型中的设计变量进行抽样，并采用改进的Morris法分析NT-net法的抽样结果，研究在翼型设计过程中各设计变量对翼型气动特性的贡献程度，并通过MCS进行验证分析；最后，研究主要设计变量对翼型外形及气动特性的影响，以期为翼型的设计提供理论参考。

1 翼型参数化模型及气动特性

1.1　翼型参数化模型

1.1.1　翼型的几何特征

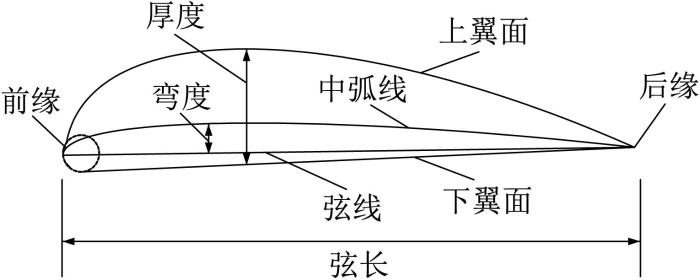
翼型为风力机叶片沿展向的某一横截面的形状，其前缘呈圆弧形，后缘呈钝形或尖形。弦线与前缘的交点为前缘点，弦线与后缘的交点为后缘点。其几何特征与气动特性密切相关。翼型的几何特征如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 翼型几何特征示意

Fig.1 Schematic of geometric characteristics of airfoil

1.1.2　翼型参数化方法

CST方法是根据翼型的几何特征，通过类函数和型函数来表示翼型外形变化的参数化方法。其优势是可以用少量的变量表达出可由计算机识别的翼型几何形状。因此，本文采用CST方法建立翼型参数化模型。以前缘点为原点O，以前缘点指向后缘点的方向为横向即 $ψ$ 向的正向，以垂直于弦线向上为纵向即 $ξ$ 向的正向，建立坐标系O- $ψ$ $ξ$ ，则翼面可以表示为：

ξ = B (ψ) G (ψ) + ψ \frac{Δ L_{e}}{c}

（1）

式中： $B (ψ)$ 为类函数； $G (ψ)$ 为型函数； $Δ L_{e}$ 为翼型后缘厚度；c为翼型的弦长。

其中：

B (ψ) = ψ^{N_{1}} {(1 - ψ)}^{N_{2}}

（2）

G (ψ) = \sum_{t = 0}^{W} A_{t + 1} \frac{W!}{t! (W - t)!} ψ^{t} {(1 - ψ)}^{W - t}

（3）

式中： $N_{1}$ 、 $N_{2}$ 为类函数系数，常取 $N_{1} = 0.5$ ， $N_{2} = 1.0$ ； t为翼型Bernstein多项式阶数，t=0，1，…， $W$ ； $A t + 1$ 为Bernstein多项式的待定系数，可由最小二乘法拟合得到。

参数化误差 $Δ y$ 为：

Δ y = y_{ψ} - ξ

（4）

式中： $y_{ψ}$ 为参数化翼型外形中横坐标为 $ψ$ 处对应的纵坐标。

1.2　翼型气动特性

翼型气动特性主要由升力系数 $C_{l}$ 和阻力系数 $C_{d}$ 表征。升阻比 $ε$ 定义为升力系数与阻力系数的比，即：

ε = \frac{C_{l}}{C_{d}}

（5）

Xfoil软件是一款交互式独立翼型的设计与分析软件。与其他CFD （computational fluid dynamics，计算流体动力学）模拟软件相比，Xfoil软件具有收敛快、效率高和易操作等优点。基于线性变换的高阶面元法，可利用Xfoil软件计算 $C_{l}$ 和 $C_{d}$ 等。

2 翼型气动特性敏感性分析方法

2.1　NT-net法

数论方法（number theory method，NTM）的实质是在 $b$ 维单位立方体 $M^{b}$ 上找到一个均匀散布的点集^［21］，该点集通常称为NT-net，偏差较小的点集称为好格子点（good lattice point，GLP）集合。

设 $P = \{g_{k} (k = 1, \dots, n)\}$ 为 $M^{b}$ 上的一个点集。对于 $r \in M^{b}$ ，令 $U (r, P)$ 为 $P$ 中满足 $g_{k} \leq r$ 的点数，则 $P$ 的偏差D（n， P）为：

D (n, P) = \underset{r \in M^{b}}{s u p} |\frac{U (r, P)}{n} - R (|0, r|)|

（6）

式中： $|0, r|$ 为边长为r的矩形， $R (|0, r|)$ 为矩形 $|0, r|$ 的体积空间。

确定最优系数 $(h_{1}, \dots, h_{b})$ 是获得GLP集合的关键环节。当维数 $b \leq 18$ 时，应用生成矢量产生GLP集合。

令生成矢量 $(n; h_{1}, \dots, h_{b})$ 满足最大公约数 $(n, h_{i}) = 1, i = 1, \dots, b$ ， $1 \leq h_{i} < h_{b}$ ， $b < n$ 及 $h_{i} \neq h_{j} (i \neq j)$ 。根据：

\{\begin{array}{l} q_{k i} \equiv k h_{i} (m o d n) \\ g_{k i} = \frac{2 q_{k i} - 1}{2 n} \end{array}

（7）

令 $q_{k i}$ 满足 $1 \leq q_{k i} \leq n$ ，则具有最小偏差的集合 $\{g_{k} = (g_{k 1}, \dots, g_{k b})\}$ 即为 $(n; h_{1}, \cdot \cdot \cdot, h_{b})$ 的GLP集合。

2.2　基于NT-net法抽样的敏感性分析方法

抽样是指将b维立方体 $M^{b}$ 的GLP集合的点映射到给定分布上的过程。敏感性分析常通过MCS来抽样模拟各种输入参数的可变性^［22］。NT-net法被称为伪MCS法，因其良好的样本收敛性而被广泛应用。Morris法是由Morris提出的全局敏感性分析方法，其敏感性指标为变量元效应的均值和标准差，可用来评价系统输入量对系统输出量的影响^［23］。

为量化每个Bernstein多项式待定系数的不确定性影响，令待定系数为服从正态分布 $N (μ, σ)$ 的设计变量 Z， $Z = (z_{1}, z_{2}, \dots, z_{b})^{T}$ ， Z 的联合分布函数为 $F (z_{i})$ 。根据样本数n及维数b，通过查找生成矢量或采用分圆域方法得到 $b$ 维立方体 $M^{b}$ 的NT-net及GLP集合，则GLP集合中的每个点g_ki 表征b维设计变量 Z 的一个样本值，由此可以建立翼型参数化模型的设计空间。

建立敏感性模型 $Q = f (Z)$ ，其中 $z_{i} \sim N (μ, σ)$ 。对于通过NT-net法抽样得到的 $g_{k i}$ ，在第 $v$ 次抽样的变量元效应 $E_{i, v}$ 及其均值 $μ_{i}$ 与标准差 $S_{i}$ 为：

E_{i, v} = \frac{\partial Q}{\partial z_{i}}

（8）

μ_{i} = \frac{1}{n} \sum_{v = 1}^{n} E_{i, v}

（9）

S_{i} = \sqrt[]{\frac{1}{n - 1} (\sum_{v = 1}^{n} E_{i, v} - μ_{i})^{2}}

（10）

针对元效应会在非单调函数中同时出现正负值的问题，Campolongo等^［24］将均值 $μ_{i}$ 改进为新均值 $\bar{μ_{i}}$ ：

\bar{μ_{i}} = \frac{1}{n} \sum_{v = 1}^{n} |E_{i, v}|

（11）

敏感性分析的首要目标是计算并选择均值较高或标准差较低的变量元效应。因此，定义变异系数 $ζ$ 为新的敏感性指标，其为变量元效应的均值与标准差的比值，即：

ζ = \frac{{\bar{μ}}_{i}}{σ_{i}}

（12）

2.3　基于NT-net法抽样的敏感性分析流程

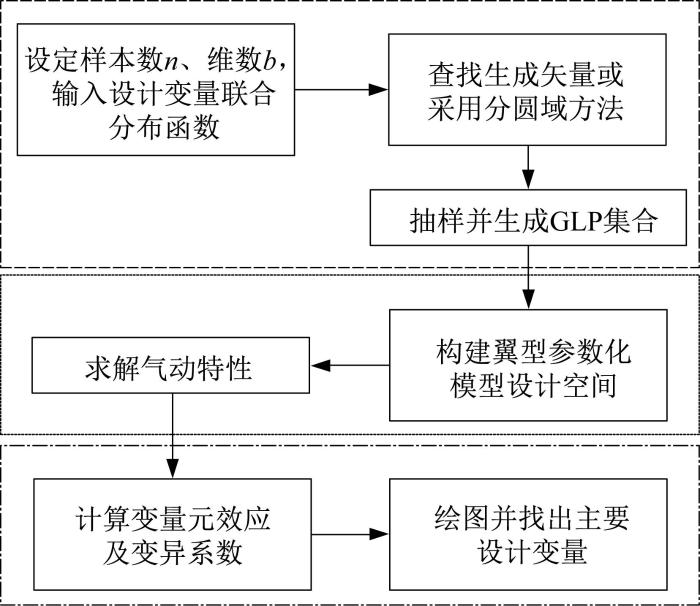
翼型气动特性敏感性分析的流程如图2所示，具体为：

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 翼型气动特性敏感性分析流程

Fig.2 Sensitivity analysis flow of aerodynamic characteristics of airfoil

1）确定设计变量 Z、样本数n和维数b，确定设计变量的分布特征；

2）根据维数b的大小选定适用方法进行NT-net抽样并生成对应设计变量 Z 的GLP集合；

3）从设计变量 Z 的GLP集合中抽取样本点，根据式（1）至式（5）构建翼型参数化模型的设计空间，利用Xfoil软件求解翼型参数化模型的气动特性；

4）基于改进的Morris法，分析设计变量的变化对气动特性的影响，根据式（12）至（16）计算翼型气动特性的变异系数 $ζ$ ，并找出影响翼型气动特性的主要设计变量。

3 算例分析

3.1　翼型参数化模型的构建及气动特性敏感性分析

3.1.1　翼型参数化模型的构建

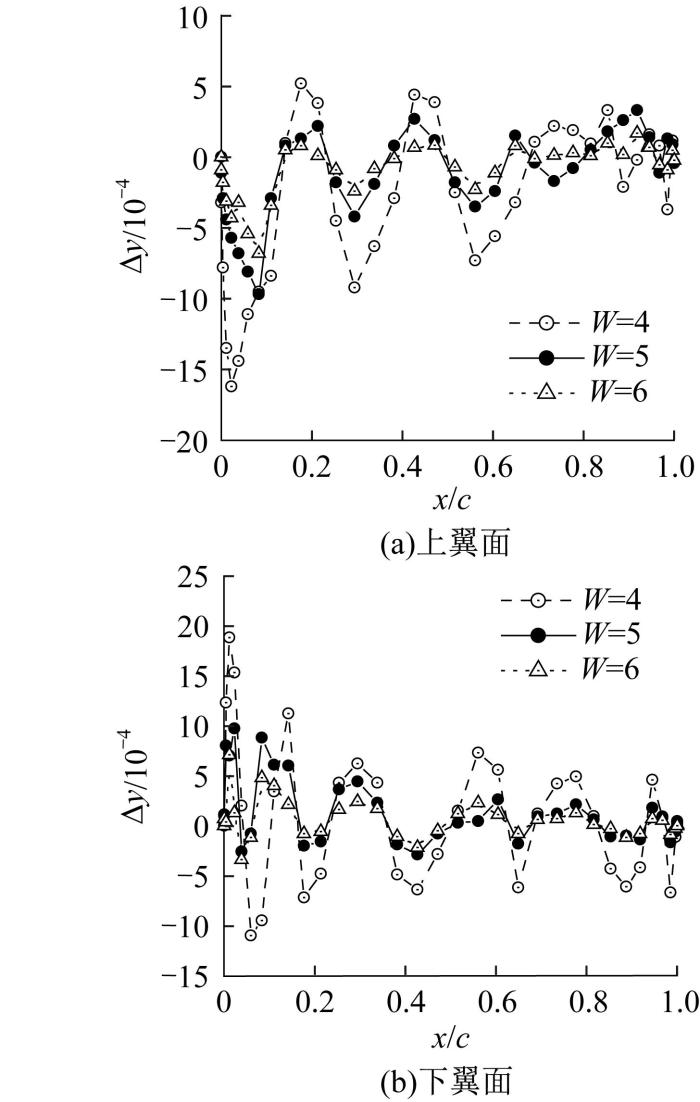
选取风力机专用翼型S832为研究对象。为了得到拟合精度较高的翼型参数化模型，取Bernstein多项式阶数 $W$ =4，5，6，采用CST方法分别对翼型的上、下翼面进行拟合并构建参数化模型。将翼型的几何外形坐标导入翼型设计软件Profili，可以更直观地表示翼型的几何外形特征。在Profili中，纵坐标y/c表示翼型几何外形的纵坐标y相对于翼型弦长c的位置关系，横坐标x/c表示翼型几何外形的横坐标x相对于翼型弦长c的位置关系。翼型模型的参数化误差如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 翼型模型的参数化误差

Fig.3 Parameterized error of airfoil model

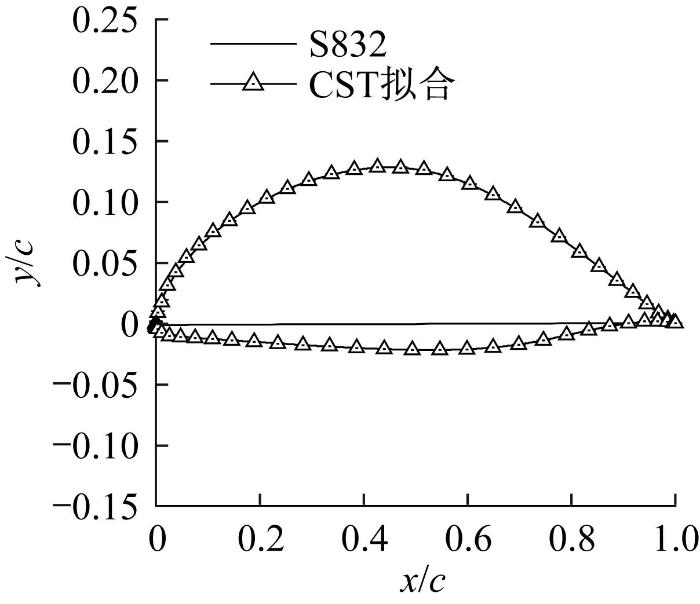
由图3可知，Bernstein多项式阶数对CST方法的拟合精度影响较大。适当提高Bernstein多项式阶数可有效提高CST方法的拟合精度，但高阶Bernstein多项式容易导致拟合过程呈病态化。当W≥5时，参数化误差最大为9.7×10^-4，已达到精度要求，因此本文选取W=5。采用5阶Bernstein时，翼型上、下翼面的参数化模型均有6个Bernstein多项式待定系数。以上翼面为例，A₁、A₂主要控制翼型前缘半径的大小，A₃、A₄主要控制翼型相对厚度和相对弯度的大小，A₅、A₆主要控制翼型后缘厚度的大小。通过CST方法对翼型几何特征进行参数化拟合，构建出计算机可识别的参数化模型，如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 翼型参数化模型

Fig.4 Parameterized model of airfoil

3.1.2　翼型气动特性敏感性分析

采用Xfoil软件求解翼型的气动特性。计算条件为稳态不可压缩气流，雷诺数Re=1.0×10⁶，来流攻角θ=5°。

令各设计变量的均值为其标准差的10倍，各概率密度分布函数不完全相同，并采用NT-net法对全部设计变量分别进行抽样，构建各设计变量样本空间。总变量维数b=12，应用生成矢量产生GLP集合。为便于快速计算，根据前文所述Bernstein多项式待定系数的影响机制及翼型几何外形的平顺性要求，将变量维数分为4组，每组维数为3，查表得到生成矢量为（101； 1， 40， 85），则GLP集合为 $\{g_{k} = (g_{k 1}, g_{k 2}, g_{k 3})\}$ 。

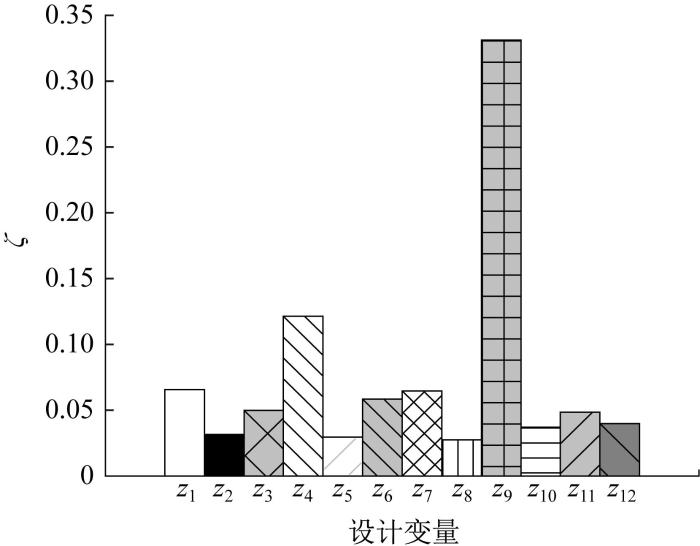
采用改进的Morris法进行翼型气动特性的全局敏感性分析。以θ=5°时S832翼型的升阻比ε为输出量，设计变量z_i （i=1，2， …，12）为输入量，其中z₁，z₂，…，z₆和z₇，z₈，…，z₁₂分别为依次对应的上、下翼面的设计变量。该12个设计变量是最小二乘法曲线拟合的数据点，依次控制5阶Bernstein多项式中的12个待定系数。以升阻比对设计变量的变异系数ζ为敏感性指标，采用改进的Morris法进行全局敏感性分析。θ=5°时升阻比对各设计变量的变异系数如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 θ=5°时升阻比对各设计变量的变异系数

Fig.5 Variation coefficient of lift-drag ratio to design variables at θ=5°

由图5可知，上、下翼面的升阻比对各设计变量的敏感性并不相同，其中对z₉、z₄、z₁、z₇、z₆的敏感性较高。z₄、z₉控制待定系数A₄、A₉，间接控制翼型最大相对厚度和最大相对弯度的大小，表示翼型气动特性主要受到翼型最大厚度和最大弯度的影响，其中以z₉的变异系数最大，表明下翼面翼型最大相对厚度和最大相对弯度对翼型气动特性的影响比上翼面翼型最大相对厚度和最大相对弯度对翼型气动特性的影响大；z₁、z₇控制着待定系数A₁、A₇，间接控制翼型的前缘半径大小，表示翼型气动特性容易受到翼型前缘半径的影响；z₆控制待定系数A₆，间接控制翼型后缘厚度大小，表示翼型后缘厚度也会影响翼型气动特性，但比前缘半径的影响程度要低。其余设计变量的变异系数均较小，表示升阻比对这些设计变量的敏感性较低，即这些设计变量对翼型气动特性的影响程度较低。

3.2　MCS验证

采用MCS法，每次抽取101个样本，共计12次，并建立翼型参数化模型，调用Xfoil软件求解翼型气动特性，然后采用Morris法进行全局敏感性分析。相对于抽样和建模时间，调用Xfoil软件及进行全局敏感性分析的时间可以忽略。在同等条件下，采用MCS法和NT-net法进行1次抽样的时间分别为205 s和180 s。采用MCS法进行全局敏感性分析所需的样本计算总数为n（i+2）^［25］，其中n=101，i=12，则采用MCS法进行全局敏感性分析的计算次数为101×（12+2）=1 414，而NT-net法的计算次数为101×12=1 212。MCS法和NT-net法的建模时长及进行全局敏感性分析的计算次数如表1所示。

表1 MCS法和NT-net法的建模时长及进行全局敏感性分析的计算次数

Table 1 Modeling time of MCS method and NT-net method and calculation times of global sensitivity analysis

方法	建模时长/s	计算次数
MCS法	205×12=2 460	1 414
NT-net法	180×12=2 160	1 212

新窗口打开| 下载CSV

由表1可知，相比于MCS法，采用NT-net法的建模时间减少了300 s，总计算次数减少了202次。因此，采用NT-net法可以有效提高翼型气动特性敏感性分析的效率。

3.3　主要设计变量对翼型外形及气动特性的影响

在来流攻角θ=5°的工况下，翼型的气动特性主要受翼型几何特征的影响。在基于NT-net法得到的各设计变量样本空间中，分析主要设计变量对翼型几何外形及气动特性的影响。当设计变量变化时，翼型的最大相对厚度和最大相对弯度几乎同时发生变化，因此本文不对翼型最大相对厚度和最大相对弯度进行单独分析。后缘厚度对翼型气动特性的影响比前缘半径的影响小。因此，本文仅对前缘半径、最大相对厚度和最大相对弯度对翼型外形及气动特性的影响作深入分析。

3.3.1　前缘半径对翼型外形及气动特性的影响

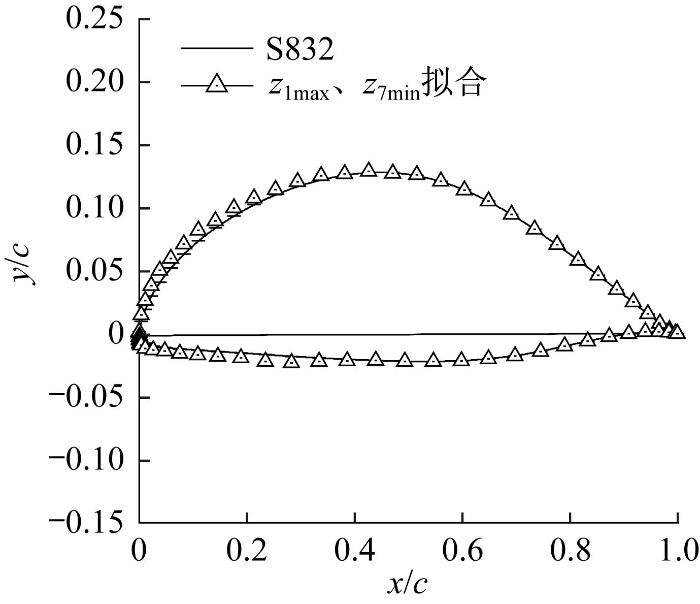
选取样本空间中间接控制上、下翼面前缘半径大小的设计变量的最大值z_1max、最小值z_7min得到对应的待定系数A₁、A₇，其余待定系数与翼型S832一致，拟合出光滑的几何外形，命名为翼型1，如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 以z_1max、z_7min间接拟合的翼型1的几何外形

Fig.6 Geometric profile of airfoil 1 indirectly fitted with z_1max、z_7min

由图6可知：当z₁、z₇分别达到z_1max、z_7min时，翼型上、下翼面对应数据点间的距离比S832的大，所控制的待定系数的变化幅度也比翼型S832的大，因此翼型1的前缘半径比翼型S832的大；针对前缘区域，上翼面的变化幅度比下翼面的变化幅度大；z₁、z₇对翼型其余部位的影响程度较小。

将翼型1的几何外形坐标导入翼型设计软件Profili和Xfoil，得到翼型1的前缘半径和升阻比。其与翼型S832的对比如表2所示。

表2 翼型1与翼型S832前缘半径和升阻比的对比

Table 2 Comparison of leading edge radius and lift-drag ratio between airfoil 1 and airfoil S832

翼型	前缘半径/mm	ε
S832	0.70	48.049 2
翼型1	0.75	48.708 3

新窗口打开| 下载CSV

由表2可知，翼型1的前缘半径比S832增加了0.05 mm，升阻比提高了0.659 1。因此，当前缘半径适当增大时，翼型的升阻比提高，气动特性增强。因此，设计时翼型的前缘半径可适当取较大的值。

3.3.2　最大相对厚度和最大相对弯度对翼型外形及气动特性的影响

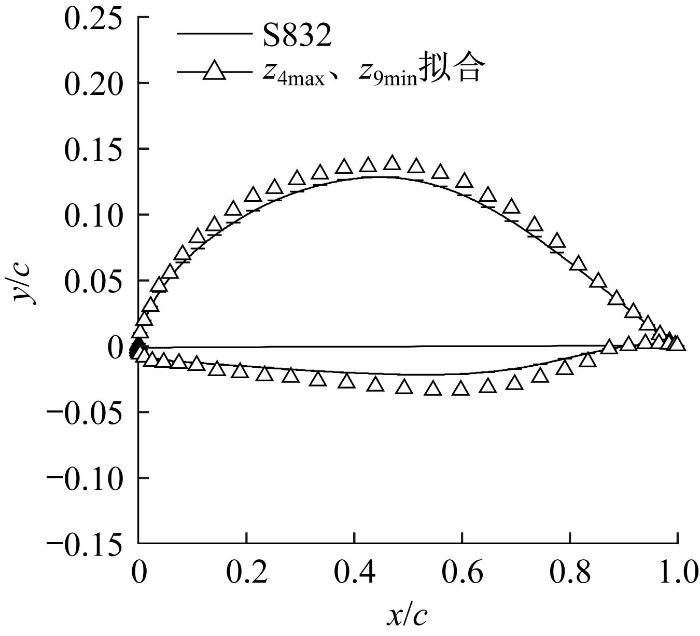
选取样本空间中控制上、下翼面最大相对厚度和最大相对弯度的设计变量最大值z_4max、最小值z_9min得到对应的待定系数A₄、A₉，其余待定系数与翼型S832的一致，拟合出光滑的几何外形，命名为翼型2，结果如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 以z_4max、z_9min间接拟合的翼型2的几何外形

Fig.7 Geometric profile of airfoil 2 indirectly fitted with z_4max、z_9min

由图7可知：当z₄、z₉分别达到为z_4max、z_9min时，翼型2上、下翼面对应数据点间的距离比翼型S832的大，所控制的待定系数的变化幅度也比翼型S832的大，因此翼型2的最大相对厚度和最大相对弯度比翼型S832的大；针对翼型的中部区域，下翼面最大相对厚度和最大相对弯度的变化幅度比上翼面的大；z₄、z₉对翼型其余部位的影响较小。

同理，可得到翼型2的最大相对厚度、最大相对弯度和升阻比。其与翼型S832的对比如表3所示。

表3 翼型2与翼型S832最大相对厚度、最大相对弯度和升阻比的对比

Table 3 Comparison of maximum relative thickness, maximum relative camber and lift-drag ratio between airfoil 2 and airfoil S832

翼型	最大相对厚度/%	最大相对弯度/%	升阻比ε
S832	14.89	5.11	48.049 2
翼型2	16.31	7.58	46.952 8

新窗口打开| 下载CSV

由表3可知，翼型2的最大相对厚度和最大相对弯度分别比S832增加了1.42%、2.47%，升阻比减小了1.096 4。因此，当最大相对厚度和最大相对弯度增大时，翼型的升阻比减小，气动特性减弱，这是由于来流攻角较小的缘故。因此，在来流攻角较小的工况下，翼型最大相对厚度和最大相对弯度可取较小值。

4 结论

1）分析了Bernstein多项式阶数对CST参数化翼型设计中拟合精度的影响。在参数拟合过程中，适当增大Bernstein多项式的阶数可有效提高CST方法的拟合精度。当阶数W=5时，采用CST方法可以达到拟合精度的要求。

2）基于NT-net法构建了翼型参数化模型。阐述了NT-net法的计算原理，基于NT-net法抽样并构建了翼型参数化模型的设计空间。经MCS法验证，采用NT-net法可以有效提高翼型参数化表达过程中不确定性传播的拟合精度及效率。

3）通过NT-net法与Morris法的结合，确定了影响翼型气动特性的主要几何因素并提出改进策略。影响翼型气动特性的主要几何因素依次为最大相对厚度和最大相对弯度、前缘半径和后缘厚度等，其中当来流攻角较小时，前缘半径适当取较大值，最大相对厚度和最大相对弯度取较小值，可以有效提高该工况下翼型的气动特性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

唐新姿，袁可人，王效禹，等.

自然风速下低雷诺数风力机翼型气动特性随机数值分析

［J］.湖南大学学报（自然科学版），2021，48（2）：45-52.