基于CSO-SVM的数控机床主轴热误差建模

doi:10.3785/j.issn.1006-754X.2022.00.036

基于CSO-SVM的数控机床主轴热误差建模

刘洪江^,^,¹, 胡腾^,¹^,², 何勇³, 董峰⁴, 罗为⁵

1.西南石油大学机电工程学院，四川成都 610500

2.四川普什宁江机床有限公司，四川都江堰 611830

3.中国石油集团川庆钻探工程有限公司培训中心，四川成都 610213

4.成都广通汽车有限公司，四川成都 611430

5.中国质量认证中心，四川成都 610065

Spindle thermal error modeling of NC machine tool based onCSO-SVM

LIU Hong-jiang^,^,¹, HU Teng^,¹^,², HE Yong³, DONG Feng⁴, LUO Wei⁵

1.School of Mechanical and Electrical Engineering, Southwest Petroleum University, Chengdu 610500, China

2.Sichuan Push Ningjiang Machine Tool Co. , Ltd. , Dujiangyan 611830, China

3.Training Center, China National Petroleum Corporation Chuanqing Drilling Engineering Co. , Ltd. , Chengdu 610213, China

4.Chengdu Guangtong Automobile Co. , Ltd, Chengdu 611430, China

5.China Quality Certification Center, Chengdu 610065, China

通讯作者: 胡腾（1985—），男，四川成都人，讲师，硕士生导师，博士，博士后研究人员，从事数控机床精度演化特性研究，E-mail：tenghu@swpu.edu.cn

收稿日期: 2021-05-03 修回日期: 2021-09-02

基金资助:

国家科技重大专项资金资助项目. 2018ZX04032001

Received: 2021-05-03 Revised: 2021-09-02

作者简介 About authors

刘洪江（1995—），男，四川巴中人，硕士生，从事数控机床热误差建模及补偿研究，E-mail：lhj055417@163.com，https：//orcid.org/0000-0002-5757-860X , E-mail：lhj055417@163.com

摘要

针对数控机床多热源所致的温升与主轴热误差之间复杂的非线性关系问题，提出一种鸡群优化（chicken swarm optimization, CSO）算法与支持向量机（support vector machines, SVM）相结合的主轴热误差预测模型（以下简称热误差模型）。以某精密数控机床的主轴单元为研究对象，采用五点法对其在空转状态下的轴向热变形进行测量，并借助热电偶传感器对机床的4个关键温度测点的温度进行采集。以SVM为理论基础，随机选取75%的数据样本进行训练，进而构建主轴热误差模型。其中，利用CSO算法优化SVM模型的惩罚参数c和核参数g，以提升热误差模型的预测能力及鲁棒性。以余下的25%的样本作为测试数据集，对所得热误差模型进行验证。利用CSO-SVM模型对不同工况下主轴的热误差进行预测，并将预测结果与测量结果进行对比。结果表明：当主轴转速为3 000 r/min时，CSO-SVM模型的平均预测精度高达97.32%，相较于多元线性回归模型和基于粒子群优化的SVM模型分别提升了6.53%和4.68%；当主轴转速为2 000， 4 000 r/min时，CSO-SVM模型的平均预测精度分别为92.53%、91.82%，表明该模型具有较高的预测能力和良好的鲁棒性。CSO-SVM模型具有较强的实用性和工程应用价值。

关键词： 数控机床 ; 主轴 ; 热误差 ; 鸡群优化 ; 支持向量机

Abstract

Aiming at the complex nonlinear relationship between temperature rise and spindle thermal error caused by multiple heat sources of numerical control (NC) machine tool, a spindle thermal error prediction model (hereinafter referred to as thermal error model) based on chicken swarm optimization (CSO) algorithm and support vector machine (SVM) was proposed. Taking the spindle unit of a precision NC machine tool as the research object, the axial thermal deformation under idle state was measured by five-point measurement method, and the temperatures of four key temperature measuring points of the machine tool were collected using thermocouple sensor. Based on SVM theory, 75% data samples were randomly selected for training, and then the spindle thermal error model was constructed. Among them, CSO algorithm was used to optimize the penalty parameter c and kernel parameter g of SVM model to improve the prediction ability and robustness of the thermal error model. The remaining 25% of the samples were used as the test data set to verify the thermal error model.The spindle thermal error under different working conditions was predicted using CSO-SVM model, and the predicted results were compared with the measured results.The results showed that when the spindle rotate speed was 3 000 r/min, the average prediction accuracy of CSO-SVM model was as high as 97.32%, which was 6.53% and 4.68% higher than that of multiple linear regression model and SVM model based on particle swarm optimization, respectively; when the spindle rotate speed was 2 000 and 4 000 r/min, the average prediction accuracy of CSO-SVM model was 92.53% and 91.82% respectively, indicating that the model had high prediction ability and good robustness. CSO-SVM model has strong practicability and engineering application value.

Keywords： CNC machine tool ; spindle ; thermal error ; chicken swarm optimization ; support vector machine

PDF (3609KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘洪江, 胡腾, 何勇, 董峰, 罗为. 基于CSO-SVM的数控机床主轴热误差建模. 工程设计学报[J], 2022, 29(3): 339-346 doi:10.3785/j.issn.1006-754X.2022.00.036

LIU Hong-jiang, HU Teng, HE Yong, DONG Feng, LUO Wei. Spindle thermal error modeling of NC machine tool based onCSO-SVM. Chinese Journal of Engineering Design[J], 2022, 29(3): 339-346 doi:10.3785/j.issn.1006-754X.2022.00.036

近年来，随着精密加工技术的不断进步，制造行业对数控机床的加工精度提出了更高的要求。热误差占数控机床总加工误差的40%以上，是影响数控机床加工精度的关键因素^［1-3］。主轴是数控机床最重要的部件之一，因此对主轴热误差的研究尤为重要。目前，主要采用误差防止法和误差补偿法来减小主轴热误差^［4］。误差防止法的本质是抑制或消除热误差，如通过优化数控机床结构、控制环境温度等方式减少主要热源产热，但是会极大地增加机床设计和制造的成本，故在工程中应用较少^［5-6］。误差补偿法是通过构建机床温度变化与主轴热误差的映射关系，由主轴的温度变化来预测主轴热误差，并通过数控系统对热误差进行补偿^［7-9］。该方法成本低、实用性好、预测的精度稳定，在实际工程中被广泛应用。

对于误差补偿法，构建精度高、鲁棒性好的热误差预测模型（以下简称热误差模型）是实现热误差补偿的重要前提^［10-11］。许多学者对热误差模型进行了深入研究。王维等^［12］采用线性回归分析法建立了热误差模型。考虑到离散的温度变量不能准确反映整个机床温度场的变化，且温度变量与热误差之间会逐渐呈现极强的非线性关系，采用线性回归分析法建模会出现一定的偏差，所以人工神经网络和机器学习被大量应用到热误差建模。谭峰等^［13］通过建立集成BP （back propagation，反向传播）神经网络模型来处理温度变量与热误差之间的非线性关系，并取得了良好的预测精度。Li等^［14］采用粒子群优化（particle swarm optimization, PSO）算法有效优化了BP神经网络的拓扑结构，从而进一步提高了BP神经网络模型的预测精度。Qiang等^［15］将灰色关联理论应用于热误差建模，以解决温度数据样本量少、信息贫乏的问题。朱星星等^［16］以进给轴为研究对象，建立了基于最小二乘支持向量机（support vector machine, SVM）的热误差模型，取得了比较理想的补偿效果。然而，以上方法都存在局限性：神经网络模型对数据样本量的需求高且收敛速度慢，在建模时，只有选择了合适的拓扑结构，才可能取得好的预测效果：SVM算法可以通过小样本数据建模，并且克服了局部收敛的问题，但预测精度对参数的选择非常敏感；PSO算法可以对神经网络模型的拓扑结构进行优化，也可以对SVM的关键参数寻优，但存在收敛速度慢、局部寻优能力较差等问题，对预测精度有较大影响。

为了解决上述问题，笔者首先采用五点法测量某数控机床主轴的热误差；其次，利用鸡群算法全局搜索能力强、搜索效率高等优点，对SVM模型的惩罚参数c和核参数g进行优化，实现鸡群优化算法（chicken swarm optimization, CSO）算法与SVM的结合，即建立基于CSO的SVM热误差模型；最后，为了验证所建模型的预测精度及鲁棒性，将该模型与多元线性回归模型和PSO-SVM模型的预测精度进行对比，并改变工况对该模型的鲁棒性进行验证。

1 主轴温度和热误差的测量

1.1　五点法测量原理

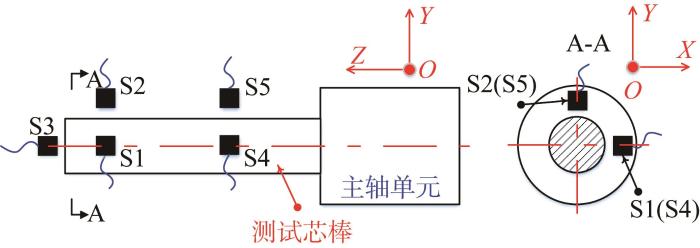
五点法测量如图1所示。主轴前端装夹了1根测试芯棒，5个位移传感器（S1至 S5）的相对位置固定。其中，S3位于芯棒中轴线方向，S1与S2以及S4与S5均沿芯棒径向布置，S1、S4用来测量主轴X向的热误差，S2、S5用来测量主轴Y向的热误差。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 五点法测量示意

Fig.1 Schematic of five-point measurement

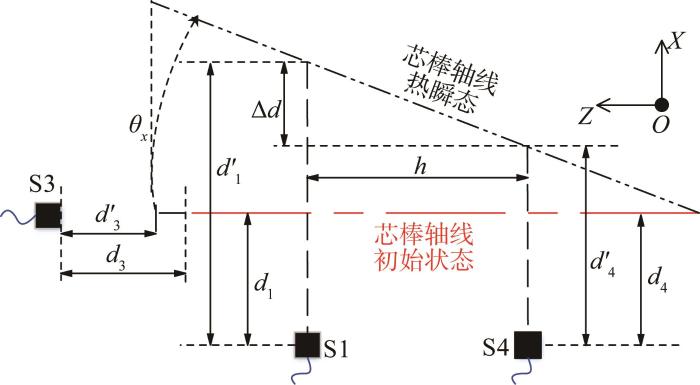
五点法测量的原理如图2所示。由于偏转角θ_x 较小，则θ_x ≈tan θ_x，即主轴Z向的热误差E和X向的热漂移误差θ_x 分别为^［17］：

E = d_{3} - d_{3}^{'}

（1）

θ_{x} \approx t a n θ_{x} = \frac{Δ d}{h} = \frac{(d_{1}^{'} - d_{1}) - (d_{4}^{'} - d_{4})}{h}

（2）

式中：d₃、 $d_{3}^{'}$ 分别为初始状态和热瞬态下S3传感器探头与测试芯棒前端面的距离；d₁、 $d_{1}^{'}$ 分别为初始状态和热瞬态下S1传感器探头到芯棒轴线的距离；d₄、 $d_{4}^{'}$ 分别为初始状态和热瞬态下S4传感器探头到芯棒轴线的距离；h为同侧传感器S4与S1之间的距离。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 五点法测量原理示意

Fig.2 Schematic of principle of five-point measurement

1.2　主轴温度和热误差的测量方法及测量结果

大量研究表明，在主轴达到热平衡的过程中，主轴轴向热误差相比其他方向的热误差更显著，所以选取主轴轴向热误差为主要研究对象，并在某数控机床进行温度和主轴热误差的测量实验。实验按照ISO230-3-2007中数控机床热误差的测量标准，采用五点法测量。选用电涡流位移传感器采集热误差数据，选取PT100热电偶温度传感器采集温度数据。

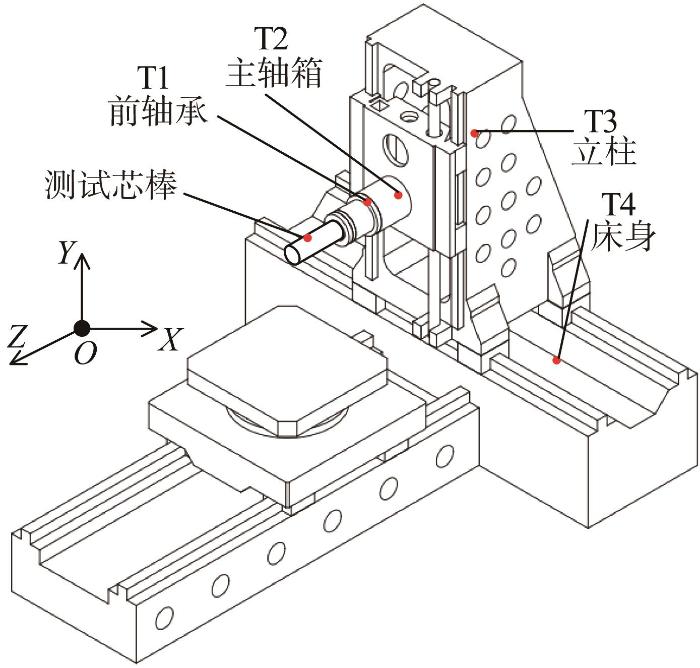
传感器探头与测试芯棒端面或法面的距离均保持为1 mm。为了准确反映机床温度场的变化，根据文献［18］提出的温度传感器布置方案及温度测点优化方案得到了4个关键温度测点，如表1所示。接着在机床的该4个测点布置好温度传感器，如图3所示。

表1 机床的关键温度测点

Table 1 Key temperature measuring points of machine tool

序号	T1	T2	T3	T4
位置	前轴承	主轴箱	立柱	床身

新窗口打开| 下载CSV

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 机床关键温度测点的分布

Fig.3 Distribution of key temperature measuring points of machine tool

机床温度和主轴热误差的测量平台如图4所示。主轴以3 000 r/min的恒定转速保持空转，每隔3 min同步采集一次温度数据和热误差数据。实验进行3 h，共采集到60组数据。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 机床温度和主轴热误差的测量平台

Fig.4 Measuring platform of machine tool temperature and spindle thermal error

待机床完全冷却后，再设置主轴转速分别为2 000 r/min和4 000 r/min进行实验，并将采集到的数据进行简要分析。

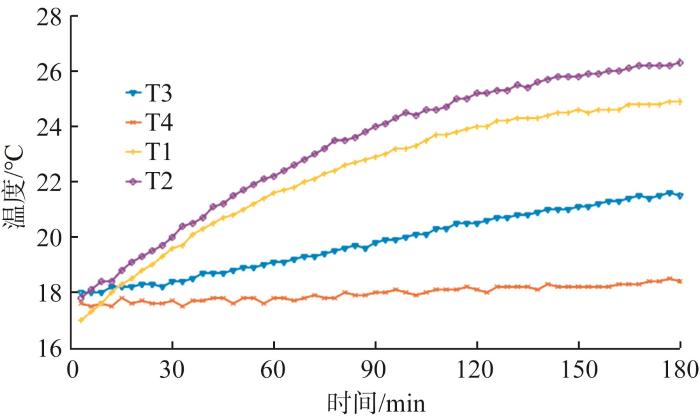
当转速为3 000 r/min时机床各关键测点的温度变化曲线如图5所示。由图可知，3 h后各测点温度基本不再变化，即主轴已经达到热平衡。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 转速为3 000 r/min时机床各关键测点的温度变化曲线

Fig.5 Temperature variation curve of key measuring points of machine tool at rotate speed of 3 000 r/min

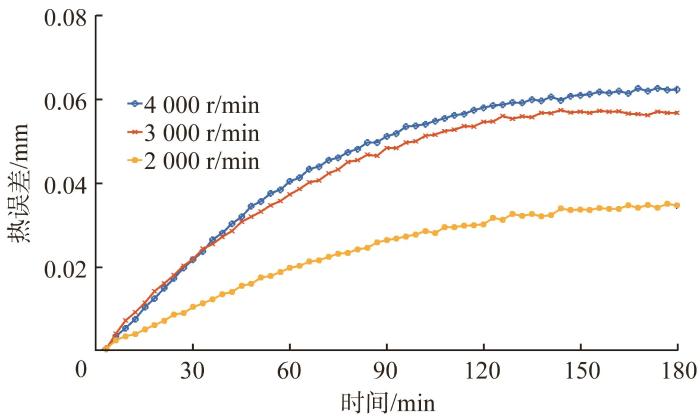
不同转速下主轴热误差变化曲线如图6所示。由图可知，在不同的转速下，主轴热误差不同。所以研究变工况下热误差模型的鲁棒性必不可少。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同转速下主轴热误差变化曲线

Fig.6 Variation curve of spindle thermal error at different rotate speeds

2 基于CSO算法的SVM热误差建模

2.1　SVM热误差建模

多元线性回归建模是较常见的机床主轴热误差建模方法。该建模方法通常需要大量实验数据来构造超越方程，其求解过程较为繁琐，计算收敛性较差，且可能不收敛。SVM是一种人工智能技术和机器学习方法，目前在模式识别、信号处理、回归预测等领域得到了大量应用。与神经网络相比，SVM能解决训练时间长和训练样本量大带来的问题，并有较强的处理非线性映射问题和全局寻优的能力^［19］。该方法的理论支撑源于结构风险最小化原则，通过选择函数子集及其判断函数，最终使风险达到最小。

对于线性问题，设f （x）=wx+b，假如对每个变量x_i （i=1，2， j，…， l），预估值f （x_i ）与实测值y_i 之间的误差都很小，即可称f （x）为最优回归曲线。其数学表达式为：

\{\begin{array}{l} \begin{array}{l} o b j . F = m i n \frac{1}{2} {‖w‖}^{2} \\ v a r . X = {w, b, μ} \end{array} \\ s . t . | w x_{i} + b - y_{i} | \leq μ \end{array}

(3)

式中：w为权重值；b为偏置；μ为实测值与预估值的最大允许误差。

在实际应用中，为了消除噪声点给模型带来的影响，引入松弛因子ξ、ξ^*，则式（3）可以改写为：

\{\begin{array}{l} \begin{array}{l} \begin{array}{l} o b j . F = m i n \frac{1}{2} {‖w‖}^{2} + c \sum_{i = 1}^{l} (ξ_{i} + ξ_{i}^{*}) \\ v a r . X = {ξ_{i}, ξ_{i}^{*}, c, w, b, μ} \end{array} \\ s . t . w x_{i} + b - y_{i} \leq μ + ξ_{i}^{*} \end{array} \\ y_{i} - w x_{i} - b \leq μ + ξ \\ ξ_{i} ξ_{i}^{*} \geq 0 \end{array}

(4)

式中：ξ_i 、ξ $_{i}^{*}$ 与训练样本点有关；c为超出最大误差范围的惩罚参数，须人为确定。

把该问题归纳为二次规划问题，则可以引入拉格朗日函数L：

\begin{array}{l} L = \frac{1}{2} {‖w‖}^{2} + c \sum_{i = 1}^{l} (ξ_{i} + ξ_{i}^{*}) - \sum_{i = 1}^{l} (η_{i} ξ_{i} + η_{i}^{*} ξ_{i}^{*}) - \\ \sum_{i = 1}^{l} α_{i} (μ + ξ_{i}^{*} + y_{i} - w x_{i} - b) - \\ \sum_{i = 1}^{l} α_{i}^{*} (μ + ξ_{i} - y_{i} + w x_{i} + b) \end{array}

(5)

式中： η_i、η $_{i}^{*}$ 分别为与ξ_i 、ξ $_{i}^{*}$ 对应的参数；α_i 、α $_{i}^{*}$ 为拉格朗日乘子。

求L对w、b、ξ $_{i}^{*}$ 的最小值，则有：

\{\begin{array}{l} \frac{\partial L}{\partial w} = w - \sum_{i = 1}^{l} x_{i} (α_{i} - α_{i}^{*}) = 0 \\ \frac{\partial L}{\partial b} = \sum_{i = 1}^{l} (α_{i}^{*} - α_{i}) = 0 \\ \frac{\partial L}{\partial ξ_{i}^{*}} = c - α_{i}^{*} - η_{i}^{*} = 0 \end{array}

(6)

即：

\{\begin{array}{l} w = \sum_{i = 1}^{l} x_{i} (α_{i} - α_{i}^{*}) \\ c = α_{i}^{*} + η_{i}^{*}, \\ \sum_{i = 1}^{l} (α_{i}^{*} - α_{i}) = 0 \end{array}

（7）

将式（7）代入式（5），将w、b、ξ $_{i}^{*}$ 消去，可得：

\{\begin{array}{l} \begin{array}{l} \begin{array}{l} o b j . F = m a x \frac{1}{2} \sum_{i, j = 1}^{l} (α_{i} - α_{i}^{*}) (α_{j} - α_{j}^{*}) - \\ μ \sum_{i = 1}^{l} (α_{i} + α_{i}^{*}) + \sum_{i = 1}^{l} y_{i} (α_{i} - α_{i}^{*}) \\ v a r . X = {α_{i}, α_{i}^{*}, α_{j}, α_{j}^{*}, μ} \end{array} \\ s . t . \sum_{i = 1}^{l} (α_{i} - α_{i}^{*}) = 0 \end{array} \\ α_{i}, α_{i}^{*} \in [0, c] \end{array}

(8)

若式（8）有解，须满足：

\{\begin{array}{l} α_{i} (μ + ξ_{i} - y_{i} + w x_{i} + b) = 0 \\ α_{i}^{*} (μ + ξ_{i}^{*} - y_{i} + w x_{i} + b) = 0 \\ ξ_{i} (c - α_{i}) = 0 \\ ξ_{i}^{*} (C - α_{i}^{*}) = 0 \\ α_{i} α_{i}^{*} = 0 \end{array}

(9)

不难看出，α_i 、α $_{i}^{*}$ 不能同时为0。当0<α_i <c且α $_{i}^{*}$ =0时，ξ_i =ξ $_{i}^{*}$ =0。对于满足0<α_i <c且α $_{i}^{*}$ =0的标准支持向量（support vector，SV），偏置b为：

b = y_{i} - μ - \sum_{J \in S V} x_{i} (α_{j} - a_{j}^{*})

(10)

式中：J为样本序列。

对所有的标准支持向量分别计算b，求其平均值，可得到拟合函数为：

f (x) = w x + b = \sum_{i = 1}^{l} x_{i} x (α_{i} - α_{i}^{*}) + b

(11)

对于非线性问题，利用核函数变换，可将低维空间映射到高维空间中，并在高维空间求解最佳拟合超平面。

本文选取的是高斯核函数：

k (e, e') = e x p \frac{- {‖e - e'‖}^{2}}{2 ρ^{2}}

(12)

式中： ρ为高斯核函数的宽度参数；e为预估值；e'为核函数的中心值。

则非线性拟合函数的表达式为：

f (x) = \sum_{i = 1}^{l} (α_{i} - a_{i}^{*}) e x p \frac{- {‖e - e'‖}^{2}}{2 ρ^{2}} + b

(13)

核函数选择为径向基函数，所以SVM模型中引入了另一个敏感参数g （g= $\frac{1}{2 ρ^{2}}$ ）。与惩罚参数c一样，核参数g也须预先设定。而c和g的选择对SVM模型的泛化能力、学习能力都有极大影响。c太大或太小都会影响模SVM模型的泛化能力。c越大，SVM模型对误差的容忍度越小，容易过拟合；c越小，则容易欠拟合。g对数据映射到高维特征空间后的分布有重大影响，g越大，支持向量就越少，而支持向量的个数决定了SVM模型的训练和预测速度。目前对c和g值的选择尚没有统一标准，网格搜索法是最简单、最广泛的参数搜索算法。该方法中，在范围内的每一个参数都须搜索验证，效率较低，并且当样本集或者待优化参数较多时，计算量很大且费时。

2.2　CSO算法

为了提升SVM模型的预测精度，常常采用遗传算法、粒子群算法等对SVM的重要参数进行寻优。然而遗传算法和粒子群算法容易出现收敛早且局部搜索能力差的问题，容易陷入局部最小值。

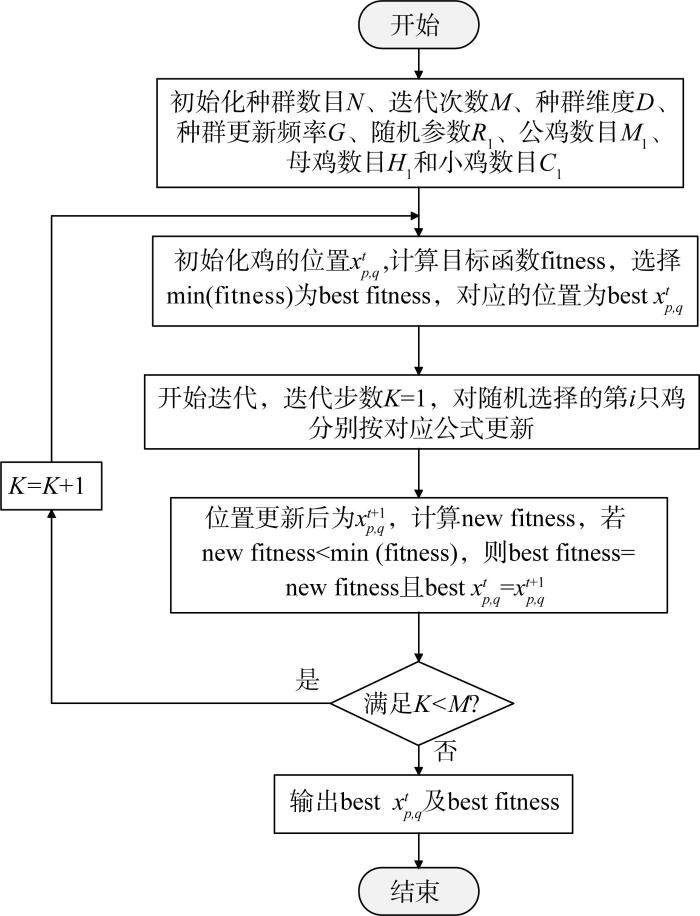
CSO算法是一种新颖的仿生群体智能算法，通过模拟具有等级秩序的鸡群觅食行为达到全局优化的效果^［20］。CSO算法根据适应度值的大小将鸡群分为多组，适应度值较小的几个被判别为公鸡，较大的几个判别为小鸡，其余则为母鸡。每组包括1只公鸡、若干母鸡和若干小鸡。鸡群跟随公鸡觅食，小鸡在母鸡周围觅食，觅食能力从强到弱依次为公鸡、母鸡、小鸡。在这种等级秩序下，不同鸡群间相互合作，协同觅食，且依据各自的运动规律不断更新位置以达到搜索食物的目的，直至寻找到最佳觅食位置。这种觅食方式不仅提升了算法的局部优化能力，其全局优化能力也得到了提升。

设搜索食物空间为D维，在t时刻第p只公鸡在q维空间的位置为x^t_p，q_{， p $\in$ ［1，2，…，M₁］， q $\in$ ［1，2，…， D］，则公鸡在t+1时刻的位置更新为：}

x_{p, q}^{t + 1} = x_{p, q}^{t} \times (1 + r a n d n (0, σ^{2}))

(14)

σ^{2} = \{\begin{array}{l} 1, f_{p} \leq f_{k} \\ e x p \frac{f_{k} - f_{p}}{|f_{p}| + ε}, f_{p} > f_{k}, k \in [1, M_{1}], k \neq p \end{array}

(15)

式（14）和式（15）中：σ² 为标准差；ε为一个常数且趋向于0；k为从公鸡组中随机挑选的第k只公鸡； f_p、f_k 分别为第p只鸡、第k只公鸡的适应度值。

在t+1时刻第p只母鸡在q维空间的位置更新为：

\begin{array}{l} x_{p, q}^{t + 1} = x_{p, q}^{t} + S_{1} \times r a n d (0,1) \times (x_{r_{1, q}}^{t} - x_{p, q}^{t}) + \\ S_{2} \times r a n d (0,1) \times (x_{r_{2, q}}^{t} - x_{p, q}^{t}) \end{array}

(16)

\{\begin{array}{l} S_{1} = e x p \frac{f_{k} - f_{p}}{|f_{p}| + ε} \\ S_{2} = e x p (f_{r_{2}} - f_{p}) \end{array}

(17)

式中：r₁为从母鸡配偶中随机挑选的第r₁只公鸡；r₂为从鸡群中随机挑选的第r₂只母鸡或公鸡。

在t+1时刻在母鸡身边觅食的第p只小鸡在q维空间的位置更新为：

x_{p, q}^{t + 1} = x_{p, q}^{t} + R_{1} \times (x_{m, q}^{t} - x_{p, q}^{t})

(18)

式中：m $\in$ ［1，C₁］；R₁ $\in$ ［0，2］为随母鸡觅食的小鸡的随机参数。

CSO算法的流程如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 CSO算法流程

Fig.7 CSO algorithm flow

2.3　SVM热误差模型的优化

SVM热误差模型的惩罚参数c和核参数g对SVM模型预测精度的影响较大。为了提高SVM模型的预测精度，采用CSO算法来优化c和g，即将CSO算法与SVM结合进行建模。把c和g的初始值作为CSO算法中鸡群的初始位置，将SVM模型的均方根误差M_SE作为CSO算法中的适应度函数，即：

f (x) = \frac{1}{n} \sum_{v = 1}^{n} (y_{v} - y_{v}^{'})^{2}

(19)

式中：y_v 为实际测量值； $y_{v}^{'}$ 为模型预测值；n为样本数量。

f （x）值越小，表示预测精度越高。根据CSO算法中鸡群的运动规律，不断迭代更新鸡群的位置，直至输出最小的适应度值和对应的最优参数c和g，即完成了CSO算法与SVM的结合，建立了基于CSO-SVM的热误差模型。

3 CSO-SVM模型的预测精度及鲁棒性验证

3.1　不同模型预测精度的对比

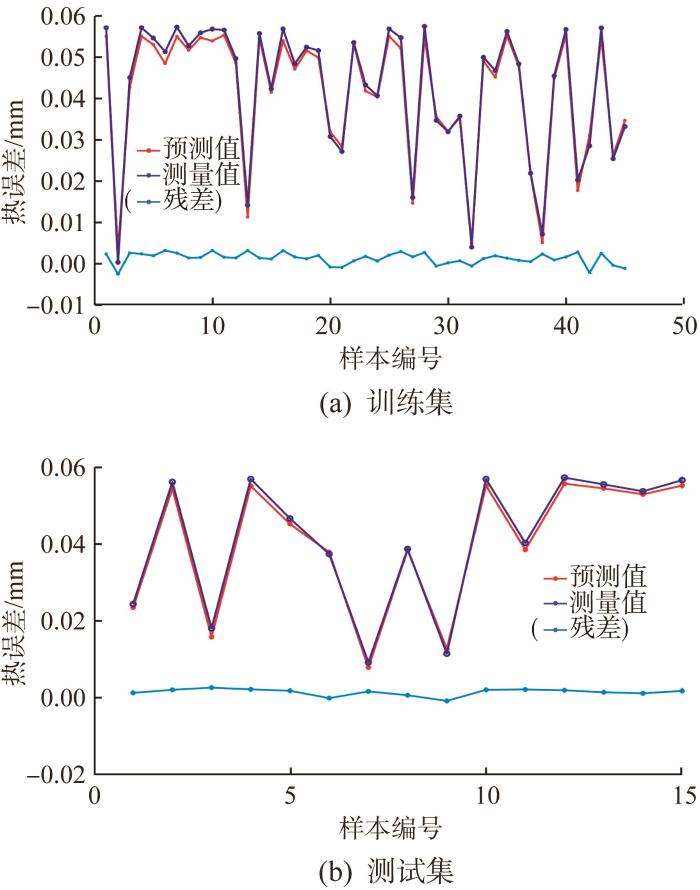
构建CSO-SVM模型后，将主轴转速为3 000 r/min时机床各关键温度测点的温度时序数据作为模型的输入，输出热误差。其中，随机选取45组数据作为训练集进行训练，训练完成后，将余下的15组数据作为测试集进行验证。CSO-SVM模型训练结果和测试结果如图8所示。可以得到CSO-SVM模型的均方根误差（即最佳适应度值）为0.002 404，计算出相应的最佳参数c和g分别为7.346 5和0.026 1。同时，得到训练集的残差为-2.9~2.9 μm，测试集的残差为 -1.2~2.5 μm。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 转速为3 000 r/min时CSO-SVM模型的热误差预测结果

Fig.8 Thermal error prediction results of CSO-SVM model at rotate speed of 3 000 r/min

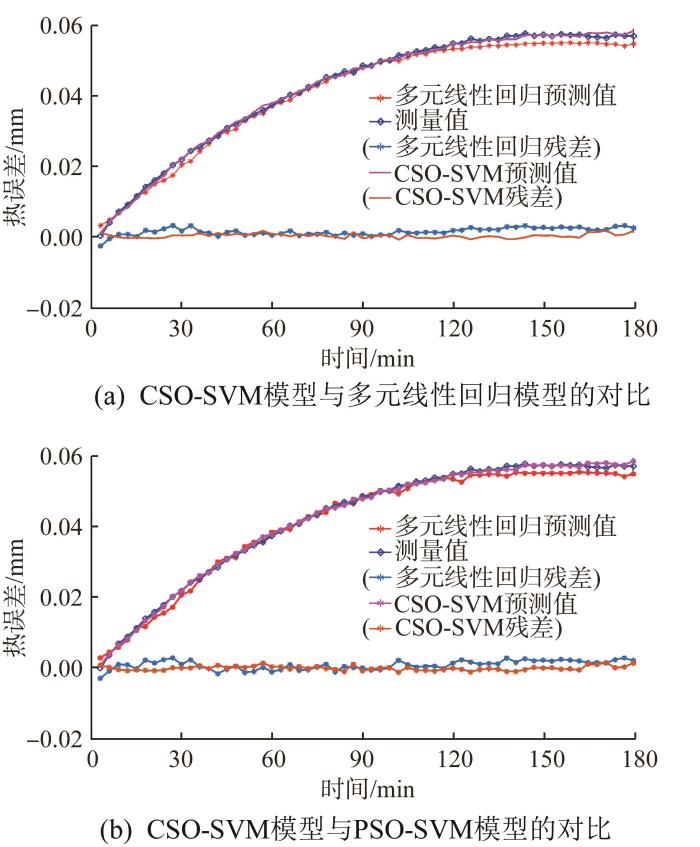
为了进一步验证CSO-SVM模型的优越性，基于转速为3 000 r/min时的实验数据，将其预测结果与多元线性回归模型、PSO-SVM模型的预测结果进行对比，结果如图9所示。由图可知，CSO-SVM模型的平均预测精度高达97.32%，相比于多元线性回归模型和PSO-SVM模型分别提升了6.53%和4.68%。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同模型预测精度的对比

Fig.9 Comparison of prediction accuracy of different models

3.2　CSO-SVM模型鲁棒性验证

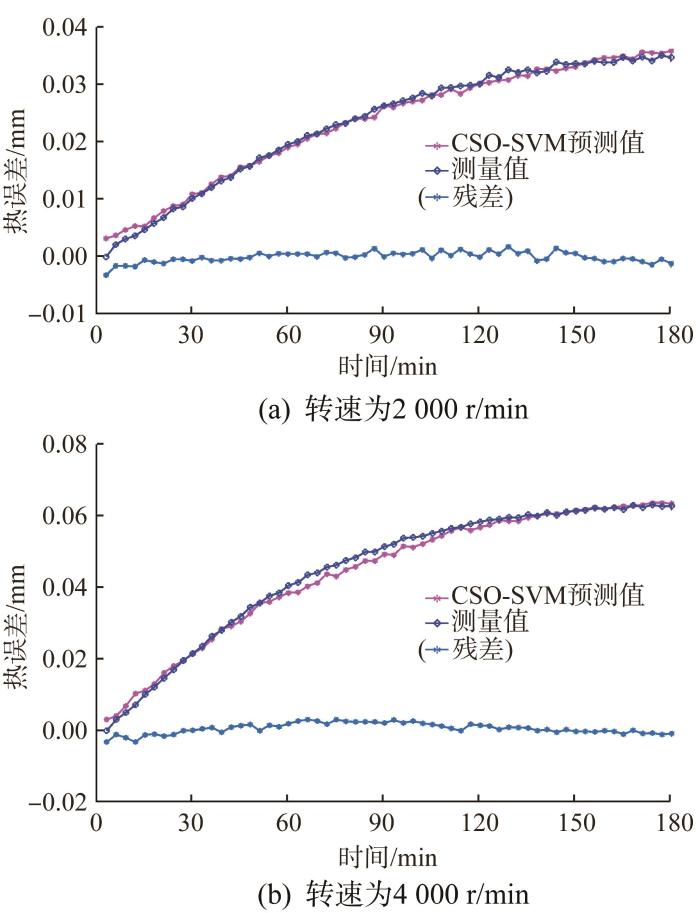
在实际工程中，工况在不断变化。为了验证CSO-SVM模型的鲁棒性，体现其实际工程价值，基于转速为2 000，4 000 r/min时的实验数据进行CSO-SVM模型热误差预测分析。预测结果如图10所示。由图可知，在2 000，4 000 r/min的主轴转速下，模型残差分别为-5.3~2.8 μm、-3.3~3.1 μm，平均预测精度分别达到了92.53%和91.82%。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同工况下CSO-SVM模型的热误差预测结果

Fig.10 Thermal error prediction results of CSO-SVM model under different working conditions

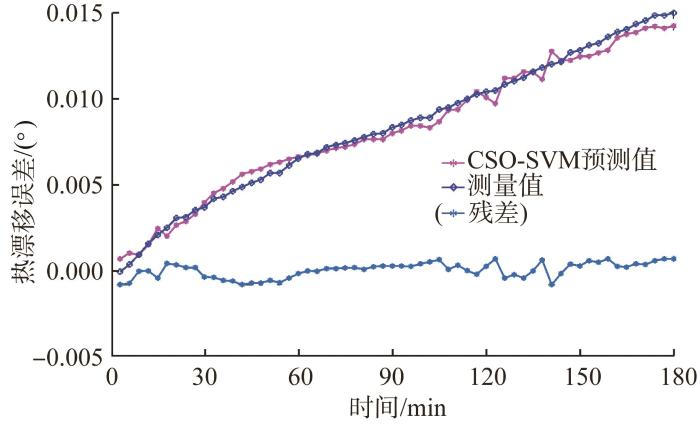
此外，当转速为3 000 r/min时对主轴径向热漂移误差进行预测分析。预测结果如图11所示。由图可知，其残差为-7.516 5×10^-4°~7.500 0×10^-4°，预测精度高达91.76%。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 转速为3 000 r/min时CSO-SVM模型的主轴径向热漂移误差预测结果

Fig.11 Prediction result of spindle radial thermal drift error of CSO-SVM model at rotate speed of 3 000 r/min

研究表明：所建CSO-SVM模型具有较高的预测精度和良好的鲁棒性，在实际工程中具有较强的应用价值。

4 结论

1）当主轴转速为3 000 r/min时，CSO-SVM模型训练集和测试集的残差分别达到了-2.9~2.9 μm、-1.2~2.5 μm，其平均预测精度高达97.32%。相比于传统的多元线性回归模型和PSO-SVM模型，平均预测精度分别提升了6.53%和4.68%，体现了CSO算法与SVM结合的优越性。

2）当主轴转速为2 000，4 000 r/min时，CSO-SVM模型热误差的平均预测精度分别为92.53%、91.82%。当主轴转速为3 000 r/min时，CSO-SVM模型主轴径向热漂移误差的平均预测精度达到91.76%。可见CSO-SVM模型具有良好的热误差预测能力和鲁棒性，拥有较强的实用性和工程应用价值。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

RAMESH

， MANNAN

M A

， POO

A N

Error compensation in machine tools： A review. part II： thermal errors

［J］. International Journal of Machine Tools and Manufacture， 2000， 40（9）： 1257-1284. doi：10.1016/s0890-6955(00)00010-9