在大飞机研制中，飞机的装配技术是一项非常重要的核心技术。研究表明，飞机装配约占整个飞机结构制造工作量的40%～50%^［1-4］。随着数字化定位装备、自动钻铆设备、制孔机器人等先进数字化设备以及异地协同平台、PDM （product data management，产品数据管理）系统、三维工艺设计系统、MES （manufacturing execution system，制造执行系统）、CATIA软件等信息化手段的应用，中航西安飞机工业集团股份有限公司基本实现了飞机部件与部件对接的数字化测量以及基于测量数据的装配。测量辅助装配（measurement assited assembly，MAA）技术成为保证装配质量的关键技术之一^［5-8］，得到了广泛重视和较快发展。

机翼是飞机最为重要的部件之一，具有提供升力、储存燃油等作用。机翼对接是飞机装配中的重要环节，其装配的准确度直接影响飞机的气动外形和飞行的平稳性^［9-12］。然而，机翼部件数量多、装配精度要求高、对接过程复杂，在装配过程中往往会积累较大的装配误差。为了实现对航空产品性能需求的快速响应，保证较高的装配质量，须对部件的质量特性进行控制，对装配过程中的容差进行合理分配。但是对每个质量特性进行控制是不现实的，须找出对产品质量有重要影响的关键特性并加以控制^［13-16］。本文通过对大飞机机翼对接中关键测量特征的研究，建立装配要求到检测要求的映射，基于关键测量特征间的几何关系，建立容差分配模型，实现机翼上测量特征点的容差分配。

在部件装配过程中关键测量特征数字化定义的技术路线如图1所示。首先，基于轻量化的产品模型，结合历史制造数据分析、风险分析和蒙特卡洛影响因子分析，确定对装配质量有决定性影响的关键测量特征，以减少不必要的测量工作^［17］；其次，根据不同几何特征的结构特点、公差要求等，将关键测量特征进一步转化为测量设备可测的离散点位数据；最后，实现不同关键测量特征的测量点集、公差信息等标准化三维可视化表达，完成关键测量特征的数字化定义。

在飞机装配过程中，不同部件之间的配合方式存在区别。配合方式的差异使得其所对应的装配几何量不同。例如：蒙皮与骨架、前缘肋与蒙皮等的对接采用曲面作为配合面，在装配过程中须保证曲面的无缝贴合；对于采用孔轴配合的翼身对接，在装配过程中须关注交点孔的位置与轴系的协调^［18-20］。同时，在装配过程中所采用的定位方法有所不同。部件的关键特征即为部件在定位、装配过程中的关键控制对象。根据部件在装配过程中的定位基准和配合方式，其关键特征主要有：曲面的贴合度、间隙、阶差，平面的平面度，定位孔的位置度和交点孔的位置度、同轴度。

装配几何量是飞机装配质量的直接反映，在实际装配时须利用数字化测量设备对其进行测定。但由于装配几何量并不具备直接可测性，且数字化测量设备采集的数据多为点位坐标，须对其进行分析并分解为直接可测的测量特征。测量特征主要是点、线和曲面等。

1）数学模型的轻量化。

为了能够将飞机部件装配的关键特征用数字量进行表达，以便直观地进行装配分析，须采用数字化测量手段对部件进行面向装配的测量。数字化测量须依赖数字化文档，包括可供数据分析参考的理论数学模型、引导测量设备自动化测量的测量点规划文档等。目前，在飞机制造中所采用的数学模型的数据量很大，其中包括许多在测量环节无效的数据，使得无法高效地测量部件。因此，须对原有的数学模型进行数据简化，在原有理论数学模型的基础上生成特定的测量数学模型和测量规划点。

在部件制造中所使用的数学模型在部件数字化测量中存在以下问题：

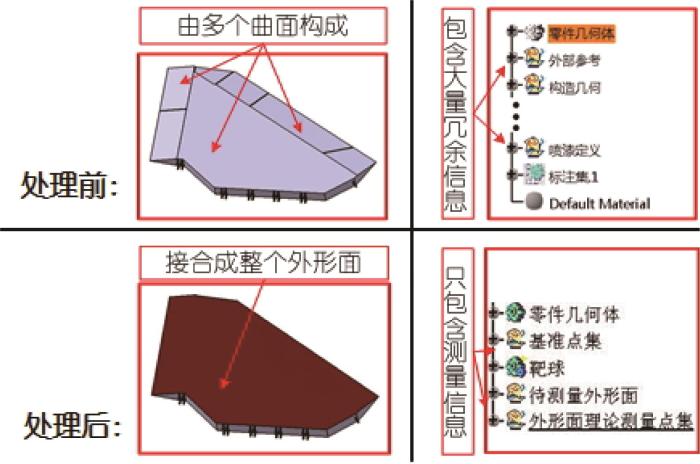
①信息冗余。数学模型包含框、梁以及工艺信息等与关键特征测量无关的信息，会对测量点的生成及后续的数据分析带来干扰。

②外形面由多张形面拼接而成，而由大量零碎曲面构成的设计外形面会给测量点的生成带来巨大工作量，并显著增大数据分析与计算量。

③容量大，导致数据分析与计算量大，效率低下。

针对上述问题，开发了测量特征提取模块，具体为：

①从数学模型中提取测量所需的外形特征，去除冗余信息。

②对部件外形面快速提取，自动拼接，形成整体外形面。

③生成轻量化的测量数学模型，减小数据分析与计算量。

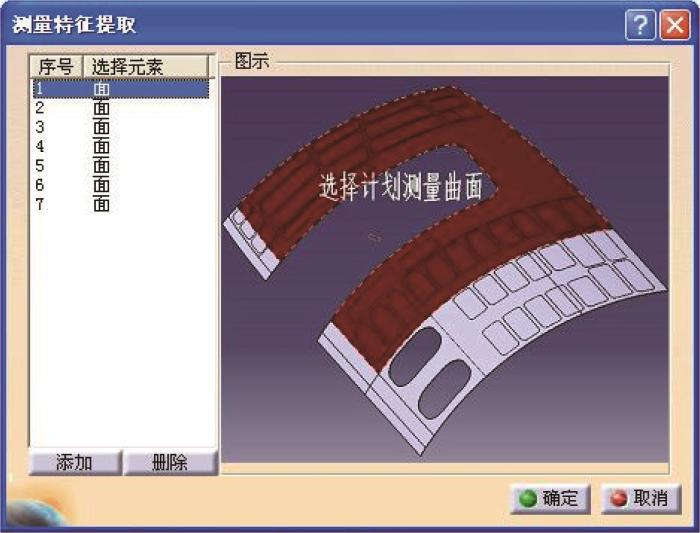
部件特征提取界面如图2所示。其功能是将零散分裂的测量特征进行合并与简化，再将所需测量的外形面进行接合后提取，从而简化模型。

通过对飞机理论数学模型的简化，将原有的数据量从10G缩小到几十兆，极大地简化了数据，提高了数据处理效率。数学模型轻量化的实施效果如图3所示。

2）测量特征的提取。

按照部件装配后对部件间的平面、位置、间隙、阶差等的要求，将这些要求逐项分解成可测量或可计算转化的点位信息，即进行测量特征提取，如将机身横向弯曲、机身纵向弯曲、机身扭转、机身与机翼的相对位置关系等转化为机身和机翼上水平测量点在飞机坐标系O-XYZ下X、Y、Z三个方向物理空间上的点位间距。其中：原点O位于飞机的质心；X向为平行于机身轴线或飞机对称面内机翼弦线指向机头的方向；Y向为垂直于飞机对称面指向右翼；Z向为飞机对称面内垂直于X向指向下方。

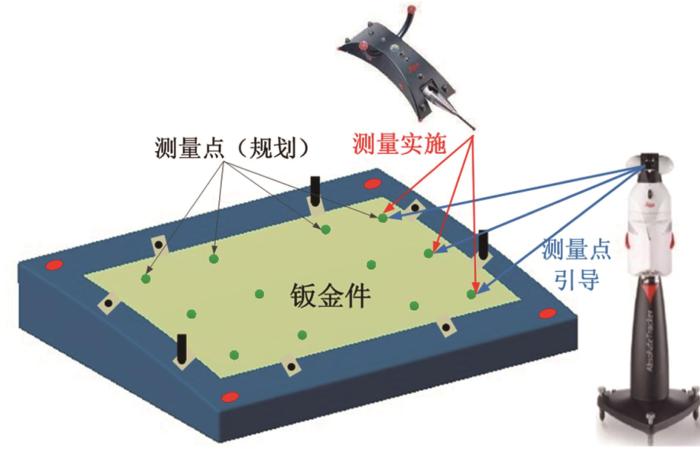
在飞机部件的装配过程中，测量对象主要为孔和曲面。孔位特征一般通过对孔心的测量获得，可采用靶球和测量基座进行测量，或者通过T-Probe探测器测量端面圆周上的离散点进行孔心拟合，也可以通过T-Scan扫描仪扫描进行数据拟合。对于曲面特征，小曲率部件可采用接触式测量设备如三坐标测量机、T-Probe探测器等进行测量，而像U形蒙皮、整体壁板等大曲率或大尺寸部件，须借助T-Scan扫描仪或激光雷达等具有扫描功能的测量设备进行测量^［21］。T-Probe探测器、激光跟踪仪的测量如图4所示。

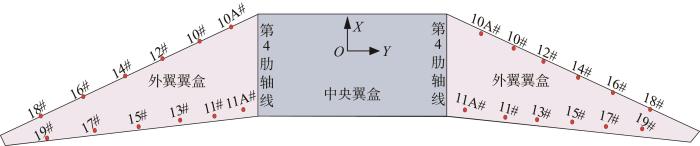
机翼对接中，首先进行前后缘组合件的型架内装配，然后在外翼翼盒总装阶段进行翼盒主体的总装配；在中央翼翼盒总装型架上完成中央翼翼盒的总装，再进行左右侧外翼翼盒与中央翼翼盒的对接装配，完成机翼固定翼面的装配；在装配型架上进行活动翼面悬挂，包括缝翼、襟翼、副翼、扰流板等的悬挂安装和调整。机翼上水平测量点的分布如图5所示。其主要用来测量和评估左右机翼的安装角、上反角和对称性。

在机翼对接过程中，须保证外翼翼盒前后梁与中央翼翼盒前后梁的对合间隙和阶差，以及中央翼与外翼在第4肋对合面上对合处的间隙和阶差。因此，在对接过程中首先须将部件按照理论位置通过水平测量点进行调平，其次进行预对合，最后根据对合间隙和阶差对外翼翼盒进行调整，在水平测量点公差范围内保证对合间隙和阶差。机翼的对接过程与机身三段的对接较为相似。因此，须根据对合要求，预先分配对合处的对接角度容差，求解相应水平测量点的容差分配。

在机翼对接过程中机翼在YOZ平面的纵向偏差如图6所示。其中Δα1、Δα21、Δα22、Δα3为纵向偏转角容差。在型架上安装阶段外翼翼盒的第4肋定位工装在其中轴线上的制造偏差影响了翼盒第4肋的定位精度，中央翼盒上左右第4肋处的定位偏差也会造成对接面上的角度偏差。为了保证对接面上对合间隙均匀，须以中央翼为基准，保持中央翼姿态不变，调整外翼翼盒姿态，因此形成水平测量点在Z向即纵向的偏差。

设左外翼翼盒上a、b两水平测量点间距的测量值为La-b，测量不确定度为uLa-b，则在对接过程中a、b两点在Z向的偏差ΔFZ0为：

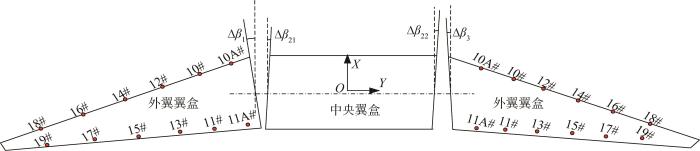
在对接过程中，机翼受对接面误差不确定性的影响，除了纵向偏转，还会产生横向偏转。机翼在XOY平面的横向偏差如图7所示。其中Δβ1、Δβ21、Δβ22、Δβ3为横向偏转角容差。

因此左、右外翼上2个对应的水平测量点A、B在X向的偏差ΔFXA、ΔFXB分别为：

式中：LA和LB分别为A、B两点距对接面距离的测量值；uLA和uLB分别为其测量不确定度。

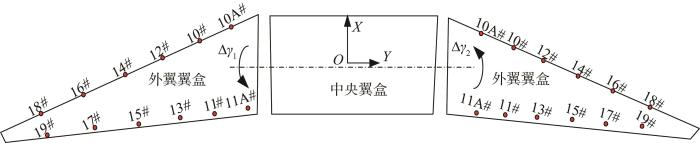
同时，在外翼对接过程中为了保证对接面的阶差均匀，须对外翼翼盒相对于中央翼翼盒进行绕Y向的调整，由此引入左、右外翼相对于中央翼盒的扭转偏差，如图8所示。其中，Δγ1、Δγ₂为扭转角容差。

扭转偏差会对纵向偏差造成影响，则a、b两点由于机翼扭转造成的Z向偏差为：

式中：Ra、Rb分别为a、b两点距外翼扭转中轴线距离的测量值；uRa和uRb分别为其测量不确定度。

扭转偏差即为机翼三段对接中安装角偏差的来源。

因此，在机翼对接过程中上反角偏差ΔF_Z 应为纵向偏差与扭转偏差之和，以左机翼为例，为：

对称性是机翼装配过程中一项重要的技术指标，直接影响飞机的飞行性能。在对称性分析过程中，用左、右外翼上2个对应的水平测量点A、B在Z向和X向的变化值来间接反映对称性（由于扭转、对接面偏差引起的Y向变化值较小，可忽略不计），则：

式中：RA和RB分别为A、B两点距扭转中心面距离的测量值；uLA和uLB分别为其测量不确定度。

在机翼数字化装配过程中，通常采用激光跟踪仪的靶球对水平测量点进行测量。激光跟踪仪的测量精度主要由角度编码器的测量精度和激光测距装置的精度决定。测量仪器自身的误差如鸟巢基距误差、靶球制造误差和校准误差等会对测量精度造成一定的影响。装配现场环境因素（温度、气压、湿度和外界干扰等）导致的误差，操作误差以及被测对象误差（热变形误差、力变形误差和制造误差等）也会对测量精度造成一定的影响。除此之外，激光跟踪仪所获取的测量值是在测量坐标系下的，须进行坐标变换得到装配坐标系下的坐标值，这又不可避免地引入了坐标变换导致的误差。因此，为了保证容差分配的可靠性和准确性，必须在容差计算中引入测量值的测量不确定度。据此，本节提出了对现场多个ERS （enhanced reference system， 增强参考系统）点进行多站位重复测量，将不同站位下的测量值通过坐标变换统一到同一坐标系下，分析各点的坐标变化，来计算现场测量值的测量不确定度。

采用统计分析方法计算所有点测量值的标准差。对单个测量点进行n次多站位测量，坐标变换后得到的测量点为P1,P2,…，Pn-1,Pn，求出这些点集的重心P，即坐标平均值。计算所有测量点与重心的距离d1,d2,…，dn-1,dn。通过计算实验标准差来获得现场测量值的测量不确定度^［22］。

对单个测量点进行n次多站位测量，其平均值的实验标准差s为：

对于m个ERS点，进行n次多站位测量，则其平均值的实验标准差为：

在某飞机机翼装配现场选取15个ERS点进行10个站位的测量。表1为第1个ERS点在10个站位的测量值。

以第1个站位为基准，将所有测量值统一到同一坐标系下，则根据式（8）算得的实验标准差s₁₅=0.0 433 mm。

所以，激光跟踪仪现场测量不确定度为0.0 433 mm。

在机翼对接过程中，安装角根据上翼面两水平测量点由于机翼扭转造成的Z向偏差ΔZ进行调控。所以，须对ΔZ进行计算，包括ΔZ10A#-11A#、ΔZ10#-11#等。

以ΔZ10A#-11A#的计算过程为例。根据外翼制造容差，预分配扭转角容差Δγ1=Δγ2=±12500 （单位为rad，予以省略。下同），10A#水平测量点距扭转中轴线的距离R10A#=1 698 mm，11A#水平测量点距扭转中轴线的距离R11A#=2 469 mm，由于同处于左机翼，扭转方向相同，根据公式（3），可知测量点10A#与11A#由于机翼扭转造成的Z向偏差ΔZ1为：

式中：Δi为尺寸链中第i个基本环的误差；Ai为误差Δi对累计误差传递的尺寸因子，或称传递系数。

采用概率法中的实用经验公式^［13］求解半带宽ωZ，则：

式中：H为修正系数，一般为1~1.8。

在机翼对接过程中，测量点10A#与11A#的理论位置高度差为24.5 mm，则机翼安装角的容差分配为：

同理，对ΔZ10#-11#进行计算。R10#=296 mm，R11#=3 763 mm，可得由于机翼扭转造成的Z向偏差ΔZ₂为：

在机翼对接过程中，测量点10#与11#的理论位置高度差为7.5 mm，则机翼安装角的容差分配为：

在机翼对接过程中，上反角根据上翼面的翼尖与翼根的两水平测量点的纵向偏差与扭转偏差之和ΔF_Z 进行调控。所以，须进行ΔF_10A#-12A#、ΔF_10#-14#等的计算。

以左机翼ΔF_10A#-12#的计算过程为例。L10A#-12#=7937mm，根据对接面装配工装的制造精度及第4肋的平面度，预分配对接面处的纵向偏转角容差Δα1=Δα21=±110000，预分配扭转角容差Δγ1=Δγ2=±12500，R10A#=1 698 mm，R12#=2 085 mm，根据公式（4），可得：

在机翼对接过程中，测量点10A#与12#的理论位置高度差为374.7 mm，则机翼上反角的容差分配为：

同理，针对左机翼测量点10#与14#，L10#-14#=8068mm，Δα1=Δα21=±110000，Δγ1=Δγ2=±12500，R_10#=296 mm，R_14#=3 926 mm，根据公式（4），可得：

ΔFZ2=3.302mm=∑i=1kAiΔi

在机翼对接过程中，测量点10#与14#的理论位置高度差为555 mm，则机翼上反角的容差分配为：

以12#左右两个水平测量点为例进行对称性分析。

L12#左=L12#右=9 902 mm，R12#左=R12#右=2 287 mm，对接过程中角度容差预分配值与前述相同，Δα1=Δα21=110000,Δγ1=12500,Δα3=Δα22=-110000，Δγ2=-12500，根据公式（5），可得：

在机翼对接过程中，机翼12#左右测量点的Z向对称性容差分配为：

在X向，将L12#左=L12#右=9902 mm，Δβ1=Δβ21=110000,Δβ22=Δβ3=-110000代入式（6），可得：

在机翼对接过程中，机翼12#左右测量点的X向对称性容差分配为：

同理，对18#点进行对称性计算。L18#左=L118#右=20941 mm，R18#左=R18#右=7497 mm，对接过程中角度容差预分配值与前述相同，根据公式（5），可得：

在机翼对接过程中，机翼18#左右测量点的Z向对称性容差分配为：

同理，在X向，根据式（6），可得：

在机翼对接过程中，机翼18#左右测量点的X向对称性容差分配为：

综上所述，在某型飞机机翼对接过程中水平测量要求如表2所示。

通过对大飞机机翼对接装配关键测量特征的研究，实现了装配要求到检测要求的映射，减少了部件数字化测量的次数，能够提高实测数据的利用率和生产效率。基于关键测量特征间的几何关系，引入现场测量设备的测量不确定度，建立了容差分配模型，对机翼的安装角、上反角和对称性等进行容差分配。本文提出的基于关键测量特征的容差建模与分析方法不仅可以应用于机翼对接，对于机身对接，翼身对接以及机翼、机身架外安装等，都能取得不错的应用效果。