工程设计学报

工程设计学报, 2022, 29(3): 286-292 doi: 10.3785/j.issn.1006-754X.2022.00.033

设计理论与方法

基于互信息与支持向量回归的盾构掘进载荷预测方法研究

周皓,, 刘尚林, 杨凯弘, 周思阳, 张茜,,

天津大学 机械工程学院，天津 300350

Research on prediction method of driving load of shield machine based on mutual information and support vector regression

ZHOU Hao,, LIU Shang-lin, YANG Kai-hong, ZHOU Si-yang, ZHANG Qian,,

School of Mechanical Engineering, Tianjin University, Tianjin 300350, China

通讯作者: 张 茜（1984—），女，天津人，教授，博士生导师，博士，从事实验固体力学研究，E-mail：zhangqian@tju.edu.cn，https：//orcid.org/0000-0001-7210-654X张 茜（1984—），女，天津人，教授，博士生导师，博士，从事实验固体力学研究，E-mail：zhangqian@tju.edu.cn，https：//orcid.org/0000-0001-7210-654X

收稿日期: 2019-12-19   修回日期: 2021-09-03  

基金资助: 国家重点研发计划资助项目.  2018YFB1702500
国家自然科学基金资助项目.  12022205.  11872269

Received: 2019-12-19   Revised: 2021-09-03  

作者简介 About authors

周皓（1997—），男，湖北黄冈人，硕士生，从事工程数据分析研究，E-mail：1239939145@qq.com , E-mail：1239939145@qq.com

摘要

掘进载荷是盾构施工中的重要控制量，直接关系着施工安全与效率。通过对掘进载荷影响因素的分析，建立了一种基于工程实测数据分析的掘进载荷特征选择及预测方法。首先，对工程实测数据进行极值归一化预处理，以降低不同参数间量纲和量级的差异产生的支配性影响；其次，通过参数分析和基于互信息的特征选择选取主要的影响参数作为输入；最后，通过支持向量回归（support vector regression，SVR）建立掘进载荷的预测模型，并结合天津地铁9号线盾构施工工程案例检验其预测表现。结果表明，所建立的掘进载荷预测方法能够在工程实测数据包含的众多影响参数中筛选出少量关键特征，实现对掘进载荷的合理预测。研究结果可以为盾构掘进参数的调控提供参考，也为具有众多参数的工程实测数据的分析提供一种思路。

关键词： 盾构 ; 工程实测数据 ; 掘进载荷 ; 特征选择 ; 支持向量回归

Abstract

driving load is an important control parameter in shield construction, which is directly related to construction safety and efficiency. Through the analysis of influencing factors of driving load, a feature selection and prediction method of driving load based on the analysis of engineering measured data was established. Firstly, the engineering measured data were extreme valuenormalized and preprocessed to reduce the dominant influence caused by dimensional and magnitude differences between different parameters; secondly, through parameter analysis and feature selection based on mutual information, the main influence parameters were selected as input; finally, the prediction model of driving load was established by support vector regression (SVR), and its prediction performance was tested by the actual shield construction engineering case of Tianjin Metro Line 9. The results showed that the established driving load prediction method could select a small number of key features from many influencing parameters contained in the engineering measured data, and realize the reasonable prediction of driving load. The research results can provide a reference for the regulation of shield tunneling parameters, and also provide an idea for the analysis of engineering measured data with many parameters.

Keywords： shield machine ; engineering measured data ; driving load ; feature selection ; support vector regression

PDF (1446KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

周皓, 刘尚林, 杨凯弘, 周思阳, 张茜. 基于互信息与支持向量回归的盾构掘进载荷预测方法研究. 工程设计学报[J], 2022, 29(3): 286-292 doi:10.3785/j.issn.1006-754X.2022.00.033

ZHOU Hao, LIU Shang-lin, YANG Kai-hong, ZHOU Si-yang, ZHANG Qian. Research on prediction method of driving load of shield machine based on mutual information and support vector regression. Chinese Journal of Engineering Design[J], 2022, 29(3): 286-292 doi:10.3785/j.issn.1006-754X.2022.00.033

盾构是一种用于地下隧道掘进的机械装备，能够进行隧道一体成型的工厂化作业，具有重型巨载、结构复杂等特点［1］。掘进载荷是在施工过程中装备控制的重要指标，其主要包括掘进总推力和刀盘扭矩。掘进总推力即为推动盾构向前的动力，刀盘扭矩则使刀盘不断旋转而对土体进行切削破坏。掘进载荷如果调控不当，不仅会影响切削破坏效果，还可能给盾构带来额外损伤，甚至可能引起工程事故，造成经济损失和人员伤亡。因此，正确预测掘进载荷是预估和优化盾构施工时间及成本的重要基础［2-3］。

盾构的掘进是机械装备与周围地质不断作用的过程，受到地质条件、操作参数等众多因素的耦合影响［4］，这给掘进载荷的分析造成了一定的困难。在施工过程中所记录的工程实测数据包含了大量运行信息［5］，是分析盾构掘进规律的重要信息基础［6］。许多学者利用工程实测数据建立反演回归模型对掘进参数进行了分析。例如：Zhang等［7］利用工程实测数据建立了掘进比能的反演识别模型；郑峥［8］基于工程实测数据进行残差分析，并通过时序分析方法对残差建模，以修正掘进推力的预测模型；褚东升［9］在分析掘进参数相关性的基础上，以掘进速度、总推力、土仓压力和刀盘转速为自变量，建立了刀盘扭矩的经验模型；Song等［10］综合考虑了地质参数、掘进参数和刀盘结构参数对刀盘扭矩的影响，结合实测数据，采用多元非线性回归方法建立了刀盘扭矩的预测模型，并通过对实测数据的统计分析，提出了基于马尔科夫决策的载荷规划；张志奇等［11］统计了不同地质分段的盾构掘进参数，开展了针对盾构掘进速率和刀盘扭矩的多元回归分析，得到了适用于复杂地层的掘进参数回归模型，而胡祥涛等［12］基于实测数据验证了该回归模型的准确性，并对刀盘扭矩进行预测；Avunduk等［13］基于积累的现场实测数据，利用多元回归分析了各种软土参数对掘进总推力和刀盘扭矩的影响；Sun等［14］利用随机森林方法，根据地质参数和掘进参数来预测盾构掘进的动态载荷；Gao等［15］利用时序神经网络建立了对推力、扭矩等关键参数的实时预测模型。综上可知，目前利用工程实测数据对掘进载荷进行分析和建模预测的相关工作主要是基于工程经验考虑掘进速度、刀盘转速、土仓压力等若干核心参数对掘进载荷的影响。然而在盾构掘进过程中影响掘进载荷的因素种类繁多，因此，有效地挖掘工程实测数据，分析众多影响参数对载荷的敏感度，建立适用于盾构数据特征的机器学习模型，是掘进载荷分析与预测的重要研究内容。

本文建立了一种基于工程实测数据分析的掘进载荷特征选择及预测方法。首先，对原始工程实测数据进行极值归一化预处理，以降低不同参数间量纲和量级的差异带来的支配性影响；其次，对在掘进过程中实时记录的众多影响因素进行分析和筛选，并采用互信息算法选择对掘进载荷影响较大的若干主要参数作为输入；接着，采用支持向量回归（support vector regression， SVR）方法提取掘进参数间的非线性耦合关系，对掘进载荷进行预测建模；最后，以采用土压平衡式盾构施工的天津地铁9号线工程为例，对本文建立的方法进行讨论和验证，比较并分析掘进载荷特征选择方式对模型预测表现的影响。

1 基于工程实测数据分析的掘进载荷特征选择及预测建模

本文提出的掘进载荷的分析和预测建模方法主要包括以下3步：1）为了降低盾构工程实测数据中不同参数间量纲和量级的差异带来的支配性影响，对数据进行极值归一化预处理；2）采用非参数检验方法中的互信息算法筛选出对掘进载荷较为敏感的关键参数作为输入特征；3）采用SVR方法对掘进载荷进行预测建模。

1.1　数据预处理

在盾构掘进过程中实时记录有关机器运行的众多信息，如油缸推力、刀盘转速、掘进速率、导向姿态和密封舱压力等。这些不同类别的工程参数的量纲各异，且数值量级差距也十分悬殊。例如，掘进总推力可达上万kN，而掘进速率往往仅为几十mm/min，而它们都是表征机器运行状态的重要因素。

考虑到大多数特征选择及机器学习算法并不具有伸缩不变性，为了防止在数据挖掘时由于数值量级上的差异而可能使某些参数起到支配性的作用，在进行数据分析前须对所有参数进行极值归一化处理，即：

xpre=x-xminxmax-xmin

式中：xpre为归一化处理后的无量纲参数；x为归一化处理前的原始数据；xmin为该参数原始数据中的最小值；xmax为该参数原始数据中的最大值。

极值归一化处理可以将有量纲的参量无量纲化，并将值映射至0~1的区间，使得在后续分析中不同量纲和量级的参数能够尽可能地被平等对待，此外，在实际求解时还有利于提升收敛速度及效果。

1.2　特征选择

由传感器采集的工程实测数据包含众多工程参数，而根据工程经验，只须选择关键性的装备性能参数和地质参数用于数据分析［16-17］。因此，为了充分挖掘不同参数与掘进载荷间的变化规律，实现有效的掘进载荷预测，须合理、准确地选取对掘进载荷变化较为敏感的参数作为后续机器学习的输入特征，即特征选择。通过特征选择，可以从众多参数中剔除冗余参数，保留关键特征，以降低模型的复杂度，有利于增强预测效果，降低经验风险。

工程数据往往不服从已知常见的数据分布形式，且它们通过组合的方式对目标变量产生影响［18］。因此，本文采用互信息算法进行特征选择。

互信息是信息论中一种有用的信息度量，它被认为是在一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不确定性［19］。对于2个连续随机变量X、Y，其互信息I为［20］：

I(X;Y)=∫Y∫Xp(x, y)logp(x, y)p(x)p(y)dxdy

式中：p（x， y）为自变量X和因变量Y的联合概率密度函数；p（x）和p（y）分别为X和Y的边缘概率密度函数。

如果2个变量完全独立，则它们的互信息值为0；互信息值越大，2个变量越不独立，则自变量X更可以作为因变量Y的特征［21］。相较于相关系数等相关性评价指标，互信息的优势在于非参数检验，不要求数据服从特定的已知分布，能更加普适地度量2个变量之间的相关程度，因此适合对关系复杂、分布不明的盾构掘进参数进行特征选择。

1.3　SVR方法

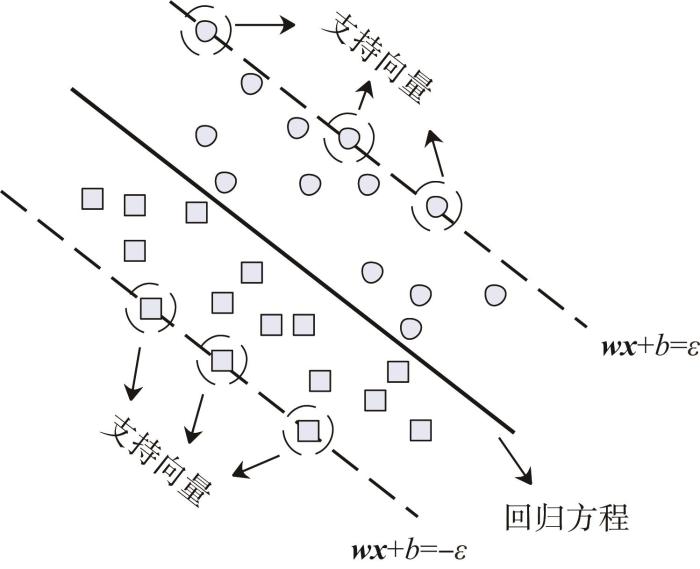
在盾构掘进过程中影响掘进载荷的参数众多，并且参数间的影响呈现复杂的非线性关系。对于此类高维非线性的数据分析问题，为了达到较高的模型精度，学习模型所需要的样本量与特征维度呈指数增长关系，因而对于特征维度高的数据，样本量往往显得不足［22］。SVR作为一种基于统计学理论的机器学习方法，在处理样本量少的非线性数据回归问题时有独特的优势［23-24］。该方法的计算复杂度取决于支持向量的数目，在一定程度上避免了高维样本带来的维数灾难，而灵活的核函数技巧使得该方法能够较为优秀地解决盾构掘进参数间的非线性关系问题。同时，工程实测数据由于在采集时受到工作环境和数据传输的影响，不可避免地含有噪声和离群值［25-26］，而采用SVR方法建模时无须依赖整个训练集，仅需少数样本点作为支持向量即可确定预测模型，对噪声和离群值具有一定的鲁棒性［27］。

SVR的基本思路是寻找一个样本空间中的超平面作为预测方程［28］，使得若干样本点到该平面的距离最小，而支持向量为距离超平面最远的点。SVR算法如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   SVR算法

Fig.1   SVR algorithm


因此，SVR算法的优化依据即为通过式（3）计算得到的样本点距离该超平面的距离。在非线性问题下，SVR算法通过核函数将原始训练样本映射到更高维中，在扩维后的样本空间中进行计算。

min12w2s.t.zi-wxi+b≤ε,∀i

式中：w为权重向量；b为偏置项；ε为偏差； xi 为第i个输入向量；zi 为目标值。

将经过极值归一化预处理并通过互信息方法筛选出的参数作为输入，利用SVR方法构建掘进载荷预测模型，对掘进总推力和刀盘扭矩进行预测。其预测流程如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   掘进载荷预测流程

Fig.2   Predicting process of driving load


2 工程实例

利用所构建的盾构掘进载荷预测方法，对在天津地铁9号线隧道某标段约960环（每环约1.2 m）施工区间所采集的工程实测数据进行分析。该施工区间的地质主要为黏土和粉土等软土，记录的原始数据包含334个参数。对原始数据进行类别及特征分析，首先剔除对掘进载荷预测无明显关联的参数，包括开关类状态参数，常数类参量及与掘进载荷明显不相干的参数如记录时刻、环号、千斤顶选择时间等。获得初步约简后的特征子集，其包含90个特征参数。盾构施工中的部分主要参数如表1所示。

表1   盾构施工中的部分主要参数

Table 1  Some main parameters in shield construction

参数最大值最小值均值标准差
掘进速度/(mm/min)55.6816.8435.2310.04
掘进总推力/kN24 878.5010 944.4116 063.762 920.61
刀盘扭矩/kNm1735.17810.461281.44152.04
刀盘转速/(r/min)1.100.400.950.14

新窗口打开| 下载CSV


原始数据初筛后的子集仍包含较多特征，因此进一步采用互信息方法进行特征选择。在高维特征的分析中，须综合考虑训练精度、计算成本及可能的过拟合等问题，选取适当个数的特征作为回归模型训练的有效输入。因此，首先就不同特征选取数对掘进载荷预测效果的影响进行讨论。

回归问题的常见评价指标有决定系数R2、平均绝对误差MAE和均方误差MSE，其计算表达式分别如式（4）至式（6）所示。

R2=1-∑i=1nyi-ŷi2∑i=1nyi-y¯2
MAE=1n∑i=1nŷi-yi
MSE=1n∑i=1n(ŷi-yi)2

式中：yi为实测值；ŷi为预测值；y¯=1n∑i=1nyi，为实测均值；n为样本数。

通过R2随特征数的变化情况来选取最终的特征个数，然后按照互信息计算得到的排序结果依次添加特征参数作为输入。同时考虑计算和特征获取的成本、算法训练复杂程度等因素，确定最优输入特征。

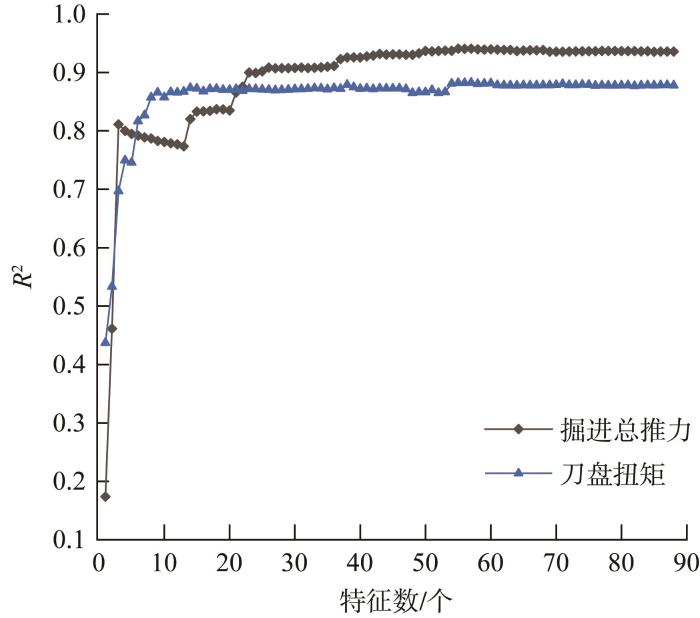
采用互信息方法对特征排序后，R2随特征数的变化曲线如图3所示。由图可知，掘进总推力和刀盘扭矩训练模型的R2均基本逐步上升，最终达到稳定的状态，具有较好的预测表现。当输入特征数达到15个左右时，R2均达到0.8以上，预测效果较优。此后，随着输入特征数的增多，R2虽有增大但增长缓慢。当输入特征数达到55个时，R2已经接近最大值，约为0.9。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   R2随特征数的变化曲线

Fig.3   Variation curve of R2 with the number of characteristics


根据实测数据互信息分析结果给出了该工程中对掘进总推力和刀盘扭矩的预测较为敏感的15个排序靠前的特征参数。掘进载荷与各特征参数之间的互信息分析结果如表2所示。由表2可知，掘进总推力与注浆上限、掘进速度、盾构掘进姿态参数等较相关；刀盘扭矩与电气参数、注浆参数等较相关。

表2   掘进载荷与各特征参数之间的互信息分析结果

Table 2  Mutual information analysis results between driving load and feature parameters

序号掘进总推力互信息值刀盘扭矩互信息值
1注浆上限0.570 52号高压变压器二次电流0.640 6
2掘进速度0.564 51号高压变压器二次电流0.355 6
3垂直偏差(铰接)0.557 5注浆累计平均值0.272 5
4垂直偏差(前端)0.557 5注浆上限0.252 6
5目标水准偏差0.557 4注浆下限0.238 9
6垂直偏差(后端)0.557 2掘进速度0.206 5
7测边差0.556 8土压平均值0.197 4
8Robotec方位偏差0.556 8注浆累计加权平均值0.195 7
9水平偏差(前端)0.556 8土压上限0.185 7
10水平偏差(铰接)0.556 8加泥上限0.173 0
11水平偏差(后端)0.556 8俯仰角0.153 9
12方位位移量0.556 8目标俯仰角偏差0.152 7
13开始时累计水准0.551 1俯仰角差0.152 5
14注浆下限0.542 0右千斤顶速度0.135 6
15俯仰角差0.523 4土压下限0.135 6

新窗口打开| 下载CSV


为了进一步验证所建立的特征选择与预测建模方法的准确性，将天津地铁9号线盾构施工工程中预留的独立数据验证集用于检验模型预测效果。该数据集未参与模型的训练过程。当输入特征数为15和55个时掘进总推力和刀盘扭矩的实测值与预测值的对比分别如图4和图5所示。图中同时给出了R2、MAE和MSE的值。由图可知，掘进总推力、刀盘扭矩实测值与预测值的变化趋势基本一致，说明选择互信息分析结果中排序靠前的少量参数作为敏感特征并用作模型的输入是合理的。特征数的增多在一定程度上有助于提升模型预测性能，但同时会导致模型复杂度、计算时间和成本增大。因此，在实际建模时，可根据需求确定特征数，平衡特征维度与准确度的关系。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   掘进总推力实测值与预测值的对比

Fig.4   Comparison between measured value and predicted value of total driving thrust


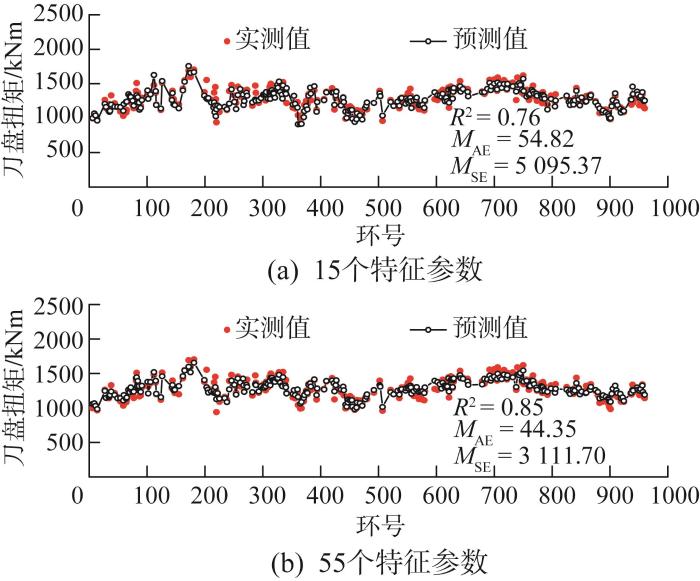
图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   刀盘扭矩实测值与预测值的对比

Fig.5   Comparison between measured value and predicted value of cutter head torque


上述研究表明，所建立的基于互信息的特征选择与SVR相结合的盾构掘进载荷预测方法能够从工程实测数据的众多特征中筛选出对掘进总推力和刀盘扭矩较为敏感的参数作为输入特征，来对掘进总推力和刀盘扭矩进行合理、准确的预测。

3 总 结

本文围绕盾构施工工程中实测数据分析与掘进载荷预测问题，建立了一种基于互信息的特征选择与SVR相结合的掘进载荷预测方法。对实测数据进行极值归一化预处理，基于互信息计算分析各类参数对掘进载荷影响的敏感度，确定适当的输入特征子集，并通过SVR方法对掘进总推力和刀盘扭矩进行建模预测。结合天津地铁9号线盾构施工工程的实测数据进行了掘进载荷的计算与分析，验证了所提出预测方法的合理性和有效性，并分析了特征数变化对掘进总推力和刀盘扭矩预测表现的影响。结果表明，通过互信息方法选取的少量特征可以建立相对较优的SVR回归模型，当输入特征数逐渐增多时，预测性能逐步上升并达到稳定状态。研究结果为盾构掘进载荷的预测提供了一种思路，也为具有高维、多参量非线性耦合等特点的工程实测数据的分析提供了参考。

参考文献

ARMAGHANI D J， KOOPIALIPOOR M， MARTO A， et al.

Application of several optimization techniques for estimating TBM advance rate in granitic rocks

［J］. Journal of Rock Mechanics and Geotechnical Engineering， 2019， 11（4）： 779-789. doi：10.1016/j.jrmge.2019.01.002

[本文引用: 1]

BILGIN N， ALGAN M.

The performance of a TBM in a squeezing ground at Uluabat， Turkey

［J］. Tunnelling and Underground Space Technology， 2012， 32： 58-65. doi：10.1016/j.tust.2012.05.004

[本文引用: 1]

夏毅敏，林赉贶，罗德志，等.

复合式土压平衡盾构盘形滚刀布置规律

［J］.中南大学学报（自然科学版），2013（9）：3652-3657.

[本文引用: 1]

XIA Yi-min， LIN Lai-kuang， LUO De-zhi， et al.

Disc cutter layout law for composite EPB shield

［J］. Journal of Central South University （Science and Technology）， 2013（9）： 3652-3657.

[本文引用: 1]

孙伟，马宏辉，丁鑫，等.

TBM刀盘驱动系统分层次建模及动力学特性研究

［J］.机械工程学报，2018，54（1）：44-55. doi：10.3901/jme.2018.01.044

[本文引用: 1]

SUN Wei， MA Hong-hui， DING Xin， et al.

Hierarchical modeling and dynamic analysis of cutterhead driving system in TBM

［J］. Journal of Mechanical Engineering， 2018， 54（1）： 44-55.

DOI:10.3901/jme.2018.01.044      [本文引用: 1]

ENTACHER M， WINTER G， GALLER R.

Cutter force measurement on tunnel boring machines： Implementation at Koralm tunnel

［J］. Tunnelling and Underground Space Technology， 2013， 38： 487-496. doi：10.1016/j.tust. 2013. 08.010

[本文引用: 1]

LIU B， GUO Q， LIU Z， et al.

Comprehensive ahead prospecting for hard rock TBM tunneling in complex limestone geology： A case study in Jilin， China

［J］. Tunnelling and Underground Space Technology， 2019， 93： 103045. doi：10.1016/j.tust.2019.103045

[本文引用: 1]

ZHANG Q， QU C， KANG Y， et al.

Identification and optimization of energy consumption by shield tunnel machines using a combined mechanical and regression analysis

［J］. Tunnelling and Underground Space Technology， 2012， 28： 350-354. doi：10.1016/j.tust. 2011.12.003

[本文引用: 1]

郑峥.

盾构掘进载荷的力学分析与反演识别

［D］.天津：天津大学，2013：31-37. doi：10.3901/jme.2014.21.031

[本文引用: 1]

ZHENG Zheng.

Mechanical analysis and inverse identification on load of shield tunneling machine

［D］. Tianjin： Tianjin University， 2013： 31-37.

DOI:10.3901/jme.2014.21.031      [本文引用: 1]

褚东升.

长沙地铁下穿湘江土压平衡盾构隧道掘进参数研究

［D］.长沙：中南大学，2012：85-91.

[本文引用: 1]

CHU Dong-sheng.

Study of EPB shield tunnelling parameters of Changsha metro passing beneath Xiangjiang River

［D］. Changsha： Central South University， 2012： 85-91..

[本文引用: 1]

SONG X， LIU J， GUO W.

A cutter head torque forecast model based on multivariate nonlinear regression for EPB shield tunneling

［C］//2010 International Conference on Artificial Intelligence and Computational Intelligence， New York： IEEE， 2010： 104-108. doi：10.1109/aici. 2010.261

[本文引用: 1]

张志奇，李彤，韩爱民，等.

复杂地层盾构掘进速率和刀盘扭矩预测模型及其地层适应性研究

［J］.隧道建设，2016，36（12）：1449-1455. doi：10.3973/j.issn.1672-741X.2016.12.007

[本文引用: 1]

ZHANG Zhi-qi， LI Tong， HAN Ai-min， et al.

Prediction models of advancing speed and cutterhead torque of shield tunneling in complex strata and its adaptability to strata

［J］. Tunnel Construction， 2016， 36（12）： 1449-1455.

DOI:10.3973/j.issn.1672-741X.2016.12.007      [本文引用: 1]

胡祥涛，张红旗，李自成，等.

基于部分可观测Markov决策过程理论的盾构推进载荷规划

［J］.机械工程学报，2014，50（21）： 84-91. doi：10.3901/jme.2014.21.084

[本文引用: 1]

HU Xiang-tao， ZHANG Hong-qi， LI Zi-cheng， et al.

POMDP-based planning model of driving force during shield tunneling

［J］. Journal of Mechanical Engineering， 2014， 50（21）： 84-91.

DOI:10.3901/jme.2014.21.084      [本文引用: 1]

AVUNDUK E， COPUR H.

Empirical modeling for predicting excavation performance of EPB TBM based on soil properties

［J］. Tunnelling and Underground Space Technology， 2018， 71： 340-353. doi：10.1016/j.tust. 2017.09.016

[本文引用: 1]

SUN W， SHI M， ZHANG C， et al.

Dynamic load prediction of tunnel boring machine （TBM） based on heterogeneous in-situ data

［J］. Automation in Construction， 2018， 92： 23-34. doi：10.1016/j.autcon. 2018.03.030

[本文引用: 1]

GAO X， SHI M， SONG X， et al.

Recurrent neural networks for real-time prediction of TBM operating parameters

［J］. Automation in Construction， 2019， 98： 225-235. doi：10.1016/j.autcon.2018.11.013

[本文引用: 1]

LI S， LIU B， XU X， et al.

An overview of ahead geological prospecting in tunneling

［J］. Tunnelling and Underground Space Technology， 2017， 63： 69-94. doi：10.1016/j.tust.2016.12.011

[本文引用: 1]

YAMAMOTO T， SHIRASAGI S， YAMAMOTO S， et al.

Evaluation of the geological condition ahead of the tunnel face by geostatistical techniques using TBM driving data

［J］. Tunnelling and Underground Space Technology， 2003， 18（2/3）： 213-221. doi：10.1016/s0886-7798（03）00030-0

[本文引用: 1]

ZHOU C， DING L Y， SKIBNIEWSKI M J， et al.

Data based complex network modeling and analysis of shield tunneling performance in metro construction

［J］. Advanced Engineering Informatics， 2018， 38： 168-186. doi：10.1016/j.aei.2018.06.011

[本文引用: 1]

AMIRI F， YOUSEFI M R， LUCAS C， et al.

Mutual information-based feature selection for intrusion detection systems

［J］. Journal of Network and Computer Applications， 2011， 34（4）： 1184-1199. doi：10.1016/j.jnca.2011.01.002

[本文引用: 1]

COVER T M， THOMAS J A. Elements of information theory［M］. New Jersey： Wiley-Interscience， 2006： 5-12.

[本文引用: 1]

VERGARA J R， ESTÉVEZ P A.

A review of feature selection methods based on mutual information

［J］. Neural Computing and Applications， 2014， 24（1）： 175-186. doi：10.1007/s00521-013-1368-0

[本文引用: 1]

张长水.

机器学习面临的挑战

［J］.中国科学（信息科学），2013，43（12）：1612-1623. doi：10.1360/n112013-00074

[本文引用: 1]

ZHANG Chang-shui.

Challenges in machine learning

［J］. Scientia Sinica （Informationis）， 2013， 43（12）： 1612-1623.

DOI:10.1360/n112013-00074      [本文引用: 1]

赖永标.

支持向量机在地下工程中的应用研究

［D］.青岛：山东科技大学，2004：22-24. doi：10.7666/d.Y671299

[本文引用: 1]

LAI Yong-biao.

Application and study of support vector machine in the underground engineering

［D］. Qingdao： Shandong University of Science and Technology， 2004： 22-24.

DOI:10.7666/d.Y671299      [本文引用: 1]

王健.

基于机器学习的TBM掘进性能预测与岩体参数表征方法研究

［D］.济南：山东大学，2017：20-23.

[本文引用: 1]

WANG Jian.

Research on TBM performance prediction and rock mass parameters characterization method based on machine learning

［D］. Jinan： Shandong University， 2017： 20-23.

[本文引用: 1]

YANG J P， CHEN W Z， LI M， et al.

Structural health monitoring and analysis of an underwater TBM tunnel

［J］. Tunnelling and Underground Space Technology， 2018， 82： 235-247. doi：10.1016/j.tust. 2018.08.053

[本文引用: 1]

TANG Z， LIU X， XU Q， et al.

Stability evaluation of deep-buried TBM construction tunnel based on microseismic monitoring technology

［J］. Tunnelling and Underground Space Technology， 2018， 81： 512-524. doi：10.1016/j.tust.2018.08.028

[本文引用: 1]

BOSER B E， GUYON I M， VAPNIK V N.

A training algorithm for optimal margin classifier

［C］//Proceedings of the fifth Annual Workshop on Computational Learning Theory. New York： Association for Computing Machinery， 1992： 144-152. doi：10.1145/130385.130401

[本文引用: 1]

周志华.机器学习［M］.北京：清华大学出版社，2016：121-136. doi：10.21436/inbom.12382432

[本文引用: 1]

ZHOU Zhi-hua. Machine learning［M］. Beijing： Tsinghua University Press， 2016： 121-136.

DOI:10.21436/inbom.12382432      [本文引用: 1]

/

〈 〉