通常电力系统都处于一个相对稳定状态，即电流、电压和功率在一个有限范围内变化，系统频率保持一致. 一旦这种平衡被打破，就会导致整个系统失稳. 例如，当电力系统中某个元件发生故障时，即使此时故障原件被切除，仍然可能导致电力系统振荡失稳^[1]. 对于一个处于动态平衡的电力系统，动态响应不是一直能够保持在一个绝对的稳定平衡点上，而是在某一个特定的空间拓扑区域，该区域称为稳定域^[2-3]. 动力学系统的稳定域表征了该系统的抗扰动能力，是量化系统稳定性的重要指标^[4]. 只要能够将电力系统的工作状态保持在稳定域范围内，就不会有失稳的风险，因此稳定域的确定对于保障电力系统安全运行具有重要意义.

稳定域的计算方法很多，主要包括Lyapunov能量函数法^[5-6]、可达集方法^[7-9]、蒙特卡洛方法^[10]等，但这些方法都存在一定的缺陷. 例如Lyapunov能量函数主要依赖于Lyapunov能量函数，得到的稳定域保守性较强. 对于蒙特卡洛方法，初始点取得越多，得到的稳定域精度越高；但初始点取得过多，会导致计算机运算时间太长. 林玉章等^[11]提出基于可达集理论确定电力系统的稳定域；该方法的主要思路如下：首先在电力系统表示的状态空间内找到一个较小的稳定区域并将其作为目标集，然后通过逆时间求解该目标集得到可达集，将可达集作为电力系统的稳定域. 该方法的缺点主要是基于最优控制求取Hamilton-Jacobi方程的最优解，而寻找最优控制的过程较繁琐且消耗时间较长.

近年来，Chiang等^[12-14]提出基于流形理论求解非线性的稳定域，但该方法只被用于计算二维系统的稳定域. 李颖晖等^[15-18]在理论上对流形理论计算稳定域进行推导，并在二阶的Normal Form变换确定受扰动后的电力系统稳定性方面取得了一定的成果. 本文在前人的基础上，首先提出基于流形理论开展电力系统的稳定域计算，引入轨道弧长法^[19]实现高维稳定边界构造. 以三阶单机无穷大系统作为仿真案例，与蒙特卡洛方法（Monte Carlo）确定的稳定域对比，验证了利用流形方法计算稳定域的有效性. 通过与可达集方法进行对比，验证了利用流形理论计算稳定域方法的高效性.

1 流形理论构造稳定域

提出的基于流形理论方法求解稳定域是以稳定平衡点（stable equilibrium point, SEP）稳定边界上的I型不稳定平衡点（unstable equilibrium point, UEP）的稳定流形的并集作为稳定边界. 利用该方法能够精确地构造高阶电力系统稳定域，因此能够作为对电力系统进行安全性分析的有力工具.

1.1 流形的基本理论

非线性动力学系统可以表示为以下微分方程形式：

${{\dot x}} = f({ x}).$

(1)

对于系统(1)，如果存在一个点x₀，使f(x₀)=0，则x₀为系统的一个平衡点. 如果在平衡点x₀处的Jacobi矩阵的特征值的实部不为零，则x₀为系统的双曲平衡点. 若特征值的实部全为负，则x₀为稳定的平衡点；反之，若存在实部大于零的特征值，则x₀为不稳定的平衡点. 实部小于零的特征值所对应的特征向量 $\left\{ {{v_1},{v_2},\cdots,{v_l}} \right\}$ 张成稳定的特征空间E^s；实部大于零的特征值所对应的特征向量 $\left\{ {{v_{l + 1}},{v_{l + 2}},\cdots,{v_n}} \right\}$ 张成不稳定的特征空间E^u. 全空间表示为Rⁿ=E^s+E^u.

双曲平衡点x₀的稳定流形W^s(x₀)和不稳定流W^u(x₀)定义如下：

$ \left.\begin{aligned} {W^{\rm s}}({{ x}_0}) = \left\{ {{ x}\left| {\mathop {\lim }\limits_{t \to \infty } \phi (t,{ x}) = {{ x}_0}} \right.} \right\}\, , \\ {W^{\rm u}}({{ x}_0}) = \left\{ {{ x}\left| {\mathop {\lim }\limits_{t \to - \infty } \phi (t,{ x}) = {{ x}_0}} \right.} \right\}\, . \end{aligned} \right\}$

(2)

式中： $\phi {\rm{(}}t,{ x}{\rm{)}}$ 为系统(2)始于 ${ x}$ 的解.

稳定平衡点x_s的稳定域A(x_s)可以定义为W^s(x_s)，边界称为稳定域的边界，记为 $\partial $ A(x_s)，是一个(n-1)维的闭不变集.

Chiang等^[20]指出，当满足以下条件(A1~A3)时，非线性动力学系统的稳定边界是由稳定平衡点的稳定边界上的I型不稳定平衡点（特征值中只有其中一维的特征值具有正实部)的稳定流形的并集构成.

1）所有在稳定边界上的平衡点都是双曲平衡点.

2）在稳定边界上平衡点的稳定和不稳定流 形都必须满足横截性条件.

3）当 $t \to \infty $ 时，稳定边界上的每一条解轨线都收敛于某一个稳定平衡点.

下面给出流形理论求解稳定域的具体方法. 对于微分系统 ${{\dot x}} = f({ x})$ ，首先令f(x)=0，求得系统所有的平衡点；然后通过求解平衡点处Jacobian矩阵的特征值，判断平衡点的稳定性；以其中的一个稳定平衡点作为工作点，同时从求得的所有不稳定平衡点中分析得到在工作点稳定边界上的I型不稳定平衡点；最后利用边界上的I型不稳定平衡点的稳定流形，刻画系统的稳定边界.

1.2 筛选出位于稳定边界上的不稳定平衡点

当通过解系统方程f(x)=0确定出若干个不稳定平衡点后，需要找到那些位于稳定边界上的I型不稳定平衡点，判断方法是稳定边界上的I型不稳定平衡点的正时间方向积分最终会收敛于选定的稳定平衡点. 具体步骤如下.

1) 以I型不稳定平衡点 ${{ x}_i}$ 为中心，取半径为 $\varepsilon $ 的n维超球体. 在超球体内部每个球面上均匀取点，第 $m$ 个球面上的点 $ {{ y}_m} = [ - \varepsilon ,{d_1},{d_2},\cdots,{d_{n - 1}},$ $\varepsilon ] + {{ x}_i}$ ，其中 ${d_j}(j = 1,2,\cdots,n - 1)$ 为 ${\rm{( - }}\varepsilon ,\varepsilon {\rm{)}}$ 内均取的点， $m = 1,2,\cdots,n$ .

2) 以步骤1)中取的点为初始点，对非线性系统进行反时间积分. 若所得轨线都能够保持在超球体内部，则进入3）；反之，将球体半径取为 $\alpha \varepsilon {\rm{(0}} < \alpha < {\rm{1)}}$ ，返回1）.

3） 以满足步骤2）中所取的 ${{ x}_i}$ 上不稳定流形上的各点为初始点，对系统进行正向数值积分. 判定当 $t \to \infty $ 时，积分轨线是否会收敛于稳定平衡点x_s.

4） 若步骤3）中的积分轨线会收敛于稳定平衡点x_s，则不稳定平衡点 ${{ x}_i}$ 为稳定平衡点x_s稳定边界上的点.

1.3 非线性系统稳定域边界构造

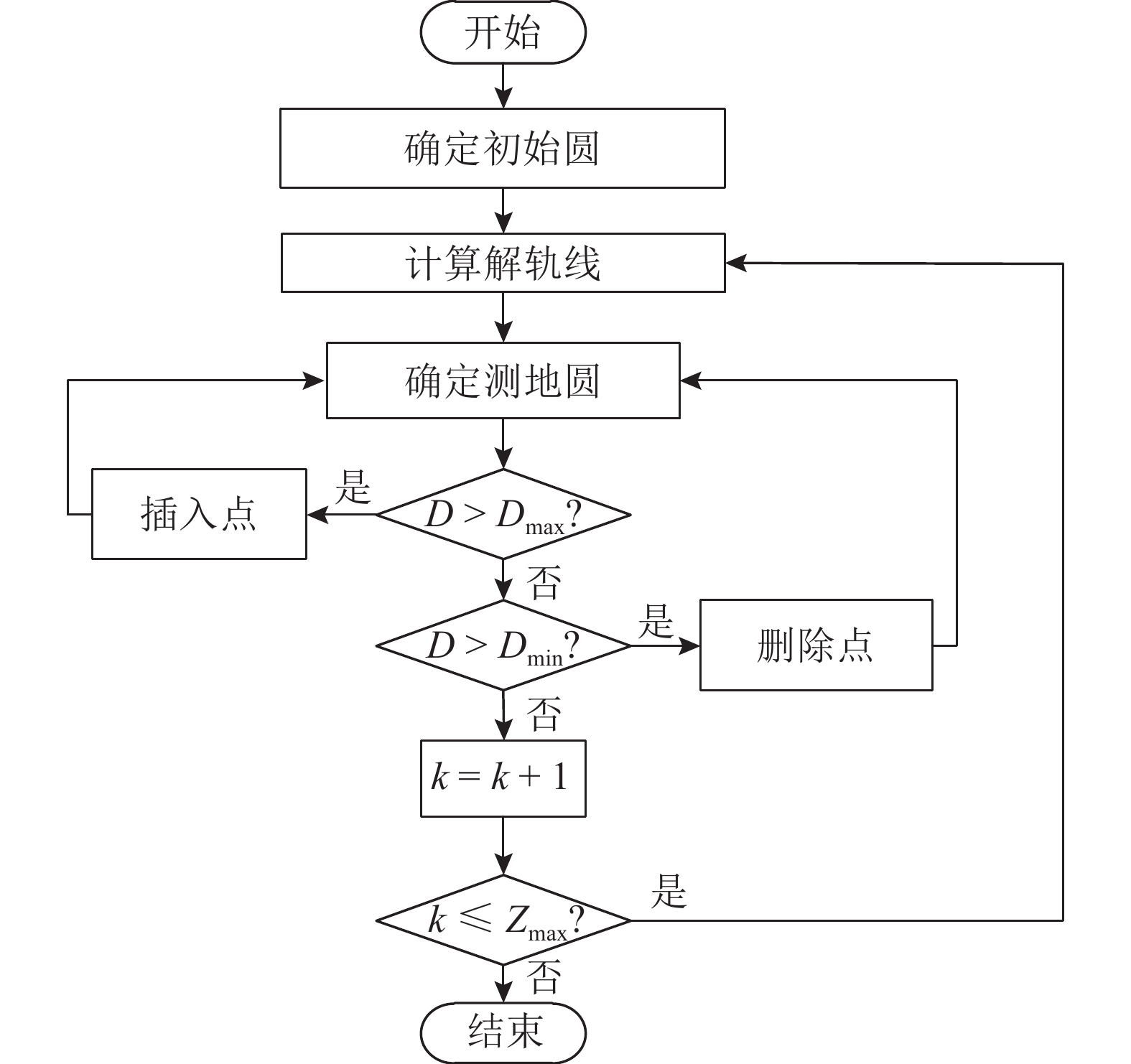
利用1.2节筛选得到的稳定边界上的I型不稳定平衡点，确定稳定边界. 其中稳定域边界的构造主要基于轨道弧长法，流程图如图1所示. 稳定域边界的具体构造步骤如下.

1）确定初始圆. 首先利用不稳定平衡点x_i的Jacobian矩阵求特征向量，将稳定的特征向量张成稳定流形的特征子空间（即切平面）；然后在确定的切平面上，以 ${{ x}_i}$ 为中心，r为半径作圆，其中r的取值略大于计算机浮点计算精度. 在圆上均匀取N个点 $\left\{ {{p_{1,1}},{p_{1,2}},\cdots,{p_{1{\rm{,}}N}}} \right\}$ .

2）求解轨线. 以点集 $\left\{ {{p_{1,1}},{p_{1,2}},\cdots,{p_{1,N}}} \right\}$ 为初始点，分别对系统进行反时间积分，当轨线长度达到设定值L时停止，得到第一代轨线 $\left\{ {{T_{1,1}}},{T_{1,2}},\cdots,\right. $ $\left.{{T_{1,N}}} \right\}$ ，将各条轨线的终点记为 $\left\{ {{p_{2,1}},{p_{2,2}},\cdots,{p_{2{\rm{,}}N}}} \right\}$ .

3）轨线间疏密程度判定. 检验各条轨线间的距离，若2条轨线间的距离大于D_max，则轨线太疏，在这两条轨线的初始点间插入一个新初始点. 反之，若2条轨线间的距离小于D_min，则2条轨线过密，删除其中一条轨线的初始点. 最后重新调整初始点集，返回2），直至满足要求，进入4）.

4） 以步骤3）中确定的轨线终点为二代初始点，重复步骤2）和3），迭代次数达到Z_max时停止.

5）连接相邻代的轨线，并将始于相邻初始点的轨线连接，形成边界面.

6）将稳定平衡点稳定边界上各个不稳定平衡点利用轨道弧长法所构造的边界面全部拼接在一起，所得界面为系统稳定域的边界.

2 可达集计算稳定域

可达集方法作为一种现在比较常用的稳定域确定方法，通过求解动力学系统稳定平衡点附近较小的稳定区域的反向可达集，并将该反向可达集作为系统的稳定域. 计算过程主要是基于可达集工具箱^[21]，下面介绍该方法的实现原理.

2.1 可达集的基本理论

非线性系统的动力学特性可以表示为以下微分方程形式：

$\dot{ x}{\rm{ = }}f{\rm{(}}{x}{\rm{,}}t{\rm{,}}{u}{\rm{)}}.$

(3)

式中： ${x} \in {{\bf{R}}^n}$ 为 $n$ 维状态空间， $t$ 表示时间， ${u} \in U$ 为控制量，其中 $f{\rm{:}}\;{{\bf{R}}^n} \times {\rm{[0,}}T{\rm{]}} \times U \to {{\bf{R}}^n}$ 有界且为Lipschitz连续.

系统的初始状态在控制量 ${u} \in U$ 的作用下，若满足在一定时间 $t \in {\rm{[0,}}\tau {\rm{]}}$ 内到达目标集，则这些所有初始状态的集合为可达集.

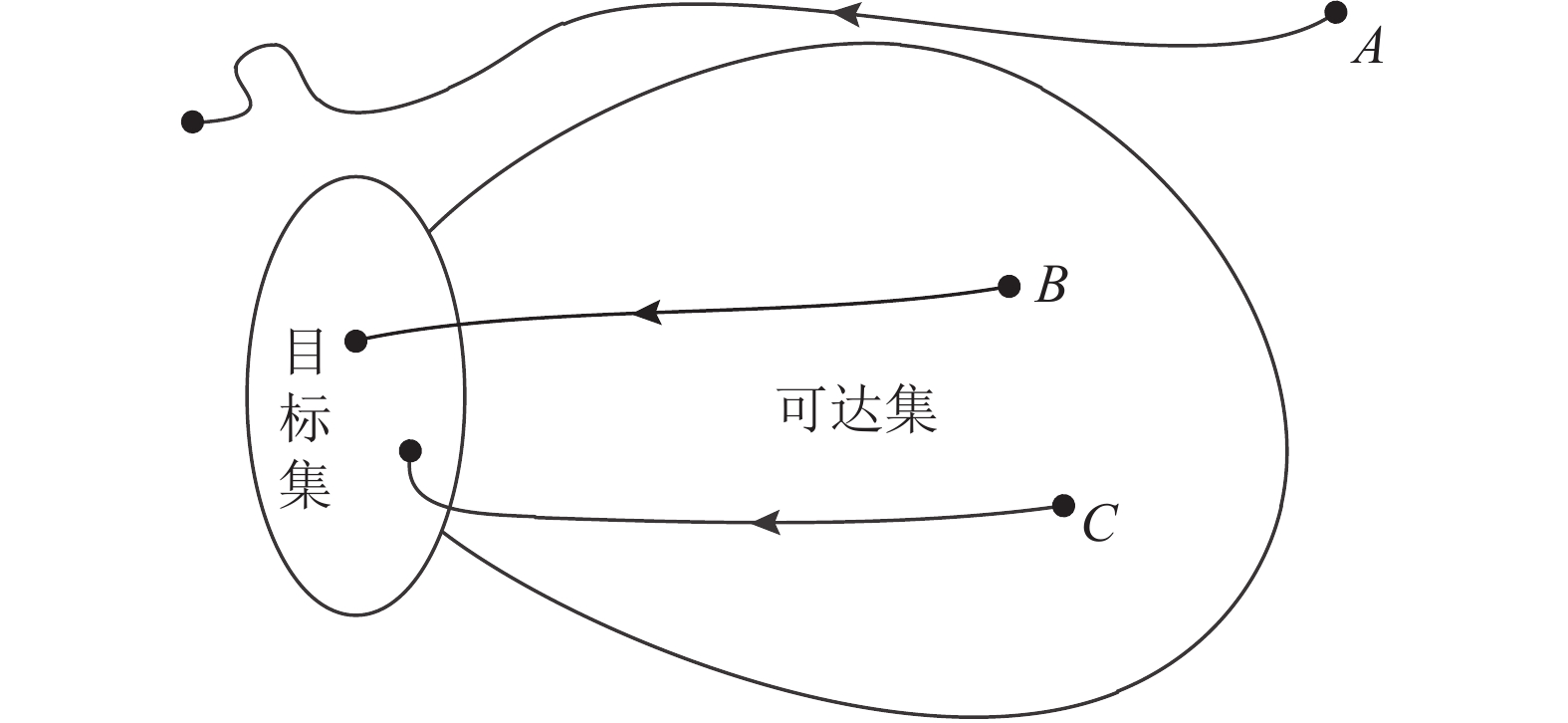
当开展系统方程分析时，由上述可达集的定义可知，可达集内的状态都能够在某一控制下经过给定时间后进入目标集；可达集外的状态点则无论何种控制，都不能在给定时间内进入目标集. 如图2所示，B和C点都是可达集内的状态点，在某一控制量作用下，经过一定时间最终都会到达目标集；可达集外的状态点A无法通过控制进入目标集.

水平集方程可以表示为

$\frac{{\partial \phi {\rm{(}}{x}{\rm{,}}t{\rm{)}}}}{{\partial t}}{\rm{ + }}f \cdot \Delta \phi {\rm{ = }}0.$

(4)

式中： $\phi {\rm{(}}{x}{\rm{,}}t{\rm{)}}$ 为水平集函数；目标集 ${G_0}$ 可以由水平集函数表示为

${G_0}{\rm{ = \{ }}{x} \in {{\bf{R}}^n}{\rm{|}}\phi {\rm{(}}{x}{\rm{,}}0{\rm{)}} \leqslant {\rm{0\} }}{\rm{.}}$

(5)

通过计算如下Hamilton-Jacobi方程的黏性解，能够得到目标集 ${G_0}$ 对应的可达集：

$\left.\begin{aligned} \displaystyle\frac{{\partial \phi \left( {{ x},t} \right)}}{{\partial t}} + \min \left[ {0,\;H\left( {{ x},\displaystyle\frac{{\partial \phi \left( {{ x},t} \right)}}{{\partial { x}}}} \right)} \right] = 0,\;{x} \in {{\bf{R}}^n},\;{{t < 0}};\\ \phi {\rm{(}}{x}{\rm{,}}t{\rm{) = }}\phi {\rm{(}}{x}{\rm{),}}\;{x} \in {{\bf{R}}^n},\;{t}{\rm{ = }}0 . \end{aligned}\right\}$

(6)

Hamilton函数 $H{\rm{(}}{x}{\rm{,}}{p}{\rm{)}}$ 为

$H{\rm{(}}{x}{\rm{,}}{p}{\rm{) = }}\mathop {\max }\limits_{{u} \in U} {{p}^{\rm{T}}}f{\rm{(}}{x}{\rm{,}}t{\rm{,}}{u}{\rm{)}}{\rm{.}}$

(7)

式中： $p = \partial \phi \left( {x,t} \right)/\partial x$ . 求最大可达集，要求使Hamilton函数值取最大，则此时的输入表示为

${{u}^{\rm{*}}}{\rm{(}}{x}{\rm{,}}{p}{\rm{) = arg max }}\;{{p}^{\rm{T}}}f{\rm{(}}{x}{\rm{,}}t{\rm{,}}{u}{\rm{)}}.$

(8)

将最优控制量 ${{u}^{\rm{*}}}$ 代入式（6）、（7）中求得可达集，可达集可以表示为

${P_\tau }{\rm{(}}{G_{\rm{0}}}{\rm{) = \{ }}{x} \in {{\bf{R}}^n}{\rm{|}}\phi {\rm{(}}{x}{\rm{,}}\tau {\rm{)}}\leqslant {\rm{0\} }}.$

(9)

2.2 可达集计算

在可达集的计算过程中，使用 Lax-Friedrichs格式得到Hamilton函数的近似值^[2]，具体为

$H\left({x}{\rm{,}}{{ p}^{\rm{ + }}}{\rm{,}}{{ p}^{\rm{ - }}}\right): = H\left({x}{\rm{,}}\frac{{{ p}{\rm^{ + }}{\rm{ + }}{{ p}^{\rm{ - }}}}}{2}\right) - \frac{{\rm{1}}}{{\rm{2}}}{{ k}^{\rm T}}\left({{ p}^{\rm{ + }}}{\rm{ - }}{{ p}^{\rm{ - }}}\right){\rm{.}}$

(11)

式中：

$p_i^{\rm{ - }}{\rm{ = }}\displaystyle\frac{{\phi \left({x_i}{\rm{,}}t\right) - \phi {\rm{(}}{x_{i{\rm{ - }}1}}{\rm{,}}t{\rm{)}}}}{{{x_i}{\rm{ - }}{x_{i{\rm{ - }}1}}}}$ ， $p_i^{\rm{ + }}{\rm{= }}\displaystyle\frac{{\phi {\rm{(}}{x_{i{\rm{ + }}1}}{\rm{,}}t{\rm{) - }}\phi {\rm{(}}{x_i}{\rm{,}}t{\rm{)}}}}{{{x_{i{\rm{ + }}1}}{\rm{ - }}{x_i}}}$ ，

其中 ${x_i}$ 、 ${x_{i{\rm{ - }}1}}$ 、 ${x_{i{\rm{ + }}1}}$ 为相邻网格点的状态；对于状态空间的第 $i$ 个维度 ${k_i}$ ，可以表示为

${k_i}{\rm{ = ma}}{{\rm{x}}_{{p_i} \in {\rm{[}}{p}_{i{{\rm{min},}}}{p}_{i{{\rm{max]}}}}}}\left| {\frac{{\partial {{H}}}}{{\partial {p_i}}}} \right|{\text{，}}$

(12)

其中， ${p}_{i{{\rm{min}}}}{\rm{ = }}\min {\rm{(}}{p_i}^{\rm{ + }},{p_i}^{\rm{ - }}{\rm{)}}$ ， ${p}_{i{{\rm{max}}}}{\rm{ = }}\max {\rm{(}}{p_i}^{\rm{ + }},{p_i}^{\rm{ - }}{\rm{)}}$ . 结合式(6)、(11)，可以求得可达集.

3 应用实例 3.1 三阶单机无穷大系统

为了对该方法进行有效性验证，引入电力系统中的三阶单机无穷大系统(SMIB)进行仿真计算. 数学模型可以表示如下：

$\left. {\begin{aligned}{} {{{T'}_{{\rm do}}}{{\dot E'}_q} = {E_{\rm f}} - {{E'}_q} - \left( {{X_d} - {{X'}_d}} \right){I_d}}, \\ {{T_{\rm j}}\dot \omega = {P_{\rm m}} - {P_{\rm e}} - D\left( {\omega - 1} \right)}, \\ {\dot \delta = {\omega _{\rm b}}\left( {\omega - 1} \right)}. \end{aligned}} \right\}$

(13)

式中：

$\left. {\begin{aligned}{} {{I_d} = {\left.{\left( {{{E'}_q} - U\cos \delta } \right)}\right/{\left( {X + {{X'}_d}} \right)}}}, \\ {{I_q} = {{U\sin \delta }\left/{\left( {X + {X_q}} \right)}\right.}}, \\ {{P_{\rm e}} = {{E'}_q}{I_q} - \left( {{{X'}_d} - {X_q}} \right){I_d}{I_q}}, \\ {X = {X_{\rm l}} + {X_{\rm t}}} . \end{aligned}} \right\}$

(14)

其中，ω为转子转速，ω_b为基准转速，δ为攻角，X_d为d轴电抗，X_q为q轴电抗，X′_d为d轴暂态电抗，X_t为变压器阻抗，X_l为线路阻抗，T′_do为励磁绕组的时间常数，T_j为转动惯量，E′_q为q轴暂态电压，P_m为机械输入功率，P_e为发电机提供的有效功率，I_d和I_q分别为d轴和q轴电流，D为阻尼系数，U为无穷大母线电压. 此外，将E′_q、ω和δ作为电力系统的状态变量，系统的相关参数如下：

$\left.\begin{split}{} {X_q} = 0.72 ,\quad{T_{\rm j}} = 8.75 ;\\ {X_d} = 1.035\;4, \quad {{T'}_{{\rm do}}} = 8.0; \\ {{X'}_d} = 0.36,\quad D = 3.0 ;\\ {X_{\rm l}} = 0.413,\quad U = 1.0 ; \\ {X_{\rm t}} = 0.15 ,\quad{P_{\rm m}} = 0.7;\\ {\omega _{\rm b}} = 2\pi \times 50 .\\ \end{split}\right\}$

(15)

3.2 利用流形理论计算三阶单机无穷大系统稳定域

以（E′_q，ω，δ）作为状态变量，选取系统的初始工作点为（0.886，314.16，1.05），经过解微分方程（13），得到2个平衡点A、B，如表1所示.

A、B两点的特征值分别为

A： $\begin{aligned} {\lambda _{1{\rm{,}}2}} = - 0.05 \pm 0.241\;1{\rm i} , {\lambda _3} = - 0.117 ;\end{aligned} $

B： $\begin{aligned} {\lambda _{1{\rm{,}}2}} = - 0.164 \pm 0.176\;5{\rm i} , {\lambda _3} = 0.109\;6 .\end{aligned} $

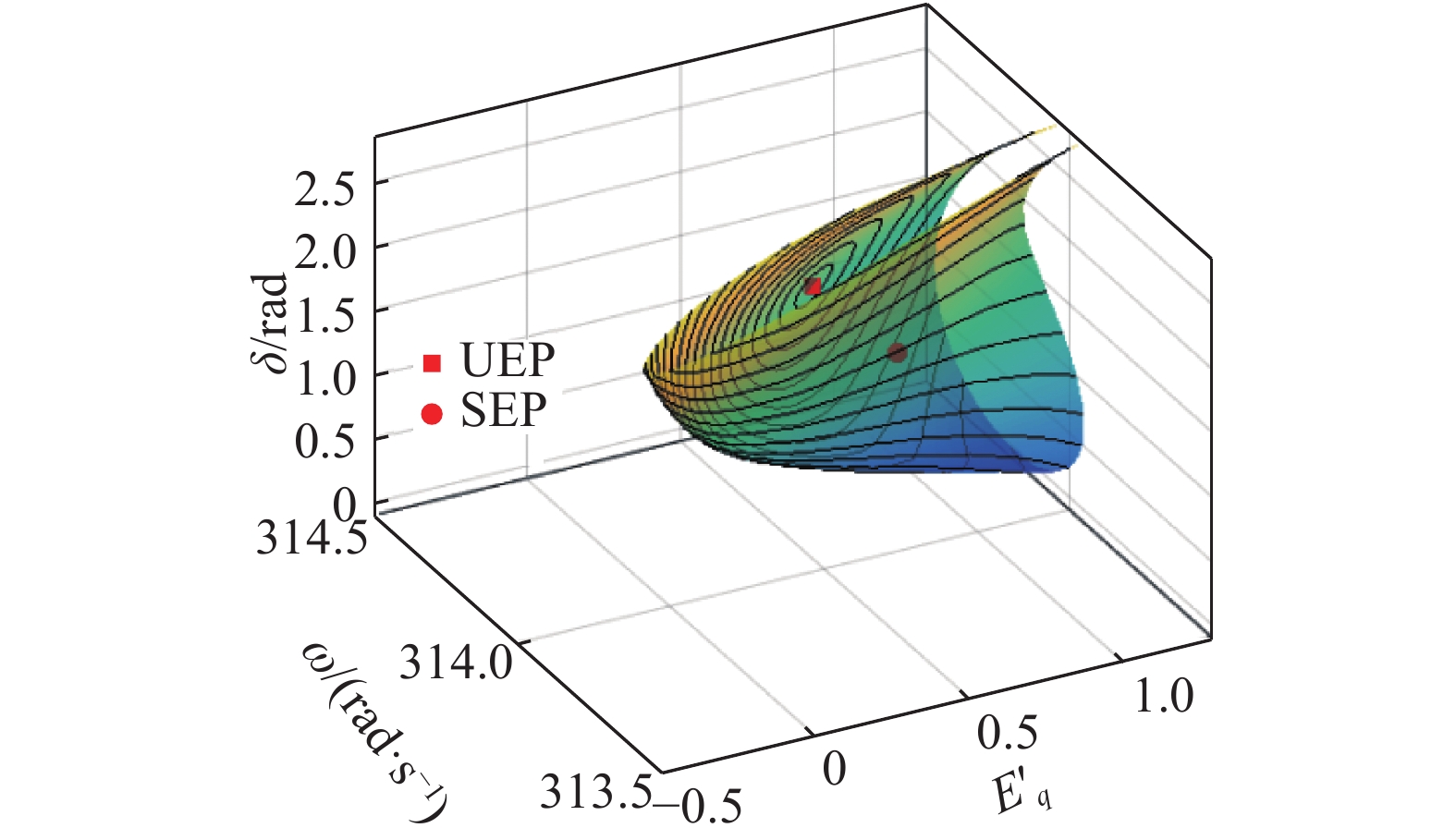
由特征值可知，A为稳定的平衡点，B为I型不稳定平衡点，利用轨道弧长法在I型不稳定平衡点B处求稳定域，得到的稳定域如图3所示.

3.3 利用蒙特卡洛方法计算三阶单机无穷大系统稳定域

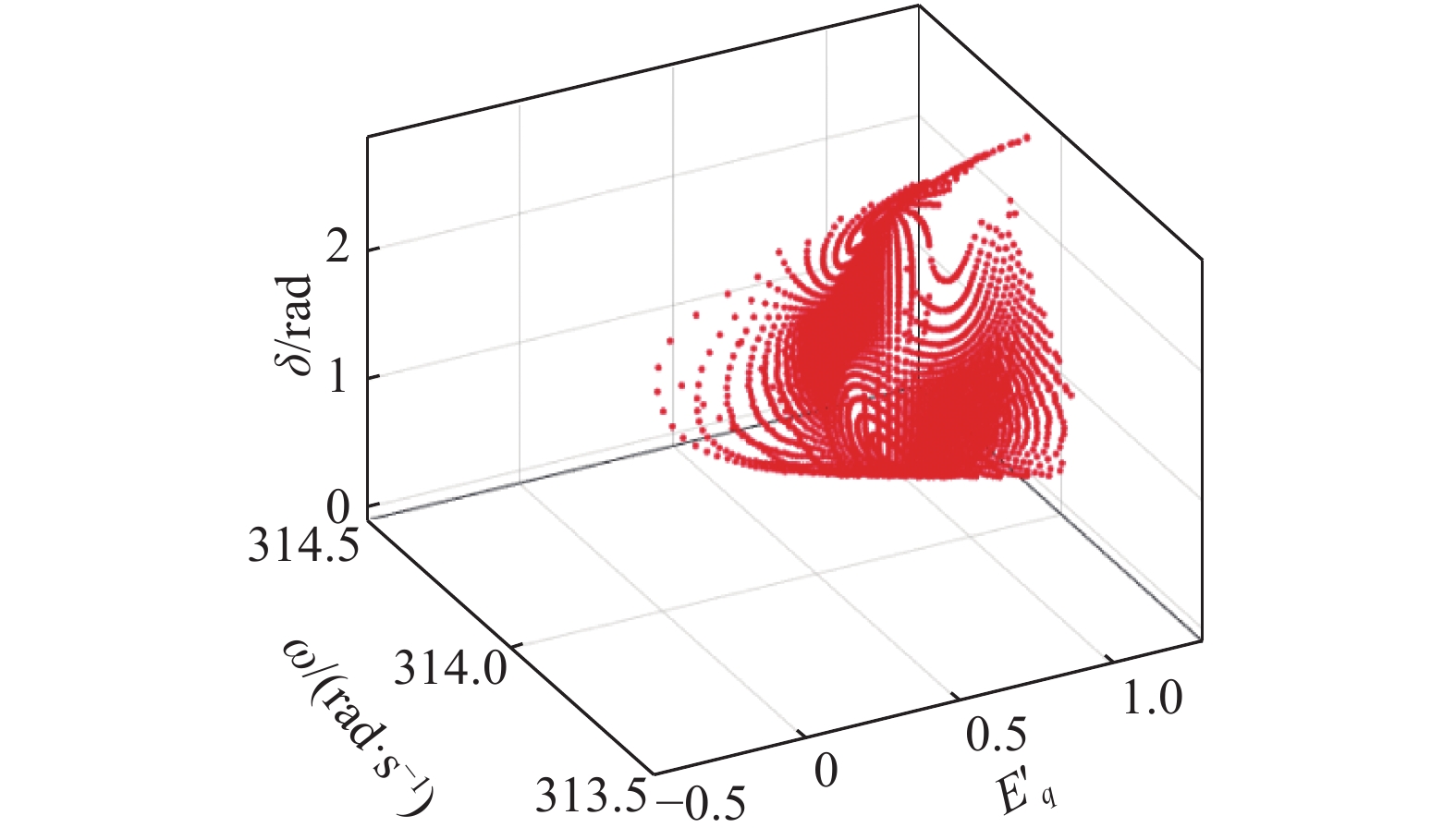
利用蒙特卡洛方法计算三阶单机无穷大系统的稳定域，主要步骤如下. 首先求解系统（13）的微分方程，得到系统的稳定平衡点；然后在该电力系统所确定的状态空间附近，大量取初始点，并在初始点处对系统进行正向数值积分求解轨线；最后将解轨线能够收敛于稳定平衡点的初始点保存下来，利用蒙特卡洛方法所确定的稳定域是由这些初始点围成的空间组成. 蒙特卡洛方法作为一种较成熟的方法，十分便于计算机实现. 在求解轨线过程中，初始点取得越多，得到的稳定域精度越高，但初始点取得过多，会导致计算机运算时间过长. 在计算中，将初始点数控制为 $50 \times 50 \times 50$ 个点，利用蒙特卡洛方法所确定的稳定域如图4所示.

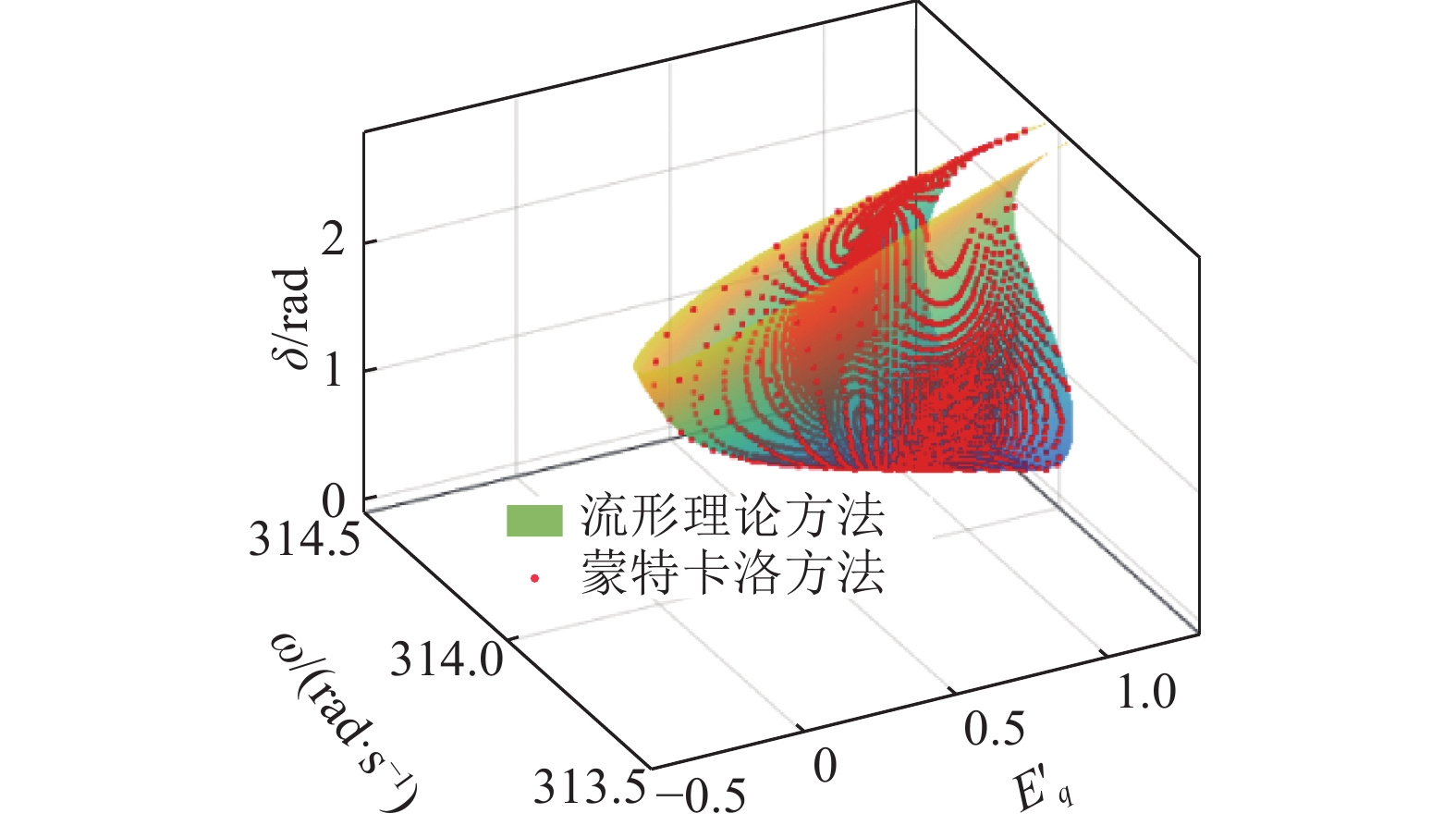
将蒙特卡罗法与流形方法所确定的稳定域进行对比，对比图如图5所示.

从图5可以看出，利用流形方法确定的稳定域能够与蒙特卡洛方法确定的稳定域完全吻合，从而验证了流形方法确定稳域的有效性，具有较高的精度.

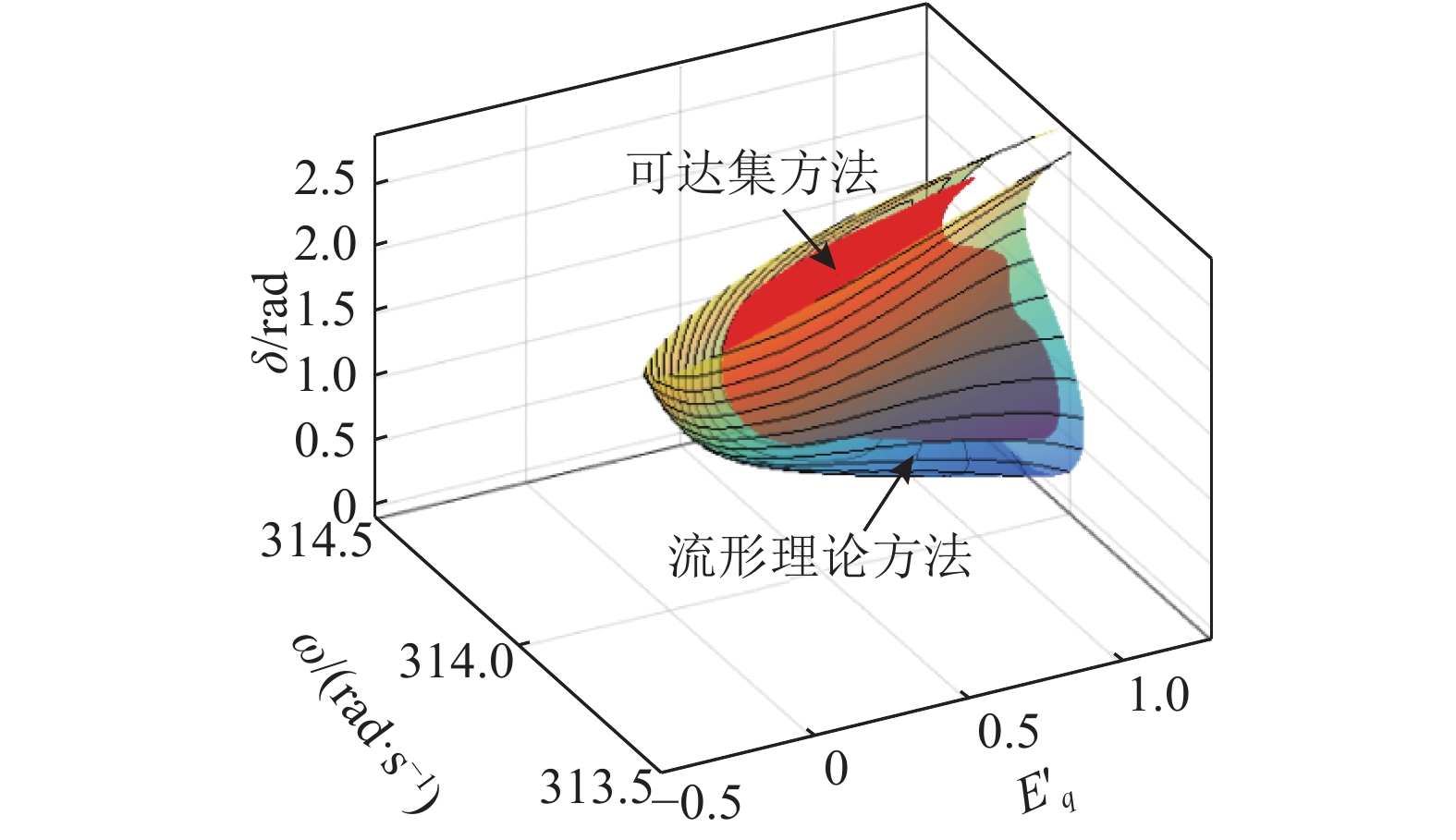
3.4 利用可达集理论计算三阶无穷大系统稳定域

2章对如何求非线性系统的可达集进行了较详细的介绍，主要过程如下. 首先在系统（13）的状态空间中，找到一个较小的稳定初始区域作为目标集；然后对目标集进行逆时间求解，得到可达集；最后将求得的可达集，作为电力系统的稳定域. 利用流形理论与可达集方法确定稳定域的对比图如图6所示.

图6中，内侧曲面表示基于可达集方法确定的三阶单机无穷大系统的稳定域. 可以看出，与流形理论方法相比，基于可达集理论计算得到的单机无穷大系统的稳定域保守性较强.

4 仿真分析

分别基于流形理论、蒙特卡洛方法、可达集方法，确定电力系统中的三阶单机无穷大系统的稳定域. 经过实验仿真，证明了利用这3种方法都能够很好地实现非线性系统的稳定域确定. 仿真环境在Intel (R) Core (TM) i7-4790 处理器下开展，其中流形理论算法中选择的圆弧向外增长长度（步长）为0.01，向外扩展圈数为10圈. 蒙特卡洛方法作为对所提算法的有效性验证方法，在满足精度要求的前提下，将初始点数控制在 $ 50 \times 50 \times$ $ 50$ . 可达集方法计算稳定域已在文献[11]中有所体现，因此将文献[11]的方法与本文算法进行对比分析. 可达集方法的特点是网格点取得越密，相对精度越高，但是取得过密，所消耗时间更长. 本文参照文献[11]的网格点数目，计算三阶单机无穷大系统的稳定域，并将可达集方法与流形理论方法所确定的稳定域进行对比. 算法对比如表2所示.

从表2可以看出，基于流形理论方法确定稳定域，相较蒙特卡洛方法与可达集方法，在仿真时间上具有明显优势. 流形理论不仅能够实现稳定域的快速确定，而且具有较高的精度. 相较于传统方法，本文基于流形理论提出的稳定域确定方法在精度和响应时间上都有了较大的提升.

5 结　论

（1）利用流形方法能够精确地构造电力系统的稳定域，改善了传统方法构造稳定域保守性较强的缺点；该方法与蒙特卡洛方法及可达集方法相比，具有耗时短的优点，为实现电力系统安全稳定分析打下基础.

（2）基于可达集方法在一定程度上虽然能够精确地确定稳定域，但该方法主要受限于初始网格点数，网格点数取得越密，精度越高，但是会导致较长的耗时，因此在一定程度上限制了可达集方法在控制领域的应用前景，对该方法进行改良是实验室下一步的研究目标.

（3）流形方法相较于传统方法和可达集方法，更加适用于电力系统的稳定域确定，在电力系统的安全性分析及控制领域具有更广的应用前景.