径向磁轴承是一种利用磁力使转子悬浮的新型支承技术,具有无机械接触、无磨损、无需润滑、寿命长等优点,在柔性转子、飞轮储能、涡轮机械、航空航天、医疗设备等领域得到了广泛的关注和应用[1-3]. 根据磁极配置方式的不同,径向磁轴承通常可以分为异极型和同极型2种类型[1]. 与后者相比,异极型径向磁轴承(HeRMB)轴向长度短、结构简单、造价便宜、易于制造安装,应用更成熟[4].
精确的电磁模型是磁轴承设计和优化的关键. 目前,已有的建模方法主要包括有限元法和解析法. Matsuzaki等[5-7]采用有限元法,分析各类磁轴承. 有限元法应用成熟,具有精度高、非线性计算能力强的特点,但是存在建模复杂、计算时间过长等问题,所以在磁轴承设计的初始阶段,往往会采用解析法. Liu等[8-11]采用等效磁路法,对各类磁轴承进行建模、设计优化和分析. 等效磁路法是一种实现简单、计算快速的解析法,能够得到磁轴承结构参数和电磁性能之间的明确物理关系,但是等效磁路法的计算精度相对较低,无法得到气隙磁通密度分布情况. Pichot等[12-13]的研究表明,通过分析磁轴承的气隙磁通密度分布可以定性地预测分析转子铁耗,方便设计方案的选择和优化. Wang等[14]采用子域法,对一台永磁偏置径向磁轴承进行建模和分析. 子域法是一种高精度的解析法[15],但没有考虑铁磁材料的饱和效应. 饱和效应对磁轴承的最大静承载力和动态响应有很大的影响[16-17].
针对上述解析法中的不足,本文提出结合等效磁路法和气隙磁导函数的非线性解析模型,计算HeRMB的气隙磁通密度分布和电磁力等性能. 通过计算磁轴承磁路各部分,包括定、转子铁芯的集中磁导,建立计及饱和效应的等效磁路,得到的非线性方程采用牛顿法计算. 利用考虑齿槽效应和转子偏心的气隙磁导函数计算得到气隙磁通密度,进而计算出作用在转子上的电磁力;利用有限元法,验证了该解析模型的计算精度. 利用建立的解析模型,研究偏置电流对HeRMB性能的影响和x、y 2个方向之间的耦合效应.
1 非线性解析模型HeRMB的结构如图1所示. 图中,ri和rr分别是转子的内外半径,rs和ro分别是定子内外半径,ry是定子轭部的内半径,k为定子磁极的编号,θs和θτ分别是槽宽和槽距对应的弧度. HeRMB主要包括转子、定子和线圈,在线圈中通有偏置电流和控制电流,分别产生偏置磁通和控制磁通,在气隙中得到合成磁场. 通过施加合适的控制电流来调整气隙磁场,产生所需的电磁力支撑转子悬浮. 以y方向为例,图1中带箭头的虚线为偏置磁通,带箭头的实线为y方向的控制磁通,两者在转子上方的气隙中方向相同、相互叠加,在转子下方的气隙中方向相反、相互抵消,从而产生y方向的电磁力作用在转子上.
|
图 1 HeRMB的结构和尺寸标注 Fig. 1 Structure and dimensions of HeRMB |
为了计算气隙磁通密度和电磁力,首先建立计及饱和效应的等效磁路,计算得到气隙中通过的磁通. 然后根据得到的磁通,采用考虑齿槽效应和转子偏心的气隙磁导函数计算得到气隙磁通密度,进而计算出电磁力. 一般HeRMB的定转子铁芯采用硅钢片叠压而成[1],故不考虑涡流的影响. 先将HeRMB的转子、定子齿部、定子轭部和气隙分别分成Np份,其中Np为磁极个数,计算每一部分的等效磁导,建立考虑铁磁材料非线性的等效磁路,如图2(a)所示. 图2(b)给出覆盖2个极的等效磁路局部,显示了等效磁路与轴承结构之间的对应关系.

|
图 2 HeRMB的等效磁路 Fig. 2 Equivalent magnetic circuit of HeRMB |
图2中,N为线圈匝数,Ik为施加在磁极k的线圈上的电流,Λsyk、Λstk、Λrk和Λgk分别为第k份定子轭部、定子齿部、转子和气隙所对应的等效磁导. 各个等效磁导的表达式[18]如下:
| ${\varLambda _{{\rm{sy}}k}} = 1\left/\left[ { \displaystyle\frac{{{\theta _{\rm{s}}}}}{{{\mu _{\rm{r}}}({H_{{\rm{sy}}k}}){\mu _0}l\ln \;({r_{\rm{o}}}/{r_{\rm{y}}})}} + \frac{\text{π}}{{2{\mu _{\rm{r}}}({H_{{\rm{sy}}k}}){\mu _0}l}}} \right]\right.,$ | (1) |
| ${\varLambda _{{\rm{st}}k}} = ({\theta _{\rm{\tau }}} - {\theta _{\rm{s}}})l{\mu _{\rm{r}}}({H_{{\rm{st}}k}}){\mu _0}/\ln\; ({r_{\rm{y}}}/{r_{\rm{s}}}),$ | (2) |
| ${\varLambda _{{\rm{r}}k}} = 1\left/\left[ { \displaystyle\frac{{{\theta _{\rm{s}}}}}{{{\mu _{\rm{r}}}({H_{{\rm{r}}k}}){\mu _0}l\ln\; ({r_{\rm{r}}}/{r_{\rm{i}}})}} + \frac{\text{π}}{{2{\mu _{\rm{r}}}({H_{{\rm{r}}k}}){\mu _0}l}}} \right]\right.,$ | (3) |
| $\begin{split} {\varLambda _{{\rm{g}}k}} =& \frac{{4{\mu _0}l}}{\pi }\ln\left(\frac{{g\left(\left(k - 0.5\right){\theta _{\rm{\tau }}}\right) + \pi {r_{\rm{s}}}{\theta _{\rm{s}}}/4}}{{g((k - 0.5){\theta _{\rm{\tau }}})}}\right) + \\ & {\rm{ }}\frac{{{\mu _0}\left({\theta _{\rm{\tau }}} - {\theta _{\rm{s}}}\right){r_{\rm{s}}}l}}{{g\left(\left(k - 0.5\right){\theta _{\rm{\tau }}}\right)}}. \end{split} $ | (4) |
式中:k = 1, 2, ···, Np,l为轴承轴向长度,μ0为真空的磁导率,μr(H)为铁芯的相对磁导率,Hsyk、Hstk和Hrk分别为第k份定子轭部、定子齿部、转子的磁场强度,g(θ)为等效气隙长度. 考虑转子偏心[14],则
| $g(\theta ) = {g_0} - \varepsilon \cos \;(\theta - \alpha ).$ | (5) |
式中:ε和α为转子偏心的距离和角度. 转子在X和Y方向的位移为
| $x = \varepsilon \cos \alpha ,$ | (6) |
| $y = \varepsilon \sin \alpha .$ | (7) |
对磁路中的节点和支路进行编号,共有m = 3Np 个节点和n = 4Np个支路. 根据基尔霍夫定律,可得
| ${{A\varPhi }} = {\bf 0}.$ | (8) |
式中:
| ${{\varPhi}} ={{ \varLambda (}}{{{A}}^{\rm{T}}}{{V + U)}}.$ | (9) |
式中:Λ为支路磁导对角矩阵,Λ = diag [Λ1, Λ2, ···, Λn];V为节点磁势向量,V = [Vi]m×1;U为支路磁源磁动势向量,U = [uj]n×1.
将式(9)代入式(8),可得磁路节点磁位的非线性方程:
| ${{A\varLambda }}{{{A}}^{\rm{T}}}{{V + A\varLambda U}} = {\bf{0}}.$ | (10) |
采用牛顿法进行迭代求解. 在每步迭代中,计算定子轭部、定子齿部、转子的磁场强度Hsyk、Hstk和Hrk. 通过所使用的硅钢叠片材料DW250-35的B-H曲线,求得各对应铁芯部分在当前饱和程度下的磁导率,对支路磁导矩阵进行更新. 在迭代过程收敛结束后,通过式(9)计算得到支路磁通向量Φ.
计及齿槽效应的气隙磁导函数[19]为
| ${\varLambda _{\rm{g}}}(\theta ) = {\mu _0}/g'(\theta ).$ | (11) |
式中:
| $\begin{array}{l} g'(\theta ) = \\ \left\{ \begin{array}{l} g(\theta ),\;\;\;\;\;\;\;\;(k - 1){\theta _{\rm{\tau }}} + {\theta _{\rm{s}}}/2 \leqslant \theta \leqslant k{\theta _{\rm{\tau }}} - {\theta _{\rm{s}}}/2;\\ g(\theta ) + \displaystyle\frac{{{\text{π}} {r_{\rm{s}}}}}{2}\left[ {\displaystyle\frac{{{\theta _{\rm{s}}}}}{2} - \left| {\theta - (k - 1){\theta _{\rm{\tau }}}} \right|} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(k - 1){\theta _{\rm{\tau }}} - {\theta _{\rm{s}}}/2 \leqslant \theta \leqslant (k - 1){\theta _{\rm{\tau }}} + {\theta _{\rm{s}}}/2. \end{array} \right. \end{array}$ | (12) |
气隙磁导函数Λg(θ)与等效磁路计算得到的Φ相结合,得到异极型径向磁轴承的径向气隙磁通密度分布:
| $B(\theta ) = {\varPhi _{{\rm{g}}k}}{\varLambda _{\rm{g}}}(\theta )/{\varLambda _{{\rm{g}}k}}.$ | (13) |
式中:Φgk为通过第k段气隙的磁通,在支路磁通向量Φ中得到. 在沿转子表面整个圆周径向气隙磁通密度的基础上,根据Maxwell张量法,忽略切向电磁力分布对总电磁力的贡献,通过积分计算得到作用在转子上x、y方向总的电磁力:
| ${F_{x}} = \int_0^{2{\text{π}}} {\left[ {\left.{r_{\rm{s}}}l{B^2}(\theta )\cos\theta \right/(2{\mu _0})} \right]{\rm{d}}\theta } ,$ | (14) |
| ${F_{y}} = \int_0^{2{\text{π}} } {\left[ {\left.{r_{\rm{s}}}l{B^2}(\theta )\sin \theta \right/(2{\mu _0})} \right]{\rm{d}}\theta } .$ | (15) |
为了讨论方便,以立式的磁轴承系统作为分析对象,不考虑重力. HeRMB采用差分控制模式,即同一方向的线圈通入的控制电流相等,产生的控制磁通与偏置电流产生的偏置磁通在一侧气隙中叠加而在另一侧气隙中相减,从而生成该方向上的电磁力. 在该模式下,可以将电磁力在工作点附近关于控制电流和转子位移进行线性化[1]:
| ${F_{x}} = {k_{x{\rm{s}}}}x + {k_{x{\rm{i}}}}{I_{x{\rm{c}}}},$ | (16) |
| ${F_{y}} = {k_{y{\rm{s}}}}y + {k_{y{\rm{i}}}}{I_{y{\rm{c}}}}.$ | (17) |
式中:Ixc、Iyc分别为x、y方向上的控制电流,kxs、kxi分别为x方向的位移刚度和电流刚度,kys、kyi分别为y方向的位移刚度和电流刚度.
2 有限元验证为了验证所提出的解析模型的计算精度,分别采用该解析模型与有限元法,分析一台8极HeRMB. 该轴承的主要参数如表1所示. 表中,Ib为偏置电流. 在差分控制模式下,施加在各个线圈上的电流Ik为
| 表 1 8极HeRMB的主要参数 Table 1 Main parameters of 8-pole HeRMB |
| $ - {I_1} = {I_8} = {I_{\rm{b}}} - {I_{x{\rm{c}}}}{\rm{ }}{I_4} = - {I_5} = {I_{\rm{b}}} + {I_{x{\rm{c}}}};$ | (18) |
| ${I_2} = - {I_3} = {I_{\rm{b}}} - {I_{y{\rm{c}}}},{\rm{ }}{I_6} = - {I_7} = {I_{\rm{b}}} + {I_{y{\rm{c}}}}.$ | (19) |
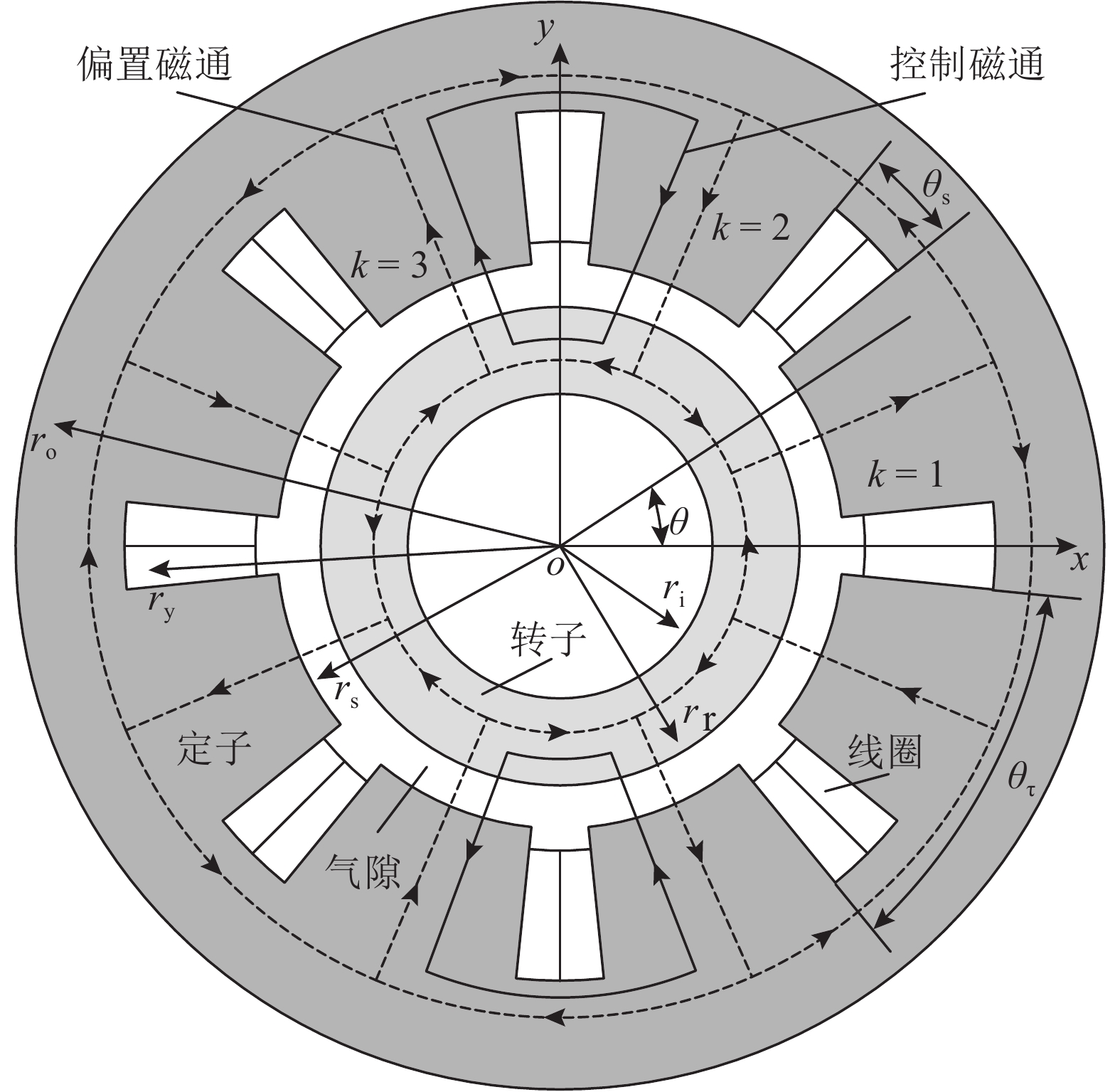
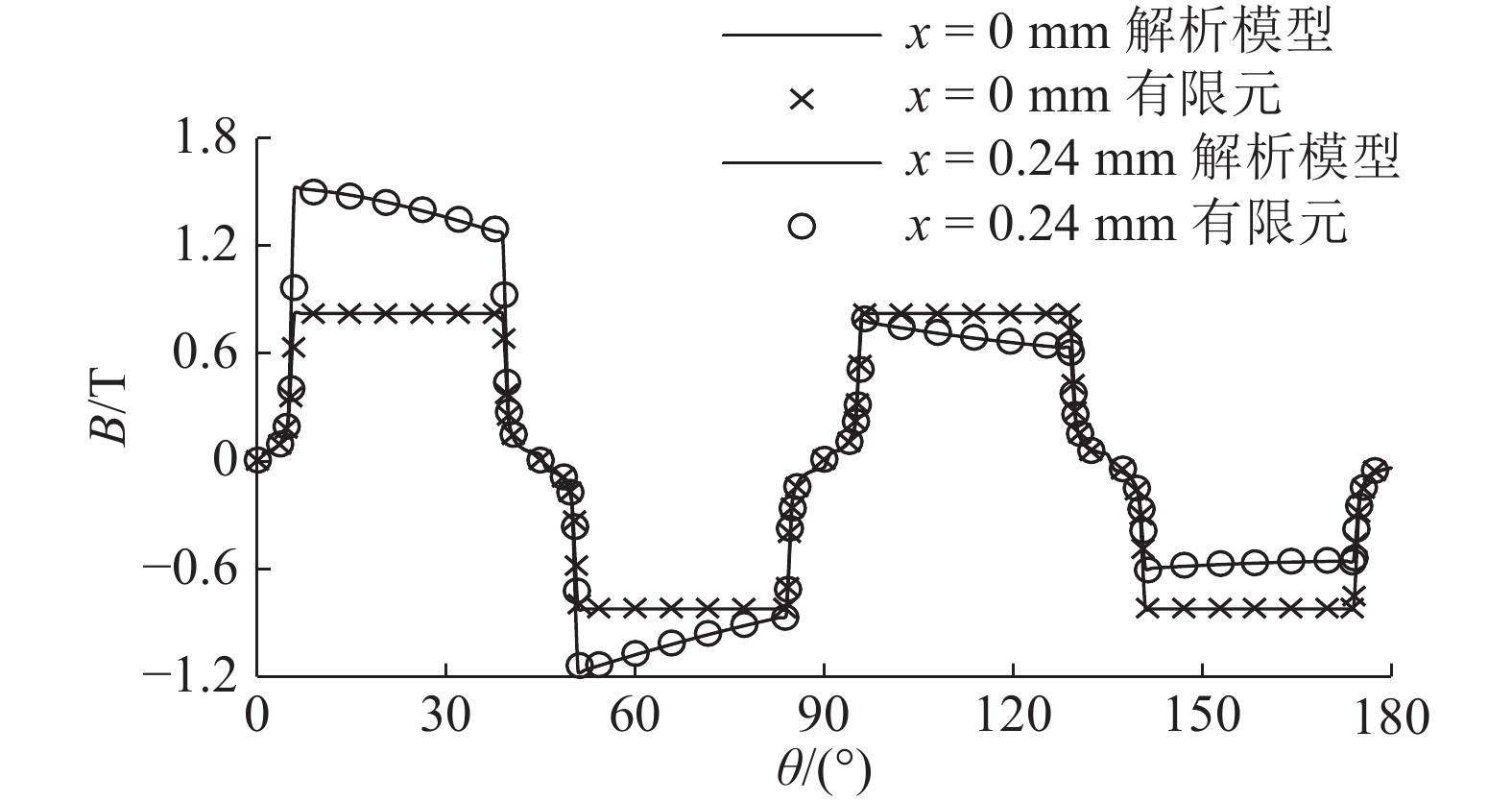
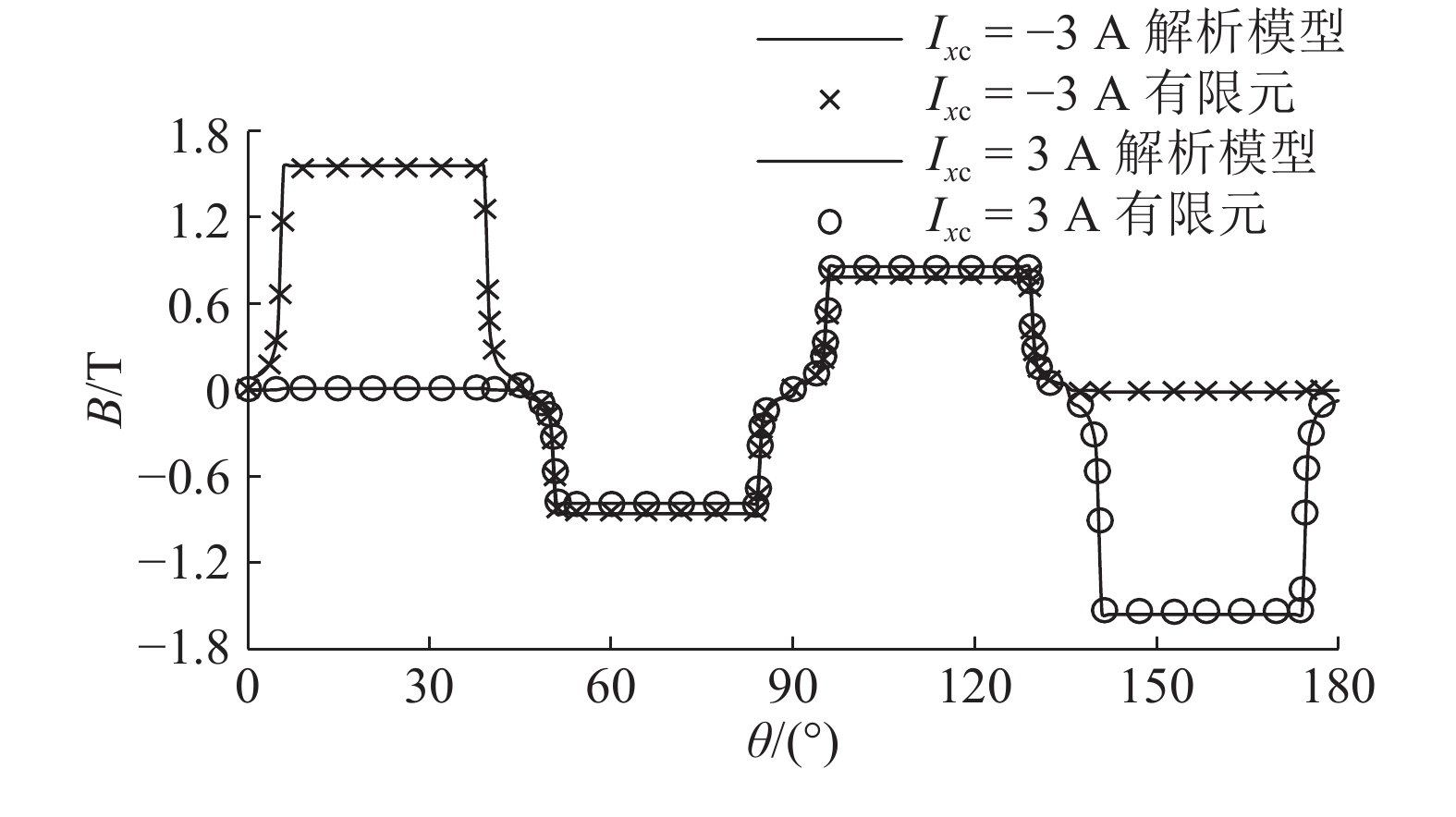
8极HeRMB的有限元模型如图3所示,总的剖分的单元数为15 438,气隙单元最大边长为0.3 mm. 采用解析模型与有限元法,计算得到不同控制电流和位移情况下的径向气隙磁通密度分布,如图4~6所示. 因为HeRMB结构对称,只给出半个气隙的径向磁通密度分布情况,以便于查看分析.

|
图 3 8极HeRMB的有限元模型 Fig. 3 FEM model of 8-pole HeRMB |
|
图 4 无控制电流时不同x方向位移下的径向气隙磁通密度分布 Fig. 4 Radial air gap flux density distribution with different x direction displacement when control current is 0 A |
|
图 5 无位移时不同x方向控制电流下的径向气隙磁通密度分布 Fig. 5 Radial air gap flux density distribution with different x direction control current when displacement is 0 mm |
|
图 6 x方向位移为0.24 mm时不同x方向控制电流下的径向气隙磁通密度分布 Fig. 6 Radial air gap flux density distribution with different x direction control current when x direction displacement is 0.24 mm |
对比不同情况下的磁通密度分布情况可知:当转子没有位移时,一个极下的气隙磁场是均匀分布的;当转子产生位移时,气隙磁场会出现畸变,产生不平衡力. 此时需要施加合适的控制电流以调整气隙磁场,产生所需的电磁力,使转子悬浮在工作位置. 图5中,当施加在线圈上的总电流达到6 A时,最大的气隙磁通密度超过1.5 T,表明铁磁材料达到了饱和区域. 由图4~6可知,解析模型与有限元法的计算结果一致,表明利用提出的解析模型,能够准确计算不同工作状态下HeRMB的径向气隙磁通密度的分布情况. 转子铁耗和气隙磁通密度分布的大小与形状相关,根据气隙磁通密度分布,可以对转子铁耗进行定性的分析比较,从而在设计优化时起到指导作用[12-13].
利用2种方法得到的电磁力和控制电流及转子位移的关系,如图7、8所示. 在全工况范围内,利用解析模型和有限元法所得的结果一致. 当转子没有位移时,磁轴承气隙均匀,且铁磁材料工作在线性区域,所以电磁力与控制电流呈线性关系. 当转子位移较大时,磁轴承气隙不均匀,铁芯饱和,导致电磁力与控制电流呈非线性关系. 电磁力与转子位移的关系整体呈非线性,但在位移较小时近似为线性. 当正常工作时,磁轴承转子位移很小,所以电磁力-控制电流和电磁力-位移关系可以按式(16)、(17)在工作点线性化以方便控制,得到的电流刚度和位移刚度如表2所示. 与有限元结果相比,利用解析模型计算得到的位移刚度误差为4.4%,电流刚度的误差为1.7%,验证了该模型的准确性.
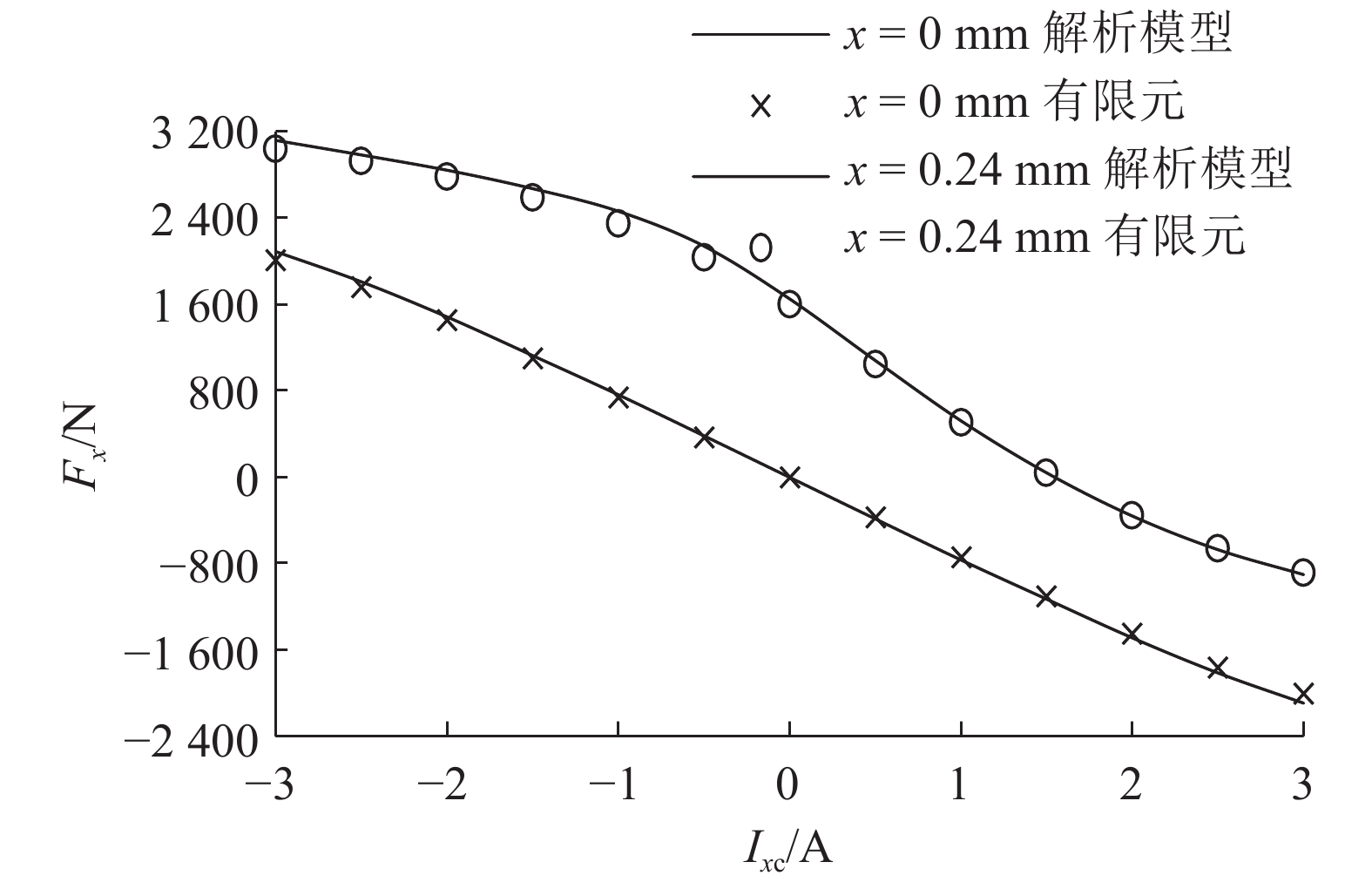
|
图 7 电磁力和控制电流的变化关系 Fig. 7 Variation of electromagnetic force with control current |
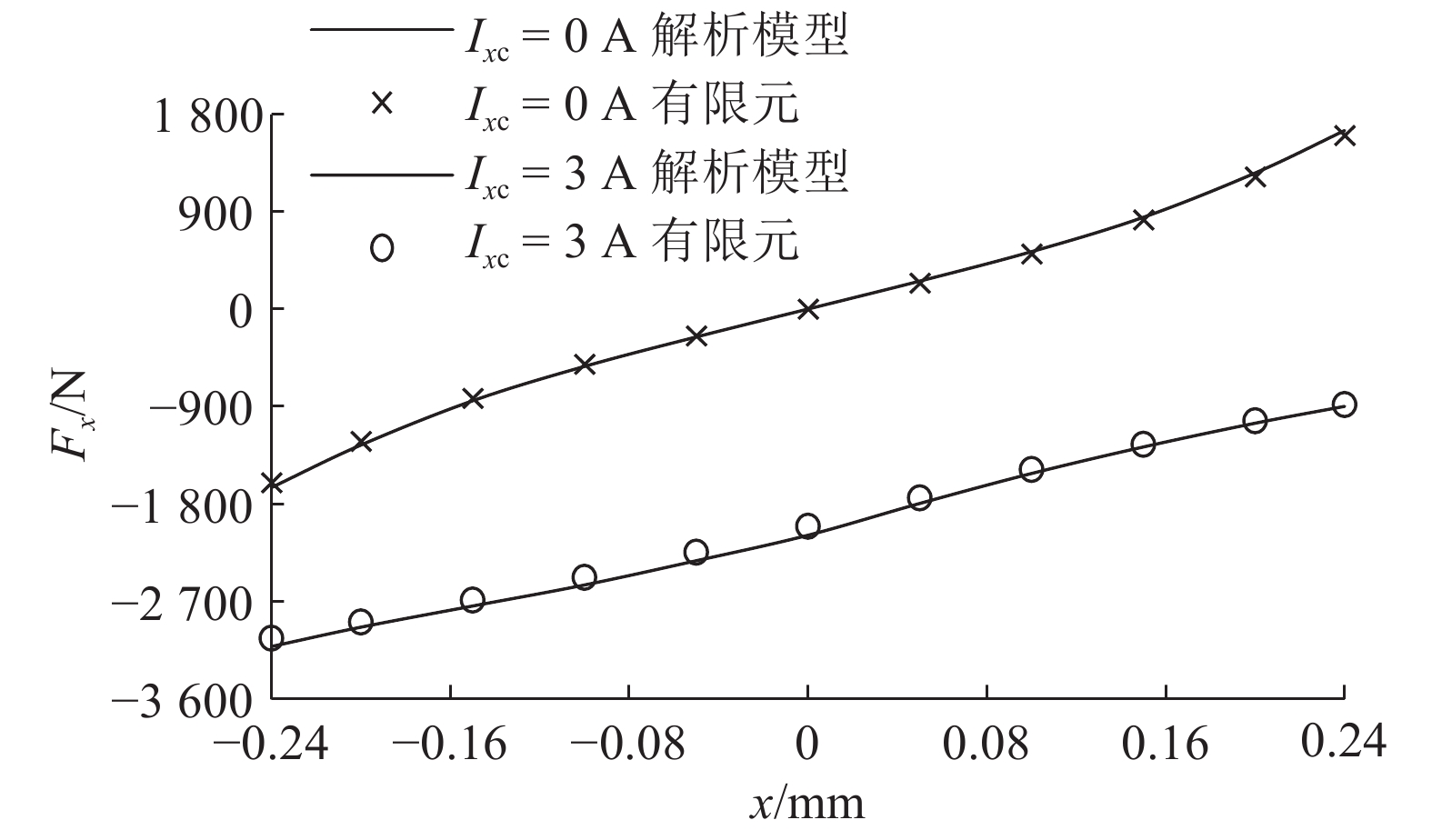
|
图 8 电磁力和位移的变化关系 Fig. 8 Variation of electromagnetic force with displacement |
| 表 2 8极HeRMB的电流刚度和位移刚度 Table 2 Current and displacement stiffnesses of 8-pole HeRMB |
在HeRMB设计过程中,偏置电流是很重要的参数. 为了研究偏置电流的选择规律,利用建立的解析模型,分析偏置电流对电磁力特性的影响.
偏置电流对电磁力-控制电流关系和电磁力-位移关系的影响如图9所示. 电磁力关于控制电流和位移的变化特性是对称的,为了易于观察,图9只给出电磁力为正数的曲线部分. 图9(a)中,在不同的偏置电流下,都保证控制电流不大于偏置电流. 随着偏置电流的增大,相同控制电流下的电磁力随之增大;当偏置电流超过5 A时,因铁磁材料的饱和效应,电磁力减小. 偏置电流对电磁力-位移关系的影响如图9(b)所示,随着偏置电流的增大,相同位移下的电磁力随之增大;当偏置电流超过5 A时,电磁力减小. 当对磁轴承进行控制时,过大的位移刚度会导致系统不稳定[20]. 电磁力-控制电流关系的线性度随着偏置电流的增大而降低. 当确定偏置电流时,需要综合考虑轴承的承载力和控制特性的稳定性及线性度,一般选择饱和电流的一半左右. 以本文为例,该轴承的饱和电流约为5 A,偏置电流为3 A,稍大于饱和电流的一半,既满足控制特性的稳定性及线性度,也提高了轴承的承载力,所以是合理的.

|
图 9 偏置电流对电磁力特性的影响 Fig. 9 Influence of bias current on force characteristics |
在HeRMB的控制中,一般x、y方向独立控制. 若2个方向之间存在耦合,则会影响控制的效果. 采用建立的解析模型,研究x、y方向之间的耦合效应. 图10给出y方向控制电流对x方向电磁力-控制电流关系的影响. 图10(a)中,转子无偏心,y方向控制电流对x方向的电磁力没有影响,2个方向是解耦的. 一般情况下,转子都会工作在中心点附近很小的范围内,偏心很小,因此可以不考虑耦合. 采用式(16)、(17)所示的线性解耦模型和表2的刚度系数,对HeRMB进行控制. 若转子受到很大干扰,出现较大偏心的情况(x = y = 0.24 mm),则x、y方向之间会存在耦合,如图10(b)所示. 通过建立的非线性解析模型,可以计算出全工况下的电磁力;在设计控制策略时,考虑偏移较大情况下会出现的耦合影响. 以x = y = 0.24 mm时为例,利用所建立的模型计算得到电磁力,在该偏心位置进行线性化,得到受y方向控制电流影响的x方向电磁力:
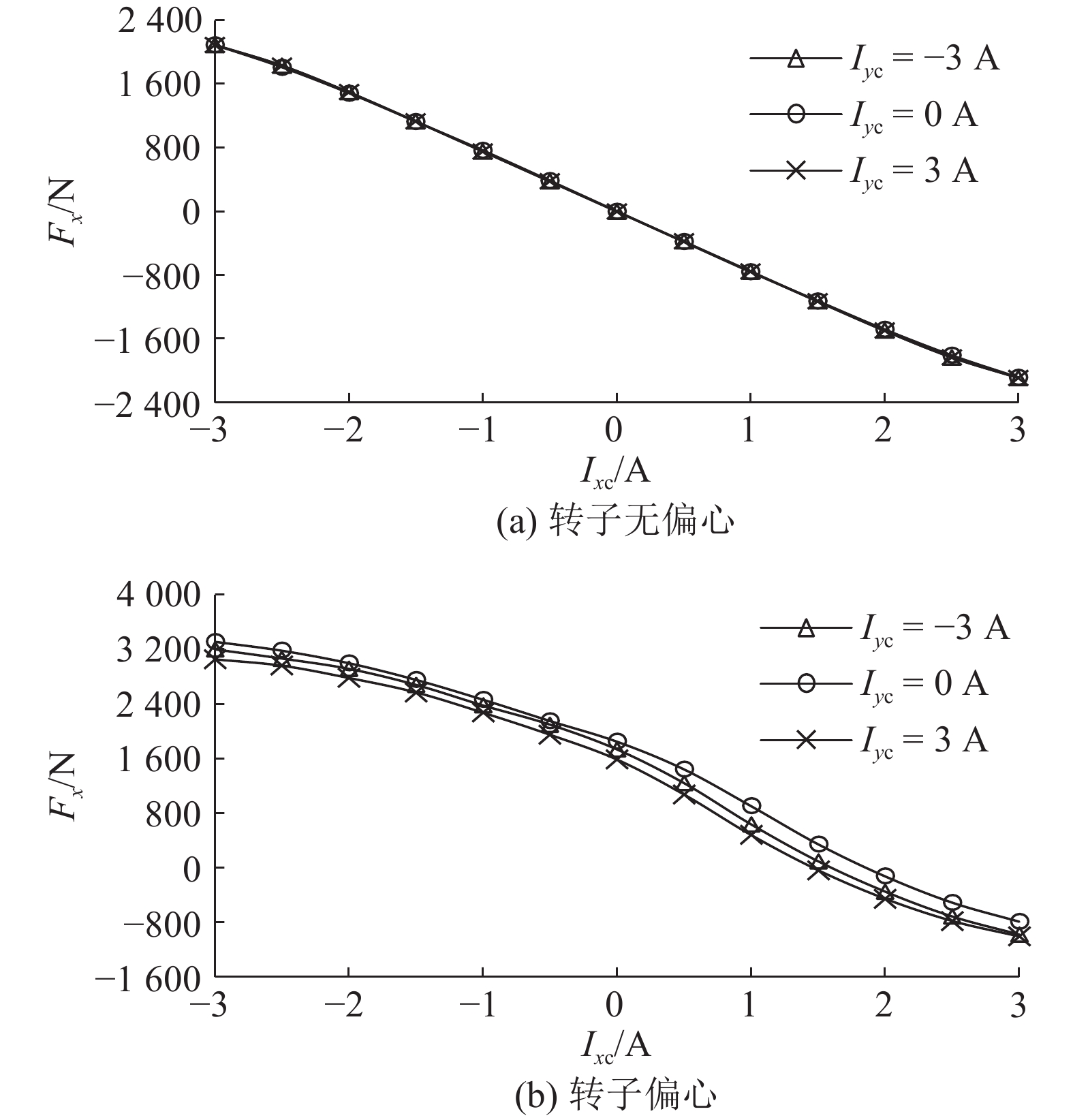
|
图 10 y方向控制电流对x方向电磁力-控制电流关系的影响 Fig. 10 Influence of y direction control current on relationship between x direction electromagnetic force and control current |
| $\begin{split} {F_{x}}\left| {_{x = y = 0.24{\rm{mm}}}} \right. =& 9\;824.5(x - 0.24) + \left( - 9.2I_{y{\rm{c}}}^2 - 2.9{I_{y{\rm{c}}}} -\right. \\ &\Big. 830.1\Big){I_{x{\rm{c}}}} + \left( - 23.9I_{y{\rm{c}}}^2 - 25.3{I_{y{\rm{c}}}} + 1\;820.9\right). \end{split} $ | (20) |
y方向的电磁力同理.
4 结 论(1)利用提出的非线性解析模型,可以准确计算HeRMB的气隙磁通密度分布和电磁力等电磁性能,为该类磁轴承的分析、设计和优化提供了支持.
(2)该解析模型结合了等效磁路法和气隙磁导函数. 利用等效磁路法,可以计算铁磁材料的饱和效应;气隙磁导函数能够考虑定子齿槽效应和转子偏心,计算出气隙磁通密度分布情况. 这一思想可以运用在其他类型磁轴承的建模分析上.
(3)偏置电流对HeRMB的电磁力特性有明显的影响. 随着偏置电流的增加,相同控制电流下的电磁力和相同位移下的电磁力都随之增大;当偏置电流超过饱和电流时,电磁力会减小. 综合考虑轴承的承载力和控制特性的稳定性及线性度,偏置电流一般选择饱和电流的一半左右.
(4)当转子无偏心时,x、y 2个方向是解耦的. 当转子有偏心时,2个方向之间会存在耦合. 利用建立的非线性解析模型,可得到全工况下的电磁力,从而在设计控制策略时,将耦合情况考虑进去.
| [1] |
SCHWEITZER G, MASLEN E H. Magnetic bearings: theory, design, and application to rotation machinery [M]. Berlin, Germany: Springer, 2009: 82–84.
|
| [2] |
蒋科坚, 祝长生. 电磁轴承-柔性转子系统多目标加权的主动振动控制[J]. 浙江大学学报: 工学版, 2016, 50(10): 1946-1951. JIANG Ke-jian, ZHU Chang-sheng. Vibration suppressing with mixed weight for multi-targets in active magnetic bearing-flexible rotor system[J]. Journal of Zhejiang University: Engineering Science, 2016, 50(10): 1946-1951. |
| [3] |
袁野, 孙玉坤, 张维煜, 等. 新型飞轮储能备用轴承磁力数值分析[J]. 电机与控制学报, 2016, 20(7): 95-101. YUAN Ye, SUN Yu-kun, ZHANG Wei-yu, et al. Magnetic force numerical analysis of auxiliary bearings in optimized flywheel storage system[J]. Electric Machines and Control, 2016, 20(7): 95-101. |
| [4] |
LE Y, FANG J, WANG K. Design and optimization of a radial magnetic bearing for high-speed motor with flexible rotor[J]. IEEE Transactions on Magnetics, 2015, 51(6): 1-13. |
| [5] |
MATSUZAKI T, TAKEMOTO M, OGASAWARA S, et al. A basic study of a novel homopolar-type magnetic bearing unifying four C-shaped cores for high output and low loss[J]. IEEE Transactions on Magnetics, 2015, 51(11): 1-4. |
| [6] |
朱熀秋, 张仲, 诸德宏, 等. 交直流三自由度混合磁轴承结构与有限元分析[J]. 中国电机工程学报, 2007, 27(12): 77-81. ZHU Huang-qiu, ZHANG Zhong, ZHU De-hong, et al. Structure and finite element analysis of an AC-DC three degrees of freedom hybrid magnetic bearing[J]. Proceedings of the CSEE, 2007, 27(12): 77-81. DOI:10.3321/j.issn:0258-8013.2007.12.014 |
| [7] |
杨志轶, 赵韩, 田杰, 等. 采用有限元法分析径向永磁轴承的力学特性[J]. 合肥工业大学学报: 自然科学版, 2001, 24(4): 477-481. YANG Zhi-yi, ZHAO Han, TIAN Jie, et al. Analysis of mechanical characteristics of radial permanent bearings using finite element method[J]. Journal of Hefei University of Technology: Natural Science, 2001, 24(4): 477-481. |
| [8] |
LIU X, HAN B. The multiobjective optimal design of a two-degree-of-freedom hybrid magnetic bearing[J]. IEEE Transactions on Magnetics, 2014, 50(9): 1-14. |
| [9] |
XU S, SUN J. Decoupling structure for heteropolar permanent magnet biased radial magnetic bearing with subsidiary air-gap[J]. IEEE Transactions on Magnetics, 2014, 50(8): 1-8. |
| [10] |
张云鹏, 刘淑琴, 李红伟, 等. 基于磁路分析的轴向混合磁轴承径向承载力解析计算[J]. 电工技术学报, 2012, 27(5): 137-142. ZHANG Yun-peng, LIU Shu-qin, LI Hong-wei, et al. Calculation of radial electromagnetic force of axial hybrid magnetic bearing based on magnetic circuit analysis[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 137-142. |
| [11] |
王曦, 房建成, 樊亚洪, 等. 轴向力偏转五自由度永磁偏置磁轴承及磁路解耦设计[J]. 中国电机工程学报, 2011, 31(17): 91-98. WANG Xi, FANG Jian-cheng, FAN Ya-hong, et al. Axial force tilting permanent-magnet-biased magnetic bearing with five degrees of freedom and magnetic field decoupling design[J]. Proceedings of the CSEE, 2011, 31(17): 91-98. |
| [12] |
PICHOT M A, DRIGA M D. Loss reduction strategies in design of magnetic bearing actuators for vehicle applications[J]. IEEE Transactions on Magnetics, 2005, 41(1): 492-496. DOI:10.1109/TMAG.2004.839289 |
| [13] |
MATSUZAKI T, TAKEMOTO M, OGASAWARA S, et al. Novel structure of three-axis active-control-type magnetic bearing for reducing rotor iron loss[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-4. |
| [14] |
WANG K, WANG D, SHEN Y, et al. Subdomain method for permanent magnet biased homo-polar radial magnetic bearing[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-5. |
| [15] |
WU L J, ZHU Z Q, STATON D, et al. Comparison of analytical models for predicting electromagnetic performance in surface-mounted permanent magnet machines [C] // Proceedings of IEEE Vehicle Power and Propulsion Conference. Lille: IEEE, 2010: 1–6. https://www.researchgate.net/publication/224224186_Comparison_of_analytical_models_for_predicting_electromagnetic_performance_in_surface-mounted_permanent_magnet_machines
|
| [16] |
MASLEN E H, HERMANN P, SCOTT M, et al. Practical limits to the performance of magnetic bearings: peak force, slew rate, and displacement sensitivity[J]. Journal of Tribology, 1989, 111(2): 331-336. DOI:10.1115/1.3261918 |
| [17] |
KANG K, PALAZZOLO A. Homopolar magnetic bearing saturation effects on rotating machinery vibration[J]. IEEE Transactions on Magnetics, 2012, 48(6): 1984-1994. DOI:10.1109/TMAG.2012.2182776 |
| [18] |
郭凤仪. 电器学[M]. 1版. 北京: 机械工业出版社, 2013.
|
| [19] |
ZHU Z Q, HOWE D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. III. effect of stator slotting[J]. IEEE Transactions on Magnetics, 2002, 29(1): 124-135. |
| [20] |
WU L, WANG D, SU Z, et al. Analytical model of radial permanent magnet biased magnetic bearing with assist poles[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(7): 1-5. |



