2. 天津大学 机构理论与装备设计教育部重点实验室,天津 300072
2. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education, Tianjin University, Tianjin 300072, China
全断面岩石掘进机(full face rock tunnel boring machine,TBM)是集机、电、液、光于一体的高技术大型隧道施工装备,具有施工速度快、施工质量高、利于环保、综合效益高等优点. TBM在隧道施工中经常会遇到岩石强度、硬度、研磨性不一的复合岩层. 众多实践工程表明,复合岩层TBM施工容易引发诸如刀具、刀盘磨损、刀盘变形、刀盘偏置振动过大等一系列问题. 其中刀盘不同部位刀具的磨损程度不同,使得部分滚刀因受力过大而损坏,导致换刀次数增加,不仅会延误施工工期,而且会增加施工成本,造成较大的经济损失. 研究复合岩层地质下TBM刀盘的滚刀布局设计具有重要意义.
目前,国内外学者在滚刀布局及复合地层方面进行大量的研究,取得了许多有价值的研究成果. Liu等[1]以滚刀受力模型为基础,建立整个刀盘的载荷模型,通过滚刀受力与磨损情况的对比,提出分区域、分原则的滚刀布置准则;张照煌等[2]给出螺旋线型布刀模式的应用原理,分析螺旋线的条数和螺旋角对滚刀布局的影响;朱殿华等[3]结合现有螺旋线布刀规律的研究分析,提出变速螺旋线滚刀布局设计方法;Sun等[4-5]以刀盘实际施工的要求作为依据,确立刀具布置的非线性约束方程,分别采取智能算法、协同进化算法,优化刀盘滚刀的布置. Ma等[6]介绍复合地层下TBM掘进时存在的问题及解决办法;刘建琴等[7]研究复合地层下岩石单轴抗压强度、截面圆分层比对刀盘动态掘进载荷的影响及推力-扭矩之间的复杂关系;尹怀秀[8]结合南昌地铁一号线,依据复合地层的地质参数,从刀盘结构、刀具布置、开口率、注入口等因素出发,开展针对复合地层的刀盘设计;程永亮等[9]综合考虑掘进地质条件、刀盘结构参数和掘进参数,建立刀具布置、开口、盘体设计等关键参数计算模型,提出相应的TBM刀盘地质适应性设计方法.
滚刀在刀盘上的位置由滚刀径向位置和周向位置共同确定. 在现有的滚刀布局研究中,大多只考虑滚刀的径向安装位置,很少涉及滚刀的周向布置. 针对TBM在复合岩层掘进过程中,滚刀磨损程度不同、刀盘受力不均、施工效率低下等问题[10-11],没有相应的滚刀布局设计理论方法. 本文提出基于滚刀等磨损速率的极径设计方法和基于刀盘载荷分布均匀的多螺旋线分区域极角设计方法.
1 刀盘载荷及滚刀磨损速率分析 1.1 刀盘载荷分析复合岩层对于TBM来说,表现为沿隧道纵断面或横断面上交替出现软硬不均匀岩层,致使刀盘受力不均,引起冲击振动,严重时将导致刀盘开裂或变形等,给TBM的正常施工造成了严重影响.
通过对TBM隧道横向开挖面地层形式的调查统计可知,大型隧道掘进机主要穿越2类地形组成的复合岩石地层. 假定:断面内复合岩层为二元地层结构. 定义岩石截面圆分层比:
| $\lambda = \frac{{{S_{\rm I}}}}{{{S_{\rm O}}}}.$ | (1) |
式中:
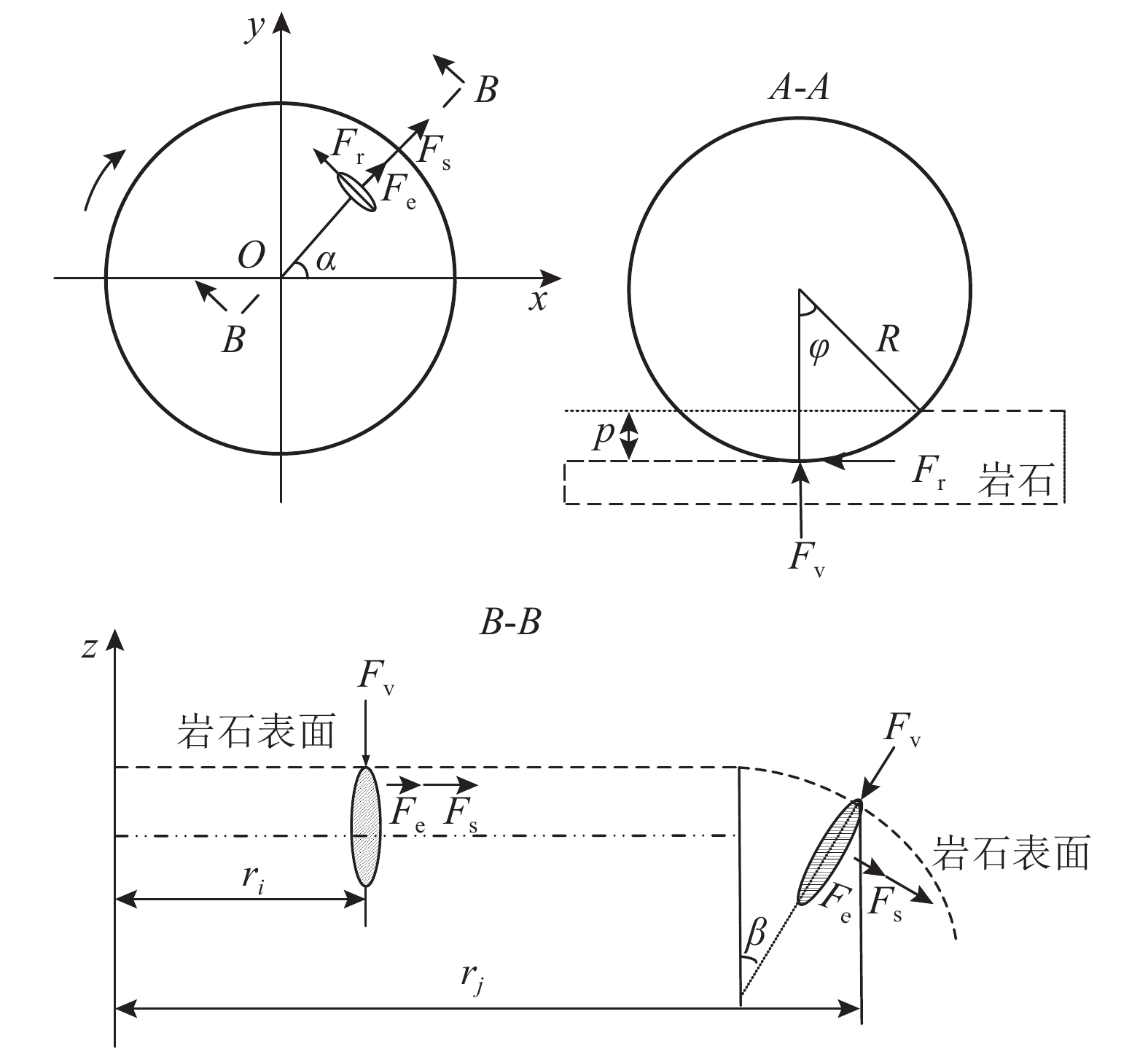
|
图 1 刀盘上滚刀不同位置受力示意图 Fig. 1 Forces of cutters on different positions on cutter-head |
由于TBM掘进复合岩层时受到的各种摩擦阻力、摩擦力矩极其复杂而难以计算. 定义刀盘所受推力为推动刀具破岩所需的合力;刀盘所受扭矩为推动刀具破岩所需的合力矩,即有效推力
| ${F_{{\rm th}}} = \sum\limits_{i = 1}^n {{F_{{\rm v}i}}} \cos \;{\beta _i}{\text{,}}$ | (2) |
| ${T_{{\rm tor}}} = \sum\nolimits_{i = 1}^n {{F_{{\rm r}i}}} {r_i}\cos \;{\beta _i}.$ | (3) |
由作用力与反作用力的关系可知,刀盘掘进过程中受到来自掌子面上不同大小、方位的岩石反作用力,对刀盘产生复合影响. 如图2所示为刀盘径向不平衡力和倾覆力矩示意图. 计算如下:
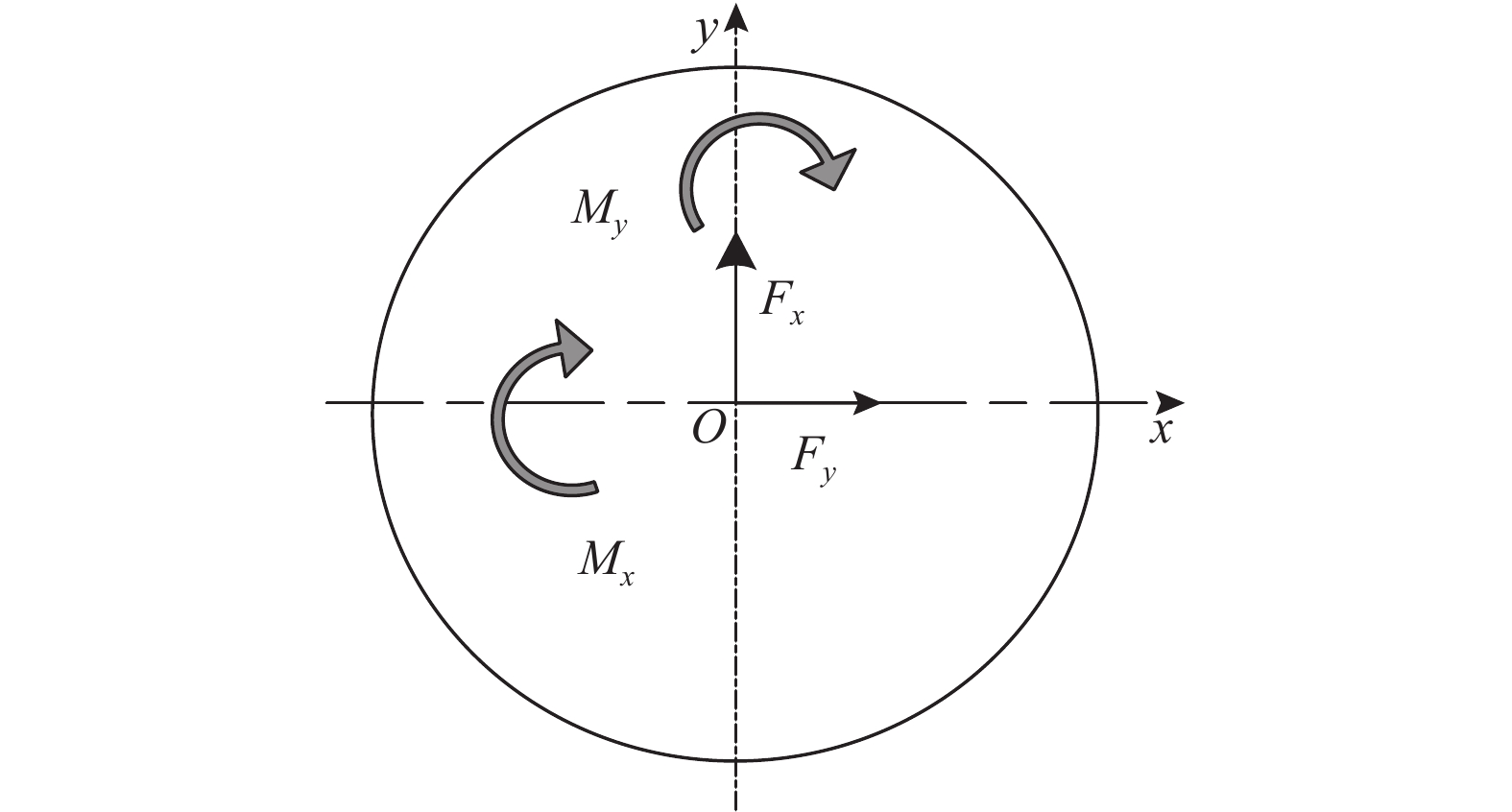
|
图 2 刀盘径向不平衡力和倾覆力矩示意图 Fig. 2 Schematic diagram of radial force and overturning moment on cutter-head |
| $\left. \begin{aligned} & {F_x} = \sum\limits_{i = 1}^n {\left( {{F_{{\rm s}i}}\cos {\alpha _i}\cos \;{\beta _i} + {F_{{\rm e}i}}\cos {\alpha _i}\cos \;{\beta _i} + } \right.} \\ & \qquad \left. {{F_{{\rm r}i}}\sin {\alpha _i} - {F_{{\rm v}i}}\cos \;{\alpha _i}\sin \;{\beta _i}} \right){\text{,}}\\ & {F_y} = \sum\limits_{i = 1}^n {\left( {{F_{{\rm s}i}}\sin {\alpha _i}\cos {\beta _i} + {F_{{\rm e}i}}\sin {\alpha _i}\cos \;{\beta _i} - } \right.} \\ & \qquad \left. {{F_{{\rm r}i}}\cos {\alpha _i} - {F_{{\rm v}i}}\sin {\alpha _i}\sin \;{\beta _i}} \right){\text{,}}\\ & {F_{xy}} = \sqrt {F_x^2 + F_y^2} . \end{aligned} \right\} $ | (4) |
| $\left. \begin{aligned} & {M_x} = \sum\limits_{i = 1}^n {\left( {{F_{{\rm v}i}}{r_i}\sin {\alpha _i}\cos \;{\beta _i} + {M_i}\sin {\alpha _i}\cos \;{\beta _i} + } \right.} \\ & \qquad \left. {{F_{{\rm e}i}}R\sin {\alpha _i}\cos \;{\beta _i} + {F_{{\rm s}i}}{r_i}\sin {\alpha _i}\sin \;{\beta _i}} \right){\text{,}}\\ & {M_y} = \sum\limits_{i = 1}^n {\left( {{F_{{\rm v}i}}{r_i}\cos {\alpha _i}\cos \;{\beta _i} + {M_i}\cos {\alpha _i}\cos \;{\beta _i} + } \right.} \\ & \qquad \left. {{F_{{\rm e}i}}R\cos {\alpha _i}\cos \;{\beta _i} + {F_{{\rm s}i}}{r_i}\cos {\alpha _i}\sin \;{\beta _i}} \right){\text{,}}\\ & {M_{xy}} = \sqrt {M_x^2 + M_y^2} . \end{aligned}\right\} $ | (5) |
式中:
对于某一实际刀盘,刀盘半径、滚刀参数(
| ${F'_{{\rm th}}} = \sum\limits_{i = 1}^j {{F_{{\rm v}i}}_1} \cos\; {\beta _i} + \sum\limits_{i = 1}^{n - j} {{F_{{\rm v}i2}}} \cos \;{\beta _i}{\text{,}}$ | (6) |
| ${T'_{{\rm tor}}} = \sum\limits_{i = 1}^j {{F_{{\rm r}i}}_1} {r_i}\cos \;{\beta _i} + \sum\limits_{i = 1}^{n - j} {{F_{{\rm {\rm r}}i2}}} {r_i}\cos \;{\beta _i}{\text{,}}$ | (7) |
| ${F'_{xy}} = \sqrt {{{({F_{x1}} + {F_{x2}})}^2} + {{({F_{y1}} + {F_{y2}})}^2}} {\text{,}}$ | (8) |
| ${M'_{xy}} = \sqrt {{{({M_{x1}} + {M_{x2}})}^2} + {{({M_{y1}} + {M_{y2}})}^2}} .$ | (9) |
式中:
TBM在复合岩石地层作业时,施工效率低,滚刀磨损程度不同且磨损量极严重;当磨损量超过一定的极值后,必须停机更换新的滚刀,这在增加了施工成本的同时,降低了TBM的利用效率,耽误了工期.
如图3所示为秦岭隧道某区间段TBM开挖推进5 621 m后更换刀具的分类统计图. 图中,Nch为换刀数量. 可以看出,由于正滚刀刀圈磨损而正常更换滚刀的次数高达1 612次,在正滚刀更换总数的1 949把中占了83%. 在复合岩石地层的施工中,正滚刀磨损增加、换刀间期更短是一个必须得重视的问题,在开展复合岩石地层的刀盘设计时,应该更多地考虑滚刀磨损.
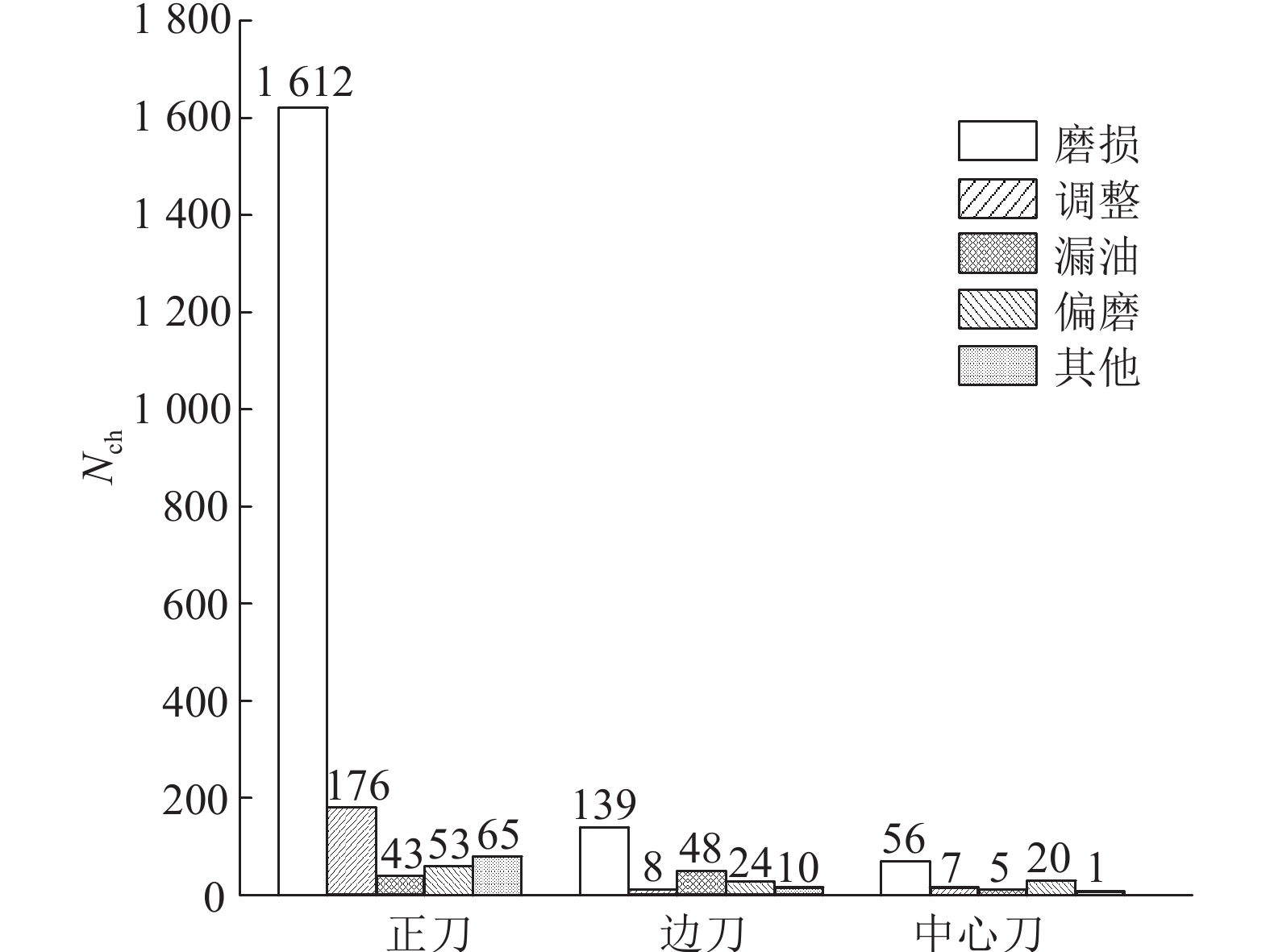
|
图 3 秦岭隧道出口开挖推进5 621 m后换刀分类统计图 Fig. 3 Classification statistics of cutters change after tunneling 5 621 m in Qinling Mountains |
杨延栋等[12]在深入研究滚刀磨损机理后,基于磨粒磨损方程和CSM滚刀破岩力模型,通过函数微分近似计算和数学推导,建立滚刀直接磨损的磨损速率(TBM单位掘进距离滚刀刀圈的径向磨损量)预测模型.
滚刀每转动一圈,刀圈的径向磨损量
| ${X_0} = \frac{{{Q_0}{l_0}}}{{\text{π} {D_0}T}}.$ | (10) |
式中:
| ${Q_0} = {K_{\rm s}}\frac{W}{{{\text{π}} {\sigma _{\rm s}}}} {\text{,}}$ | (11) |
其中,
| $W = 0.8{T^{\frac{5}{6}}}{S^{\frac{1}{3}}}D_0^{\frac{1}{2}}{\sigma _{\rm c}}{h^{\frac{1}{3}}} {\text{;}}$ | (12) |
| ${l_0} = {R_0}\varphi \approx \sqrt {{D_0}h} {\text{,}}$ | (13) |
其中
| ${X_0} = 0.08{K_{\rm s}}\frac{{{S^{{1}/{3}}}{\sigma _{\rm c}}{h^{{1}/{3}}}}}{{{T^{{1}/{6}}}{\sigma _{\rm s}}}}.$ | (14) |
滚刀直接磨损的磨损速率方程为
| $w = \frac{X}{L} = \frac{{{X_0}{R_{\rm i}}/{R_0}}}{h} = 0.16{K_{\rm s}}\frac{{{S^{{1}/{3}}}{\sigma _{\rm c}}{R_{\rm i}}}}{{{T^{{1}/{6}}}{D_0}{\sigma _{\rm s}}{h^{{1}/{6}}}}}.$ | (15) |
式中:
式(15)直观地反映了滚刀磨损速率与滚刀尺寸材料参数(
为了更加简洁、清楚地表达出刀盘上滚刀的具体坐标,分别选取直角坐标
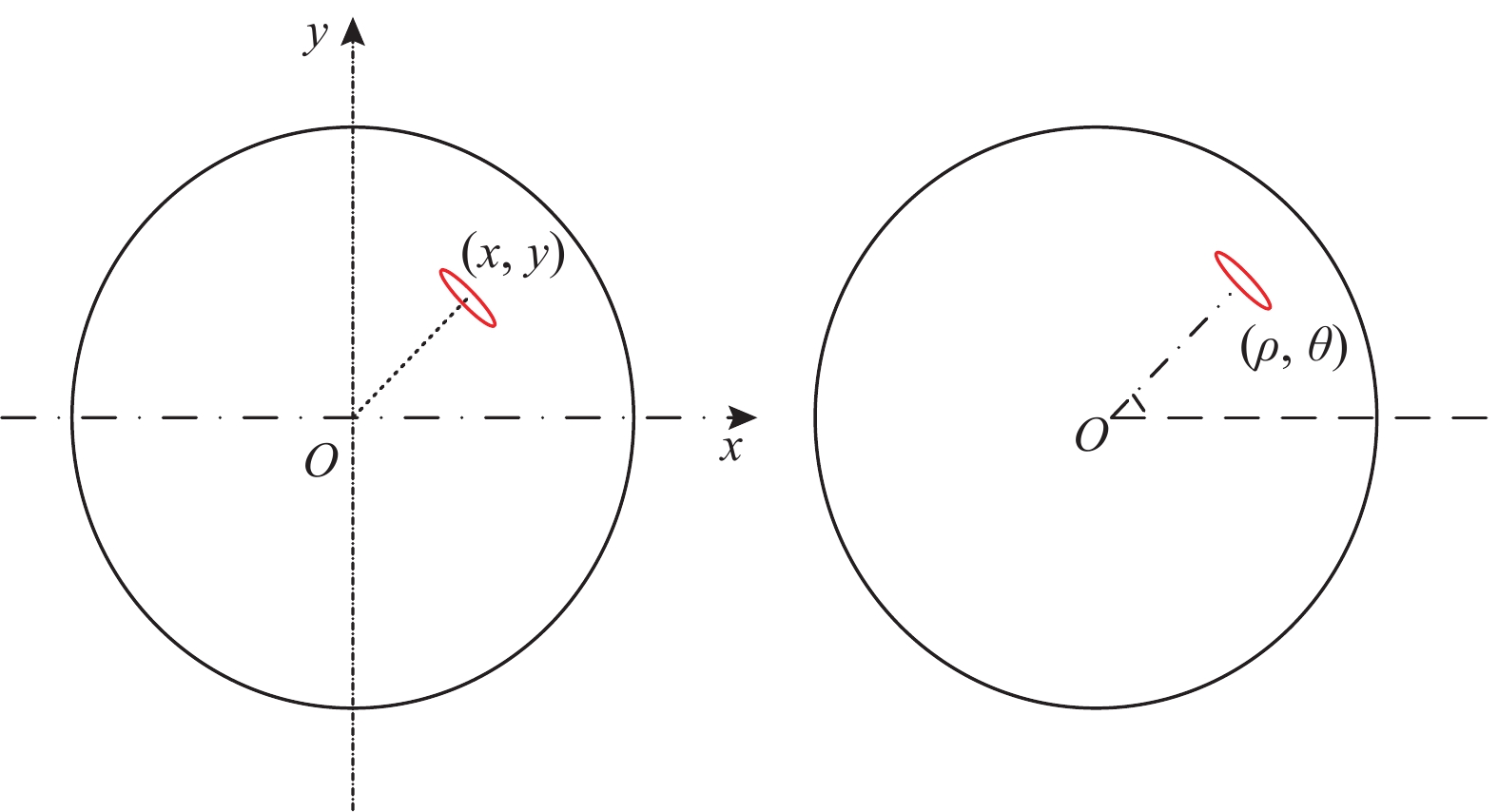
|
图 4 滚刀布置示意图 Fig. 4 Schematic of cutter layout |
刀盘上第
| $ X = \left\{ {{x_1},{x_2},\cdots,{x_n}} \right\};{x_i} = ({\rho _i},{\theta _i},{\beta _i}),i = 1,2,\cdots,n. $ |
滚刀磨损速率差异量由滚刀磨损速率的方差
| $E' = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{w_i} - E'(w)} \right)}^2}} .$ | (16) |
以秦岭隧道TB880E施工刀盘为例,建立基于正滚刀磨损速率方差最小的非线性数学模型及约束. 以所有51把正滚刀的磨损速率方差为目标函数,当目标函数取得最小值时,得到的最优解集合是滚刀极径布置的最佳方案.
最优极径解搜寻:
目标函数:
| $\min f(x) = \frac{1}{n}\left[ {{{({w_1} - \bar w)}^2} + {{({w_2} - \bar w)}^2} + \cdots +{{({w_i} - \bar w)}^2}} \right].$ | (17) |
约束条件:
| $({x_1} + {x_2} + {x_3} +\cdots + {x_{51}}) = {R_{\rm f}} {\text{,}}$ | (18) |
| $T < {x_i} < 2h\tan \;\beta {\text{,}}$ | (19) |
| ${w_i} = {x_i}^{\frac{1}{3}} ({R_{\rm a}} + {x_1} + {x_2} +\cdots + {x_{{i}}}) {\text{,}}$ | (20) |
| $\bar w = \frac{1}{n}({w_1} + {w_2} + {w_{\rm{3}}} + \cdots + {w_{{\rm{51}}}}).$ | (21) |
式中:
| 表 1 正滚刀优化后的极径布置参数 Table 1 Pole diameter layout parameters of cutters after optimized |
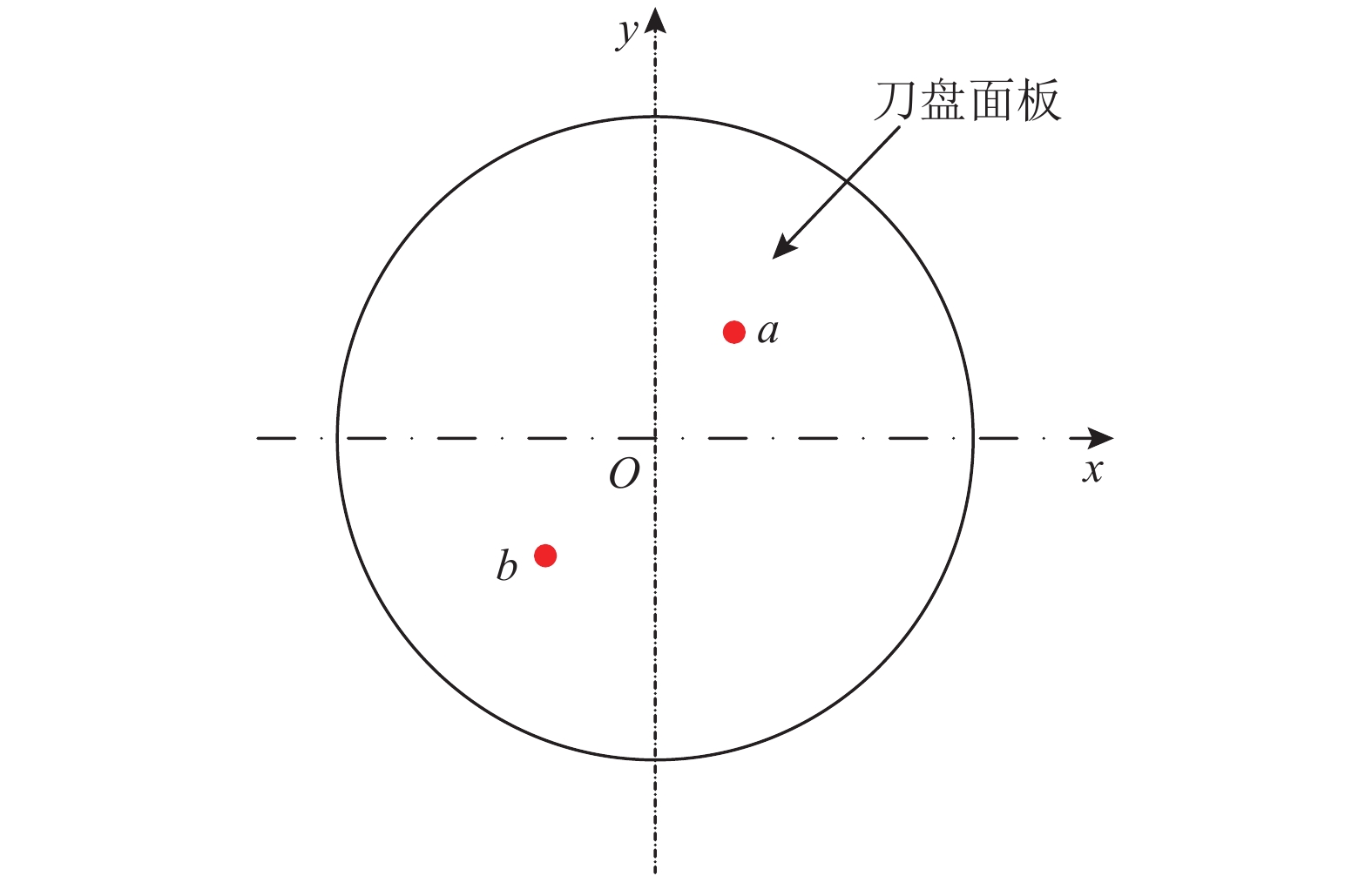
当进行滚刀布局设计时,设计人员将目标区域分成几块子区域,按照约束条件和布置原则把滚刀布置到各个子区域. 布置区域划分与滚刀布置设计密切关联,在区域划分方式时应考虑与滚刀布置相结合,建立合理、有效的子区域和滚刀分配方案. 通常将圆形刀盘区域划分为偶数块面积相等的扇形区域,相邻滚刀为一组进行对称布置,如图5所示,即若滚刀布置在
|
图 5 临近滚刀对称分布示意图 Fig. 5 Schematic diagram of symmetrical distribution of cutters |
刀盘在复合岩石地层中掘进时,载荷分布极不均匀,倾覆力矩、径向不平衡力对刀盘影响较大,因此在对正滚刀极角进行设计时,为了更好地满足刀盘载荷分布的均匀性、减少刀盘载荷的波动幅度,提出多螺旋线极角布置方法. 先将圆形刀盘面板划分成偶数块相等面积的扇形子区域,以一条等速螺旋线作为基准,通过选择旋转、增加螺旋线数目进行布置. 利用多螺旋线布置方法能够较好地满足相位角要求和滚刀顺次破岩的要求,多螺旋线曲线方程所需参数的计算方法与等速螺旋线相同.
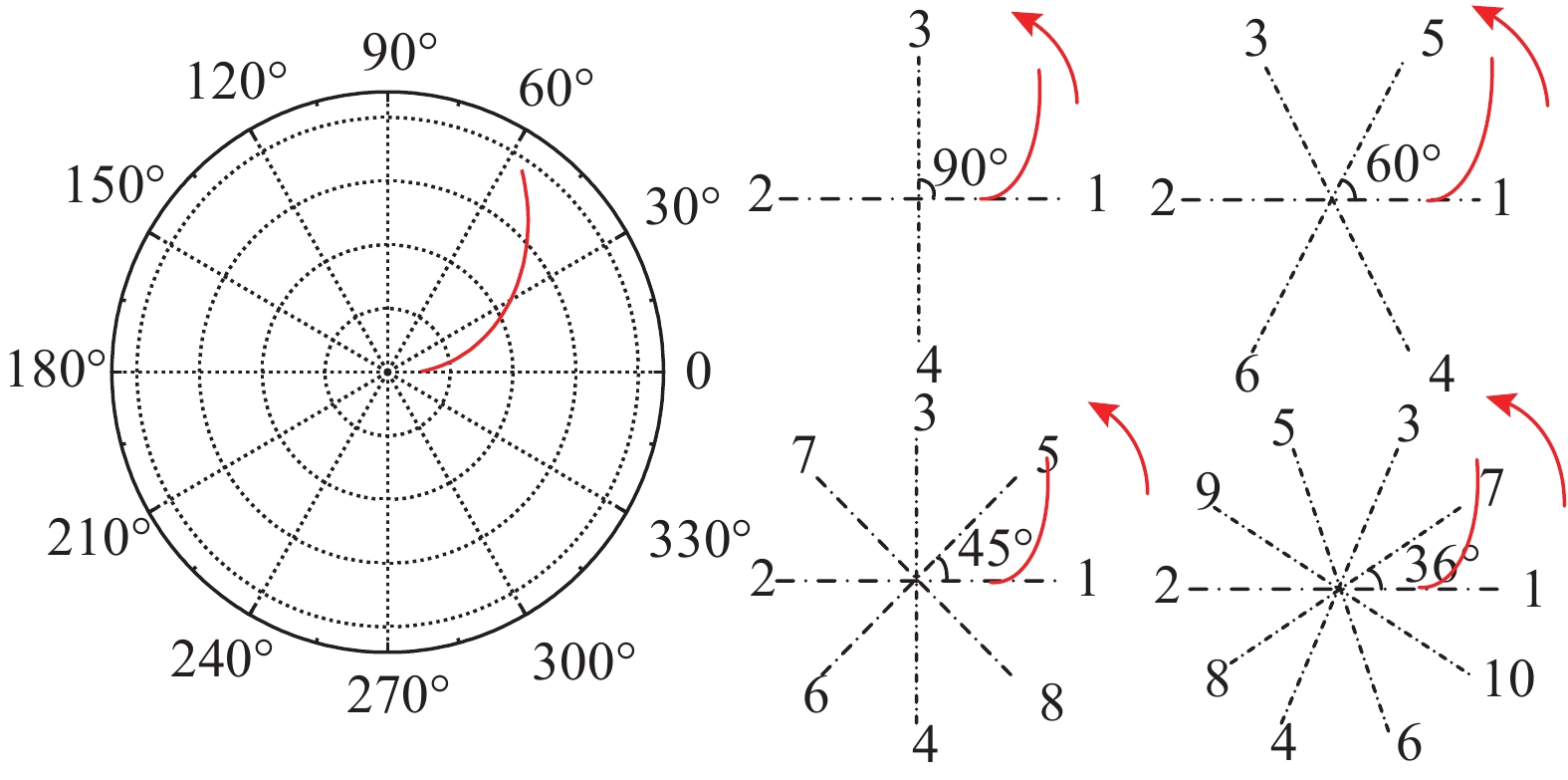
以TB880E刀盘为例,每把滚刀的极径已知,限定极角为0~90°,计算出51把滚刀的极角坐标. 首先计算螺旋线系数,确定该段螺旋线转过的度数,即最后一把中心滚刀到最后一把正滚刀螺旋线转过的角度,当转过的角度无限趋近于零时,刀盘布置变成米字型. 对于4、6、8、10条螺旋线刀盘,分别以4、6、8、10把滚刀为一大组、相邻2把滚刀为一对称小组,按照如图6所示的布置顺序,从第一把滚刀到分组中最后一把滚刀旋转依次布置,辅助直线的夹角分别为90°、60°、45°、36°,不同形式刀盘各51把滚刀的布置示意图如图7所示. 由此可知,对于任意一个不同布置形式的刀盘,2条相邻螺旋线之间的面积相等,这可以有效地降低刀盘分块子区域内的载荷集中性.
|
图 6 螺旋线旋转顺序示意图 Fig. 6 Helix rotation sequence diagram |

|
图 7 不同正滚刀布置形式的刀盘示意图 Fig. 7 Cutter-head's schematic of different cutters layout |
滚刀布置性能的好坏,很大程度上决定了刀盘整体性能的好坏. 滚刀的安装布置不是随意的,需要遵循一定的规律和要求. 为了使刀盘保持平衡稳定,以减少掘进机在掘进过程中的振动和噪声,滚刀在刀盘上的布局需要满足以下基本要求[13].
1)对于刀盘的径向不平衡力,越小越好.
2)对于刀盘的倾覆力矩,越小越好.
3)刀盘上所有滚刀整体的质心距离刀盘中心越近越好. 通常通过建立数学模型进行约束,滚刀群X轴方向质心
| ${X_{\rm c}} = \displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^n {m{r_i}\sin {\alpha _i}} }}{{nm}},{Y_{\rm c}} = \displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^n {m{r_i}\cos {\alpha _i}} }}{{nm}} {\text{,}}$ | (22) |
| ${L_{\rm p}} = \sqrt {{X_{\rm c}}^2 + {Y_{\rm c}}^2} .$ | (23) |
4)滚刀在破岩过程中尽可能地等量磨损,方便停机统一更换,节省施工过程中的不必要时间.
选取刀盘滚刀磨损速率方差、倾覆力矩、径向不平衡力及质心偏斜量4项,作为滚刀布置性能的评价指标. 基于对复合地层刀盘载荷的分析,考虑滚刀布置参数、刀盘的结构参数等,采用数值计算的方法,分别求解原始刀盘随机型布置方式及以上所设计的不同布局形式刀盘的4项指标,结果整理如下.
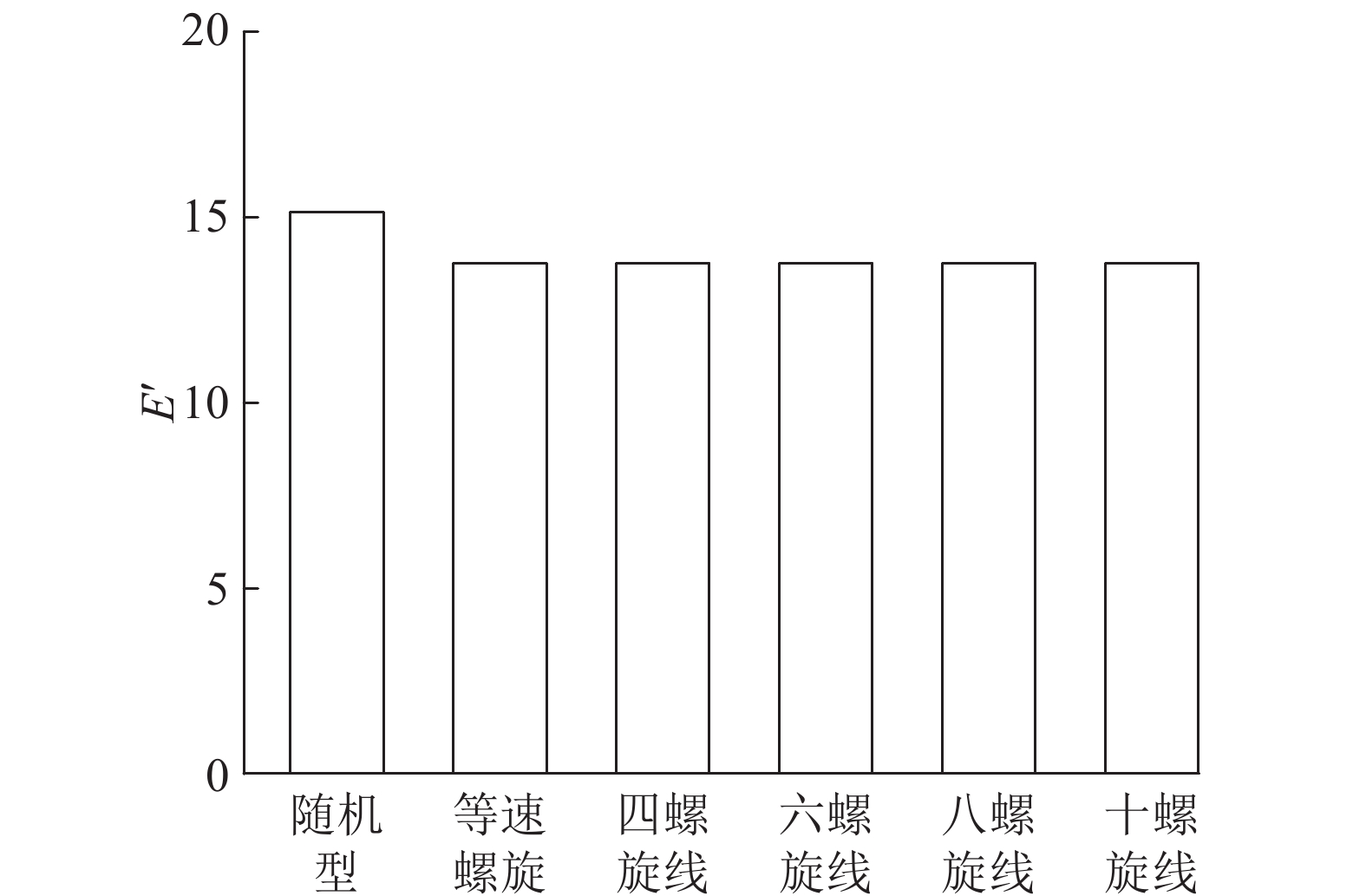
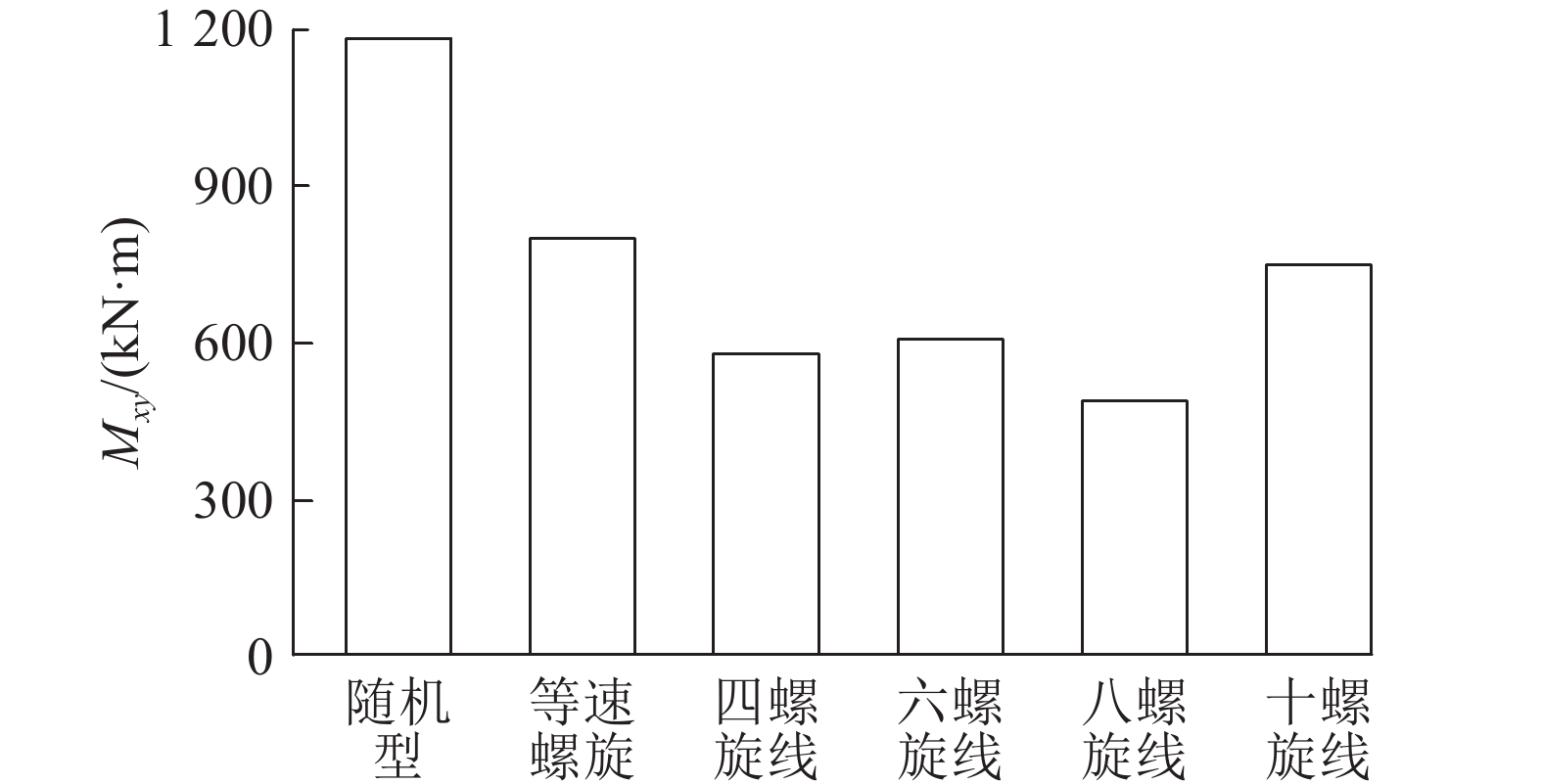
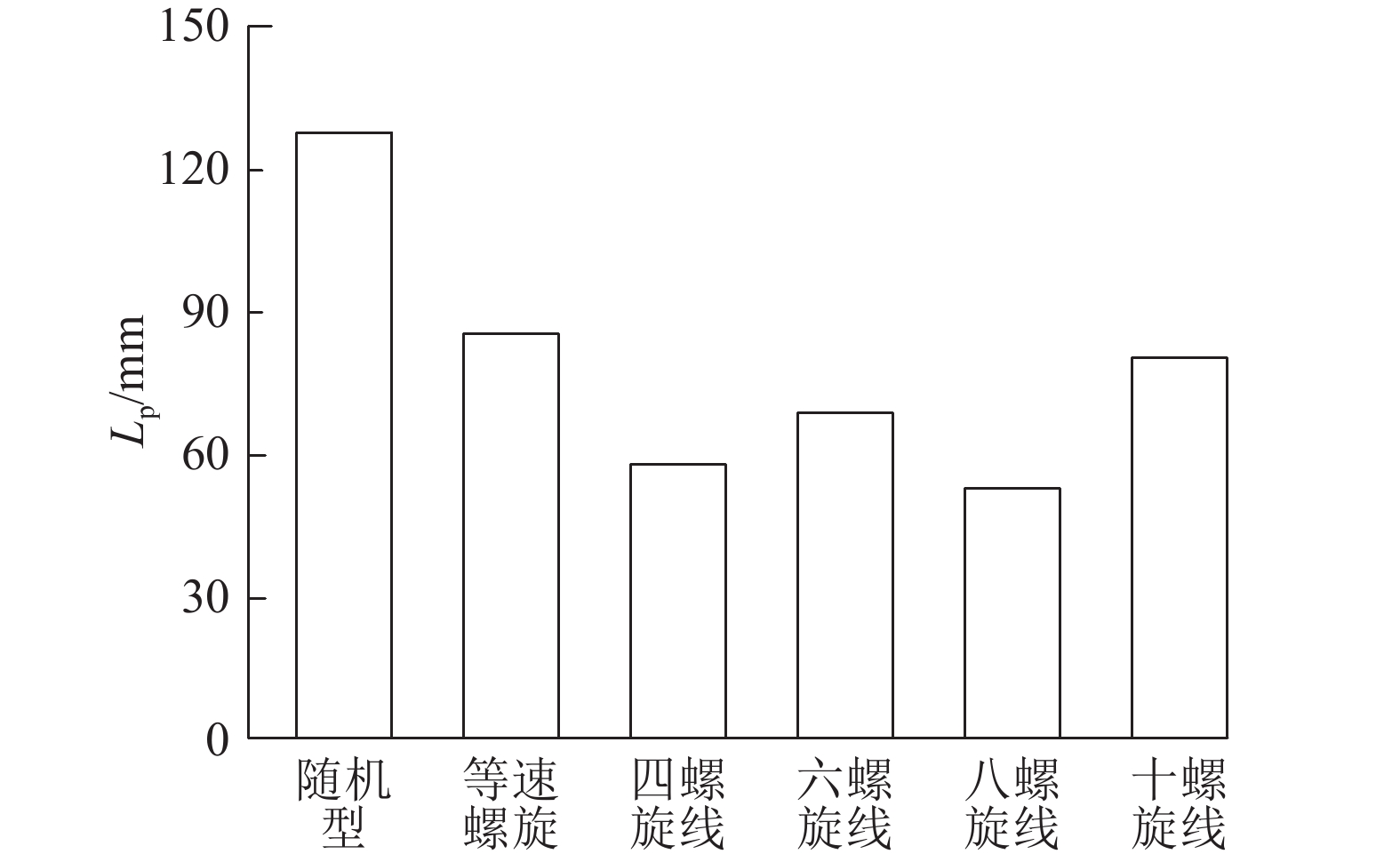
如图8~11所示分别为原始随机型刀盘、等速螺旋线型刀盘、多螺旋线型刀盘(4条、6条、8条、10条螺旋线)在复合地质条件下刀盘滚刀的磨损速率方差、倾覆力矩、径向不平衡力、质心偏斜量对比图. 可知,经过改进设计的多螺旋线型刀盘各指标都比原始TB880E刀盘优异,但是不同螺旋线条数的刀盘在各指标上有所差异.
|
图 8 不同正滚刀布置形式刀盘滚刀磨损速率方差对比 Fig. 8 Variance comparison of wear rate of cutters with different cutter arrangement |
|
图 9 不同正滚刀布置形式刀盘倾覆力矩对比 Fig. 9 Comparison of overturning moment of cutter-head with different cutter arrangement |

|
图 10 不同正滚刀布置形式刀盘径向不平衡力对比 Fig. 10 Comparison of radial unbalance force of cutter-head with different cutter arrangement |
|
图 11 不同正滚刀布置形式刀盘质心偏斜量对比 Fig. 11 Comparison of centroid deflection of cutter-head with different cutter arrangement |
采用各指标相对原始随机型的优越程度作为最终的决策度量,决策度量越小,刀盘的综合性能水平越优. 假设
| $\left. \begin{gathered} {{C'}_1} = E'/{{E'}_0} {\text{,}} \hfill \\ {{C'}_2} = {M_{xy}}/{M_0} {\text{,}} \hfill \\ {{C'}_3} = {F_{xy}}/{F_0} {\text{,}} \hfill \\ {{C'}_4} = {L_{\rm p}}/{L_0}. \hfill \\ \end{gathered} \right\}$ | (24) |
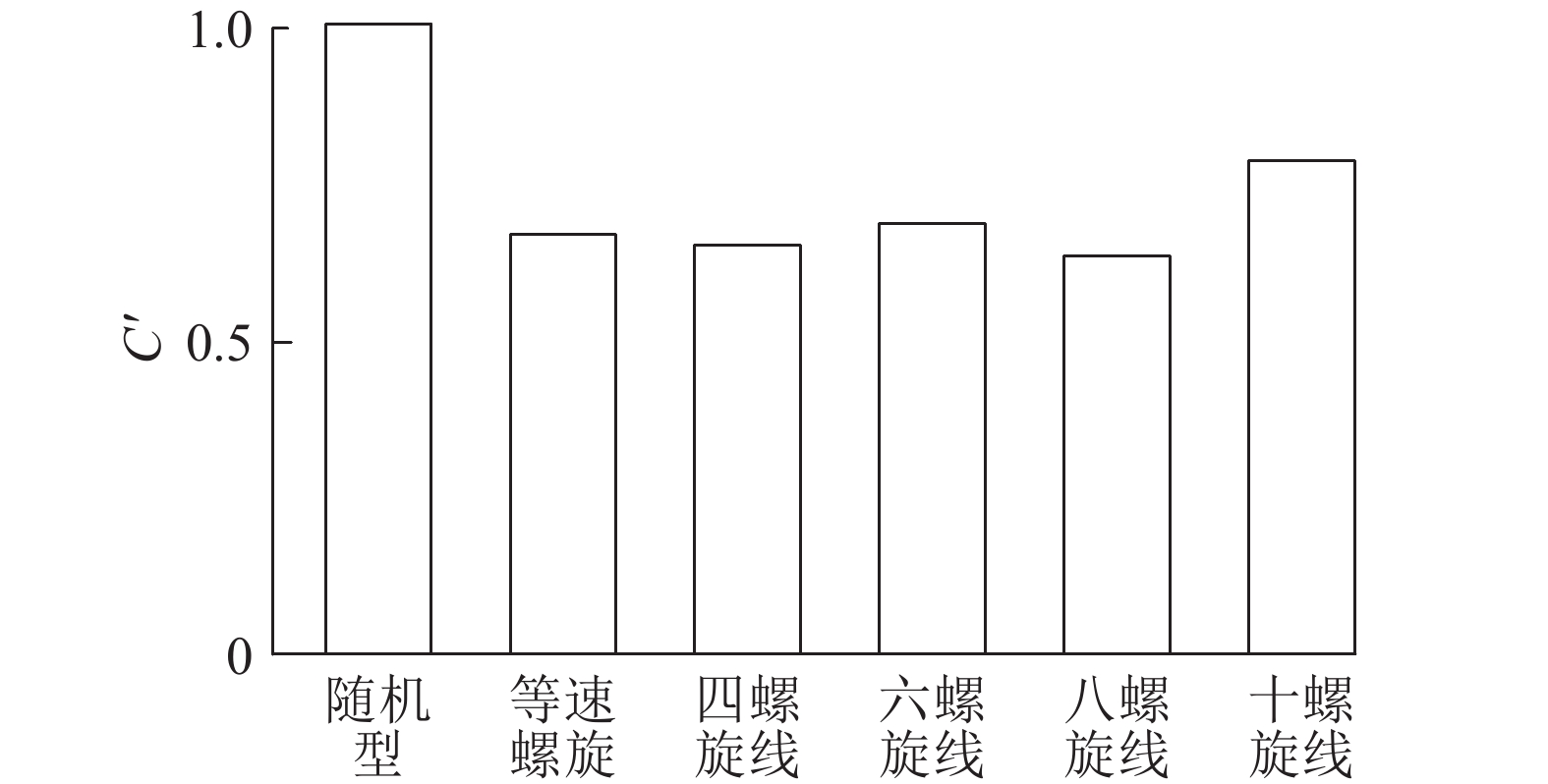
计算结果如图12所示,8条螺旋线型刀盘滚刀布置性能综合水平最优.
|
图 12 不同正滚刀布置形式的综合决策结果 Fig. 12 Comprehensive decision results of different cutter layout |
(1)通过分析秦岭隧道某区间段TB880E刀盘开挖推进5 621 m后刀盘上正滚刀的换刀次数,提出基于等磨损速率的正滚刀极径设计方法. 利用新的设计方法,滚刀的等磨损速率方差相对降低了10.45%.
(2)结合复合岩石地层中刀盘盘体载荷的分布特性,提出新的多螺旋线旋转分区域的极角设计方法. 该方法使得任意不同布置形式的刀盘中2条相邻螺旋线之间的面积相等,可以有效地降低刀盘分块子区域内的载荷集中性.
(3)分析对比随机型刀盘、等速螺旋线型刀盘、多螺旋线型刀盘在复合地质条件下刀盘滚刀的磨损速率方差、倾覆力矩、径向不平衡力和质心偏斜量. 结果表明,所设计的多螺旋线型刀盘的各项指标都比原始刀盘优异. 以各指标的相对优化程度作为最终的决策度量,实现对滚刀布置性能的综合评价,得出8条螺旋线型刀盘滚刀布置性能综合水平最优.
| [1] |
LIU J, REN J, WEI G. Thrust and torque characteristics based on a new cutter-head load model[J]. Chinese Journal of Mechanical Engineering, 2015, 28(4): 801-809. DOI:10.3901/CJME.2015.0504.066 |
| [2] |
张照煌, 乔永立. 全断面岩石掘进机盘形滚刀布置规律研究[J]. 工程力学, 2011, 28(5): 172-177. ZHANG Zhao-huang, QIAO Yong-li. Study on the cutters’ layout of cutter-head for full face tunnel boring machine[J]. Engineering Mechanics, 2011, 28(5): 172-177. |
| [3] |
朱殿华, 孙斌. 基于均衡破岩量的TBM正滚刀多目标优化布局[J]. 机械设计, 2017, 34(11): 1-6. ZHU Dian-hua, SONG Bin. Multi-objective optimal layout of TBM normal cutters based on balanced rock breaking[J]. Journal of Machine Design, 2017, 34(11): 1-6. DOI:10.3969/j.issn.2095-509X.2017.11.001 |
| [4] |
SUN W, HUO J Z, CHEN J, et al. Disc cutters’ layout design of the full-face rock tunnel boring machine (TBM) using a cooperative evolutionary algorithm[J]. Journal of Mechanical Science and Technology, 2011, 25(2): 415-427. DOI:10.1007/s12206-010-1225-3 |
| [5] |
程军, 巩亚东, 李伟, 等. 基于数字样机技术的隧道掘进机刀盘破岩机理分析[J]. 中国机械工程, 2013, 24(14): 1847-1853. CHENG Jun, GONG Ya-dong, LI Wei, et al. Analysis of breaking mechanism of tunnel boring machine cutter based on digital prototype technology[J]. China Mechanical Engineering, 2013, 24(14): 1847-1853. DOI:10.3969/j.issn.1004-132X.2013.14.001 |
| [6] |
MA H, YIN L, GONG Q, et al. TBM tunneling in mixed-face ground: problems and solutions[J]. International Journal of Mining Science and Technology, 2015, 25(4): 641-647. DOI:10.1016/j.ijmst.2015.05.019 |
| [7] |
刘建琴, 宾怀成, 郭伟. 复合岩层下岩石掘进机刀盘载荷特性研究[J]. 哈尔滨工程大学学报, 2018, 39(3): 575-583. LIU Jian-qin, BIN Huai-cheng, GUO Wei. Study on load characteristics of TBM cutter-head under mixed-face rock ground condition[J]. Journal of Harbin Engineering University, 2018, 39(3): 575-583. |
| [8] |
尹怀秀. 针对复合式地层的刀盘设计[J]. 混凝土与水泥制品, 2017, 44(8): 69-71. YIN Huai-xiu. Design of cutter-head for mixed-face rock ground[J]. China Concrete and Cement Products, 2017, 44(8): 69-71. DOI:10.3969/j.issn.1000-4637.2017.08.017 |
| [9] |
程永亮, 钟掘, 暨智勇, 等. TBM刀盘地质适应性设计方法及其应用[J]. 机械工程学报, 2018, 54(1): 1-9. CHENG Yong-liang, ZHONG Jue, JI Zhi-yong, et al. Geological adaptaive design method and application of TBM cutter-head[J]. Journal of Mechanical Engineering, 2018, 54(1): 1-9. |
| [10] |
吴起星, 安关峰, 周小文, 等. 软硬复合地层中盾构掘进刀盘受力分析与计算[J]. 土木工程学报, 2015, 48(2): 321-326. WU Qi-xing, AN Guan-feng, ZHOU Xiao-wen, et al. Stress analysis and calculation of shield driven cutter-head in soft and hard composite stratum[J]. Journal of Civil Engineering, 2015, 48(2): 321-326. |
| [11] |
王贺. 复合地层TBM破岩过程滚刀磨损机理及掘进效率研究[D]. 重庆: 重庆大学, 2016. WANG He. Study on the mechanism of cutter wear and driving efficiency in the process of TBM rock breaking in mixed-face rock ground [D]. Chongqing: Chongqing University, 2016. |
| [12] |
杨延栋, 陈馈, 李凤远, 等. 盘形滚刀磨损预测模型[J]. 煤炭学报, 2015, 40(06): 1290-1296. YANG Yan-dong, CHEN Kui, LI Feng-yuan, et al. Disc cutter wear prediction model[J]. Journal of China Coal Society, 2015, 40(06): 1290-1296. |
| [13] |
刘蒙蒙. 硬岩隧道掘进机滚刀布局关键问题研究[D]. 天津: 天津大学, 2014. LIU Meng-meng. Research on key problems of cutters’ layout in hard rock tunnel boring machine [D]. Tianjin: Tianjin University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10056-1015017450.htm |


