2. 上海卫星装备研究所,上海 200240
2. Shanghai Institute of Satellite Equipment, Shanghai 200240, China
长期以来,航天器上存在的微振动由于产生来源多,时刻影响着航空航天活动[1],对高精度航天器及敏感载荷上存在的微振动进行抑制和隔离的要求越来越迫切. 对微振动进行隔离的方法大体可以分为被动隔振和主动隔振. 被动隔振虽然结构简单、可靠性强,取得了不错的隔振效果[2-8],但对于频率较低且干扰源复杂的微振动环境是无能为力的. 主动隔振由于其低频控制能力,在针对空间微振动干扰的控制应用中越来越受到重视.
目前,研究最多的主动隔振平台是基于Stewart构型的主动隔振平台[9-16],如欧洲航天局开发的MAIS (multi-purpose active isolation system)主动隔振系统等. 其次便是基于洛伦兹力作动器的非接触式隔振平台[17-22],如马歇尔太空飞行中心研发的STABLE (suppression of transient accelerations by levitation)和g-LIMIT (glovebox integrated microgravity isolation technology)隔振装置、中科院空间应用工程与技术中心研发的MAIS (microgravity active vibration isolation system)主动隔振系统等. 此外,有根据其他不同工作原理作动器设计的微振动主动隔振平台[23-25]. 非接触式隔振平台由于具有无机械接触的特点,更加适合空间微重力环境下的微振动控制. 国内外目前已有的上述各非接触式隔振平台,作动器的激励线圈均采用传统的手工绕制方案,严重限制了作动器及平台的工作性能. 设计一款性能优良的非接触式二轴作动器,并依此研制一款结构紧凑、控制精确、隔振效果好的非接触式主动隔振平台是十分必要和迫切的.
对于主动隔振平台,其在轨工作前的另一个工作重点是地面试验. 其中,原理样机的试验方法主要有落塔法、抛物飞行法、水浮法、悬吊法、气悬浮法等[26],但相关样机试验的成本均较高. 鉴于此,沈建等[27-34]利用ADAMS及MATLAB等仿真分析软件在设计阶段对主动隔振平台的各项工作性能进行试验分析,高效、可靠而准确地为平台的各项工作性能进行验证,支持平台的设计和试验.
针对现有非接触式主动隔振装置在作动器设计、关键元器件空间布置等方面的不足,本文提出一款非接触式定位隔振平台(下文简称平台),对平台的激励单元、位置测量单元、加速度测量单元及控制系统进行设计. 利用ADAMS和MATLAB软件,分别建立平台的机械系统仿真模型和控制系统仿真模型,获得平台机电联合仿真模型. 利用联合仿真模型对平台的定位和隔振性能进行仿真分析,验证了平台的各项工作能力.
1 平台工作原理平台以工作于微重力环境的高精度航天器及其上的敏感载荷为服务对象,三维模型如图1所示. 采用空间对称布置方案,主要包括浮台、基台、位置测量单元、激励单元、加速度测量单元、限位单元及控制器等. 平台的浮台与基台之间无机械接触,通过非接触式激励单元进行相互作用. 浮台与基台之间的相对位置变化通过位置测量单元获得;浮台的加速度变化通过加速度测量单元获得. 控制器连接上述各单元,构成对浮台进行定位隔振控制的闭环系统. 在实际应用中,可以将基台与大型航天器固定,浮台作为工作台面与敏感载荷固定,实现敏感载荷与航天器间的无接触连接和定位隔振控制.
1.1 激励单元平台的激励单元如图1所示,由3套二轴电磁作动器构成. 各套作动器均由磁轭、永磁体及激励线圈构成,其中磁轭为高导磁材料,磁轭与永磁体共同形成闭合磁路并被安装在浮台上,所形成的闭合磁路在工作间隙处产生强而均匀的磁场. 作动器的激励线圈采用多层印制电路板工艺进行设计制造. 每块激励线圈均包含2组相互独立的多层激励绕组:一组在工作间隙处沿水平向绕制,另一组在工作间隙处沿垂直向绕制,激励线圈与基台固定安装. 由于采用的是印制电路板工艺,所设计作动器激励线圈的走线更精确、紧凑、垂直和水平线圈间的正交性更好,厚度更薄,有利于作动器输出大且相互垂直的二轴作用力,提升平台控制性能.
当激励线圈安装在工作间隙时,向2组激励绕组分别通入电流后,将在激励线圈与闭合磁路间产生如图1所示的2个相互独立且正交的作用力

|
图 1 非接触式定位隔振平台及其作动器三维模型 Fig. 1 Three-dimensional model of contactless positioning and vibration isolation platform and its actuator |
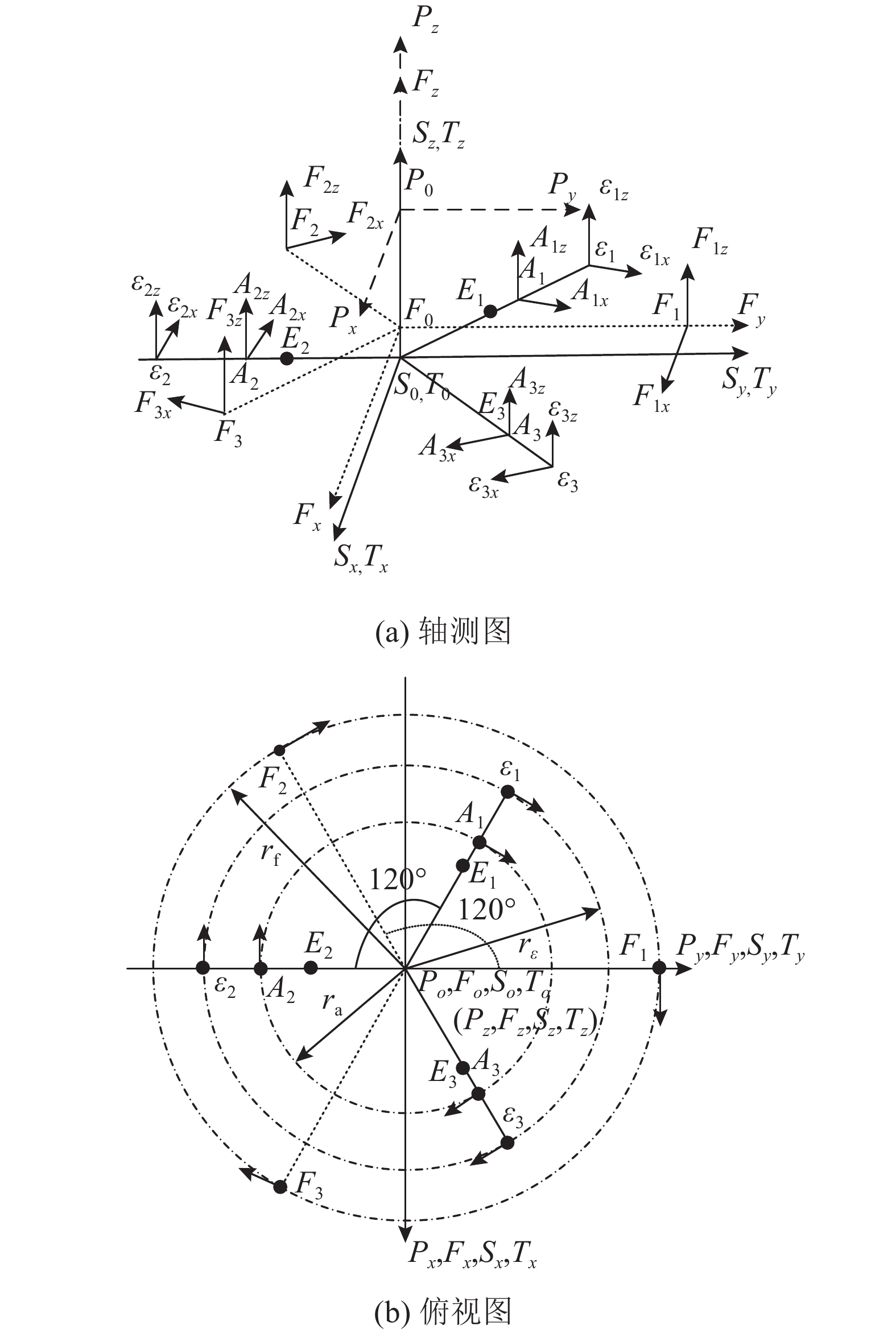
根据平台设计可知,3套电磁作动器的输出作用力如图2所示,在
|
图 2 平台坐标系建立及各关键元器件的空间布置 Fig. 2 Coordinates-setting of platform and spatial layouts of its key components |
根据图2所示的激励单元空间布置方案可知,各作用力在浮台坐标系
| $\left[ {\begin{array}{*{20}{c}} {{{\theta}} _{{\rm{ F1}}z}^{\rm{T}}} \\ {{{\theta}} _{{\rm{ F1}}x}^{\rm{T}}} \\ {{{\theta}} _{{\rm{ F2}}z}^{\rm{T}}} \\ {{{\theta}} _{{\rm{ F2}}x}^{\rm{T}}} \\ {{{\theta}} _{{\rm{ F3}}z}^{\rm{T}}} \\ {{{\theta}} _{{\rm{ F3}}x}^{\rm{T}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&0&1 \\ 1&0&0 \\ 0&0&1 \\ { - {1 / 2}}&{{{\sqrt 3 } / 2}}&0 \\ 0&0&1 \\ { - {1 / 2}}&{ - {{\sqrt 3 } / 2}}&0 \end{array}} \right].$ | (1) |
式中:
| $\left[ {\begin{array}{*{20}{c}} {{{R}}_{{\rm{F1}}}^{\rm{T}}} \\ {{{R}}_{{\rm{F2}}}^{\rm{T}}} \\ {{{R}}_{{\rm{F3}}}^{\rm{T}}} \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} 0&{{r_{\rm{f}}}}&{ - {d_{\rm{f}}}} \\ { - {{\sqrt 3 {r_{\rm{f}}}} / 2}}&{ - {{{r_{\rm{f}}}} / 2}}&{ - {d_{\rm{f}}}} \\ {{{\sqrt 3 {r_{\rm{f}}}} / 2}}&{ - {{{r_{\rm{f}}}} / 2}}&{ - {d_{\rm{f}}}} \end{array}} \right].$ | (2) |
式中:
令
| $\left[ {\begin{array}{*{20}{c}} {M{{{I}}_{3 \times 3}}}&{\bf 0} \\ {\bf 0}&{{J}} \end{array}} \right] {{A}} = {{{K}}_{\rm{f}}}{{{F}}_{\rm{f}}}.$ | (3) |
式中:
| ${{{K}}_{\rm{f}}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&{ - \displaystyle\frac{1}{2}}&0&{ - \displaystyle\frac{1}{2}} \\ 0&0&0&{\displaystyle\frac{{\sqrt 3 }}{2}}&0&{ - \displaystyle\frac{{\sqrt 3 }}{2}} \\ 1&0&1&0&1&0 \\ {{r_{\rm{f}}}}&0&{ - \displaystyle\frac{1}{2}{r_{\rm{f}}}}&{\displaystyle\frac{{\sqrt 3 }}{2}{d_{\rm{f}}}}&{ - \displaystyle\frac{1}{2}{r_{\rm{f}}}}&{ - \displaystyle\frac{{\sqrt 3 }}{2}{d_{\rm{f}}}} \\ 0&{ - {d_{\rm{f}}}}&{\displaystyle\frac{{\sqrt 3 }}{2}{r_{\rm{f}}}}&{\displaystyle\frac{1}{2}{d_{\rm{f}}}}&{ - \displaystyle\frac{{\sqrt 3 }}{2}{r_{\rm{f}}}}&{\displaystyle\frac{1}{2}{d_{\rm{f}}}} \\ 0&{ - {r_{\rm{f}}}}&0&{ - {r_{\rm{f}}}}&0&{ - {r_{\rm{f}}}} \end{array}} \right].$ | (4) |
由此,根据式(3)及上述各作动器的空间布置,利用上述3套二轴电磁作动器,可以对浮台的6自由度运动进行控制.
1.2 位置测量单元平台的位置测量单元由3组二维位置敏感探测器(position sensitive detector,PSD)和对应的激光器构成,如图2所示. 图中,
根据图2所示的各PSD布置,可以将测量坐标系原点到PSD敏感面上照射点的位置矢量表示为
| ${}^{({{T }})}{{{\delta}} _i} = {}^{(T/S)}{{Q}}\left[{}^{{{(S}}/{\varepsilon _i})}{{{Q}}^{({\varepsilon _i})}}{{{ \varepsilon }} _i} + {}^{({{S}})}{{{R}}_{{{\varepsilon}}i}} - {}^{({{S}})}{{{r}}_{\rm{c}}}\right];\;i = 1, 2, 3.$ | (5) |
式中:
| ${}^{{{(T /S)}}}{{Q}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} 1&{{\theta _{{{T }}z}}}&{ - {\theta _{{{T}}y}}} \\ { - {\theta _{{{T }}z}}}&1&{{\theta _{{{T }}x}}} \\ {{\theta _{{{T }}y}}}&{ - {\theta _{{{T}}x}}}&1 \end{array}} \right];$ | (6) |
| $\begin{split}& ^{{{(S}}/{\varepsilon _1})}{{Q}} = \left[ {\begin{array}{*{20}{c}} {{{\sqrt 3 } / 2}}&{{1 / 2}}&0 \\ { - {1 / 2}}&{{{\sqrt 3 } / 2}}&0 \\ 0&0&1 \end{array}} \right], ^{{{(S}}/{\varepsilon _2})}{{Q}} = \left[ {\begin{array}{*{20}{c}} 0&{ - 1}&0 \\ 1&0&0 \\ 0&0&1 \end{array}} \right], \\ & ^{({{S}}/{\varepsilon _3})}{{Q}} = \left[ {\begin{array}{*{20}{c}} { - {{\sqrt 3 } / 2}}&{{1 / 2}}&0 \\ { - {1 / 2}}&{ - {{\sqrt 3 } / 2}}&0 \\ 0&0&1 \end{array}} \right], \end{split}$ | (7) |
其中,
| $\left[ {\begin{array}{*{20}{c}} {^{\left( {{S}} \right)}{{R}}_{{\rm{\varepsilon }}1}^{\rm{T}}} \\ {^{\left( {{S}} \right)}{{R}}_{{\rm{\varepsilon }}2}^{\rm{T}}} \\ {^{\left( {{S}} \right)}{{R}}_{{\rm{\varepsilon }}3}^{\rm{T}}} \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} { - {{\sqrt 3 {r_{\rm{\varepsilon }}}} / 2}}&{{{{r_{\rm{\varepsilon }}}} / 2}}&0 \\ 0&{ - {r_{\rm{\varepsilon }}}}&0 \\ {{{\sqrt 3 {r_{\rm{\varepsilon }}}} / 2}}&{{{{r_{\rm{\varepsilon }}}} / 2}}&0 \end{array}} \right].$ | (8) |
其中,
| $\left. \begin{array}{l} l_x = {l_{Tx}}{\rm{ + }}{d_{\rm{t}}}\sin {\theta _{Ty}},\\ l_y = {l_{Ty}} - {d_{\rm{t}}}\sin {\theta _{Tx}},\\ l_z = {l_{Tz}} - {d_{\rm{t}}}\left( {1 - \cos {\theta _{Tx}}\cos {\theta _{Ty}}} \right),\\ {\theta _x} = {\theta _{Tx}},\\ {\theta _y} = {\theta _{Ty}},\\ {\theta _z} = {\theta _{Tz}}. \end{array} \right\}$ | (9) |
平台的加速度测量单元由6个安装在浮台上的单轴加速度计构成,如图2所示,6个加速度计与位置测量单元的激光器一起安装在测量坐标系上,两两一组分别安装在图中的
根据刚体动力学原理可知,上述布置方案中的6个单轴加速度计测得的加速度可以表示为
| ${A_i} = {{\theta}} _{{\rm{A}}i}^{\rm{T}} {{A}_l} ^{\rm{T}} + {{\theta}} _{{\rm{A}}i}^{\rm{T}}{\widetilde { A}_\theta } {{R}}_{{\rm{A}}i} + {{\theta}} _{{\rm{A}}i}^{\rm{T}}{\tilde {{\omega}} ^2}{{R}}_{{\rm{A}}i}.$ | (10) |
式中:
| $\left[ {\begin{array}{*{20}{c}} {{{\theta}} _{{\rm{A}}1z}^{\rm{T}}} \\ {{{\theta}} _{{\rm{A}}1x}^{\rm{T}}} \\ {{{\theta}} _{{\rm{A}}2z}^{\rm{T}}} \\ {{{\theta}} _{{\rm{A}}2x}^{\rm{T}}} \\ {{{\theta}} _{{\rm{A}}3z}^{\rm{T}}} \\ {{{\theta}} _{{\rm{A}}3x}^{\rm{T}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&0&1 \\ {{1 / 2}}&{{{\sqrt 3 } / 2}}&0 \\ 0&0&1 \\ { - 1}&0&0 \\ 0&0&1 \\ {{1 / 2}}&{ - {{\sqrt 3 } / 2}}&0 \end{array}} \right];$ | (11) |
| $\left[ {\begin{array}{*{20}{c}} {{{R}}_{{\rm{A}}1z}^{\rm{T}}} \\ {{{R}}_{{\rm{A}}1x}^{\rm{T}}} \\ {{{R}}_{{\rm{A}}2z}^{\rm{T}}} \\ {{{R}}_{{\rm{A}}2x}^{\rm{T}}} \\ {{{R}}_{{\rm{A}}3z}^{\rm{T}}} \\ {{{R}}_{{\rm{A}}3x}^{\rm{T}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {{\sqrt 3 {r_{\rm{a}}}} / 2}}&{{{{r_{\rm{a}}}} / 2}}&{ - {d_{\rm{t}}}} \\ { - {{\sqrt 3 {r_{\rm{a}}}} / 2}}&{{{{r_{\rm{a}}}} / 2}}&{ - {d_{\rm{t}}}} \\ 0&{ - {r_{\rm{a}}}}&{ - {d_{\rm{t}}}} \\ 0&{ - {r_{\rm{a}}}}&{ - {d_{\rm{t}}}} \\ {{{\sqrt 3 {r_{\rm{a}}}} / 2}}&{{{{r_{\rm{a}}}} / 2}}&{ - {d_{\rm{t}}}} \\ {{{\sqrt 3 {r_{\rm{a}}}} / 2}}&{{{{r_{\rm{a}}}} / 2}}&{ - {d_{\rm{t}}}} \end{array}} \right], $ | (12) |
其中,
根据式(10)及上述6个加速度计所测得的加速度
上文对平台的各测量和作动单元进行了设计,平台的另一个关键单元是控制器,用于将上述测量和作动单元联系起来,构成对浮台6自由度位移及加速度进行控制的闭环控制系统.
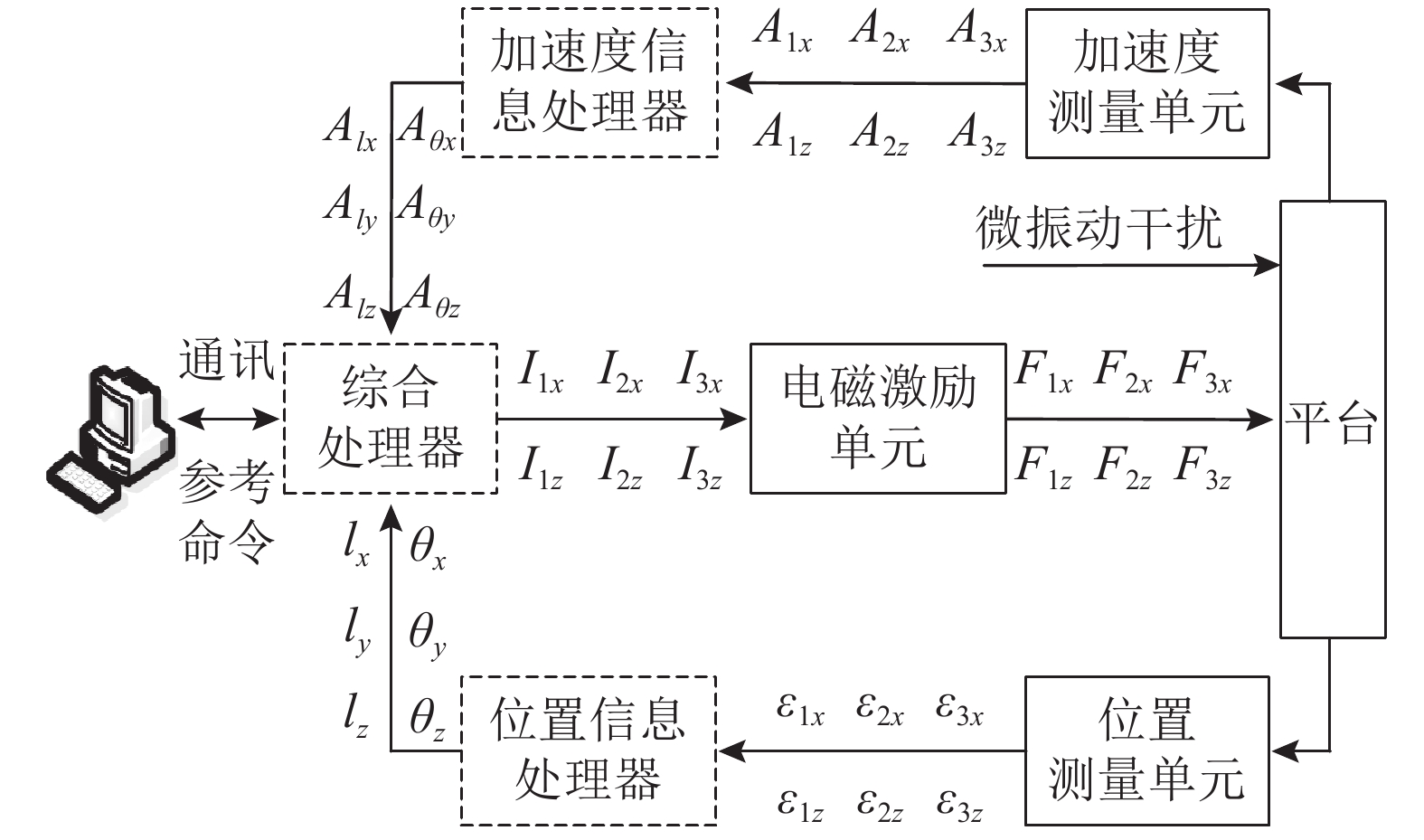
如图3所示,控制系统的控制器主要包含图中虚线框所示的加速度信息处理器、位置信息处理器和综合处理器. 在工作过程中,控制器实时采集各测量元器件的输出值,利用加速度信息处理器及位置信息处理器解算得到浮台的位移与加速度信息;综合处理器将测得的6自由度运动信息,分别与各自由度方向的位置、加速度参考命令进行比较,并经控制策略处理后,得到对浮台进行位置和加速度控制各自由度方向所需的输出力和力矩;综合处理器将6自由度控制力及力矩转换为各电磁作动器所需的激励电流,通过电磁激励单元将激励电流转换为作用力输出,完成对浮台的控制.
|
图 3 非接触式定位隔振平台控制系统框图 Fig. 3 Control system block diagram of contactless positioning and vibration isolation platform |
平台控制器的工作模式分为定位模式和隔振模式. 在定位模式中,控制器利用所采集的位置与姿态信息,对浮台与基台间的相对位移进行控制,采用的控制策略为PID控制;在隔振模式中,控制器主要利用所采集的加速度信息,对浮台的加速度进行控制,采用的控制策略为PI控制,同时结合采集的位置信息,根据PI控制策略对浮台与基台的相对位置进行控制,避免浮台与基台间发生碰撞. 根据控制系统设计,在隔振模式下,平台在6自由度方向的加速度与所受干扰力间的传递函数可以分别表示为
| ${G_i}(s) = \frac{{{M_{{\rm{b}}i}}{s^3} + {k_{{\rm{pe}}i}}{s^2} + {k_{{\rm{ie}}i}}}}{{{M_{{\rm{b}}i}}{\rm{(}}{M_i} + {k_{{\rm{a}}i}}{\rm{)}}{s^3} + {M_{\rm{b}}}{k_{{\rm{d}}i}}{s^2} + [{M_i}{k_{{\rm{pe}}i}} + {M_{\rm{b}}}_i{\rm{(}}{k_{{\rm{pe}}i}} + {k_{{\rm{p}}i}}{\rm{)}}]s{\rm{ + (}}{M_i} + {M_{\rm{b}}}_i{\rm{)}}{k_{{\rm{ie}}i}}}}.$ | (13) |
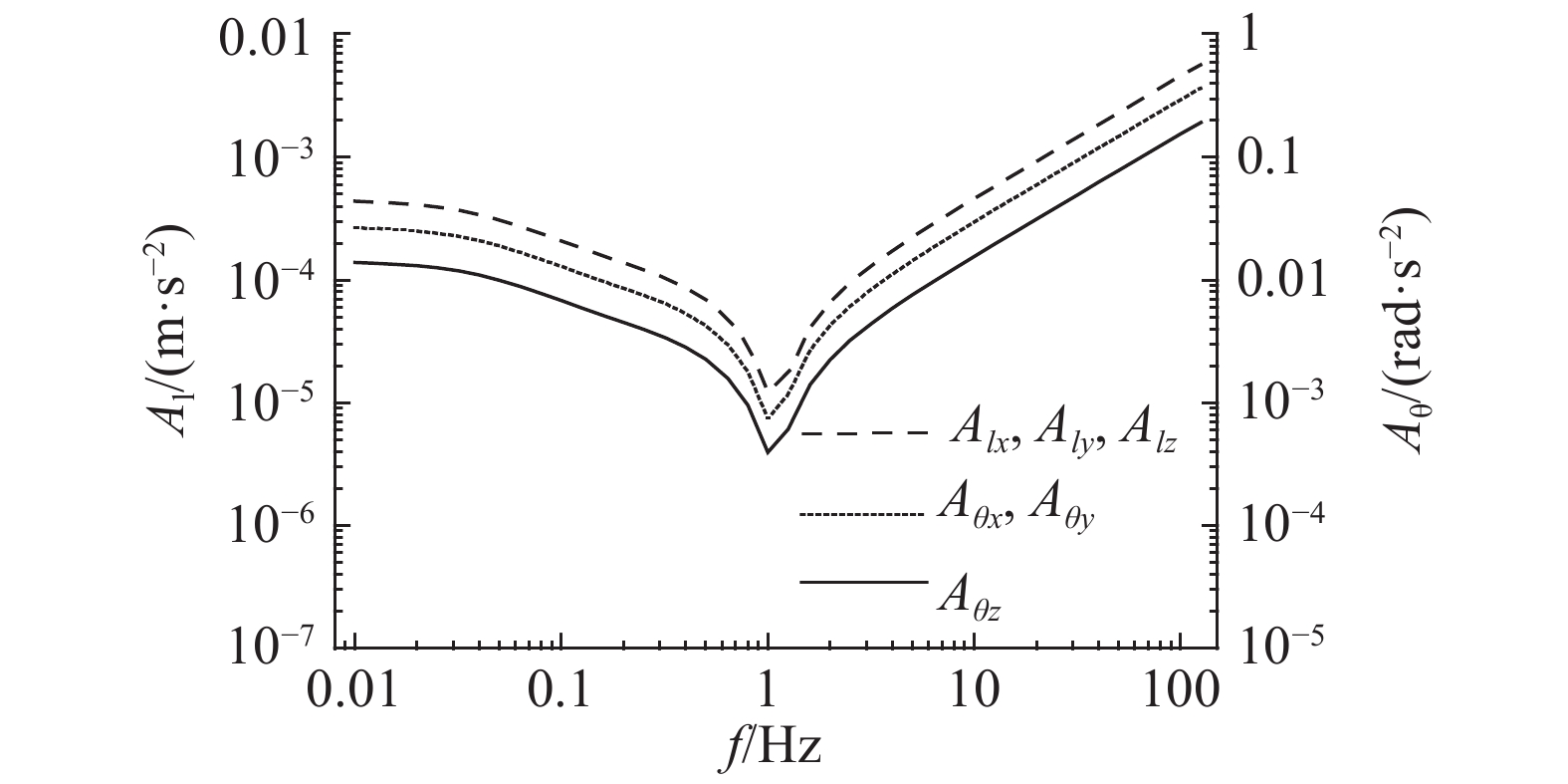
式中:i用于标识对应的6自由度控制方向,分别为
|
图 4 单位力或力矩作用下平台6自由度加速度频率响应 Fig. 4 Six-DOF acceleration frequency responses of platform under disturbance of unit force or torque |
ADAMS即机械系统动力学自动分析,采用拉格朗日方程建立系统动力学方程,可以对机械系统进行静力学、运动学和动力学分析[35]. Simulink即simulation和link的合成,将一系列仿真模块连接起来,构成复杂的系统模型[36]. 利用ADAMS与MATLAB/Simulink联合仿真,可以有效地结合各自在机械系统与控制系统建模上的优势,使得仿真过程更简便,结果更可靠. 在联合仿真中,加速度测量单元、位置测量单元、电磁激励单元等平台机械部分由ADAMS仿真,控制器由MATLAB/Simulink软件仿真. 此外,在进行机械系统仿真设置前,将利用SolidWorks软件所建立的平台机械系统三维模型转换为.x_t格式后,导入ADAMS.
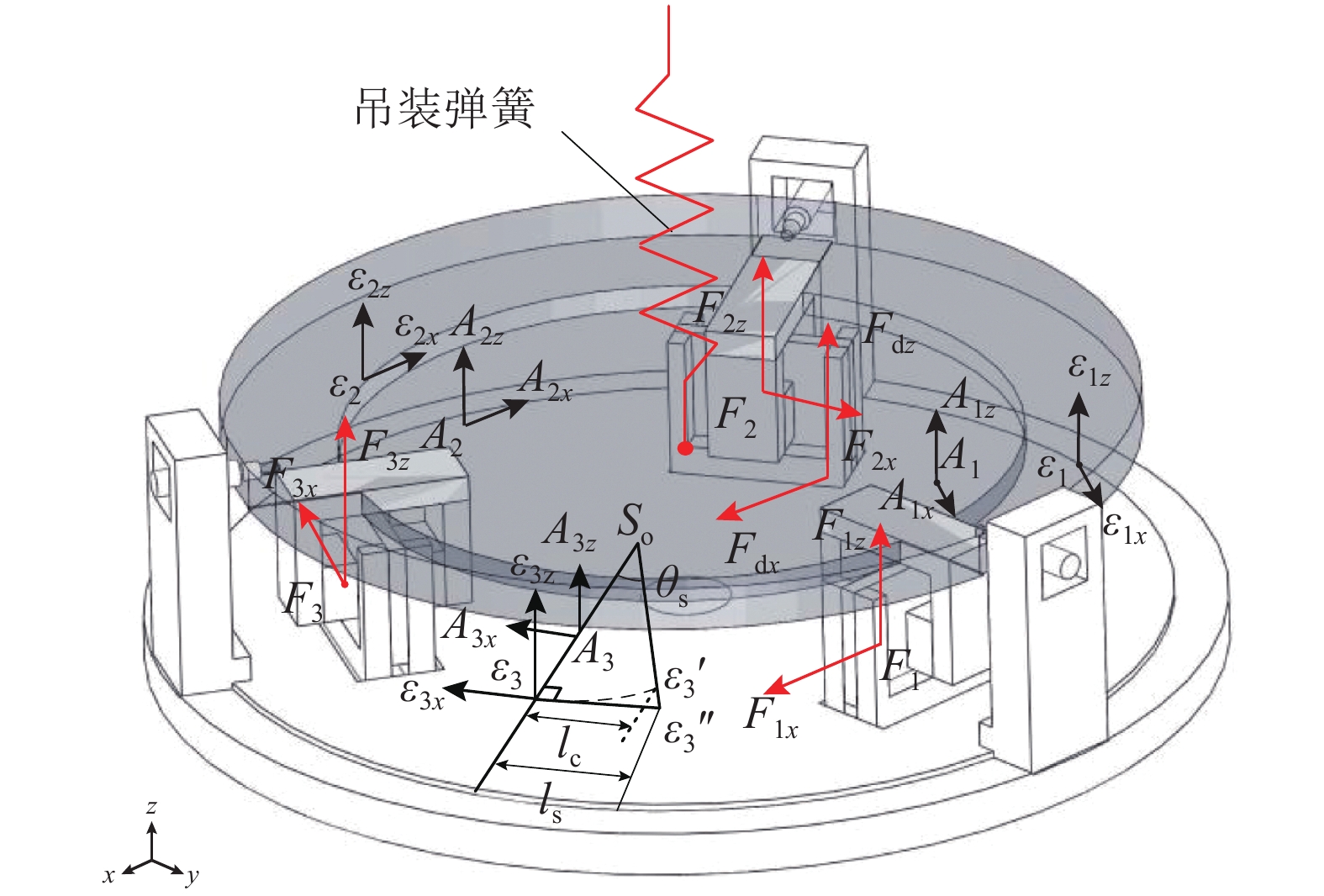
如图5所示为平台模拟地面试验时所进行的仿真设置,工作环境设置为重力环境,基台与基础固定,浮台通过吊装弹簧进行单点吊装. 本文仿真条件是空间微重力环境,将工作环境设置为无重力环境并去掉吊装弹簧. 3套二轴电磁作动器分别设置在图5的
|
图 5 基于ADAMS的平台机械系统仿真模型 Fig. 5 Mechanical system simulation model of platform built by ADAMS |
如图5所示,位置测量单元仿真设置了
如图5所示,在台面的相应位置设置有直接干扰力,当图5所示的2个干扰力同时作用时,浮台在多个自由度方向均受到直接振动干扰. 在设置平台的机械系统仿真模型后,利用ADAMS/Control模块将机械系统仿真模型导出,与图6所示的利用Simulink搭建的控制系统仿真模型进行联合仿真.

|
图 6 基于Simulink的平台控制系统仿真模型 Fig. 6 Control system simulation model of platform built by Simulink |
图6的接口模块为导入的机械系统仿真模型,同时用于连接控制系统模型与机械系统仿真模型. 在仿真前,需要对接口模块的求解器类型、动画模式、仿真模式、通讯时间间隔等参数进行设置. 其中动画模式若选为interactive,则仿真过程中ADAMS软件会被自动打开并与控制系统模型一起进行联合仿真,仿真过程可以在ADAMS中通过动画显示;若设置为batch,则联合仿真仅在MATLAB/Simulink中开展,仿真结果不在ADAMS中通过动画显示.
如图6所示,所建立的控制系统仿真模型包含激励模块、干扰模块、位置处理模块、加速度处理模块、控制处理模块及显示存储模块等. 其中激励模块为作用力分配放大模块,模拟了控制器的D/A转换、功率放大及激励解耦等操作,用于将6自由度控制信号转换并放大为作动器的6个作用力,并通过接口模块作用到虚拟平台上. 干扰模块为干扰力输入模块,在偏心位置设置了2个正交的干扰力,通过接口模块传递给虚拟平台,对浮台在多个自由度方向进行微振动干扰. 位置处理模块用于将虚拟PSD输出的6个位置测量值转换为沿浮台坐标系相对基台在6个自由度方向的位移和角位移. 加速度处理模块用于将仿真测量得到的6个加速度传感器测量值转换为沿浮台坐标系6个自由度方向的线加速度和角加速度. 控制处理模块模拟综合处理器,用于将采集到的6自由度位移信息和加速度信息分别与6自由度参考信息作比较;利用控制算法得到对6自由度方向进行定位或隔振操作各方向所需输出的作用力,输出6自由度控制信号. 显示存储模块用于对平台的位置与姿态及各向加速度信息进行显示和存储,方便仿真过程中对控制系统的各个参数进行调试.
利用ADAMS和MATLAB/Simulink分别建立平台的机械系统仿真模型和控制系统仿真模型,进而建立平台的机电联合仿真模型.
3 联合仿真分析 3.1 定位功能分析平台定位功能主要用于敏感载荷与航天器间的定位控制,使得相互间无机械接触的同时可以在6自由度方向进行微小的相对位置与姿态调整.
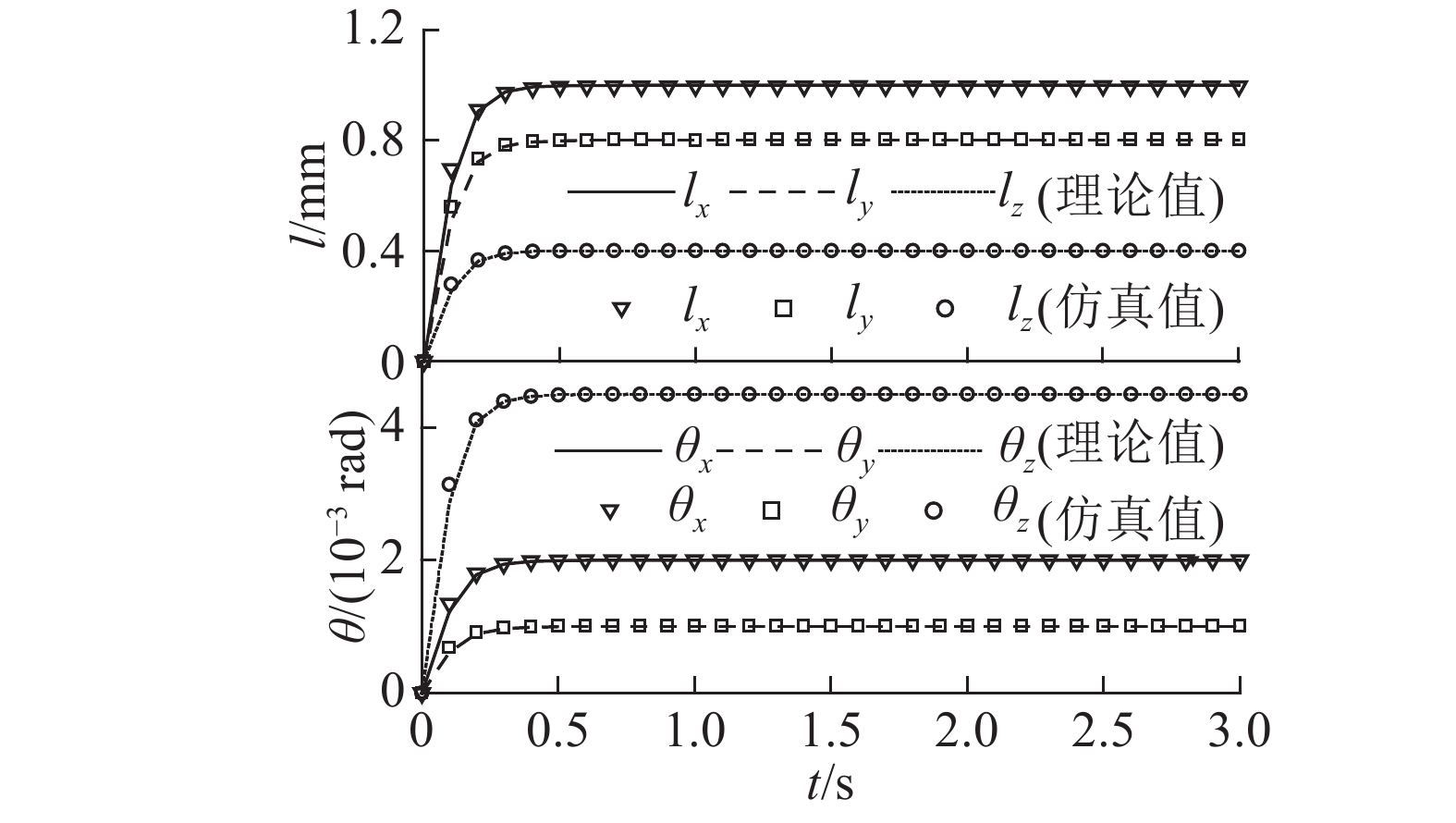
定位仿真试验在无外界干扰及无重力条件下开展,在仿真过程中主要利用位移反馈PID控制对浮台进行位置与姿态闭环控制. 由于定位功能仅用于对敏感载荷的微小位置与姿态进行控制,在仿真过程中,将浮台相对基台沿3个轴向的位移参考值分别设置为1 000、800和400 μm;将角位移参考值分别设置为2×10−3、10−3和4.5×10−3 rad. 仿真结果如图7所示. 图中,
|
图 7 定位仿真试验平台的浮台与基台间的6自由度相对位移曲线 Fig. 7 Six-DOF relative displacement diagrams between floater and base of platform during positioning simulation test |
平台的隔振功能主要用于对安装于浮台上的敏感载荷进行6自由度微振动干扰抑制. 相关的隔振仿真试验在无重力条件下开展. 在隔振控制过程中,利用加速度反馈和位置反馈对平台进行控制,使得浮台在加速度控制过程中能够跟随基台进行低频运动,不至于与基台发生碰撞. 根据上述设计,首先利用浮台上设置的干扰力对浮台开展20 Hz和100 Hz正弦直接干扰抑制仿真试验. 在试验中,将上述2个干扰力 (0.3 N)均设置在垂直于y轴的方向,进而相对浮台在除y轴平动方向外的其他5个方向进行振动干扰.
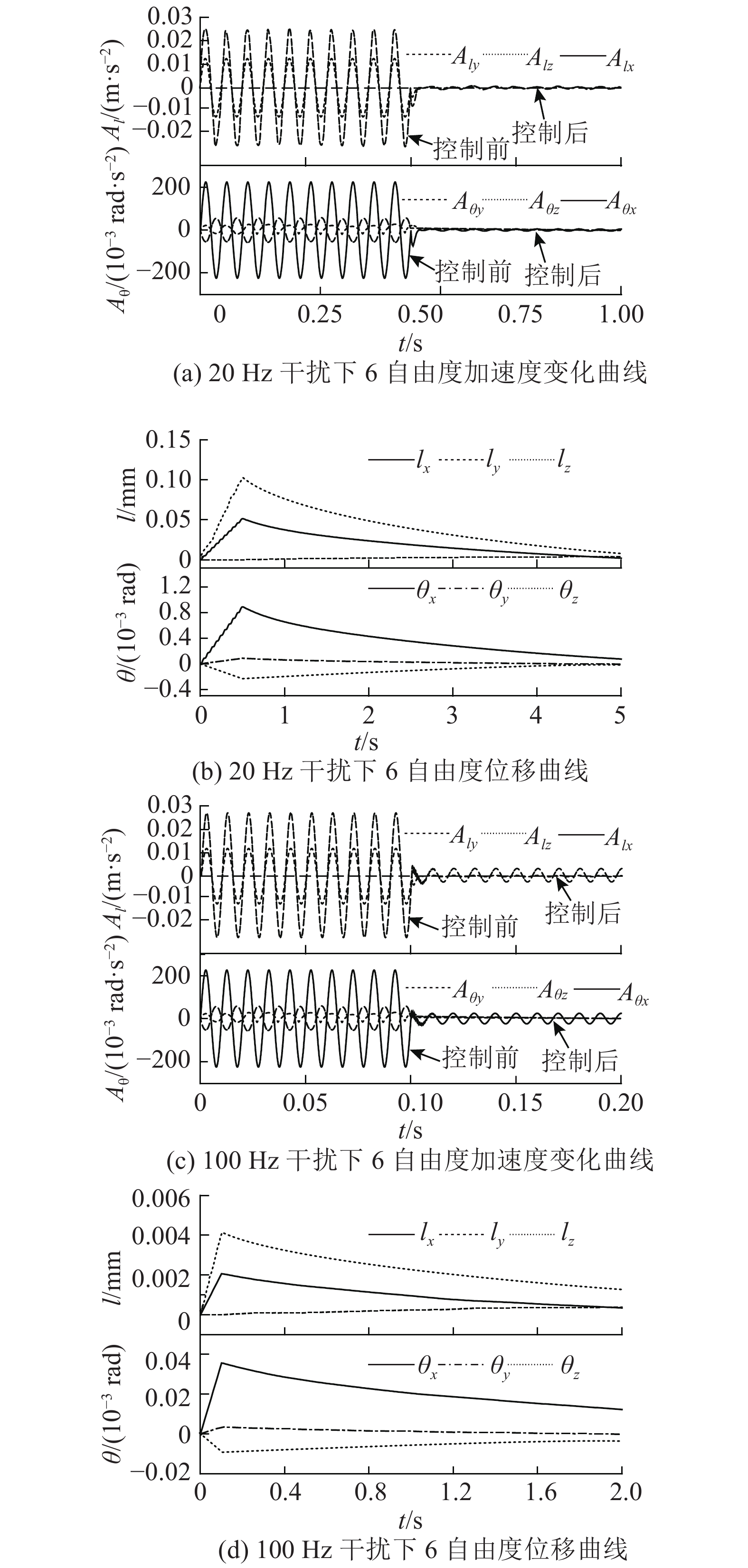
隔振试验结果分别如图8所示. 如图8(a)所示为浮台受20 Hz正弦直接干扰后沿6自由度方向的加速度变化曲线. 可以看出,在0.5 s进行隔振控制后,沿各轴的加速度
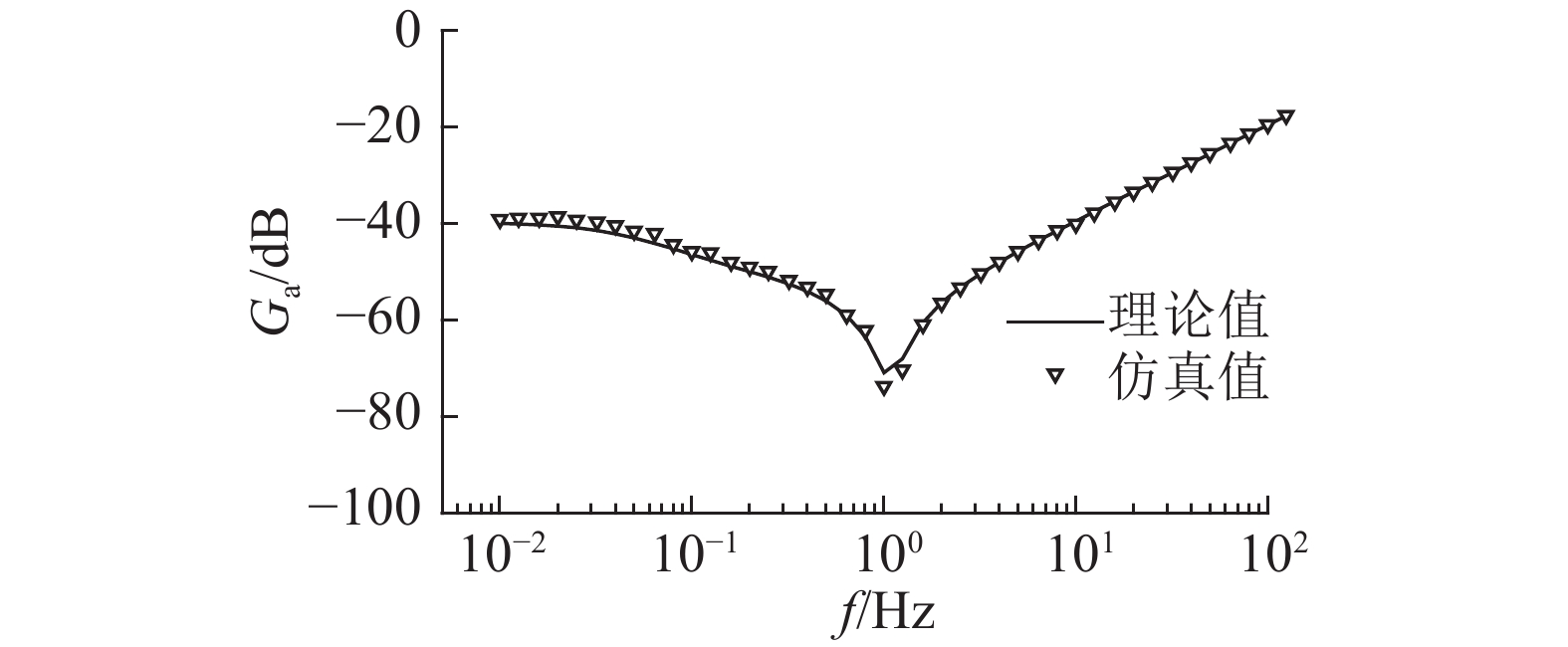
根据理论计算和对不同频率点的仿真分析,得到平台对0.01~100 Hz微振动干扰进行抑制的频率响应,如图9所示. 图中,Ga为微振动干扰加速度抑制效率,即隔振后的加速度与无控制时干扰加速度的比值. 根据图9所示,各频率点振动抑制效率的理论值和仿真值基本一致,对于0.01~1 Hz正弦直接干扰具有39~73 dB的抑制效率,且在1 Hz时达到最大;在1~100 Hz正弦直接干扰作用下,平台的抑制效率随着频率的增大而减小,在100 Hz时达到最小值,约为19 dB. 如图9所示,对20 Hz干扰的振动抑制效率约为33 dB,100 Hz对应为19.35 dB,与图8所示的结果一致.
|
图 8 20 Hz或100 Hz正弦干扰下浮台的6自由度加速度及浮台与基台间6自由度相对位移的控制结果 Fig. 8 Control results of 6-DOF accelerations of floater and 6-DOF relative displacements between floater and base under 20 Hz or 100 Hz sinusoidal disturbances |
|
图 9 平台对0.01~100 Hz正弦干扰进行抑制过程中浮台的加速度抑制效率频率响应 Fig. 9 Acceleration suppression efficiency frequency response of floater during suppression process of 0.01~100 Hz sinusoidal disturbances by platform |
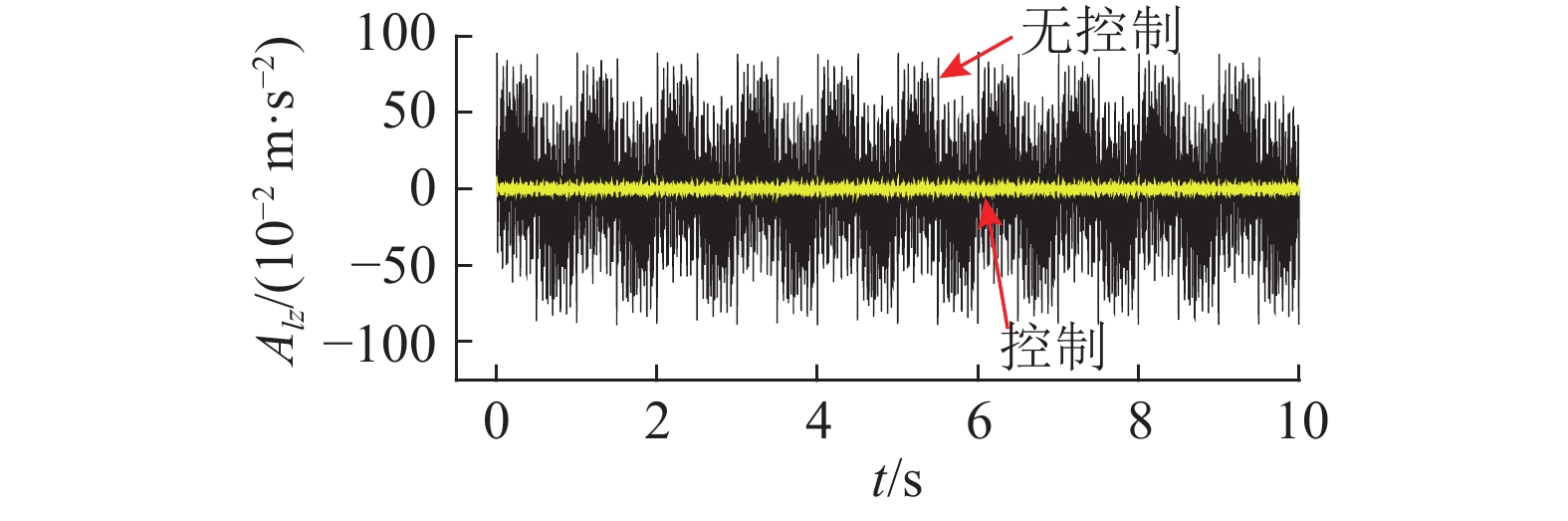
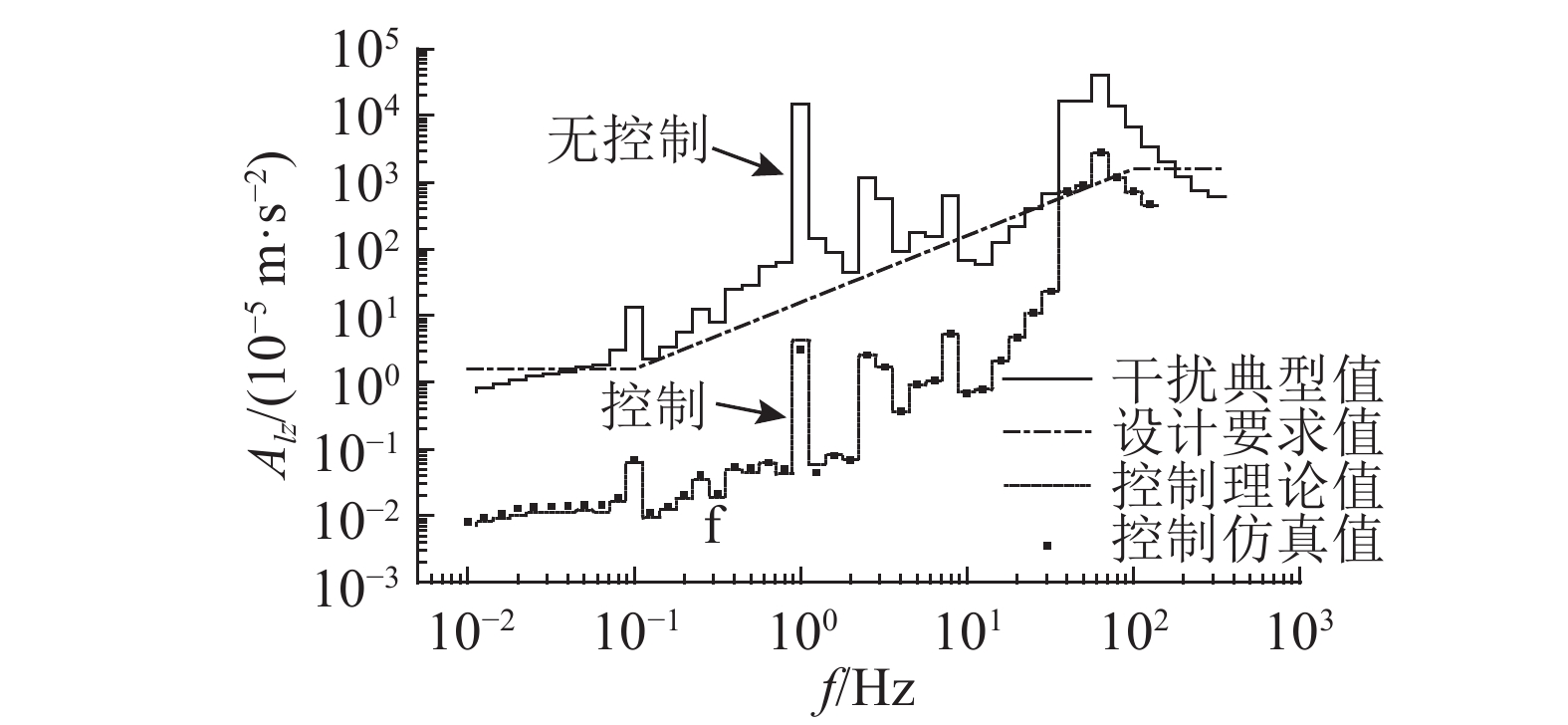
为了进一步分析平台的实际工作能力,将文献[17]所列出的ISS空间站典型微振动干扰直接输入到浮台的z轴开展振动抑制试验. 如图10所示为对上述典型干扰进行抑制的10 s时长的时域结果. 可以看出,在不进行控制的情况下,振动加速度最大值约为0.9 m/s2,进行隔振控制后的加速度最大值约为0.086 m/s2,干扰抑制效果明显. 如图11所示为对上述典型干扰进行抑制的频域结果. 其中,实线为空间站在0.01~100 Hz的典型干扰加速度,较大的干扰主要出现在1和64 Hz附近,都远远超出了空间站的设计要求. 平台在控制系统设计过程中,考虑了这一实际干扰情况,所设计的控制器对1 Hz附近的干扰具有很强的抑制作用. 根据图11所示平台控制结果的理论值及仿真值可以看出,平台对0.01~100 Hz微振动干扰进行了有效控制,除个别点(64 Hz)外,频率范围内的振动加速度量级基本都满足了空间站的设计要求.
|
图 10 空间典型干扰作用下浮台的加速度时域变化曲线 Fig. 10 Time domain change curves of floater acceleration under effect of space typical disturbances |
|
图 11 空间典型干扰作用下浮台的加速度频率响应 Fig. 11 Frequency response of floater acceleration under effect of space typical disturbances |
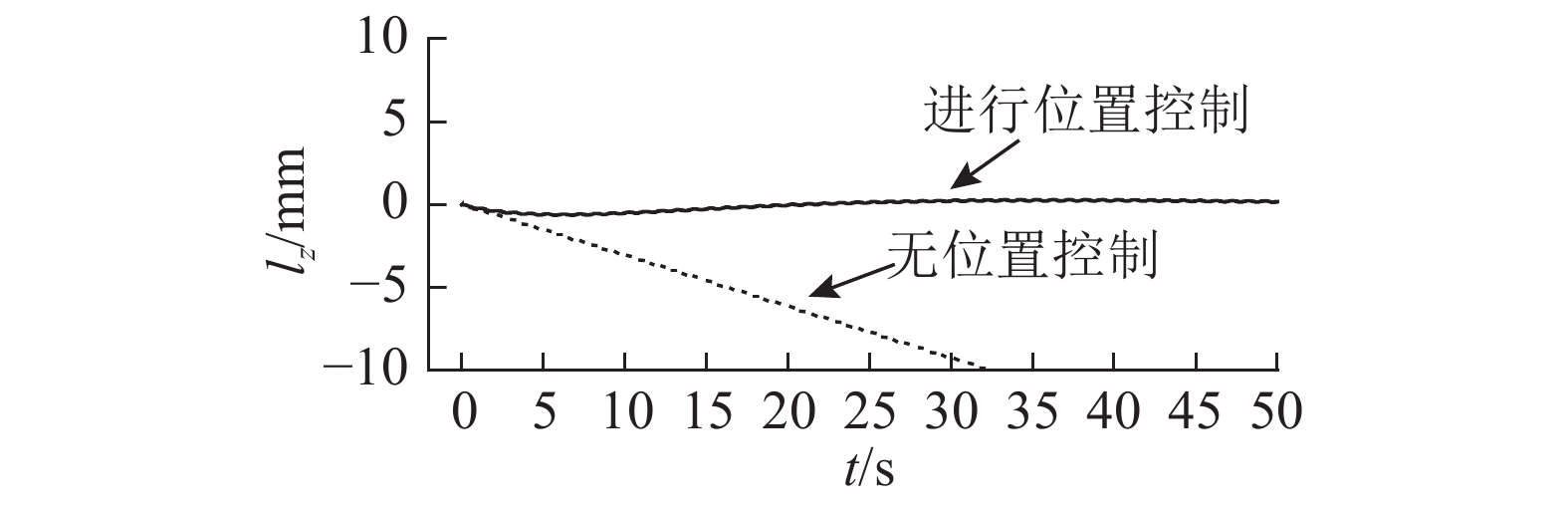
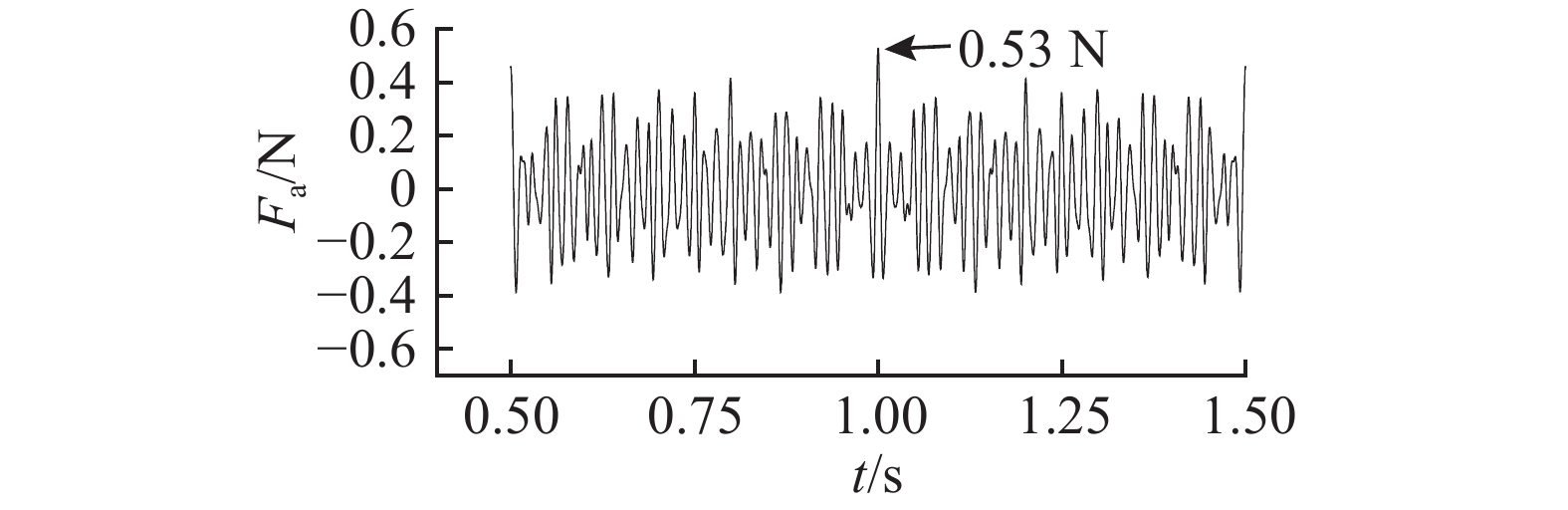
在对空间典型微振动干扰进行控制的过程中,对浮台与基台的相对位移和各作动器的输出力进行监测. 如图12所示为隔振控制过程中浮台与基台在初始50 s时的相对位移. 可以看出,若无位置控制,则浮台与基台间的相对位移随时间不断增大,在32.5 s附近超出了设计的±10 mm运动范围限制;在正常的隔振跟随控制下,浮台与基台间的相对位移虽在初始时刻稍有波动,但最大值不超过1 mm,且随着时间的增长,最终稳定在原点附近. 如图13所示为控制过程中某一主作动器的输出力随时间的变化曲线,图示的最大值0.53 N为控制过程中的最大力输出. 所设计二轴电磁作动器的各向额定输出力均为3 N,因此可以满足控制需要. 通过分析可知,所设计的定位隔振平台具备较强的隔振跟随能力.
|
图 12 空间典型干扰下浮台与基台的相对位移曲线 Fig. 12 Relative displacement curves between floater and base under effect of space typical disturbances |
|
图 13 空间典型干扰抑制过程中作动器输出力变化曲线 Fig. 13 Output force changing curves of actuator during space typical disturbances suppression process |
在上述各项试验中,各项仿真值均与理论值相当接近,说明了联合仿真结果的可靠性. 由于实际装置涉及各元器件的安装误差和实际性能偏差,仅对仿真中可能存在的较大误差进行分析. 相较于其他误差,最大的误差来源于相对位置测量单元. 如图5所示,当进行相对位置测量时,利用初始时刻分别在浮台和基台上的相应位置设置3组两两重合的“Marker”点,利用上述各组两点相对位移的测量值解算,得到浮台与基台的相对位置变化. 以图示的
| $\Delta { \varepsilon} {\rm{ = [}}\!\!\begin{array}{*{20}{c}} {\Delta {\varepsilon _{{{1x}}}}},\;{\Delta {\varepsilon _{{{1z}}}}},\;{\Delta {\varepsilon _{{{2x}}}}},\;{\Delta {\varepsilon _{{{2z}}}}},\;{\Delta {\varepsilon _{{{3x}}}}},\;{\Delta {\varepsilon _{{{3z}}}}} \end{array}\!\!{{\rm{]}}^{\rm{T}}}, $ | (14) |
则位置测量单元的测量误差可以表示为
| $\Delta { e}{\rm{ = }}G({ \varepsilon} )\Delta { \varepsilon} , $ | (15) |
式中:
(1)基于非接触式二轴电磁作动器,设计采用空间对称布置的非接触式隔振平台,实现敏感载荷与航天器间的无接触连接和定位隔振控制.
(2)基于ADAMS和MATLAB/Simulink软件,分别建立平台的机械系统仿真模型和控制系统仿真模型;利用得到的平台机电联合仿真模型,对定位和隔振性能进行仿真试验.
(3)仿真结果表明,利用ADAMS与MATLAB所建立的联合仿真模型,可以有效开展平台的动力学仿真试验;所设计的非接触式隔振平台具备高精度6自由度定位和姿态控制能力,在开展小范围定位控制时,沿各自由度方向的线位移误差和角位移误差分别小于10 μm和2×10−5 rad;所设计的非接触式隔振平台可以对浮台6自由度进行有效的隔振和跟随控制,针对典型空间微振动,对0.01~1 Hz正弦直接干扰具有39~73 dB的抑制效率且效率随着频率的增大而增大,对1~100 Hz正弦直接干扰具有19~73 dB的抑制效率且效率随着频率的增大而减小,在控制过程中浮台与基台的相对位移小于1 mm.
| [1] |
张振华, 杨雷, 庞世伟. 高精度航天器微振动力学环境分析[J]. 航天器环境工程, 2009, 26(6): 528-534. ZHANG Zhen-hua, YANG Lei, PANG Shi-wei. Jitter environment analysis for micro-precision spacecraft[J]. Spacecraft Environment Engineering, 2009, 26(6): 528-534. DOI:10.3969/j.issn.1673-1379.2009.06.007 |
| [2] |
徐道临, 赵智, 周加喜. 气动可调式准零刚度隔振器设计及特性分析[J]. 湖南大学学报: 自然科学版, 2013, 40(6): 47-52. XU Dao-lin, ZHAO Zhi, ZHOU Jia-xi. Design and analysis of an adjustable pneumatic vibration isolator with quasi-zero-stiffness characteristic[J]. Journal of Hunan University: Natural Sciences, 2013, 40(6): 47-52. |
| [3] |
HUANG X C, ZHANG Z G, SUN J Y, et al. Analytical stiffness model of a fluid-filled U-shaped bellows based three-parameter fluid damper for micro-vibration suppression[J]. Aerospace Science and Technology, 2017, 69: 357-369. DOI:10.1016/j.ast.2017.07.004 |
| [4] |
刘乃军, 牛军川. 2-PRC-PR(C)并联机构减振平台及其动力学特性[J]. 中南大学学报: 自然科学版, 2017, 48(4): 925-935. LIU Nai-jun, NIU Jun-chuan. 2-PRC-PR(C) parallel mechanism platform for vibration isolation and its dynamics[J]. Journal of Central South University: Science and Technology, 2017, 48(4): 925-935. |
| [5] |
LEE D O, PARK G, HAN J H. Experimental study on on-orbit and launch environment vibration isolation performance of a vibration isolator using bellows and viscous fluid[J]. Aerospace Science and Technology, 2015, 45: 1-9. DOI:10.1016/j.ast.2015.04.012 |
| [6] |
LEE D O, PARK G, HAN J H. Hybrid isolation of micro vibrations induced by reaction wheels[J]. Journal of Sound and Vibration, 2016, 363: 1-17. DOI:10.1016/j.jsv.2015.10.023 |
| [7] |
WANG C X, CHEN Y H, ZHANG Z Y. Simulation and experiment on the performance of a passive/active micro-vibration isolator[J]. Journal of Vibration and Control, 2018, 24(3): 453-465. DOI:10.1177/1077546316650130 |
| [8] |
LI W P, HUANG H, ZHOU X B, et al. Design and experiments of an active isolator for satellite micro-vibration[J]. Chinese Journal of Aeronautics, 2014, 27(6): 1461-1468. DOI:10.1016/j.cja.2014.10.012 |
| [9] |
DEFENDINI A, VAILLON L, TROUVE F, et al. Technology predevelopment for active control of vibration and very high accuracy pointing systems [C] // Proceedings of the 4th ESA International Conference on Spacecraft Guidance, Navigation and Control Systems. Noordwijk:[s.n.], 1999: 385–391.
|
| [10] |
SANNIBALE V, ORTIZ G G, FARR W H. A sub-hertz vibration platform for a deep space optical communication transceiver [C] // Proceedings of Volume 7199, Free-Space Laser Communication Technologies XXI. San Jose: SPIE, 2009.
|
| [11] |
LUO Q, LI D X, JIANG J P. Analysis and optimization of microvibration isolation for multiple flywheel systems of spacecraft[J]. AIAA Journal, 2016, 54(5): 1719-1731. DOI:10.2514/1.J053885 |
| [12] |
WU Y, YU K P, JIAO J, et al. Dynamic modeling and robust nonlinear control of a six-DOF active micro-vibration isolation manipulator with parameter uncertainties[J]. Mechanism and Machine Theory, 2015, 92: 407-435. DOI:10.1016/j.mechmachtheory.2015.06.008 |
| [13] |
KONG Y F, HUANG H. Vibration isolation and dual-stage actuation pointing system for space precision payloads[J]. Acta Astronautica, 2018, 143: 183-192. DOI:10.1016/j.actaastro.2017.11.038 |
| [14] |
刘勺斌, 杨洪波, 刘洋, 等. 基于Stewart平台的空间光学仪器主动隔振系统研究[J]. 噪声与振动控制, 2008, 28(2): 10-13. LIU Shao-bin, YANG Hong-bo, LIU Yang, et al. Study on an active vibration isolation system for spaceborne optical instrument based on Stewart platform[J]. Noise and Vibration Control, 2008, 28(2): 10-13. DOI:10.3969/j.issn.1006-1355.2008.02.004 |
| [15] |
YANG J F, XU Z B, WU Q W, et al. Dynamic modeling and control of a 6-DOF micro-vibration simulator[J]. Mechanism and Machine Theory, 2016, 104: 350-369. DOI:10.1016/j.mechmachtheory.2016.06.011 |
| [16] |
钱承, 鄂加强, 刘明, 等. Stewart 6自由度并联平台动力学模型振动分析[J]. 湖南大学学报: 自然科学版, 2016, 43(2): 36-42. QIAN Cheng, E Jia-qiang, LIU Ming, et al. Vibration analysis of the dynamic model of Stewart platform with six degrees of freedom[J]. Journal of Hunan University: Natural Sciences, 2016, 43(2): 36-42. |
| [17] |
GRODSINSKY C M, WHORTON M S. Survey of active vibration isolation systems for microgravity applications[J]. Journal of Spacecraft and Rockets, 2000, 37(5): 586-596. DOI:10.2514/2.3631 |
| [18] |
KIN Y K, WHORTON M S. Equations of motion for the g-LIMIT microgravity vibration isolation system [R]. Huntsville, Alabama: Marshall Space Flight Center, NASA/TM-2001-211301.
|
| [19] |
ZHANG Y K, DONG W B, LIU W, et al. Verification of the microgravity active vibration isolation system based on parabolic flight[J]. Microgravity Science and Technology, 2017, 29(6): 415-426. DOI:10.1007/s12217-017-9559-4 |
| [20] |
WU Q Q, YUE H H, LIU R Q, et al. Simulation of multi-closed loop control with feed forward control of micro-vibration isolation platform [C] // Proceeding of the ASME 2014 International Mechanical Engineering Congress and Exposition. Montreal: ASME , 2014.
|
| [21] |
YU Y P, CHEN S Q, WANG Y. Cascade active disturbance rejection optimal control for microgravity active vibration isolation system [C] // 2017 32nd Youth Academic Annual Conference of Chinese Association. Hefei: IEEE, 2017: 602–607.
|
| [22] |
YUN Y, WANG L, ZHANG B, et al. Design, experiments and multidisciplinary optimization of 2 degrees-of-freedom electromagnetic actuator for application in space vibration isolation[J]. Advances in Mechanical Engineering, 2017, 9(12): 1-15. |
| [23] |
SUN X Q, YANG B T, ZHAO L, et al. Optimal design and experimental analyses of a new micro-vibration control payload-platform[J]. Journal of Sound and Vibration, 2016, 374: 43-60. DOI:10.1016/j.jsv.2016.04.007 |
| [24] |
ZHANG X Y, DING X, WU D, et al. A component-level frequency tunable isolator for vibration-sensitive chips using SMA beams[J]. Review of Scientific Instruments, 2016, 87(6): 066106. DOI:10.1063/1.4953922 |
| [25] |
STABILE A, AGLIETTI G S, RICHARDSON G, et al. Design and verification of a negative resistance electromagnetic shunt damper for spacecraft micro-vibration[J]. Journal of Sound and Vibration, 2017, 386: 38-49. DOI:10.1016/j.jsv.2016.09.024 |
| [26] |
齐乃明, 张文辉, 高九州, 等. 空间微重力环境地面模拟试验方法综述[J]. 航天控制, 2011, 29(3): 95-100. QI Nai-ming, ZHANG Wen-hui, GAO Jiu-zhou, et al. The primary discussion for the ground simulation system of spatial microgravity[J]. Aerospace Control, 2011, 29(3): 95-100. |
| [27] |
沈建. 动量飞轮隔振平台性能仿真与最优控制研究[D]. 长沙:湖南大学, 2012. SHEN Jian. Study on performance simulation and optimal control of momentum flywheel isolation platform[D]. Changsha: Hunan University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10532-1012480314.htm |
| [28] |
ZHANG Y, XU S J. Vibration isolation platform for control moment gyroscopes on satellites[J]. Journal of Aerospace Engineering, 2012, 25(4): 641-652. DOI:10.1061/(ASCE)AS.1943-5525.0000156 |
| [29] |
ALAM M N, AKHLAQ A, RAHMAN N U. Dynamic analysis and vibration control of a multi-body system using MSC Adams[J]. Latin American Journal of Solids and Structures, 2015, 12(8): 1505-1524. DOI:10.1590/1679-78251598 |
| [30] |
YANG L H, SU K, LIU S Y, et al. Study on active vibration isolation system using neural network sliding mode control[J]. Journal of Vibroengineering, 2017, 19(8): 6904-6104. |
| [31] |
TANG C Y, ZHAO G Y, ZHOU W, et al. Research on suspension system based on fuzzy logic control [C] // Advanced Computer Control (ICACC), 2nd International Conference. Shenyang: IEEE, 2010: 5–8.
|
| [32] |
NAN Y H, XUAN D J, KIM J W, et al. Control of an active suspension based on fuzzy logic [C] // International Conference on Computer and Electrical Engineering. Phuket: IEEE, 2008: 303–307.
|
| [33] |
YANG C F, HE J F, JIANG H Z, et al. Modeling and simulation of 6-DOF parallel manipulator based on PID control with gravity compensation in Simulink/ADAMS [C] // International Workshop on Modelling, Simulation and Optimization. Hong Kong: IEEE, 2008: 391–395.
|
| [34] |
ZHU D L, QIN J Y, ZHANG Y, et al. Research on co-simulation using ADAMS and MATLAB for active vibration isolation system [C] // International Conference on Intelligent Computation Technology and Automation. Changsha: IEEE, 2010: 1126–1129.
|
| [35] |
陈志伟, 董月亮. MSC Adams多体动力学仿真基础与实例解析[M]. 北京: 中国水利水电出版社, 2012.
|
| [36] |
刘白雁.机电系统动态仿真: 基于MATLAB/Simulink[M]. 北京: 机械工业出版社, 2012.
|



