2. 上海卫星工程研究所,上海 200240
2. Shanghai Institute of Satellite Engineering, Shanghai 200240, China
在高分辨率光学遥感成像中,高分辨率与宽视场是矛盾的,主要原因在于成像器件的像元尺寸、像元数量受到工艺水平的限制,单一器件的高分辨成像视场较小. 一种有效的解决方法是利用传感器获取多幅包含一定重叠区域的高分辨率窄视场遥感图像,通过配准拼接成一幅高分辨率宽视场遥感图像.
随着敏捷成像技术的发展,越来越多的高分辨率遥感图像将由敏捷卫星获取,随着卫星姿态和其他成像条件的变化,图像配准的残余误差是不可避免的. 图像配准精度将对拼接质量和人眼视觉感官效果有重大的影响.
图像配准技术在近几十年发展迅速,基于特征的图像配准应用最广泛. Mikolajczyk等提出Harris-Laplace[1]与Harris-Affine[2]特征算子,分别具有尺度不变性以及仿射不变性. Lowe[3]提出SIFT特征点检测算子,通过在高斯差分尺度空间内寻找极值点的方法,获取同时具有尺度不变性、仿射不变性的特征点,精度达到亚像素级. Bay等[4]提出SURF特征检测算子,用Haar小波响应计算特征描述子,相比SIFT具有更好的光照强度不变性,速度能够达到SIFT的3倍. Rublee等[5]提出ORB特征,将FAST[6]特征与BRIEF[7]特征描述子进行结合与改进,相比于SIFT和SURF具有极高的效率.
在国内研究方面,冯宇平等[8]提出基于频域相位相关方法改进图像序列排序并确定重叠区域,用改进的Harris算子提取图像角点,效率提升40%. 何宾等[9]结合基于区域和基于特征的图像配准方法,提出快速的F-SIFT算法,发挥了FFT的运算快的特点. 李玉峰等[10]提出基于区域分块的SIFT拼接算法,通过分块减少无用搜索,效率提高50%. 在地面民用场合,Gao等[11]针对全景图像前、后景距离不一致引起的配准效果欠佳,提出将前、后景分割,使用2个单应性矩阵变换,消除拼接时前、后景错位的方法.
信息丰富、场景类型多样是高分辨率遥感图像的重要特征. 与海洋、田野等信息较少的区域相比,对那些包含道路、房屋的丰富细节区域有更高的拼接精度要求[12].
本文将包括2种具有明显特征区别场景的遥感图像定义为双场景类型遥感图像. 从人眼视觉出发,主观设定的遥感图像场景类型包括城市、森林、海洋、乡村田野、军港机场等. 当一幅遥感图像同时包括2种场景时,即符合本文所处理的图像对象范围.
为了符合人眼视觉的观察特点,本文从配准拼接算法的流程出发,根据图像内容,利用分块信息熵聚类的方法进行大区域分割,优化特征点匹配残余误差目标函数,对区域误差权重进行再分配,减小细节丰富区域特征点匹配残差,提高拼接精度,从而提升该类图像的拼接质量.
本文使用SIFT特征点检测算子进行图像特征点检测.
1 图像配准方法遥感图像具备无穷远成像(物距相同)、信息量大、细节丰富、景物关联性强等特征.
如图1所示,通常人们更关心的是图像上半区域(建筑道路部分)的配准拼接质量.

|
图 1 一幅包括2种场景的典型遥感图像 Fig. 1 Typical remote sensing image consists of two scene types |
对于2幅有重叠区域的遥感图像,传统的方法如下:分别对2幅图像进行SIFT特征点提取,进行特征点匹配,采用RANSAC[13](随机抽样一致)等方法去除误匹配点,获得描述2幅图像之间投影变换的单应性矩阵.
针对图1所示的这一类具有明显特征区域区别的遥感场景,在上述步骤之后对单应性矩阵进行优化:将图像规则分割为若干子块,进行分块信息熵聚类,将图像分割为若干大区域;根据聚类分割结果与信息熵统计信息,优化特征点匹配残差这一目标函数;使用Levenberg-Marquardt[14]算法,迭代求解微小增量矩阵,获得优化后的单应性矩阵;开展羽化融合拼接. 方法流程如图2所示.

|
图 2 基于误差权重再分配的遥感图像配准拼接优化算法流程 Fig. 2 Flow chart of registration and stitching optimization algorithm for remote sensing image based on weighted value reassignment in RMSE |
采用投影变换模型,2幅有重叠区域的图像间的几何变换关系可以通过单应性矩阵
| $\left[ {\begin{array}{*{20}{c}} \!\!\! X \!\!\! \\ \!\!\! Y \!\!\! \\ \!\!\! 1 \!\!\! \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \!\!\! {{h_{00}}}&{{h_{01}}}&{{h_{02}}} \!\!\! \\ \!\!\! {{h_{10}}}&{{h_{11}}}&{{h_{12}}} \!\!\! \\ \!\!\! {{h_{20}}}&{{h_{21}}}&{{h_{22}}} \!\!\! \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \!\!\! x \!\!\! \\ \!\!\! y \!\!\! \\ \!\!\! 1 \!\!\! \end{array}} \right] \sim \left[ {\begin{array}{*{20}{c}} \!\!\! {{h_1}}&{{h_2}}&{{h_3}} \!\!\! \\ \!\!\! {{h_4}}&{{h_5}}&{{h_6}} \!\!\! \\ \!\!\! {{h_7}}&{{h_8}}&1 \!\!\! \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \!\!\! x \!\!\! \\ \!\!\! y \!\!\! \\ \!\!\! 1 \!\!\! \end{array}} \right].$ | (1) |
转换矩阵
由于通常获取的匹配特征点组远远超过4对,且在这些匹配的特征点组中存在误匹配的情况,选用RANSAC方法来剔除误匹配的特征点组,并优选4组匹配的特征点组. 具体的方法如下:在一个循环次数足够多的过程中,每次随机选择4组匹配的特征点来求解
| ${\rm RMSE} = \sqrt {{{\left( {{x_i}' - {X_i}} \right)}^2} + {{\left( {{y_i}' - {Y_i}} \right)}^2}} \leqslant \varepsilon .$ | (2) |
式中:
根据式(3)、(4),可以将待配准图像向参考图像进行坐标变换
| $x' = \frac{{{h_1}x + {h_2}y + {h_3}}}{{{h_7}x + {h_8}y + 1}},$ | (3) |
| $y' = \frac{{{h_4}x + {h_5}y + {h_6}}}{{{h_7}x + {h_8}y + 1}}.$ | (4) |
由随机4组对应特征点得到的单应性矩阵初始解,虽然完全匹配该4组对应特征点,但通常情况下不是最优解(最优解通常不完全符合任意4组对应特征点,但对于所有特征点来说是全局最优解). 对
| ${{H}} \leftarrow \left( {{{I + D}}} \right){{H}}.$ | (5) |
式中:D为微小增量矩阵,
| ${{D}} = \left[ {\begin{array}{*{20}{c}} {{d_1}}&{{d_2}}&{{d_3}} \\ {{d_4}}&{{d_5}}&{{d_6}} \\ {{d_7}}&{{d_8}}&0 \end{array}} \right]\text{;}$ |
| $x'' = \frac{{\left( {1 + {d_1}} \right)x' + {d_2}y' + {d_3}}}{{{d_7}x' + {d_8}y' + 1}},$ | (6) |
| $y'' = \frac{{{d_4}x' + \left( {1 + {d_5}} \right)y' + {d_6}}}{{{d_7}x' + {d_8}y' + 1}}.$ | (7) |
优化的目的是使得
| $E\left( {\tilde { d}} \right) = \left\| {{x}'' - {X}} \right\|_2^2 = \sum\limits_i {{{\left| {\tilde { x}'{'_i} - {{\tilde { X}}_i}} \right|}^2} \approx } \sum\limits_i {{{\left| {{{J}_{{i}}}\tilde { d} + {{{\varepsilon}} _i}} \right|}^2}} .$ | (8) |
式中:
| $\begin{aligned} {J} = & {\left. {\frac{{\partial \widetilde { x}''}}{{\partial \widetilde d}}} \right|_{\tilde d = 0}} = \\ & \left[ {\begin{array}{*{20}{c}} {x'}&{y'}&1&0&0&0&{ - x{'^2}}&{ - x'y'}\\ 0&0&0&{x'}&{y'}&1&{ - x'y'}&{ - y{'^2}} \end{array}} \right]; \end{aligned}$ | (9) |
目标函数中已知粗优化后的
对于如图1所示,很明显拥有2种或以上场景类型的遥感图像,通常对于细节丰富区域的拼接要求更高,例如城市道路、楼房;对于大海、田野细节不丰富的区域,人眼敏感度低,拼接要求较低. 若将细节丰富、细节较少的区域区别对待,重新分配特征点匹配残差,则可在不牺牲图像总体视觉效果的前提下,提升细节丰富区域的拼接质量. 具体来说,可以通过修改剩余误差目标函数来实现,将式(8)改写为
| $E\left( {\tilde { d}} \right) = \sum\limits_{j = 1}^n {{w_j}} \sum\limits_i {{{\left| {{{{J}}_i}\tilde { d} + {{ \varepsilon} _i}} \right|}^2}} .$ | (10) |
式中:
| $\sum\limits_{j = 1}^n {{w_j}} = n.$ | (11) |
针对优化后的匹配残差优化函数,可以利用Levenberg-Marquardt算法来求解最优增量矩阵
| $\widetilde { d} = {\left( {{{{J}}^{\rm T}}{{J}} + \lambda {\rm diag}\left( {{{{J}}^{\rm T}}{{J}}} \right)} \right)^{ - 1}}{{{J}}^{\rm T}}{ \varepsilon} .$ | (12) |
式中:
由1.1节可知,优化的关键在于根据图像信息,赋予多纹理区域更高的权重,从而提升细节丰富区域的配准拼接效果.
纹理信息是一种局部的统计信息,无法从单一像素获取. 尽管随着区域的移动,图像纹理细节发生变化,图像内容能够归类到为数不多的几种场景类型,如森林、海洋、沙漠、城市(道路、楼房)等;可以将一片区域内的同一类场景进行相同处理,即赋予相同的特征点残差优化权值.
针对遥感图像的上述特点,提出分块图像信息熵聚类的方法. 将遥感图像分割成2个或以上大场景区域,按照每一个分割的统计信息,对同一场景类型的区域赋予特征残差再分配的权值.
如图3所示为2幅包含重叠区域的待配准图像,截取自WorldView-2拍摄的一幅法国遥感图像,分辨率为0.5 m,两者之间的亮度存在一定差异. 将第1张称为参考图像,第2张称为配准图像.

|
图 3 2幅包含重叠区域、存在亮度差异的待配准遥感图像 Fig. 3 Two remote sensing images to be registered with overlap regions and different radiation conditions |
将参考图像进行周期性规则的分块,取每一块大小为30×30像素,如图4所示.

|
图 4 参考图像周期性规则分块 Fig. 4 Regular segmentation of reference image |
计算每一子块的熵,用来度量局部信息量的多少,即细节的丰富程度,图像熵[17]的定义如下:
| $H = - \sum {{P_i}} {\log _a}{P_i}.$ | (13) |
式中:
信息熵在信息论中所代表的是变量的不确定性(随机性). 变量的不确定性越大,熵越大. 图像熵反映灰度分布的分散程度,像素灰度的随机性大,表示选取到任一灰度的概率趋向于相同. 以8位灰度图像为例,可以证明:图像熵H最大值为8,当且仅当256个灰度级概率均为1/256 时能够取到最大值;最小值为0,当且仅当只存在1个灰度级,该灰度级概率为1,其他灰度级概率都为0时能够取到最小值.
简而言之,灰度级概率分布越均匀(随机性高),图像熵越高,灰度级越多,纹理细节更加丰富;灰度级概率分布越不均匀(随机性低),图像熵越低,纹理细节会相对较少(极端情况是仅存在一个灰度级,所有像素为同一灰度,不存在任何纹理细节).
通常而言,人眼视觉对纹理细节更丰富(信息熵较高)的区域更感兴趣,对细节相对较少(信息熵较低)的区域兴趣较低.
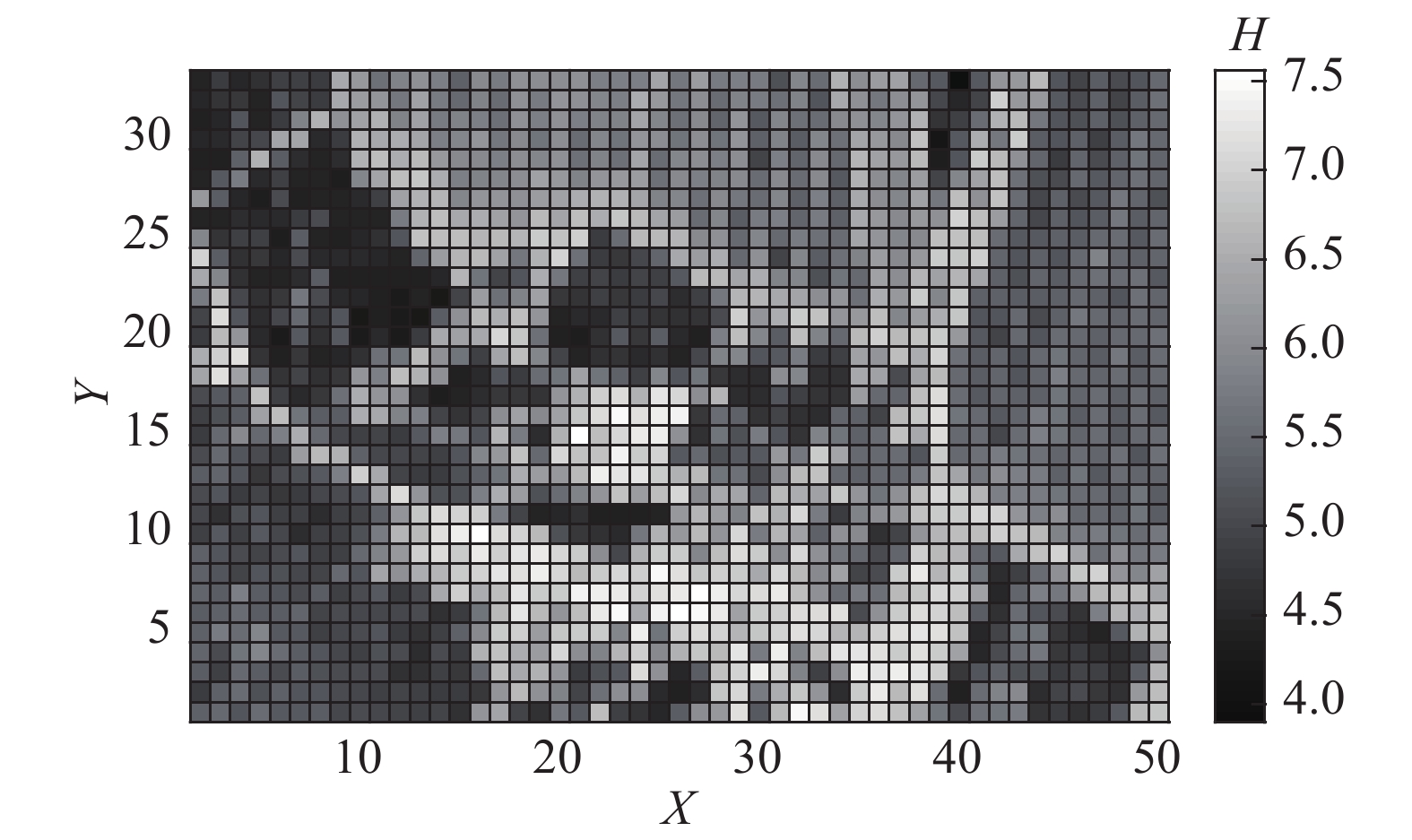
|
图 5 参考图像信息熵图 Fig. 5 Entropy map of reference image |
根据每一子块的信息熵,使用k-means方法进行聚类. 本文针对的是双场景类型遥感图像,聚类数量为2.
k-means方法的使用步骤如下:将尺寸为34×50的信息熵图展开为1×1 700的数组,数组中的每个值为30×30大小子块的信息熵;选取任意2个值为初始中心值,计算剩余子块到这2个中心的距离,选取较小的距离划分入2个类别;计算每一类别内子块信息熵的均值,作为2类区块各自的新中心值;重复上述操作,直到前、后两次的聚类不再发生变化,这样得到的2类区块即对应图像上按照信息熵划分的2类场景. 结果如图6所示,参考图像大致分为楼房树木(白色)、田野(黑色)两大场景,特征点按照位置被归入这2个区域.

|
图 6 参考图像信息熵k-means聚类结果 Fig. 6 Segment result of reference image after k-means clustering |
利用k-means方法得到的2个聚类中心E1=6.526 0,E2=5.170 7,各自表征每一场景类型的信息熵均值. 根据该值,给出特征点匹配残差再分配的权重为
| ${w_1} = \frac{{2{E_1}}}{{{E_1} + {E_2}}},$ | (14) |
| ${w_2} = \frac{{2{E_2}}}{{{E_1} + {E_2}}}.$ | (15) |
将式(14)、(15)代入式(10),对目标函数进行优化.
为了考察特征点误差权重再分配的实际效果,开展2组实验:A组,不进行权重分配,即

|
图 7 全局优化与权重再分配优化配准拼接结果对比 Fig. 7 Result comparison between unweight global optimization and weighted reassignment optimization |
比较图7(b)、(c)可知,A组的图像右侧草地边缘存在错位,B组正常. 比较图7(d)、(e)可知,A组院子的边缘存在错位,B组正常. 比较图7(f)、(g)可知,B组人工加入的十字标记完全重合,说明配准精确,在亚像素级;A组的十字标记未完全重影,且存在模糊,结合均值融合的操作表明,配准存在较大误差,至少超过1像素.
A组采用一般的全局优化方法,B组采用提出的按照权重分配残差的方法,对于权重分配较高的区域具有良好的配准效果提升. 原因是全局优化的方法具有较大的随机性. RANSAC过程不可能遍历所有的4对特征点组合,因此单应性矩阵的初始解存在随机性;在全局优化中,各区域的特征点对于匹配残差函数的贡献权重相同,SIFT算子对于遥感图像各类场景的特征点搜索能力都十分强,因此有较大概率出现人眼视觉不感兴趣(信息熵较低)的场景区域配准精度高,人眼视觉感兴趣(信息熵较高)的场景区域配准精度低的情况. 该方法根据图像信息熵的统计特征,为不同区域的特征点按照人眼视觉的一般感受强制分配优化权重,避免了全局优化方法的随机性,提高了配准过程的稳定程度.
2 遥感图像拼接实验结果与讨论为了进一步说明该方法针对这类双场景类型遥感图像提高拼接精度的有效性,使用上述步骤开展遥感场景拼接实验,利用特征点配准残差RMSE作为指标定量考察. 如图8所示为2幅存在重叠区域的遥感图像. 从人眼视觉的角度可以看出,遥感图像包含两大类型的场景.

|
图 8 2幅待配准遥感图像与聚类分块预处理 Fig. 8 Two remote sensing images to be registered and clustering segmentation preprocessing |
使用基于信息熵聚类的区域误差权重再分配对配准进行优化,采用羽化融合的方法进行拼接. 分块信息熵的聚类结果如图8(c)所示,聚类数量设置为2,整幅图像被分为2块大的场景区域,分别为城市建筑、山地. 拼接结果如图9所示.

|
图 9 两幅遥感图像的羽化拼接结果 Fig. 9 Feathering and stitching results of two remote sensing images |
对于该组遥感图像,计算配准之后的特征点匹配残差. 通过特征点初始查找、匹配,再利用RANSAC方法去除误匹配点之后,得到初始单应性矩阵(无优化). 对单应性矩阵进行全局优化(不分配权重),可以计算所有特征点的剩余匹配误差;对单应性矩阵使用基于信息熵聚类的区域误差权重再分配方法进行优化,同样计算所有特征点的剩余匹配误差. 以该误差作为判据,评价拼接效果,如表1、2所示.
| 表 1 参考图像特征点数量 Table 1 Number of feature points in reference image |
| 表 2 无优化、全局优化、权重再分配优化方法在全局、细节丰富区域、细节较少区域的特征点匹配残差结果比较 Table 2 Comparison of residual error of feature points among no optimization,unweighted global optimization and weighted reassignment optimization approaches,separately in global region,rich detail area and poor detail area |
在该组实验中,细节丰富的区域为城市建筑区域,细节较少的区域为山地森林区域. 根据1.3节可知,从人眼主观观察的角度证明可以提升细节丰富区域的拼接效果. 以下从客观指标来分析.
由表1可知,细节丰富的区域特征点数远多于细节较少的区域.
由表2可知,与仅使用RANSAC计算初始单应性矩阵相比,使用无差别优化(不分配权重)的方法,全局、细节丰富区域、细节较少区域的特征点匹配残差均减小,说明了原始无差别优化方法的有效性;与仅使用RANSAC方法计算初始单应性矩阵相比,提出的基于信息熵聚类的区域误差权重再分配方法,全局、细节丰富区域、细节较少区域的特征点匹配残差都减小;与无差别优化方法相比,提出方法在保持全局特征点匹配残差变化不大的情况下,细节丰富区域特征点匹配残差降低了14%,细节较少区域特征点匹配残差仅增加7%,即一定程度上牺牲了山地森林区域(细节较少区域)的配准拼接质量,提升了城市道路区域(细节丰富区域)的配准拼接质量,说明了该方法在针对特定遥感场景提升图像配准拼接质量的有效性.
综合上述分析,该方法能够基于图像的信息特征,利用分块信息熵聚类的方法,将图像分为2个较大区域的场景类型;利用平均信息熵,衡量图像各区域的信息丰富程度,作为特征点匹配残差优化目标函数中的权重值参数,进行单应性矩阵(转换矩阵)的迭代优化,从而实现特征点残差的再分配,减小细节丰富区域的特征点匹配残差,提升该区域的配准拼接质量,避免全局优化方法的随机性,提高配准过程的稳定程度. 本文方法充分结合了遥感图像的场景特性与观测需要.
3 结 语针对一类包括2个具有明显特征区别场景的遥感图像,提出基于误差权重再分配的配准拼接优化算法. 利用子块图像信息熵聚类的方法,将遥感图像分割成2个大区域,对应遥感场景中的城市道路建筑、森林、海洋等场景类型. 统计每一大区域的平均信息熵,作为误差权重分配的依据,优化了特征点匹配残差的目标函数;根据重新分配的误差权重,减小细节丰富区域特征点匹配残差,提高拼接精度,降低随机性,提升配准过程的稳定程度,保证图像整体的拼接质量不发生太大变化. 实验表明,利用本文方法能够大幅提升细节丰富区域(如道路、建筑等)的配准精度,细节丰富区域特征点匹配残差降低14%,从而提升拼接质量,满足人眼视觉特性的需求,符合高分辨率遥感卫星常规对地成像任务的一般要求.
| [1] |
MIKOLAJCZYK K, SCHMID C. Indexing based on scale invariant interest points [C] // Proceedings of the 8th IEEE International Conference on Computer Vision (ICCV). Vancouver: IEEE, 2001: 525–531. https://www.researchgate.net/publication/3906069_Indexing_based_on_scale_invariant_interest_points
|
| [2] |
MIKOLAJCZYK K, SCHMID C. Scale and affine invariant interest point detectors[J]. International Journal of Computer Vision, 2004, 60(1): 63-86. DOI:10.1023/B:VISI.0000027790.02288.f2 |
| [3] |
LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [4] |
BAY H, ESS A, TUYTELAARS T, VAN GOOL L. Speeded-Up Robust Features (SURF)[J]. Computer Vision and Image Understanding, 2008, 110(3): 346-359. DOI:10.1016/j.cviu.2007.09.014 |
| [5] |
RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB: an efficient alternative to SIFT or SURF [C] // Proceedings of 2011 IEEE International Conference on Computer Vision (ICCV). Barcelona: IEEE, 2012: 2564–2571. https://www.researchgate.net/publication/221111151_ORB_an_efficient_alternative_to_SIFT_or_SURF
|
| [6] |
ROSTEN E, DRUMMOND T. Machine learning for high-speed corner detection [C] // 9th European Conference on Computer Vision. Graz, Austria: Springer, 2006: 430–443. https://link.springer.com/chapter/10.1007%2F11744023_34
|
| [7] |
CALONDER M, LEPETIT V, STRECHA C, et al. Brief: binary robust independent elementary features [C] // 11th European Conference on Computer Vision. Heraklion, Crete, Greece: Springer, 2010: 778–792.
|
| [8] |
冯宇平, 戴明, 孙立悦, 等. 图像自动拼接融合的优化设计[J]. 光学精密工程, 2010, 18(2): 470-476. FENG Yu-ping, DAI Ming, SUN Li-yue, et al. Optimized design of automatic image mosaic[J]. Optics and Precision Engineering, 2010, 18(2): 470-476. |
| [9] |
何宾, 陶丹, 彭勃. 高实时性F-SIFT图像拼接算法[J]. 红外与激光工程, 2013, 42(增 2): 440-444. HE Bin, TAO Dan, PENG Bo. High real-time F-SIFT image mosaic algorithm[J]. Infrared and Laser Engineering, 2013, 42(增 2): 440-444. |
| [10] |
李玉峰, 李广泽, 谷绍湖, 等. 基于区域分块与尺度不变特征变换的图像拼接算法[J]. 光学精密工程, 2016, 24(5): 1197-1205. LI Yu-feng, LI Guang-ze, GU Shao-hu, et al. Image mosaic algorithm based on area blocking and SIFT[J]. Optics and Precision Engineering, 2016, 24(5): 1197-1205. |
| [11] |
GAO J, KIM S J, BROWN M S. Constructing image panoramas using dual-homography warping [C] // Proceedings of 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Colorado Springs: IEEE, 2011: 49–56. https://www.researchgate.net/publication/224254795_Constructing_image_panoramas_using_dual-homography_warping
|
| [12] |
CHEN J, FENG H, PAN K, et al. An optimization method for registration and mosaicking of remote sensing images[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(2): 697-703. DOI:10.1016/j.ijleo.2013.07.034 |
| [13] |
WU X, ZHAO Q, BU W. A SIFT-based contactless palmprint verification approach using iterative RANSAC and local palmprint descriptors[J]. Pattern Recognition, 2014, 47(10): 3314-3326. DOI:10.1016/j.patcog.2014.04.008 |
| [14] |
WANG Z, KIEU H, NGUYEN H, et al. Digital image correlation in experimental mechanics and image registration in computer vision: similarities, differences and complements[J]. Optics and Lasers in Engineering, 2015, 65(1): 18-27. |
| [15] |
SZELISKI R. Image alignment and stitching: a tutorial[J]. Foundations and Trends® in Computer Graphics and Vision, 2006, 2(1): 1-104. DOI:10.1561/0600000009 |
| [16] |
CHANG C H, SATO Y, CHUANG Y Y. Shape-preserving half-projective warps for image stitching [C] // Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Columbus: IEEE, 2014: 3254–3261. https://www.researchgate.net/publication/286594558_Shape-Preserving_Half-Projective_Warps_for_Image_Stitching
|
| [17] |
BRINK A D. Image models and the definition of image entropy applied to the problem of unsupervised segmentation [D]. Johannesburg: University of the Witwatersrand, 2016.
|



