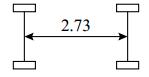运营状态中的公路桥梁车辆荷载实质上是一个复杂的随机过程，描述车辆荷载状态的车辆间距、车速、车辆总重、车辆轴重、车辆横向分布等参数均具有很强的随机性；车辆荷载具有地域性、路段性的特点，加之近年来车流量的快速增长和车辆的超载现象，如何建立与桥梁运营状态中交通组成相适应的车辆荷载，开展结构计算已成为一个亟待解决的问题. 采用实测车辆数据建立随机车流模型，根据该模型开展桥梁荷载效应研究，对桥梁设计及运营安全评估均具有重大的现实意义.

目前，国内外众多学者对公路桥梁的随机车流及荷载效应开展大量卓有成效的研究工作. Mayrai^[1]利用移动称重系统，对美国新泽西州的一座桥梁车重数据进行统计分析，提出预测最大车辆荷载和车辆荷载效应的新方法，利用该方法预测不同重现期的最大载荷. Castillo等^[2]采用贝叶斯理论，运用Gamma随机变量建立车流量的预测模型. Jabari等^[3]利用元胞自动机(CA)，建立能够模拟车辆加速、减速和超车等行为的随机车流模型. 余志武等^[4]建立预测交通量增长的灰色高斯混合模型，利用Markov链得到考虑交通量增长的随机车流模型. 孙守旺等^[5]基于动态称重系统得到的车辆信息，以轴组类型为依据，对所有车辆进行分类及筛选，建立6种主要车型的车重、车距、车道交通量、轴重与轴距的统计模型，基于损伤等效原则给出6种车型的疲劳等效标准车辆. 郭彤等^[6]基于实测数据，建立用于公路桥梁可靠性评估的车辆荷载多峰分布概率模型. 宗周红等^[7]基于WIM系统，开展特定对象（新沂河大桥）的车辆荷载模型研究. 目前，在随机车流模拟中，对各参数的相关性，尤其是对荷载效应有直接影响的轴重的相关性研究比较缺乏，如何建立考虑轴重相关的随机车流模型并分析荷载效应是一个亟待研究的问题.

本文基于宜泸高速公路车辆动态称重系统(WIM)的实测数据，对该路段实际行驶的车辆进行分类，建立典型车辆并统计车型、车道所占比例. 对日车流量、车辆间距等进行统计，建立概率模型. 分析各车型轴重相关性，建立考虑相关性的轴重联合概率模型. 应用MATLAB平台编制随机车流模拟程序，采用影响线加载法，分析随机车流的荷载效应，与设计规范的荷载效应进行对比，探讨考虑轴重相关与不考虑时荷载效应的差别.

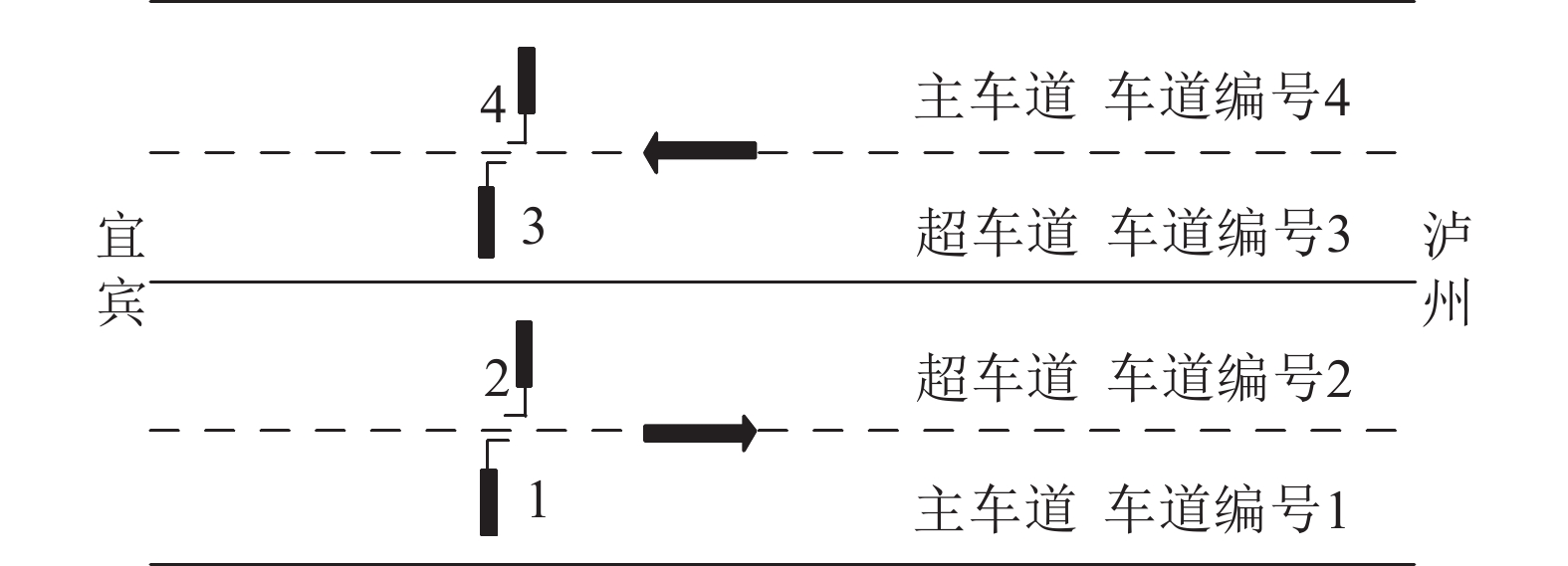
1 随机车流模拟

南溪长江大桥是宜泸高速公路上一座跨越长江的特大钢箱梁悬索桥，桥梁建成后为对桥梁通行车辆情况进行监测，安装了车辆动态称重系统(WIM). 采集车辆的车流量、车道、车型、车速、轴重和总重等信息，该系统平面布置如图1所示，利用该系统2015年6月—2016年7月的实测数据.

1.1 车型分类及占有率

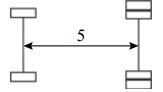
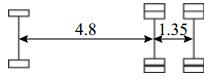
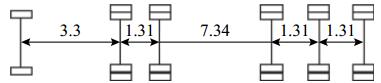
该桥梁上行驶的车辆种类繁多，按照车型相近、轴数相等原则对相近车型进行统计. 采用的6种典型车型如表1所示. 采用实测数据，各车道的车辆占有率如表2所示. 表中，p₁~p₄分别为1~4车道的车辆占有率. 6种典型车型在各车道的车辆占有率如表3所示.

1.2 日车流量

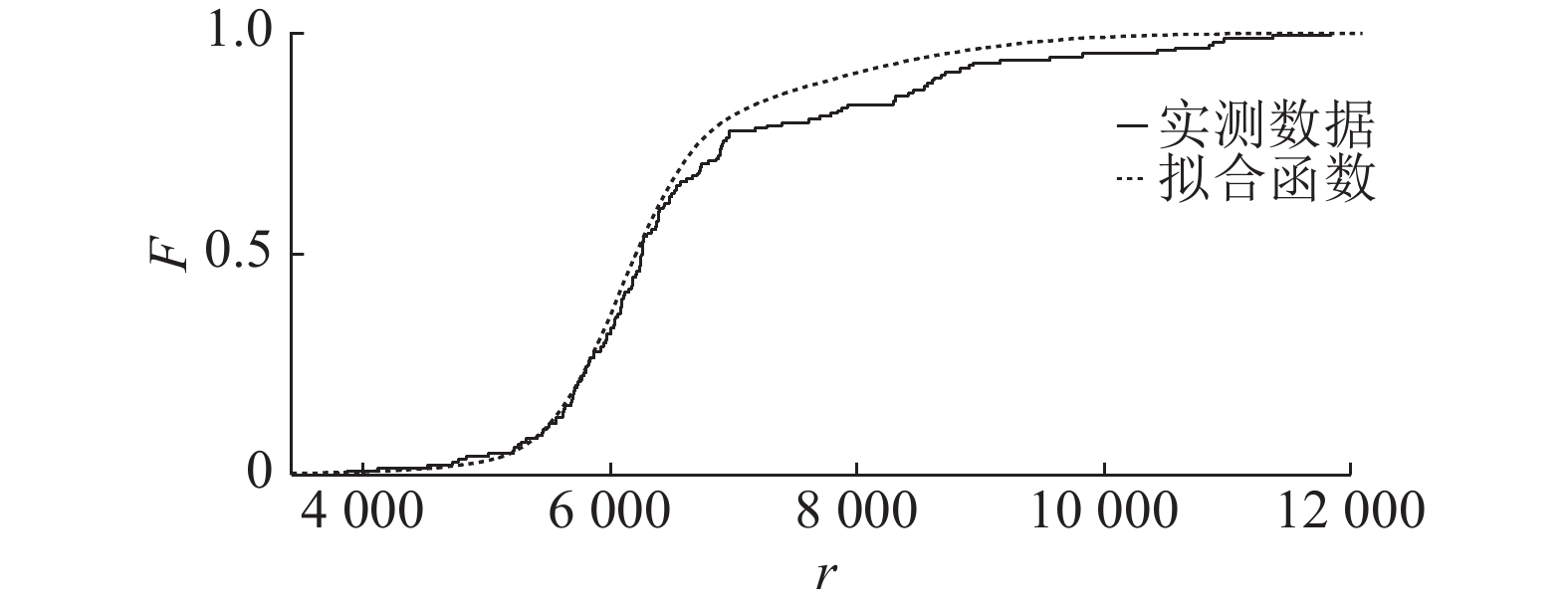
对实测日车流量进行统计分析，采用高斯混合分布对日车流量r进行拟合, 利用K-S法对拟合优度进行检验. 显著性水平为0.05时的拟合结果满足K-S检验，分布函数拟合情况见图2. 图中，F为累积概率. 相关参数见表4.

1.3 车距

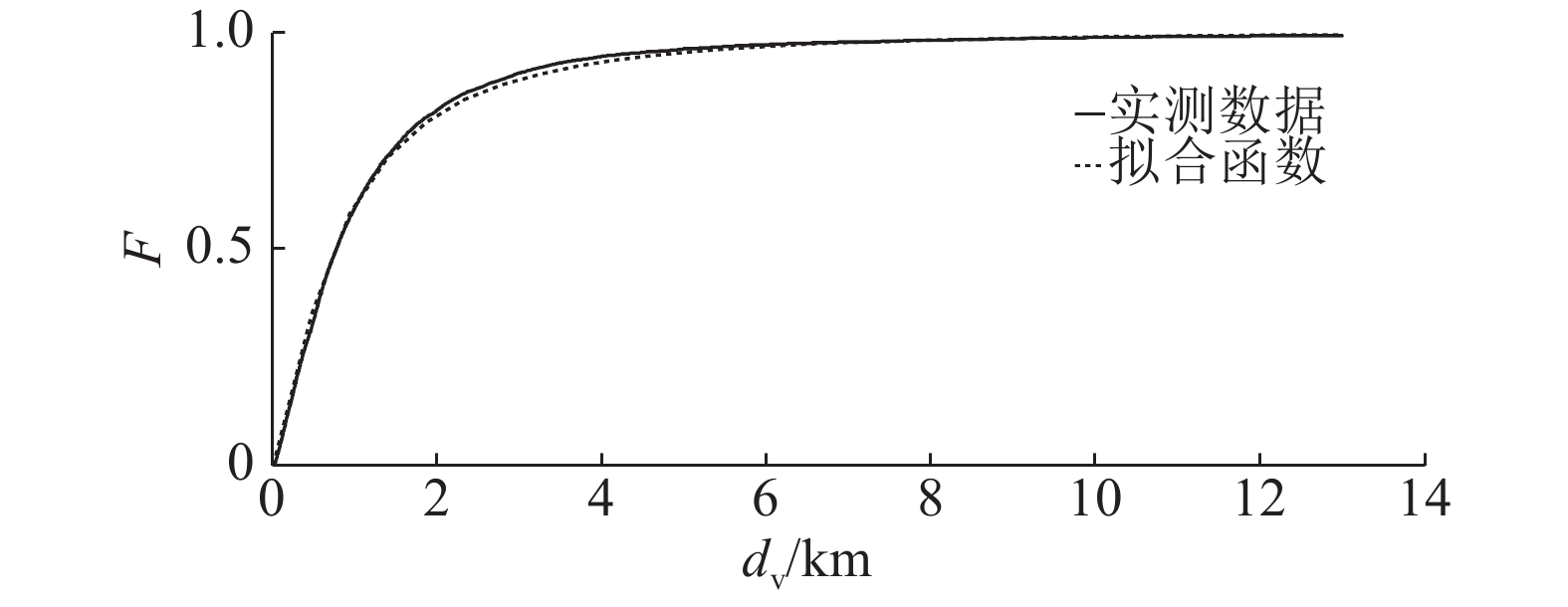
通常根据车距（时间间隔界限值往往为3 s），将车流分为一般运行状态和密集运行状态，分别开展研究^[8]. 本文主要研究随机车流作用引起的极端响应，不考虑运行状态. 利用实测数据进行拟合,开展显著性水平为0.05的K-S拟合优度检验，表明各车道车距均服从对数正态分布，1~4车道的概率密度函数参数值分别为：μ=6.582 1，σ=1.152 6；μ=6.473 2，σ=1.142 8；μ=6.497 1，σ=1.138 7；μ=6.584 5，σ=1.158 7. 以车道1为例，车距分布函数的拟合情况如图3所示. 图中，d_v为车距.

1.4 轴重 1.4.1 轴重实测数据分析

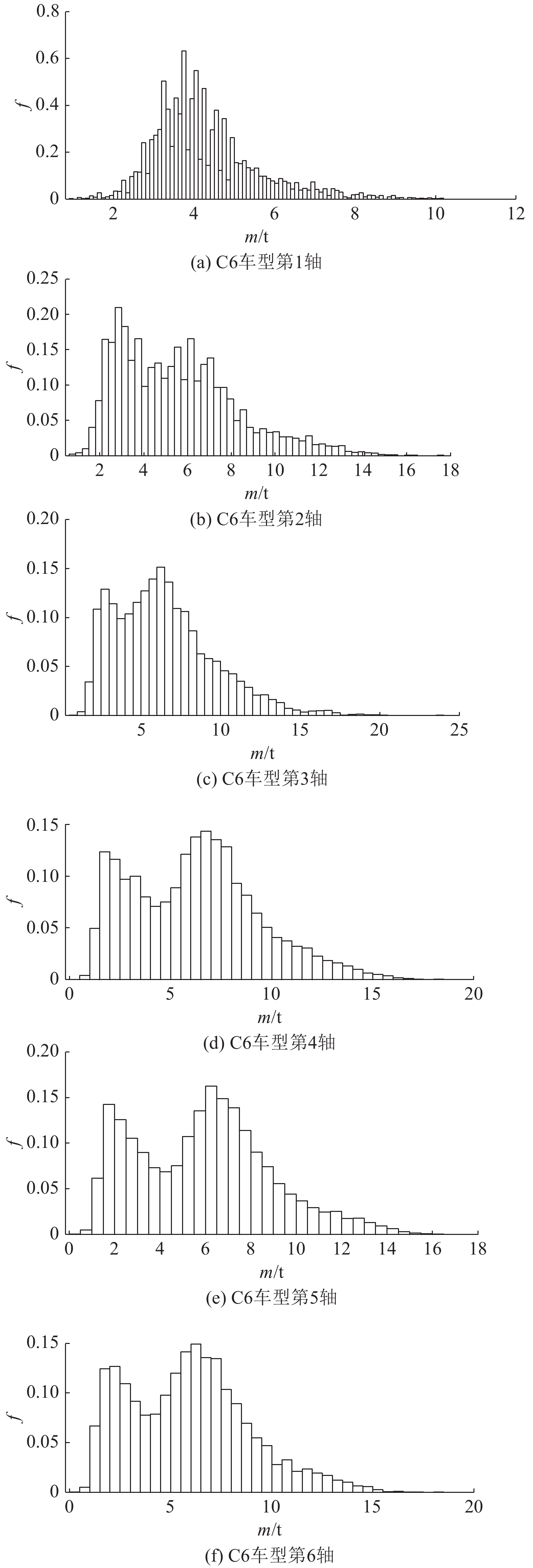
行驶中的车辆由于载重的不同，可以分为空载、一般载重和重载3种情况，因此车辆荷载将呈现多峰分布的特点^[9]. 由于车辆设计中的部分车轴为联轴设计，车辆各轴重之间应具有一定的相关性. 采用实测数据，首先对各车型轴重边缘分布特征进行分析. 结果表明，各车型轴重边缘分布呈现多峰特点. 限于篇幅，C6车型的各轴轴重统计直方图见图4. 图中，m为轴重，f为概率密度.

目前，常用描述变量相关程度的指标有：Pearson相关系数、Kendall秩相关系数和Spearman秩相关系数. 由于Pearson相关系数适用于变量为正态分布或接近正态的单峰分布，考虑到车辆轴重具有多峰的特点，选择采用对变量分布形态要求不严格的Kendall秩相关系数和Spearman秩相关系数，对轴重相关性进行分析. 分析结果表明，各车型轴重之间具有相关性，甚至某些轴重之间具有很强的相关性，随机车流的准确模拟必须考虑轴重之间的相关性. 以C6车型为例，Kendall秩相关系数见表5，Spearman秩相关系数见表6. 表中，R为各轴轴重与该行轴号所表示轴重的相关系数.

1.4.2 Copula函数

由概率论可知，若多维随机变量的边缘分布服从同一标准分布，如正态分布、t分布或者均匀分布，则在已知多维随机变量相关系数的情况下，可以得出较准确的多维联合分布函数. 车辆轴重不属于上述标准分布，很难直接得出轴重的联合分布函数.

Sklar于1959年提出Copula理论，提出可以将任意一个n维联合分布函数分解为n个边缘分布和一个Copula函数，边缘分布描述的是各随机变量的累积分布，且各随机变量的边缘分布不必相同，Copula函数用于描述变量之间的相关性^[10]. Nelsen给出更严格的Copula函数定义^[11]，采用Copula函数构造的n维联合累积分布函数表达式：

$F({x_1},\cdots,{x_n}) = C({F_1}({x_1}),\cdots,{F_n}({x_n})).$

(1)

式中：F为n维联合分布函数, F_i为各变量的边缘分布函数，C为n维Copula函数.

应用Copula理论构造n维联合分布函数，须经过以下几个步骤. 1) 确定各变量的边缘分布函数；2) 选取能够合理描述变量间相关特点的Copula函数，建立联合分布；3) 估计Copula函数中的参数.

1.4.3 边缘分布拟合

首先基于实测数据对各轴轴重边缘分布进行拟合. 通过实测数据估计概率密度函数，目前常用的有参数法和非参数法. 参数法需要先假定概率密度函数，再由实测数据估计其中的参数，该方法的关键是假定概率密度函数，但这往往是非常困难的；非参数法不存在这方面的困难. 利用非参数法——核密度估计，得到轴重的边缘分布.

设 $\hat f({x^j})$ 为变量 ${x^j}$ 的非参数核密度估计，表达式为

$\hat f ({x^j}) = \frac{1}{{N{h_j}}}\sum\limits_{i = 1}^N {{K_j}\left(\frac{{{x^j} - x_i^j}}{{{h_j}}}\right)} .$

(2)

式中： ${K_j}$ 为核函数，常用的核函数有Gaussian核函数、Box核函数、Triangle核函数和Epanechnikov核函数； ${h_j}$ 为光滑参数； $x_i^j$ 为变量 ${x^j}$ 的实测数据. 变量 ${x^j}$ 在点 $x_i^j$ 的分布函数估计值 $X_i^j$ 为

$X_i^j = \int_{ - \infty }^{x_i^j} {\hat f ({x^j}){\rm{d}}{x}} .$

(3)

拟合及K-S优度检验结果表明，采用不同核函数的非参数核密度估计均能够很好地拟合轴重的边缘分布. 以C6车型的各轴轴重边缘分布拟合为例，各轴轴重概率密度及分布函数拟合情况见图5. 采用Gaussian核函数的核密度估计，拟合各轴轴重边缘分布.

1.4.4 Copula函数的选择

在确定轴重的边缘分布后，需要选取能够合理描述变量间相关特点的Copula函数. 目前，常用的Copula函数有多元正态Copula函数、多元t-Copula函数、二元Frank-Copula函数、二元Gumbel-Copula函数和二元Clayton-Copula函数. 由于典型车型多数轴数多于2轴，对多元正态Copula函数、多元t-Copula函数进行比较. 多元正态Copula函数的分布函数和密度函数表达式为

$C({u_1},{u_2}, \cdots ,{u_N};{{\rho }} ) = {\varPhi _\rho }\left[ {{\varPhi ^{ - 1}}({u_1}),{\varPhi ^{ - 1}}({u_2}), \cdots ,{\varPhi ^{ - 1}}({u_N})} \right],$

(4)

$c({u_1},{u_2}, \cdots ,{u_N};{{\rho }} ) = {\left| {{\rho }} \right|^{ - {1}/{2}}}\exp \left[ { - \frac{1}{2}{\zeta '}({{{\rho }} ^{ - 1}} - I)\zeta } \right].$

(5)

式中：ρ为多角线上的元素全为1的N阶对称正定矩阵； ${\varPhi _\rho }$ 为相关系数矩阵为ρ的多元标准正态分布的分布函数，边缘分布均为标准正态分布； ${ \zeta '}{\rm{ = }}\left[ {{\varPhi ^{ - 1}}({u_1}),{\varPhi ^{ - 1}}({u_2}), \cdots ,{\varPhi ^{ - 1}}({u_N})} \right]$ ；I为单位矩阵. 多元t-Copula函数的分布函数和密度函数表达式为

$C({u_1},{u_2}, \cdots ,{u_N};{ \rho} ,k) = {{{t}} _{{ \rho} ,k}}\left[ {({t} _k^{ - 1}({u_1}),{{t}} _k^{ - 1}({u_2}), \cdots ,{t} _k^{ - 1}({u_N})} \right],$

(6)

$ \begin{split} c({u_1},{u_2}, \cdots ,{u_N};{ \rho} ,k) =& {\left| { \rho} \right|^{ - {1}/{2}}}\frac{{\varGamma \left(\frac{{k + N}}{2}\right){{\left[ {\varGamma \left( {\frac{k}{3}} \right)} \right]}^{N - 1}}}}{{\varGamma^{N} {{\left(\frac{{k + 1}}{2}\right)}}}}\times \\ & \frac{{{{(1 + \frac{1}{k}{{ \zeta} '}{{ \rho} ^{ - 1}}{ \zeta} )}^{\frac{{k + N}}{2}}}}}{{\mathop \Pi \limits_{i = 1}^N {{\left(1 + {{{{{ \zeta}}} _i^2}}/{k}\right)}^{\frac{{k + 1}}{2}}}}}. \end{split} $

(7)

式中： ${{{t}} _{\rho ,k}}$ 表示相关系数矩阵为ρ、自由度为k的标准多元t分布的分布函数, ${{ \zeta} '}\!\!{\rm{ = }}\!\left[ {({{t}} _k^{ - 1}({u_1}),{{t}} _k^{ - 1}({u_2}), \cdots \!,{{t}} _k^{ - 1}({u_N})} \right]$ .

现有研究表明，正态Copula函数和t-Copula函数均具有对称尾部，但t-Copula函数对随机变量尾部相关的变化较敏感，能够更好地描述变量之间对称的尾部相关关系^[12]. 分析轴重数据分布特征可知，各典型车型轴重数据分布具有对称性，大部分轴重数据相关性的差别表现为尾部数据的变化，选择t-Copula函数更合理.

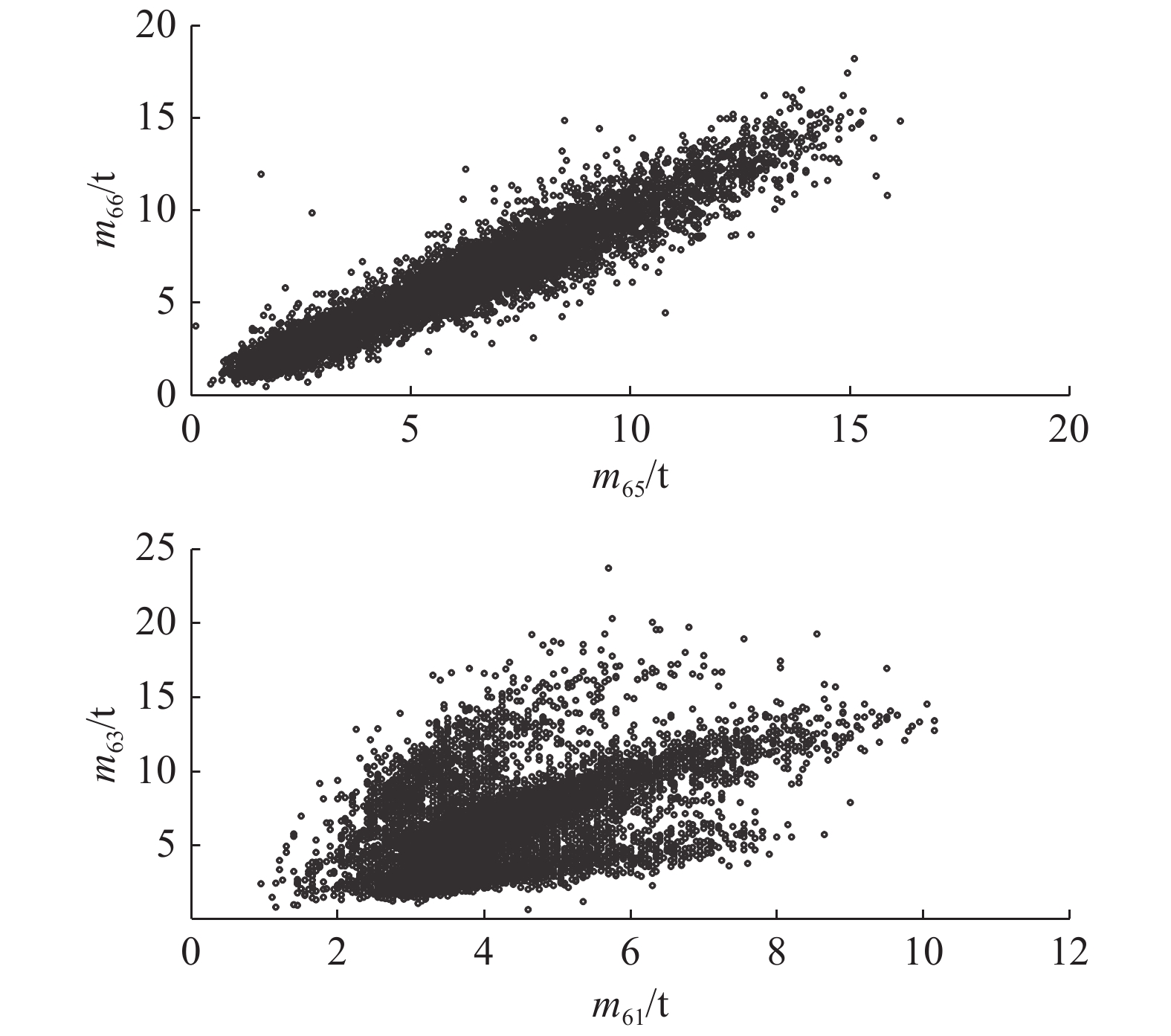
以典型车型中最复杂的C6车型轴重实测数据为例，分别选取表5、6中相关系数除1外的最大值涉及到的轴重数据（m₆₅-m₆₆）和最小值涉及到的轴重数据（m₆₁-m₆₃），数据分布特征见图6. 图中，m下标的第1个数字表示车型编号，第2个数字表示轴号.

为了比较正态Copula函数和t-Copula函数的差别，开展模型评价. 利用最大似然估计确定参数后，建立各车型以t-Copula函数为连接函数的n维轴重联合分布函数和以正态Copula函数为连接函数的n维轴重联合分布函数，其中n为各典型车型车轴数.

目前，对Copula函数选择的判定标准尚不统一，但基本从以下2个方面进行评价：1）变量间的相关程度；2）变量间的相关特点. 常用的方法为通过秩相关系数的对比判断相关程度的拟合情况，通过与经验Copula函数的对比，判断相关特点的拟合情况. 采用平方欧式距离作为对比量化指标，分别判断相关程度与相关特点的拟合情况.

秩相关系数的平方欧式距离表达式为

$s_{{\rm{gau}}}^2 = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{{\left| {R_{ij}^{{\rm{gau}}} - R_{ij}^{\rm{y}}} \right|}^2}} } ,$

(8)

$s_{\rm{t}}^{\rm{2}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{{\left| {R_{ij}^{\rm{t}} - R_{ij}^{\rm{y}}} \right|}^2}} } .$

(9)

式中： $R_{ij}^{{\rm{gau}}}$ 为正态Copula函数的秩相关系数矩阵 ${{R}}^{{\rm{gau}}}$ 中的值， $R_{ij}^{\rm{t}}$ 为t-Copula函数的秩相关系数矩阵 ${{R}}^{\rm{t}}$ 中的值， $R_{ij}^{\rm{y}}$ 为样本数据的秩相关系数矩阵 ${{R}}^{\rm{y}}$ 中的值，n为矩阵维数， $s_{{\rm{gau}}}^2$ 为正态Copula函数的平方欧式距离， $s_{\rm{t}}^{\rm{2}}$ 为t-Copula函数的平方欧式距离. 平方欧式距离越小，表明描述变量间的相关程度越准确.

假定 $\left( {x_i^1,x_i^2, \cdots ,x_i^n} \right)\left( {i = 1,2, \cdots ,m} \right)$ 是n维总体 $\left( {x^1,x^2, \cdots ,x^n} \right)$ 的一个样本， $x^1,x^2, \cdots ,x^n$ 的分布函数为 ${{{F}} _1}\left( {{x^1}} \right),{{{F}} _2}\left( {{x^2}} \right), \cdots ,{{{F}} _n}\left( {{x^n}} \right)$ ，定义经验Copula函数的表达式为

$ \begin{array}{l} {C^{\rm j}}({u^1},{u^2}, \cdots ,{u^n}) = \displaystyle\frac{1}{m}\sum\limits_{i = 1}^m {{I_{\left[ {{{{F}}_1}\left( {{x{_i}\!\!\!^1}} \right) \leqslant {u^1}} \right]}}{I_{\left[ {{{{F}}_2}\left( {{x{_i}\!\!\!^2}} \right) \leqslant {u^2}} \right]}} \cdots }\\ {I_{\left[ {{{{F}}_n}\left( {{x{_i}\!\!\!^n}} \right) \leqslant {u^n}} \right]}} ;\;{u^1},{u^2}, \cdots ,{u^n} \in \left[ {0,1} \right]. \end{array} $

(10)

式中： ${{{I}} _{\left[ {} \right]}}$ 为示性函数，当 ${F_n}\left( {{x{_i}\!\!\!^n}} \right) \leqslant {u^n}$ 时， ${{{I}} _{\left[ {} \right]}} = 1$ ，否则为0. 经验Copula函数的平方欧式距离表达式为

$d_{{\rm{gau}}}^2 = \sum\limits_{i = 1}^m {{{\left| {{C^{\rm{j}}}(u_i^1,u_i^2, \cdots ,u_i^n) - {C^{{\rm{gau}}}}(u_i^1,u_i^2, \cdots ,u_i^n)} \right|}^2}} ,$

(11)

$d_{\rm{t}}^{\rm{2}} = \sum\limits_{i = 1}^m {{{\left| {{C^{\rm{j}}}(u_i^1,u_i^2, \cdots ,u_i^n) - {C^{\rm{t}}}(u_i^1,u_i^2, \cdots ,u_i^n)} \right|}^2}} .$

(12)

式中： $u_i^n = {{{F}} _n}\left( {x_i^n} \right)$ ， $d_{{\rm{gau}}}^2$ 为正态Copula函数的平方欧式距离， $d_{\rm{t}}^{\rm{2}}$ 为t-Copula函数的平方欧式距离. 若 $d_{\rm{t}}^{\rm{2}} < d_{{\rm{gau}}}^{\rm{2}}$ ，则表明t-Copula函数更能够准确地描述变量间的相关特点，反之亦然.

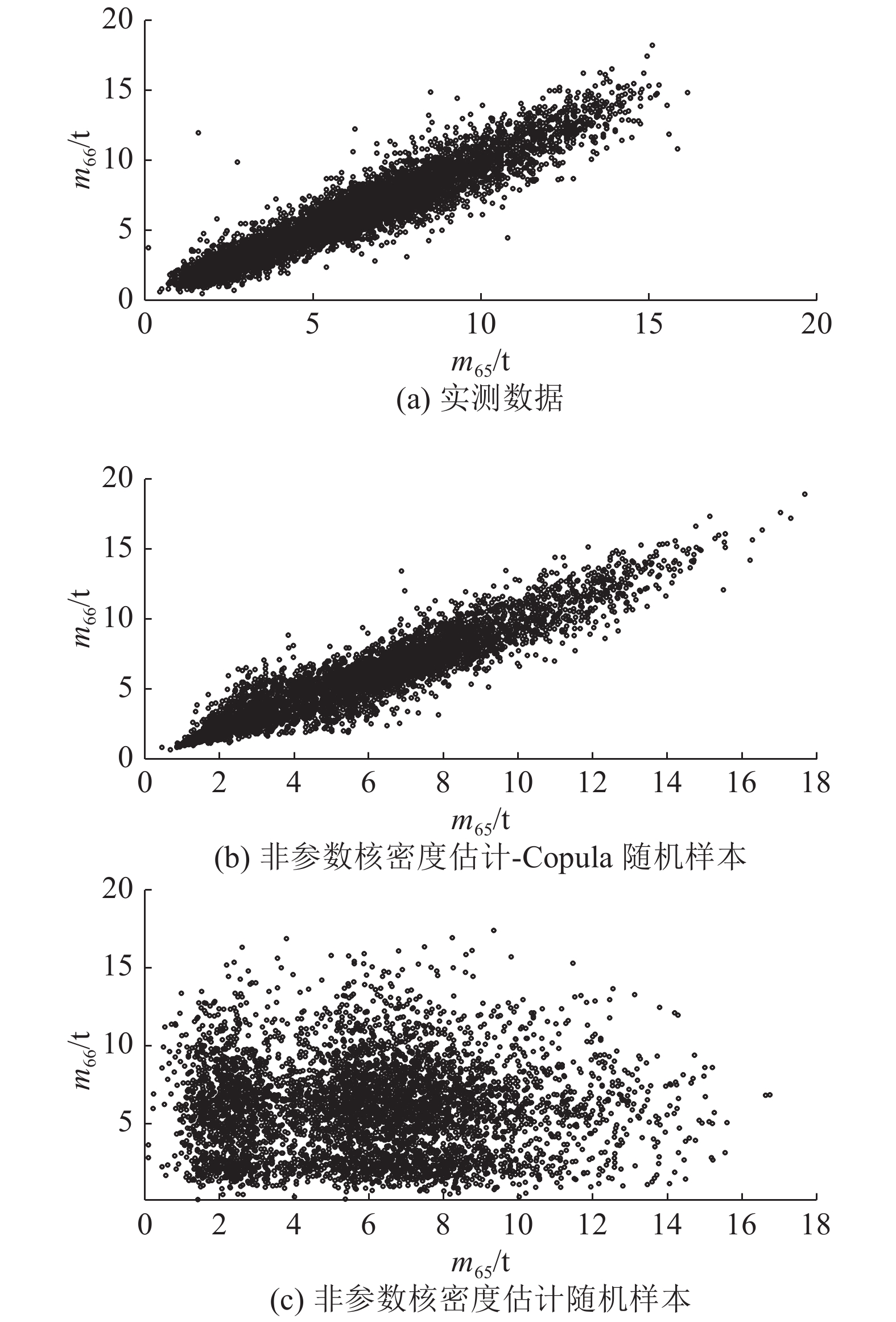
正态Copula函数和t-Copula函数平方欧式距离计算结果如表7所示. 表中，s²为秩相关系数的平方欧式距离，d²为采用不同Copula函数的概率模型的分布函数值与采用实测数据的经验Copula函数的分布函数值的平方欧式距离. 可知，正态Copula函数和t-Copula函数评价指标值均很小，表明均能够很好地描述轴重的联合分布. 正态Copula函数除C4车型Spearman相关系数的平方欧式距离小于t-Copula函数外，其他均大于t-Copula函数，表明选择t-Copula函数作为连接函数，对轴重相关程度和相关特点的描述更好. 选择t-Copula函数作为连接函数，建立考虑相关性的轴重联合分布函数非参数核密度估计-Copula构造方法. 若不考虑轴重之间的相关性，则可以直接用非参数核密度估计构造轴重的边缘分布. 限于篇幅，典型车型中最复杂的C6车型第5轴和第6轴实测数据、非参数核密度估计-Copula随机样本和非参数核密度估计随机样本的数据分布特征如图7所示.

1.5 随机车流建模

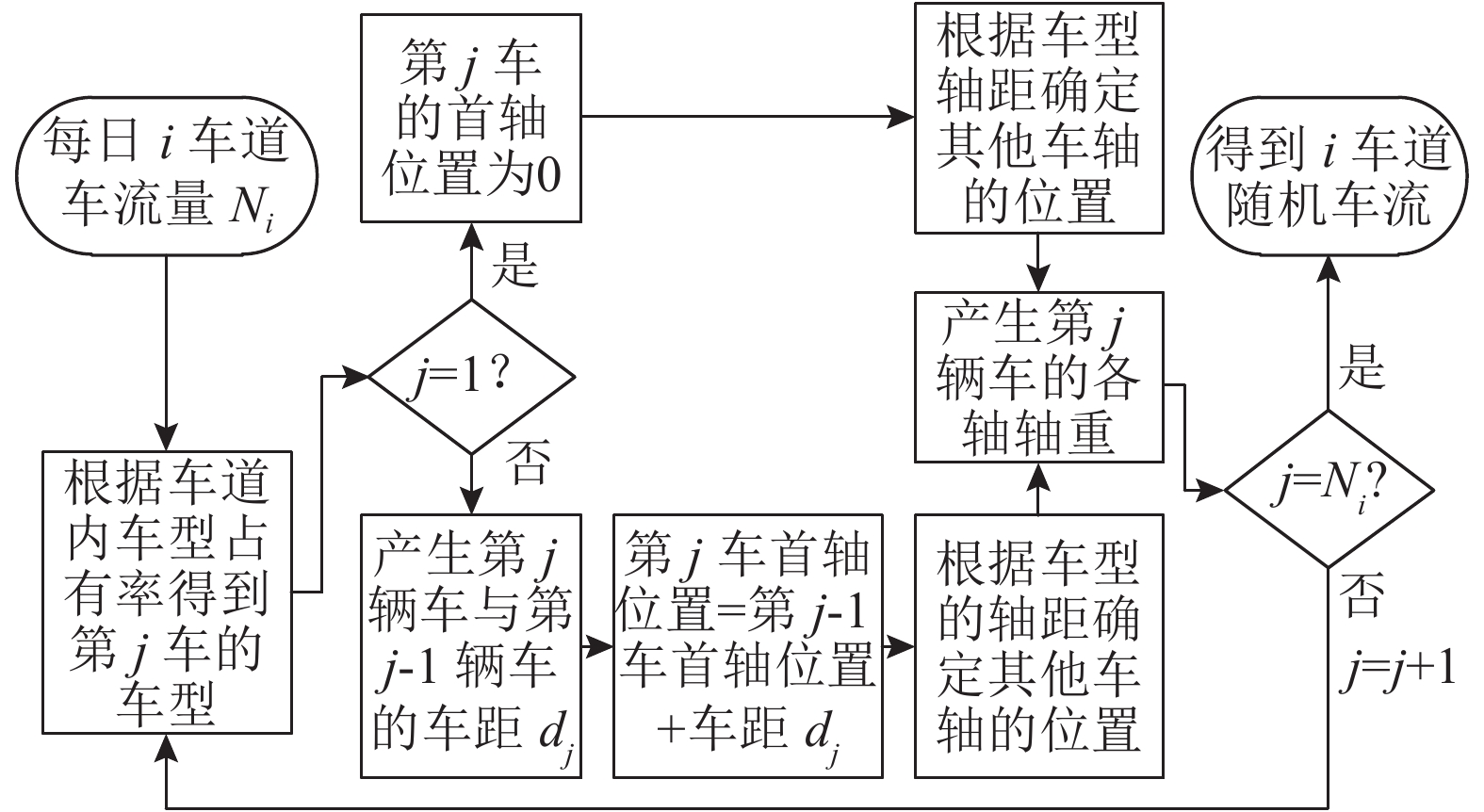
在完成车辆参数分析后，应用MATLAB编制随机车流模拟程序. 程序中随机车流的产生流程见图8，程序模拟的考虑轴重相关和不考虑的日随机车流样本的部分车流见图9. 图中，x为车轴位置.

2 荷载效应分析

由于车流的随机性，桥梁在运营过程中的结构响应有显著的差异，对于桥梁设计和运营安全评估，往往重点关注运营重现期内由车辆荷载引起的极端响应. 公路桥梁车辆荷载研究课题组^[13]基于经典极值理论的最大值外推方法，对我国公路桥梁车辆荷载开展研究；采用上述方法，对随机车流的荷载效应进行研究. 首先确定最大值取值区间（1天、1月或者1年），综合考虑汽车荷载的时变特性和数据利用率，阮欣等^[14]研究认为取用1天作为最大值取值区间较能兼顾，本文选择1天作为最大值取值区间. 然后选取取值区间内的最大值作为观测样本，最后对若干个取值区间内的最大值观测样本进行拟合和优度检验. 荷载效应研究的桥梁背景为占我国在建和已建桥梁大部分的简支梁桥，跨径分别取6、8、10、20、30及40 m.

采用编制的随机车流程序，生成各车道3 000个考虑轴重相关的日随机车流样本，开展影响线加载. 取每天跨中弯矩的最大值作为效应观测样本（各车道观测样本数为3 000），对观测样本进行拟合及优度检验，表明均服从对数正态分布. 为了验证随机车流模拟实测车流荷载效应的准确性，采用1车道的实测车流数据，按照上述方法开展同样的加载、取值、拟合和优度检验. 结果表明，实测车流的每天跨中弯矩最大值服从对数正态分布.

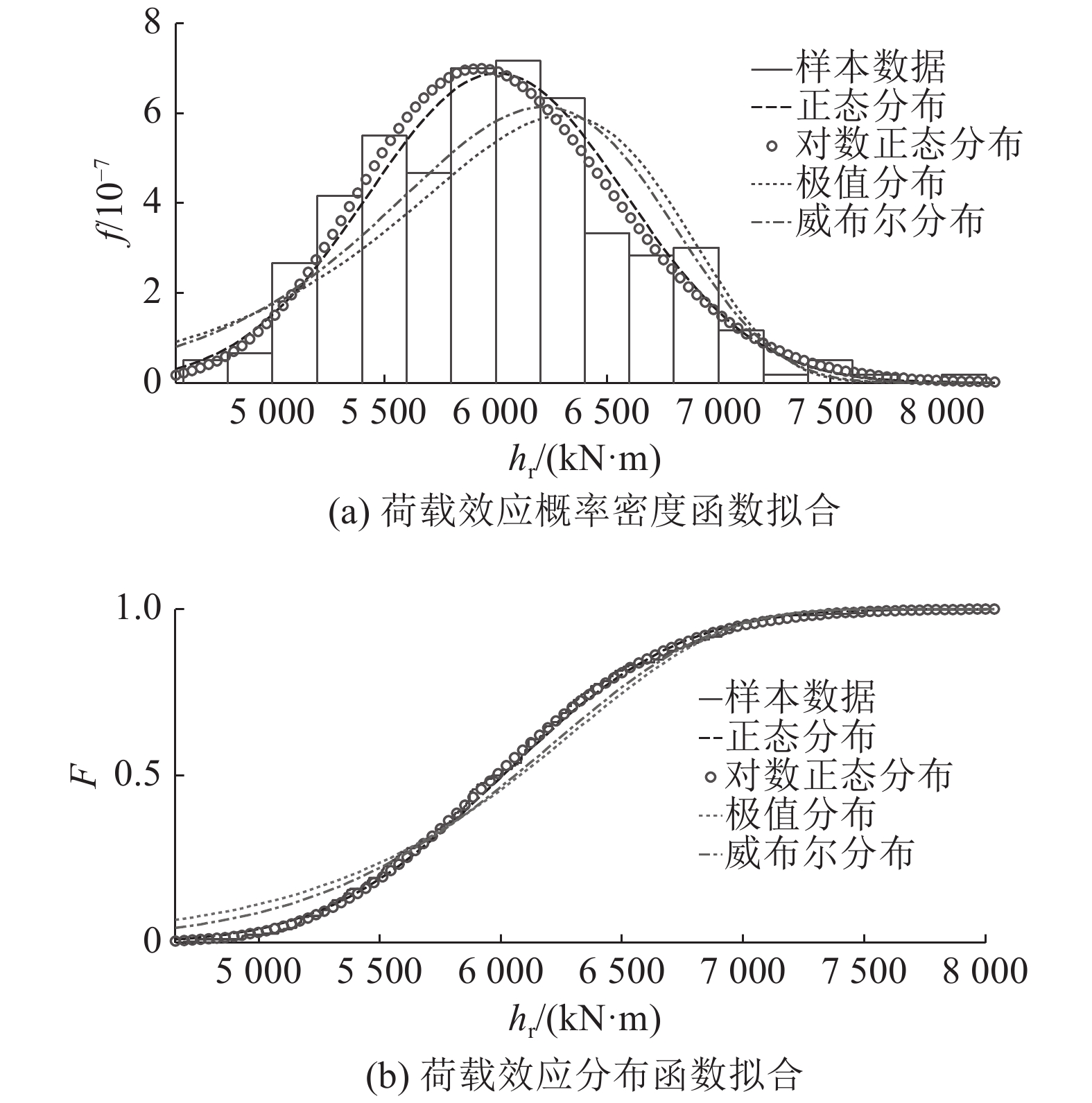
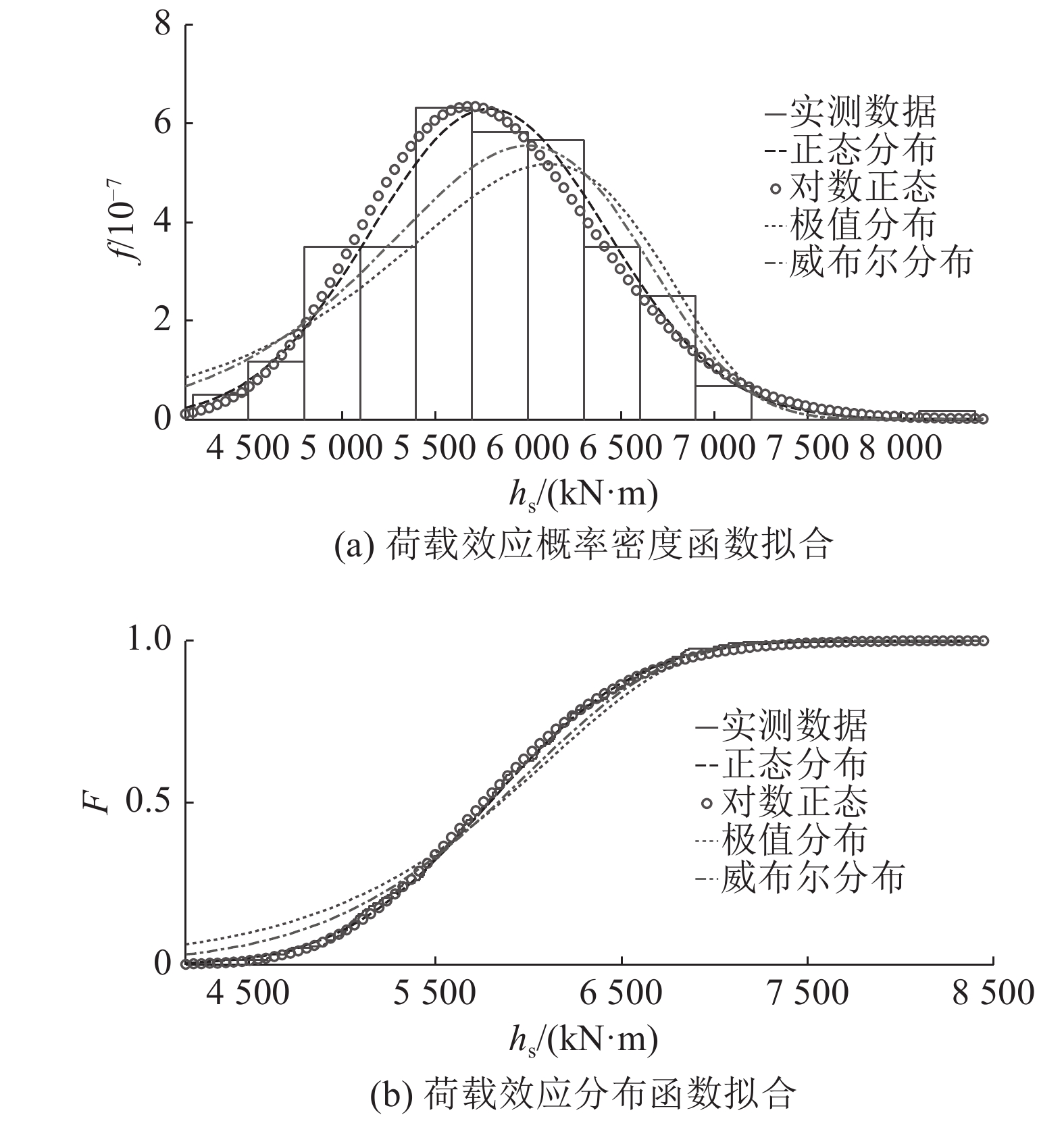
限于篇幅，40 m简支T梁在1车道随机车流作用下的观测样本分布拟合情况如图10所示. 图中，h_r为考虑轴重相关的随机车流荷载效应. 40 m简支T梁在1车道实测车流作用下的荷载效应分布拟合情况如图11所示. 图中，h_s为实测车流荷载效应.

取分布函数的0.95分位值作为随机车流及实测车流荷载效应的代表值，计算我国现行2014年规范^[15]及该项目设计时执行的2003规范^[16]中公路-І级车道荷载作用下的跨中弯矩，有关结果如表8所示. 表中，l为跨径，h_g为规范荷载效应.

由表8可知，宜泸高速各车道随机车流对各跨径简支梁桥的荷载效应代表值差别不大；随机车流荷载效应代表值均超过了现行2014年规范^[15]及该项目设计时执行的2003规范^[16]中公路-І级车道荷载的荷载效应，但超出各规范的幅度有差异，且受到跨径的影响；1车道随机车流荷载效应代表值与实测车流荷载效应代表值的差别不大.

为了分析跨径对超出幅度的影响，取随机车流荷载效应代表值与现行2014年规范^[15]（以下简称14规范）及该项目设计时执行的2003规范^[16]（以下简称03规范）中公路-І级车道荷载的荷载效应比值(简称14效应比和03效应比)作为研究对象，效应比随跨径变化的情况如图12所示. 图中，y₁₄、y₀₃分别为14效应比和03效应比.

从图12可以看出，随着跨径的增加，14效应比呈现两边小、中间大的趋势，最大值为1.34，最小值为1.18；03效应比总体上呈现逐渐减小的趋势，由1.77减小为1.31，03效应比的变化趋势及大小与14规范编制时所做的实测结果基本一致. 2个效应比的差异主要是因为14规范将跨径<50 m时的车道集中荷载最小值由03规范的180 kN提高到了270 kN.

利用随机车流程序，产生3 000个不考虑轴重相关的1车道日随机车流样本. 采用同样的荷载效应分析方法，得到不考虑轴重相关时的各跨径简支梁桥荷载效应，分析各跨径简支梁桥在2种情况下的荷载效应代表值，计算考虑与不考虑时代表值的比值（简称增大比）z，结果见表9. 表中，h_ry为不考虑轴重相关的随机车流荷载效应，h₀₃为2003规范荷载效应，h₁₄为2014规范荷载效应.

由表9可知，不考虑轴重相关时的荷载效应代表值小于14规范中的公路-І级车道荷载的荷载效应值及实测数据的荷载效应值，但大于03规范中的公路-І级车道荷载的荷载效应值；考虑轴重相关的随机车流荷载效应更接近实测车流荷载效应；考虑轴重相关的荷载效应代表值比不考虑时平均高约45%.

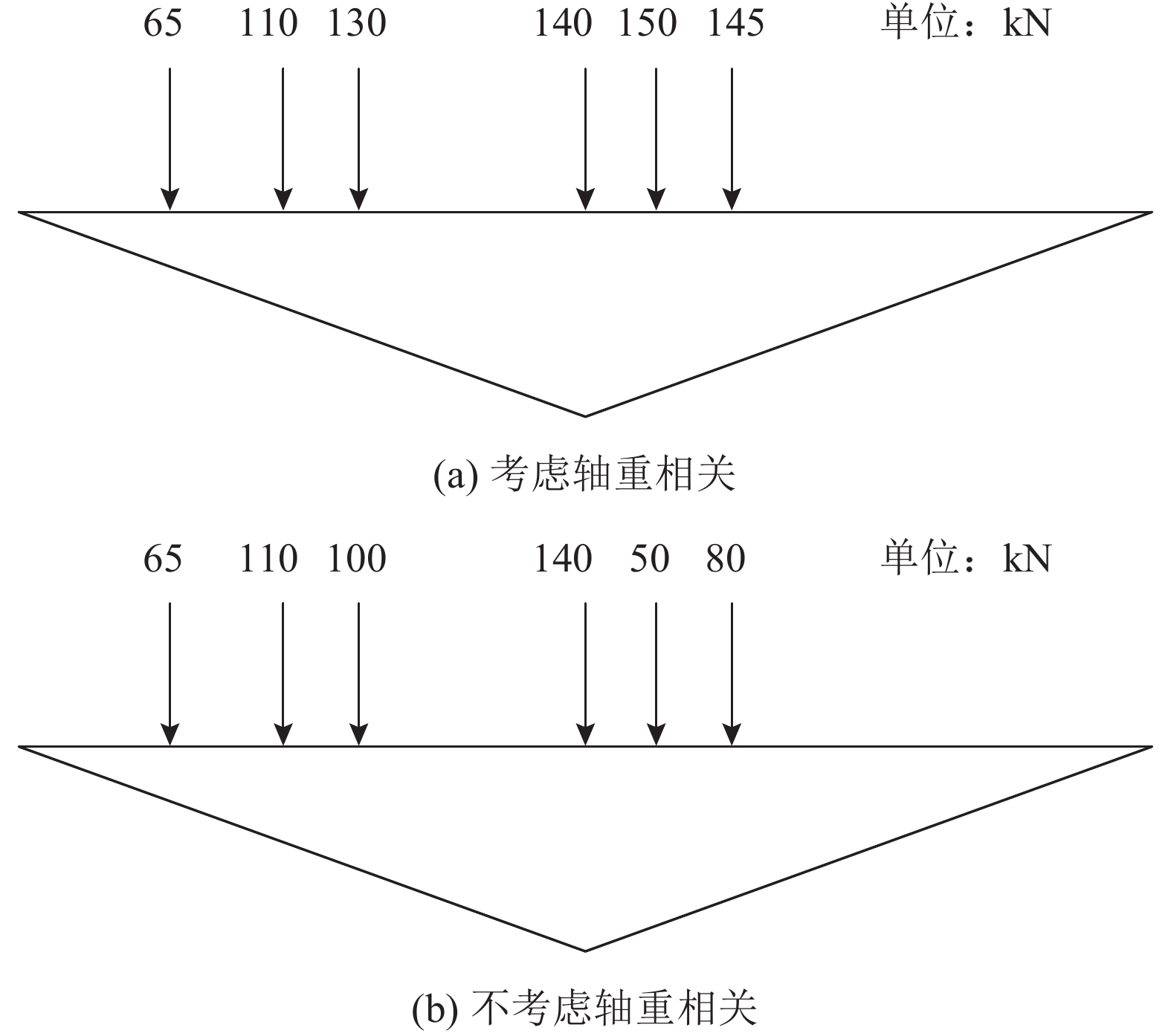
考虑到荷载效应的极值很大程度上是由于重型货车引起的，以C6车型为例，分析造成上述荷载效应差异的原因. 将1辆C6车型的货车加载到40 m跨径的简支梁桥上，假定车辆第4轴位于跨中，保持车辆的第1轴、第2轴和第4轴轴重不变. 由于车辆的第3轴、第4轴、第5轴和第6轴之间的相关性较强，由图7可知，考虑轴重相关性后，轴重的样本值将较接近（与实际情况比较吻合），不考虑轴重相关性，样本值的轻重差异较大（与实际情况不符）. 车辆轴重及在跨中弯矩影响线的加载情况见图13.

对上述2种情况进行计算，考虑轴重相关的跨中弯矩为5 771 kN·m，不考虑轴重相关的跨中弯矩为4 081 kN·m，考虑相关比不考虑相关大41.1%. 若不考虑轴重相关性而进行独立抽样，则容易造成一辆重型货车的轴重轻重差异较大，对荷载效应的极值结果造成很大的影响.

3 结　论

(1) 各车型轴重呈现多峰分布，且轴重之间具有较强的相关性，甚至某些轴重之间具有很强的相关性. 当建立随机车流模型时，若不考虑车辆轴重的相关性，则会造成较大误差.

(2) 各车型轴重选择t-Copula函数作为连接函数，对相关程度和相关特点均能够很好地进行描述. 采用非参数核密度估计-Copula构造方法建立的联合分布函数，可以较准确地描述车辆轴重的联合分布.

(3) 考虑轴重相关情况下的荷载效应代表值比不考虑时高约45%，更接近实测车流的荷载效应代表值，表明利用随机车流分析荷载效应时，应考虑随机车流轴重的相关性. 考虑到荷载效应的极值很大程度是由于重型货车引起，若不考虑轴重相关性而进行独立抽样，则容易造成一辆重型货车的各轴轴重轻重差异较大，对荷载效应的极值结果造成很大的影响.

(4) 宜泸高速各车道随机车流对各跨径简支梁桥的跨中弯矩荷载效应代表值差别不大，但均已超过14规范公路-І级车道荷载的荷载效应，考虑到最小效应比已达1.18，建议加强对超载车辆的管理.