盾构掘进会对周围土体产生扰动,引起土体应力状态的改变,造成土体变形,这种影响在双线水平平行盾构施工中尤为明显. 地表变形的监测是研究盾构施工引起土体变形最常见的方法,监测结果能够直观地体现土体变形. 通过合理的施工控制技术减小地表变形,能够有效地提高盾构施工的安全性,因此在实际施工中经常以地表变形来指导盾构施工[1-2].
很多学者对盾构施工引起的地表变形进行研究. Peck[3]研究大量地铁施工引起的地表变形数据及工程资料后,得出地表沉降槽服从正态分布的理论. Sagaseta[4]分析近地点某处由土体损失引起的土体应变场,以绝对位移为变量,求解地面以下土体的位移场和应力场,得到不排水条件下的三维地面变形计算公式. 关于双线盾构施工引起的土体变形研究,目前主要包括基于Peck公式的实测分析与理论对比[5-7]、随机介质法[8]、有限元法[9-10]、模型试验法[11]. 其中,基于Peck公式的双线平行盾构施工引起的地表沉降预测经验公式主要可以分为以下2类.
1)采用Peck公式直接计算地表沉降总变形曲线:Peck[3]认为双线隧道引起的沉降槽为对称分布,在沉降槽计算时,用一个大圆代替双线隧道来描述沉降槽宽度的增加,该方法的计算结果没有考虑二次扰动效应且无法解释2条隧道间距增大时沉降槽呈现W形的原因;New等[12]考虑最大沉降点的偏移,对Peck公式进行修正,但在计算时偏移距离没有具体的取值方法.
2)采用Peck公式,分别求先行隧道和后行隧道开挖引起的地面沉降曲线;然后叠加,得到总的地面沉降曲线. 刘波等[13]假定无二次扰动效应,先行隧道和后行隧道开挖引起的地面沉降相同,即土体损失率与沉降槽宽度相同,采用单线Peck公式分别计算2条地面沉降曲线,叠加得到总的地面沉降曲线;Suwansawat等[14]考虑先行隧道开挖对后行隧道的影响,假定后行隧道土体损失率与沉降槽宽度的取值与先行隧道不同,该方法需要分别确定先、后行线的土体损失率和沉降槽宽度.
本文对杭州地铁2号线某双线盾构区间施工进行现场实测,分析双线盾构施工过程中地表变形的规律,研究盾构施工参数与地表变形之间的相关性;分析双线Peck公式在软土地区的适用性,给出软土地区土体损失率的建议值及控制方法.
1 现场试验 1.1 试验概况该试验的研究对象为杭州地铁2号线丰潭路站—古翠路站盾构区间段,区间线路位于杭州市文二西路,呈东西向敷设,区间全长503.866 m. 隧道纵断面为人字坡,埋深为7.78~9.66 m,先行线与后行线之间的轴线距离为15 m,盾构机采用可以自动采集各施工参数的日本石川岛土压平衡盾构机(EPB),刀盘开口率为40%,刀盘形式如图1所示.

|
图 1 刀盘形式 Fig. 1 Component of cutter head |
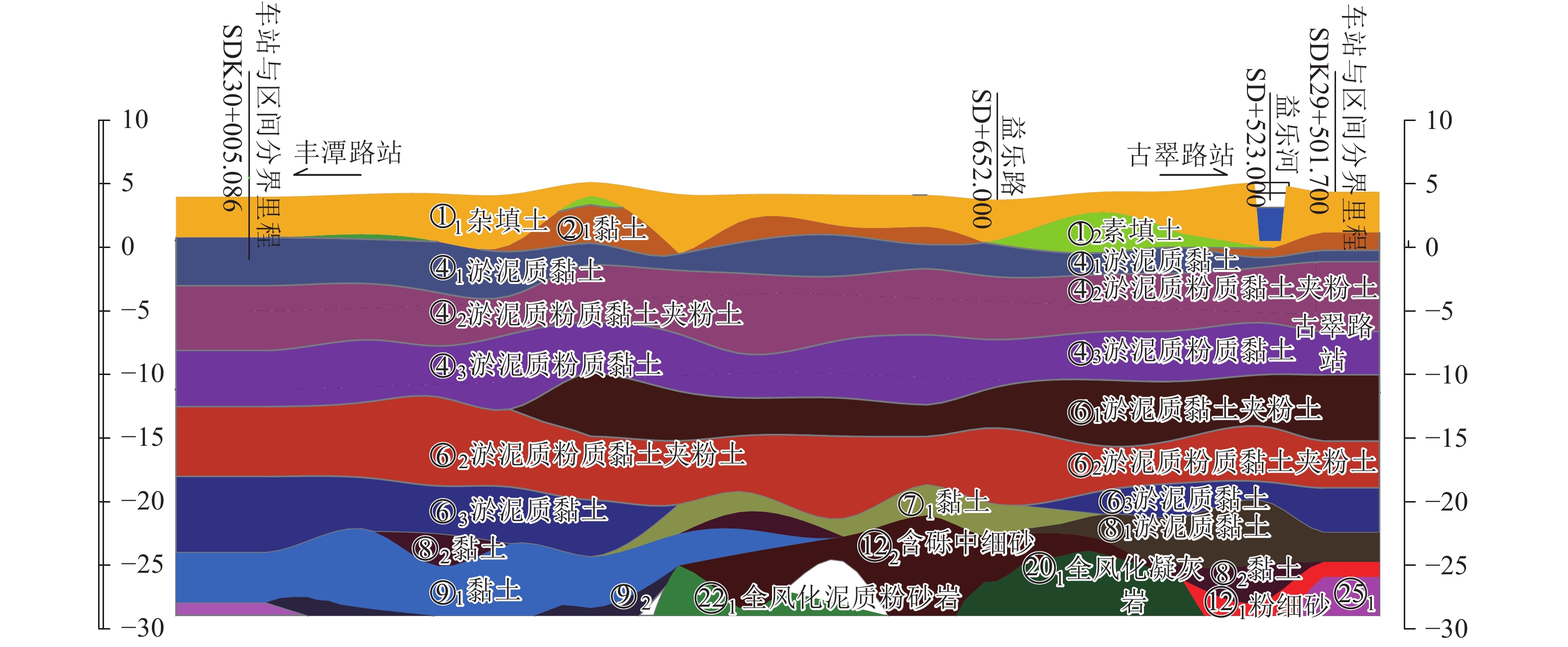
隧道衬砌结构为装配式钢筋混凝土管片,采用错缝拼装,管片内径为5.5 m,外径为6.2 m,环宽为1.2 m,厚0.35 m. 土层分布情况及参数见表1. 表中,γ为重度,c为黏聚力,φ为摩擦角,ES为压缩模量. 盾构下穿地质剖面见图2.
|
图 2 盾构下穿地质剖面图 Fig. 2 Geological profile of shield tunnel under construction |
| 表 1 土体参数 Table 1 Parameters of soils |
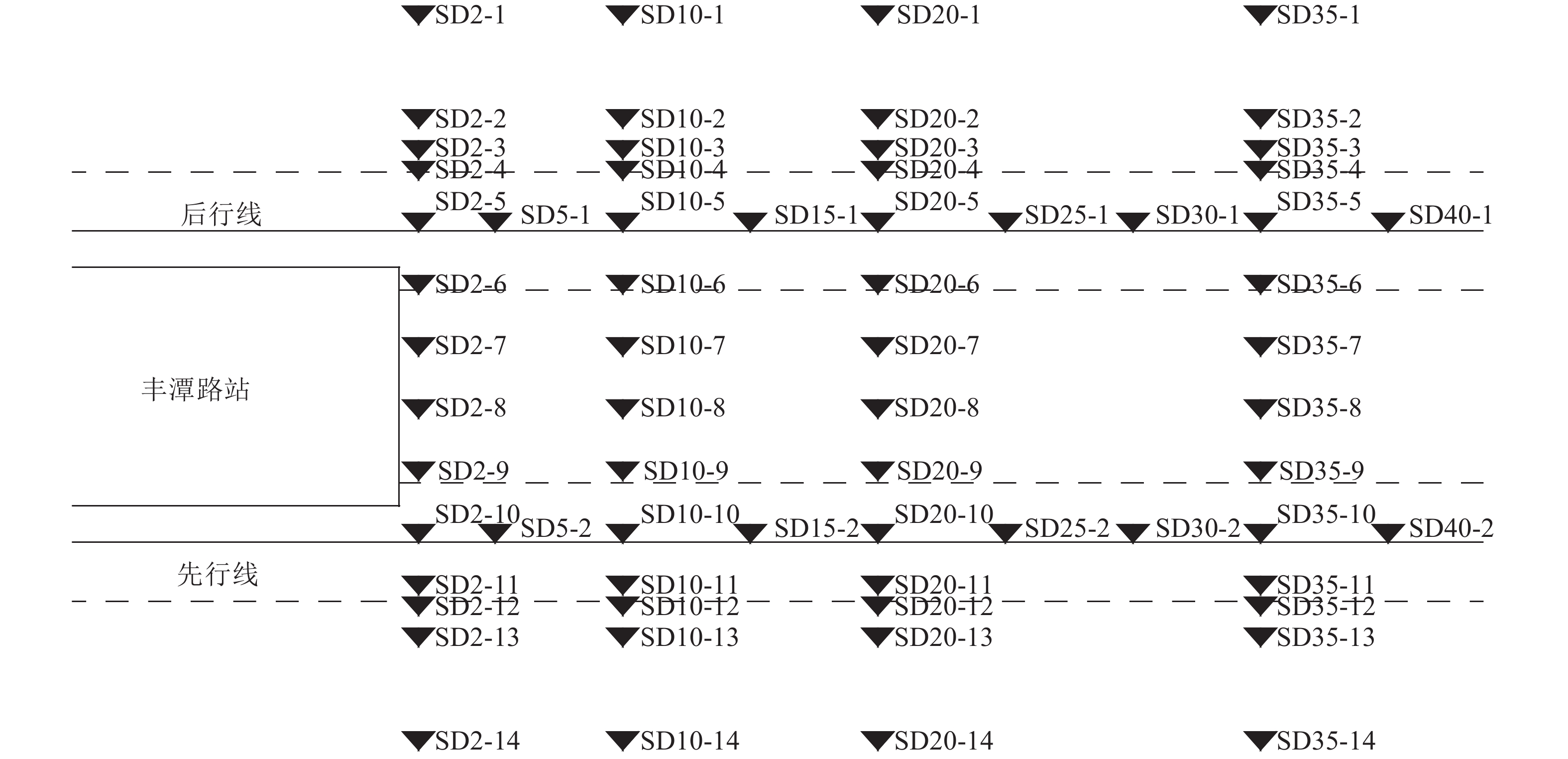
通过本次现场试验,测试了软土区双线盾构掘进过程中的地表变形. 测点布置如下:沿区间隧道中心轴线走向布设纵向剖面测点,垂直于隧道中心轴线布设横向剖面测点. 该试验地表沉降的监测以地铁公司提供的深桩水准点为起算点,区间内每100~200 m布置一个水准工作基点,共布置4个基点,按二等水准测量精度要求实施观测. 在轴线上每5环布一个沉降测点,每30 m布设一个沉降监测剖面,监测剖面处2条区间隧道轴线内每隔3 m布置一个测点,轴线外2.5、3.5、5和10 m处各布一个测点. 若遇特殊地质条件,监测断面距离加密为10环,共布置446个沉降监测点. 当盾构在进、出洞50 m内时,在2环、10环、20环、35环、45环,布设5组监测断面,具体的布置情况见图3.
|
图 3 地表实测部分测点布置 Fig. 3 Arrangement of measuring point on surface |
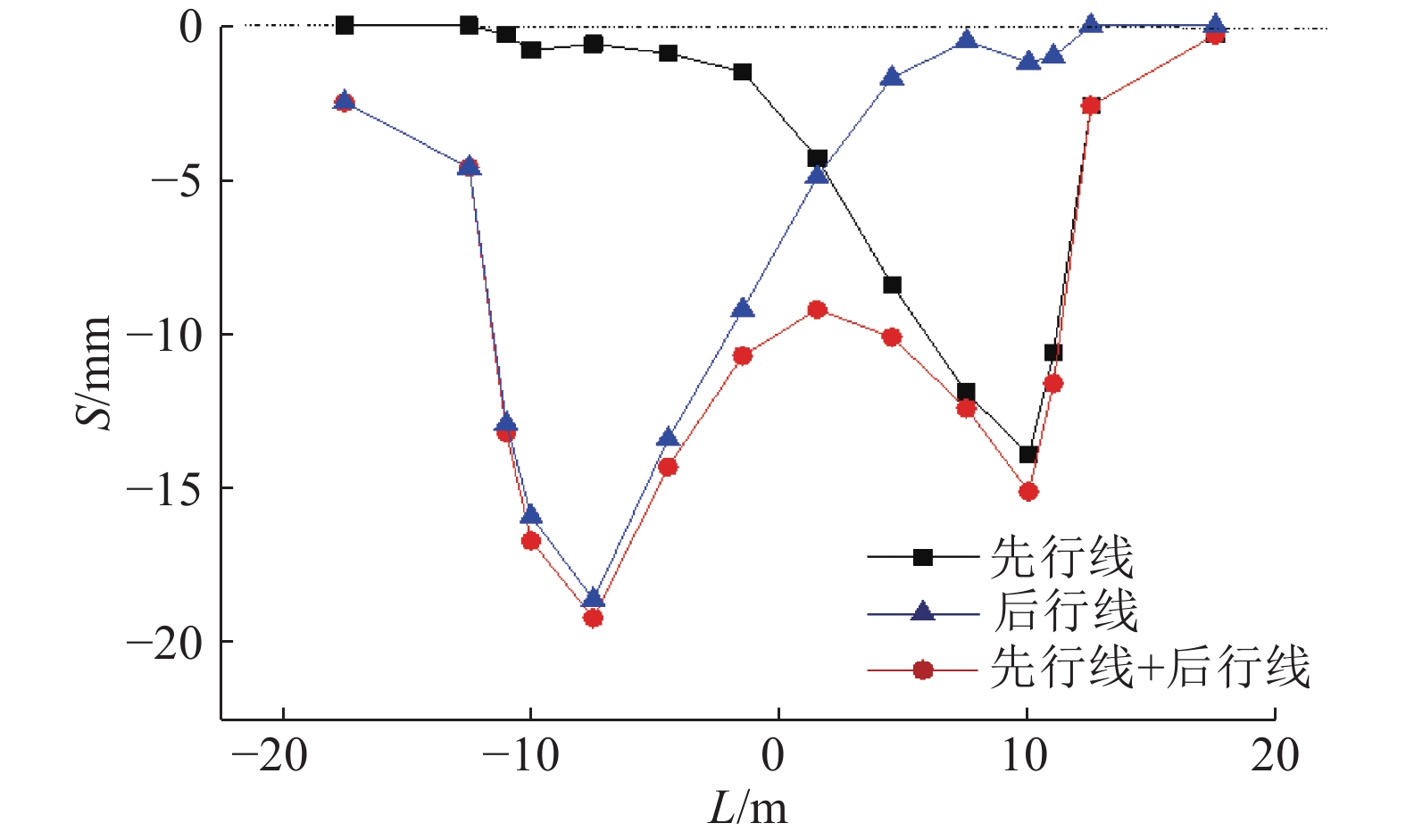
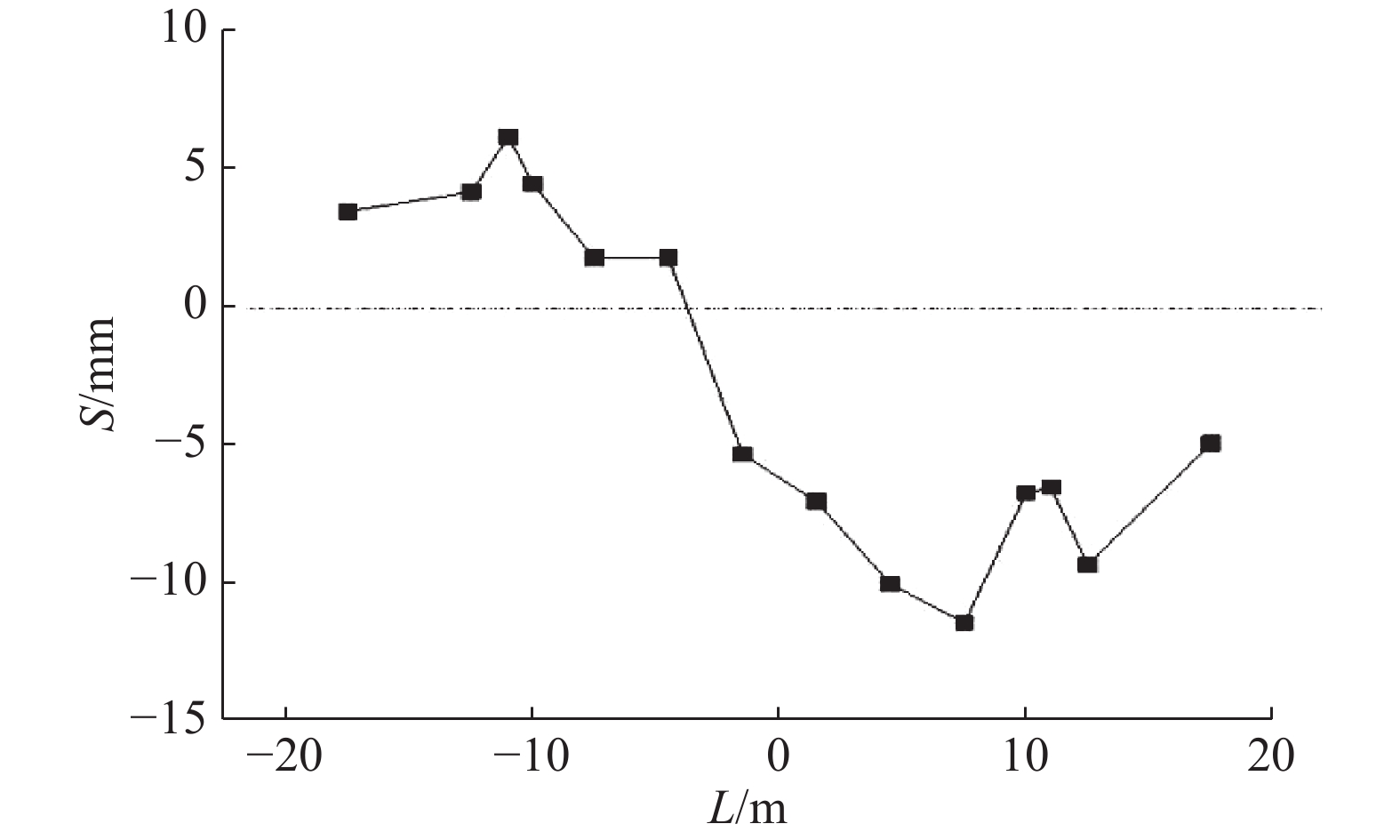
通过分析试验中监测断面原始地表变形监测数据发现,断面的沉降曲线大多为双峰形曲线,如图4所示(即地表变形S与测点距中线水平距离L的关系),且后行线(左线)轴线上方的地表沉降大于先行线,实测各个断面的二次扰动效应存在一定的差异.
由图4可以看出,因后行隧道施工造成的二次扰动效应较明显,以后行线掘进引起的断面最大沉降与先行线掘进引起的断面最大沉降的比值N为控制因素,对试验中变形曲线符合理论公式预测的断面二次扰动效应进行分析,进一步与其他学者的研究成果进行对比并记录,如表2所示.
|
图 4 SD185断面地表变形实测曲线 Fig. 4 Surface deformation of section SD185 |
由表2可知,在杭州淤泥质土地区,双线盾构施工时后行线掘进引起的二次扰动效应明显大于其他土质,且实测先行线和后行线的平均沉降分别为9.53和14.68 mm,沉降绝对值大于其他大部分地区. 若在施工过程中控制不到位,则很容易发生地表沉降报警,从而影响施工安全,因此在杭州淤泥质土地区进行双线盾构施工时,需要对二次扰动效应给予重视. 关于该试验中二次扰动效应造成的额外沉降明显的原因,笔者推测与杭州湾地区软土含水率较高有关.
| 表 2 不同土质地区N对比 Table 2 Contrast of Nin different area |
施工参数会对盾构掘进过程中的地表变形产生影响,张恒等[18]通过数值模拟及现场监测,分析盾构掘进参数对地表沉降的影响;魏新江等[19]通过分析杭州地铁1号线的监测数据,研究盾构施工参数之间的相关性以及对地层位移的影响. 从施工参数的角度,研究各断面二次扰动效应差异的原因.
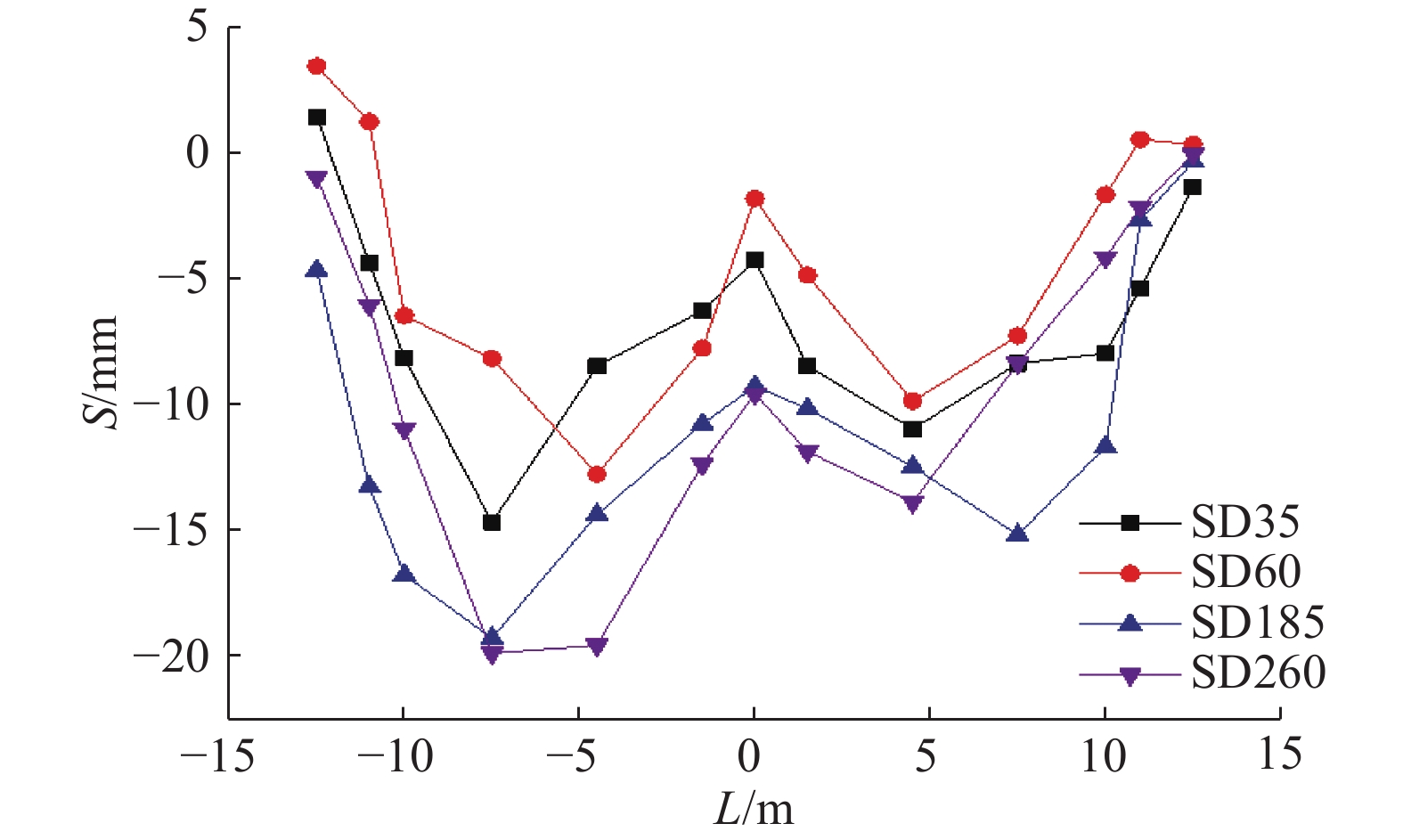
如图5所示为部分断面地表变形曲线. 可知,不同断面的沉降曲线形状和绝对沉降都存在差异,这是由于在盾构掘进过程中施工参数的差异所引起的. 表3记录了各断面的单环排土量Q(盾构施工过程中推进一环所排出的土体)和盾尾注浆压力p. 表中,Smax为最大沉降.
|
图 5 部分断面地表变形实测曲线 Fig. 5 Surface deformation measured curves of sections |
| 表 3 部分断面沉降与施工参数记录表 Table 3 Settlement and construction parameters of sections |
由表3很难直接看出地表最终沉降和施工参数之间的关系,因此定义:
| $ K{\rm{ = }}(Q/p) \times {10^{{\rm{ - }}1}}. $ | (1) |
式中:Q为单环排土量.
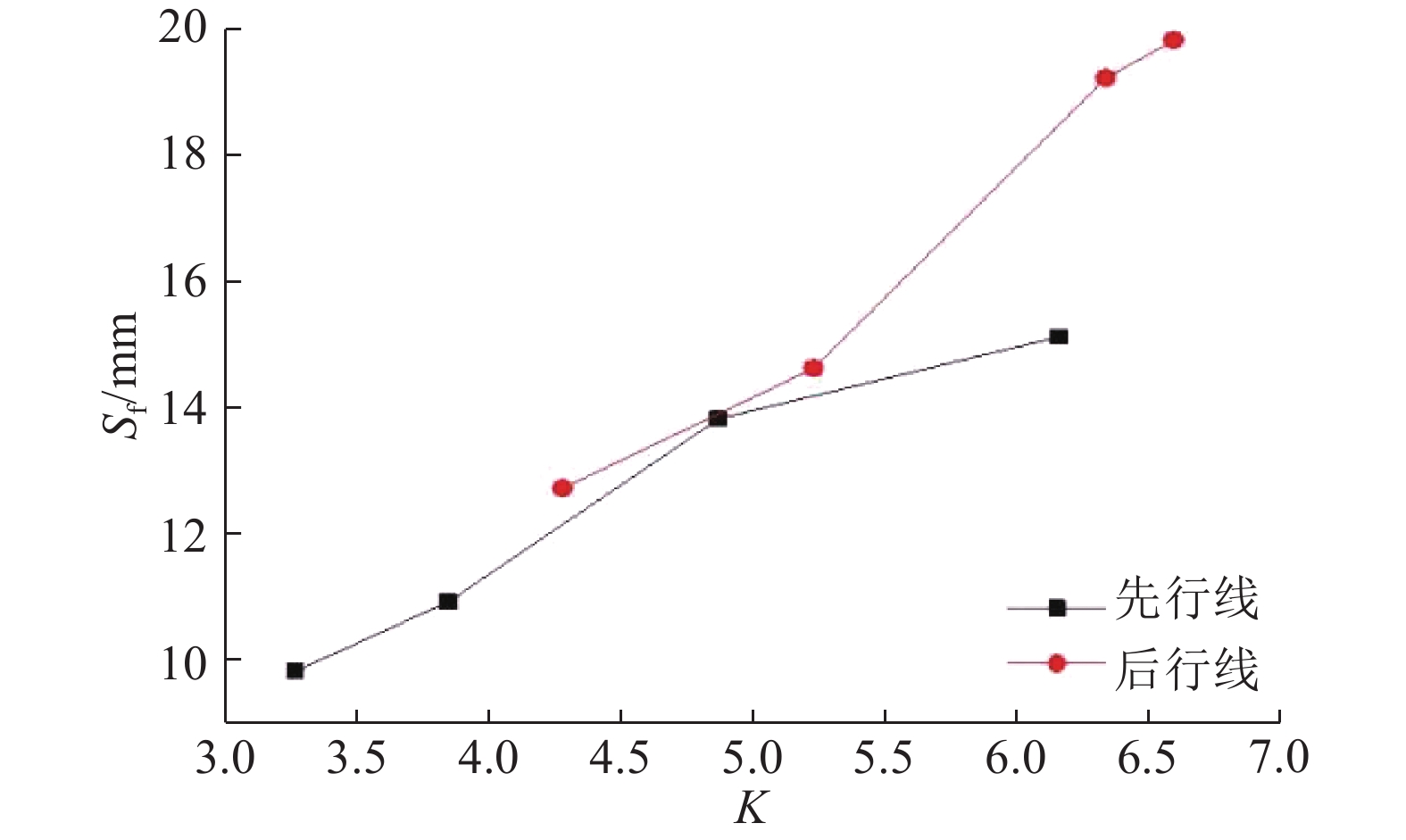
如图6所示为地表最终沉降Sf与K的关系. 可知,Sf和K之间存在较好的正相关,K越大则Sf越大,即盾构掘进过程中的单环排土量和Sf之间存在一定的正相关性,盾尾注浆压力和地表最终沉降之间的关系为负相关,且后行线的K普遍大于先行线.
|
图 6 地表最终沉降与K的关系图 Fig. 6 Relationships between surface final settlement and K |
在试验中,部分监测断面的沉降曲线与经验公式预测结果存在较大的差异,如图7所示. 图7中,当SD110先行线掘进时,地表变形曲线与Peck公式预测结果的匹配度较好;在后行线掘进完成后,整个监测断面变形曲线与经验公式的预测结果完全不同,断面后行线的单环排土量为25.42 m3,盾尾注浆压力高达1.18 MPa,K仅为2.15,导致断面上方土体产生了隆起,验证了K越大则地表最终沉降越大的结论.
|
图 7 SD110地表横向变形实测曲线 Fig. 7 Lateral surface deformation measured curve of section SD110 |
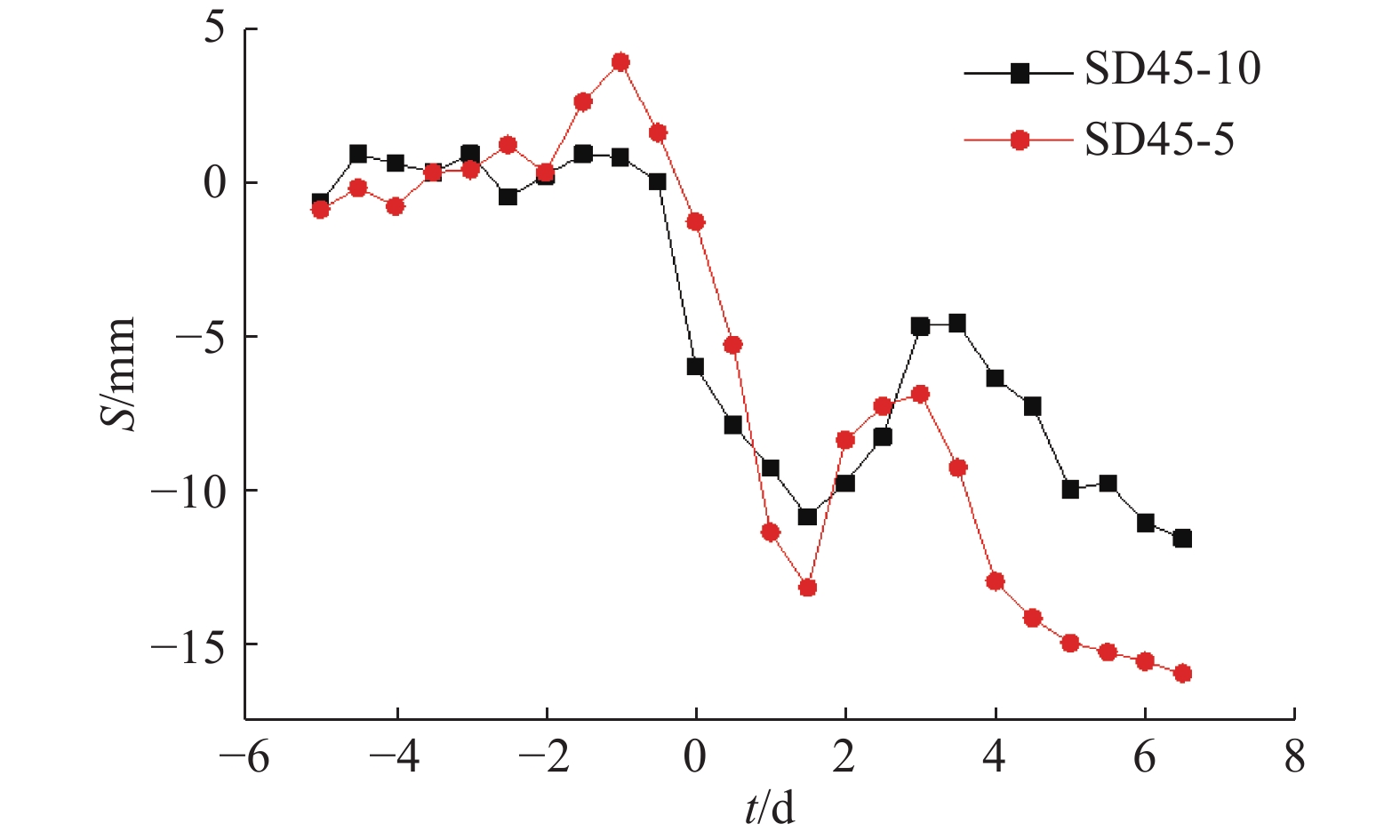
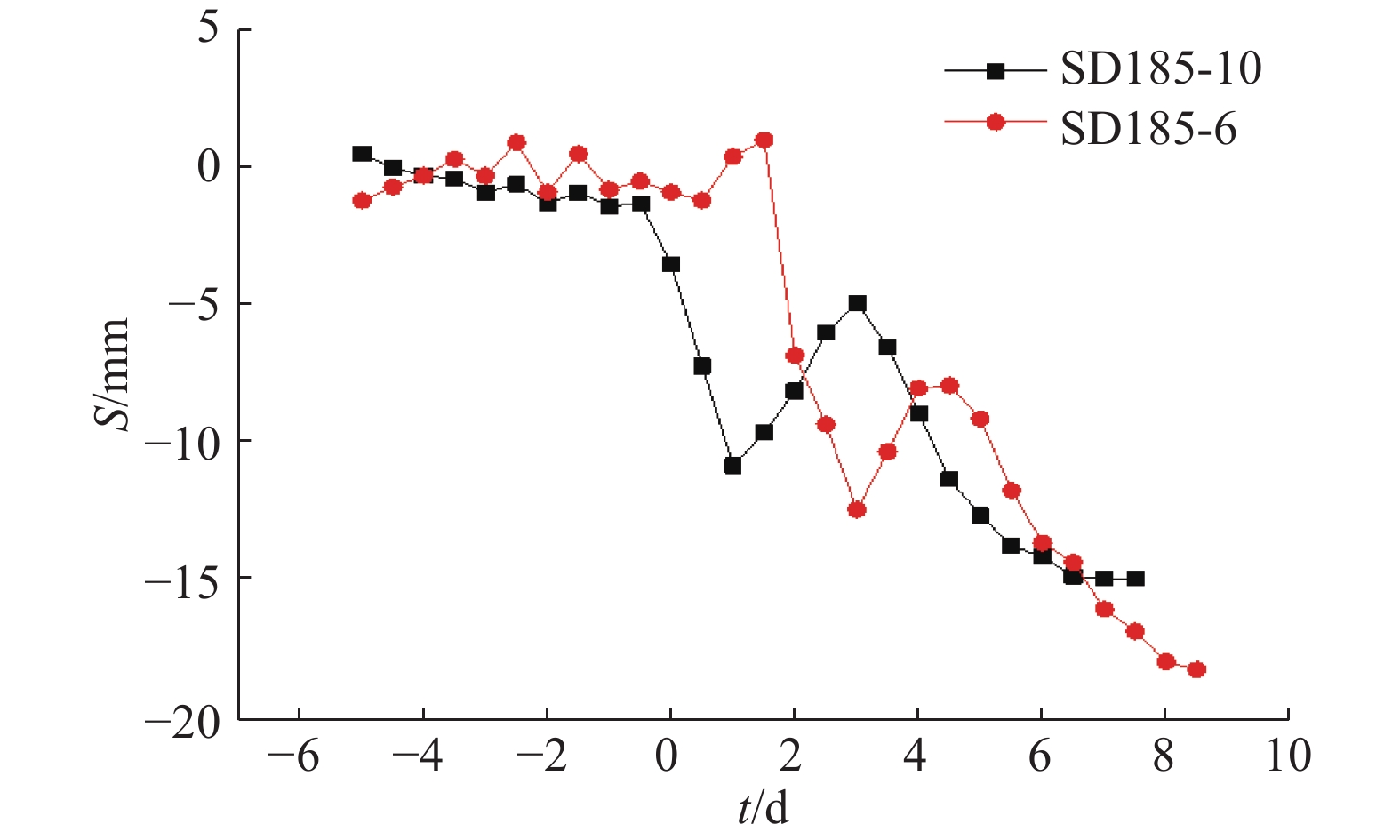
在盾构机推进过程中,地表会随着掘进的不同阶段产生相应的隆起或沉降. 在分析地表变形规律时,分别选取先行和后行隧道施工过程中断面内变形最大的测点进行分析研究. 如图8、9所示分别为SD45断面与SD185断面中最大变形点的S随时间t增加的累计变形曲线.
|
图 8 SD45断面测点累计变形曲线 Fig. 8 Deformation of monitoring points in section SD45 |
|
图 9 SD185断面测点累计变形曲线 Fig. 9 Deformation of monitoring points in section SD185 |
分析图8、9可知,从整体的变化趋势来看,土体在盾构机到达前1天左右开始急剧沉降,盾尾通过时由于盾尾注浆导致土体有一定的回弹,盾尾通过后土体继续沉降且沉降速度逐渐变缓最终趋于稳定. 对比先行线和后行线的变形规律可以发现,在双线盾构掘进过程中,后行线的土体受扰动后的变形更加明显,图8、9的监测断面处后行线最大沉降分别为先行线的1.37倍和1.24倍,这是由土体的二次扰动效应造成的.
3 杭州湾软土地区Peck公式适用性分析Peck[3]对大量实测数据进行统计可知,在假定土体不排水,土体损失体积等于沉降槽体积的情况下,提出单线隧道上方地表变形呈符合正态分布的槽型分布,单线盾构引起的横向地表沉降公式为
| $ S(x) = {S_{\max }}\exp \left( - \frac{{{x^2}}}{{2{i^2}}}\right)\;\;, $ | (2) |
| $ {S_{\max }} = \frac{{{V_{{\rm{loss}}}}}}{{i\sqrt {2{\text{π}}} }}{\rm{ = }}\frac{{\text{π} {R^2}\eta }}{{i\sqrt {2{\rm{\text{π}}}} }}\;\;. $ | (3) |
式中:x为距隧道轴线的水平距离,
马克栓[6]在Peck公式的基础上,研究双线盾构隧道地表变形公式:
| $ \begin{aligned} \delta (x) = & \frac{{\text{π} {R^2}{\eta _1}}}{{\sqrt {2\text{π} } {i_1}}}\exp\left [ - \frac{{{{(x - D/2)}^2}}}{{2i_1^2}}\right] +\\ & \frac{{\text{π} {R^2}{\eta _2}}}{{\sqrt {2\text{π} } {i_2}}}\exp \left[ - \frac{{{{(x + D/2)}^2}}}{{2i_2^2}}\right]. \end{aligned} $ | (4) |
式中:
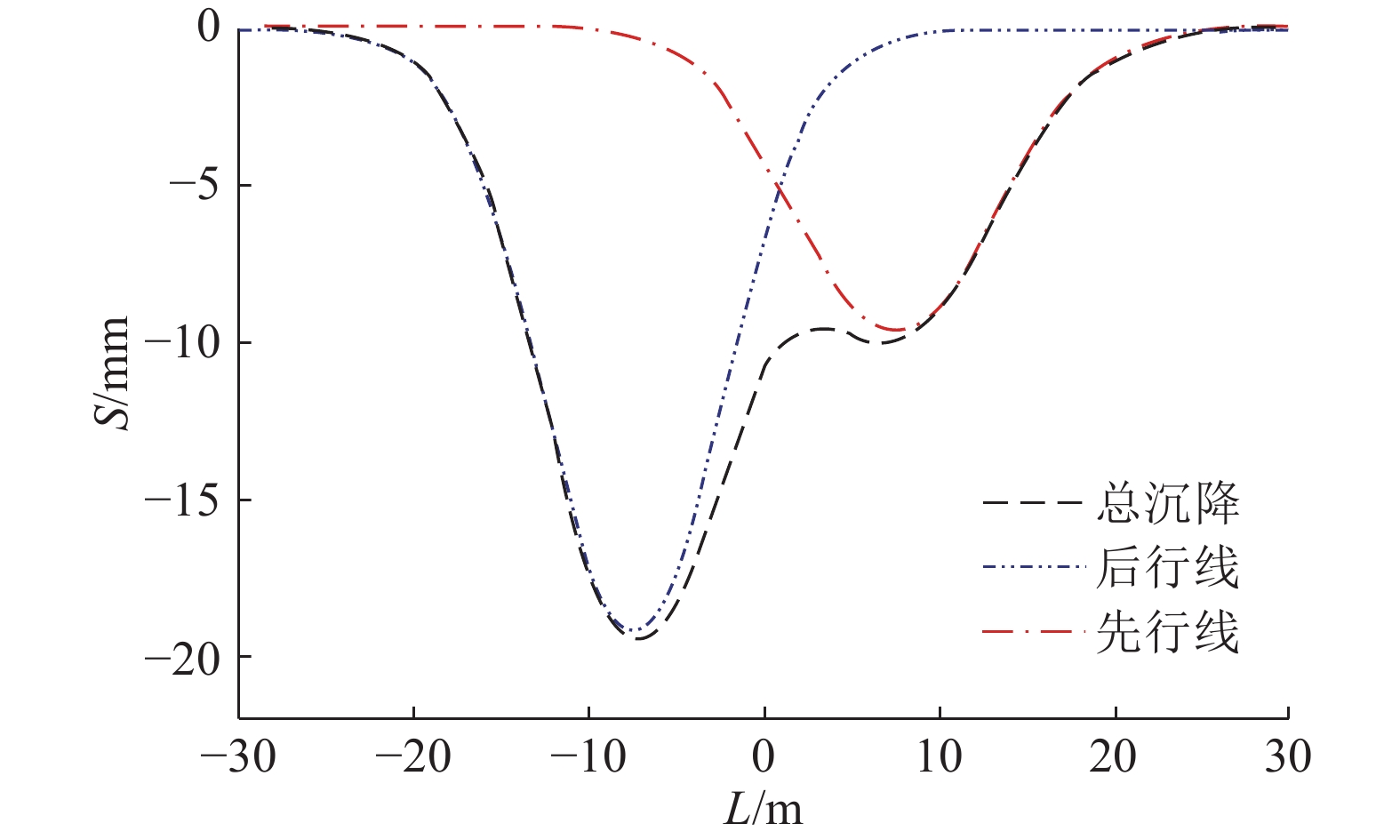
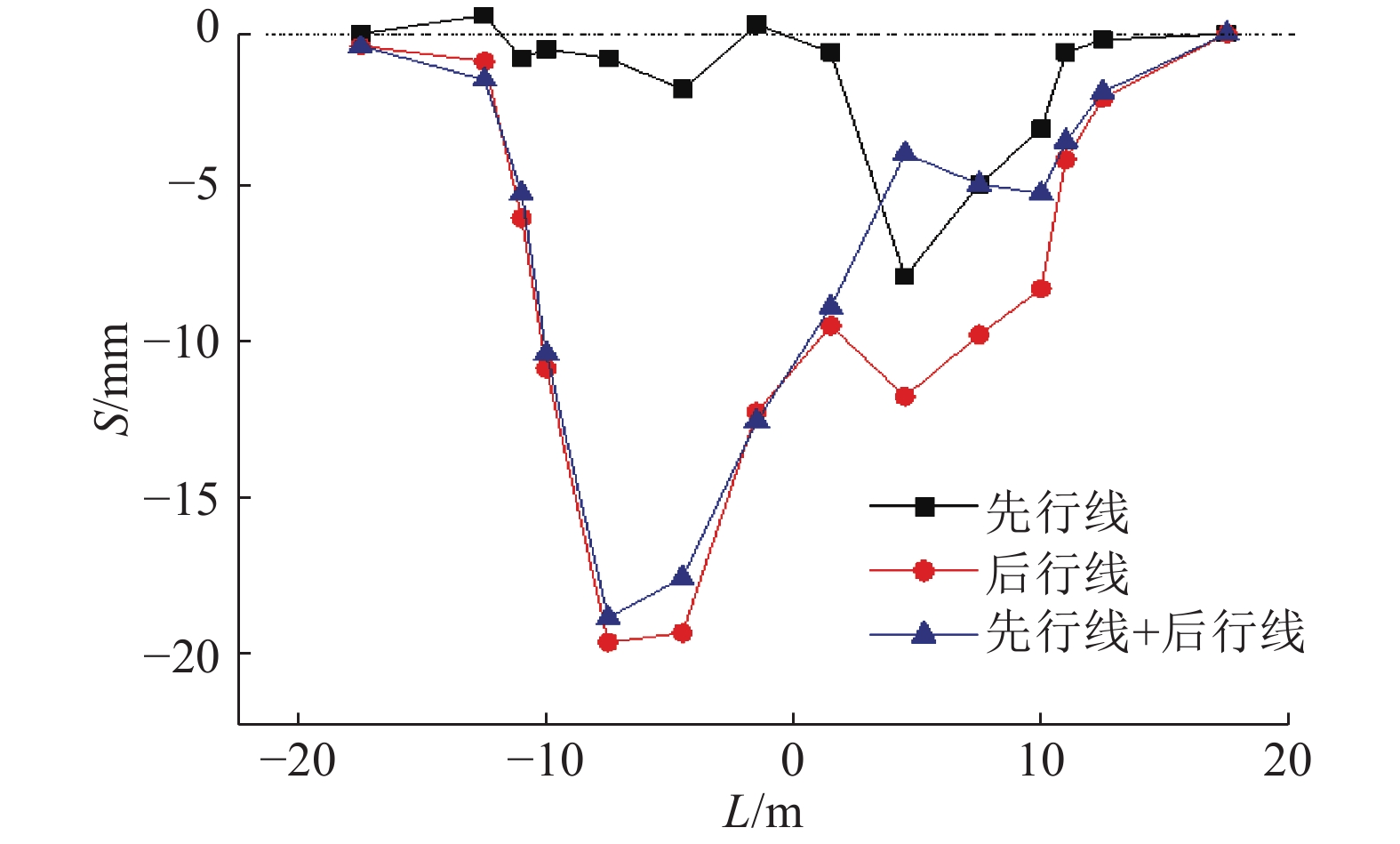
采用反算法计算式(4)中的相应参数,对SD260监测断面的地表变形进行预测,预测结果和实测地表变形如图10、11所示. 对比图10、11可知,SD260断面的实测变形曲线与预测曲线均为双峰状,且其他监测断面实测变形曲线大都与预测曲线形状相似,但地表变形绝对值存在一定的差异,可见利用双线Peck公式预测杭州湾软土地区双线盾构掘进引起的地表变形结果是可供参考的,采用式(4)进行预测的关键是式(4)中沉降槽宽度和土体损失率的取值,地表沉降是由土体损失率决定的,因此确定参数的选取方法是研究Peck公式在杭州湾软土地区适用性的关键.
|
图 10 SD260断面地表横向变形预测图 Fig. 10 Prediction of lateral surface deformation of section SD260 |
|
图 11 SD260断面地表横向变形实测曲线 Fig. 11 Lateral surface deformation of section SD260 |
现有关于Peck公式参数取值的研究中,Peck等[3, 20]研究沉降槽宽度的取值;魏纲对前人提出的公式进行系统的分析,基于大量实测数据提出黏性土的沉降槽宽度计算公式. 关于土体损失率,目前尚未有统一的取值方法. 本文结合实测数据,利用反算法得到土体损失率并分析软土区双线盾构施工过程中土体损失率的变化规律,在反算点的选取过程中仅选取变形曲线符合Peck公式预测的断面,所得的各断面土体损失率分布如表4所示.
由表4可知,该试验中各有效监测断面的土体损失率的主要分布区间为0.2%~0.8%,占总数的88.46%,其中0.2%~0.5%数量最多,占总数的50%,与文献[21~23]的结论吻合. 后行线左线的土体损失率平均值为先行线右线的1.24倍,左、右线中土体损失率为0.5%~0.8%的比例分别为42.86%和33.33%,可见受到二次扰动效应的影响,后行线的土体损失率较先行线会有一定的增大,因此当采用双线Peck公式预测杭州湾软土区地表变形时,建议取后行线的土体损失率为先行线的1.25倍.
| 表 4 土体损失率分布规律 Table 4 Distribution of loss rate of soil |
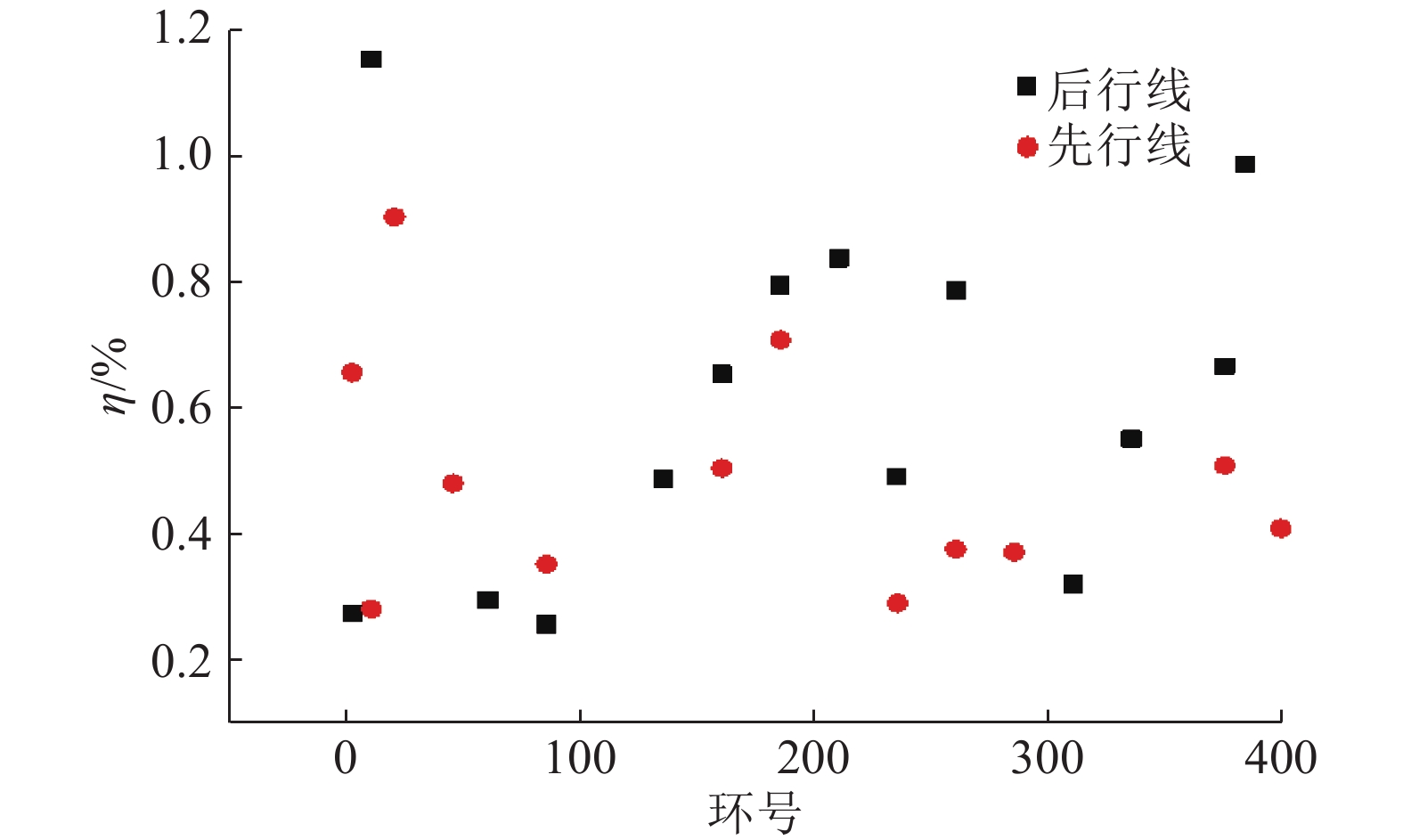
研究试验过程中的土体损失率η,如图12所示为各断面先行线和后行线的土体损失率. 可知,土体损失率没有明显的变化规律,这是因为土体损失率与盾构掘进过程中的施工参数有关,施工参数的调整会极大程度地影响土体损失率的取值. 分析土体损失率与单环排土量的关系,对二者的关系进行玻尔兹曼曲线拟合,如图13、14所示.
|
图 12 各监测断面的土体损失率 Fig. 12 Loss rate of soil of all sections |
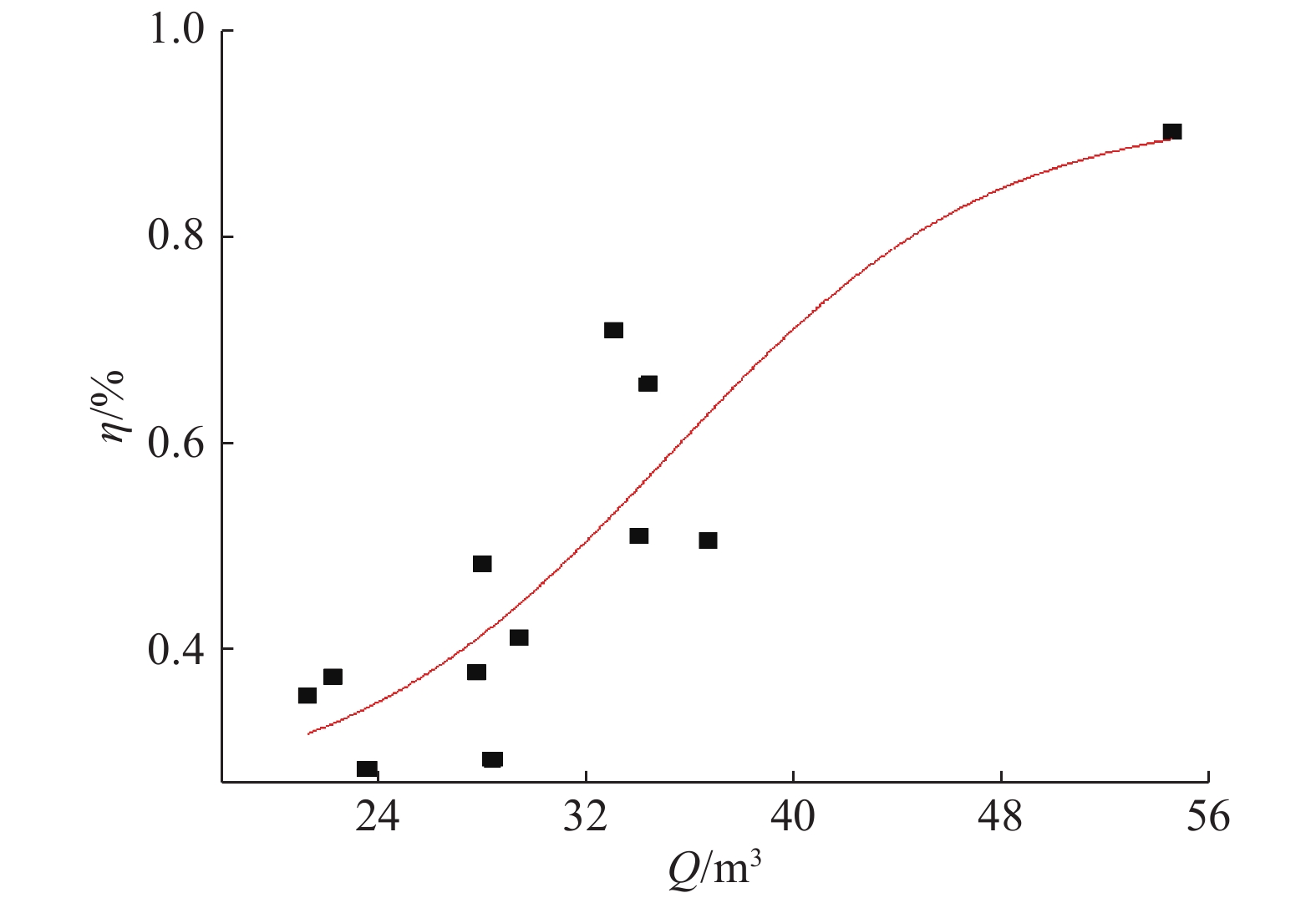
由图13可得,先行线的土体损失率与单环排土量之间满足玻尔兹曼分布规律,拟合检验参数R2为0.518 4;A1和A2分别为上限和下限,即在盾构正常施工的情况下,土体损失率为0.248%~0.924%,且土体损失率随着单环排土量的增大而增大,变化速率如图12所示,该拟合曲线在分布区间中点X0处的斜率为0.169.
|
图 13 先行线土体损失率与单环排土量关系图 Fig. 13 Relationships between loss rate and single ring excavated soil of forward line |
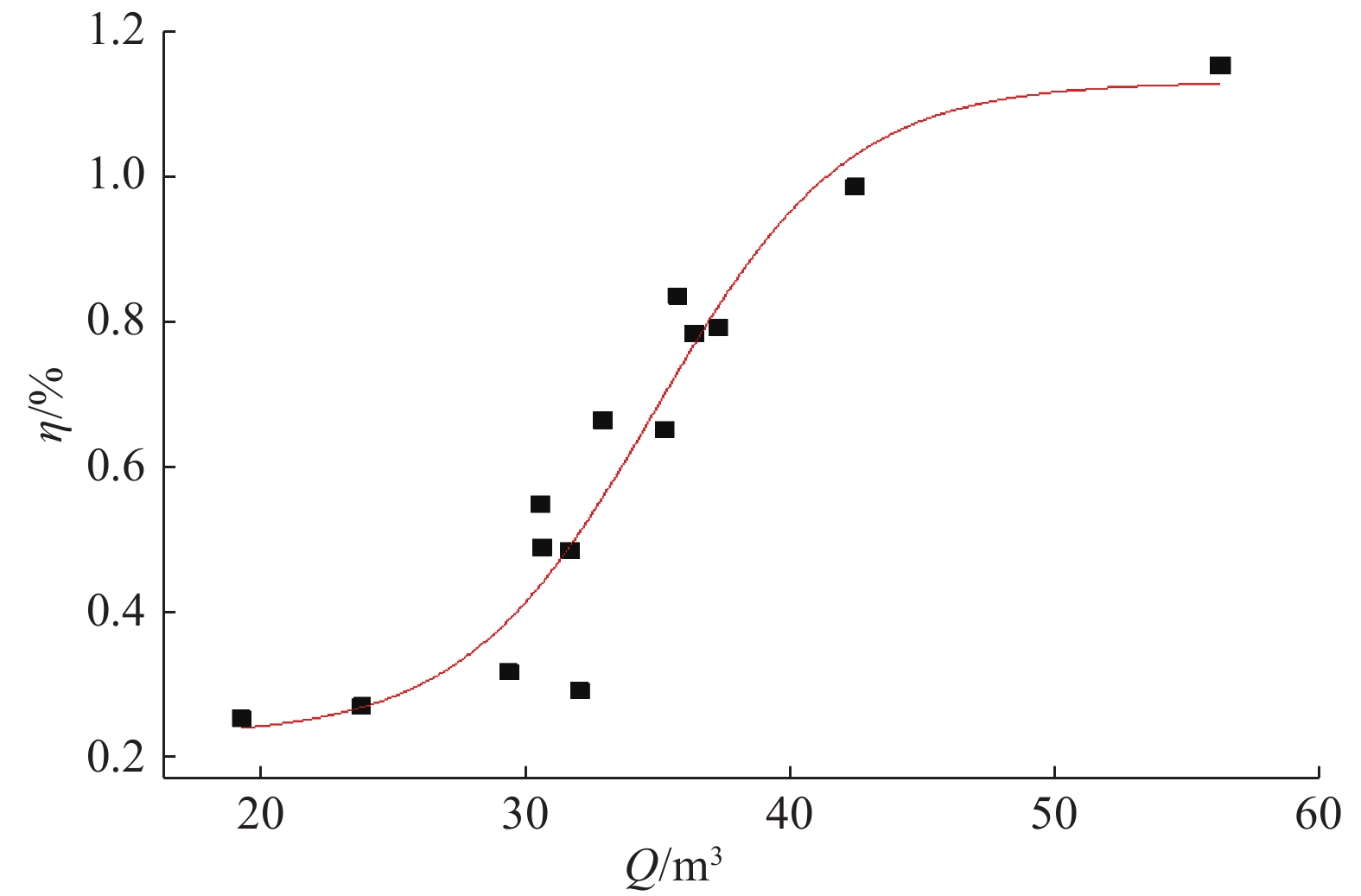
如图14所示为后行线土体损失率与单环排土量之间的关系满足玻尔兹曼分布规律,拟合检验参数R2为0.770 4,高于先行线. 后行线的土体损失率为0.232%~1.130%,拟合曲线在X0处的斜率为0.225,为先行线的1.33倍. 对比先、后行线的拟合曲线可以发现,后行线土体损失率的分布区间更广,对单环排土量的敏感性更高. 结合表3中土体损失率的区间分布规律可知,在软土区双线盾构施工中,将单环排土量控制为30 m3,能够有效地控制土体损失率接近实测平均值.
|
图 14 后行线土体损失率与单环排土量关系图 Fig. 14 Relationships between loss rate and single ring excavated soil of back line |
(1)将后行线与先行线掘进引起的断面最大沉降比值作为分析二次扰动效应的控制因素,分别对比武汉、上海和佩思地铁施工中的N. 研究分析可得软土地区双线盾构掘进引起的沉降绝对值较大且二次扰动效应明显强于其他土质,在施工中应予以重视.
(2)分析实测变形曲线,定义单环排土量与盾尾注浆压力的比值,分析可得地表最终沉降和K之间存在较好的正相关,即盾构掘进过程中的单环排土量和地表最终沉降值之间存在一定的正相关,盾尾注浆压力和地表最终沉降之间呈负相关.
(3)该试验中各有效监测断面的土体损失率的主要分布区间为0.2%~0.8%,占总数的88.46%,其中0.2%~0.5%的分布数量最多,占总数的50%,后行线左线的土体损失率平均值为先行线右线的1.24倍. 受到二次扰动效应的影响,后行线的土体损失率较先行线会有一定的增大,因此在采用双线Peck公式预测杭州湾软土区地表变形时,建议取后行线的土体损失率为先行线的1.25倍.
(4)土体损失率与单环排土量之间满足玻尔兹曼分布规律,即在盾构正常施工的情况下,土体损失率分布在一个上限和下限之间,且土体损失率随着单环排土量的增大而增大. 在软土区双线盾构施工中,建议通过合理的施工管控(螺旋输送机)将单环排土量控制为30 m3.
| [1] |
魏纲, 张鑫海, 华鑫欣. 考虑多因素的双线水平平行盾构施工引起地表隆陷研究[J]. 防灾减灾工程学报, 2017, 37(6): 923-930. WEI Gang, ZHANG Xin-hai, HUA Xin-xin. Research on surface heave and subsidence caused by multi-factor in double-line shield tunnels construction[J]. Journal of Disaster Prevention and Reduction Engineering, 2017, 37(6): 923-930. |
| [2] |
邱明明, 杨果林, 吴镇清, 等. 双孔平行地铁隧道盾构施工地表沉降分布规律研究[J]. 现代隧道技术, 2017, 54(2): 96-105. QIU Ming-ming, YANG Guo-lin, WU Zhen-qing, et al. Distribution laws of surface settlement induced by shield construction of twin-tube metro tunnels[J]. Modern Tunnelling Technology, 2017, 54(2): 96-105. |
| [3] |
PECK R B. Deep excavations and tunneling in softground [C] // Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico City: [s. n.], 1969: 225–290.
|
| [4] |
SAGASETA C. Analysis of undrained soil deformation due to ground loss[J]. Geotechnique, 1987, 37(3): 301-320. DOI:10.1680/geot.1987.37.3.301 |
| [5] |
李忠超, 陈仁朋, 孟凡衍, 等. 软黏土中盾构掘进地层变形与掘进参数关系[J]. 浙江大学学报: 工学版, 2015, 49(7): 1268-1275. LI Zhong-chao, CHEN Ren-peng, MENG Fan-yan, et al. Tunnel boring machine tunneling-induced ground settlements in soft clay and influence of excavation parameters[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(7): 1268-1275. |
| [6] |
陈春来, 赵城丽, 魏纲, 等. 基于Peck公式的双线盾构引起的土体沉降预测[J]. 岩土力学, 2014, 35(8): 2212-2218. CHEN Chun-lai, ZHAO Cheng-li, WEI Gang, et al. Prediction of soil settlement induced by double-line shield tunnel based on Peck formula[J]. Rock and Soil Mechanics, 2014, 35(8): 2212-2218. |
| [7] |
WEI Gang. Prediction of soil settlement caused bydouble-line parallel shield tunnel construction[J]. Disaster Advances, 2013, 6(6): 23-27. |
| [8] |
胡斌, 刘永林, 唐辉明, 等. 武汉地铁虎泉-名都区间隧道开挖引起的地表沉降研究[J]. 岩石力学与工程学报, 2012, 31(5): 908-913. HU Bin, LIU Yong-lin, TANG Hui-ming, et al. Researchon ground subsidence due to tunnel excavation inHuquan-Mingdu section of Wuhan subway[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(5): 908-913. DOI:10.3969/j.issn.1000-6915.2012.05.006 |
| [9] |
CHEHADE F H, SHAHROUR I. Numerical analysis of the interaction between twin-tunnels: influence of the relative position and construction procedure[J]. Tunnelling and Underground Space Technology, 2008, 23(2): 210-214. DOI:10.1016/j.tust.2007.03.004 |
| [10] |
NGOC A D, DANIEL D, PIERPAOLO O. Three-dimensional numerical simulation of mechanized twin stacked tunnels in soft ground[J]. Journal of Zhejiang University: Science A, 2014, 15(11): 896-913. DOI:10.1631/jzus.A1400117 |
| [11] |
孙兵, 仇文革. 双孔盾构隧道地表位移离心机模型试验研究[J]. 铁道建筑, 2010(2): 38-41. SUN Bing, QIU Wen-ge. Study on surface displacementinduced by parallel twin shield tunnel with centrifuge model test[J]. Railway Engineering, 2010(2): 38-41. DOI:10.3969/j.issn.1003-1995.2010.02.013 |
| [12] |
NEW B M, BOWERS K H. Ground movement model validation at the heathrow express trial tunnel[J]. Tunnelling, 1994(3): 301-329. |
| [13] |
刘波, 陶龙光, 丁城刚, 等. 地铁双隧道施工诱发地表沉降预测研究与应用[J]. 中国矿业大学学报, 2006, 35(3): 356-361. LIU Bo, TAO Long-guang, DING Cheng-gang, et al. Predictionfor ground subsidence induced by subway double tube tunneling[J]. Journal of China University of Mining and Technology, 2006, 35(3): 356-361. DOI:10.3321/j.issn:1000-1964.2006.03.014 |
| [14] |
SUWANSAWAT S, EINSTEIN H H. Describing settlement troughs over twin tunnels using a superposition technique[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(4): 445-468. DOI:10.1061/(ASCE)1090-0241(2007)133:4(445) |
| [15] |
白海卫, 宋守信, 王剑晨. Peck公式在双线盾构隧道施工地层变形中的适应性分析[J]. 北京交通大学学报, 2015, 39(3): 30-34. BAI Hai-wei, SONG Shou-xin, WANG Jian-chen. An adaptability study of Peck formula applied to predicting ground settlements induced by double shield tunneling[J]. Journal of Beijing Jiaotong University, 2015, 39(3): 30-34. |
| [16] |
赵华松, 周文波, 刘涛, 等. 双线平行盾构施工引起的土体位移分析及其软件开发[J]. 上海大学学报: 自然科学版, 2015, 11(4): 416-422. ZHAO Hua-song, ZHOU Wen-bo, LIU Tao, et al. Numerical simulation and software development of soil displacement due ti double-tube parallel tunnels[J]. Journal of Shanghai University: Natural Science, 2015, 11(4): 416-422. |
| [17] |
GIMA V M, BARRY M L. Numerical back-analyses of greenfield settlement during tunnel boring[J]. Canadian Geotechnical Journal, 2013, 50(2): 145-152. DOI:10.1139/cgj-2011-0358 |
| [18] |
张恒, 陈寿根, 邓稀肥. 盾构掘进参数对地表沉降的影响分析[J]. 现代隧道技术, 2010, 47(5): 48-53. ZHANG Heng, CHEN Shou-gen, DENG Xi-fei. Analysis of the influence of shield driving parameters on ground settlements[J]. Modern Tunneling Technology, 2010, 47(5): 48-53. DOI:10.3969/j.issn.1009-6582.2010.05.009 |
| [19] |
魏新江, 周洋, 魏纲. 土压平衡盾构掘进参数关系及其对地层位移影响的试验研究[J]. 岩土力学, 2013, 34(3): 59-65. WEI Xin-jiang, ZHOU Yang, WEI Gang. Research of EPB shield tunneling parameter relations and their influence on stratum displacement[J]. Rock and Soil Mechanics, 2013, 34(3): 59-65. |
| [20] |
魏纲. 盾构法隧道地面沉降槽宽度系数取值的研究[J]. 工业建筑, 2009, 39(12): 74-79. WEI Gang. Study on calculating for width parameter of surface settlement trough induced by shield tunnel[J]. Industrial Construction, 2009, 39(12): 74-79. |
| [21] |
O’REILLY M P, NEW B M. Settlements above tunnels in the United Kingdom-their magnitude and prediction [C] // Proceedings of Tunnelling’82. London: Institution of Mining and Metallurgy, 1982: 173–181.
|
| [22] |
ATTEWELL P B. Ground movements caused by tunnelling in soil [C] // Conference on Large Ground Movements and Structures. London: Pentech Press, 1978: 812–948.
|
| [23] |
MAIR R J. Settlement effects of bored tunnels [C] // Proceedings of International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground. London: Balkema, 1996: 43–53.
|


