岩石、混凝土等固体材料的力学参数具有尺寸效应,它们随着试样的尺寸或/和形状的变化而变化. 在混凝土尺寸效应的研究中,对强度参数的研究较多,对变形参数的研究较少;对含有粗骨料的混凝土研究较多[1-5],对无粗骨料的活性粉末混凝土(RPC)研究较少[6-8];静态加载研究较多,动态加载研究较少.
RPC是Richard等[9]发明的一种超高强、超高耐久性的混凝土材料. 关于RPC强度尺寸效应的研究,只停留在单轴条件下. 刘数华等[6]对素RPC和含钢纤维RPC的、边长分别为4、10 cm的立方体试样以及尺寸为10 cm×10 cm×30 cm的棱柱体试样,开展无减摩单轴试验. 秦子鹏等[7]在研究RPC尺寸效应时,使用3种立方体试样(边长分别为40、70.7和100 mm)及1种棱柱体试样(40 mm×40 mm×160 mm),每种试样在龄期分别为7 d和28 d时进行无减摩加载. An等[8]为了研究素RPC和含钢纤维RPC的强度尺寸效应,对边长分别为50、70.7、100和150 mm的立方体试样进行单轴不减摩压缩试验. 归纳文献[6~8]得到以下2个结论:1)当形状相同时,在一定的尺寸范围内,尺寸越大,强度越低;2)当截面相同时,在一定的高度范围内,试块越高,强度越低.
岩石与混凝土材料的常规三轴试验研究已不鲜见,然而在这些试验中,对试样端部采取减摩措施的较少. 余自若等[10]对含钢纤维RPC进行常规三轴试验,采取一定的端部减摩措施;余自若等[10]的研究结果表明:RPC的抗压强度、弹性模量以及轴向峰值应变与围压均呈线性关系. 上述研究没有对比不同的端部减摩方式对RPC力学性能的影响.
当采用霍普金森杆和轻气炮对RPC施加冲击荷载时,试样的长度一般小于试样的直径;目前的准静态和低速加载使用的试样长度通常为直径的2.0~3.0倍,为了能够使冲击加载试验结果与低速及静态加载结果具有可比性,需要使试样具有相同的尺寸.
本文研究长径比对RPC在静态加载条件下的力学特性的影响,考虑加载过程中端部减摩条件和围压的影响.
1 试验概述 1.1 材料配比及试样制备RPC的制备材料:P.O 525水泥(冀东水泥厂盾石牌),硅灰(购于埃肯国际贸易有限公司),石英粉(购于北京开碧源贸易有限责任公司),海砂(购于福建彰德,粒径为0.35~1.00 mm),石英砂(购于河北振胜矿业,粒径为0.16~0.63 mm),3301L型聚羧酸减水剂(购于西卡公司),FAQ型消泡剂(购于北京建筑工程研究院),北京市海淀区自来水.
制备RPC的详细配合比如表1所示.
| 表 1 活性粉末混凝土材料用量 Table 1 Raw materials proportion of RPC |
搅拌成型过程如下:将水泥、硅灰、石英粉、海砂和石英砂倒入卧式搅拌机中进行干混,直到混匀;将水等分成2份;将减水剂溶入一份水中混匀,然后倒入搅拌机内搅拌;将消泡剂溶入另一份水中,混匀之后倒入搅拌机内,继续搅拌,直到使浆料呈稳定的流动状态. 将搅拌完成的RPC浆料浇筑至350 mm×200 mm×140 mm表面有塑胶层的木制模具中;再将浇筑有浆料的模具放至振动台上振动1 min;振动完成后,在浇筑的浆料表面覆盖一层保鲜膜,将模具放入标准养护室内;48 h后拆模,并继续放在标养室养护28 d;28 d后,将成型的RPC大块搬出养护室,在室内存放.
试样制备:在室内存放约23到24个月后,用钻机从RPC大块中钻取圆柱试样;圆柱芯样先用切割机切割,然后用磨平机磨平. RPC试样分别按长径比为0.5、1.0、2.0和3.0来加工,试样直径均控制在43.6 mm左右.
该试验的所有试样均取自于同一个RPC大块.
1.2 加载设备和试样密封方法该试验所用的主要设备为北京交通大学土木建筑工程学院XTR-01型电液伺服岩石三轴试验机,与该设备配套的三轴压力室具有液压自平衡功能.
试样的加载方式如图1所示. 图中,
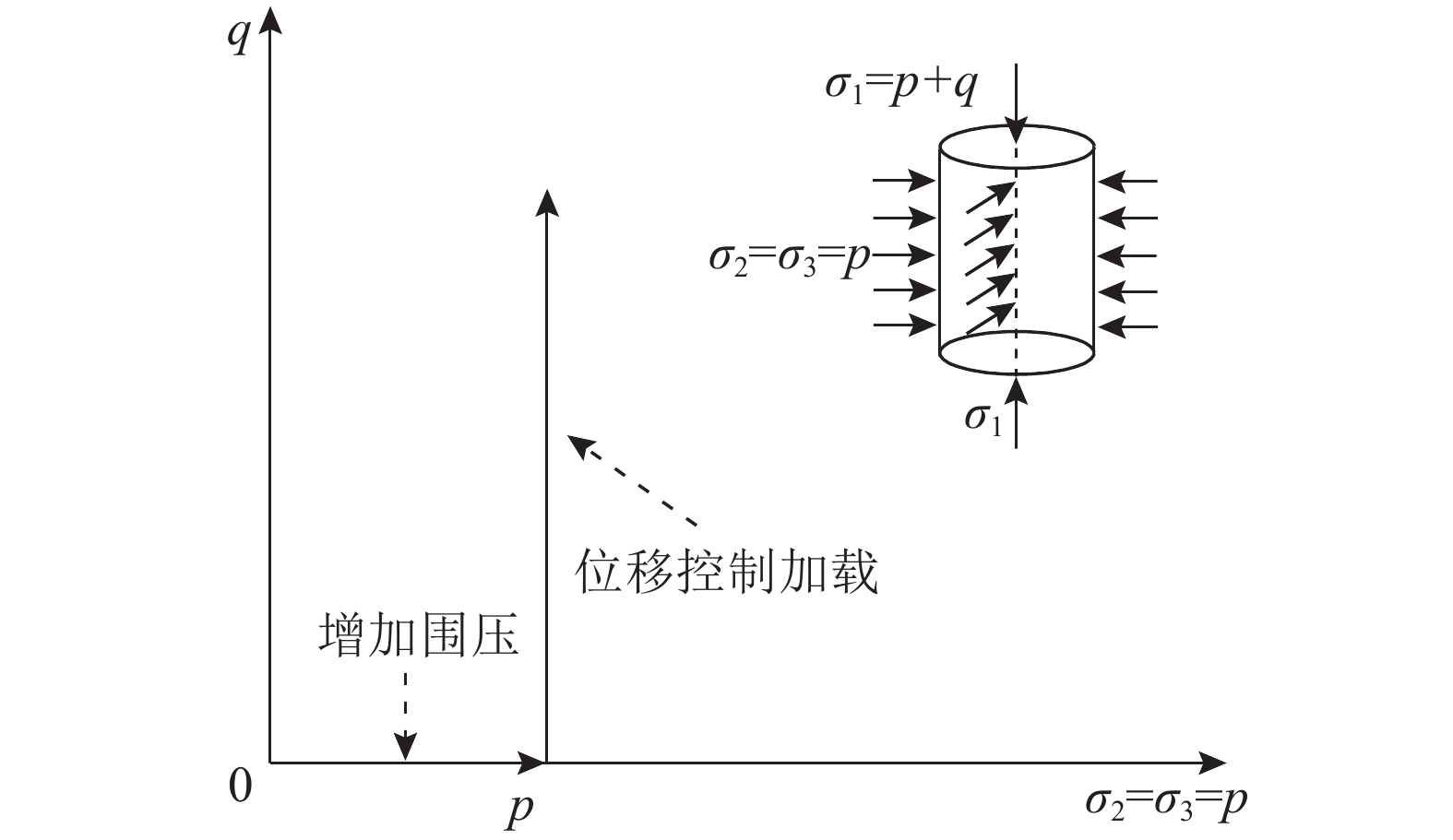
|
图 1 常规三轴加载方式 Fig. 1 Loading regime of conventional triaxial device |
试样两端直接与上、下压头相接触,上压头(带球铰)直径为50 mm,下压头直径为53 mm. 上、下压头直径都比试样直径大;这样处理可以保证在试样因轴向受压发生侧向膨胀时,端部不超出压头范围. 由于受到三轴室内柱塞行程的限制,不同长径比试样所搭配的下压头高度会作相应的调整,但上压头不作更换. 由于试样直径小于上、下压头直径,为了使试样端面圆心与上、下压头端面圆心对中以及使包裹试样的热缩管可以在试样与压头接触处顺畅过度,在试样的上、下端粘有断面呈阶梯状的软质聚氯乙烯(PVC)条. 上、下压头与试样用热缩管套住. 在与上、下压头接触的热缩管两端用伸缩性良好的筒状橡胶带封住,以防液压油从热缩管与压头之间的缝隙处渗入.
1.3 变形测量在试验过程中,试样的轴向与径向变形分别用轴向及径向引伸计(试验机配套YSY60-6/2引伸计)测量,如图2所示. 在对所有试样的轴向变形测量中,测量标距均为180 mm;除长径比为0.5的试样没测径向变形外,其他均测量了试样中部的径向变形.

|
图 2 RPC圆柱试样变形的测量 Fig. 2 Measurement of deformation of RPC cylindrical specimen |
由于轴向引伸计的测量标距恒定,试样长度越小,压头的变形占据的份额越大. 为了消除压头变形的影响,假设试样的总变形量为测量标距范围内的总变形量减去在该范围内的压头变形量. 这样处理没有考虑减摩层变形的影响.
在计算压头变形时,压头材料的弹性模量取为206 GPa. 在轴向引伸计的标距范围内,直径为50 mm的上端压头长度远小于直径为53 mm的下端压头长度;在计算上、下压头的合计变形量时,近似地将上压头的直径取为53 mm.
1.4 加载过程和端部减摩条件整个加载过程分为以下5步:1)通过计算机控制,对试样施加一个较小的轴向预压力,这是为了让带有球铰的上端压头调整到上表面与柱塞端面平行;2)增加围压,使其到达目标值;3)保持围压和轴压不变,并持续一段时间,这是为了释放掉试样两端减摩层的黏塑性变形和热缩套的黏塑性变形;4)继续保持围压恒定,单调地增加试样的轴向变形;5)在轴向变形达到一定程度后,先减少柱塞加给试样的轴向压力,直到接近或等于0,然后再把围压卸载到0.
采用0.1 mm厚的聚四氟乙烯薄膜作为减摩垫层. 试样的端部减摩条件有以下3种,分别如下:1)试样两端不作减摩处理,试样端面直接与金属压头接触,相应的试样称为条件A试样;2)试样两端分别垫有2层聚四氟乙烯薄膜,相应的试样称为条件B试样;3)试样两端分别垫有3层聚四氟乙烯薄膜,薄膜与薄膜之间涂有黄甘油,薄膜与试样以及薄膜与压头均直接接触,相应的试样称为条件C试样.
2 试验结果及分析 2.1 应力-应变曲线分析如图3所示为根据试验数据绘制出的偏差应力

|
图 3 不同长径比下试样的偏差应力-应变曲线 Fig. 3 Differential stress-strain curves of specimen under different length-diameter ratios |
图3(a)中,当围压为5 MPa,长径比为0.5时,条件A试样的峰值偏差应力达到250 MPa左右,条件B与条件C试样均约为150 MPa. 当围压为70 MPa,长径比为0.5时,条件A试样的
图3中,对于不同减摩条件下的所有长径比试样,当围压为70 MPa时,
对于素RPC试样,
观察图3中所有试样的曲线可以发现:在相同长径比及相同围压的条件下,条件B和条件C试样的
图3(c)中,当围压为20、35 MPa时长径比为2.0的试样只列了部分曲线,全部试验曲线见图4. 另外,对长径比为2.0的条件C试样进行单轴压缩试验,试验曲线如图5所示. 可以看出,在到达峰值点之前,曲线的主体部分是直线.
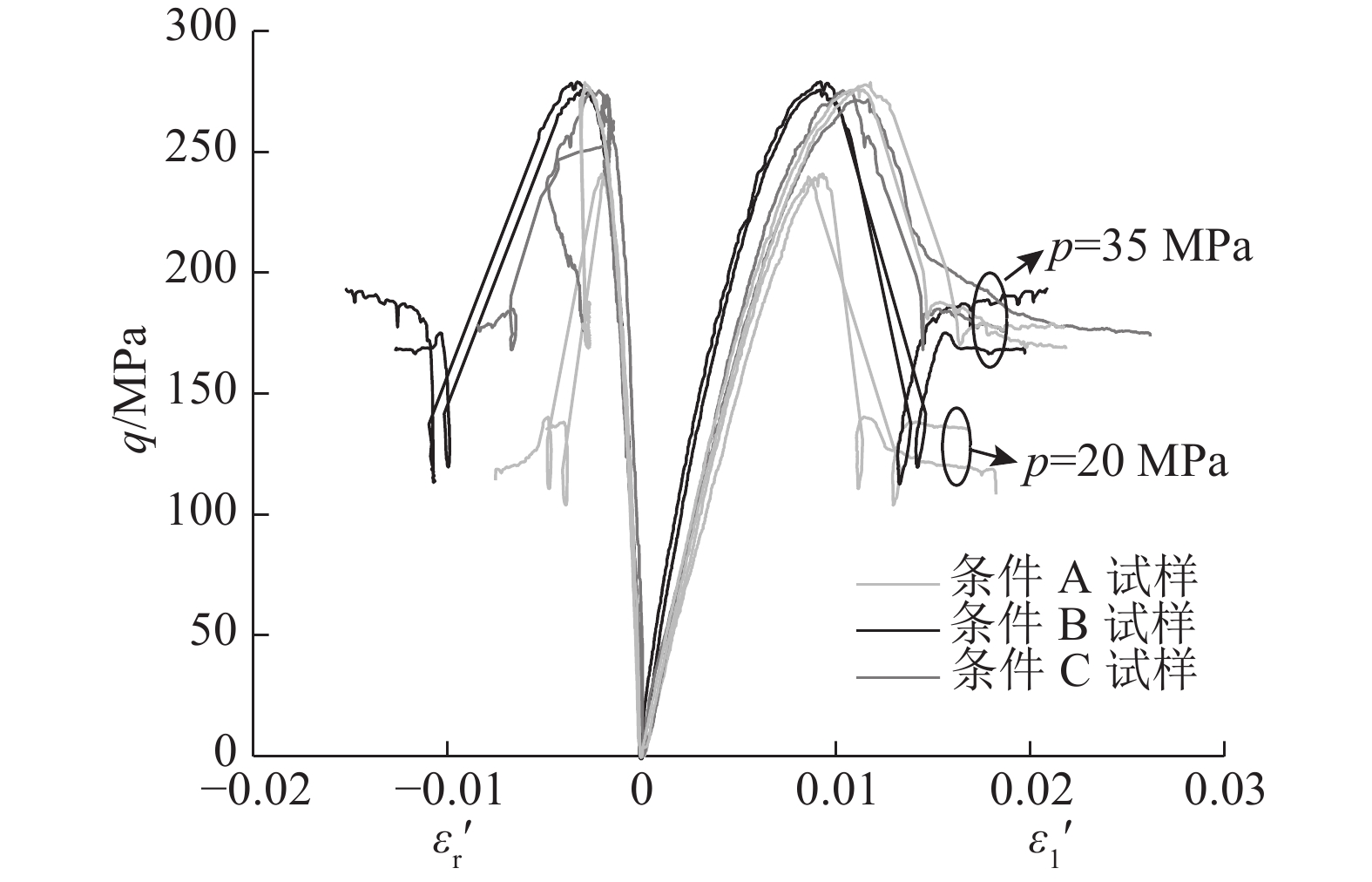
|
图 4 围压为20及35 MPa时长径比为2试样的偏差应力-应变曲线 Fig. 4 Differential stress-strain curves of specimen with length-diameter ratio is 2 when confining pressure is 20 MPa and 35 MPa |
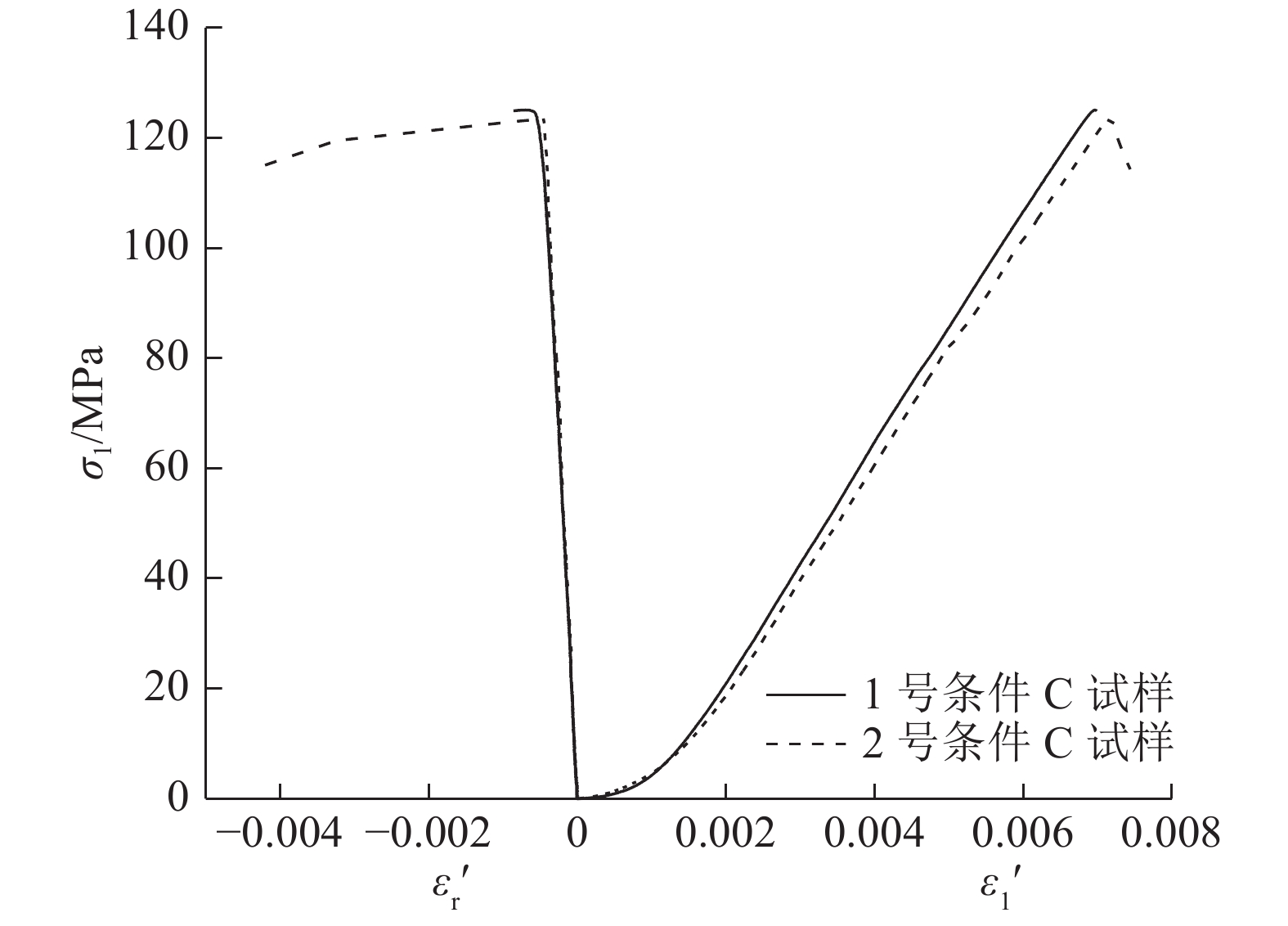
|
图 5 长径比为2的条件C试样单轴应力-应变曲线 Fig. 5 Uniaxial stress-strain curves of specimen with condition C when length-diameter ratio is 2 |
如图6所示,对于长径比为0.5的试样,无论采用哪种减摩条件以及哪一档围压,从试样的2个端面以及侧面都能够看到多个破坏面与试样表面的交线,其中多数破坏面贯穿整个试样的高度,并与试样的轴线之间有一定角度. 对于条件A试样,无论围压高低,在试样端面都出现了环形的白圈,白色为裂隙中的粉末颜色. 对于条件B和C试样,无论围压高低,在试样的两端都出现了多条裂缝,裂缝之间彼此相交. 当围压为5 MPa时,无论是哪种减摩条件,试样侧面的贯通裂缝多数是张开的;在同样的围压下,条件A试样上、下端面的裂隙是闭合的,条件B和C试样的两端面裂缝有些是张开的. 当围压为70 MPa时,条件A试样和条件B试样的侧面以及上、下端面上,所有裂缝都是闭合的.

|
图 6 长径比为0.5试样的破坏模式 Fig. 6 Failure mode of RPC specimen when length-diameter is 0.5 |
如图7所示,对于长径比为1.0的试样,当围压为5 MPa时,条件B试样和条件C试样中会出现一条或多条贯穿整个高度的主裂纹,这些主裂纹在试样的上、下端面均可见;试样侧面的相邻主裂纹可能会合并,出现V形,但没有出现X形相交的裂纹. 当围压为70 MPa时,试样只有一端出现裂纹,另一端较完好;试样侧面能够出现X形相交的剪切裂纹.
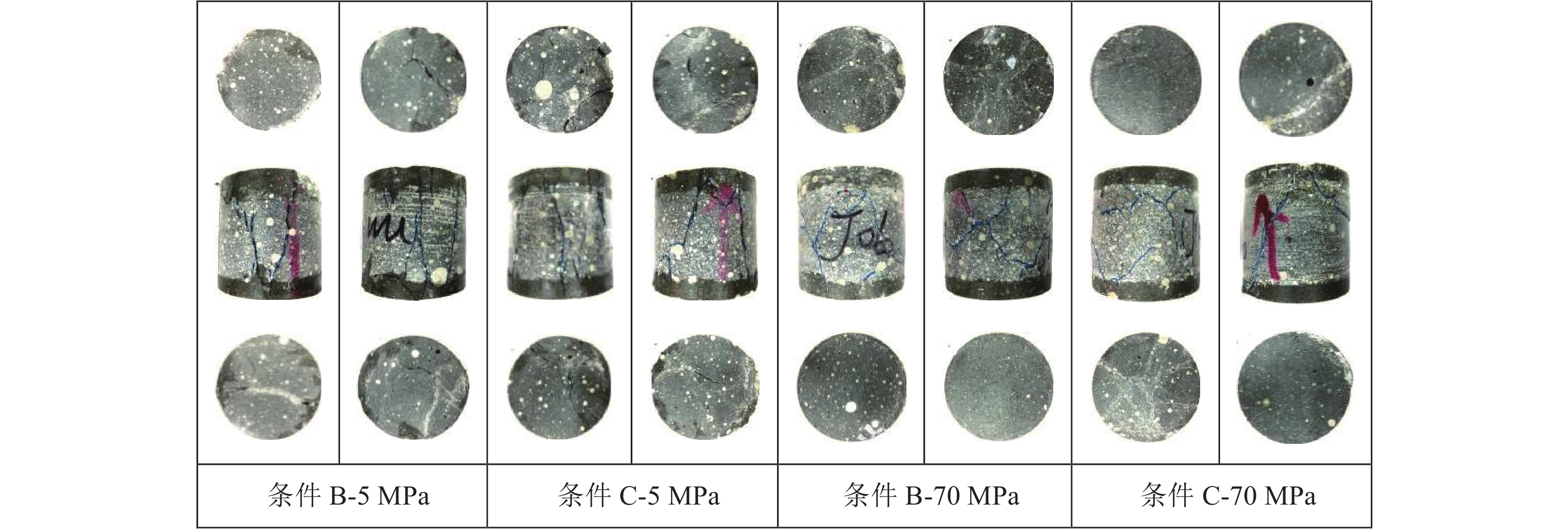
|
图 7 长径比为1试样的破坏模式 Fig. 7 Failure mode of RPC specimen when length-diameter is 1 |
如图8所示,对于长径比为3.0的试样,当围压为5 MPa时,条件A试样的2个端面都没有出现裂缝;条件C试样的一端出现了裂缝,另一端没有裂缝. 当围压为70 MPa时,条件A试样的两端没有出现裂缝;2块条件C试样中,有一块在一端出现裂缝、另一端完好,另一块则两端均无裂缝. 在这2种围压、2种减摩条件的4种组合中,每个试块的侧面出现的主裂缝只有1、2条.

|
图 8 长径比为3.0试样的破坏模式 Fig. 8 Failure mode of RPC specimen when length-diameter is 3.0 |
记
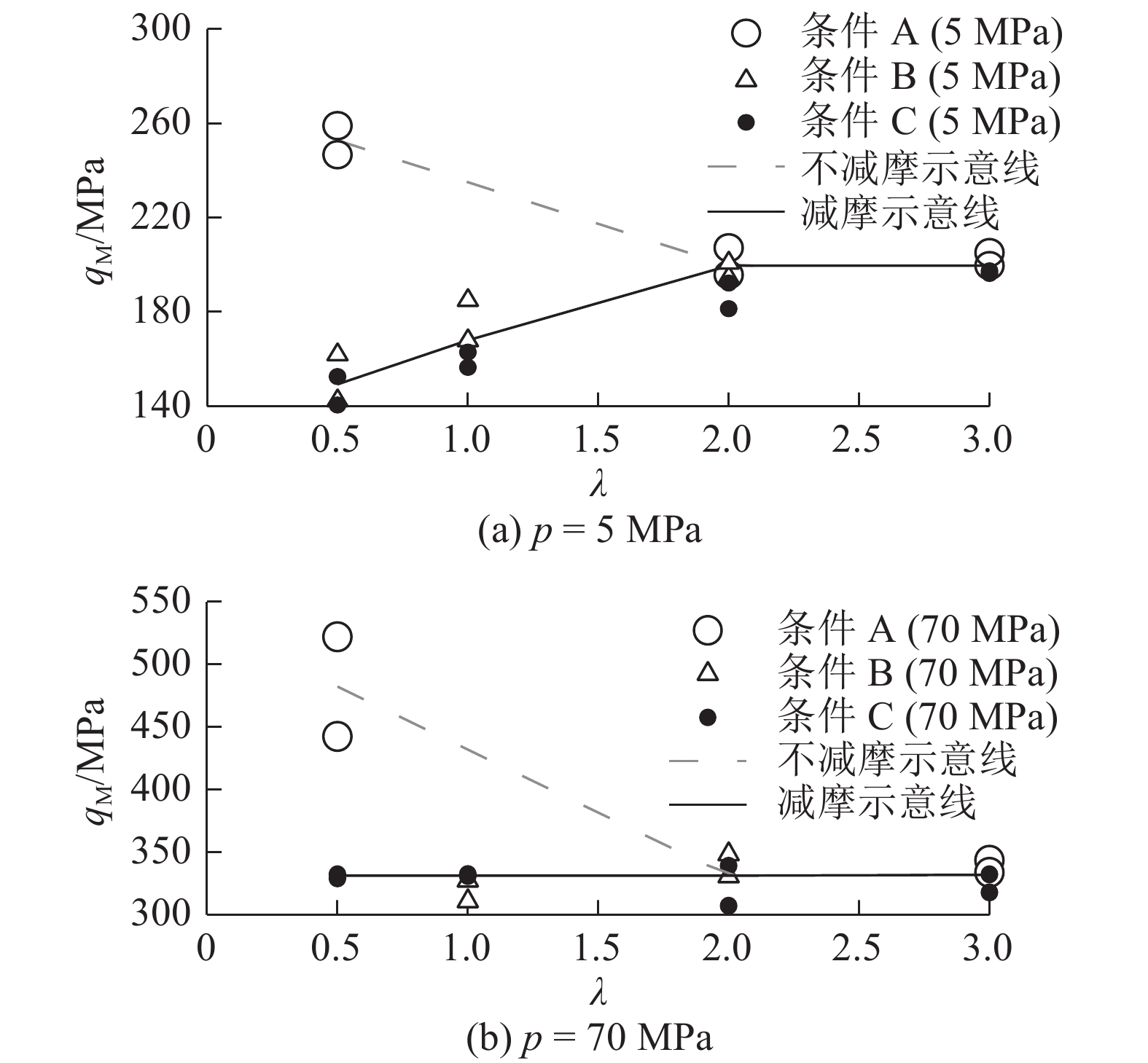
图9(a)给出当围压为5 MPa时,几种端部减摩条件试样的偏差应力峰值
图9(b)给出70 MPa围压下几种减摩条件试样的
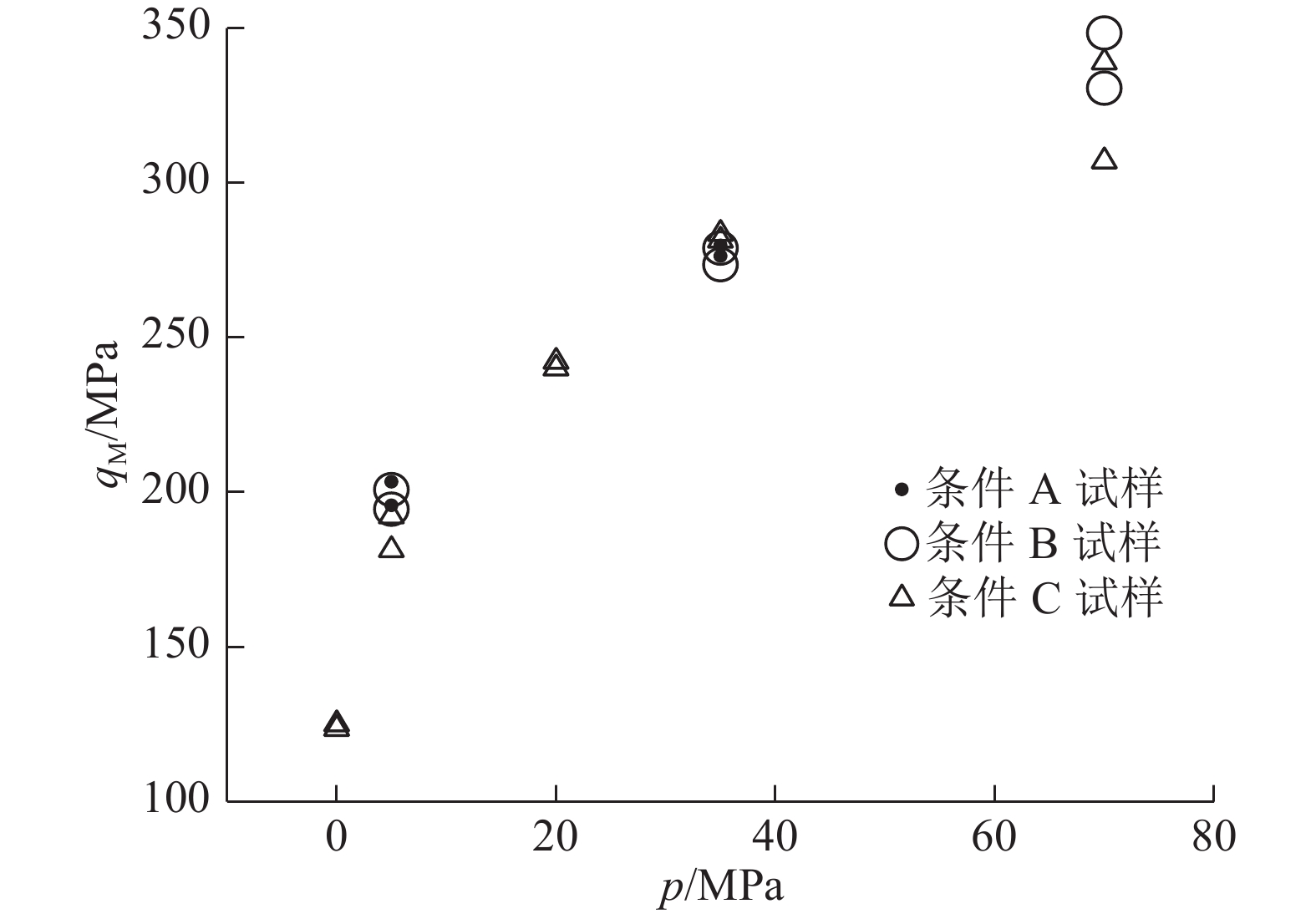
图10给出当长径比为2.0时,不同端部减摩条件试样的
|
图 10 长径比为2.0时RPC试样的峰值偏差应力与围压的关系 Fig. 10 Relationship between peak differential stress of RPC specimen and confining pressure when length-diameter ratio is 2.0 |
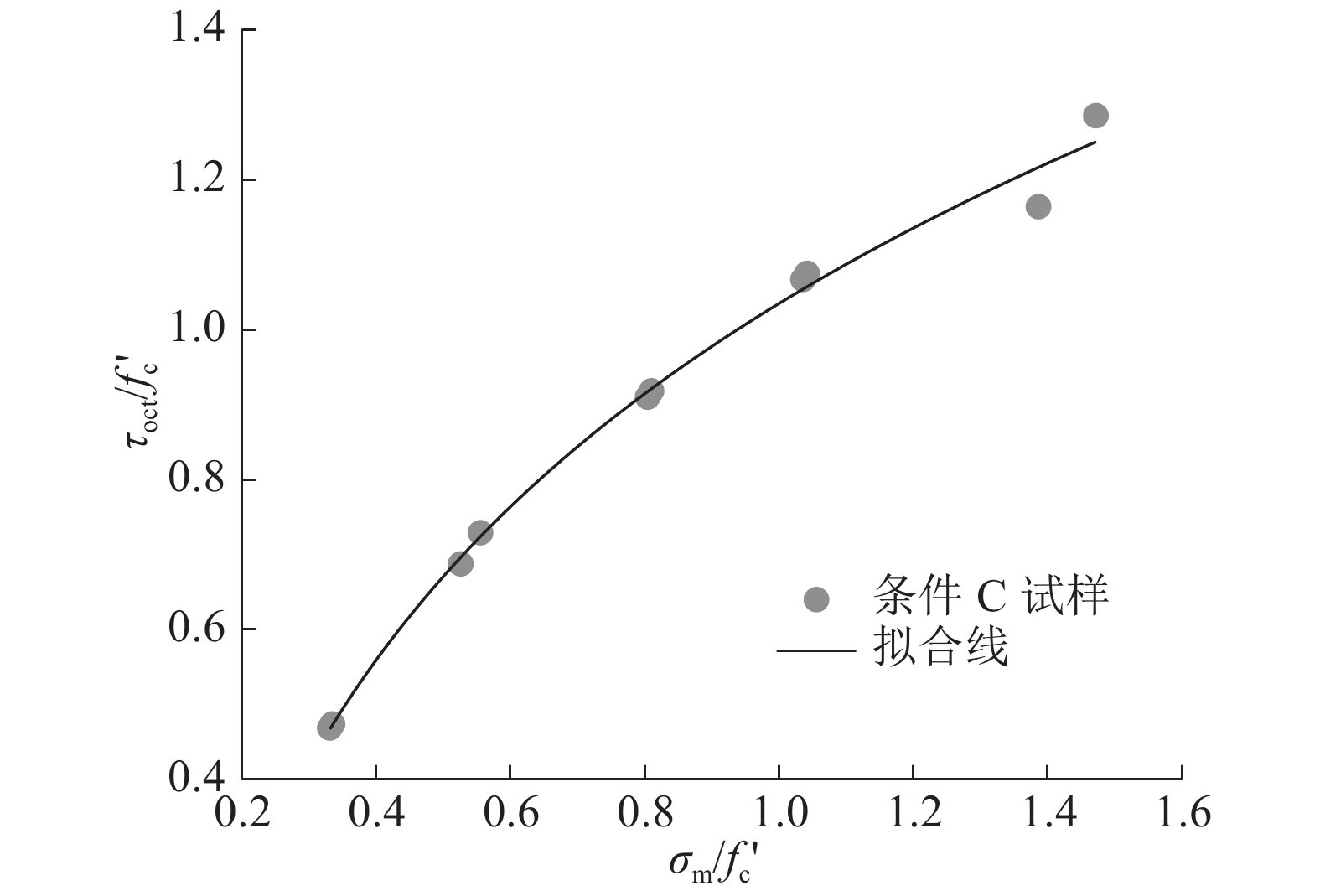
图11给出当长径比为2.0时,条件C试样的
|
图 11
长径比为2.0时条件C试样的
|
根据拟合式:
| ${\tau _{{\rm{oct}}}}/f_{\rm{c}}' = {a_0} + {a_1}{\left( {{\sigma _{\rm{m}}}/f_{\rm{c}}'} \right)^{{a_2}}},$ | (1) |
对图11的数据进行拟合. 式中:
| ${\tau _{{\rm{oct}}}} = \frac{1}{3}\sqrt {{{({\sigma _{\rm{1}}} - {\sigma _{\rm{2}}})}^2} + {{({\sigma _{\rm{2}}} - {\sigma _{\rm{3}}})}^2} + {{({\sigma _{\rm{3}}} - {\sigma _{\rm{1}}})}^2}} ;$ |
| ${\sigma _{\rm{m}}} = \frac{1}{3}({\sigma _{\rm{1}}} + {\sigma _{\rm{2}}} + {\sigma _{\rm{3}}});$ |
拟合结果为
| ${\tau _{{\rm{oct}}}}/f_{\rm{c}}' = - 3.908\;52 + 4.943\;51{\left( {{\sigma _{\rm{m}}}/f_{\rm{c}}'} \right)^{0.110\;45}}.$ |
该结果适用于围压为0~70 MPa下的条件C试样,超出范围需要重新验证. 拟合相关系数为0.991 71,拟合效果较好.
所有试样的峰值偏差应力数据详见表2. 表中,试样的组合编号,例如“A-35”,前面的“A”、“B”和“C”表示不同减摩条件的试样,后面的数字表示试验过程中所施加的围压(单位为MPa).
| 表 2 各试样的峰值偏差应力 Table 2 Peak differential stress of tested specimen |
试样的破坏过程受到长径比、围压及端部减摩条件的影响,三者协同作用共同决定着包含裂纹的萌生、扩展、贯通在内的试样破坏机理.
2.4.1 减摩层对试样承载能力的影响1)减摩层产生的应力场.
当圆形减摩层受到轴向正应力挤压时,会向四周流动,假设流动后减摩层的形状可以保持不变,且圆心位置保持固定. 这种流动会产生作用在试样端部的切应力. 该切应力的方向是从试样端面的圆心指向四周,呈辐射状分布,在试样端部附近区域产生径向拉应力场.
在平行于试样端面的平面上,试样轴心位置的径向拉应力最大,靠近试样侧面时径向拉应力变小. 在平行于试样轴线的直线上,各点的径向拉应力随着所在点与试样端部之间距离的增加而减小.
减摩层的影响范围是指试样端部附近的一个区域,在其内由减摩层引起的径向拉应力高于设定的阈值,该阈值可以直接取为区域内最大拉应力的某一个百分比,例如5%. 假设:当端部减摩试样处在弹性状态时,若在试样内部轴线上某点与试样端面的垂直距离小于试样的直径,则该点的径向拉应力要考虑减摩层的贡献;当该点与端面的垂直距离大于直径时,可以忽略该端面减摩层对该点径向拉应力的影响. 在弹性状态下减摩层影响范围的高度可以定为试样的直径. 当试样进入到塑性状态时,减摩层影响范围的高度会减小.
当长径比为0.5时,无论试样处在弹性状态还是塑性状态,2个端部减摩层的影响范围之间会出现重叠. 当计算某一端面上的径向拉应力时,除了考虑与之接触的减摩层贡献外,还要考虑另一个端面上减摩层的影响.
当长径比为1.0时,在弹性状态下,试样端部减摩层影响范围的高度认为约等于试样的直径;在塑性状态下,该范围会减小. 当长径比为1.0时,无论材料处在弹性还是塑性状态,试样一端的减摩层对另一端面上的径向拉应力影响很小;但是在试样轴线附近的某个高度范围内,两端减摩层影响范围会出现重叠,所产生的径向拉应力会出现叠加. 这种径向拉应力的叠加,有利于裂缝的扩展. 试样某一端一旦产生了裂缝,该裂缝就很容易扩展到另一端,或与另一端的裂缝贯通.
当长径比大于或等于2.0时,无论试样处在弹性状态还是塑性状态,2个端面减摩层的影响范围基本上不会重叠.
2)围压对减摩层力学作用的影响.
当围压低于某一值(包括单轴情况)时,试样发生的破坏为弹脆性破坏;在
试样的实际受力状态是减摩层产生的拉应力、试样受到的围压以及轴向荷载三者叠加的结果. 在单轴条件下,由减摩层引起的径向拉应力对试样破坏产生的影响最大;在有围压条件下,径向拉应力的效果被削弱;在高围压条件下,径向拉应力几乎没有影响.
围压对应力场的影响包含2种方式:a)直接与由减摩层引起的径向拉应力进行叠加,改变应力;b)通过影响试样在破坏前是处于弹性还是塑性状态,影响由减摩层引起的拉应力以及受减摩层影响的空间范围.
3)减摩层对端部表面微小凹陷助裂作用的影响.
试样的表面在宏观上是平面,但是表面上分布着各种缺陷. 除了有少数1~4 mm直径的小坑外,还分布着更多的直径为几微米至几百微米的微小凹陷. 这些微小凹陷易受到减摩层的影响. 对于条件B试样,在试样加载过程中,减摩层会被挤入这些微小凹陷;当凹陷的直径和深度与减摩层厚度相近或略小于减摩层厚度时,减摩层会填满这些微小凹陷,进而对侧壁施加压应力,这会诱发微裂缝的萌生,引起已有裂缝的扩展. 对于条件C试样,除了减摩层之外,黄甘油也会被挤入微小凹陷中,这更容易诱发微裂缝和造成裂缝扩展.
总之,试样的破坏过程是以下几个因素共同作用的结果:a)轴向压应力;b)由减摩层引起的拉应力与围压的叠加应力场;c)试样破坏前是处在弹性状态还是塑性状态;d)减摩层挤入端部微小凹陷后,对凹陷侧壁施加的压应力.
4)根据以上讨论分析试验现象.
图3中,对于4种长径比下的条件B和条件C试样,当围压为5 MPa时,
当围压为70 MPa时,在试样内任一点的径向应力中,端部减摩层引起的拉应力占据的份额远远小于围压所占的份额,所以端部减摩层产生的拉应力可以忽略. 另外,对于图3中70 MPa围压、4种长径比试样的
|
图 9 RPC试样的峰值偏差应力与长径比的关系 Fig. 9 Relationship between peak differential stress of RPC specimen and length-diameter ratio |
与有减摩层时相反,当试样直接与压头接触时,压头会在试样端部产生约束切应力,该切应力方向由试样端部边缘指向试样轴心. 在试样破坏时,一般端部有圆锥体出现(要求试样高度大于2个圆锥体的高度),圆锥体占据的范围可以认为是压头约束的作用范围,不妨称为锥形区. 锥形区的高度约为0.75~1.0倍试样直径. 在理想状况下,两端锥形区的轴线与试样轴线应重合. 锥形区内的材料承载能力高于锥形区之外的. 当长径比为0.5和1.0时,试样两端的锥形区有一部分会相互重叠,整体呈沙漏状,相互重叠的锥形区在试样一半高度处,其垂直于试样轴线的截面面积最小,该面积的大小是决定试样最终承载能力的主要影响因素. 当长径比为0.5时,该截面面积大于长径比为1.0时的情况,故长径比为0.5时试样的峰值强度大于长径比为1的试样. 当长径比大于或等于2.0时,两端的锥形区不发生重叠,此时决定试样承载力的是锥形区范围外的区域,故长径比为2.0和3.0时试样的强度均相差不大,且都小于长径比为1.0和0.5时试样的抗压强度.
2.4.3 有减摩层与没有减摩层试样的强度分析当长径比为0.5和1.0时,无论有、无减摩层,试样两端切应力的影响范围都会重叠. 当有减摩层时,减摩层削弱两端切应力影响范围内的试样承载能力;当无减摩层时,压头对试样端部的摩擦约束力会增大约束区内试样的承载能力. 当长径比为0.5和1.0时,不减摩试样的承载能力大于减摩试样.
当长径比为2.0和3.0时,试样端部切应力的影响区域不会发生重叠. 对于减摩试样,远离端部的区域(高度一半处附近)是整个试样中承载能力最高的区域;对于不减摩试样,远离端部的区域是整个试样中承载能力最低的区域. 在单轴和低围压条件下,减摩试样的强度会略低于不减摩试样的强度;在高围压条件下,减摩层作用占据的份额变小,减摩试样的强度与不减摩试样的强度几乎没有差异. 这解释了破坏形态:当长径比为2.0和3.0时,对于不减摩试样,2个端面都比较完整;对于减摩试样,一般会有1个端面发生破坏,70 MPa围压下会出现两端面都完好的情况.
2.5 尺寸效应分析对于围压为5 MPa、不同长径比的条件A试样与条件C试样,2种不同减摩处理方式下的素RPC试样在抗压强度上均表现出了一定的尺寸效应.
Kim等[11-16]对尺寸效应作出了大量研究. 本文对Kim等[16]提出的尺寸效应公式稍加修改,得到
| ${f_{3{\rm c}}} = \alpha {f'_{3{\rm c}}} + \displaystyle\frac{{B{{f'}_{3{\rm c}}}}}{{\sqrt {1 + \displaystyle\frac{1}{{{\alpha _0}}}(\lambda - 1)} }}.$ | (2) |
式中:
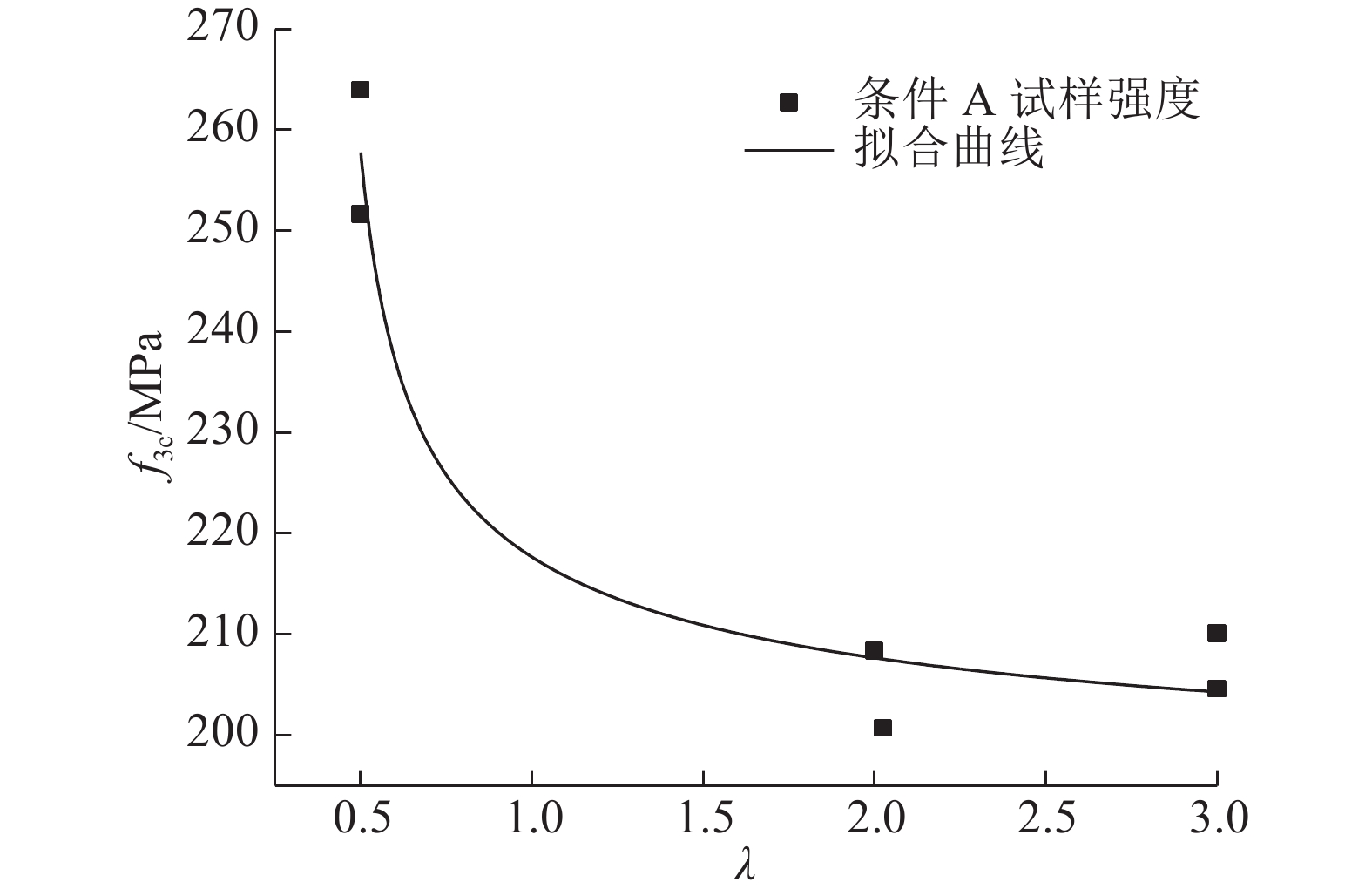
利用式(2),对5 MPa围压下条件A试样的强度与长径比关系进行拟合,以5 MPa下长径比为3.0的条件A试样的强度均值作为标准试样的抗压强度. 拟合结果如图12所示.
|
图 12 5 MPa下条件A试样强度与长径比的关系 Fig. 12 Relationship between strength of specimen with condition A and length-diameter ratio when confining pressure is 5 MPa |
拟合式为
| ${f_{3{\rm c}}} = 0.926{f'_{3{\rm c}}} + \displaystyle\frac{{0.123{{f'}_{3{\rm c}}}}}{{\sqrt {1 + \displaystyle\frac{1}{{0.589}}(\lambda - 1)} }}.$ |
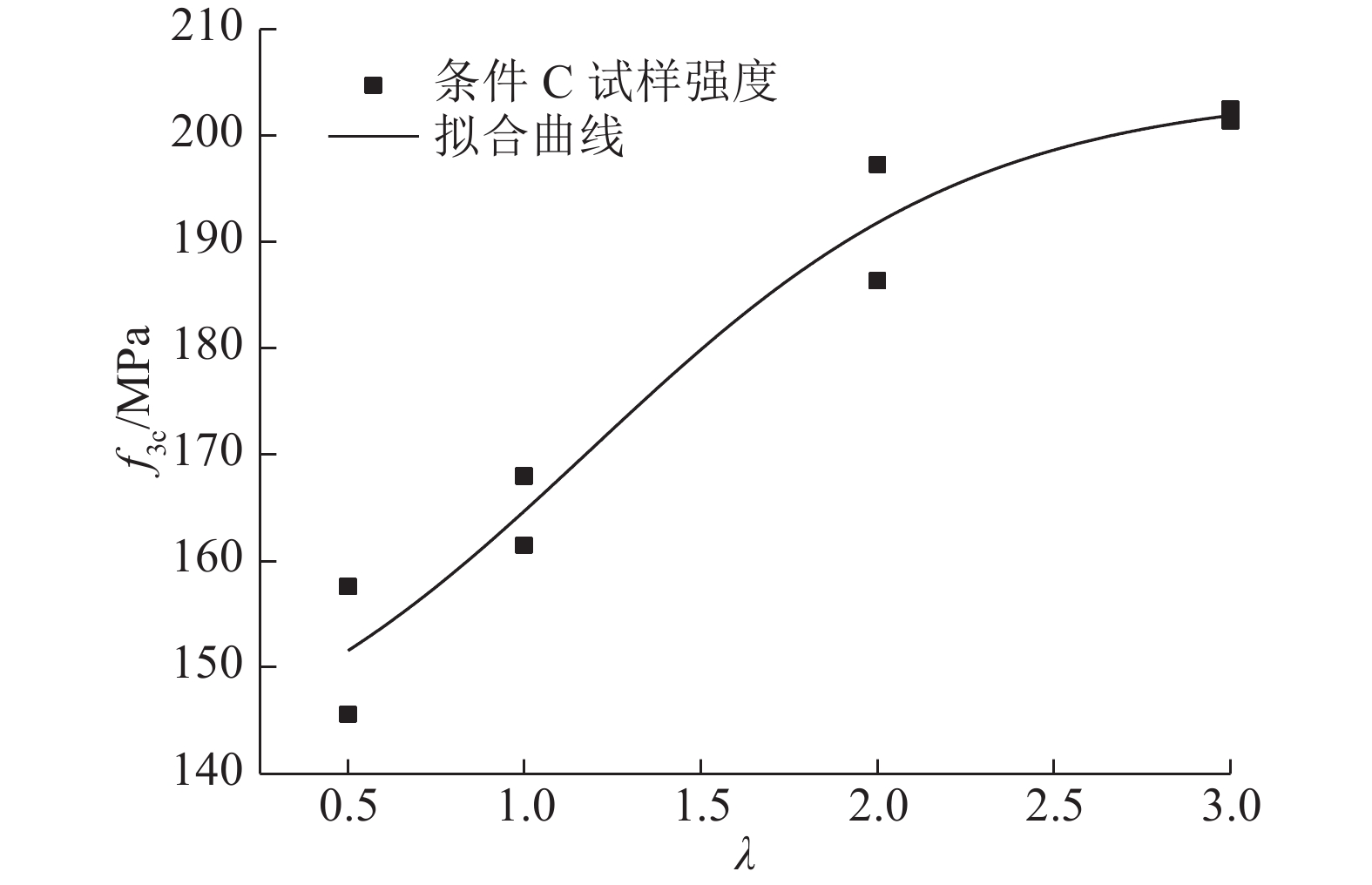
运用Boltzmann函数,对围压5 MPa下条件C试样的强度与长径比的关系进行拟合,如图13所示. 拟合后的表达式为
|
图 13 5 MPa下条件C试样强度与长径比的关系 Fig. 13 Relationship between strength of specimen with condition C and length-diameter ratio when confining pressure is 5 MPa |
| ${f_{3{\rm c}}} = 204.268\;21 - \displaystyle\frac{{67.756\;62}}{{ {1{\rm{ + }}{{\rm{exp}}\;{\big[1.828\;18(\lambda - 1.184\;62)\big]}}} }}.$ |
由图12、13并结合拟合结果可知,当围压为5 MPa时,条件A试样的强度随着长径比的增加而减小;条件C减摩试样的强度随着长径比的增加而增加. 两者的尺寸效应规律正好相反.
当围压为70 MPa时,由于条件A试样对应的长径比只有2种,不再回归强度与长径比的关系式.
3 结 论(1)对素RPC试样进行常规三轴试验. 根据试验结果可得,试样的强度与围压、长径比、端部减摩条件有关.
(a)当围压较低时,对于条件A试样,当长径比为0.5~2.0时,强度随着长径比的增加而减小;当长径比为2.0~3.0时,强度不受长径比的影响. 在相同的围压下,对于条件B和条件C试样,当长径比为0.5~2.0时,强度随着长径比的增加而增加;当长径比为2.0~3.0时,强度保持不变,与条件A试样同条件下的强度基本相等.
(b)当围压较高时,对于条件A试样,当长径比为0.5~2.0时,推断强度随着长径比的增加而减小;当长径比为2.0~3.0时,推断强度不受长径比的影响. 在相同的围压下,对于条件B和条件C试样,当长径比为0.5~3.0时,强度基本保持不变,推断强度与条件A试样在长径比为2.0~3.0时的强度基本相等.
(2)讨论试样的破坏机理,分析围压、长径比、端部减摩条件对裂纹的萌生、扩展、贯通的影响,对本文的试验现象给出统一的解释.
| [1] |
苏捷, 方志. 普通混凝土与高强混凝土抗压强度的尺寸效应[J]. 建筑材料学报, 2013, 16(6): 1078-1081. SU Jie, FANG Zhi. Scale effect on cubic compressive strength of ordinary concrete and high-strength concrete[J]. Journal of Building Materials, 2013, 16(6): 1078-1081. |
| [2] |
惠弘毅, 李宗利, 杨华, 等. 不同强度等级混凝土尺寸效应试验研究[J]. 混凝土, 2015(7): 31-34. XI Hong-yi, LI Zong-li, YANG Hua, et al. Experimental study on impact of strength grade on size effect of concrete strength[J]. Concrete, 2015(7): 31-34. DOI:10.3969/j.issn.1002-3550.2015.07.008 |
| [3] |
周红. 混凝土强度尺寸效应的实验研究[D]. 大连: 大连理工大学, 2010. ZHOU Hong. Experiment study on size effect on concrete strength [D]. Dalian: Dalian University of Technology, 2010. |
| [4] |
唐欣薇, 石建军, 郭长青, 等. 自密实混凝土强度尺寸效应的试验与数值仿真[J]. 水力发电学报, 2011, 30(3): 145-151. TANG Xin-wei, SHI Jian-jun, GUO Chang-qing, et al. Test and numerical simulation of size effect on the strength of self-compacting concrete[J]. Journal of Hydroelectric Engineering, 2011, 30(3): 145-151. |
| [5] |
NEVILLE A M. The influence of size of concrete test cubes on mean strength and standard deviation[J]. Magazine of Concrete Research, 1956, 8(23): 101-110. DOI:10.1680/macr.1956.8.23.101 |
| [6] |
刘数华, 阎培渝, 冯建文. 超高强混凝土RPC强度的尺寸效应[J]. 公路, 2011(3): 123-127. LIU Shu-hua, YAN Pei-yu, FENG Jian-wen. Size effect on strength of ultra-high strength concrete RPC[J]. Highway, 2011(3): 123-127. |
| [7] |
秦子鹏, 杜应吉, 田艳. 高强活性粉末混凝土尺寸效应的研究[J]. 中国农村水利水电, 2013(9): 92-94. QIN Zi-peng, DU Ying-ji, TIAN Yan. A study of the size effect of high-strength reactive powder concrete[J]. China Rural Water and Hydropowder, 2013(9): 92-94. DOI:10.3969/j.issn.1007-2284.2013.09.027 |
| [8] |
AN Ming-zhe, ZHANG Li-jun, YI Quan-xin. Size effect on compressive strength of reactive powder concrete[J]. International Journal of Mining Science and Technology, 2008, 18(2): 279-282. |
| [9] |
RICHARD P, CHEYREZY M. Reactive powder concretes with high ductility and 200-800 MPa compressive strength[J]. Aci Special Publication, 1994, 114(24): 507-518. |
| [10] |
余自若, 秦鑫, 安明喆. 活性粉末混凝土的常规三轴压缩性能试验研究[J]. 中国铁道科学, 2012, 33(2): 40-44. YU Zi-ruo, QIN Xin, AN Ming-zhe. Experimental research on the conventional triaxial compressive properties of reactive powder concrete[J]. China Railway Science, 2012, 33(2): 40-44. |
| [11] |
KIM J K, EO S H, PARK H K. Size effect in concrete structures without initial crack [C] // Fracture Mechanics: Application to Concrete, SP-118. Detroit: ACI, 1989: 179–196.
|
| [12] |
KIM J K. Size effect in concrete specimens with dissimilar initial cracks[J]. Magazine of Concrete Research, 1990, 42(153): 233-238. DOI:10.1680/macr.1990.42.153.233 |
| [13] |
BAŽANT Z P. Fracture energy of heterogeneous materials and similitude [M] // Fracture of concrete and rock. New York: Springer, 1989: 229–241.
|
| [14] |
BAŽANT Z P. Size effect in compression and tensile quasibrittle fracture[J]. Journal of the Mechanical Behavior of Materials, 2000, 11(1-3): 7-12. |
| [15] |
BAŽANT Z P, XIANG Y. Size effect in compression fracture: splitting crack band propagation[J]. Journal of Engineering Mechanics, 1997, 123(123): 162-172. |
| [16] |
KIM J K, YI S T, PARK C K, et al. Size effect on compressive strength of plain and spirally reinforced concrete cylinders[J]. ACI Structural Journal, 1999, 96(1): 88-94. |


