机器人喷涂大量应用于各种工业产品的生产,如飞机进气道[1-2]、飞机外表面[3]和船体[4]等,这些产品大都包含复杂形面. 喷涂涂层厚度模拟是机器人喷涂复杂形面的一个重要环节,采用函数型喷涂成膜模型进行涂层厚度模拟计算是目前常用的方法[5-6]. 弧面是一种典型的曲面,可与其他形面组成多种工件的复杂形面,开展圆弧面喷涂数值模拟研究具有重要理论意义及工程价值.
随着计算流体动力学(computational fluid dynamics,CFD)及计算机的发展,CFD已应用于喷涂成膜的数值模拟中. 喷涂时,空气冲击使涂料流变成细小微粒,随后涂料、在高速空气的带动下运,工件表面并撞击、黏附于工件表面或湿膜表面,形成最终涂料膜. 因此,喷涂成膜过程可以描述为空气—涂料两相流场,其建模方法有2种:欧拉—拉格朗日法[7-13]和欧拉—欧拉法[14-16]. 前者能够详细地对单个液滴运动进行跟踪和计算,但对于描述喷雾流场中大批量的涂料液滴的流动非常困难. 后者可以有效地描述大批涂料液滴与空气的相互作用,可以给出液滴相在空间分布的详细信息,也能较好地描述液滴在气流中的湍流混合过程.
动态喷涂模拟可以使用动喷枪法或动壁面法[12]. 其中,动喷枪法是指喷枪移动,壁面位置固定的喷涂方法,不仅符合实际作业情况,也可较好地模拟喷雾流场随喷枪移动而发生的变化. 目前,未见对圆弧面动态喷涂进行详细研究的报道.
本文采用欧拉—欧拉法建立由喷雾流场模型和碰撞黏附模型构成的喷涂成膜模型;采用动网格模型,对圆弧面动态喷涂进行计算. 通过实验验证所提出的模型可以用于研究圆弧面动态喷涂数值模拟.
1 喷涂成膜模型 1.1 喷雾流场模型 1.1.1 两相流基本控制方程两相流喷雾流场模型基于流体力学的连续介质模型,对流场中各相分别建立质量守恒方程和动量守恒方程.
1)质量守恒方程为
| $\frac{{\partial {\alpha _q}{\rho _q}}}{{\partial t}} + {\nabla} \cdot ({\alpha _q}{\rho _q}{{{v}}_q}) = 0. $ | (1) |
式中:t为时间,
2)动量守恒方程为
| $\begin{split}&\frac{\partial }{{\partial t}}\left( {{\alpha _q}{\rho _q}{{{v}}_q}} \right) + \nabla \cdot ({\alpha _q}{\rho _q}{{{v}}_q}{{{v}}_q}) = \\ &\quad - {\alpha _q}\nabla p + \nabla \cdot {\tau _q} + {\alpha _q}{\rho _q}{{g}} + {F^{{\text{td}}}}\!\!\!\!\!\!{_{q}} + {{{F}}_q} . \end{split}$ | (2) |
式中:p为相共用的压力,τq为q相的黏性应力,
动量方程(2)中相间作用力Fq是曳力Fd、举力Fl和虚拟质量力Fv之和,本研究忽略举力Fl和虚拟质量力Fv,仅考虑由于两相间的速度差引起的曳力:
| ${{{F}}_{\rm{d}}} = 0.75{{\rm{C}}_{\rm{D}}}{\alpha _q}{\rho _q}\left| {{{{v}}_p} - {{{v}}_q}} \right|\left( {{{{v}}_p} - {{{v}}_q}} \right). $ | (3) |
式中:CD为曳力系数,本研究取0.44.
1.1.2 湍流模型湍流模型是模拟时需要处理好的一个重要问题. 喷雾流场内涂料液滴的体积分数虽然比较小,但是液滴对空气有比较明显的影响,因此,湍流模型既需要考虑气相的湍动,同时还需考虑液相对气相的影响.
雷诺平均法(Reynolds average numerical simulation,RANS)对工程实际应用可以取得很好的预测效果,是目前使用最广泛的湍流模型,因此,本研究采用雷诺平均法求解湍流流动. 黏涡模型不直接求解雷诺应力项,将其表示为湍流黏度μt的函数. 湍流黏度可以用下式计算:
| ${\mu _{\rm{t}}} = \rho {{\rm{C}}_\mu }\frac{{{k^2}}}{\varepsilon }. $ | (4) |
式中:
针对气液混合相,引入标准k-ε湍流模型(standard k-ε turbulent model)来封闭动量方程,其中湍流动能k和湍流动能耗散率ε对应的输送方程分别为
| $\begin{split}& \frac{\partial }{{\partial t}}\left( {{\rho _{\rm{m}}}k} \right) + \nabla \cdot \left( {{\rho _{\rm{m}}}{{{v}}_{\rm{m}}}k} \right) =\\ & \quad\nabla \cdot \left( {\frac{{{\mu _{{\rm{t,m}}}}}}{{{\sigma _k}}}\nabla k} \right) + {G_{k,{\rm{m}}}} - {\rho _{\rm{m}}}\rho + {\varPi _{{k_{\rm{m}}}}}\end{split}$ | (5) |
| $\begin{split} \frac{\partial }{{\partial t}}&\left( {{\rho _{\rm{m}}}\varepsilon } \right) + \nabla \cdot \left( {{\rho _{\rm{m}}}{{{v}}_{\rm{m}}}\varepsilon } \right) = \nabla \cdot \left( {\frac{{{\mu _{{\rm{t,m}}}}}}{{{\sigma _\varepsilon }}}\nabla \varepsilon } \right) + \\ &\frac{\varepsilon }{k}\left( {{{\rm{C}}_{{\rm{1\varepsilon }}}}{G_{k,{\rm{m}}}} - {{\rm{C}}_{2\varepsilon }}{\rho _{\rm{m}}}\varepsilon } \right) + {\varPi _{{\varepsilon _{\rm{m}}}}}. \end{split}$ | (6) |
式中:
由于喷雾内液相相对于气相要稀疏得多,液相的运动主要取决于气相,无需对液相建立单独的湍流模型. 同时喷雾内大批量的涂料液滴会对空气流动产生较大的影响,因此多相流的湍流模型还需考虑液相对气相湍流的扰动. 使用分散湍流模型(dispersed turbulence model)描述液相对气相的影响. 液相的运动主要取决于气相,对液相采用Tchen-theory关系式,利用均匀湍流离散粒子的传播来表征液相的湍流的大小,并通过
上述建立的标准k-ε湍流模式针对充分发展的湍流才有效. 但是喷涂目标壁面附近区域,湍流发展不够充分,因此,在近壁面区域需要采用特殊的近壁区壁面函数配合k-ε模型使用. 其思路如下:在核心区使用标准k-ε模型求解湍流流动,在近壁区不直接求解湍流流动,而是使用一组公式将近壁区内物理量与核心区内与之对应的求解变量联系起来.
1.2 碰撞黏附模型 1.2.1 液相沉积模型喷雾流场中在涂料液相接触壁面并沉积成膜过程中,液相的质量和动量从喷雾流场两相流中移出,作为源项加入到液膜的质量守恒方程和动量守恒方程中.
单位壁面面积液膜的质量源项为
| ${\dot m_{\rm{s}}} = {\alpha _{\rm{d}}}{\rho _{\rm{d}}}{v_{{\rm{dn}}}}A. $ | (7) |
式中:
液膜动量源项为
| ${\dot {{q}}_{\rm{s}}} = {\dot m_{\rm{s}}}{{{v}}_{\rm{d}}}. $ | (8) |
由于壁面上液膜的厚度比圆弧面壁面的曲率半径要小得多,可以认为液膜流动平行于壁面,液膜方程在平行于壁面的局部坐标内求解. 壁面上液膜模型包括质量守恒方程、动量守恒方程和能量守恒方程.
质量守恒方程为
| $\frac{{\partial h}}{{\partial t}} + {\nabla _{\rm{S}}} \cdot (h \cdot {{{v}}_{\rm{l}}}) = \frac{{{{\dot m}_{\rm{s}}}}}{{{\rho _{\rm{l}}}}}. $ | (9) |
式中:
动量守恒方程为
| $\frac{{\partial h{{{v}}_{\rm{l}}}}}{{\partial t}} + {\nabla _{{{\rm S}}}} \cdot (h{{{v}}_{{l}}}{{{v}}_{{l}}}) = - \frac{{h{\nabla _{\rm{S}}}{{{p}}_{\rm{1}}}}}{{{\rho _{\rm{l}}}}} + \frac{3}{{2{\rho _{\rm{l}}}}}{{{\tau}} _{{\rm{fs}}}} - \frac{{3{\nu _{\rm{l}}}}}{h}{{{{ v}}}_{\rm{l}}} + \frac{{{{\dot {{q}}}_{\rm{s}}}}}{{{\rho _{\rm{l}}}}}. $ | (10) |
式中:右侧第1项代表液膜压力
动网格模型是动态喷涂成膜CFD模拟计算中的一个重要模型,实现计算中网格的动态变化,以解决流场由于边界运动随时间改变的问题. 动网格法常用的模型有3种:铺层模型、弹性光顺模型和局部重构模型. 模拟研究表明,弹性光顺模型结合局部重构模更适合于动喷枪法喷涂模拟[17]. 本研究进行动态喷涂成膜CFD模拟计算时,采用弹性光顺模型结合局部重构模型,如图1所示. 随着喷枪向右移动,喷枪右侧的网格被压缩,而左侧的网格被拉伸,当网格扭曲率过大或尺寸过小时,网格自动局部重构以满足网格扭曲率和尺寸的要求.

|
图 1 喷嘴移动导致的网格动态变化 Fig. 1 Mesh dynamic change due to nozzle’s motion |
喷枪空气喷嘴模型见图2,空气喷嘴中心是涂料孔,孔径为1.1 mm;涂料孔外侧是环形的中心雾化孔,外径为2 mm,内径为1.6 mm;中心雾化孔两侧分别排列2个辅助雾化孔,孔径均为0.5 mm;空气喷嘴两侧牛角形结构上分别布置2个扇面控制孔,孔径均为0.8 mm.

|
图 2 喷枪空气喷嘴的三维模型 Fig. 2 3D geometric model of the air spray gun’s nozzle |
由于运动区域和喷枪的运动路径、移动速度都是已知并提前规划好的,可以将控制域划分为2个区域,其中一个为运动区域,另一个为静止区域,以减少计算量,同时增加运算精度.
平面喷涂控制域划分见图3,控制域内包括一个喷枪运动区域,喷枪在该区域内沿直线运动,网格随喷枪的移动而变化. 除运动区域之外,控制域内其他区域为静止区域,静止区域内网格不发生变化. 为保证计算精度,同时限制总的网格数和网格尺寸,运动区域内网格划分要加密,静止区域内的网格划分可相对稀疏.

|
图 3 平面动态喷涂控制域划分 Fig. 3 Division of control domain for dynamically spray painting flat wall |
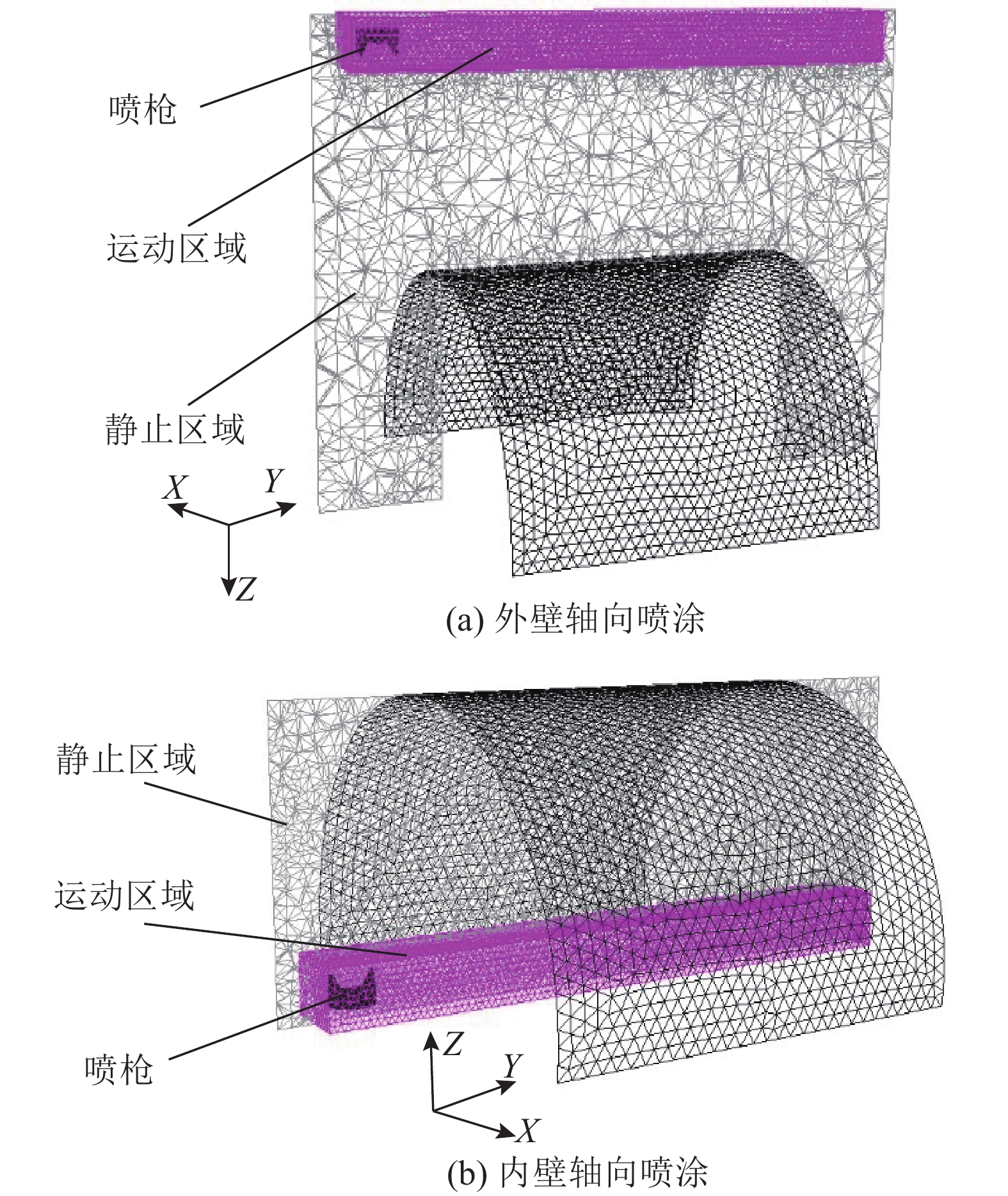
本研究的圆弧面动态喷涂包括外壁轴向和内壁轴向喷涂. 与平面喷涂控制域划分类似,圆弧面动态喷涂控制域也分为运动区域和静止区域,喷枪在运动区域内沿直线运动,如图4所示.
|
图 4 圆弧面动态喷涂控制域划分示意图 Fig. 4 Division of control domain for spray painting arc surfaces with moving paint nozzle |
对喷雾流场定义2个相,其中第1相为气相,表示喷雾流场中的空气,第2相为液相,表示流场中的涂料液滴. 其中液相粒径为20 μm,液相黏度为0.096 86 kg/(m·s),密度为1.2×103 kg/m3.
空气喷嘴的涂料孔设为质量入口,液相的质量流量为1.32×10−3 kg/s,气相质量流量为5×10−6 kg/s,液相初始速度为5 m/s,液相在入口处体积率为0.2,湍流参数设定为湍流强度I=15%,水力直径为D=0.002 m. 其他入口设为压力入口,喷枪雾化压力为140 kPa,扇面控制压力为150 kPa,重力加速度设为9.8 m/s2,操作压力为一个大气压.
动态喷涂开始计算时时间步长设为Δ t =1×10−4 s,待喷雾流场稳定后,时间步长逐渐增大到Δ t =1×10−3 s. 当喷枪沿轴向移动喷涂圆弧面时,喷枪从距离壁面50 mm处开始喷涂,喷枪移动速度v =0.1 m/s.
分别将平面和圆弧面喷涂的三维模型导入ANSYS Fluent,配置相关模型和计算参数,利用有限体积法求解动态喷涂成膜模型,离散格式采用二阶迎风格式,采用PC-SIMPLE算法(多相耦合的SIMPLE算法)计算离散后的代数方程. 软件运行平台为Windows 64位操作系统的10核心Xeon CPU工作站,运行内存为64 G.
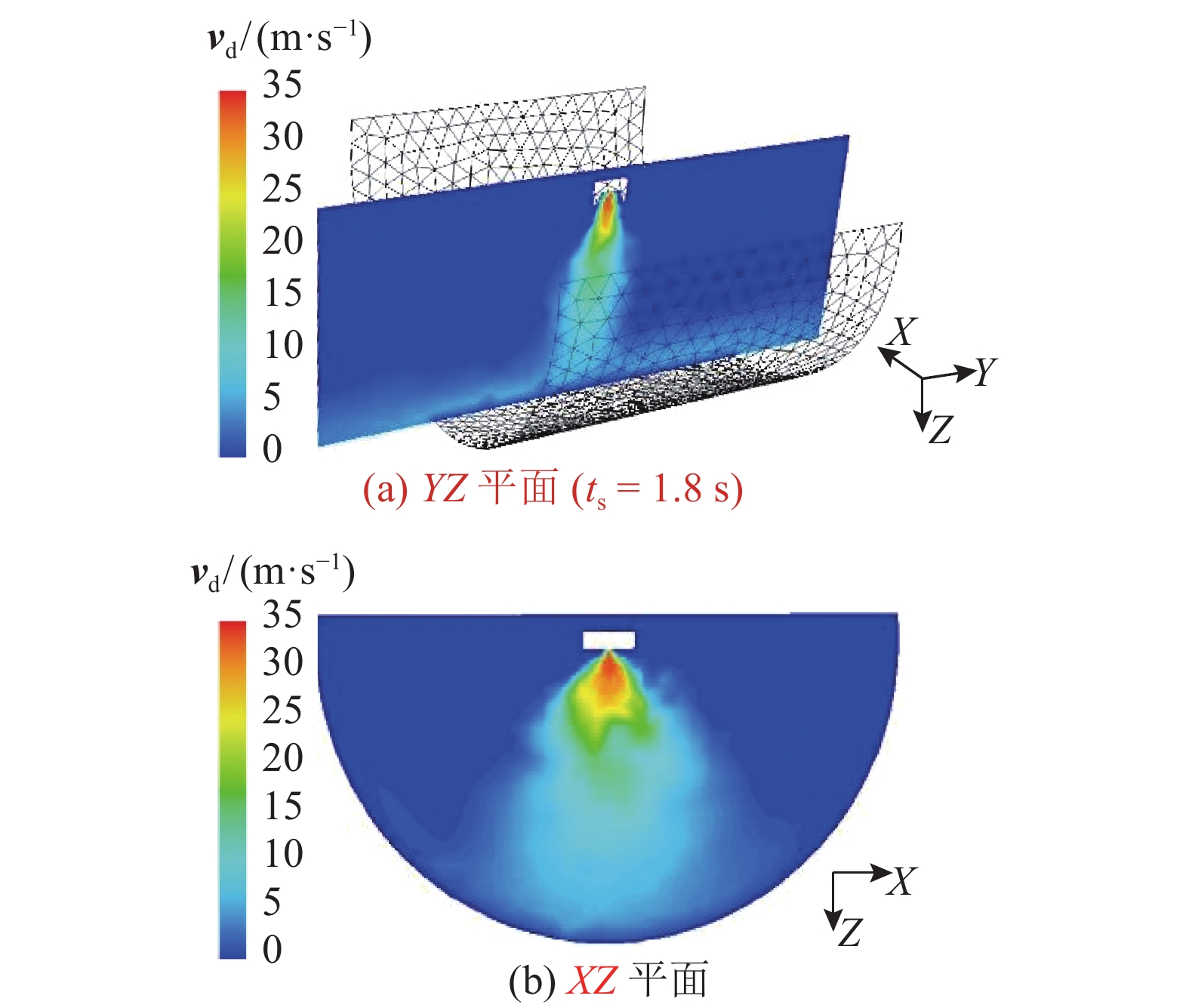
2.3 计算结果与分析 2.3.1 喷雾流场圆弧面外壁轴向动态喷涂的喷雾流场见图5,其中图5(a)为XZ平面上的液相速度分布,基本不随喷涂时间变化;图5(b)~(d)分别喷涂时间ts为0.8、1.8和3.4 s时基本不随喷涂时间变化;YZ平面上的液相速度分布. 圆弧面内壁轴向动态喷涂的喷雾流场如图6所示,其中图6(a)为XZ平面上的液相速度分布. 由于圆弧面内壁轴向动态喷涂的喷雾流场与外壁喷涂相似,本研究仅给出1.8 s时YZ平面内的喷雾流场,如图6(b)所示.

|
图 5 圆弧面外壁轴向动态喷涂液相速度分布 Fig. 5 Velocity distribution of liquid phase of axially spray painting the outer arc surface with moving paint nozzle |
由图5和6可知,喷雾流场在XZ平面内比YZ平面的范围要大,这是由于在扇面控制孔气流的冲击下,喷雾流场在Y方向被压扁,在X方向扩张. 由图5(b)~(d)可知,由于喷枪的移动,喷雾流场向喷枪移动的后方略微倾斜.
|
图 6 圆弧面内壁轴向动态喷涂液相速度分布 Fig. 6 Velocity distribution of liquid phase of axially spray painting inner arc surface with moving paint nozzle |
圆弧面内壁和外壁的喷涂方式涂膜厚度分布见图7. 由图可知,壁面上不同位置涂膜的喷幅和厚度均有一定的差别. 对每个截面涂膜厚度做平均,可得涂膜平均厚度分布. 使用平均涂膜厚度分布研究涂膜特性的前提,是各截面涂膜厚度分布与平均涂膜厚度分布相似.

|
图 7 圆弧面内、外壁涂膜厚度分布云图 Fig. 7 Film thickness distribution contours on outer and inner arc surfaces |
以圆弧面外壁轴向喷涂为例分析涂膜截面厚度. 分别取Y=50、150和250 mm截面,对比不同截面涂膜厚度分布与平均涂膜厚度分布,如图8所示. 由图可知,涂膜平均厚度分布曲线最大值为61.7 μm. Y=50 mm截面上的涂膜最大厚度为53.9 μm,明显小于平均涂膜厚度,这是由于喷枪刚移动到壁面上方,喷雾流场还不够稳定. Y=150和250 mm的截面涂膜厚度在平均涂膜厚度上下浮动. 这2个截面厚度分布曲线与平均厚度分布曲线很相似,拟合度分别为95.7%和99.2%. 由此可得:虽然不同截面上涂膜厚度分布有一定的差别,但总体来看,各截面涂膜厚度分布规律是相同的,与平均涂层厚度分布的误差都在可接受范围内;Y方向喷涂厚度不均匀是正常的现象,是喷雾流场的湍流造成两相流动的不确定性所导致的,并且喷枪的运动会加剧这种两相流的不确定性. 因此,平均涂膜厚度分布曲线能够反映整体涂膜厚度分布,而且能够近似表示圆弧面上每个截面的涂膜厚度分布.

|
图 8 外壁轴向喷涂的截面涂膜厚度 Fig. 8 Sectional film thickness of axial external spray painting |
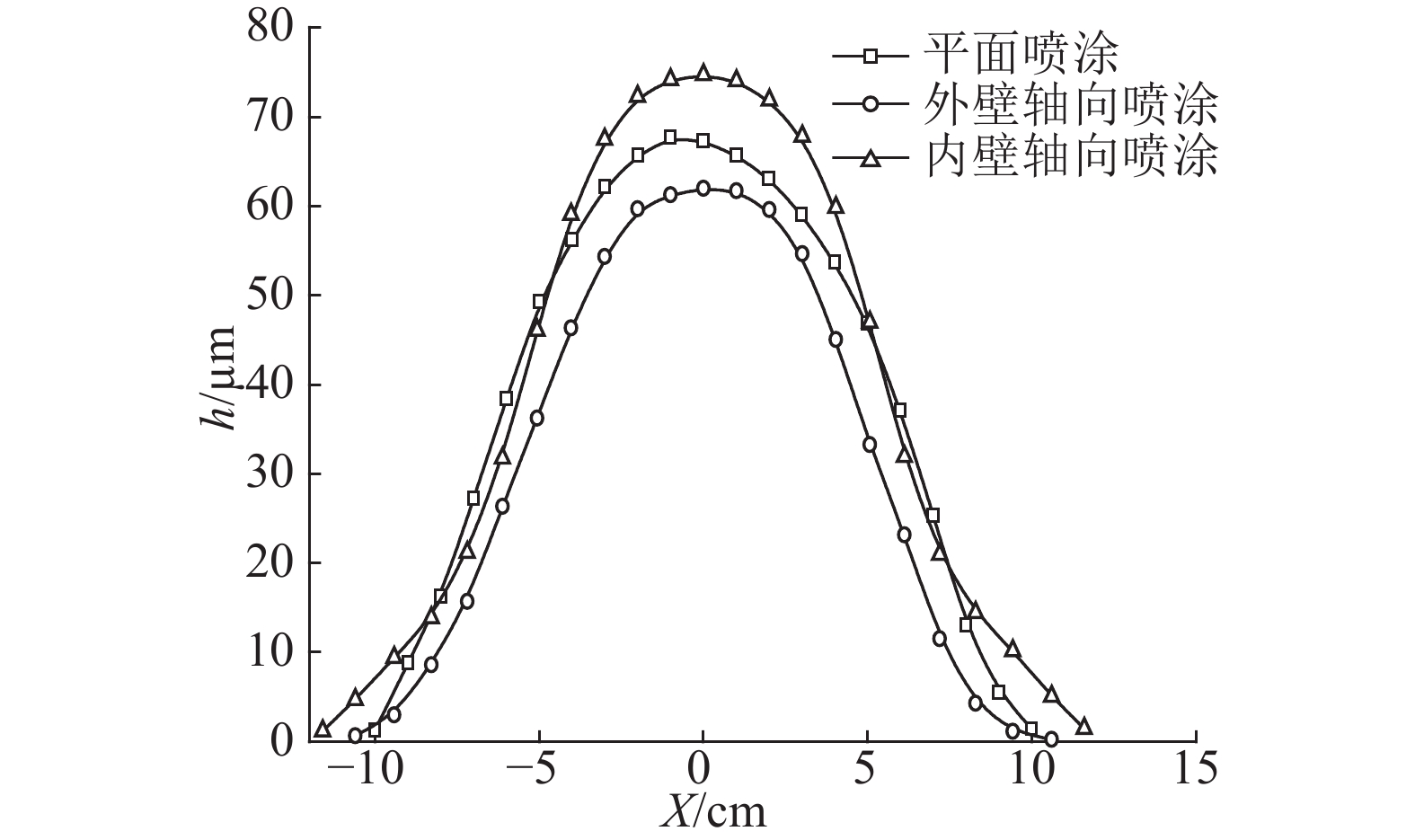
涂膜平均厚度分布曲线可以反应涂膜厚度分布特性,圆弧面轴向喷涂的涂膜平均厚度分布与平面喷涂涂膜厚度分布对比如图9所示. 圆弧面轴向喷涂涂膜厚度分布与平面喷涂涂膜厚度分布有一定的差别. 平面喷涂涂膜最大厚度为67.7 μm,内壁涂膜中间区域厚度明显大于平面喷涂涂膜厚度,最大厚度为74.5 μm. 外壁喷涂涂膜厚度整体明显小于平面喷涂涂膜厚度,涂膜最大厚度为61.9 μm.
|
图 9 不同形面的涂膜平均厚度分布 Fig. 9 Average film thicknesses on different surfaces |
平面喷涂涂膜宽度为20.0 cm,外壁喷涂涂膜宽度略大于平面喷涂,为21.2 cm. 内壁喷涂涂膜宽度明显小于平面喷涂涂膜厚度,涂膜最大厚度为23.2 cm.
由上述分析可知,圆弧面轴向喷涂涂膜厚度分布与平面喷涂涂膜厚度分布有较大的区别. 因此对于轴向喷涂圆弧面,在计算涂层厚度、优化相邻2个喷涂轨道间距时,必须考虑轴向普通喷涂涂膜厚度分布与平面涂膜厚度分布的差异.
3 动态喷涂实验与分析数值模拟直接得到的涂层厚度为湿膜厚度h1,若要与实验结果进行对比,必须根据涂料固体组份体积分数将其转化为干膜厚度h2[18].
为验证本文的仿真结果,进行平面和圆弧面喷涂实验. 喷漆过程中喷枪始终垂直于平面和圆弧面工件,运动参数与模拟参数保持一致. 喷涂完成后3 d内不能压碰漆膜. 待油漆完全固化后,使用涂层测厚仪测量涂膜厚度,记下该点的圆弧面展开坐标系坐标及涂膜厚度. 在测量涂膜厚度时,每隔1 cm测量一个点的厚度,每个点位测量5次,取其平均值作为该点位的涂膜厚度.
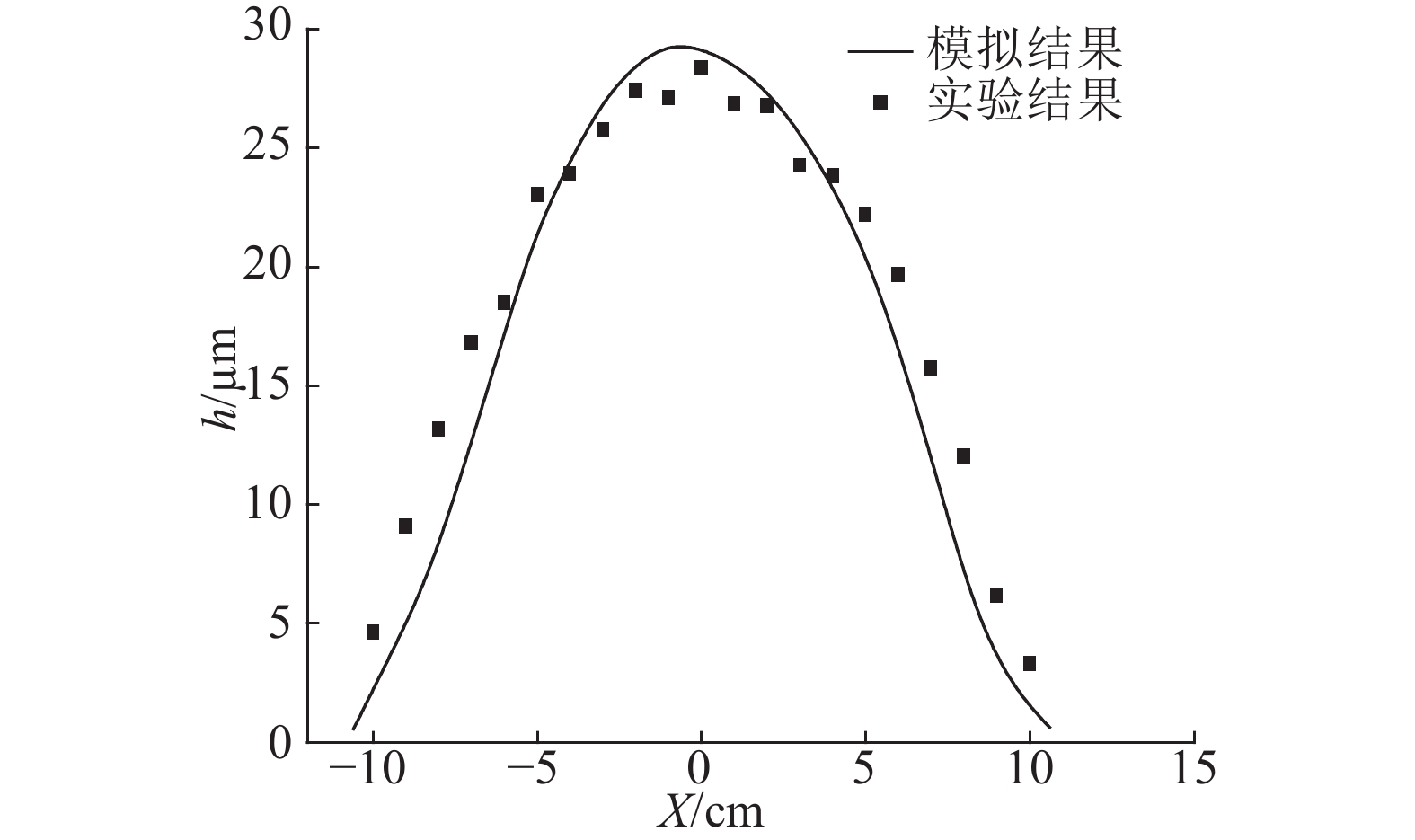
对比动态平面喷涂涂膜厚度模拟结果与实验结果,如图10所示. 由图可知,模拟涂膜厚度与实验厚度吻合较好.
|
图 10 平面喷涂涂膜厚度模拟结果与实验结果 Fig. 10 Simulated and measured film thickness results for spray painting flat wall |
动态轴向喷涂半径为180 mm的圆弧面涂膜厚度模拟结果与实验结果对比见图11,其中图11(a)为外壁轴向喷涂,图11(b)为内壁轴向喷涂,可见模拟计算出的涂层厚度与实验获得的涂层厚度吻合较好.

|
图 11 圆弧面轴向喷涂涂膜厚度模拟结果与实验结果 Fig. 11 Simulated and measured film thickness results for axially spray painting arc surfaces |
(1)在扇面控制孔气流的冲击下,喷雾流场在Y方向被压扁,在X方向扩张. 由于喷枪的移动,喷雾流场向喷枪移动的后方略微倾斜.
(2)圆弧面内壁、外壁轴向喷涂涂膜厚度分布与平面喷涂涂膜厚度分布有一定的差别:圆弧面内壁喷涂的最大涂层厚度(74.5 μm)大于平面喷涂(67.7 μm),外壁喷涂的最大平面喷涂涂层厚度(61.9 μm)小于平面喷涂;圆弧面内壁喷涂的涂膜宽度(23.2 cm)大于平面喷涂(20.0 cm),外壁喷涂的涂膜宽度(21.2 cm)也大于平面喷涂.
(3)通过对比试验和仿真得到的喷雾图形和涂层厚度分布,证实了本研究所建立的喷涂成膜模型用于研究圆弧面喷涂喷雾流场特性是可行的.
| [1] |
CHEN W Z, CHEN Y, CHEN K, et al. Design of redundant robot painting system for long nonregular duct[J]. Industrial Robot: an International Journal, 2016, 43(1): 58-64. DOI:10.1108/IR-06-2015-0113 |
| [2] |
CHEN Y, CHEN W Z, CHEN K, et al. Motion planning of redundant manipulators for painting uniform thick coating in irregular duct[J]. Journal of Robotics, 2016, 1-12. |
| [3] |
缪东晶, 吴聊, 徐静, 等. 飞机表面自动喷涂机器人系统与喷涂作业规划[J]. 吉林大学学报: 工学版, 2015, 45(2): 547-553. MIAO Dong-jing, WU Liao, XU Jing, et al. Automatic spraying robot system for aircraft surfaces and spraying operation planning[J]. Journal of Jilin University: Engineering and Technology Edition, 2015, 45(2): 547-553. |
| [4] |
YE Q, SHEN B, TIEDJE O, et al. Investigations of spray painting processes using an airless spray gun[J]. Journal of Energy and Power Engineering, 2013, 1: 74-81. |
| [5] |
CHEN Y, CHEN W Z, LI B, et al. Paint thickness simulation for painting robot trajectory planning: a review[J]. Industrial Robot: an International Journal, 2017, 44(5): 629-638. DOI:10.1108/IR-07-2016-0205 |
| [6] |
曾勇, 龚俊, 许宁, 等. 面向犄角型曲面的喷涂机器人喷涂轨迹优化[J]. 浙江大学学报: 工学版, 2014, 48(5): 791-798. ZENG Yong, GONG Jun, XU Ning, et al. Tool trajectory optimization of spray painting robot for horns surface[J]. Journal of Zhejiang University: Engineering Science, 2014, 48(5): 791-798. |
| [7] |
HICKS P G, SENSER D W. Simulation of Paint transfer in an air spray process[J]. Journal of Fluids Engineering, 1995, 117(4): 713-719. DOI:10.1115/1.2817327 |
| [8] |
FOGLIATI M, FONTANA D, GARBERO M, et al. CFD simulation of paint deposition in an air spray process[J]. Journal of Coating Technology and Research, 2006, 3(2): 117-125. DOI:10.1007/s11998-006-0014-5 |
| [9] |
刘国雄. 空气雾化涂料喷枪喷涂流场仿真及特性研究[D]. 杭州: 浙江大学, 2012: 31–49. LIU Guo-xiong. Simulation study on the spray flow field of air atomized paint spray gun [D]. Hangzhou: Zhejiang University, 2012: 31–49. http://cdmd.cnki.com.cn/Article/CDMD-10335-1012321161.htm |
| [10] |
YE Q, SHEN B, TIEDJE O, et al. Numerical and experimental study of spray coating using air-assisted high pressure atomizers[J]. Atomization and Sprays, 2015, 25(8): 643-656. DOI:10.1615/AtomizSpr.v25.i8 |
| [11] |
YE Q, PULLI K. Numerical and experimental investigation on the spray coating process using a pneumatic atomizer: influences of operating conditions and target geometries[J]. Coatings, 2017, 7(1): 13. DOI:10.3390/coatings7010013 |
| [12] |
TOLJIC N, ADAMIAK K, CASTLE G S P, et al. A full 3D numerical model of the industrial electrostatic coating process for moving targets[J]. Journal of Electrostatics, 2013, 71(3): 299-304. DOI:10.1016/j.elstat.2012.12.032 |
| [13] |
OSMAN H, ADAMIAK K, CASTLE P G S, et al. Comparison between the numerical and experimental deposition patterns for an electrostatic rotary bell sprayer [C] // Proceedings of the 2015 International Mechanical Engineering Congress and Exposition. Houston: IMECE, 2015: 1–8.
|
| [14] |
杨庆功, 李萌盛. 双流体模型模拟喷涂飞行区内的速度分布[J]. 合肥工业大学学报: 自然科学版, 2006, 29(9): 1120-1123. YANG Qing-gong, LI Meng-sheng. Simulation of the velocity distribution in the spray cone based on the two-phase flow model[J]. Journal of Hefei University of Technology: Natural Science, 2006, 29(9): 1120-1123. |
| [15] |
陈雁, 何少炜, 张钢, 等. 空气喷涂平面成膜的双流体模型模拟[J]. 后勤工程学院学报, 2015, 31(6): 82-86. CHEN Yan, HE Shao-wei, ZHANG Gang, et al. Two-fluid Model simulation of paint deposition on flat wall in an air spray process[J]. Journal of Logistical Engineering University, 2015, 31(6): 82-86. DOI:10.3969/j.issn.1672-7843.2015.06.015 |
| [16] |
陈雁, 陈文卓, 何少炜, 等. 圆弧面空气喷涂的喷雾流场特性[J]. 中国表面工程, 2017, 30(6): 122-131. CHEN Yan, CHEN Wen-zhuo, HE Shao-wei, et al. Spray flow characteristics of painting cylindrical surface with a pneumatic atomizer[J]. China Surface Engineering, 2017, 30(6): 122-131. |
| [17] |
YE Q. Using dynamic mesh models to simulate electrostatic spray-painting [C] // High Performance Computing in Science and Engineering' 05. Berlin: Springer, 2006, 5: 173–182.
|
| [18] |
GOLDSCHMIDT A, STREITBERGER H J. BASF Handbook on Basics of Coating Technology [M]. Münster: Vincentz Network, 2005: 330–331.
|



