根据美国癌症协会统计的数据,结直肠癌是美国三大最常见癌症之一. 截止2017年6月,美国约有135 430个新的结直肠癌确诊案例,以及50 260个死亡病例[1],而在中国,结直肠癌在男性和女性中分别是最常见的排名第5和第4的癌症[2]. 虽然手术方式以及辅助治疗手段等都在不断发展,但术后癌症的转移、复发的几率很高,因此结直肠癌根治性手术后患者的生存率并不算高.
随着机器学习的进步与发展,各种相关技术已被应用于癌症研究,进行预测模型的开发、准确决策的提供[3-4]. 然而现在机器学习在癌症预测诊断的主流方向是早期病症辅助筛查,癌症术后的治疗主要靠医生定期随访、病人定期到院复查,这大大降低了术后治疗方案的实时性和方便性. 若利用机器学习对结直肠癌患者的术后生存期进行预测,有助于筛选出可能需要进行预防性治疗的高风险患者并针对性进行术后预防性治疗,提高患者的术后生存率.
当前癌症存活期预测较多采用随机森林、回归算法和人工神经网络等[5-7]. 随机森林对处理维度高、数量大的数据具有优势,且对缺省值问题也能获得较好结果[8]. 回归算法包括多元自适应回归、比例风险回归、混合逻辑回归等. 在一项3 632例乳腺癌患者样本的研究中,人工神经网络对存活期的预测效果优于回归算法[7].
结直肠癌术后生存期数据较难获取,样本总量小且存在信息缺失. 同时结直肠癌的预后因素很多,如年龄、TNM分期、p53、β-连环蛋白、化疗与否等[9-10]. 这是机器学习中较为常见的受数据样本量和维数的限制的问题[11]. 在实际工作当中,研究者为了避免遗漏信息,往往在研究初期尽可能多地考虑相关因素,力求以高维数据收集更全面的信息量. 但这会给后期数据挖掘带来“维数灾难”[12],即在一定样本数量下,维数过高会导致训练出来的模型难以具备足够的泛化能力. 针对上述问题,对样本进行降维,优化特征选择方案是形成有效的癌症预测模型的重要途径之一[11]. 传统的降维方法主成分分析[13]虽然应用广泛但主要运用线性转换来降维,有时降维效果并不理想且存在缺乏解释性的问题;奇异值分解[14]主要用于信息修复或在统计中减少维数,也缺乏解释性;域分解[15]是将数据集分成许多子集并采用简单的相似性测量,使得高维计算可以在一些小的子集中进行,但这种方法并没有直接减少维数. 聚类分析作为数据挖掘技术中一种重要的方法,常常用于样本的聚类划分,很少用来进行变量聚类并降维.
本研究基于模糊C均值(fuzzy C-means,FCM)聚类,提出一种结合场景认知和隶属度排序的变量聚类方法,降低高维样本的维数,并利用筛选出来的特征变量训练BP神经网络,以得到一个能够准确预测结直肠癌术后生存期的模型,为病患术后进行预防性治疗提供新方法.
1 模糊C均值聚类 1.1 FCM聚类简介模糊C均值聚类算法[16]是一种基于柔性划分的聚类方法,其思想是把n个聚类对象分为c个模糊组,同一模糊组里的聚类对象相似度最大.
在聚类过程中,FCM需要确定2个参数:一个是模糊组个数c,另一个是加权指数m. 一般来说,c>1且远小于聚类样本的总个数;m作为一个控制算法的柔性的参数,Pal等[17]从聚类有效性出发总结出[1.5, 2.5]是m的最佳选取区间,区间中值m=2为无特殊要求的情况下的取值.
1.2 FCM变量聚类提出一种基于FCM聚类算法的降维方法,这种方法先结合场景认知,根据目标变量将总样本分为多个子样本集,然后针对不同场景的子样本集进行变量聚类,对比隶属度排序,从过多的特征变量中筛选出少量对目标变量影响最明显的特征变量,参与后续的分析和建模.
设S表示有s个样本的数据集合,每个样本包含p维特征变量和1维目标变量,记为
| $S{\rm{ = }}\left\{ {{a_1}\left( {{X_1},{Y_1}} \right),{a_2}\left( {{X_2},{Y_2}} \right),\,\cdots\,,{a_s}\left( {{X_s},{Y_s}} \right)} \right\}.$ | (1) |
式中:
用FCM进行变量聚类从而达到降维、筛选变量的目的,步骤如下.
1)基于先验知识和场景认知,总结出场景规则
| ${Z_j}{\rm{ = }} \left\{ {{a_{jk}}\left( {{X_{jk}}} \right)|\;k = 1,2,\,\cdots\,,{N_j},\;1 \leqslant {N_j} \leqslant s,{a_{jk}} \in S} \right\}.$ | (2) |
式中:
2)一般在进行样本聚类的时候,是将每个样本作为聚类对象输入;本文提出的变量聚类是将特征变量作为聚类对象输入,将初始样本集转化为变量聚类的输入样本集,记为
| $\begin{split}D =& \{ {x_1}({a_1},{a_2},\,\cdots\,,{a_n}),{x_2}({a_1},{a_2},\,\cdots\,,{a_n}),\,\cdots\,,\\ &{x_p}({a_1},{a_2},\,\cdots\,,{a_n})\} .\end{split}$ | (3) |
式中:
3)结合1)和2)可知,每个场景子样本集
| ${D_j} \!=\! \left\{ {{x_i}\!\left( {{a_{j1}},{a_{j2}},\,\!\!\cdots\!\!\,,{a_{j{N_j}}}} \right)\!|\,i \!=\! 1,2,\,\!\cdots\!\,,p,{x_i} \in X,{a_{jk}} \!\in \!{L_j}} \right\}.$ | (4) |
式中:
4)基于FCM聚类算法将每个输入样本集
5)隶属度排序:基于
| ${{{R}}_{jv}} = \left[ {{x_{v1}},{x_{v2}},\,\cdots\,,{x_{vi}},\,\cdots\,,{x_{v{M_v}}}} \right].$ | (5) |
6)筛选出具有标签意义的特征变量:根据隶属度排序,设特征变量
7)筛选出所有具有标签意义的特征变量
这样筛选出来的变量具有标签意义,原因如下:在FCM的隶属度是表示某变量隶属于某个类的程度,若某个特征在某一场景中的排序数(排序数反映了在这个场景的这个聚类组中的隶属度在整个组中的大小水平)明显高于或低于在其他场景中的排序数,则这个特征在这个场景中的情况显著异于其他场景. 换句话说,当病人处在这个场景时这个特征就会突变,这种突变的量在术后预测中是有标签意义.
2 基于变量聚类的BP神经网络模型人工神经网络理论[18]最早是在20世纪40年代初由心理学家McCulloch和数理逻辑学家Pitts提出的神经元模型,经历60多年的曲折发展,人工神经网络在众多科学领域的应用方面显示出了巨大的潜力和广阔的应用前景. 反向传播网络(back propagation network,BP神经网络)就是当前运用的最成功和最广泛的神经网络模型之一.
本研究以结直肠癌患者数据样本的特征变量构造输入空间,运用FCM算法先进行变量聚类,筛选特征变量;再以这些特征变量作为输入层,以结肠癌患者术后生存期作为输出层对BP神经网络进行训练,得到训练后的模型. 该模型结构如图1所示.

|
图 1 基于模糊C均值(FCM)变量聚类的BP神经网络结构图 Fig. 1 Structure of BP neural network with fuzzy C-means(FCM) variable cluster |
在建模过程中,由于原始数据可能存在杂乱性、重复性和不完整性,先对原始数据进行预处理,包括数据清理、数据集成、数据归一化等. 将预处理后得到的高维样本数据集合进行FCM变量聚类,对高维样本数据集合进行降维,得到d个特征变量,这些特征变量对结直肠癌术后生存期有标签影响意义. 设置神经网络的输入层神经元个数为d;对于隐含层层数、每层神经元个数的选择,本模型采用“试错法”,分别从2~10逐步增加试验,权衡模型的复杂度和输出结果精度,选择最优的网络结构;神经网络输出层设置1个神经元,输出对结直肠癌术后生存期的预测值. 先利用训练集对BP神经网络进行训练得到预测模型,再用测试集测试其准确率.
3 实例分析收集到222例结直肠癌病人的样本数据,每个样本有1个目标变量(生存期)和35个特征变量. 通过数据预处理,最终得到可用样本217例,每例数据含1个目标变量和20个特征变量(p=20),分别为远处转移情况、饮酒史、尿糖、CD68间质计数、组织学类型、心血管病史、浸润深度、癌旁淋巴细胞浸润、发病部位、脉管侵犯、生长方式、化疗与否、确诊时年龄、5-Fu、CD68实质计数、β连环蛋白、p53率、家族肿瘤史、Ppar-γ、胆道疾病史.
3.1 FCM变量聚类通过对目标变量生存期的分析可知,在临床上,3 a生存率和5 a生存率是用来评价手术和治疗效果的指标,即3 a和5 a是一个病患术后生存状况的分水岭. 基于此场景认知,得出场景规则:
| $f{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {{a_i} \in S{L_1},\quad0 \leqslant {a_i}(Y) < 3}; \\ {{a_i} \in S{L_2},\quad3 \leqslant {a_i}(Y) < 5}; \\ {{a_i} \in S{L_3}, \quad{a_i}(Y) \geqslant 5}. \end{array}} \right.$ | (6) |
式中:
根据每个样本的生存期将217个样本分别划分到对应的一类,得到3个场景子样本集

|
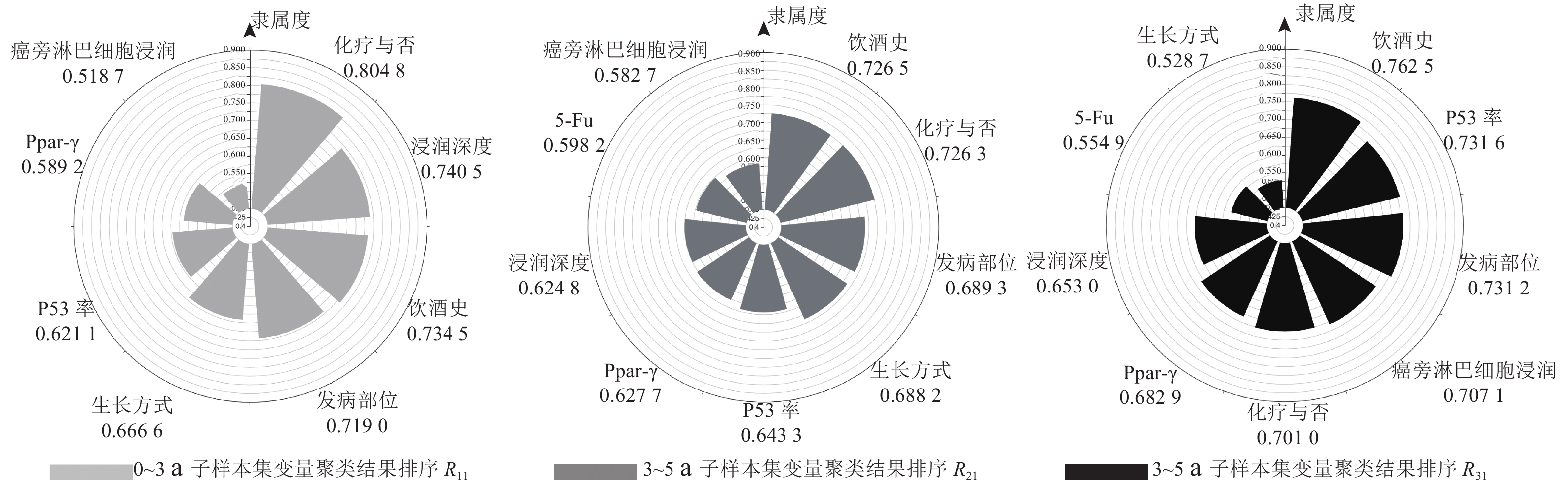
图 2 聚为类I的特征变量的隶属度及排序 Fig. 2 Membership degree and its rank of variables belonging to cluster I |
|
图 3 聚为类II的特征变量的隶属度及排序 Fig. 3 Membership degree and its rank of variables belonging to cluster II |
把类I看作是影响结直肠癌术后生存期的因素一,类II为因素二. 通过比较各个特征变量在3个样本集中隶属度排序的变化情况,可筛选出6个对3个生存期段(
1)对于聚为类I的特征变量.
a)脉管侵犯:脉管侵犯在
b)CD68实质计数:CD68实质计数在
c)家族肿瘤史:家族肿瘤史在
2)对于聚为类II的特征变量.
a) 化疗与否:化疗与否在
b) 浸润深度:浸润深度在
c) p53率:p53率在
结合现有的研究结果发现,通过FCM变量聚类筛选出来的对生存期有标签意义的特征变量也在结直肠癌研究领域被发现对术后生存期有重要的影响,具有较高的相关性和解释性:脉管内侵犯是恶性肿瘤常见的病理特征,肿瘤通过脉管侵犯,形成微转移,最终在远处形成转移灶,被认为与多种肿瘤的预后有关系,其中包括结直肠癌[19];结直肠癌中和肿瘤相关的巨噬细胞与结直肠癌患者肝转移发生率有关,CD68作为可靠的检测造血系统内单核−巨噬细胞系统的特异性标志,将有助于结直肠癌的预后[20];家族肿瘤史与结直肠癌术后癌症复发和死亡有着显著关系[21];化疗属于辅助治疗手段,有多个研究表明,化疗对结直肠癌患者的生存率有显著影响[22];肿瘤浸润肠壁深度与预后有直接关联,浸润深度在现阶段被研究者作为结直肠癌的独立预后因素[23];P53基因是一种人体抑癌基因,该基因编码一种野生型p53蛋白,是结直肠癌患者预后的独立因素[3-4].
3.2 术后生存期预测本研究采用6-6-5-1的神经网络结构模型:由FCM变量聚类从20个特征变量中筛选出6个特征变量作为BP神经网络的输入,分别为脉管侵犯、CD68实质计数、家族肿瘤史、化疗与否、浸润深度、p53;利用“试错法”得出采用2层隐含层的BP神经网络适合本例,神经元个数分别为6和5;输出层神经元个数为1,输出为对术后生存期的预测. 最大参数训练次数设置为3 000次.
首先随机选取全样本集的85%(185例)作为训练集对BP神经网络进行训练,生成预测模型,再用样本集的剩余32例作为测试集,对预测模型进行测试,计算准确率,测试集预测结果如图4所示. 图中T为生存期. 图中实心圆表示每个样本的真实术后生存时间,空心圆表示每个样本预测的术后生存时间. 可以看到,大部分真实值和预测值很接近但存在误差. 由于在实际中,病人和医生只需知道生存期在一定范围内,无需关注月份或天数的偏差,临床上也是更关注3 a存活率和5 a存活率,本文仍然将生存期分为0~3 、3~5 和5~n(n>5)3个时间区间来统计准确率,即只要最终的预测值和实际值处在于同一个区间,则视为预测准确.
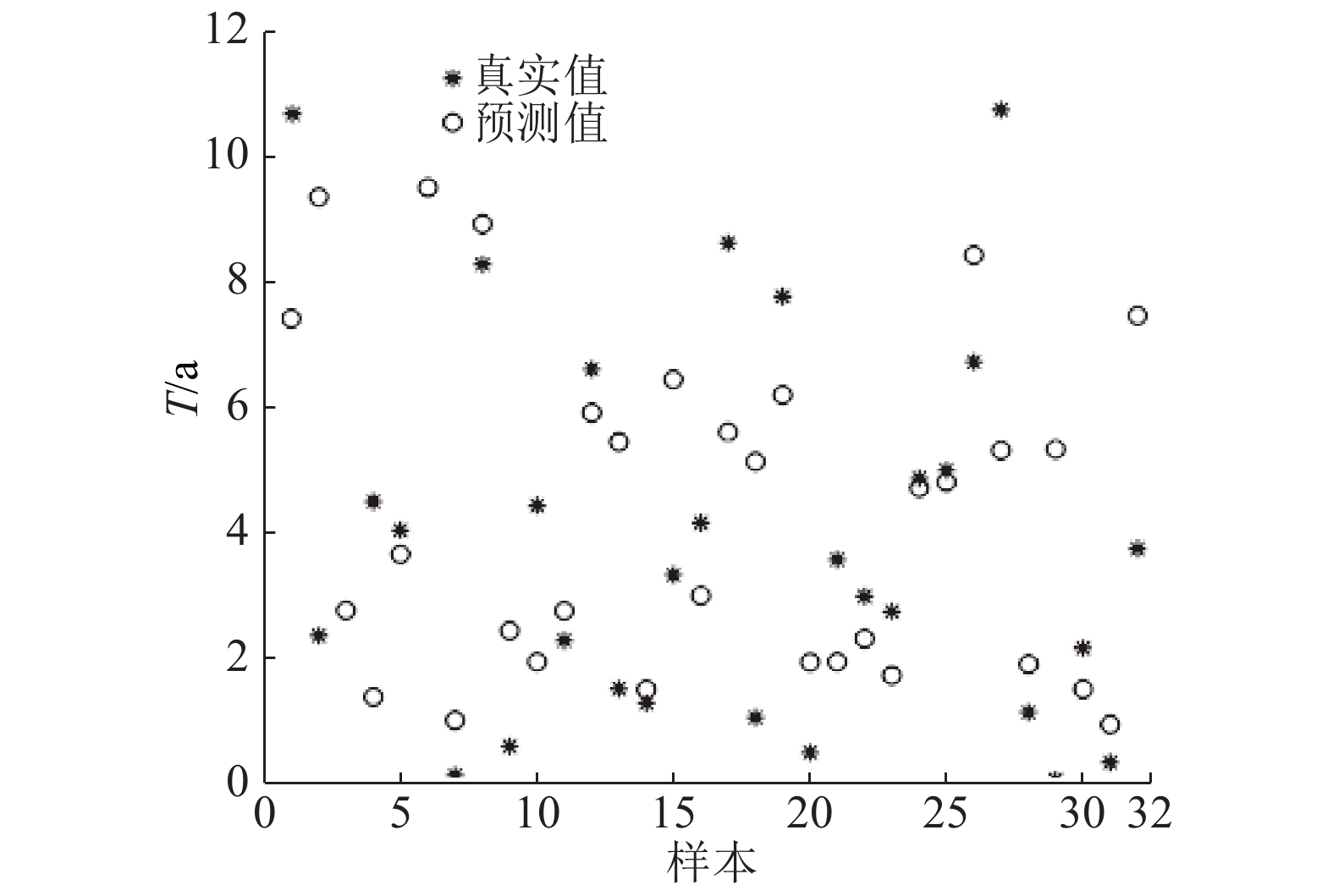
|
图 4 基于FCM变量聚类的BP神经网络预测模型测试结果 Fig. 4 Test results of BP neural network prediction model with FCM variable cluster |
同时本研究利用传统的主成分分析法(principal component analysis, PCA)对样本进行降维,筛选出特征变量作为输入,重新训练BP神经网络,对比准确率. 确保2个网络模型的参数一致,对比结果如表1所示. 表中N1为筛选前变量个数,N2为筛选后变量个数,R为各时间段预测准确率.
| 表 1 基于FCM及PCA的BP神经网络模型的测试准确率对比 Table 1 Comparison of accuracy between BP neural network models based on FCM and PCA |
虽然现有的医疗AI诊断已有个案应用,准确度可高达80%,甚至90%,但医疗术后预测不同于医疗诊断,医疗早期诊断区间一般在0.5~2 a,而本研究的术后预测区间为10 a以上,长时间区间的医学数据、生物结构和病理特征的变化性和复杂性使得预测的难度大大提高,本研究所得的准确度已能反映方法的有效性. 除此之外,通过对比结果可以看到,FCM-BP模型在3个时间段的准确率都比PCA-BP模型的准确率高,其中0~3 a高30.94%,3~5 a高33.32%,5~n a高92.61%,进一步表明基于场景认知的FCM变量聚类进行高维变量降维和筛选是有效的.
不容忽视的是,无论是FCM-BP模型还是PCA-BP模型,3~5 a区间的准确率都非常低,且大部分被误预测为0~3 a区间,而另外2个区间准确率较高. 导致这一现象的主要原因如下.
1)根据现实情况,0~3 a这个区间是特征很明显的一个时间段. 临床上,癌症病人术后3 a之内发生转移和复发的概率极大,约占80%,因此患者特征变量中恶性特征明显,这就有助于神经网络通过训练较好捕捉到蕴含其中的恶性特征,从而较为准确地预测这个区间的生存期;
2)根据现实情况,5~n a这个区间也是特征很显著的一个时间段. 临床上,如果5 a内不复发,再次复发的几率将非常小,因此患者特征变量的良性特征明显,这有助于神经网络通过训练较好捕捉到这些良性特征,从而较为准确地预测这个区间的生存期;
3)临床中,5 a存活率是一个很重要的指标,5 a之前都属于不太稳定的状态,说明3~5 a生存期的病人特征与0~3 a较为接近,即展现出一定的恶性特征,因此在神经网络训练过程中很容易误识别为0~3 a死亡的一类. 这一类病人如果不及早接受治疗和改善生活习惯,也容易在0~3 a内死亡[24]. 这样的预测结果恰好能够对生存期在3~5 a内的病人起到警示作用.
进一步地,样本数量较小是本研究需要攻克的一个难点. 在大数据时代,采集大量的数据进行训练是人们惯用的研究方式. 然而不可否认的是,在小样本的基础上提高精度也是一个不可或缺的研究方向,因为“数据越多越好”的思想并不能带领人们走向真正的人工智能[25],真正的人工智能除了需要数据的积累还需要依靠算法的改进. 本研究想要做的就是在有限的样本数下通过算法提高预测精度,为推进人工智能作出微小的贡献. 本研究提出的基于场景认知的变量聚类正是为了弥补样本少的缺陷. 如果没有此变量聚类方法的变量筛选(筛选出了具有预后一样的变量),那么直接训练的效果将差很多.
4 结 语基于FCM聚类,本研究提出了一种变量聚类方法,能够筛选出对目标变量有较高相关性和解释性的特征变量. 并结合BP神经网络,设计了预测结直肠癌术后生存期的模型,同时与传统的主成分分析法进行对比,结果表明,本文的模型预测精确度更高,具有重要的研究意义. 在研究过程中,该变量聚类方法加入了对场景的认知,这是筛选出重要特征变量的关键,也是其优于无解释性的主成分分析方法的原因.
虽然提出的模型准确率更高,但是仍然存在3~5 a的区间准确率较低的问题,因此,未来的研究重点将聚焦于进一步优化算法,提高预测准确率. 同时,如何将此模型沿用到其他类型癌症上将是下一步研究的重点.
| [1] |
SIEGEL R L, MILLER K D, FEDEWA S A, et al. Colorectal cancer statistics, 2017[J]. CA: a Cancer Journal for Clinicians, 2017, 67(3): 177-193. DOI:10.3322/caac.v67.3 |
| [2] |
CHEN W, ZHENG R, BAADE P D, et al. Cancer statistics in China, 2015[J]. CA: a Cancer Journal for Clinicians, 2016, 66(2): 115-132. DOI:10.3322/caac.21338 |
| [3] |
HORNBROOK M C, GOSHEN R, CHOMAN E, et al. Early colorectal cancer detected by machine learning model using gender, age, and complete blood count data[J]. Digestive Diseases and Sciences, 2017, 62(10): 2719-2727. DOI:10.1007/s10620-017-4722-8 |
| [4] |
MONTAZERI M, MONTAZERI M, MONTAZERI M, et al. Machine learning models in breast cancer survival prediction[J]. Technology and Health Care Official Journal of the European Society for Engineering and Medicine, 2015, 24(1): 31-42. |
| [5] |
THONGKAM J, XU G, ZHANG Y. AdaBoost algorithm with random forests for predicting breast cancer survivability[C] // IEEE International Joint Conference on Neural Networks. Hong Kong: IEEE, 2008: 3062–3069.
|
| [6] |
YAO D, YANG J, ZHAN X. Predicting breast cancer survivability using random forest and multivariate adaptive regression splines [C] // International Conference on Electronic and Mechanical Engineering and Information Technology. Harbin: IEEE, 2011: 2204–2207.
|
| [7] |
HUANG S H, LOH J K, TSAI J T, et al. Predictive model for 5-year mortality after breast cancer surgery in Taiwan residents[J]. Chinese Journal of Cancer, 2017, 36(4): 23. |
| [8] |
SVETNIK V, LIAW A, TONG C, et al. Random forest: a classification and regression tool for compound classification and QSAR modeling[J]. Journal of Chemical Information and Computer Sciences, 2003, 43(6): 1947. DOI:10.1021/ci034160g |
| [9] |
KUNIZAKI M, SAWAI T, TAKESHITA H, et al. Clinical value of serum p53 antibody in the diagnosis and prognosis of colorectal cancer[J]. Anticancer Research, 2016, 36(8): 4171-4175. |
| [10] |
WANG P, LIANG J, WANG Z, et al. The prognostic value of p53 positive in colorectal cancer: a retrospective cohort study[J]. Tumour Biology, 2017, 39(5): 1010428317703651. |
| [11] |
KOUROU K, EXARCHOS T P, EXARCHOS K P, et al. Machine learning applications in cancer prognosis and prediction[J]. Computational and Structural Biotechnology Journal, 2015, 13(C): 8-17. |
| [12] |
JAIN A K, CHANDRASEKARAN B. 39 dimensionality and sample size considerations in pattern recognition practice[J]. Handbook of Statistics, 1982, 2(39): 835-855. |
| [13] |
FRANCO G D. Principal component analysis and factor analysis[J]. Principal Component Analysis, 2002, 150-166. |
| [14] |
KLEMA V, LAUB A J. The singular value decomposition: Its computation and some applications[J]. IEEE Transactions on Automatic Control, 1980, 25(2): 164-176. DOI:10.1109/TAC.1980.1102314 |
| [15] |
姜园, 张朝阳, 仇佩亮, 周东方. 用于数据挖掘的聚类算法[J]. 电子与信息学报, 2005(4): 655-662. JIANG Yuan, ZHANG Chao-yang, QIU Pei-liang, et al. Clustering algorithm for data mining[J]. Journal of Electronics and Information Technology, 2005(4): 655-662. |
| [16] |
BEZDEK J C, EHRLICH R, FULL W. FCM: The fuzzy C-means clustering algorithm[J]. Computers and Geosciences, 1984, 10(2): 191-203. |
| [17] |
PAL N R, BEZDEK J C. On cluster validity for the fuzzy C-means model[J]. IEEE Transactions on Fuzzy Systems, 2002, 3(3): 370-379. |
| [18] |
PITTS W. A logical calculus of the ideas immanent in nervous activity[J]. Bulletin of Mathematical Biology, 1943, 5(4): 115-133. |
| [19] |
王彦东, 吴佩. 肿瘤的脉管内侵犯与转移[J]. 国际外科学杂志, 2007, 34(3): 209-212. WANG Yan-dong, WU Pei. Intravascular invasion and metastasis of tumor[J]. International Journal of Surgery, 2007, 34(3): 209-212. DOI:10.3760/cma.j.issn.1673-4203.2007.03.021 |
| [20] |
KHORANA A A, RYAN C K, COX C, et al. Vascular endothelial growth factor, CD68, and epidermal growth factor receptor expression and survival in patients with stage II and stage III colon carcinoma: a role for the host response in prognosis[J]. Cancer, 2003, 97(4): 960-968. DOI:10.1002/(ISSN)1097-0142 |
| [21] |
CHAN J A, MEYERHARDT J A, NIEDZWIECKI D, et al. Association of family history with cancer recurrence and survival among patients with stage III colon cancer[J]. Jama the Journal of the American Medical Association, 2008, 299(21): 2515-2523. DOI:10.1001/jama.299.21.2515 |
| [22] |
宫媛, 吴本俨, 苏斌斌. 272例直肠癌患者的预后影响因素分析[J]. 解放军医学杂志, 2008, 33(5): 608-610. GONG Yuan, WU Ben-yan. Analysis of prognostic factors in 272 patients with rectal cancer[J]. Medical Journal of Chinese People's Liberation Army, 2008, 33(5): 608-610. DOI:10.3321/j.issn:0577-7402.2008.05.043 |
| [23] |
NAKAMURA T, MITOMi H, KANAZAWA H, et al. Tumor budding as an index to identify high-risk patients with stage II colon cancer[J]. Diseases of the Colon and Rectum, 2008, 51(5): 568-572. DOI:10.1007/s10350-008-9192-9 |
| [24] |
WULFKUHLE J D, LIOTTA L A, PETRICOIN E F. Proteomic applications for the early detection of cancer[J]. Nature Reviews Cancer, 2003, 3(4): 267. DOI:10.1038/nrc1043 |
| [25] |
MARCUS G. Deep Learning: a critical appraisal [EB/OL]. (2018-01-02)[2018-04-18]. https://arxiv.org/abs/1801.00631.
|


