2. 结构风工程与城市风环境北京市重点实验室,北京 100044
2. Beijing Key Laboratory of Structural Wind Engineering and Urban Wind Environment, Beijing 100044, China
常处于大风浪等的恶劣自然条件下的跨海大桥,在设计时必须考虑波浪荷载. 由桩基、承台和桥墩组成的跨海桥梁下部结构[1],波浪荷载计算十分复杂,主要体现在本身结构型式的复杂以及由于波浪入射方向不同、波浪与结构物的相对高度不同而表现出的各向异性. 准确计算桥梁下部结构波浪力,分析不同因素的影响规律,对跨海桥梁设计具有重要意义.
组合结构的下部多为群桩,称为群桩基础,被广泛用于跨海大桥建设中[2]. 当只有下部桩基的部分受波浪作用时,桩间距和波浪入射方向角是桩基受力的主要影响因素,很多学者对此进行了不同程度的研究[3-5]. 当桩及上部承台与桥墩均遭遇波浪作用时,由于承台属于大尺度结构物,产生的波浪绕射对下部小尺度桩柱所受波浪荷载具有不可忽略的减小作用[6],因此承台的存在使得桥梁整个下部结构波浪力的计算难度大大增加. 多数研究仅针对平床条件,未考虑近海岸底部坡度的影响. 在近海岸浅水区,由于水深变浅,波高迅速增加,波面发生变形[7],近岸处的跨海桥梁下部结构将面临更加复杂的波浪力场,波浪荷载分析变得更加困难[8]. 此外,现有相关研究多针对单桩[9-11]或双柱[12]以及桩柱位置等对波浪荷载的影响,较少考虑桥梁下部群桩、承台与桥墩组合型式的结构所遭遇的波浪力计算.
针对桥梁下部结构设计的复杂性以及所遭遇的波浪特征(如:相对波高),本文采用水流运动方程的雷诺时均Navier-Stokes(RANS)方程和k-ε湍流模型,研究近岸跨海桥梁下部组合结构(墩+承台+桩基础)与波浪的相互作用,包括相对波高、波浪入射方向与结构物产生的各向异性特征对波浪力的影响.
1 数值计算模型 1.1 控制方程及数值求解方法本文采用描述不可压缩流体运动的雷诺时均Navier-Stokes(RANS)方程来模拟水波时均量,其控制方程包括连续方程和动量方程.
1)连续方程
| $\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0.$ | (1) |
2)动量方程
| $\frac{{\partial {u_i}}}{{\partial t}} + {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + {g_i} + \frac{\partial }{{\partial {x_j}}}\left( {\upsilon \frac{{\partial {u_i}}}{{\partial {x_j}}} - \overline {{{u'}_i}{{u'}_j}} } \right).$ | (2) |
式中:i、j为直角坐标方向循环指标,分别取值1、2和3;ui、uj分别为i、j方向流体运动的时均速度;t为时间;ρ为流体密度;p为压强;gi为重力加速度;υ为流体的运动黏度;
| $ - \overline {{{u'}_i}{{u'}_j}} = {\nu _t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}k{\delta _{ij}}.$ | (3) |
其中,
式(1)和(2)采用两步投影的有限体积法求解[14],第一步是预测步,第二步是校正步. 采用线性最小二乘重构法来估计单元中心变量梯度[15],时间导数项采用前差格式离散,水的自由表面计算采用体积分数法[16]. 结构物受到的波浪力通过对压强和黏性应力积分得到,计算公式为
| $ { F} = \int\limits_s {\left( { - p + {\tau _\upsilon }} \right){\rm d}s = } \sum\limits_{i = 1}^n \,{\left( { - p + {\tau _\upsilon }} \right)A\hat n} .$ | (4) |
式中:
| ${C_{{F_x}}} = \frac{{2{F_x}}}{{\rho g{h^2}D}}.$ | (5) |
其中,Fx为水平x方向波浪力,h为静水深,D为桩柱直径.
计算域入口为造波边界,采用Goring造波方法[17];底部和斜坡采用无滑移固壁边界条件,上部为自由表面,采用压力入口边界条件,前后侧设为对称边界. 初始时刻,设定全计算域范围内的水质点初始流速为0.
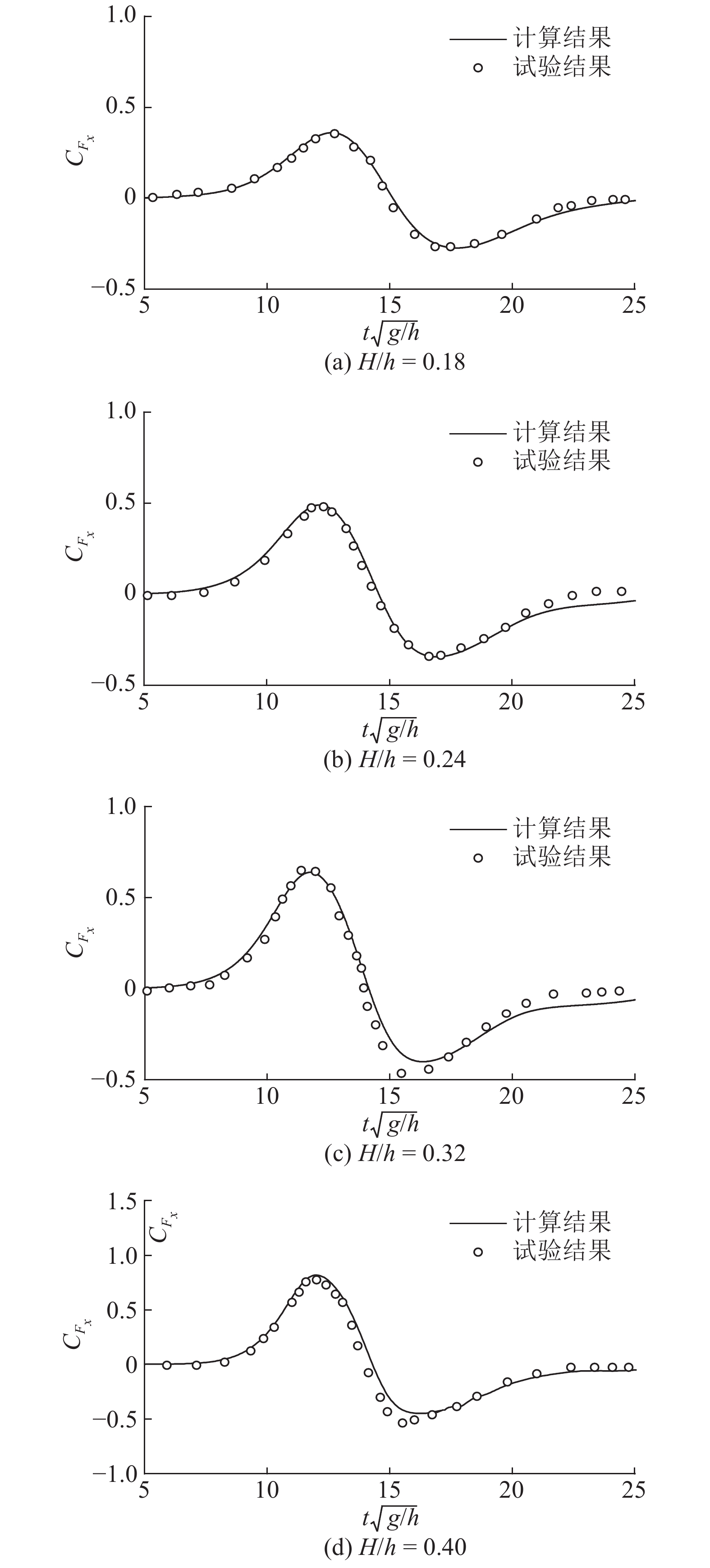
1.2 模型验证为了验证湍流模型的适用性以及波浪对结构物的作用力计算,采用Yates等[18]提出的试验模型和计算条件进行验证,具体参数详见参考文献[18],波面形态和波浪力计算结果与试验结果对比如图1和2所示. 图1为H/h=0.40(H为入射波高)条件下,墩前(Gauge 1-2)和墩后(Gauge 3-4)4个不同位置处波面高程时程曲线,同时试验数据也点绘于图中[18],其中t采用

|
图 1 波面时程曲线对比(H/h=0.40) Fig. 1 Comparison of time histories of wave surface (H/h=0.40) |
|
图 2 不同波高的波浪力时程曲线对比 Fig. 2 Comparison of time histories of wave force for different wave heights |
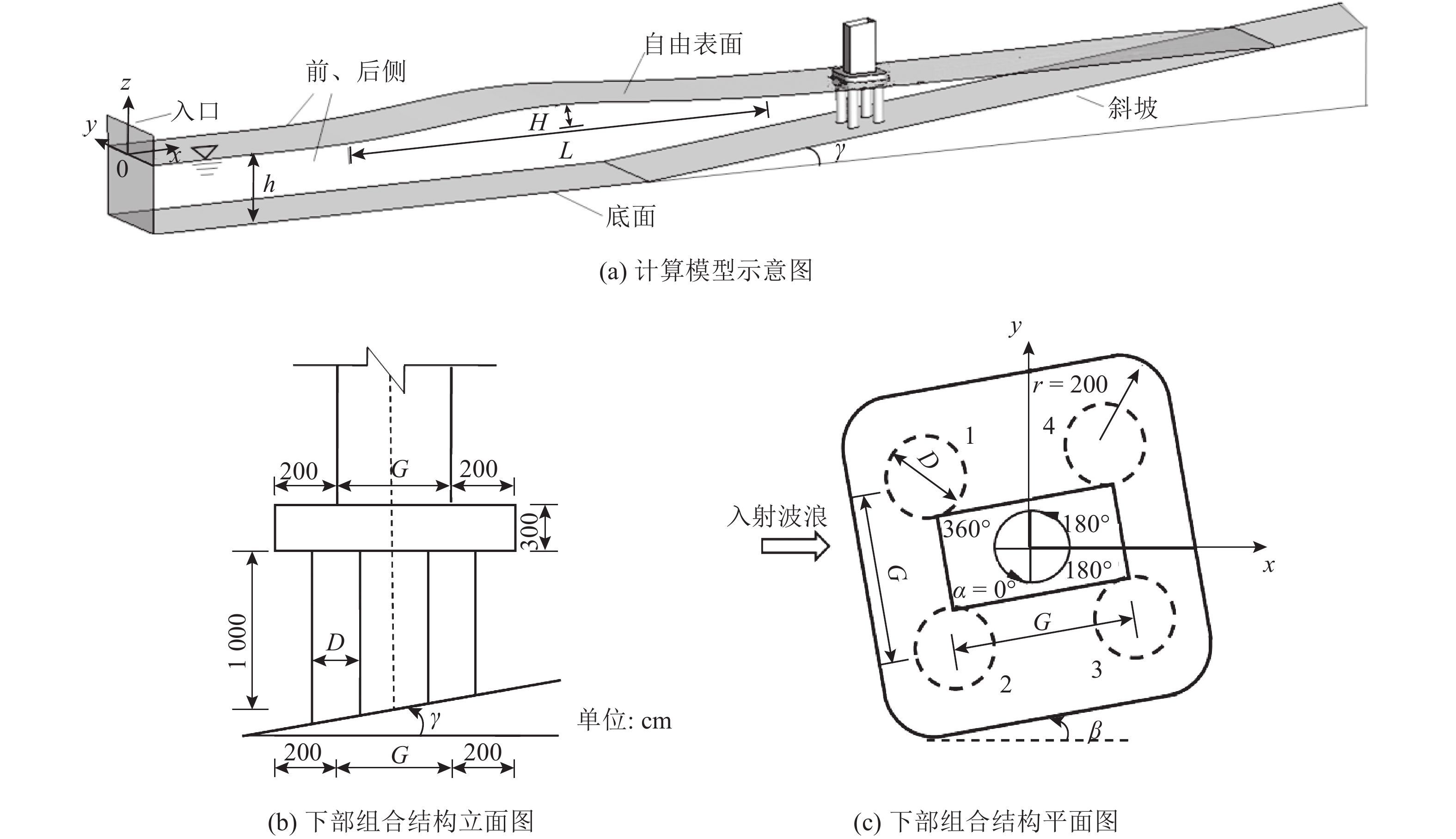
以我国跨海桥实际工程为背景,采用本文模型研究2×2布置式群桩+承台+桥墩组合结构所受波浪力的影响规律,分析入射波方向和波高变化与该结构产生的各向异性对波浪荷载的影响. 本研究中整个计算域长为440 m,宽为50 m,高为24.8 m,示意图如图3(a)所示,将近岸床面简化为单一坡度. 由于孤立波的波形与近岸浅水波相似,入射波浪采用孤立波,图中,L为波长,计算公式为
|
图 3 跨海桥梁计算模型及桥梁下部组合结构示意图 Fig. 3 Sketch of calculation model and substructure of sea-crossing bridge |
组合结构布置如图3(b)和3(c)所示,桥墩为矩形,承台为圆角方形,长×宽×高(B为承台高度)为10.25 m×10.25 m×3.00 m,圆角直径r=2.0 m,承台底部中心到床面高度为10 m,4根桩柱为等直径圆柱,直径D=2.5 m,编号1-4按照逆时针顺序排列,G为桩柱中心距,β为波浪与结构物相对方向角, 圆周角α(0° ~ 360°)定义见图3(c),其中结构前方正对波浪入射方向定义为0°(360°). 当波高和水深很小时,只有下部桩基础受到波浪作用,此时桩柱受力即是整个组合结构的受力,故下文将桩基作为单独部分进行研究.
2.2 计算条件计算条件及具体参数取值如表1所示. 其中,β取值为0°~45°;桩柱中心距G取值为G/D=1.5~5.0;相对波高H/h取值为0.109~0.470,表示波浪特征的无量纲参数KC取值为6.326~12.971,计算公式如下:
| 表 1 入射波浪及桥梁下部结构参数设置 Table 1 Parameters setting of incident wave and bridge substructure |
| ${\rm KC} = \frac{{{U_{\rm m}}T}}{{{D_y}}},\quad{U_{\rm m}} = H\sqrt {\frac{g}{h}} ,\quad T = 4\pi h\sqrt {\frac{1}{{3gH}}} .$ | (6) |
式中:Um为水质点最大水平速度,T为波浪周期,Dy为沿水槽y方向的阻水宽度. 在群桩计算中取值2D,在桥梁下部组合结构计算中,由于结构型式复杂,阻水宽度沿水深方向变化,Dy采用不同阻水宽度计算值的加权平均.
3 组合结构的下部桩基础受力分析当波高和水深很小时,波浪只作用于下部桩基础,桩柱受力问题即是整个组合结构的受力问题,故首先研究桩基础所受波浪力. 研究发现本文计算条件下群桩中桩柱受到y方向的波浪力Fy小于x方向波浪力Fx的5%,z方向上举力Fl小于x方向波浪力Fx的2%,故只分析x方向波浪力
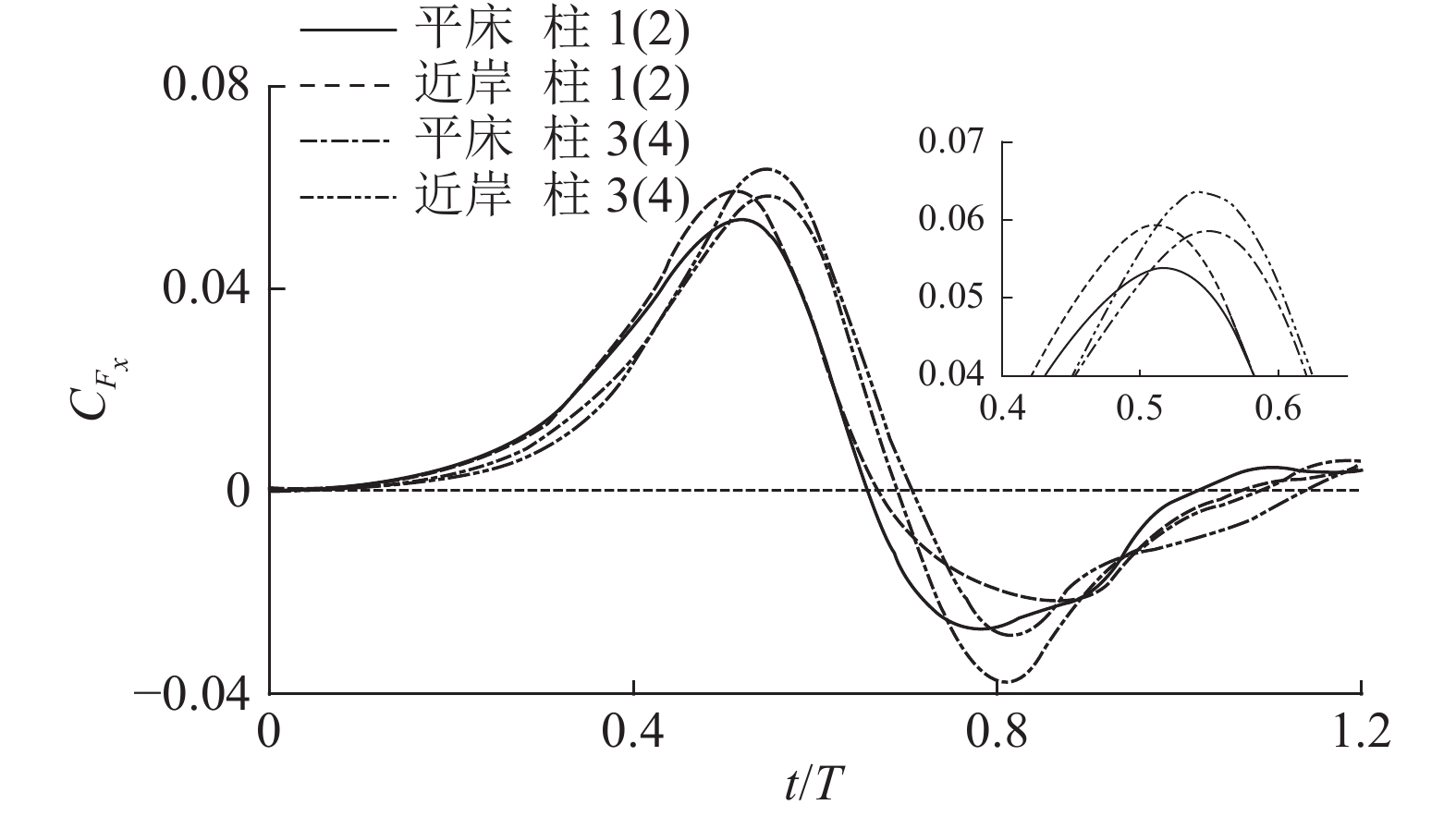
波浪变化导致桩柱受到波浪力随时间变化,将孤立波恰好到达前排桩柱位置的时刻定义为t/T=0,将各分结构受力
|
图 4 近岸和平床桩柱波浪力随时间变化(H/h=0.320) Fig. 4 Variations of wave forces with time in near-shore and flat bed (H/h=0.320) |
|
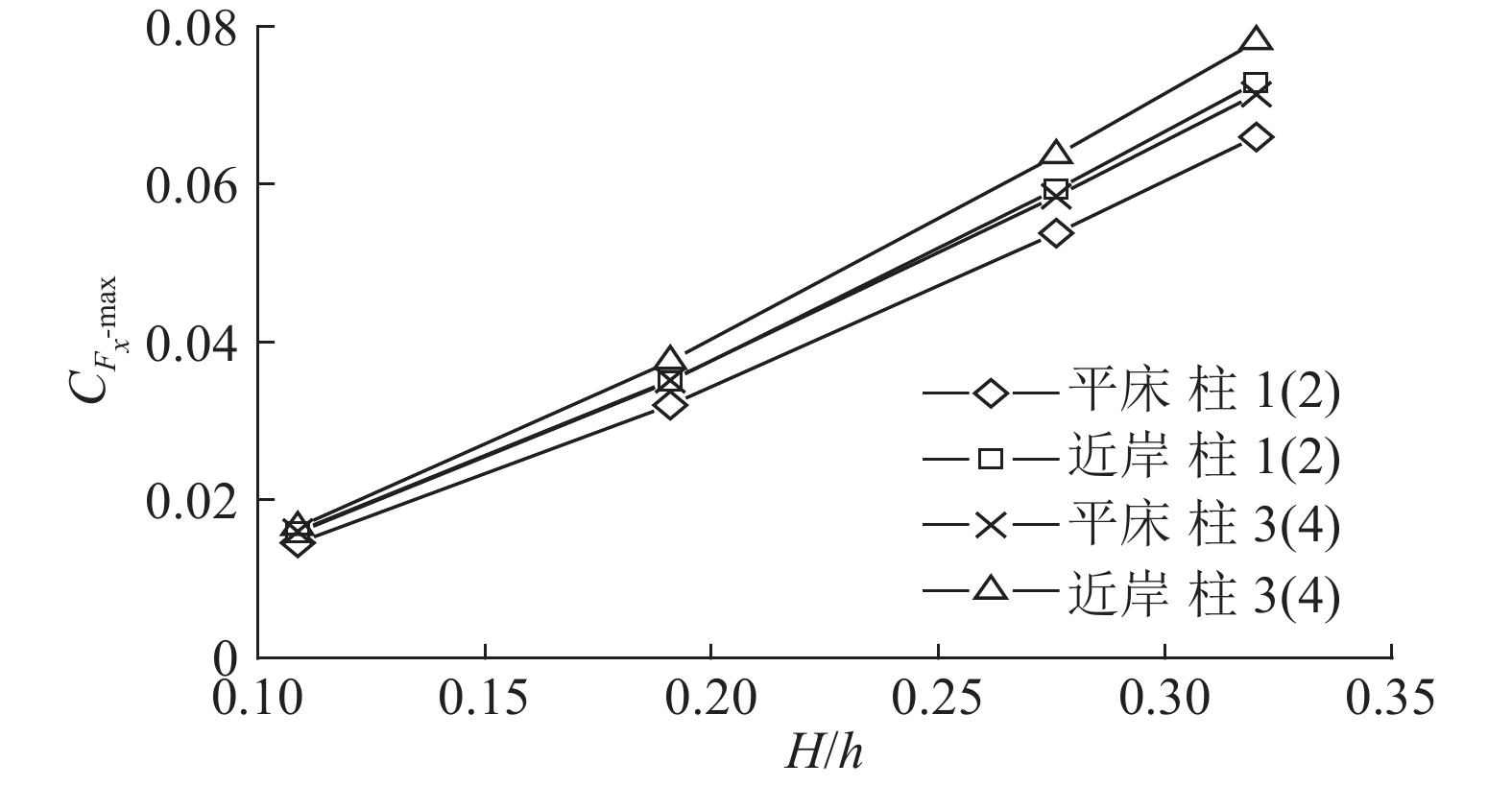
图 5 近岸和平床桩柱最大波浪力随波高比变化(β=0°,G/D=2.5) Fig. 5 Variations of maximum wave forces with wave height ratio in near-shore and flat bed (β=0°,G/D=2.5) |
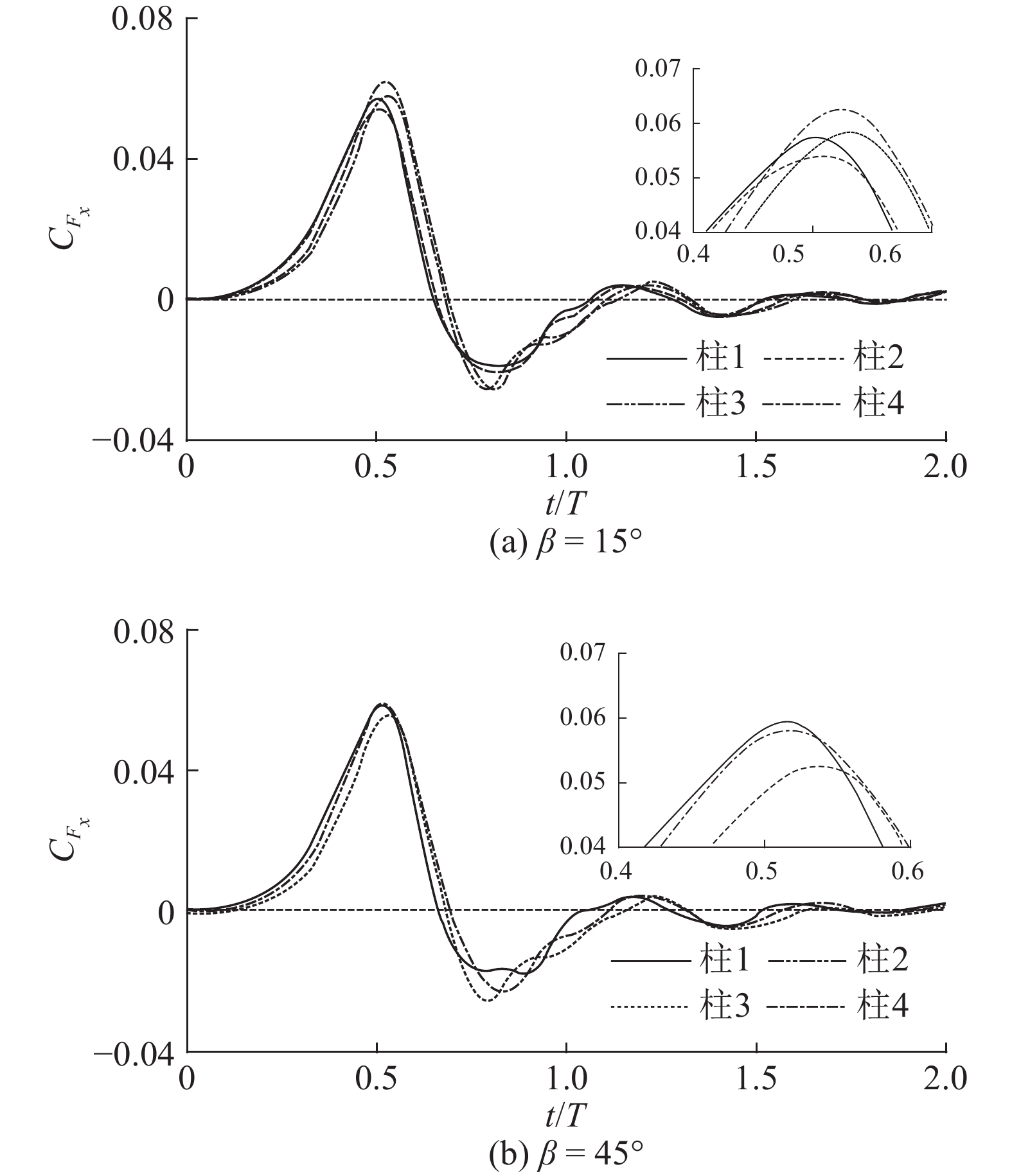
近岸条件下,不同波浪入射角β影响下的桩柱波浪力随时间变化如图6所示(β=15°和45°). 从图中可以看出,尽管波浪入射方向不同,各桩柱所受
|
图 6 波浪入射角影响下近岸桩柱波浪力随时间变化(H/h=0.274,G/D=2.5) Fig. 6 Variations of wave forces with time in near-shore under influence of incident wave direction (H/h=0.274,G/D=2.5) |
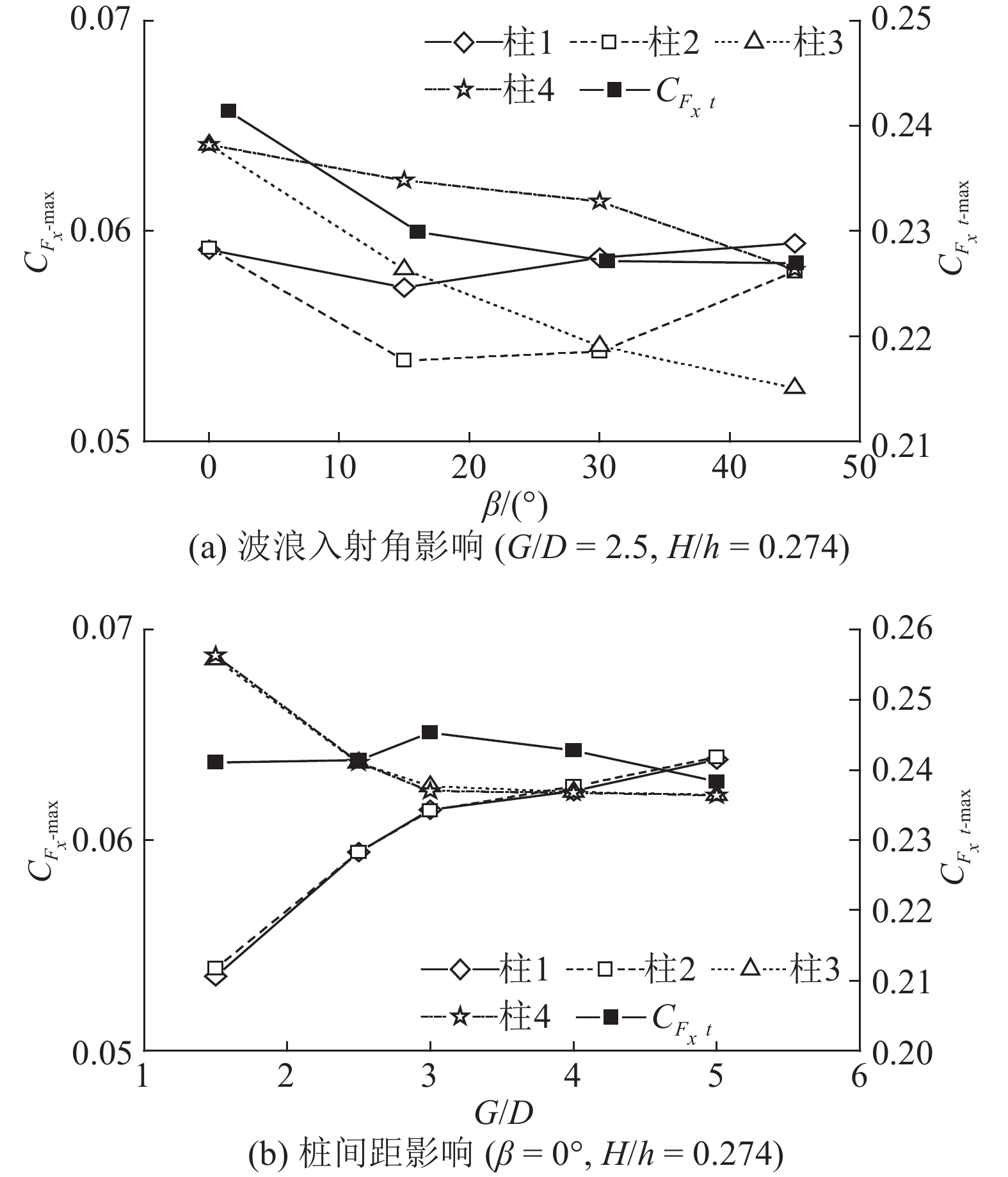
各桩柱受到的最大波浪力
|
图 7 波浪入射角和桩间距对最大波浪力的影响 Fig. 7 Influence of incident wave direction and pile spacing on maximum wave forces |
在入射波浪β=0°、H/h=0.274条件下,设置5种桩间距(G/D=1.5 ~ 5.0),其对桩柱波浪力的影响如图7(b)所示. 当G/D≤4时,前排桩柱
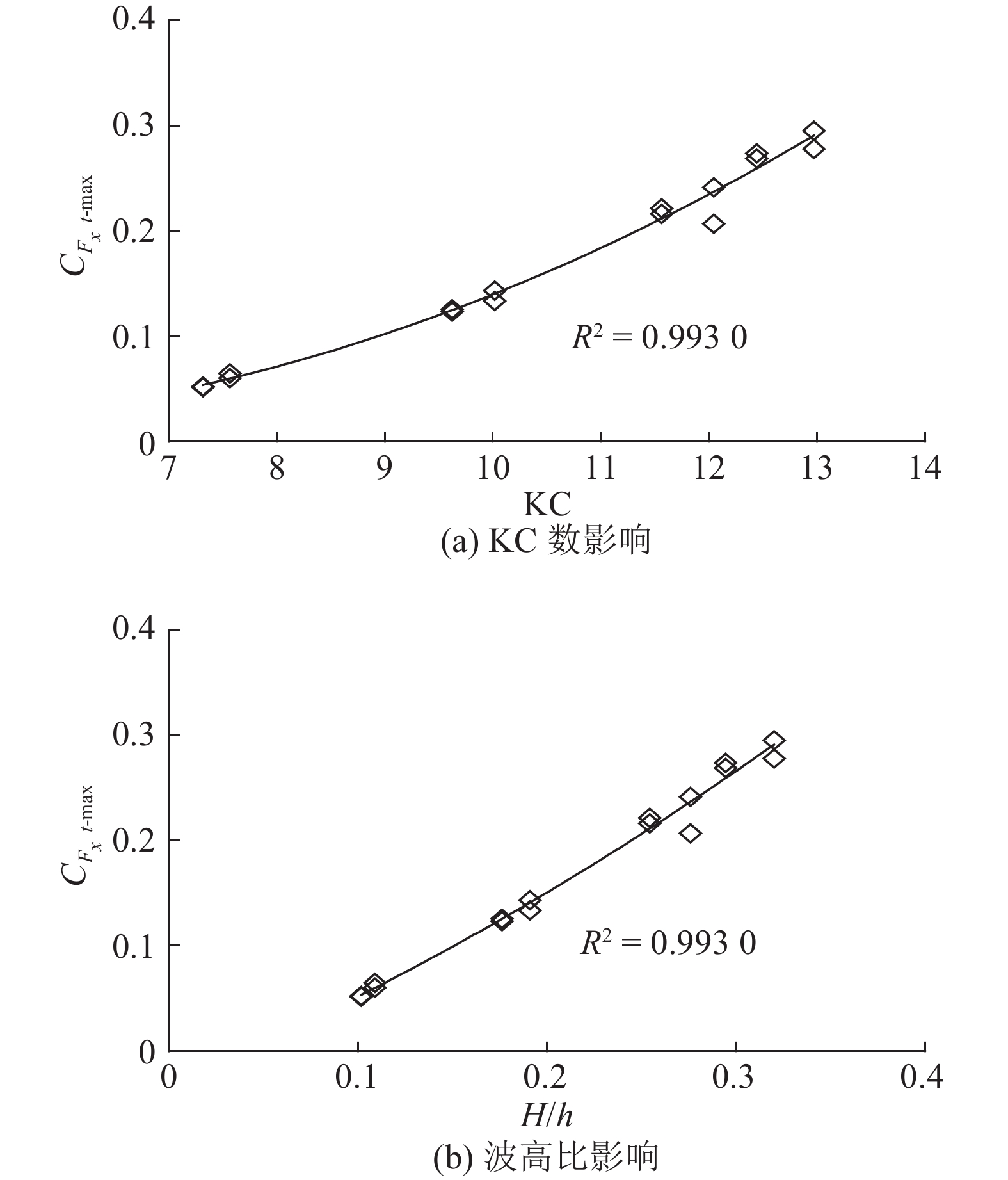
KC数是表征波浪与桩柱相互作用的重要参数,相对波高H/h是描述孤立波特性的重要参数. 在本文计算条件下,群桩受到的总波浪力最大值
|
图 8
KC数和波高比对群桩整体所受波浪力最大值
|
| ${C_{{F_xt} - \max }} = 0.000\,16{\rm{K}}{{\rm{C}}^{2.946}}.$ | (7) |
上式相关系数R2=0.993 0. 图8(b)表明,在H/h≈0.1 ~ 0.4内,
| ${C_{{F_xt} - \max }} = 1.578\,7{\left( {\frac{H}{h}} \right)^{1.472\,9}}.$ | (8) |
上式相关系数R2=0.993 0. 可见,对于群桩基础来说,KC数和相对波高H/h均能很好地反映孤立波特性对波浪力的影响规律.
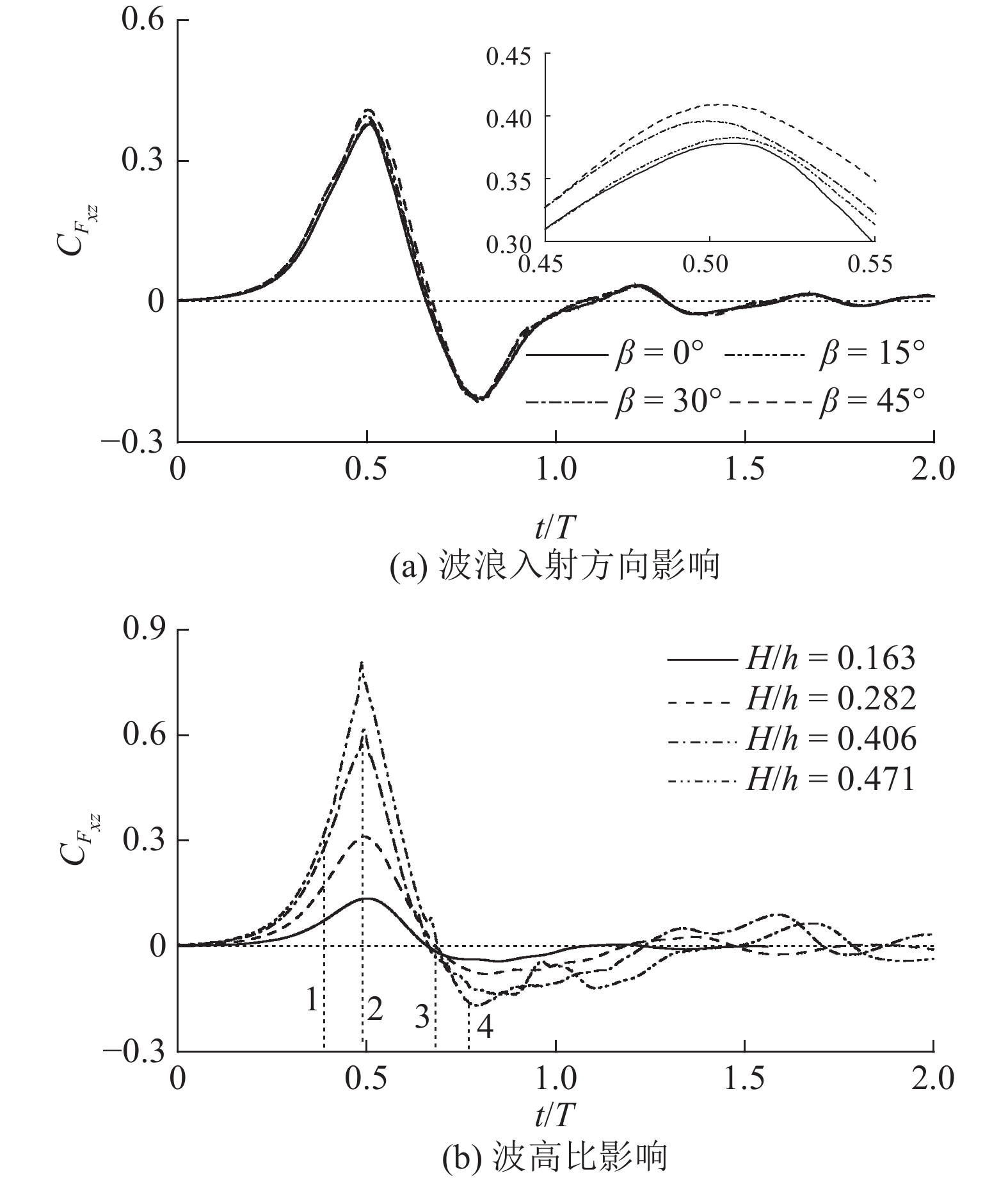
4 组合结构受力分析 4.1 波浪力时程曲线和波面分布图9给出了当波浪入射方向β=0° ~ 45°和相对波幅H/h=0.163 ~ 0.471时,桥梁下部结构整体所受波浪力
|
图 9 桥梁下部结构整体受力随时间变化 Fig. 9 Variations of wave forces on bridge substructure with time |
图9(b)中1 ~ 4分别对应
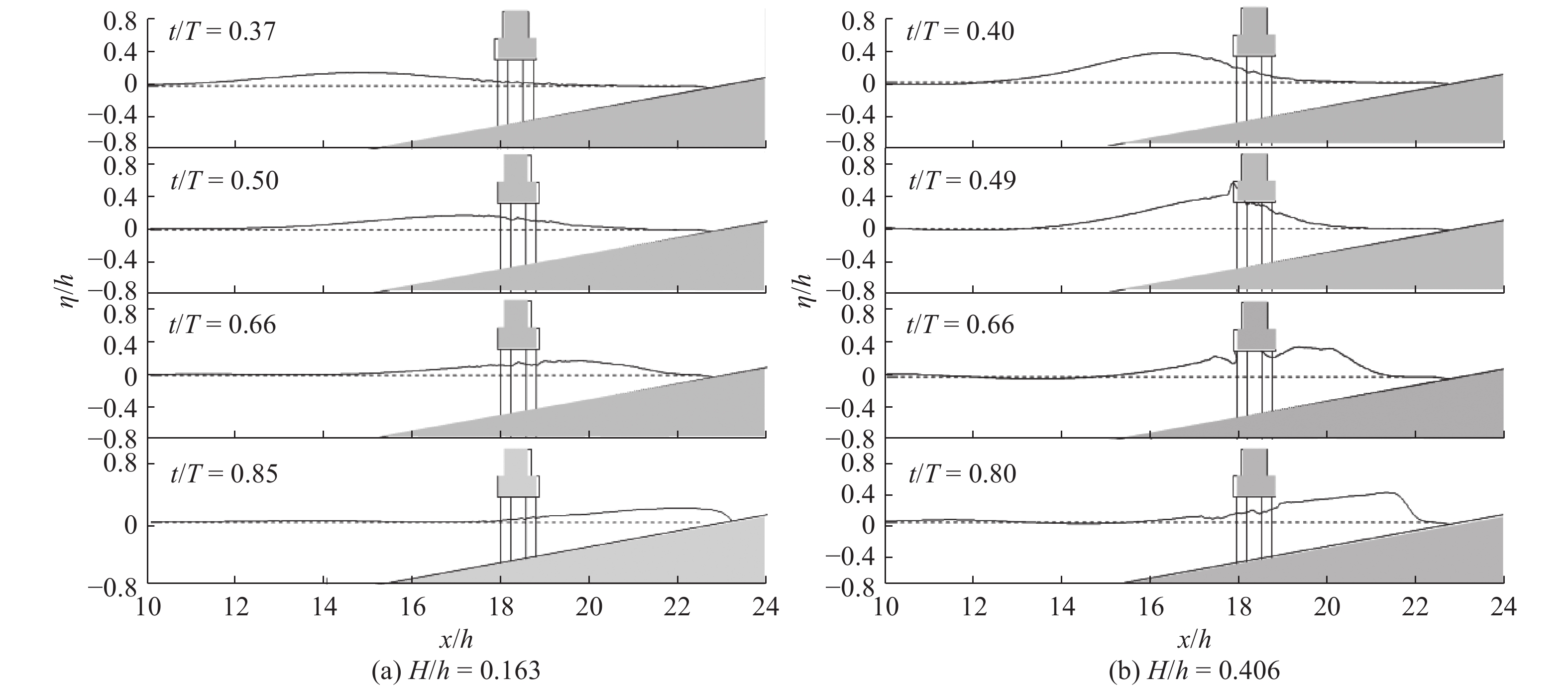
|
图 10 不同时刻波形空间分布 Fig. 10 Spatial distribution of wave surfaces at different times |
相对压强pc定义为
| ${p_{\rm c}} = \frac{{{p_\eta } - {p_0}}}{{\rho gh}}.$ | (9) |
式中,pη为桥梁下部组合结构所受x方向波浪力
当H/h=0.274时,静水面(z=0)位于承台1/2高度(B/2)处,β=0°和β=45°条件下z=0位置处承台表面测点对应的相对压强pc分布如图11所示. 可以看出,最大pc均分布在承台迎流面前驻点处(α=0°和360°),向两侧逐渐减小,背水面α=180°位置处最小. 与β=0°的结果相比,β=45°时迎流面和背流面相对压强数值均较大,但迎流面与背流面压强差值变化不大.
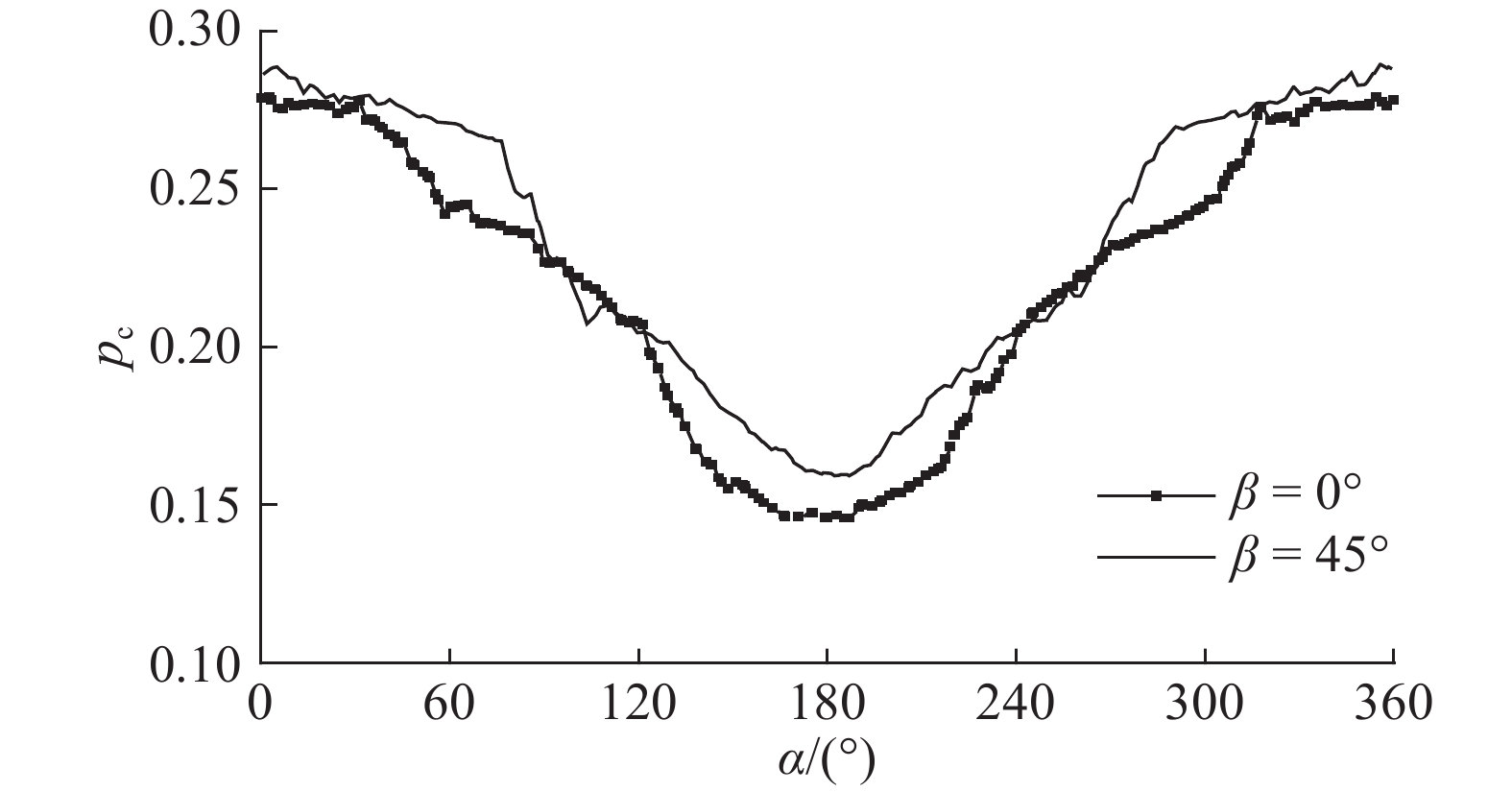
|
图 11 总波浪力达到最大值时静水面位置承台表面相对压 强分布 Fig. 11 Distribution of relative pressure on bearing platform surface for still water surface when total wave force arrives maximum |
计算结果发现,桥梁下部结构y方向波浪荷载Fy小于x方向荷载Fx的5%,z方向上举力Fl不可忽略. 此外,桥梁下部整体结构受到上举力Flz几乎不受波浪入射方向角β的影响,波浪要素的影响后续可进行深入研究,在此不过多关注,本文重点分析x方向波浪力
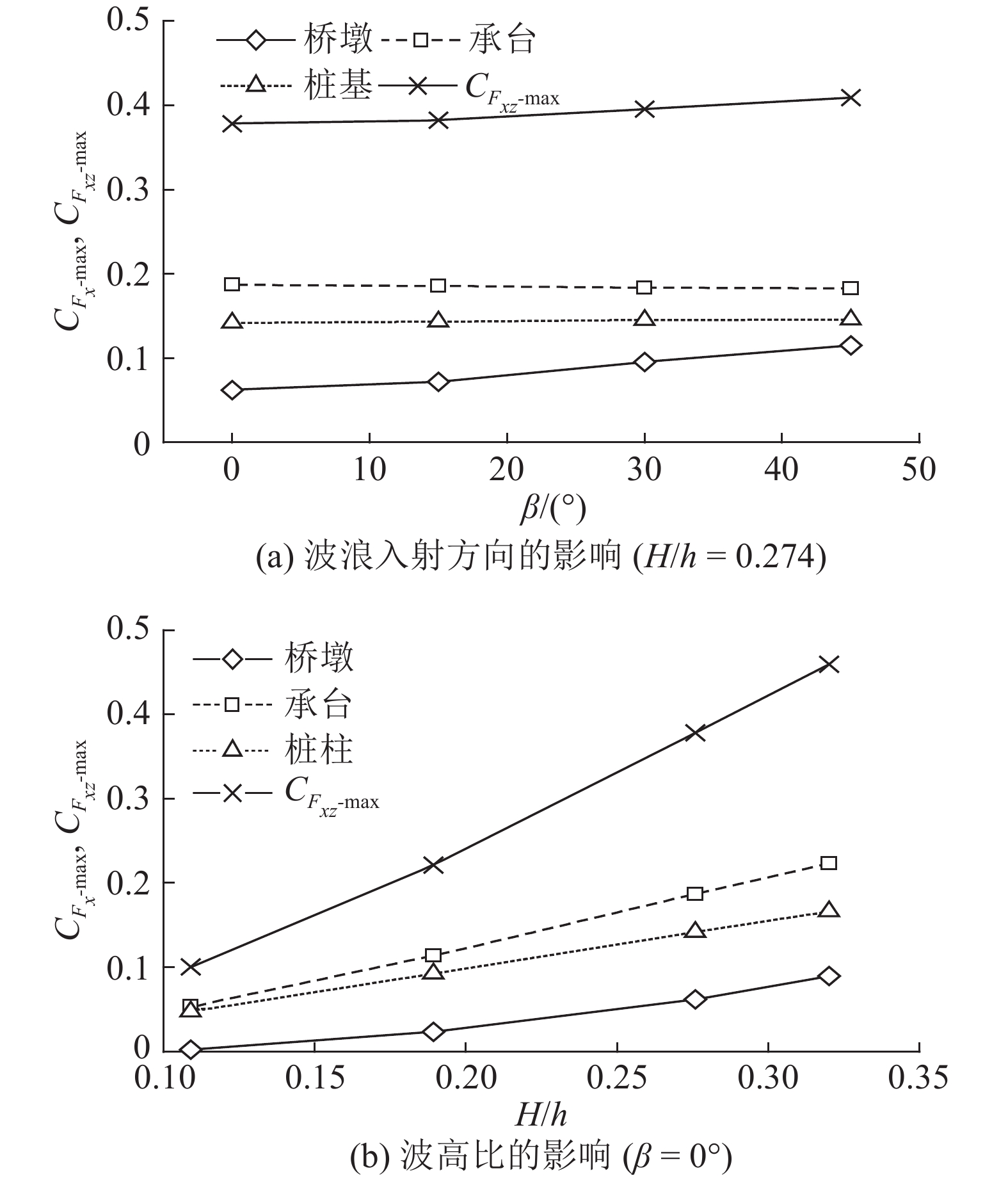
|
图 12 参变量影响下的最大波浪力 Fig. 12 Influence of different parameters on maximum wave forces |
图13表示KC数和相对波高H/h对桥梁下部整体结构所受最大波浪力
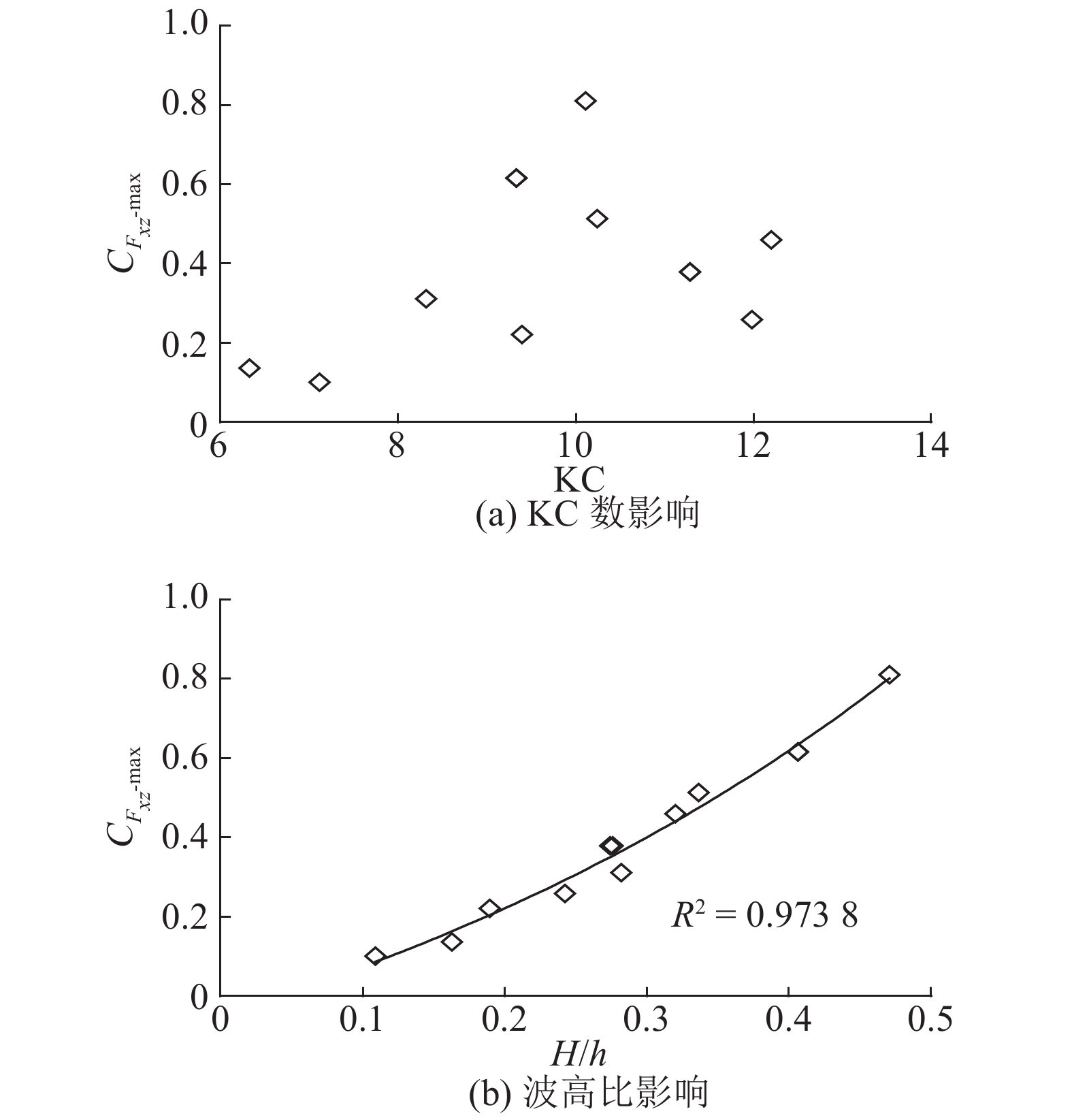
|
图 13 KC数和波高比对最大总波浪力的影响 Fig. 13 Influence of KC number and H/h on maximum of total wave forces |
| ${C_{F_{xz} {\text -} \max }} = 2.363\,3{\left( {\frac{H}{h}} \right)^{1.473\,9}}.$ | (10) |
该式相关系数R2=0.973 8. 可见,相对波高H/h能更好地反映波浪特性对桥梁下部结构整体所受波浪力的影响规律.
5 结 论(1)当波浪入射角β=0°时,与平床条件相比,近岸由于波浪浅化变形,桩柱所受波浪力增加,且增幅随相对波高H/h增加.
(2)近岸条件下,波浪入射角β=0°时前排桩柱受力随桩间距的增加而增加,后排桩柱受力随桩间距的增加而减小,但群桩整体受力随桩间距和波浪入射方向变化幅度小于10%,随KC数和H/h成幂指数规律增加.
(3)对于桥梁下部组合结构,当波浪入射方向角由0°增加到45°时,桥墩受力随之增加,桩基、承台以及桥梁下部整体结构受力随β基本不变.
(4)桥梁下部结构整体受力随H/h成幂指数规律增加,相对增幅可达704%.
(5)由于桥梁下部组合结构阻水面积沿垂向变化显著,与KC数相比,相对波高H/h能更好地反映波浪特性对桥梁下部组合结构整体受力的影响.
| [1] |
袁作祥, 吴有铭. 澳门西湾大桥主塔基础施工世界桥梁[J]. 世界桥梁, 2005, 4: 28-30. YUAN Zuo-xiang, WU You-ming. Construction of pylon foundations of Sai Van Bridge in Macau[J]. World Bridges, 2005, 4: 28-30. DOI:10.3969/j.issn.1671-7767.2005.04.008 |
| [2] |
孙国强. 杭州湾跨海大桥深水区引桥采用钢管桩基础初析[J]. 公路, 2005, 6: 39-42. SUN Guo-qiang. Analysis of steel pipe pile foundation used in deep-water approach bridge of Hangzhou Bay sea-crossing Bridge[J]. Highway, 2005, 6: 39-42. DOI:10.3969/j.issn.1671-2668.2005.03.015 |
| [3] |
ZHAO M, CHENG L, TENG B. Numerical simulation of solitary wave scattering by a circular cylinder array[J]. Ocean Engineering, 2007, 34: 489-499. DOI:10.1016/j.oceaneng.2006.03.005 |
| [4] |
YANG C, LIU Y, LIU C G. Predicting wave loads on adjacent cylinder arrays with a 3D model[J]. Journal of Hydraulic Research, 2015, 53(6): 797-807. DOI:10.1080/00221686.2015.1058864 |
| [5] |
BONAKDAR L, OUMERACI H, ETEMAD-SHAHIDI A. Wave load formulae for prediction of wave-induced forces on a slender pile within pile groups[J]. Coastal Engineering, 2015, 102: 49-68. DOI:10.1016/j.coastaleng.2015.05.003 |
| [6] |
耿宝磊, 腾斌, 宁德志, 等. 畸形波作用下海洋平台小尺度杆件波浪荷载分析[J]. 大连海事大学学报, 2010, 36(1): 39-43. GENG Bao-Lei, TENG Bin, NING De-zhi, et al. A time-domain analysis of wave force on small-scale cylinders of platform under freak waves[J]. Journal of Dalian Maritime University, 2010, 36(1): 39-43. |
| [7] |
MO W, JENSEN A, LIU L F. Plunging solitary wave andits interaction with a slender cylinder on a sloping beach[J]. Ocean Engineering, 2013, 74(1): 48-60. |
| [8] |
WIENKEA J, OUMERACI G. Breaking wave impact force on a vertical and inclined slender pile-theoretical and large-scale model investigations[J]. Coastal Engineering, 2005, 52: 435-462. DOI:10.1016/j.coastaleng.2004.12.008 |
| [9] |
XIAO H, HUANG W. Three-dimensional numerical modeling of solitary wave breaking and force on a cylinder pile ina coastal surf zone[J]. Journal of Engineering Mechanics, 2015, 141(8): A4014001. DOI:10.1061/(ASCE)EM.1943-7889.0000834 |
| [10] |
CHOI S J, LEE K H, GUDMESTAD O T. The effect of dynamic amplification due to a structure's vibration on breaking wave impact[J]. Ocean Engineering, 2015, 96: 8-20. DOI:10.1016/j.oceaneng.2014.11.012 |
| [11] |
KAMATH A, CHELLA M A, BIHS H, et al. Breaking wave interaction with a vertical cylinder and the effect of breaker location[J]. Ocean Engineering, 2016, 128: 105-115. DOI:10.1016/j.oceaneng.2016.10.025 |
| [12] |
BIHS H, KAMATH A, CHELLA M A, et al. Breaking-wave interaction with tandem cylinders under different impact scenarios[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2016, 142(5): 4016005(14). |
| [13] |
LAUNDER B E, SPALDING B. The numerical computation of turbulent flows[J]. Computer Methods in Applied Mechanics and Engineering, 1974, 3(2): 269-289. DOI:10.1016/0045-7825(74)90029-2 |
| [14] |
ISSA R I. Solution of implicitly discretized fluid flow equations by operator splitting[J]. Journal of Computational Physics, 1986, 62: 40-65. DOI:10.1016/0021-9991(86)90099-9 |
| [15] |
BARTH T J. Aspects of unstructured grids and finite-volume solvers for the Euler and Navier–Stokes equations: AGARD R-787 [R]. Brussels: Special Course on Unstructured Grid Methods for Advection Dominated Flows, 1992. https://www.researchgate.net/publication/23826802_Aspects_of_unstructured_grids_and_finite-volume_solvers_for_the_Euler_and_Navier-Stokes_equations
|
| [16] |
HIRTC W, NICHOLS D B. Volume of fluid method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39: 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [17] |
GORING D G. Tsunamis: the propagation of long waves onto a shelf: KH-R-38 [R]. Pasadena: California Institute of Technology, 1978.
|
| [18] |
YATES G T, WANG K H. Solitary wave scattering by a vertical cylinder: experimental study [C] // Proceedings of the 4th International Offshore and Polar Engineering Conference, Osaka: ISOPE, 1994, 3: 118–124.
|



