2. 南通大学 机械工程学院,江苏 南通 226019
2. College of Mechanical Engineering, Nantong University, Nantong 226019, China
潮流能作为一种清洁可再生能源正在全球范围内引起广泛关注. 作为水下风力机,水平轴潮流能水轮机被广泛用于获得潮汐运动中的动能. 作为获能关键部位,叶片性能的好坏至关重要. 为提升叶片获能系数,需对叶片进行必要的设计优化. 叶片由一系列翼型在半径方向上以不同扭角排列构建而成,叶片翼型的优化对提升潮流能水轮机性能具有重要意义. 为了提高潮流能机性能,国内外学者已经作了很多研究. 翼型试验和模拟方面:徐超等[1-2]采用Boltmann方法对水轮机叶片翼型水动力性能进行了研究;Goundar等[3]对翼型升阻力特性及空泡问题开展了数值模拟及实验研究;Bahaj等[4-8]对水平轴潮流能水轮机叶轮功率系数、推力系数、叶片空化及翼型升力系数、压力系数分布等均进行了大量实验研究. 基于试验及模拟数据,国内外学者对翼型进行了优化研究;容亮湾[9]采用形函数及Fluent平台对水轮机翼型NACA0018进行了优化研究;董一帆等[10]应用Xfoil结合遗传算法,以高升阻比为目标优化设计了潮流能水轮机翼型并进行了计算流体动力学(computational fluid dynamics,CFD)分析;Grasso[11]基于梯度方法运用RFoil软件对水轮机翼型水动力性能进行了优化设计研究;朱国俊等[12]基于径向基神经网络−遗传算法对潮流能水轮机叶片翼型进行了优化,以径向基神经网络替代优化过程中的CFD分析,提高了优化效率. 虽然众学者在潮流能水轮机优化设计方面已经取得了一些研究成果,但翼型优化方法仍不完善,在空化性能优化方面的研究更少. Grasso[11]采用的梯度方法寻优结果准确性得不到保障,遗传算法虽极大提高了获得最优解的概率但迭代过程中的CFD分析过程耗时太多,优化效率低. 朱国俊等[12]采用径向基神经网络方法解决了优化效率问题,但对翼型空化性能未作考虑且最终优翼型性能仍需CFD分析.
本文以潮流能机叶片翼型NACA63-815为研究对象,以翼型水动力性能及压力系数最小值为优化目标,在优化迭代过程中通过程序调用XFoil软件对翼型压力系数最小值以及升阻比进行分析,替代CFD计算分析过程,提高翼型优化效率. 在优化翼型空化初生性能后,为验证优化翼型全空化性能是否得到提升,对优化翼型不同空化数下的空泡分布情况进行CFD分析[13],为进一步提升潮流能水轮机叶片性能提供一种可行方法.
1 基于XFoil的翼型动力学特性预测XFoil是美国学者Drela开发的一个为设计和分析亚音速飞机独立翼型的互动式程序,可以对一种已存的翼型的黏流(无黏流)进行分析[14]. 针对直接和逆混合模型,Drela[14]开发了一种结合Karman-Tsien可压缩性校正的无黏线性涡度面板方法. 采用两方程滞后耗散积分法表示黏性层,e9类放大公式确定过渡点求解层流和湍流层. 边界层和转换方程采用全局牛顿法与无黏流场同时计算求解.
本文以NACA638-15翼型为算例计算不同攻角下翼型升力系数与阻力系数值,翼型升力系数和阻力系数定义如下:
1)升力系数
| ${C_{\rm{L}}} = {F_{\rm{L}}}\left/\left( {\frac{1}{2}\rho {A_{\rm{f}}}{u^2}} \right),\right.$ | (1) |
2)阻力系数
| ${C_{\rm{D}}} = {F_{\rm{D}}}\left/\left( {\frac{1}{2}\rho {A_{\rm{f}}}{u^2}} \right).\right.$ | (2) |
式中:
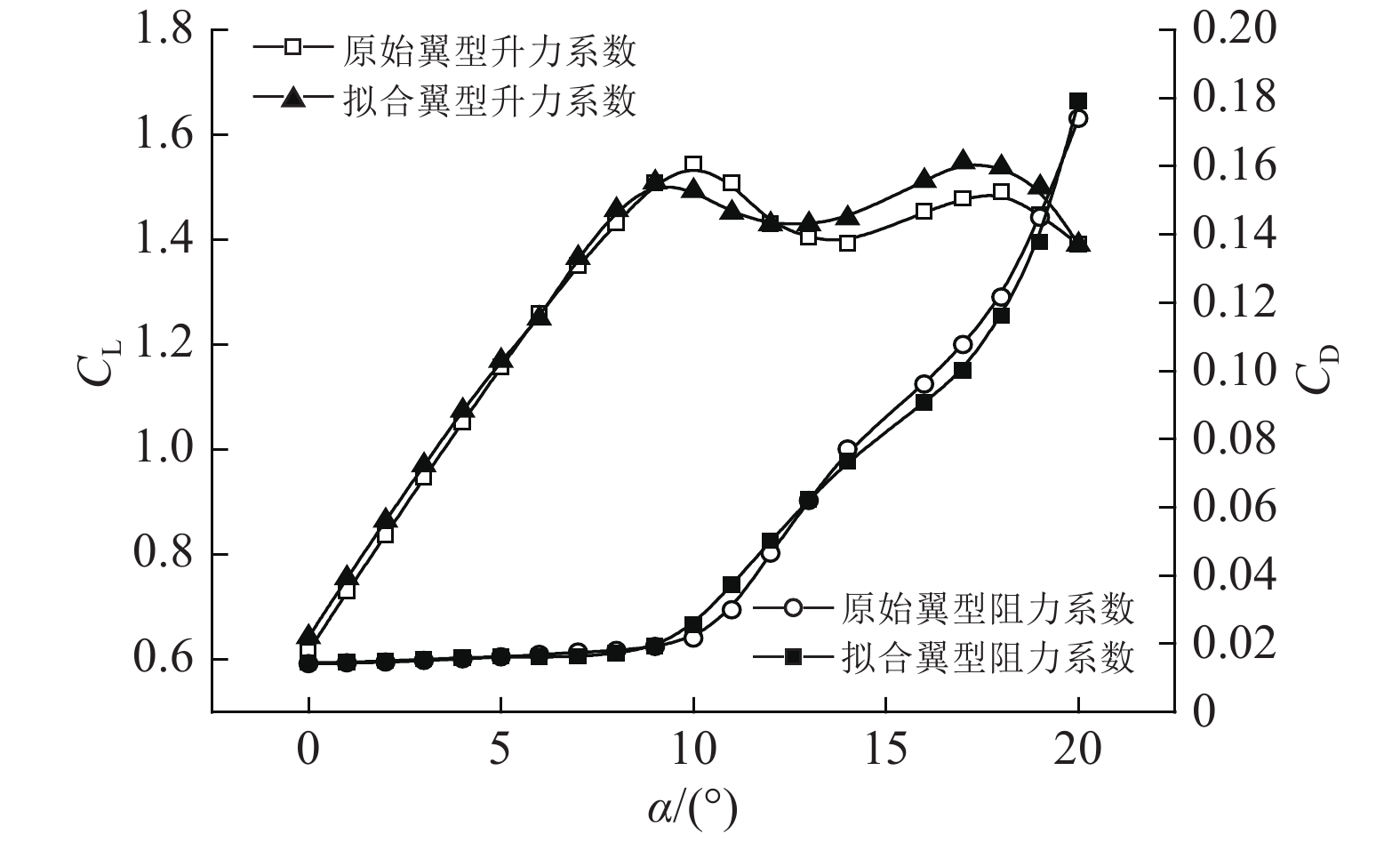
计算结果与试验对比如图1所示. 其中,α为翼型攻角. 计算结果表明,在升力系数的预测上(见图1),XFoil计算结果比实验值略小但大体上一致. 计算值比实验值略小的原因为实验所用NACA63-815翼型采用了上表面加厚,尾缘存在一定厚度,据文献[15]可知,上表面加厚翼型阻力系数较原翼型有所减小. 在阻力系数的预测上(见图1),XFoil计算值也与试验值吻合度较高. 文献[16]采用XFoil对NACA0018等其他用于潮流能水轮机的二维翼型的外特性参数进行预测,结果均表明XFoil能准确预测翼型的水动力特性参数.
|
图 1 NACA63-815翼型的XFoil验证 Fig. 1 XFoil verification for airfoil NACA63-815 |
翼型参数化方法主要有形状函数法、型函数扰动法、控制点法、CST方法及正交基函数法[17]. 本文采用几何表征能力较强的形状函数法对翼型进行参数化处理. 由于翼型形状复杂,直接对翼型进行函数拟合难度较大,特征参数较多且准确性得不到保证,对翼型进行形状变化后再进行参数化表征不仅可以提高拟合精度,还可以减少特征参数的数量. 本文先采用儒可夫斯基变换[18]对翼型进行形状变化,将复杂区域映射成简单区域,采用西奥道生法[18]及形状函数法拟合翼型. 本文采用该方法对翼型进行参数化处理,翼型曲线采用三角函数进行拟合. 采用式(3)、(4)对儒氏逆变换图形进行拟合,拟合翼型参数为
| $\begin{array}{c}{a_1} = - 0.054\,1,\;{b_1} = 0.135\,6,\\{a_2} \!=\! - 0.069\,8,\;{b_2} \!=\! - 0.038\,5,\\{a_3} \!=\! 0.030\,5,\;{b_3} \!=\! - 0.021\,1;\end{array}$ |
| ${z_{\rm c}} = 0.25\exp \;(\varphi (\theta ));$ | (3) |
| $\varphi \left( \theta \right) = \mathop \sum \limits_{i = 1}^{{n}} {{{a}}_1}{(1 - \cos \theta )^i} + \mathop \sum \limits_{j = 1}^m \,{b_1}{\sin ^j}\theta .$ | (4) |
式中:zc为复平面上拟圆函数形式,r为翼型在复平面中矢径的长度,θ为幅角.
对拟合函数曲线采用下式进行儒可夫斯基变换:
| $x = \left.\left(r + {0.25^2}\right/r\right)\cos\; \theta ,$ | (5) |
| ${{y}} = \left.\left(r - {0.25^2}\right/r\right)\sin\; \theta.$ | (6) |
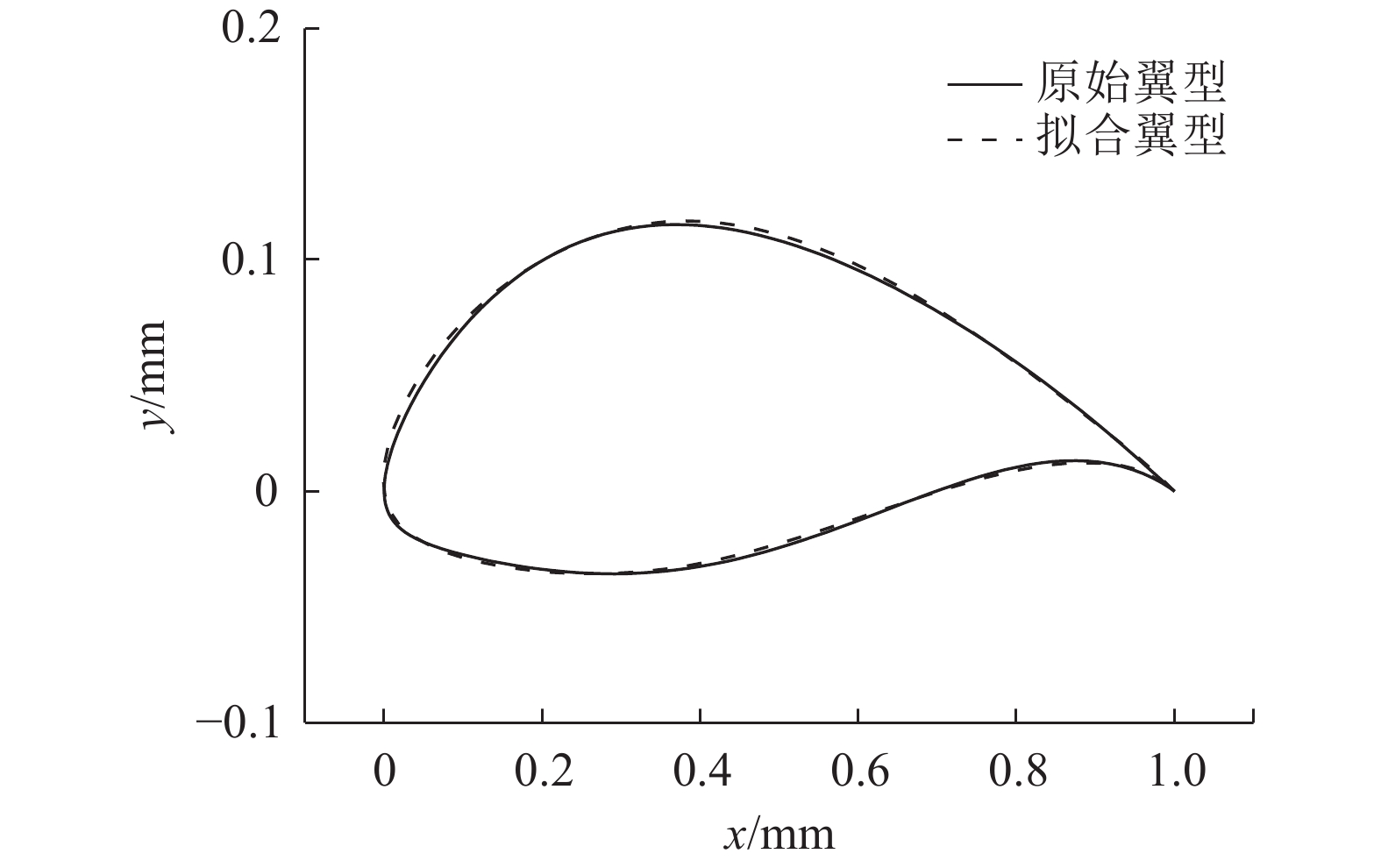
将ANCA63-815翼型函数表示成笛卡尔直角坐标系形式并与原翼型型函数进行对比,结果如图2所示.
|
图 2 原始翼型与优化翼型的几何对比 Fig. 2 Geometry comparison of initial and optimal airfoil |
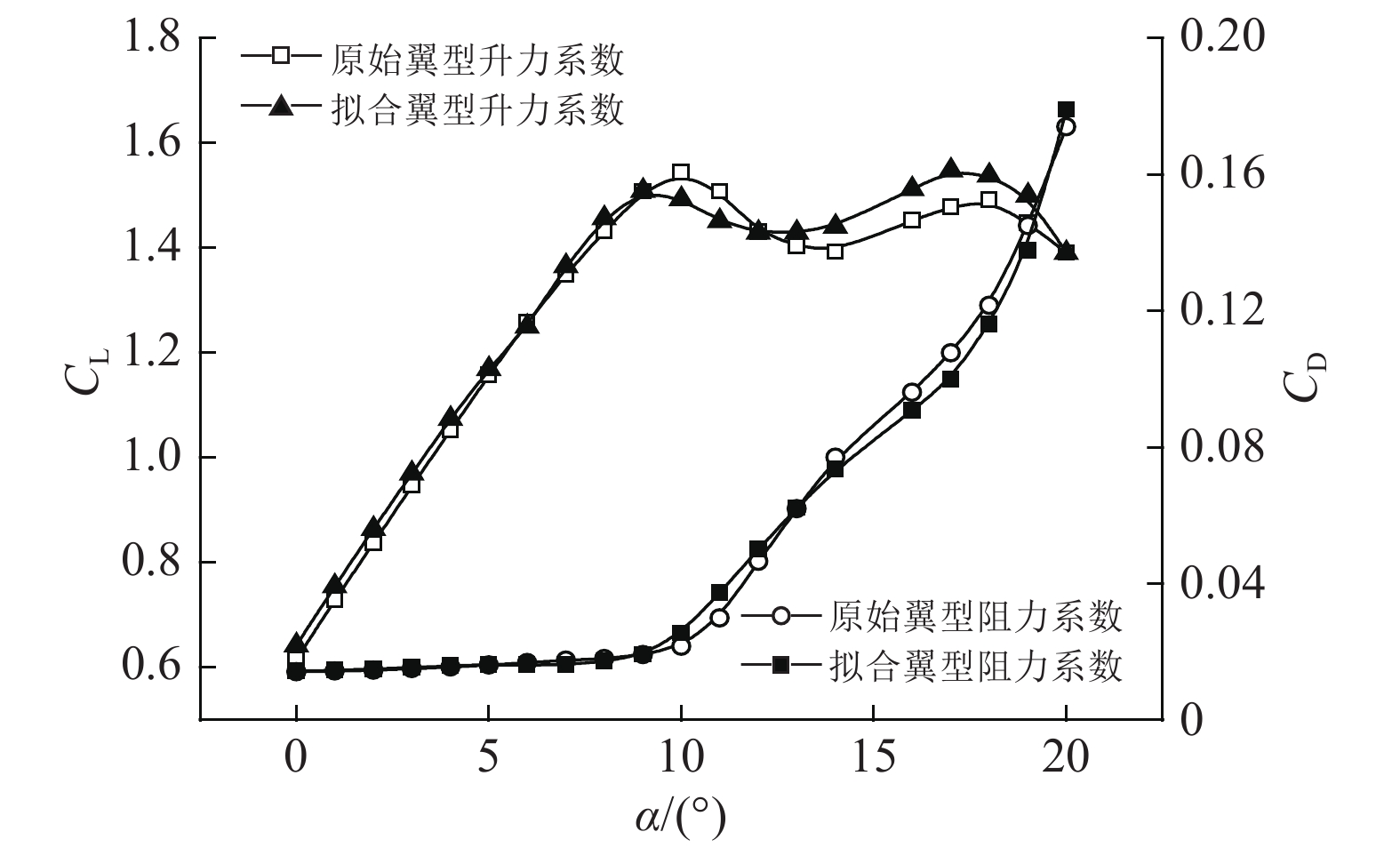
采用XFoil软件对拟合翼型进行升阻比特性预测并与原NACA63-815翼型进行对比. 升力系数与阻力系数对比如图3所示,从升力系数对比可以看出,在攻角小于8°时,拟合翼型与原翼型的升力系数值基本一致,在攻角大于10°的失速区域内,升力系数变化趋势基本一致,数值上存在一定误差,但考虑到本研究仅采用3阶三角级数对翼型进行拟合,精度上存在一定不足,误差在可接受范围内;从阻力系数对比上看出,拟合翼型与原始翼型基本一致. 综上,拟合翼型与原翼型的水动力特性基本保持一致,故采用此拟合翼型代替原翼型是可行的.
|
图 3 原始翼型与拟合翼型的水动力性能对比 Fig. 3 Hydrodynamic performance comparison of initial and fitting airfoil |
粒子群算法(particle swarm optimization, PSO)是近年来由Kennedy等[19]开发的一种新的进化算法,具有容易、精度高、收敛快等优点. PSO在六维空间中从粒子i当前位置
本研究中NACA63-815翼型多目标优化函数为
| $\begin{split}f{\rm{(}}X{\rm{)}} =& - {\rm{0}}{\rm{.2}}{C_{{\rm{pmin}}}}/4.2 - {\rm{0}}{\rm{.4}}{C^{6.8}_{\rm L}}{\rm{/1}}{\rm{.5}} - \\&{\rm{0}}{\rm{.4}}{C^{6.8}_{\rm L}}{\rm{/}}{C^{6.8}_{\rm D}}{\rm{/100}}.\end{split}$ | (7) |
式中:
目标函数包含翼型升力系数、升阻比系数、压力系数最小值. 升阻比系数代表翼型工作效率,是最能反映翼型性能的指标. 为防止在翼型升阻比增加时升力系数下降,将升力系数作为其中一个优化目标. 同时为了提升翼型空化性能,将压力系数最小值也作为优化目标. 本文采用基于PSO的最小值优化,而压力系数最小值为负值,故对压力系数最小值取相反数建立目标函数. 同理,对升力系数及升阻比也取相反数. 水动力性能为翼型的主要性能参数,故对优化对象的权重分配如下:升力系数为40%,最大升阻比系数为40%,压力系数最小值为20%. 此权重也可根据实际需要进行调整,获得最适应于各个工况的最优翼型.
3.2 优化参数界定及优化流程为保证优化后的翼型仍以原始NACA63-815翼型为基础,需要对优化参数的范围进行控制. 此外,界定参数范围可以避免在优化过程中翼型发生严重畸变导致优化失败. 优化参数以表1为基础,上、下边界最大浮动不超过25%.
在通过随机函数确定种群初始速度vi后,粒子i的进化方程如下:
| $\begin{aligned}{v_{ij}}^{k + 1} = {v_{ij}}^k + {{{C}}_1}{r_{1j}}({P_{ij}} - {x_{ij}}^k) + {{{C}}_2}{r_{2j}}({P_{ij}} - {x_{ij}}^k),\end{aligned}$ | (8) |
| ${x_{ij}}^{k + 1} = {x_{ij}}^k + {v_{ij}}^{k + 1}.$ | (9) |
式中:i为个体,j为搜索空间;C1、C2为迭代加速度,本文均设置为1.494 45;
|
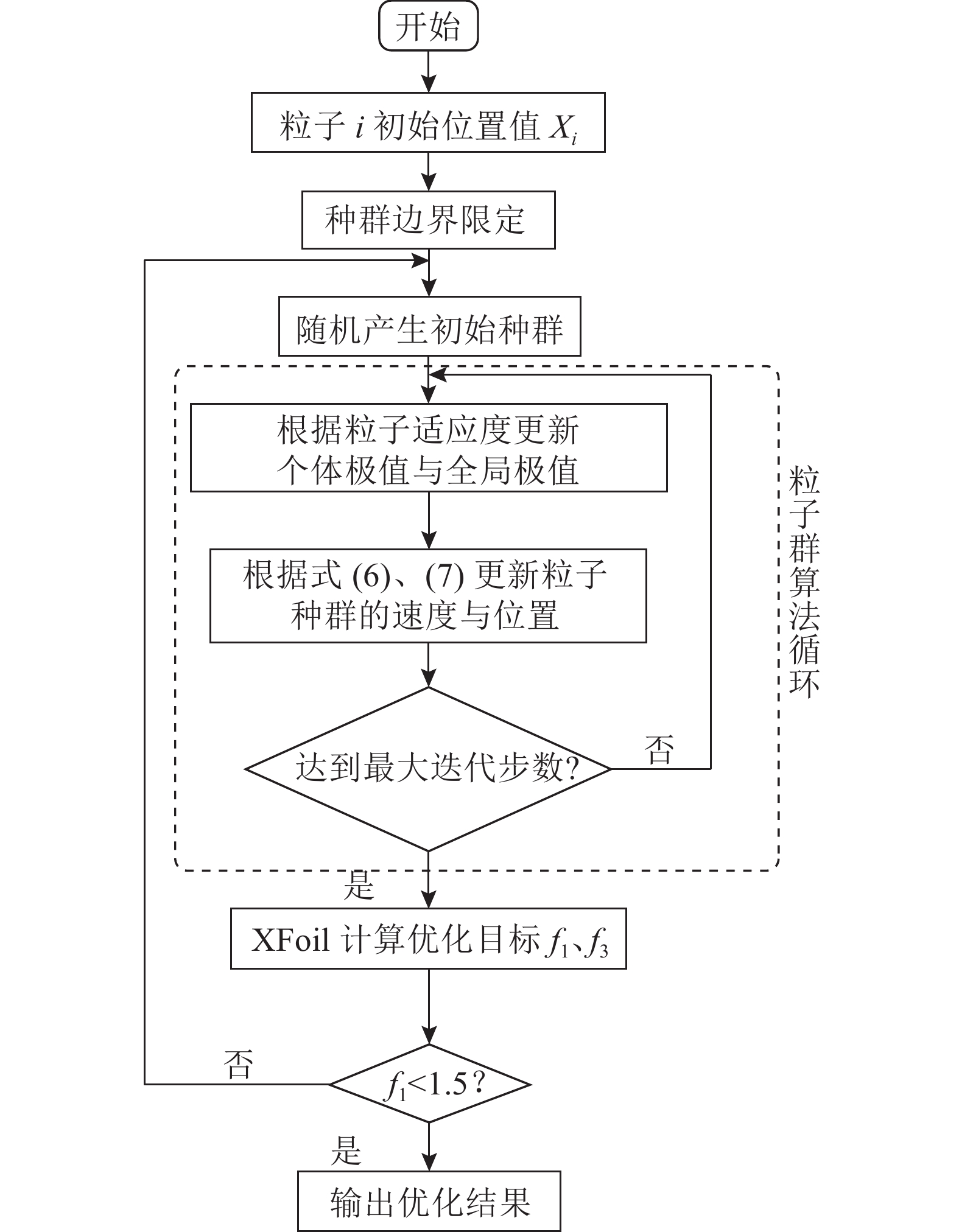
图 4 翼型多目标优化流程图 Fig. 4 Flow chart of airfoil multi-objective optimization |
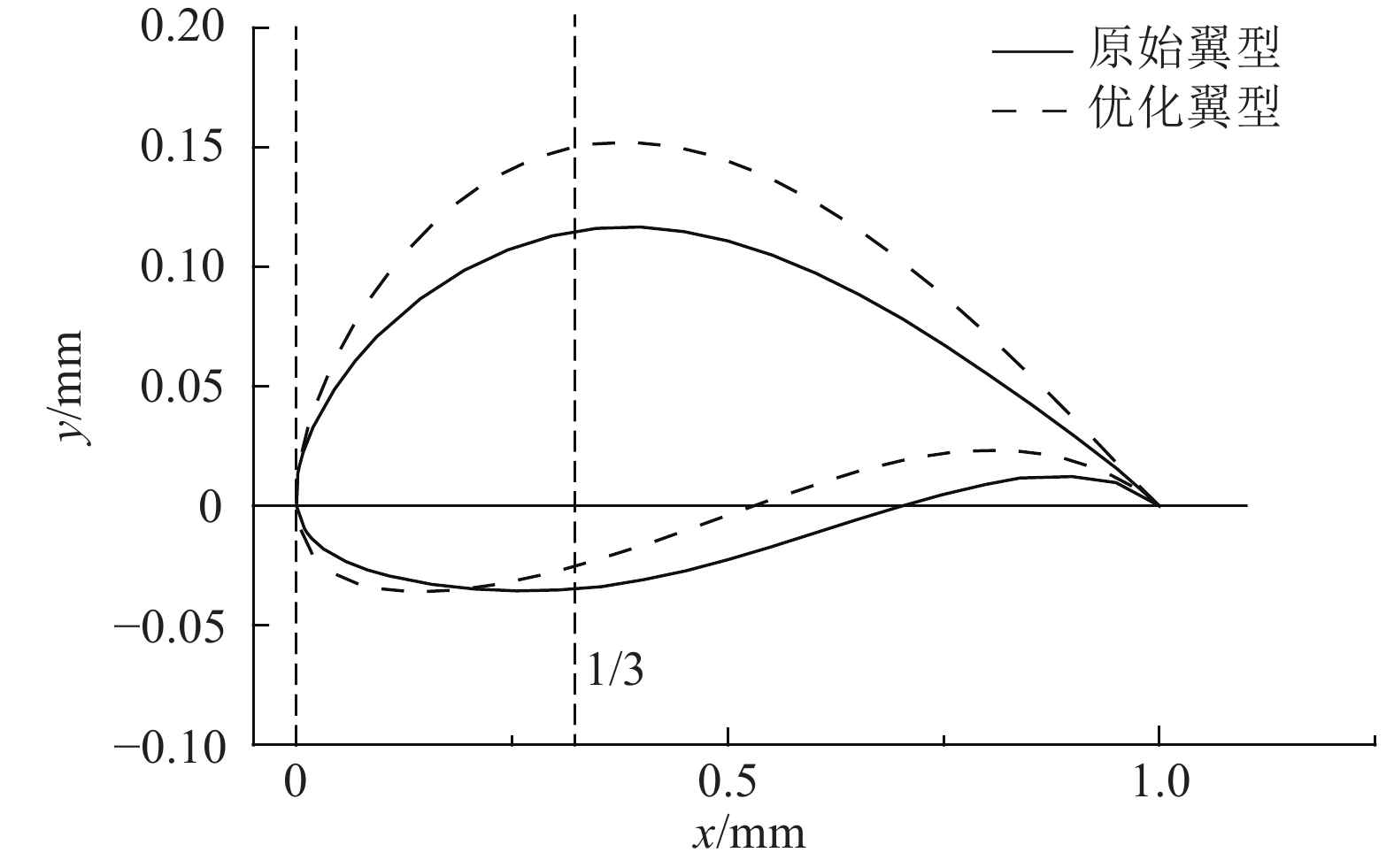
优化翼型的型函数曲线与原NACA63-815翼型的型函数曲线对比如图5所示. 在翼型前缘位置,优化翼型在滞止点下部出现了较为明显的外凸. 从弦长1/3直至翼型尾缘处,在压力面出现了较大的内凹. 优化翼型在整个吸力面出现了较大程度的加厚,翼型吸力面形状较原翼型凸起弧度更大,翼型最大厚度明显增加.
|
图 5 NACA63-815翼型与优化翼型的几何对比 Fig. 5 Geometry comparison of airfoil NACA63-815 and optimal airfoil |
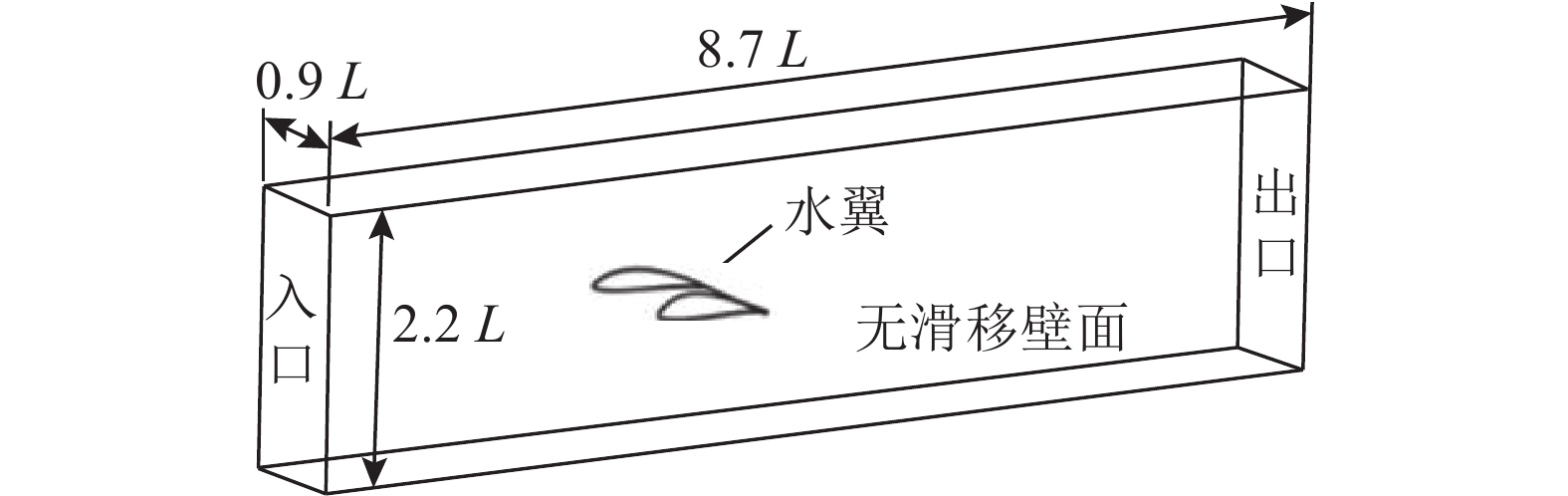
为了分析原翼型及优化翼型表面压力系数分布和空泡形态分布,本文对原翼型及优化翼型进行CFD计算分析. 为使计算分析数据能与实验值对比,计算域及边界条件按照文献[7]设定. 翼型弦长L=230 mm,翼展为210 mm,流场区域尺寸如图6所示. 入口距翼型前缘为3.2L,出口距翼型尾缘为5.5L,进口边界条件为进口速度
|
图 6 NACA63-815和优化翼型计算域及边界条件 Fig. 6 Computational domain and boundary conditions of airfoil NACA63-815 and optimal airfoil |
为使网格贴合翼型前缘形状,对翼型采用C型结构化网格划分,对翼型表面及翼型上部空泡区域进行网格加密,网格总数约为3.87×106,近壁面网格如图7所示. 计算结果显示无量纲数y+在0~15,满足SST k-ω湍流模型壁面函数计算要求.

|
图 7 NACA63-815翼型近壁面网格划分策略 Fig. 7 Near wall meshing strategy of airfoil NACA63-815 and optimal airfoil |
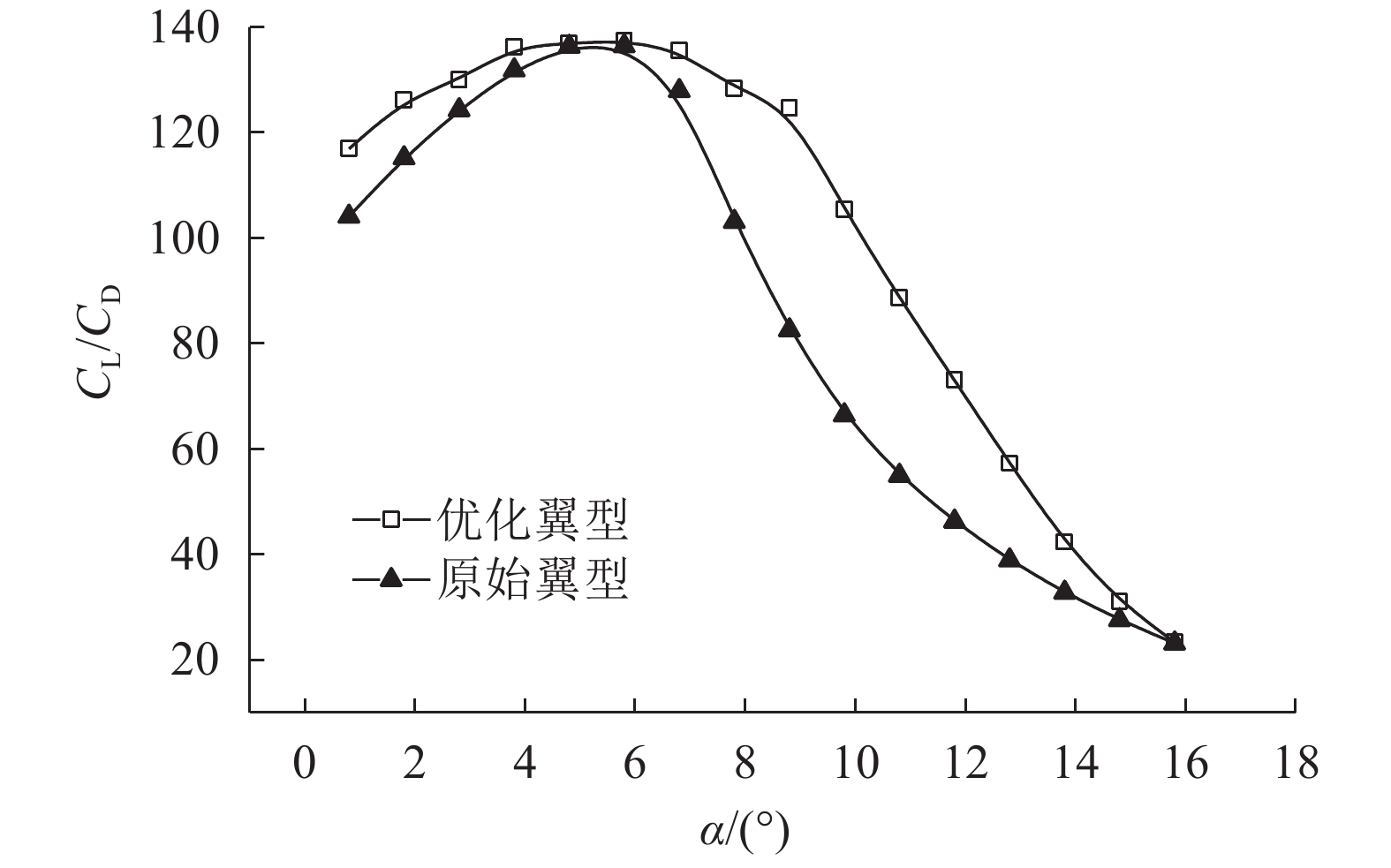
通过CFD分析计算,表1中给出了主要研究工况及1个小攻角工况下的性能数据对比. 优化翼型升阻比系数在3个工况下均大于原始翼型. 优化翼型在攻角为2.8°、6.8°和10.8°时升阻比系数分别提高了24.5%、6.0%和61.1%,全攻角范围内原翼型与优化翼型的升阻比系数对比如图8所示. 压力系数最小值在小攻角下比原翼型略低,但在小攻角下压力系数分布平缓,无明显峰值,故对空化性能影响较小. 优化攻角下压力系数最小值均得到有效优化. 优化翼型在攻角为2.8°、6.8°和10.8°时压力系数最小值分别提高了−6.5%、17.0%和45.8%.
|
图 8 优化翼型与原始翼型的水动力性能对比图 Fig. 8 Hydrodynamic performance comparison of initial airfoil and optimal foil |
| 表 1 优化前、后的翼型性能对比 Table 1 Comparison of hydrofoil’s performance before and after optimization |
为了更为详细对比优化翼型与原翼型的表面压力系数,定义无量纲压力系数Cp和空化数σ [20]:
| ${C_{\rm{p}}} = \frac{{{p_{\rm L}} - {p_0}}}{{0.5\rho u_\infty ^2}},$ | (10) |
| $\sigma = \frac{{{p_0} - {p_{\rm v}}}}{{0.5\rho u_\infty ^2}}.$ | (11) |
式中:
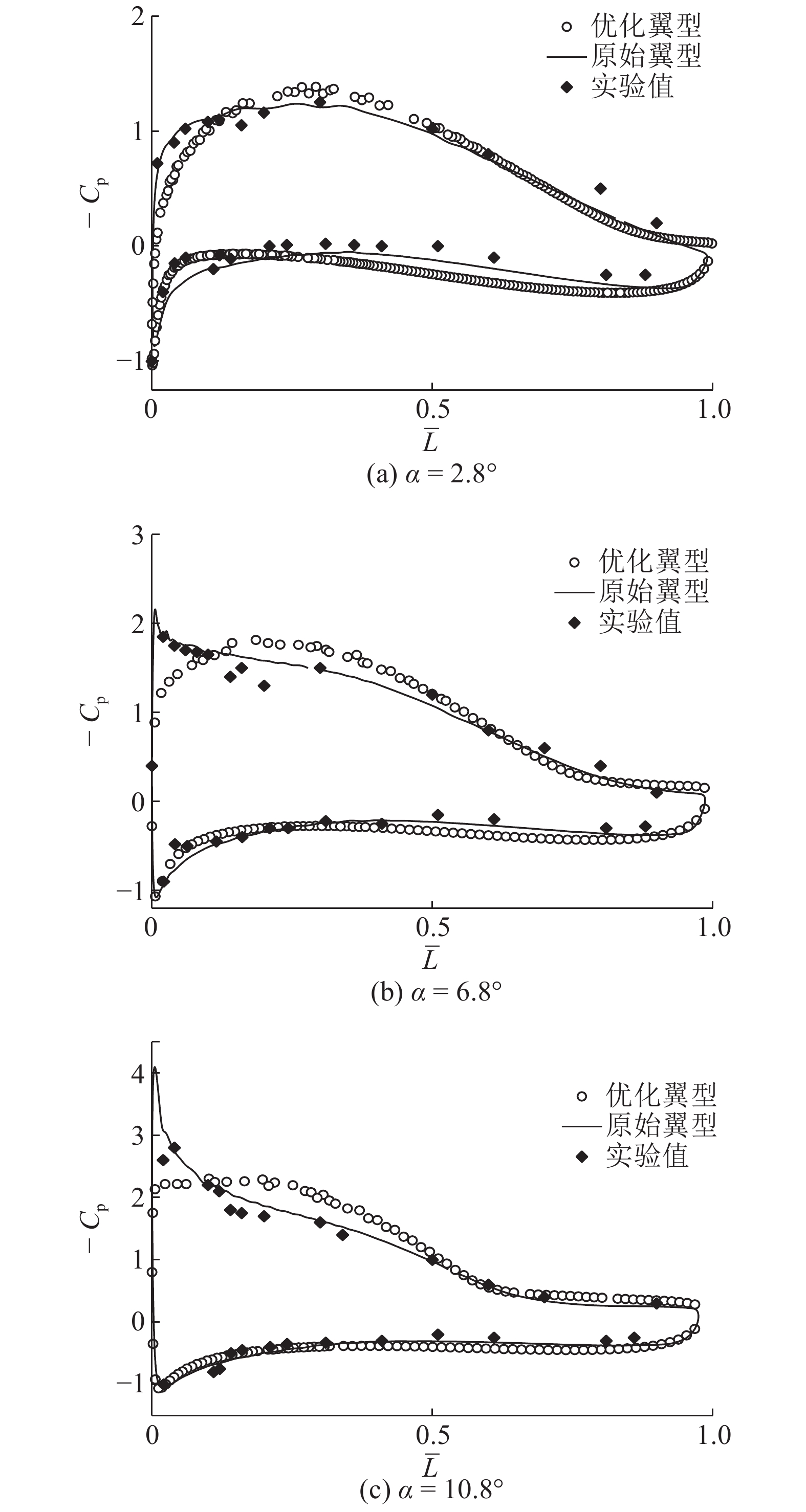
分别计算优化翼型与原翼型在σ=12工况下3个攻角的压力系数分布,并与文献[5]中的实验值进行对比,如图9所示. 图中,
|
图 9 不同攻角下的翼型表面压力系数对比 Fig. 9 Contrast of pressure coefficients of hydrofoil surface under different angles of attack |
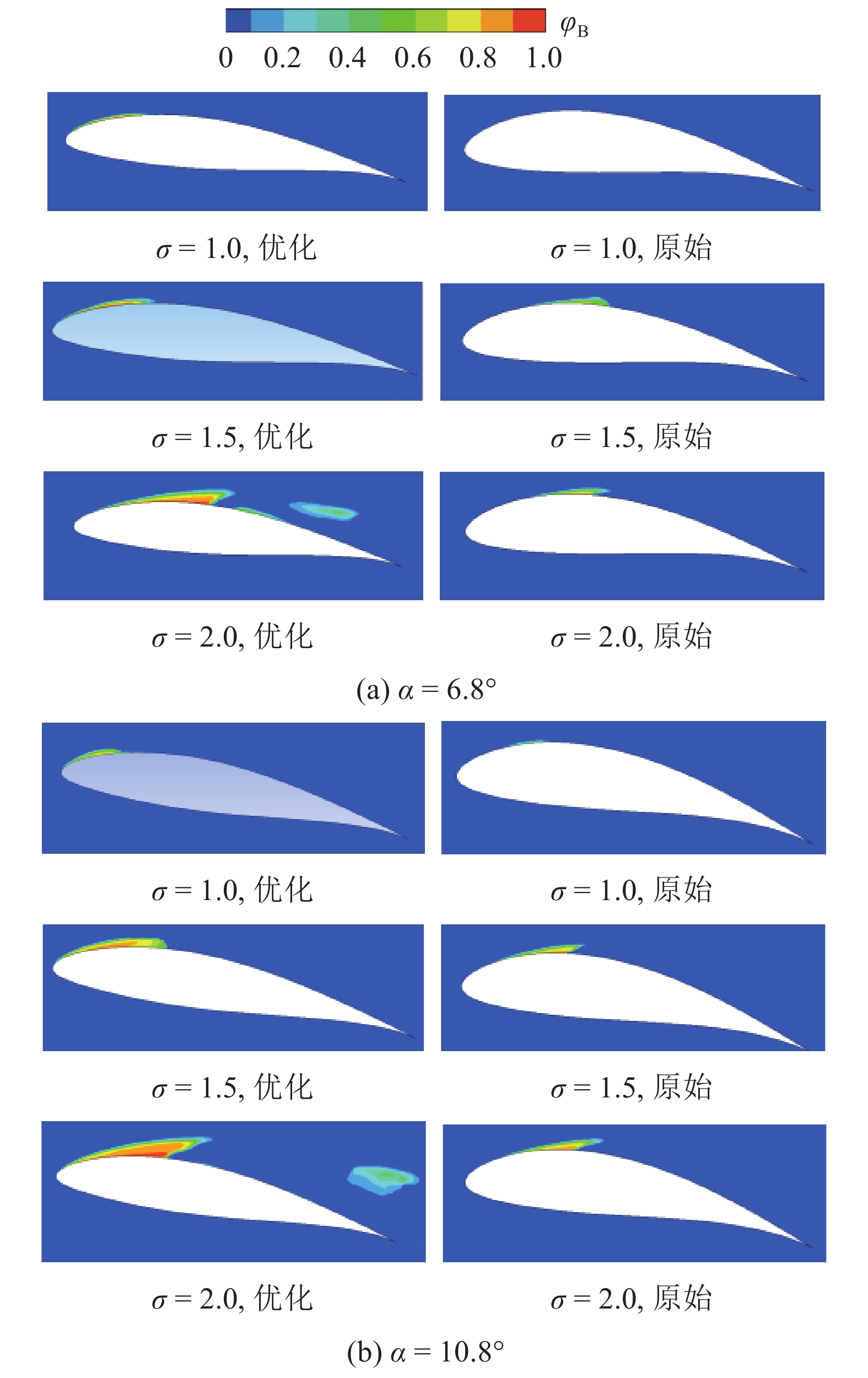
优化翼型在攻角为6.8°和10.8°时在3个不同空化数下的CFD计算结果的空泡分布如图10所示. 图中,φB为气体与水的体积比. CFD后处理时建立空气体积等值面用于表示空化区域. 当α=6.8°且σ=2.0时,可以看出原始翼型在吸力面从翼型前缘开始至相对弦长大约1/4处形成较薄表面附着空化,而优化翼型在吸力面相对弦长1/3处发生较小范围的空化. 当α=6.8°时,σ=1.5时的空泡分布情况与σ=2.0相似,翼型表面空泡体积增大;σ=1.0时可以明显看出原始翼型表面附着空泡体积较优化翼型更大,且原始翼型吸力面的空泡出现更加明显的不稳定性,空泡被较大逆压梯度切断开始脱落. 当α=10.8°时,原始翼型与优化翼型在3个空化数下的空泡对比与α=6.8°时较为类似,优化翼型仍表现出较好的空化性能.
|
图 10 不同攻角及不同空化数下的空泡分布对比 Fig. 10 Comparison of cavitation distribution with different cavitation numbers under different angles of attack |
(1)采用形状函数法并结合儒可夫斯基变换及西奥道生思想对NACA63-815翼型进行参数化处理,拟合翼型与原翼型具有基本一致的水动力性能及几何形状,证明了此参数化方法的可行性及正确性.
(2)结合实验数据,以一定攻角翼型性能参数为优化对象建立多目标优化函数. 通过程序调用XFoil对优化过程中翼型性能进行监测,节省了优化时间. CFD计算结果表明,优化翼型水动力性能在攻角为2.8°、6.8°和10.8°时分别提升了24.5%、6.0%和61.1%,水动力性能得到有效改善.
(3)CFD对空化性能的分析表明,小攻角下空化性能无明显改变,但优化翼型在攻角为6.8°和10.8°时的压力系数最小值分别提升17.0%和45.8%,吸力面压力系数分布过度平滑,无峰值,空化初生性能得到明显改善. 当空化数为1.0、1.5和2.0时,优化翼型的空泡体积较原始翼型明显减小,空化形态更稳定,验证了本文提出的翼型优化方法的可行性.
| [1] |
徐超. 基于格子Boltzmann方法的海流能水轮机翼型叶片水动力特性研究[D]. 山东: 中国海洋大学, 2010. XU Chao. Research on hydrodynamics of marine current turbine’s hydrofoil blades based on lattice Boltzmann method [D]. Shandong: Ocean University of China, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10423-1011029195.htm |
| [2] |
王英英. 基于格子Boltzmann方法的海流能水轮机大雷诺数模拟研究[D]. 山东: 中国海洋大学, 2011. WANG Ying-ying. Research on lattice boltzmann simulation on high Reynolds number flow around marine current turbine [D]. Shandong: Ocean University of China, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10423-1011229124.htm |
| [3] |
GOUNDAR J, AHEMD M. Design of a horizontal axis tidal current turbine[J]. Applied Energy, 2013, 111(11): 161-174. |
| [4] |
BAHAJ A, MOLLAND A, CHAPLIN J, et al. Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank[J]. Renewable Energy, 2007, 32(3): 407-426. DOI:10.1016/j.renene.2006.01.012 |
| [5] |
BAHAJ A, MOLLAND A, CHAPLIN J, et al. Measurements and predictions of forces, pressures and cavitation on 2-D sections suitable for marine current turbines[J]. Journal of Engineering for the Maritime Environment, 2004, 218(2): 127-138. |
| [6] |
BATTEN W, BAHAJ A, MOLLAND A, et al. The prediction of the hydrodynamic performance of marine current turbines[J]. Renewable Energy, 2008, 33(5): 1085-1096. DOI:10.1016/j.renene.2007.05.043 |
| [7] |
BATTEN W, BAHAJ A, MOLLAND A, et al. Experimentally validated numerical method for the hydrodynamic design of horizontal axis tidal turbines[J]. Ocean Energy, 2007, 34(7): 1013-1020. DOI:10.1016/j.oceaneng.2006.04.008 |
| [8] |
BAHAJ A, BATTEN W, MCCANN G. Experimental verifications of numerical predictions for the hydrodynamic performance of horizontal axis marine current turbines[J]. Renewable Energy, 2007, 32(15): 2479-2490. DOI:10.1016/j.renene.2007.10.001 |
| [9] |
容亮湾. 水轮机叶片水动力分析及翼型优化[D]. 哈尔滨: 哈尔滨工程大学. 2006. RONG Liang-wang. Hydrodynamics analysis and airfoil optimization of turbine s blades [D]. Harbin: Harbin Engineering University. 2006. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y936405 |
| [10] |
董一帆, 李晔, 戴泽霖. 水平轴潮流能水轮机优化设计[C] // 中国力学大会: 2015论文摘要集. 上海: CCTAM, 2015. DONG Yi-fan, LI Ye, DAI Ze-lin. Optimal design of a horizontal axis marine current turbine [C] // The Chinese Congress of Theoretical and Applied Mechanics. Shanghai: CCTAM, 2015. |
| [11] |
GRASSO F. Design and optimization of tidal turbine airfoil[J]. Journal of Aircraft, 2012, 49(2): 636-643. DOI:10.2514/1.C031617 |
| [12] |
朱国俊, 冯建军, 郭鹏程, 等. 基于径向基神经网络-遗传算法的海流能水轮机叶片翼型优化[J]. 农业工程学报, 2014, 30(8): 65-73. ZHU Guo-jun, FENG Jian-jun, et al. Optimization of hydrofoil for marine current turbine based on radial basis function neural network and genetic algorithm[J]. Journal of Agricultural Engineering, 2014, 30(8): 65-73. DOI:10.3969/j.issn.1002-6819.2014.08.008 |
| [13] |
王宁, 黄彪, 吴钦, 等. 绕水翼空化流动及振动特性的试验与数值模拟[J]. 排灌机械工程学报, 2016, 34(4): 321-327. WANG Ning, HUANG Biao, WU Qin, et al. Experimental and numerical simulation of vibration characteristics of hydrofoil in cavitating flow[J]. Journal of Drainage and Irrigation Machinery Engineering (JDIME), 2016, 34(4): 321-327. |
| [14] |
DRELA M. XFOIL: an analysis and design system for low Reynolds number airfoils[J]. Lecture Notes in Engineering, 1989, 54: 1-12. DOI:10.1007/978-3-642-84010-4 |
| [15] |
李仁年, 陈寅. 尾缘厚度对风力机翼型气动性能的影响[J]. 流体机械, 2012, 40(4): 13-15. LI Ren-nian, CHEN Yin. Effect of trailing edge thickness on aerodynamic performance[J]. Fluid Machinery, 2012, 40(4): 13-15. DOI:10.3969/j.issn.1005-0329.2012.04.004 |
| [16] |
GOUNDAR J, AHMED M, LEE Y. Numerical and experimental studies on hydrofoils for marine current turbines[J]. Renewable Energy, 2012, 42(1): 173-179. |
| [17] |
陈进, 张石强, EECEN, 等. 风力机翼型参数化表达及收敛特性[J]. 机械工程学报, 2010, 46(10): 132-138. CHEN Jin, ZHANG shi-qiang, EECEN, et al. Parametric representation and convergence of wind turbine airfoils[J]. Chinese Journal of Mechanical Engineering, 2010, 46(10): 132-138. |
| [18] |
蒋传鸿. 风力机结冰翼型的气动性能分析及优化设计[D]. 重庆: 重庆大学, 2014. JIANG Chuan-hong. Aerodynamic performance analysis and optimization design of wind turbine with iced airfoil [D]. Chongqing: Chongqing University, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D511367 |
| [19] |
KENNEDY J, EBERHART R. Particle swarm optimization [C] // International Conference on Neural Networks. Perth: IEEE, 1995: 1942-1948.
|
| [20] |
李仁年, 毕祯, 黎义斌, 等. 诱导轮偏转角对离心泵叶轮空化性能的影响[J]. 排灌机械工程学报, 2016, 34(6): 461-469. LI Ren-nian, BI Zhen, LI Yi-bin, et al. Effect of finducer deflection angle on impeller cavitation performance in centrifugal pump[J]. Journal of Drainage and Irrigation Machinery Engineering(JDIME), 2016, 34(6): 461-469. |


