2. 江苏省水利勘测设计研究院有限公司,江苏 扬州 225127
2. Jiangsu Surveying and Design Institute of Water Resources Co. Ltd, Yangzhou 225127, China
光纤传感器由于具有体积小、重量轻、抗电磁干扰、抗腐蚀等优越特性,且具有分布式、连续式监测和远程实时监测的潜力,近年来在土木工程结构健康监测领域倍受关注. 对光纤传感器的研究和应用多集中在石英光纤方面,最具代表性的是光纤光栅技术[1-5]. 然而石英光纤在实际应用中易发生断裂,应用能力受到了很大限制. 相比之下,塑料光纤(plastic optical fiber,POF)具有较高的断裂韧性,不仅弥补了石英光纤的不足,且具有纤芯直径大、韧性良好、可塑性高、成本低等优势. 目前,POF在结构健康监测方面的应用研究尚处于起步阶段. Liehr等[6]总结了分布式POF应变传感器在土工和砌体结构中的应用,通过模型试验探测并评估了POF对土体变形和砌体结构裂缝的监测效果. Zhang等[7]对埋入POF的土样进行了不同围压的拉拔试验,并结合试验结果导出了评估POF变形监测能力的公式,表明在不发生塑性变形的前提下,POF适用于监测土体变形. Luo等[8]通过对掺高活性粉体的混凝土梁进行四点弯曲试验分别验证了埋入式和表面粘贴式POF的裂缝监测能力. 笔者等[9-12]通过裂缝模拟试验分别验证了POF和裂缝呈不同夹角下不同直径POF的裂缝监测性能,并利用多项式回归和权值分配推导了裂缝开度预测模型.
在将POF应用于混凝土结构监测时,需要将其与被测混凝土结构通过一定的方式进行结合. 结合方式主要有2种:直接埋入式和表面粘贴式. 其中,直接埋入式是在工程的施工期直接将光纤传感器埋入结构内部,此布设方式下的光纤传感器可以全面地对施工期及运行期结构内部变形情况进行监测. 在结合后形成的多相材料复合体中,POF与混凝土之间需要具有良好的应变传递关系. 当混凝土结构在内外因素作用下发生变形时,良好的应变传递关系可以使POF与混凝土协调变形,从而实现POF对混凝土局部变化的力学感知.
关于埋入式石英光纤传感器与被测结构之间的应变传递关系,国内外学者开展了一些研究. Pak[13]研究了远场剪应力作用下,埋入式光纤与基体间的应变传递关系,以及涂覆层厚度和弹性模量对应变传递系数的影响. Ansari等[14]利用剪滞理论并假设粘贴段光纤中点的应变与涂覆层及基体的应变相同,得出了埋入式光纤轴向应变与基体真实应变关系的表达式及剪应力分布. Li等[15]对文献[14]的研究进行了扩展,在分析中假定涂覆层为理想弹塑性材料,从而计入了涂覆层塑性阶段的影响,修正了应变传递系数,扩大了其适用范围. 李东升等[16]在研究埋入式光纤光栅的应变感知原理时,进一步修正了文献[14]对粘贴段光纤中点应变与涂覆层及基体应变相同的假定,认为纤芯与涂覆层的应变梯度相同,从而给出了更合理的光纤与基体间应变传递的关系式. Sun等[17]考虑了温度变化和非轴向应力,进一步完善了文献[16]的研究. 吴永红等[18]推导了光纤光栅封装结构的应变传递关系,从而建立了光纤光栅标准化埋入式封装设计的理论模型. 吴入军等[19]建立了埋入式光纤布拉格光栅应变传递函数,并研究了传递函数各参数对测量应变的影响. 周智等[20]研究了埋入混凝土结构的光纤应变传感器的长期使用性能. Her等[21]通过Mach-Zehnder干涉试验研究了光纤埋设长度和涂覆层对应变的影响.
关于埋入式POF与被测结构之间的应变传递关系相关研究较少,常新龙等[22-23]研究了应用于固体火箭发动机壳体应变监测的聚合物光纤传感器,建立了基于线性粘弹性的埋入式聚合物光纤应变传递模型并分析了影响参数.
本文将推导埋入式塑料光纤与混凝土基体间的应变传递模型,并通过数值仿真加以验证,然后对模型中的主要参数进行敏感性分析,探索利于应变传递的参数组合.
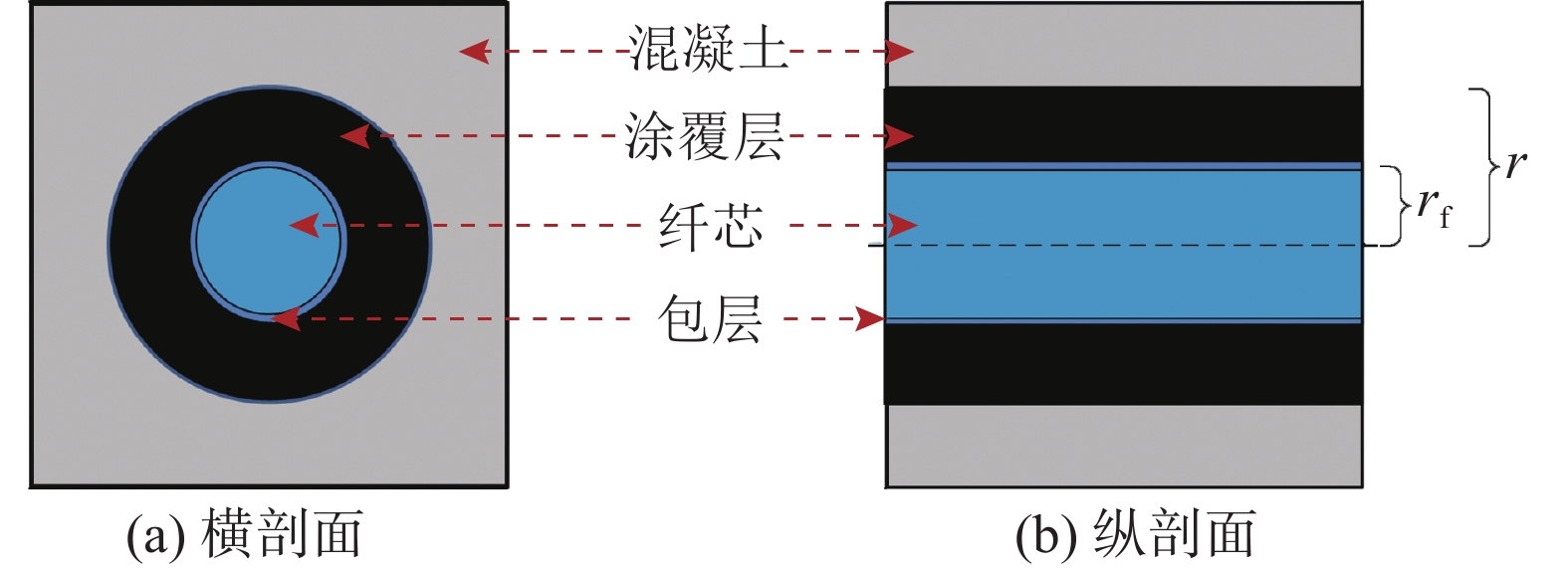
1 应变传递分析POF以光学塑料为材料,内部结构包括纤芯和包层. 在实际应用时外部需要间隔一层涂覆材料,以避免POF纤芯与混凝土直接接触,在使用过程中遭到损坏. 间隔材料为一种低弹模塑料保护层,其与POF纤芯之间存在材料差异性. 当POF−混凝土复合体中混凝土受力产生应变时,混凝土上的应变需要通过间隔材料传递至POF纤芯,材料差异必然对混凝土与POF纤芯之间的应变传递有一定影响. 埋入式POF与混凝土组成的多相材料复合体的横、纵剖面图如图1所示. 图中,rf为POF纤芯半径,r为带涂覆层纤芯的半径(纤芯半径与凃覆层厚度之和)
|
图 1 埋入式塑料光纤(POF)−混凝土复合体横、纵剖面图 Fig. 1 Transverse and longitudinal sections of embedded plastic optical fiber (POF)-concrete complex |
在分析埋入式POF与混凝土之间应变传递关系之前,先进行以下几点假定:
1)假定各层材料均为线弹性材料,混凝土层仅受POF轴线方向的外力作用,混凝土层通过传递切应力使POF纤芯层产生应变,涂覆层和纤芯层不直接承受外力.
2)假定POF纤芯与包层的机械性质相同. 由于POF包层厚度远小于纤芯直径,包层可视为纤芯的一部分. 相较于石英光纤,此假定对于POF更合理.
3)假定混凝土与涂覆层间、涂覆层与纤芯间交界面结合情况良好,无相对滑移.
以下分析过程中,下标f代表POF的纤芯,下标c代表POF的涂覆层,下标m代表混凝土,总的光纤埋设长度为
根据图1中POF−混凝土复合体横剖面呈对称性的特点,取横剖面的1/4、长度为
|
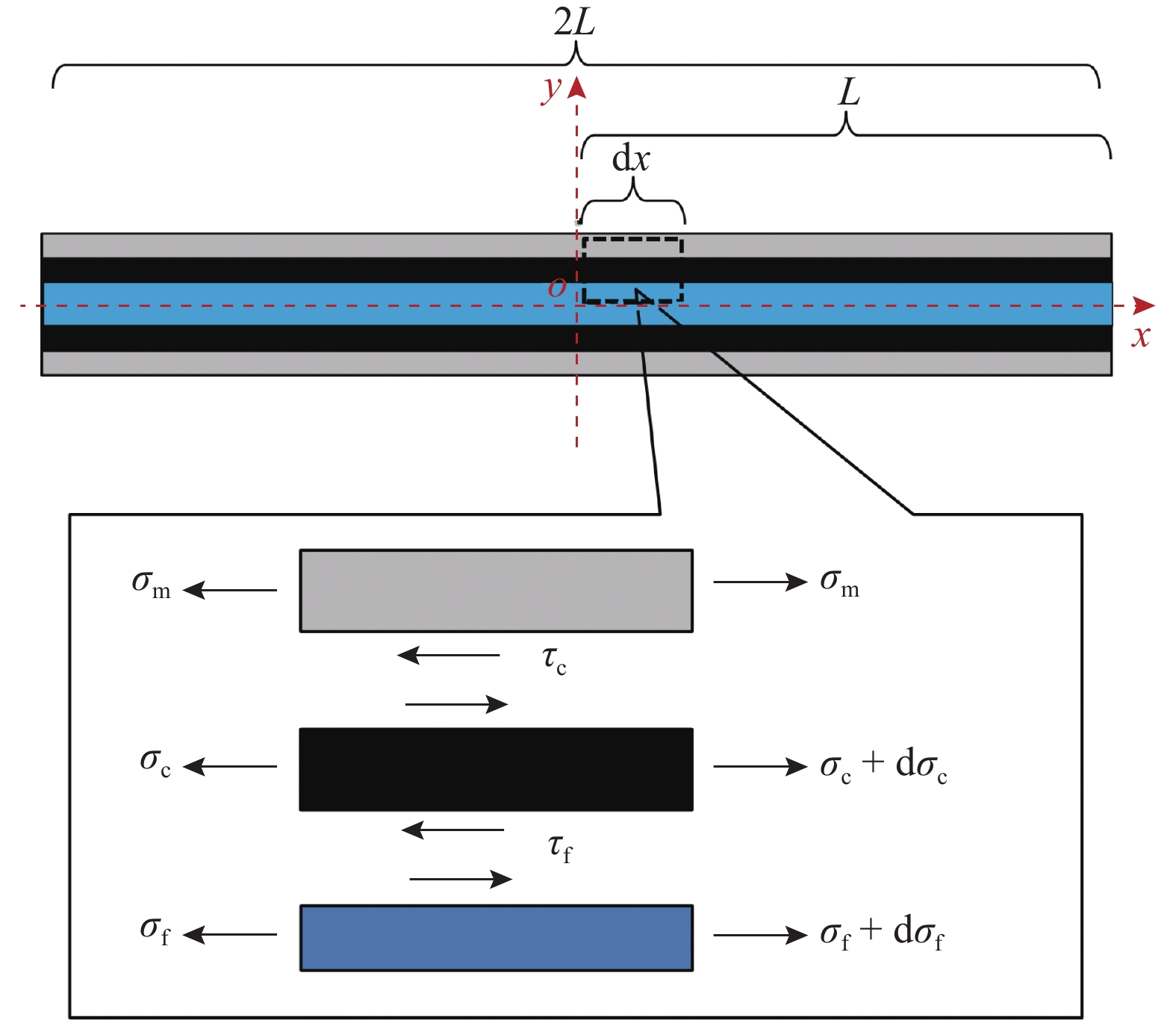
图 2 直接埋入式POF−混凝土复合体各相材料间的应力分布 Fig. 2 Stress distribution between material layers within embedded POF-concrete complex |
根据图2中POF纤芯段的受力情况,列其轴(
| $\frac{1}{2}\text{π} r_ {\rm{f}}^2{\sigma _ {\rm{f}}} = \text{π}{ r_ {\rm{f}}}{\tau _ {\rm{f}}}{\rm{d}}x + \frac{1}{2}\text{π} r_ {\rm{f}}^2({\sigma _ {\rm{f}}} + {\rm{d}}{\sigma _ {\rm{f}}}), $ | (1) |
可以得出
| $\frac{{{\rm{d}}{\sigma _ {\rm{f}}}}}{{{\rm{d}}{x} }} = - \frac{{2{\tau _ {\rm{f}}}}}{{{ r_ {\rm{f}}}}}. $ | (2) |
同样对涂覆层任一半径为r的部分列轴向力的平衡方程:
| $\begin{split} \frac{1}{2}\text{π} &({r} ^2 - r_ {\rm{f}}^2){\sigma _ {\rm{c}}} + \text{π}{ r_ {\rm{f}}}{\tau _ {\rm{f}}}{\rm{d}}x = \\ & \frac{1}{2}\text{π}({r} ^2 - r_ {\rm{f}}^2{)(}{\sigma _ {\rm{c}}} + {\rm{d}}{\sigma _ {\rm{c}}}) + \text{π}{r} \tau {\rm{d}}x ,\end{split} $ | (3) |
可以得出
| $\tau = \frac{{{ r_ {\rm{f}}}{\tau _ {\rm{f}}}}}{{r} } - \frac{{{r} ^2 - r_ {\rm{f}}^2}}{{2{r} }}\frac{{{\rm{d}}{\sigma _ {\rm{c}}}}}{{{\rm{d}}x}}. $ | (4) |
将式(2)代入式(4)得
| $\tau = - \frac{{ r_ {\rm{f}}^2{\rm{d}}{\sigma _ {\rm{f}}}}}{{2{r} {\rm{d}}x}} - \frac{{{r} ^2 - r_ {\rm{f}}^2}}{{2{r} }}\frac{{{\rm{d}}{\sigma _ {\rm{c}}}}}{{{\rm{d}}x}}. $ | (5) |
由于 POF 的轴向尺寸远大于其径向尺寸,可忽略泊松效应的影响,式(5)进一步写为
| $\tau = - \frac{{ r_ {\rm{f}}^2{\rm{d}}{\varepsilon _ {\rm{f}}}}}{{2{r} {\rm{d}}x}}{{E} _ {\rm{f}}} - \frac{{{r} ^2 - r_ {\rm{f}}^2}}{{2{r} }}\frac{{{\rm{d}}{\varepsilon _ {\rm{c}}}}}{{{\rm{d}}x}}{{E} _ {\rm{c}}}. $ | (6) |
式中:Ef为POF纤芯弹性模量,Ec为凃覆层弹性模量,εf和εc分别为POF纤芯和涂覆层的轴向应变,τ为涂覆层切应力。由于POF纤芯与涂覆层同步变形,两者的应变梯度接近,即可认为
| $\frac{{{\rm{d}}{\varepsilon _ {\rm{f}}}}}{{{\rm{d}}x}} \cong \frac{{{\rm{d}}{\varepsilon _ {\rm{c}}}}}{{{\rm{d}}x}}. $ | (7) |
将式(7)代入式(6)得
| $\tau = - \left(\frac{{ r_ {\rm{f}}^2}}{{2{r} }}{{E} _ {\rm{f}}} + \frac{{{r} ^2 - r_ {\rm{f}}^2}}{{2{r} }}{{E} _ {\rm{c}}}\right)\frac{{{\rm{d}}{\varepsilon _ {\rm{f}}}}}{{{\rm{d}}x}}. $ | (8) |
根据POF的轴向尺寸远大于其径向尺寸的特点,这里仅考虑其轴向变形,则
| $\tau = {{G} _ {\rm{c}}}\gamma \cong {{G} _ {\rm{c}}}\frac{{{\rm{d}}u}}{{{\rm{d}}r}}. $ | (9) |
式中:
| $\begin{split} \int\limits_{{ r_ {\rm{f}}}}^{{{r} _ {\rm{m}}}} {\left({{G} _ {\rm{c}}}\frac{{{\rm{d}}{u} }}{{{\rm{d}}r}}\right)} {\rm{d}}r &= \\ & \int\limits_{{ r_ {\rm{f}}}}^{{{r} _ {\rm{m}}}} {{\Bigg[} - \left(\frac{{ r_ {\rm{f}}^2}}{{2{r} }}{{E} _ {\rm{f}}} + \frac{{{r} ^2 - r_ {\rm{f}}^2}}{{2{r} }}{{E} _ {\rm{c}}}\right)\frac{{{\rm{d}}{\varepsilon _ {\rm{f}}}}}{{{\rm{d}}x}}{\Bigg]}} {\rm{d}}r .\end{split} $ | (10) |
| $\begin{split} {{u} _ {\rm{m}}} - {{u} _ {\rm{f}}} =& - \frac{{d{\varepsilon _ {\rm{f}}}}}{{{\rm{d}}x}}\frac{{1}}{{4{{G} _ {\rm{c}}}}} \times \\ & \left[ {({r} _ {\rm{m}}^2 - r_ {\rm{f}}^2){{E} _ {\rm{c}}} + 2 r_ {\rm{f}}^2({{E} _ {\rm{f}}} - {{E} _ {\rm{c}}})\ln\;\left(\frac{{{{r} _ {\rm{m}}}}}{{{ r_ {\rm{f}}}}}\right)} \right] .\end{split} $ | (11) |
其中,uf和um分别为纤芯外侧和涂覆层外侧的轴向位移,Ec/[2(1+μ)]为涂覆层剪切模量,μ为泊松比. 令
| ${{k} ^2} = 4{{G} _ {\rm{c}}}{\left[ {({r} _ {\rm{m}}^2 - r_ {\rm{f}}^2){{E} _ {\rm{c}}} + 2 r_ {\rm{f}}^2({{E} _ {\rm{f}}} - {{E} _ {\rm{c}}})\ln\;\left(\frac{{{{r} _ {\rm{m}}}}}{{{ r_ {\rm{f}}}}}\right)} \right]^{{- 1}}}. $ | (12) |
将式(12)代入式(11)得
| ${{u} _ {\rm{m}}} - {{u} _ {\rm{f}}} = - \frac{1}{{{{k} ^2}}}\frac{{{\rm{d}}{\varepsilon _ {\rm{f}}}}}{{{\rm{d}}x}}. $ | (13) |
将式(13)对
| $\frac{{{{\rm{d}}^2}{\varepsilon _ {\rm{f}}}({x} )}}{{{\rm{d}}{x^2}}} - {{k} ^2}{\varepsilon _ {\rm{f}}}({x} ) = - {{k} ^2}{\varepsilon _ {\rm{m}}}. $ | (14) |
式(14)即为POF纤芯沿轴向应变与基体应变关系的控制方程,方程的通解为
| ${\varepsilon _ {\rm{f}}}({x} ) = {{c} _1}{{\rm{e}}^{{kx} }} + {{c} _2}{{\rm{e}}^{ - {kx} }} + {\varepsilon _ {\rm{m}}}. $ | (15) |
式中:
| ${\varepsilon _ {\rm{f}}}({L} ) = {\varepsilon _ {\rm{f}}}( - {L} ) = 0. $ | (16) |
由边界条件可以求导出
| ${{c} _1} = {{c} _2} = - \frac{{{\varepsilon _ {\rm{m}}}}}{{2\cosh\;({kL} )}}. $ | (17) |
将式(17)代入式(15),可以得出POF纤芯层的轴向应变分布为
| ${\varepsilon _ {\rm{f}}}({x} ) = {\varepsilon _ {\rm{m}}}\left(1 - \frac{{\cosh\;({kx} )}}{{\cosh\;({kL} )}}\right). $ | (18) |
POF埋设段各点应变传递率为
| $\alpha ({x} ) = \frac{{{\varepsilon _ {\rm{f}}}({x} )}}{{{\varepsilon _ {\rm{m}}}}} = 1 - \frac{{{\rm{cosh\;(}}{kx} )}}{{{\rm{cosh\;(}}{kL} )}}. $ | (19) |
POF埋设段平均应变传递率为
| $\overline \alpha = \frac{{\overline {{\varepsilon _ {\rm{f}}}({x} )} }}{{{\varepsilon _ {\rm{m}}}}} = 1 - \frac{{\sinh\;({kL} )}}{{{kL} \cosh\;({kL} )}}. $ | (20) |
为验证上述理论分析结果的正确性,对POF−混凝土复合体进行有限元分析. 分析模型如图3所示,模型轴向长度取40 mm,该长度为POF的埋设长度,POF纤芯的半径为0.25 mm,带涂覆层POF的半径为0.5 mm(涂覆层厚度为0.25 mm),POF周围混凝土取一边长为2 mm的正方形区域. 拟选用的POF型号为三菱公司生产的SH2001-J,该型号POF纤芯材料为聚甲基丙烯酸甲脂(PMMA)、涂覆层材料为氟化聚合物(PE),各层材料参数的取值如表1所示. 混凝土弹性模量Em=28 GPa,泊松比μm=0.18. 分析中,在模型两端混凝土区域施加一大小为0.5 MPa的轴向拉应力,POF纤芯和涂覆层不受力,并设定模型中混凝土区域仅可发生平行于纤芯轴向的位移. 该模型轴向应变计算结果如图4所示.

|
图 3 埋入式POF-混凝土复合体有限元模型 Fig. 3 Finite element model of embedded POF-concrete complex |
| 表 1 POF纤芯和涂覆层的机械参数 Table 1 Material parameters of POF core and cladding |

|
图 4 POF−混凝土复合体及POF纤芯轴向应变分布的数值计算结果 Fig. 4 Axial strain distribution of POF-concrete complex and POF core by numerical calculation |
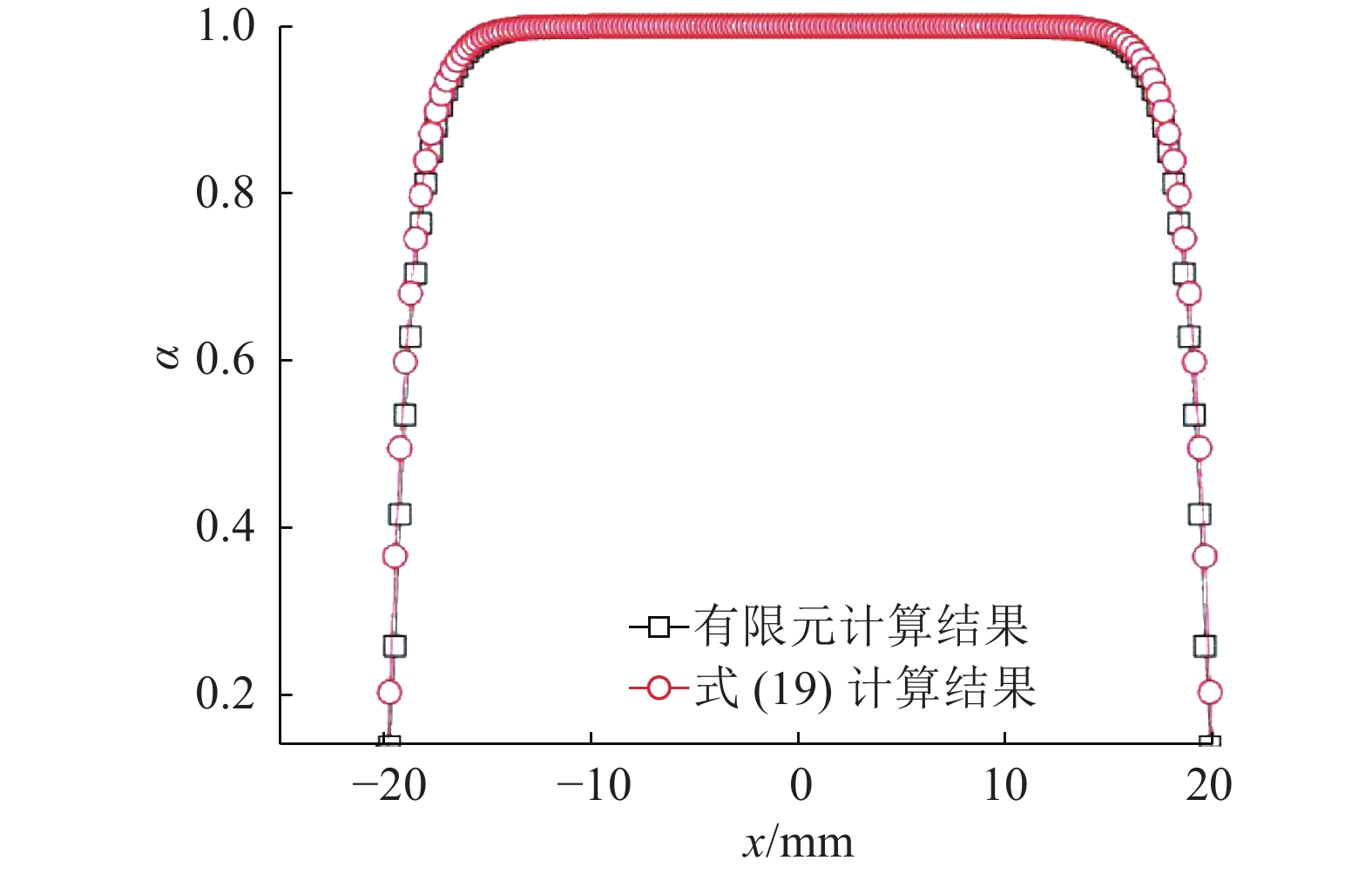
由图4可以看出,当混凝土结构受力产生应变时,POF埋设段中间大部分区域的应变与混凝土结构应变保持一致,仅两端较小区域的应变比混凝土的应变小. 这说明本研究采用的POF在直接埋设于混凝土中时,即使混凝土结构与POF纤芯之间存在一层弹性模量较低的涂覆材料,混凝土结构上的应变依然可以较好地传递至POF纤芯. 为了进一步比较数值仿真与理论分析的结果,将分析模型中POF纤芯中心轴线上各点的轴向应变和混凝土结构与涂覆层相接触处各点的应变相比较,得出埋设段POF中心轴上各点的应变传递率,并与式(19)的计算结果绘制于同一图中,如图5所示. 可以看出,数值仿真与理论分析的结果基本一致,POF埋设段中间大部分区域的应变传递率接近于1,而埋设段两端应变传递率较低. 这2种方法得出的结果在埋设段两端稍有差异,数值仿真所获得的各点应变传递率要稍高于理论分析结果,但数值上相差不大,整体相对误差仅为3.1%. 数值仿真与理论分析结果的一致性可以说明本文理论分析所得出的公式可以用于分析POF与混凝土结构之间的应变传递问题. 本研究采用的POF材料参数如表1所示,若埋设长度为40 mm,依据式(20)可知,其与混凝土间的平均应变传递率可达0.945,说明若将该POF埋入混凝土中,能够达到较好的应变传递效果,在进行裂缝监测时,混凝土内部的应变可有效传递至POF纤芯.
|
图 5 埋入式POF与混凝土间应变传递率的理论及数值计算结果 Fig. 5 Strain transmissibility between embedded POF and concrete by theoretical and numerical calculation |
在实际应用中,POF的涂覆层材料、尺寸以及其埋设长度都可根据实际情况进行选择. 由式(12)可以看出,上述因素都可能影响POF纤芯与混凝土结构之间的应变传递效果. 下面以式(20)平均应变传递率为指标,分析上述因素对应变传递率影响的敏感性.
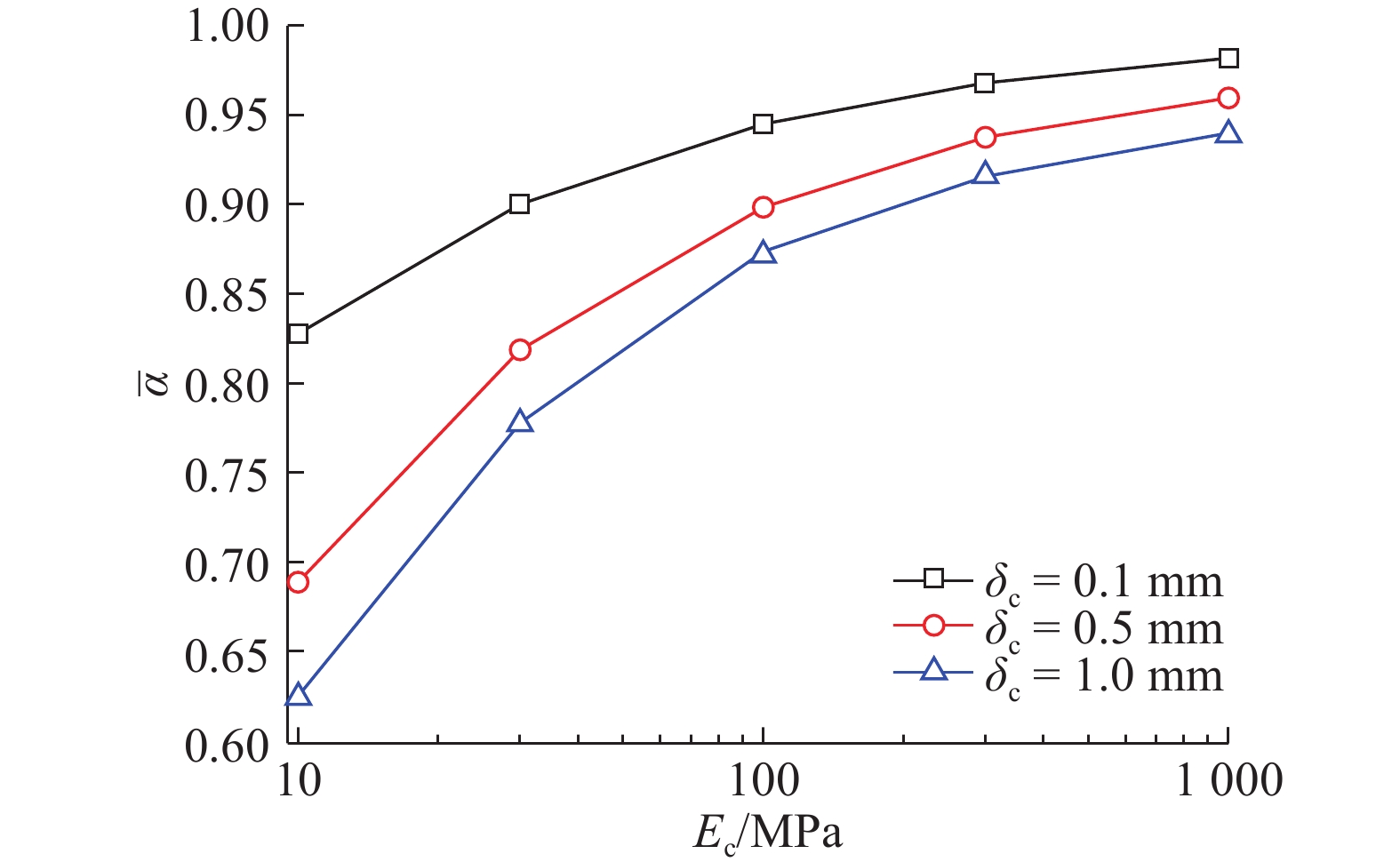
如图6所示为涂覆层厚度分别为0.1、0.5和1.0 mm时. 涂覆层的弹性模量由10 MPa增大到1 000 MPa过程中,POF纤芯与混凝土结构之间平均应变传递率的计算结果,其他参数见表1. 由图6可以看出,平均应变传递率随涂覆层弹性模量的增加呈明显上升趋势,当弹性模量增大到一定范围时,应变传递率的增加趋势变缓;曲线起始点处的平均应变传递率值差别较大,分别为0.63、0.69、0.83左右. 在涂覆层弹性模量接近1 000 MPa时,不同涂覆层厚度对应的平均应变传递率的差值明显变小,说明在高弹性模量条件下,涂覆层厚度的影响在逐渐减弱. 由于不同厚度条件下曲线的起点差异大而终点差异小,各曲线的竖向变幅不同. 具体表现如下:在厚度较小时平均应变传递率的变幅较小,而在厚度较大时,平均应变传递率的变幅较大,这说明随着涂覆层厚度的增大,涂覆层弹性模量对应变传递效果的影响在逐渐增强.
|
图 6 不同涂覆层厚度时POF纤芯与混凝土之间的平均应变传递率随涂覆层弹性模量的变化 Fig. 6 Variation of average strain transmissibility between POF core and concrete with cladding elastic modulus of cladding under different cladding thickness values |
实际应用中涂覆层的主要作用是保护纤芯,但其不可避免地对混凝土与POF纤芯间的应变传递产生一定阻碍作用. 从计算结果来看,要使埋设于混凝土内部的POF与混凝土变形协调一致,可以选用弹性模量较大(>100 MPa)的涂覆材料,并适当减小其涂覆厚度(<0.5 mm). 例如,选用弹性模量为140 MPa、涂覆厚度为0.25 mm的PE材料,此时应变传递率可达到0.933.
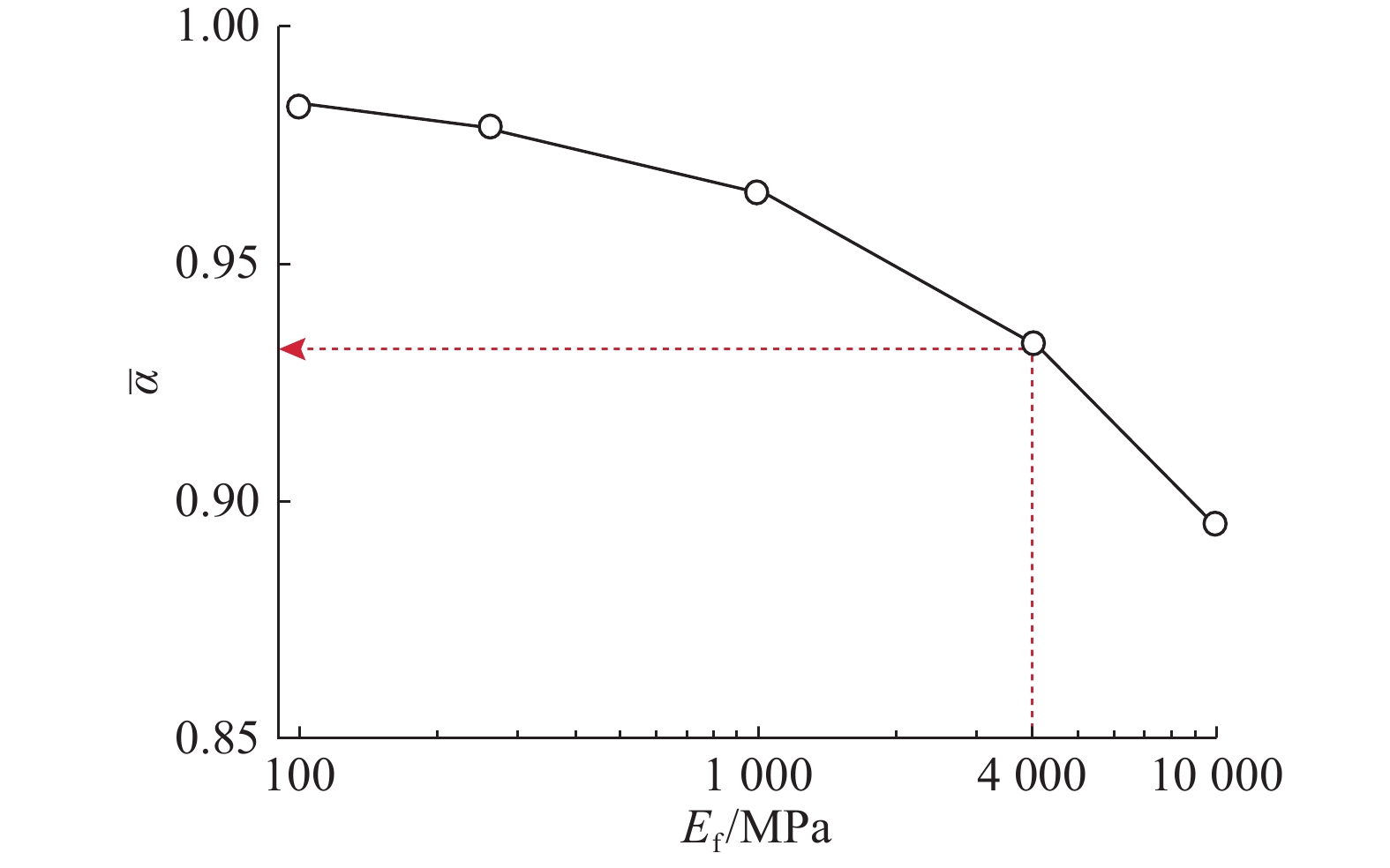
POF的纤芯由光学塑料制作,不同的光学塑料具有不同的弹性模量,因此有必要研究纤芯弹性模量对POF−混凝土间应变传递的影响. 如图7所示为纤芯弹性模量在100 ~10 000 MPa时,平均应变传递率随纤芯模量的变化情况,其他参数见表1. 由图中曲线的变化趋势可以看出,纤芯模量对平均应变传递率的影响比较明显. 在纤芯模量由100 MPa增长至10 000 MPa的过程中,平均应变传递率由0.98降为0.89,因此选择弹性模量较低的光学塑料作为纤芯材料有利于POF−混凝土间应变的传递. 典型地,若采用弹模为4 000 MPa的PMMA材料,其平均应变传递率接近于0.94.
|
图 7 POF与混凝土之间的平均应变传递率随POF纤芯弹性模量的变化 Fig. 7 Variation of average strain transmissibility between POF core and concrete with POF core elastic modulus |
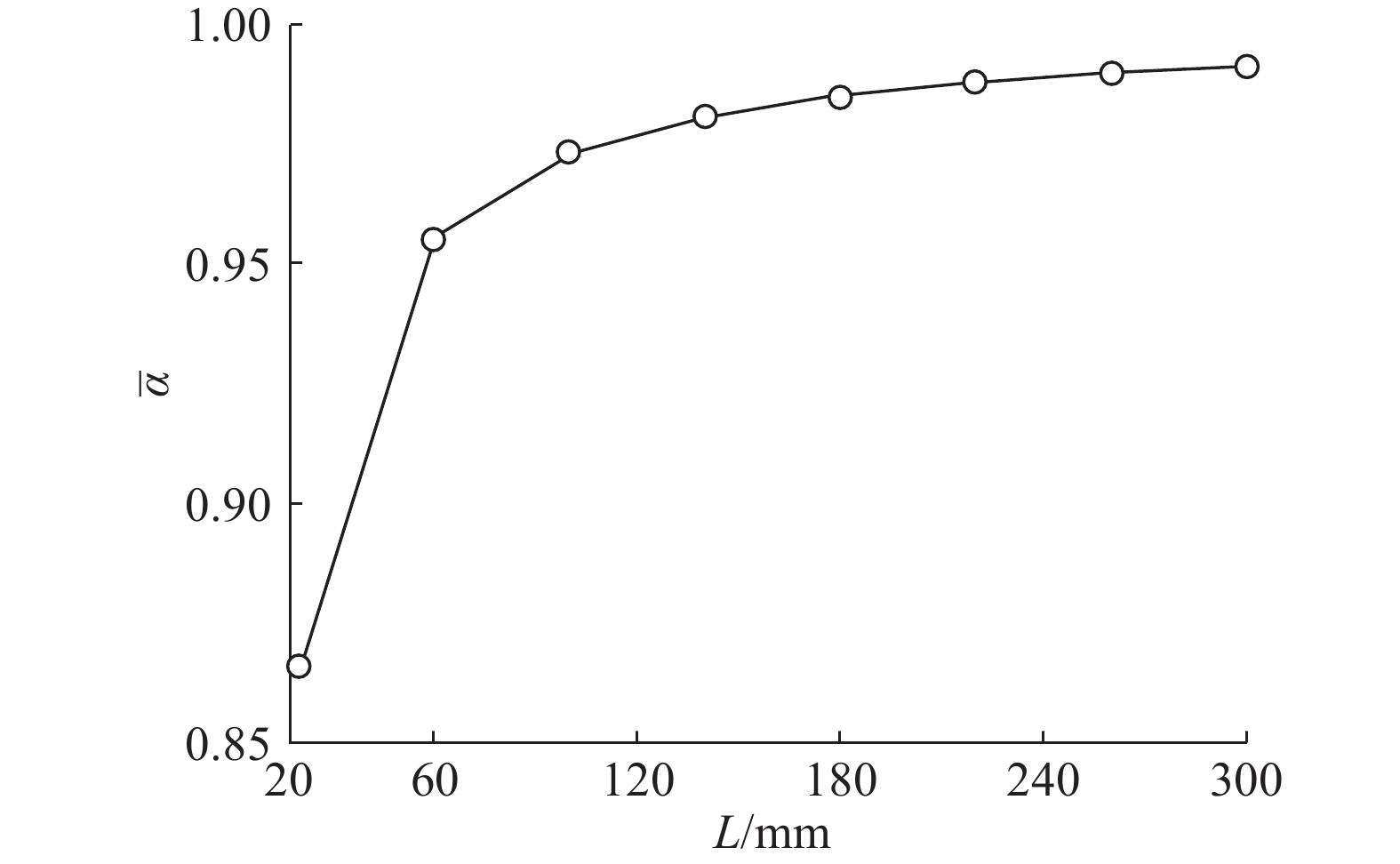
实际应用中,在混凝土结构尺寸较小的部位,还可能面临POF埋设长度的选择问题. 如图8所示为不同埋设长度条件下,POF与混凝土结构之间平均应变传递率的计算结果,其他参数见表1. 由图8可以看出,POF与混凝土结构之间的平均应变传递率随埋设长度的增大逐渐增加. 在埋设长度由20 mm增大到300 mm的过程中,平均应变传递率由0.87增加到0.99以上. 计算结果表明埋设长度对平均应变传递率有较明显的影响,由于在实际应用中一般都可以保证POF埋设长度在300 mm以上,POF与混凝土结构之间可保证较好的应变传递效果.
|
图 8 平均应变传递率随POF埋设长度的变化 Fig. 8 Variation of average strain transmissibility with embedded length |
总的来看,将现有商业POF(POF材料参数见表1)直接埋入混凝土时,POF纤芯与混凝土之间应变传递效果较好. 具体来看:埋设长度为300 mm时,POF纤芯与混凝土之间平均应变传递率能够达到0.99左右,如图8所示;而且埋设段中间大部分区域应变传递率接近于1,应变传递效果较差的区域仅出现在两端较小范围,如图5所示. 因此,当混凝土结构在外力作用下产生应变时,其与POF之间良好的应变传递关系可以使POF纤芯产生相当的应变,如此POF传感器便实现了对混凝土结构应变的感知. 混凝土结构的开裂源于结构局部应变超过其极限,POF对应变较好的感知能力说明POF同样可以感知裂缝的发生.
4 结 论(1)对埋入式POF与混凝土之间的应变传递关系进行了推导,建立了埋入式POF纤芯与混凝土间应变传递的理论模型,通过数值仿真验证了模型的正确性,并对可能影响应变传递效果的参数进行了敏感性分析.
(2)根据参数敏感性分析结论可知,为有利于埋入式POF与混凝土之间的应变传递,宜使POF的涂覆层厚度小于0.5 mm,弹性模量大于100 MPa,埋设长度大于300 mm.
(3)利用本文推导的应变传递模型计算了现有商业POF与混凝土间的应变传递率. 若纤芯半径为0.25 mm、涂覆厚度为0.25 mm、纤芯为PMMA材料、涂覆为PE材料、胶剂固化后弹模为4 GPa,在埋设长度为300 mm时,POF纤芯与混凝土间平均应变传递率可达到0.99左右,说明两者之间具有较好的应变传递效果,可使两者协调变形.
| [1] |
BARRIAS A, CASAS J R, VILLALBA S. A review of distributed optical fiber sensors for civil engineering applications[J]. Sensors, 2016, 16(5): 748. DOI:10.3390/s16050748 |
| [2] |
LEUNG C K Y, WAN K T, INAUDI D, et al. Optical fiber sensors for civil engineering applications[J]. Materials and Structures, 2015, 48(4): 871-906. DOI:10.1617/s11527-013-0201-7 |
| [3] |
AHMAD S, HUSAIN S M A, ANWAR A, et al. Application of fiber optic sensors in civil engineering[J]. International Journal of Engineering Innovation and Research, 2015, 4(3): 526-529. |
| [4] |
YE X, SU Y, HAN J. Structural health monitoring of civil infrastructure using optical fiber sensing technology: a comprehensive review[J]. The Scientific World Journal, 2014, 2014: 65329. |
| [5] |
BAO T. Distributed fiber bragg grating sensors for monitoring cracks in concrete structures[C] // Thirteenth ASCE Aerospace Division Conference on Engineering, Science, Construction, and Operations in Challenging Environments, and the 5th NASA/ASCE Workshop on Granular Materials in Space Exploration. Pasadena: ASCE, 2012: 1290–1399.
|
| [6] |
LIEHR S, LENKE P, WENDT M, et al. Polymer optical fiber sensors for distributed strain measurement and application in structural health monitoring[J]. IEEE Sensors Journal, 2009, 9(11): 1330-1338. DOI:10.1109/JSEN.2009.2018352 |
| [7] |
ZHANG C, ZHU H, SHI B, et al. Performance evaluation of soil-embedded plastic optical fiber sensors for geotechnical monitoring[J]. Smart Structures and Systems, 2016, 17(2): 297-311. DOI:10.12989/sss.2016.17.2.297 |
| [8] |
LUO D, YUE Y, LI P, et al. Concrete beam crack detection using tapered polymer optical fiber sensors[J]. Measurement, 2016, 88: 96-103. DOI:10.1016/j.measurement.2016.03.028 |
| [9] |
包腾飞, 赵津磊, 戚丹. 塑料光纤在裂缝监测中的性能[J]. 光子学报, 2015, 44(10): 82-87. BAO Teng-fei, ZHAO Jin-lei, QI Dan. Properties of plastic optical fibers in crack monitoring[J]. Acta Photonica Sinica, 2015, 44(10): 82-87. |
| [10] |
ZHAO J, BAO T, CHEN R. Crack monitoring capability of plastic optical fibers for concrete structures[J]. Optical Fiber Technology, 2015(24): 70-76. |
| [11] |
赵津磊, 包腾飞, 戚丹. 塑料光纤在裂缝监测中应用的可行性研究[J]. 光电子. 激光, 2014, 25(10): 1943-1948. BAO Teng-fei, ZHAO Jin-lei, QI Dan. Feasibility study on application of plastic optical fiber in monitoring[J]. Journal of Optoelectronics. Laser, 2014, 25(10): 1943-1948. |
| [12] |
赵津磊, 包腾飞, 戚丹. 基于塑料光纤裂缝传感器的裂缝开度预测[J]. 水电能源科学, 2015, 2(33): 131-134. BAO Teng-fei, ZHAO Jin-lei, QI Dan. Prection of crack width based on plastic optical fiber crack sensor[J]. Water Resources and Power, 2015, 2(33): 131-134. |
| [13] |
PAK Y E. Longitudinal shear transfer in fiber optic sensors[J]. Smart Materials and Structures, 1992, 1(1): 57-62. DOI:10.1088/0964-1726/1/1/008 |
| [14] |
ANSARI F, LIBO Y. Mechanics of bond and interface shear transfer in optical fiber sensors[J]. Journal of Engineering Mechanics, 1998, 124(4): 385-394. DOI:10.1061/(ASCE)0733-9399(1998)124:4(385) |
| [15] |
LI Q, LI G, WANG G, et al. Elasto-plastic bonding of embedded optical fiber sensors in concrete[J]. Journal of Engineering Mechanics, 2002, 128(4): 471-478. DOI:10.1061/(ASCE)0733-9399(2002)128:4(471) |
| [16] |
李东升, 李宏男. 埋入式封装的光纤光栅传感器应变传递分析[J]. 力学学报, 2005, 37(4): 435-441. LI Dong-sheng, LI Hong-nan. Strain transferring analysis of embedded fiber Bragg grating sensors[J]. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(4): 435-441. DOI:10.3321/j.issn:0459-1879.2005.04.008 |
| [17] |
SUN L, HAO H, ZHANG B, et al. Strain transfer analysis of embedded fiber Bragg grating strain sensor[J]. Journal of Testing and Evaluation, 2015, 44(6): 2312-2320. |
| [18] |
吴永红, 邵长江, 屈文俊, 等. 传感光纤光栅标准化埋入式封装的理论与实验研究[J]. 中国激光, 2010, 37(5): 1290-1293. WU Yong-hong, SHAO Chang-jiang, QU Wen-jun, et al. Basic theoretical model and its experimental investigation for standard embedded sensing fiber Bragg grating packaging[J]. Chinese Journal of Lasers, 2010, 37(5): 1290-1293. |
| [19] |
吴入军, 郑百林, 贺鹏飞, 等. 埋入式光纤布拉格光栅传感器封装结构对测量应变的影响[J]. 光学精密工程, 2014, 22(1): 24-30. WU Ru-jun, ZHENG Bai-lin, HE Peng-fei, et al. Influence of encapsulation structures for embedded fiber-optic Bragg grating sensors on strain measurement[J]. Optics and Precision Engineering, 2014, 22(1): 24-30. |
| [20] |
周智, 王倩, 郝孝伟, 等. 考虑混凝土基体蠕变的FBG传感器应变传递研究[J]. 中国测试, 2016, 42(5): 1-5. ZHOU Z, WANG Q, HAO X. Strain transfer analysis of the FBG sensor considering the creep of the concrete host[J]. China Measurement and Test, 2016, 42(5): 1-5. |
| [21] |
HER S C, HUANG C Y. Effect of coating on the strain transfer of optical fiber sensors[J]. Sensors, 2011, 11(7): 6926-6941. DOI:10.3390/s110706926 |
| [22] |
CHANG X, LI M. Study on strain transfer of polymer optical fiber grating sensors [C] // International Symposium on Photoelectronic Detection and Imaging 2009: Material and Device Technology for Sensors. Beijing: SPIE, 2009: 73811P.
|
| [23] |
常新龙, 李明, 王渭平, 等. 埋入式聚合物光纤传感器应变传递影响参数分析[J]. 激光与红外, 2010, 40(5): 515-519. CHANG Xin-long, LI Ming, WANG Wei-ping. Analyses of parameters influencing strain transfer of embedded polymer optical fiber sensors[J]. Laser and Infrared, 2010, 40(5): 515-519. DOI:10.3969/j.issn.1001-5078.2010.05.015 |


