随着全球气候变暖和人类活动的加剧，极端降雨和洪水事件变得更加频繁和剧烈^[1-3]，不仅造成巨大的经济损失，还威胁着人民的生命财产安全. 因此，建立有效的降雨和洪水预警系统意义重大^[4].

洪水事件的发生与大气降水直接相关，而研究发现大气环流受全球或者区域的气候类型影响显著^[5-6]. 气候类型的状态通常可以用气候指数来表示，建立气候指数与大气降水的相关性从而提高洪水预报的精度是一种较为可行的方法. Zhang等^[6]证实利用厄尔尼诺南方涛动（El Niño Southern Oscillation, ENSO）以及印度季风指数与径流的相关性能有效提高长江流域长期径流预报. 近些年，随着集合预报方法在水文气象领域中的广泛应用，气候指数也作为一种权重方法被引入到集合径流预报中^{[5, 7]}. 2012年，Najafi等^[8]通过主成分分析法得到包括太平洋年代际振荡（Pacific Decal Oscillation, PDO）指数和南方涛动指数（Southern Oscillation Index, SOI）在内的多项气候指数与科罗拉多河流域春汛洪量的关系，并根据该相关性定义集合成员的权重，发现基于气候指数加权的集合预报能明显改善春汛的估计精度. 2015年，洪宇等^[9]研究发现汉江流域降水量和气温在月尺度上与PDO和SOI有着显著的相关性. 2016年，Huang等^[10]采用主成分分析法和K均值算法分析了内蒙古自治区降雨指数与11种主要气候指数的相关性，发现ENSO和SOI与当地降雨显著相关.

降雨与气候指数的相关性研究针对长江流域已有较为深入的开展^[11-12]，结果证实ENSO影响着整个长江流域，而流域下游主要受东亚夏季风指数（East Asian Summer Monsoon Index, EASMI）影响. 此外，Shen等^[13]研究发现PDO对整个华东地区的降雨影响显著. 兰江流域位于东南地区，距离长江流域下游段约200 km，基于此本文将着重讨论PDO、SOI和EASMI指数对研究流域的影响.

根据Xu等^{[2, 14]}的研究，随着气候变化兰江流域将面临更为严峻的降雨和洪涝灾害，但是迄今为止兰江流域降雨量与气候指数的相关性还没有人进行过深入的研究，并且针对大多数其他流域的早期研究都是基于月尺度甚至更长时间尺度，本文将研究SOI、PDO和EASMI在日尺度上与兰江流域降雨的相关性，从而为流域洪水预报和水资源管理提供可靠依据.

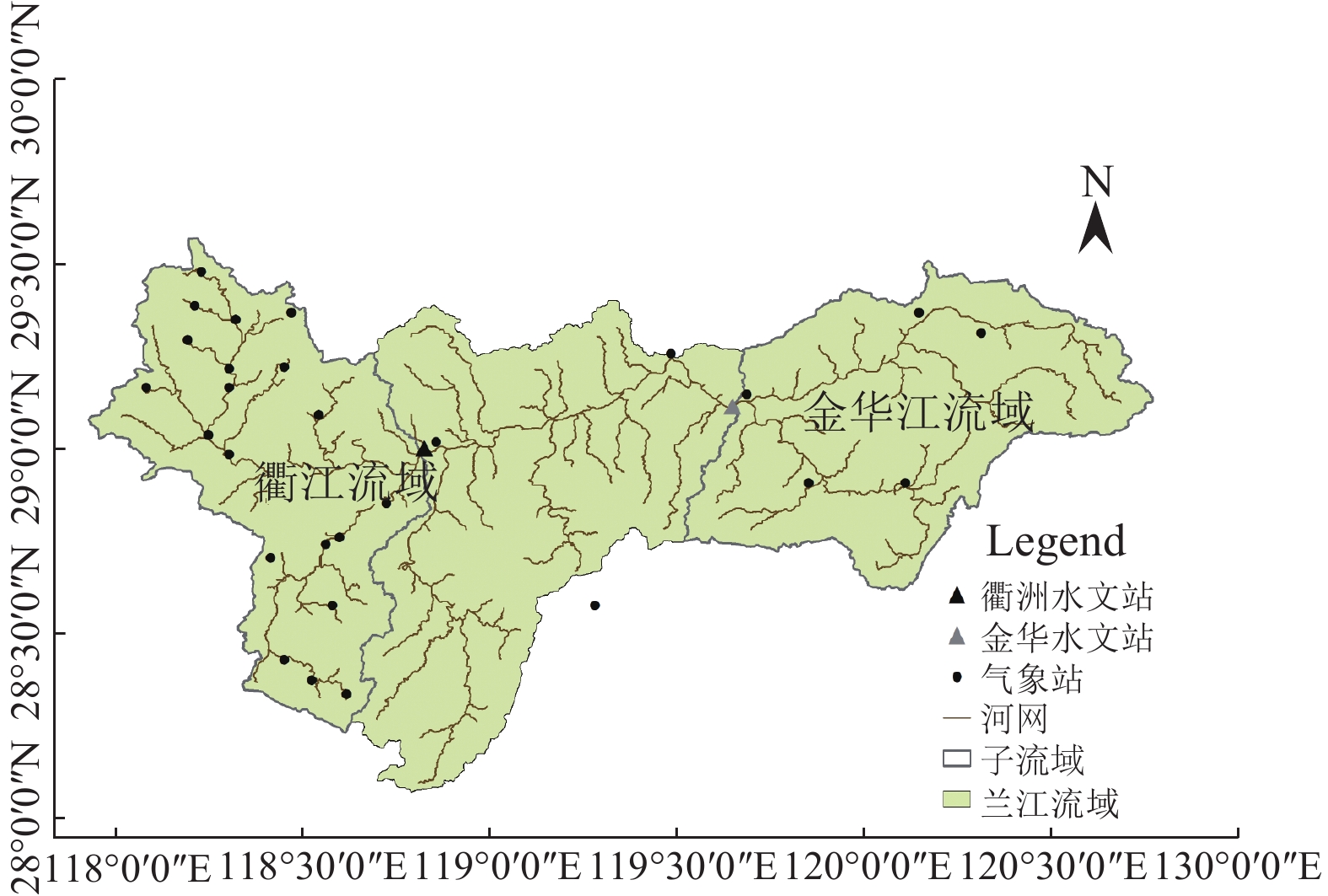
兰江流域（118°4′E~120°38′E，28°6′N~29°30′N）位于浙江省西南部，是钱塘江流域的主要支流，如图1所示. 兰溪水文站以上控制集水面积约为17 000 km². 流域位于亚热带湿润季风区，全年平均温度约为17 °C，年平均降雨量达1 600 mm，5~9月为主要的丰水期^[14]. 兰江上游西侧支流段为衢江支流，集水面积约5 600 km²，以山地和丘陵地形为主；东上游段为金华江支流，集水面积约5 900 km²，其地形主要为平原. 本文将兰江流域分为金华江和衢江两大支流分别进行研究.

图 1

图 1 兰江流域位置和气象站点分布 Fig. 1 Location of Lanjiang River and distribution of meteorology stations

所采用的降雨数据是由中国气象局和浙江省气象局提供的兰江流域28个气象站点的日值数据. 数据长度为1963—2000年.

所用的逐月PDO和SOI数据分别来自于华盛顿大学的大气海洋研究联合中心^[15]和美国国家海洋与大气管理局^[16]. EASMI数据来自于北京师范大学李建平教授的个人主页^[17]. 所有气候指数的时间跨度与降雨数据保持一致.

根据Wilks^[18]的研究，相对于线性插值样条插值方法更适用于对月平均数值的插值，可以在保持插值序列平滑的同时，产生合理的峰值.本研究也证实样条插值可以比线性插值产生更为合理的日值数据. 因此样条插值方法被选取来对月平均气候指数插值，以获取日尺度的气候指数. 考虑到流域丰水期主要集中在夏季，本研究只针对5~9月期间PDO和SOI以及7~8月期间EASMI与相应时段降雨的相关性，并通过泰森多边形法分别计算金华江流域和衢江流域的面雨量. PDO的变换周期通常为20~30年，因此主要研究其在长期尺度上与降雨的相关性. 而根据Zhang等^[6,19]的研究，SOI存在与降雨的长期相关性和短期相关性，因此，从长期和短期角度分别对SOI进行分析. 对EASMI只作短期相关性分析，一是由于EASMI数据序列较短（6~8月），二是由于EASM本身就是一年回归事件，周期较短.

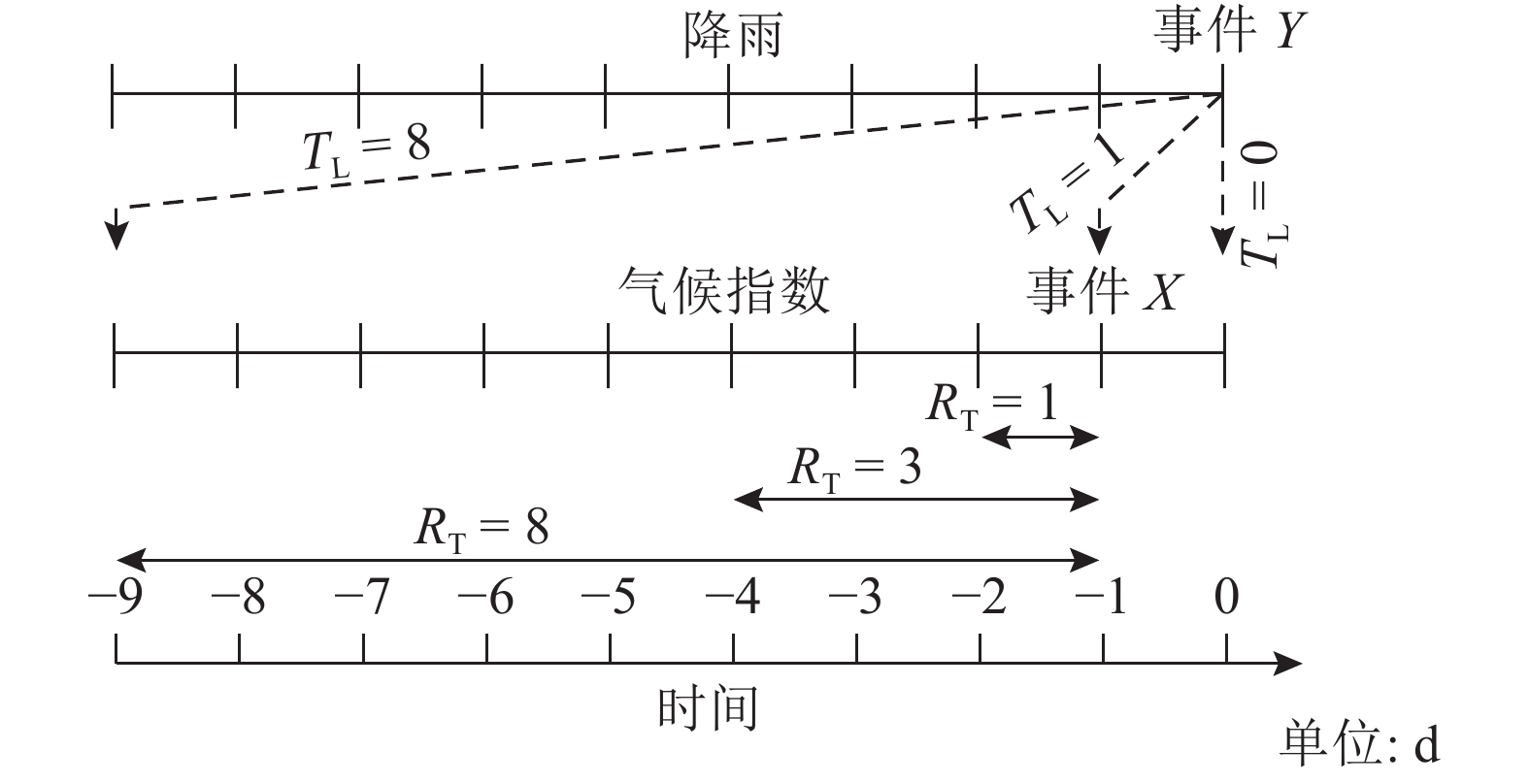
气候指数对降水的影响通常具有滞后效应^[9]. 参考Demirel等^[20-21]的研究，每一个相关性评估都存在其最佳的时间分辨率（R_T）和滞后时间（T_L），如图2所示. 例如，当事件X与Y相关性的最佳T_L为6 d、最佳R_T为3 d时，意味着当X发生6 d后，可测得X与Y的最大相关性，并且X不是某一天的值，而是3 d的平均值. 在计算最佳T_L和R_T时需要确定其最大边界值. 对于EASMI，这个边界设定8月为T_L与R_T的和不超过31 d，因为7用于选取降雨事件，剩下一个月的数据用于改变T_L和R_T. 对于SOI，其短期评估的最大边界值设定为T_L=1 a，R_T=90 d，因为其他相关研究已经发现SOI与降雨的相关性主要与一年以内的ENSO事件有关^{[19, 21]}. 最后，对于SOI和PDO的长期相关性分析，最大R_T设定为20 a^[6]，且在实际计算时，为节省计算时间，时间步长定为50 d，因为SOI与降雨每50~100 d可能呈现相反的相关性，即变化周期大于50 d. 不考虑滞后时间的影响，根据计算结果，相关性对T_L的改变不敏感，因此最大T_L设为0 d.

图 2

图 2 滞后时间和时间分辨率示意图 Fig. 2 Schematic diagram of lag time and temporal resolution

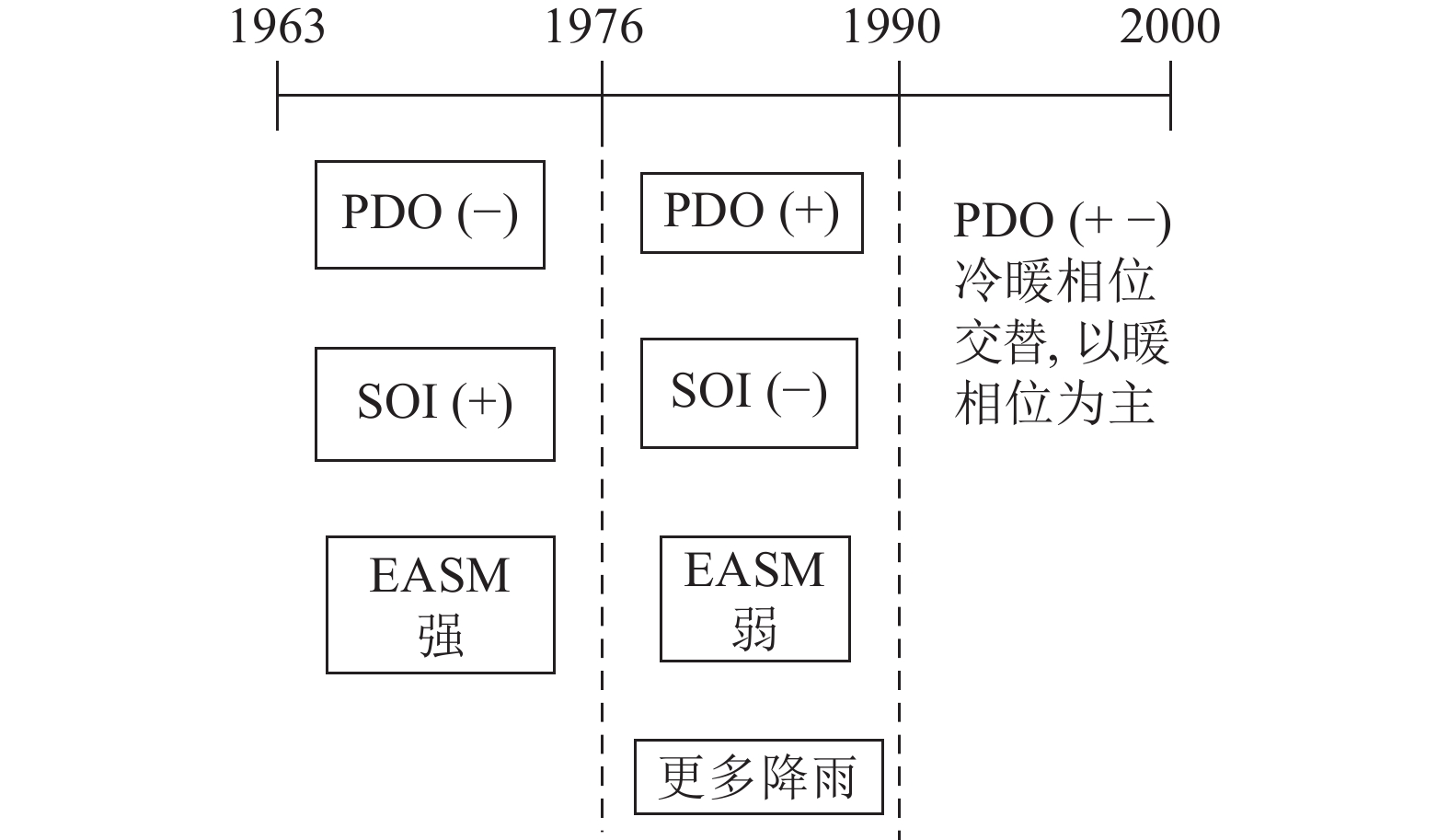
根据Feng等^[22]的研究发现，本文所涉及的3个气候指数，并非完全不相关. 总体而言，PDO和SOI基本处于负相关^[23]：当PDO处于冷相位时，会促使ENSO位于暖相位；反之，暖相位的PDO则会加强SOI的冷相位. 此外，暖相位的PDO趋向于减弱东亚夏季风（EASM），造成中国北方地区降雨减少，而长江流域降水增多^{[22, 24-25]}. 因此，本文除了对每个气候指数采用线性回归作分别的相关性分析以外，还将采用多元回归方法分析指数组合对降雨的影响. 鉴于EASMI和SOI与PDO所处的相位有着密切的联系，在对这2个指数进行分析时，将根据如图3所示的PDO的不同相位阶段，将研究期分为3个子时期，分别探究其对降雨量的影响，即1963—1976（PDO−），1977—1989（PDO+），1990—2000（PDO+−）时期. 其中线性回归分析通过计算皮尔逊相关系数获得，其计算公式如下：

图 3

图 3 按时间线表示的指数间的相互作用 Fig. 3 Interaction of climate indexes represented by timeline

式中：γ为要素X与Y之间的相关系数；X_i和Y_i为第i天的气候指数和降雨， $\overline X$ 和 $\overline Y$ 为均值，n为要素序列长度.

多元回归分析采取的指数组合为PDO-SOI，SOI-EASMI和EASMI-PDO，通过式（2）可获得降雨量y的估计值：

式中： ${x_1},{x_2},\cdots,{x_k}$ 为气候指数， ${b_1},{b_2},\cdots,{b_k}$ 为回归系数， $\hat y$ 为降雨量的估计值. 降雨量实测值y与估计值 $\hat y$ 的相关系数即为相应的指数组合与降雨量的相关系数.

式中： ${x_1},{x_2},$ $\,\cdots\,,{x_k} $ 为气候指数， ${b_1},{b_2},\,\cdots\,,{b_k}$ 为回归系数， $\widehat y$ 为降雨量的估计值.

需要注意的是，多元回归的使用前提是所涉及的变量x是相互独立的，但是本研究所采用的气候指数实际是以某种复杂的方式部分相关的. 对气候数据进行一个初步的相关性分析，发现PDO、SOI和EASMI两两之间的相关系数均小于0.15，因此假定数据基本是相互独立的.

显著性检验采用Kutner等^[26]提出的公式：

式中：n−2为自由度. 同t检验一样，该方法先建立零假设H₀和备择假设H_A，再计算检验统计量t^*，可得到显著性结论， $\beta {\rm{ = }}0$ 表示相关性不显著， $\beta \ne 0 $ 表示相关性显著.

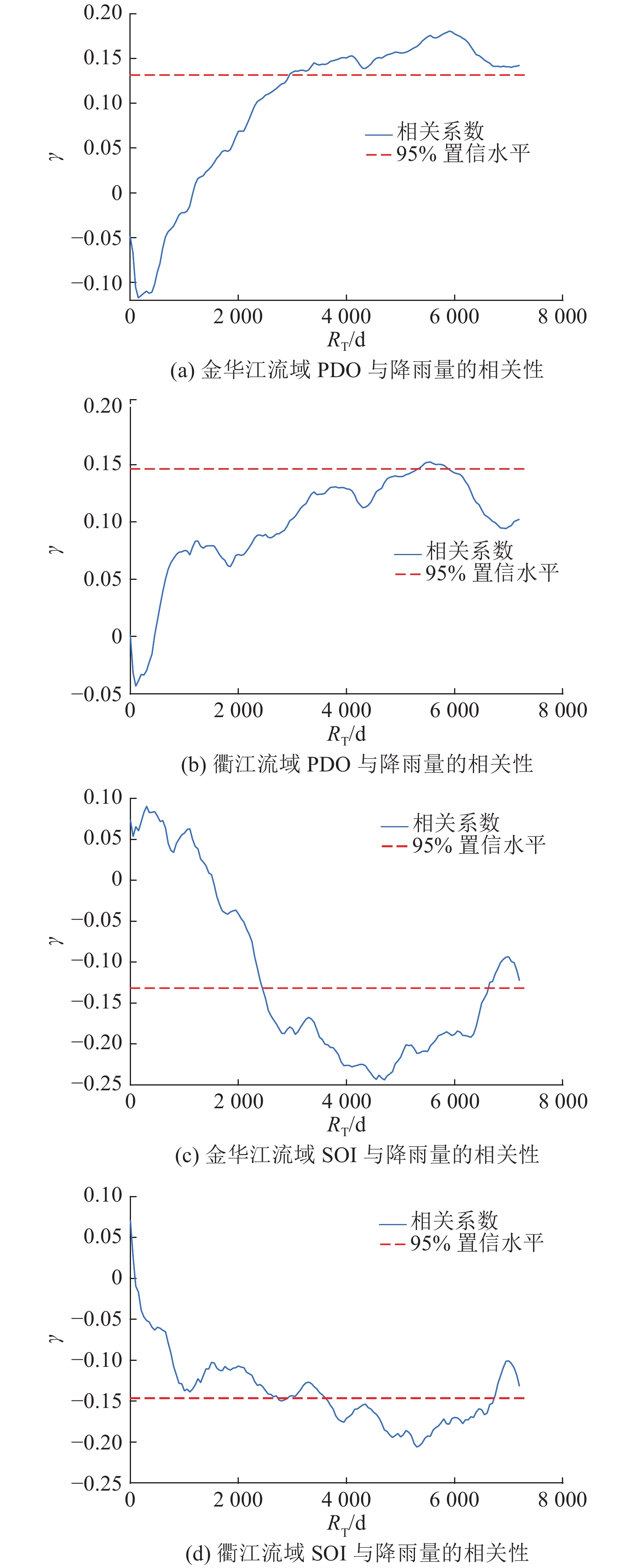
PDO和SOI在长期尺度上与降雨的相关性如图4所示，图中，γ为相关系数. 总体来说，金华江流域的相关性比衢江流域显著. 由图4(a)可知，对于金华江流域，PDO在R_T=8~18 a时可以得到与降雨量较高的相关性，极值约在R_T为16 a处出现. 而衢江流域PDO与降雨量的高相关性约出现在R_T=15~16.5 a，其显著性略高于95%置信水平，不及金华江流域显著. 考虑到PDO是一个长期指数，这个结果可以认为是合理的. 与PDO相反，SOI在2个流域均与降雨量有着显著的负相关性，其中金华江流域的最佳R_T是12~13 a，衢江流域为6.5~8 a或者10.5~11.5 a. 表1总结了如图4所示的最佳相关性的统计结果.

表 1

表 1 PDO/SOI在长期尺度上与降雨量的最佳相关性和时间分辨率 Table 1 Optimal correlation values and temporal resolutions for PDO/SOI with precipitation in long term relationship 流域 气候指数 RT/d r 金华江 PDO 3 000~6 500 0.18 SOI 3 500~6 500 −0.24 衢江 PDO 5 200~6 000 0.15 SOI 4 000~6 500 −0.21 注：下划线数据表示高于95%置信水平的显著相关性

表 1 PDO/SOI在长期尺度上与降雨量的最佳相关性和时间分辨率 Table 1 Optimal correlation values and temporal resolutions for PDO/SOI with precipitation in long term relationship

图 4

图 4 衢江流域和金华江流域降雨量与太平洋年代际振荡(PDO)以及南方涛动指数(SOI)的长期相关性 Fig. 4 Long-term correlation between precipitation and Pacific Decal Oscillation (PDO) and Southern Oscillation Index (SOI) for Jinhua subbasin and Qu subbasin

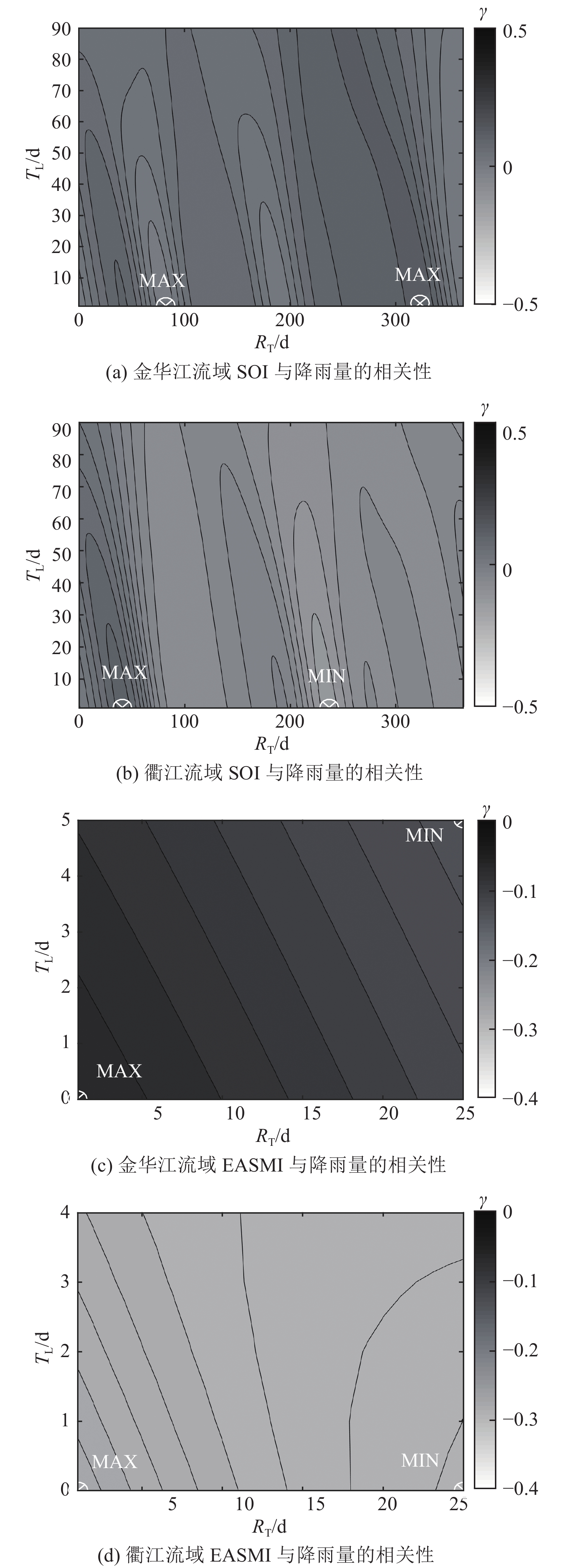
在短期尺度上，SOI与EASMI在整个研究期内随滞后时间和时间分辨率的变化情况如图5所示. 可以看出，SOI与降雨量的相关性是动荡变化的（图5（a）、（b）），每50~100 d可呈现完全相反的2种相关性. 猜想这种正负相间的相关性可能是由ENSO所处的不同阶段造成的，即厄尔尼诺和拉尼娜. 正如Jin等^[19,27]的研究所证实的，厄尔尼诺和拉尼娜与气侯的反应各不相同，同时具有完全不同的滞后效应. 相对其他2个指数来说，EASMI与降雨量具有更高的相关性，尤其是在衢江流域，具体如图5（c）、（d）所示. 在金华江流域，相关系数与T_L和R_T均呈现一定的线性关系，随着T_L和R_T的增大，相关系数不断减小. 衢江流域的相关性随T_L和R_T变化不显著，相关系数保持在−0.3左右，表现出显著的负相关性. EASMI在2个流域表现如此不同，可能与流域地理位置有关，衢州流域相比于金华江流域更偏西，处于更为内陆的地方，更少受到来自海洋等其他因素的影响^[28]。表2为图5的统计信息，γ_SOI-max为SOI与降雨量的最大相关系数，γ_SOI-min为SOI与降雨量的最小相关系数，同理，γ_EASMI-minEASMI与降雨量的最小相关系数.

表 2

表 2 SOI和EASMI在短期尺度上与降雨量的相关性 Table 2 Correlation for SOI and EASMI with precipitation in short-term scale 流域 γSOI-max γSOI-min γEASMI-min 金华江 0.019 −0.012 −0.162 衢江 0.108 −0.129 −0.287 注：下划线数据表示高于95%置信水平的显著相关性

表 2 SOI和EASMI在短期尺度上与降雨量的相关性 Table 2 Correlation for SOI and EASMI with precipitation in short-term scale

图 5

图 5 SOI和东亚夏季风指数(EASMI)与降雨量(1963—2000年)在不同滞后时间和时间分辨率时的相关性 Fig. 5 Correlation between SOI and East Asian Summer Monsoon Index (EASMI) and precipitation during 1963 to 2000 for different lag times and temporal resolutions

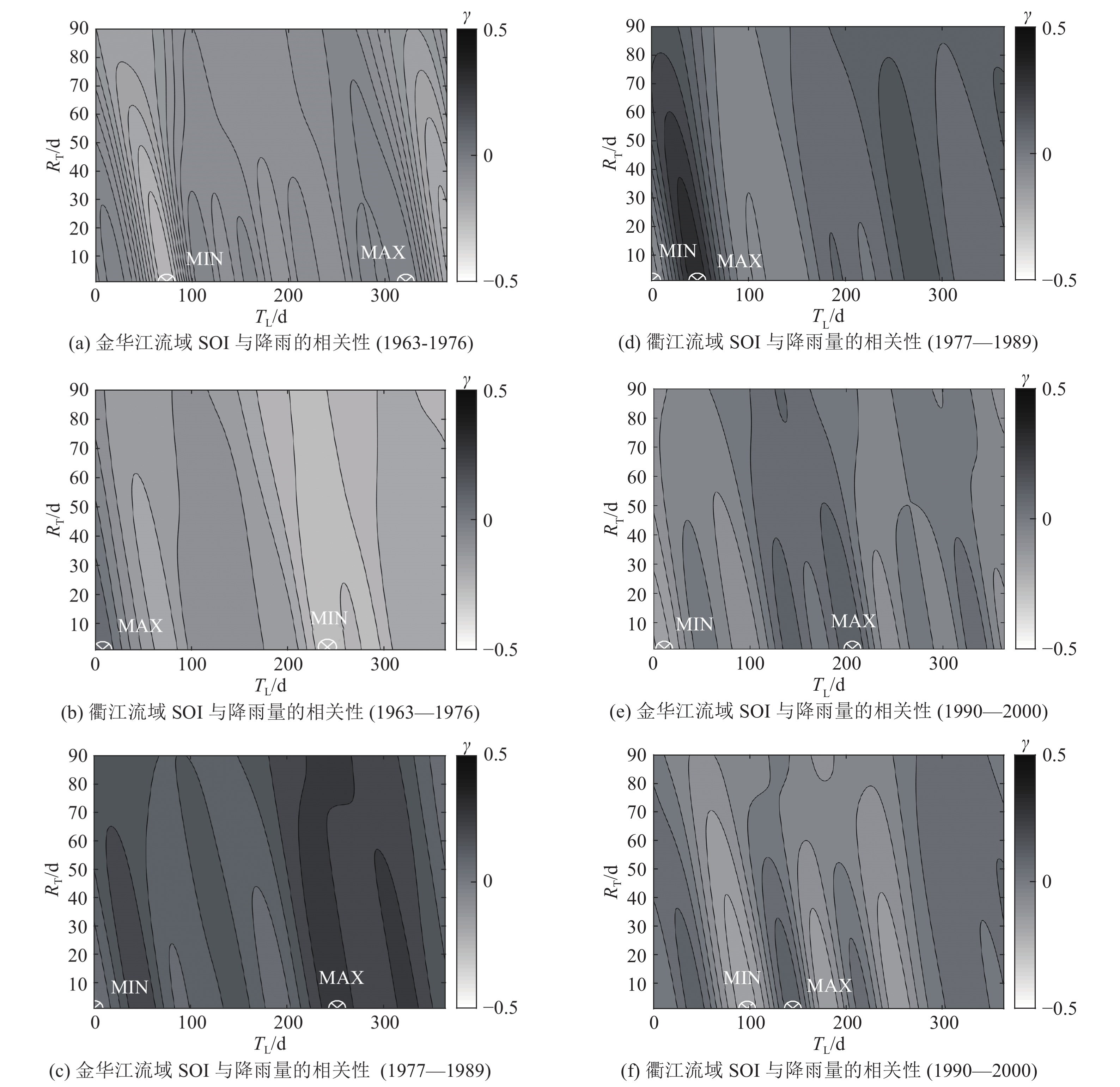
为了更深入地分析SOI和EASMI对降雨量的影响，按照如图3所示的不同PDO相位阶段划分的1963—1976，1977—1989和1990—2000三个子时期的结果如图6和7所示。可以看到大多数的相关系数极值都发生在小于一个月的时间分辨率内，这跟SOI具有的短期变化性质有关. 由表3（P为降雨量）的统计结果不难看出，SOI与降雨量在第一个子时期具有显著的负相关关系，相关系数r₁最大达到0.279. 在第二个子时期，则呈现出显著的正相关，其中衢江流域的相关系数r₂达到了0.334. 可以肯定的是，当PDO位于冷相位时，SOI与降雨量有着明显的负相关性，而PDO位于暖相位时，SOI与降雨量正相关性显著. 第三个子时期的相关系数r₃结果则较为复杂，具体可能和该时期内PDO的冷暖交替有关.

图 6

图 6 SOI与降雨量在1963—1976、1977—1989和1990—2000三个子时期内的相关性 Fig. 6 Correlation between SOI and precipitation during three different subperiods from 1963 to 1976, 1977 to 1989 and 1990 to 2000

图 7

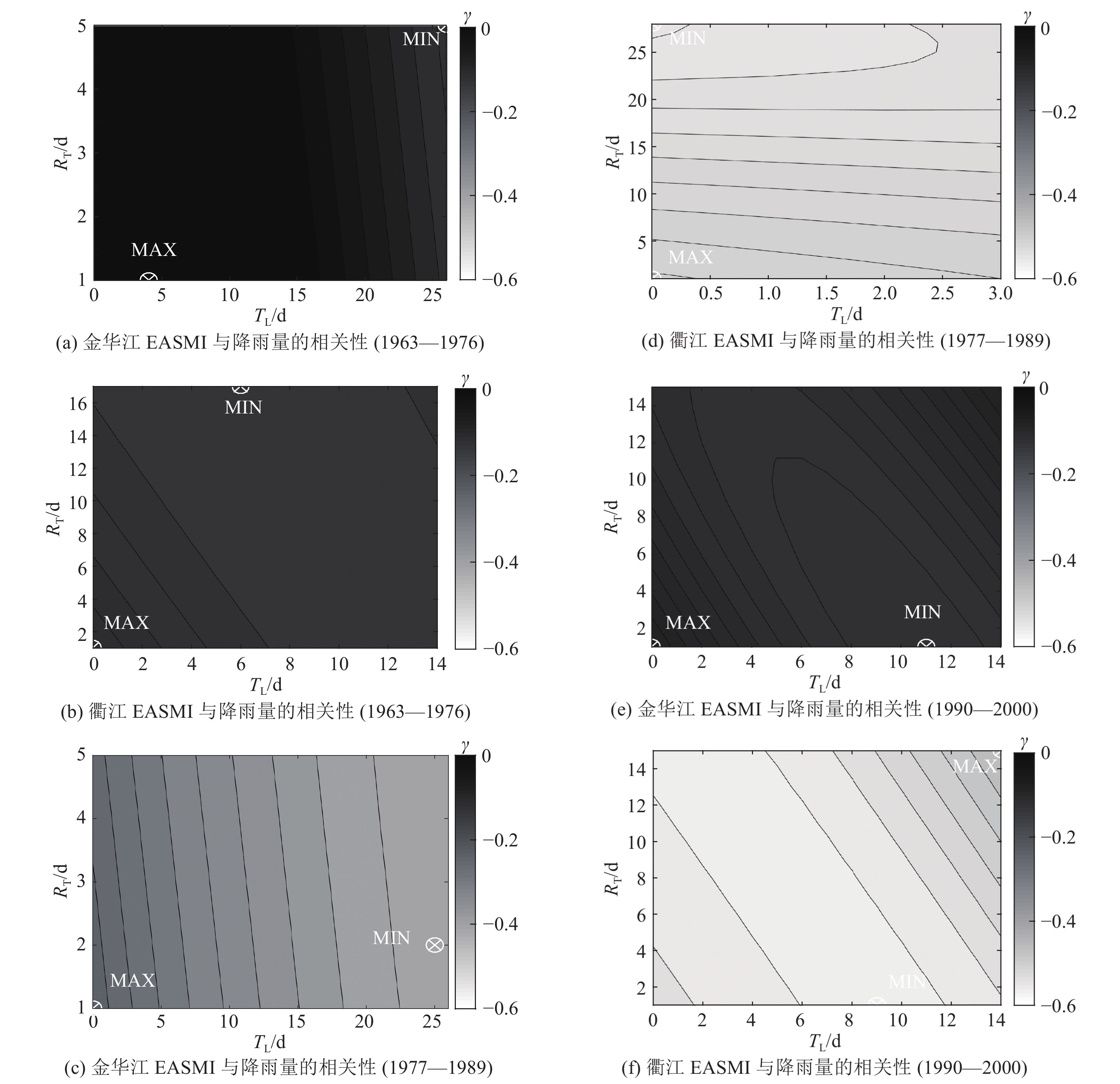
图 7 EASMI与降雨量在1963—1976、1977—1989和1990—2000三个子时期内的相关性 Fig. 7

表 3

表 3 SOI与降雨量在1963—1976、1977—1989和1990—2000三个子时期内的相关性 Table 3 Maximum correlations for SOI with precipitation for three subperiods from 1963 to 1976, 1977 to 1989 and 1990 to 2000 流域 相关性 r1 (PDO −) r2 (PDO +) r3 (PDO +/−) 金华江 SOI-P + −0.023 0.278 0.148 SOI-P − −0.240 0.031 −0.163 衢江 SOI-P + 0.085 0.334 0.137 SOI-P − −0.279 −0.078 −0.171 注：下划线数据表示高于95%置信水平的显著相关性

表 3 SOI与降雨量在1963—1976、1977—1989和1990—2000三个子时期内的相关性 Table 3 Maximum correlations for SOI with precipitation for three subperiods from 1963 to 1976, 1977 to 1989 and 1990 to 2000

如图7所示为EASMI与降雨量在3个子时期内的相关关系，可以看到，相比起其他子时期，第一个子时期（1963—1976）的相关性最为不显著，这可能和前文所提及的PDO处于冷相位时，长江流域下游及其周边区域降水较少有关. 总体而言，降雨量与EASMI存在显著的负相关性，且该相关性主要受滞后时间的影响。金华江流域最显著的相关性发生在第二个子时期，最大负相关系数达到0.407，最佳T_L=25 d，R_T=2 d. 衢江流域的相关性比金华江更为明显，第二和第三个子时期的负相关系数都达到0.5以上，其中第二子时期的最佳T_L=0，R_T达到30天，第三个子时期的最佳T_L=9 d，最佳R_T=1 d. 相应的最高相关系数的统计结果呈现在表4内，表中，γ_min为相关系数最小值；“+”表示实际的最佳值可能大于目前率定值，因为数据靠近设定的边界值。

表 4

表 4 EASMI与降雨量在1963—1976，1977—1989和1990—2000三个子时期内的相关性 Table 4 Correlations for EASMI with precipitation for three short subperiods from 1963 to 1976, 1977 to 1989 and 1990 to 2000 时期 金华江 衢江 γmin TL/d RT/d γmin TL/d RT/d 1963—1976 −0.128 26+ 5+ −0.134 6 17+ 1977—1989 −0.407 25 2 −0.527 0 28+ 1990—2000 −0.129 11 1 −0.567 9 1 注：下划线数据表示高于95%置信水平的显著相关性

表 4 EASMI与降雨量在1963—1976，1977—1989和1990—2000三个子时期内的相关性 Table 4 Correlations for EASMI with precipitation for three short subperiods from 1963 to 1976, 1977 to 1989 and 1990 to 2000

指数组合与降雨量的多元回归分析结果如图8和表5所示，其中T_L-EASMI为气候指数EASMI的滞后时间，R_T-PDO为气候指数PDO的时间分辨率，R_T-SOI为气候指数SOI的时间分辨率. 对于PDO和SOI（长期尺度），只研究R_T对其相关性的影响，而研究EASMI时则只对T_L进行调整，从图7可知，EASMI对T_L更为敏感. 多元回归分析最重要的结论是，所有的指数组合都能得到与降雨量更为显著的正相关性. PDO-SOI组合的相关系数比分别采用PDO和SOI单独评估时的相关性高很多；金华江流域PDO-SOI与降雨量的相关性达到0.39，而单独的PDO相关性为0.19，SOI为−0.24；衢江流域PDO-SOI组合与降雨量的相关性最大达到0.28，而单独的PDO和SOI与降雨量的相关系数分别仅为0.14和−0.2.可见，PDO-SOI组合可以有效地提高降雨量与气候指数的相关性. 对于EASMI相关的组合，相关系数的提高主要集中在金华江流域，其中EASMI与PDO和SOI的指数组合与降雨量的相关系数分别达到0.45和0.41，而单独的EASMI与降雨量的相关系数仅为−0.162. 多元回归后，EASMI与降雨的负相关性消失了，这是由于回归公式中EASMI的回归系数为负值. 当相关系数达到最佳时，各气候指数的回归系数总结在表6中，b₁和b₂为回归系数. 可以看到，EASMI在回归组合中的系数始终为负值，且系数通常较大，可见在组合中更多的权重倾向于分配给区域性的气候指数EASMI. 此外，从图8（a）~（d）可以看出，与图7相比，滞后时间对EASMI相关的指数组合与降雨量的相关性的影响变得微乎其微。

图 8

图 8 降雨量与气候指数多元回归分析的相关性 Fig. 8 Correlation for multiple regression analysis between precipitation and climate indexes

表 5

表 5 降雨量与气候指数组合的多元回归分析相关系数值 Table 5 Correlation values of multiple regression analysis between precipitation and climate index compositions 流域 指数组合 r RT-PDO/d RT-SOI/d TL-EASMI/d 金华江 PDO-SOI 0.39 200~1 800 4 000~5 000 − EASMI-PDO 0.45 200~800 − 25 EASMI-SOI 0.41 − 4 500~5 500 25 衢江 PDO-SOI 0.28 200~1 000 5 000~6 000 − EASMI-PDO 0.45 2 200 − 19 EASMI-SOI 0.44 − 1 300 17 注：下划线数据表示高于95% 置信水平的显著相关性

表 5 降雨量与气候指数组合的多元回归分析相关系数值 Table 5 Correlation values of multiple regression analysis between precipitation and climate index compositions

表 6

表 6 获得最佳相关性时多元回归的回归系数 Table 6 Coefficient for multiple regression analysis when optimal correlation is obtained 流域 指数组合 b1 b2 金华江 PDO-SOI −4.80 −2.92 EASMI-PDO −9.04 −6.35 EASMI-SOI −1.51 −2.85 衢江 PDO-SOI −3.70 −4.09 EASMI-PDO −8.28 5.57 EASMI-SOI −6.17 −1.42 注：b1和b2分别与相应的指数组合的第一、第二个气候指数对应。

表 6 获得最佳相关性时多元回归的回归系数 Table 6 Coefficient for multiple regression analysis when optimal correlation is obtained

兰江流域的降雨量在日尺度上均与PDO存在较为显著的正相关性，其中金华江流域的最佳时间分辨率约为16 a，衢江流域约为15 a，但显著性不及金华江流域显著. 从长期尺度来讲，SOI与降雨量存在显著的负相关性，负相关系数达到0.2以上；在短期尺度上，兰江流域受EASMI的影响更为显著，特别是衢江流域，最大负相关系数为0.278. 3个子时期的相关性评估结果证实SOI和EASMI与降雨量的相关性均受PDO所处相位的影响，当PDO位于暖相位时，SOI与降雨量正相关性明显，EASMI与降雨量的负相关性显著. 同时，由不同指数组合PDO-SOI，SOI-EASMI和EASMI-PDO的多元回归分析可得到比简单线性回归更显著的相关关系，且均为正相关.