2. 西南交通大学 土木工程学院,四川 成都 610031
2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
钢管混凝土以其承载力和稳定性高、施工方便等优点,被广泛地用于桥梁工程中[1-3]. 但是受核心混凝土收缩徐变效应影响,其长期变形和应力重分布已经逐步代替极限承载力,成为制约大跨度钢管混凝土拱桥运营安全性的关键因素之一,越来越多地受到设计人员的重视[2]. 受拱桥施工过程影响,钢管往往会首先承受荷载[4],在钢管内灌注混凝土后,钢管与混凝土才共同受力,因此钢管初始应力大小对钢管混凝土收缩徐变效应的影响是一个实际工程问题,需要着力解决. 另外,钢管与混凝土之间的黏结滑移效应又是引起结构应力重分布的关键因素. 因此,开展考虑初始应力和黏结滑移效应的钢管混凝土收缩徐变研究可进一步提高对钢管混凝土收缩徐变规律的认识.
目前已有较多学者对钢管混凝土的长期变形性能进行了理论和试验研究[1, 4-13],对其长期变形规律和应力重分布特征有了较为深入的认识[14]. 但以往的收缩徐变分析理论均认为钢管与混凝土之间符合完全黏结假定[1, 5, 7-8, 12],该假定在钢管混凝土轴压构件中的应用效果较好[7-9],但对钢管混凝土拱桥的长期变形计算的适用性值得商榷[13],且相关学者对该假定的适用条件研究较少. 现阶段相关学者仅对钢管混凝土中钢管或混凝土的收缩或徐变应变进行了单方面测试[5-6, 11-12, 15-16],对钢管与混凝土应变的综合测试和差异性对比分析研究较为欠缺[17-19]. 另外,目前相关学者对考虑初应力[4-20]和黏结滑移效应[21-22]的钢管混凝土极限承载力进行了诸多研究,研究表明初始应力较大的钢管混凝土构件极限承载力会减低[20],钢管与混凝土黏结滑移效应会直接影响到钢管与混凝土的应力重分布及刚度[13]. 但考虑钢管初始应力及屈服后,其收缩徐变性能如何,目前尚未见报道.
本文基于ANSYS有限元程序[23],建立钢管混凝土收缩徐变分析的三维实体有限元模型,通过ANSYS内部应力读写功能[24]实现钢管的初始应力模拟,并用弹簧单元模拟钢管与混凝土之间的黏结滑移效应,准确方便地实现了考虑钢管初始应力、钢管屈服和黏结滑移效应的钢管混凝土长期变形计算分析研究.
1 初始应力和收缩徐变效应模拟 1.1 初始应力在ANSYS15.0版本中,初始应力的读取仅限于高阶单元SOLID185[23],不适合于低阶单元SOLID95,因此钢管需用SOLID185单元模拟. 软件中内置的显式徐变算法仅适用于低阶单元SOLID95,不适用于高阶单元SOLID185,因此管内混凝土采用SOLID95单元模拟.
钢管初始应力的模拟分2步:1)分别建立钢管与混凝土的三维实体有限元模型,保证钢管与混凝土处于分离状态,在钢管上施加初始应力,进行钢管初始应力分析,用“INISTATE,WRITE,”命令将分析得到的钢管内节点应力存储到ANSYS根目录下的.ist文件中;2)重新建立处于分离状态的钢管与混凝土三维实体有限元模型,在钢管与混凝土之间相同坐标的2个节点之间建立3个方向上不同刚度的弹簧单元模拟钢管与混凝土之间的黏结效应. 通过“INISTATE,READ,”命令读取存储到.ist文件中的钢管初始应力,同时在钢管上施加与步骤1)相同的初始应力.
对考虑上述2种荷载作用的钢管混凝土结构进行有限元分析,即可获得较为满意的钢管初始应力. 此方法可保证混凝土内几乎无应力,且截面上不会产生初始应力变形.
1.2 混凝土徐变效应ANSYS有限元程序中自带的金属蠕变算法可用于混凝土徐变计算[23],且该方法已得到相关学者验证[24]. 本文核心混凝土的徐变采用显式蠕变算法中C6=0的徐变方程,则混凝土的徐变应变增量可表示为
| $ \Delta {\varepsilon _{{\rm{cr}}}} = {C_{\rm{1}}}{\sigma ^{{C_{\rm{2}}}}}\varepsilon _{}^{{{\rm{C}}_{\rm{3}}}}{e^{ - {C_{\rm{4}}}/T}}\Delta t .$ | (1) |
式中:Δεcr为混凝土徐变应变增量;C1、C2、C3、C4为系数,
| $ {C_1} = \frac{{\Delta \varphi }}{{\Delta t\left[ {\varphi (t, {t_0}) + 1} \right]}},\quad{C_2} = {C_4} = 0,\;{C_3} = 1; $ |
σ为混凝土总应力;ε为徐变应变;T为混凝土单元温度;Δt为时间增量;Δφ为徐变系数增量;φ(t,t0)为t时刻,加载龄期为t0的徐变系数,可按文献[25]计算.
1.3 混凝土收缩效应目前在使用ANSYS有限元程序进行混凝土的收缩计算时,主要采用等效降温荷载法[9].
假定t时刻混凝土的收缩应变为εsh(t,t0),可按CEB90模型计算[25];混凝土的参考温度为T0,取293 K;热膨胀系数为α,取1×10−5 °C−1,则混凝土收缩应变可转化为t时刻的等效温度荷载:
| $ T(t) = - {\varepsilon _{{\rm{sh}}}}(t, {t_0})/\alpha + {T_0} .$ | (2) |
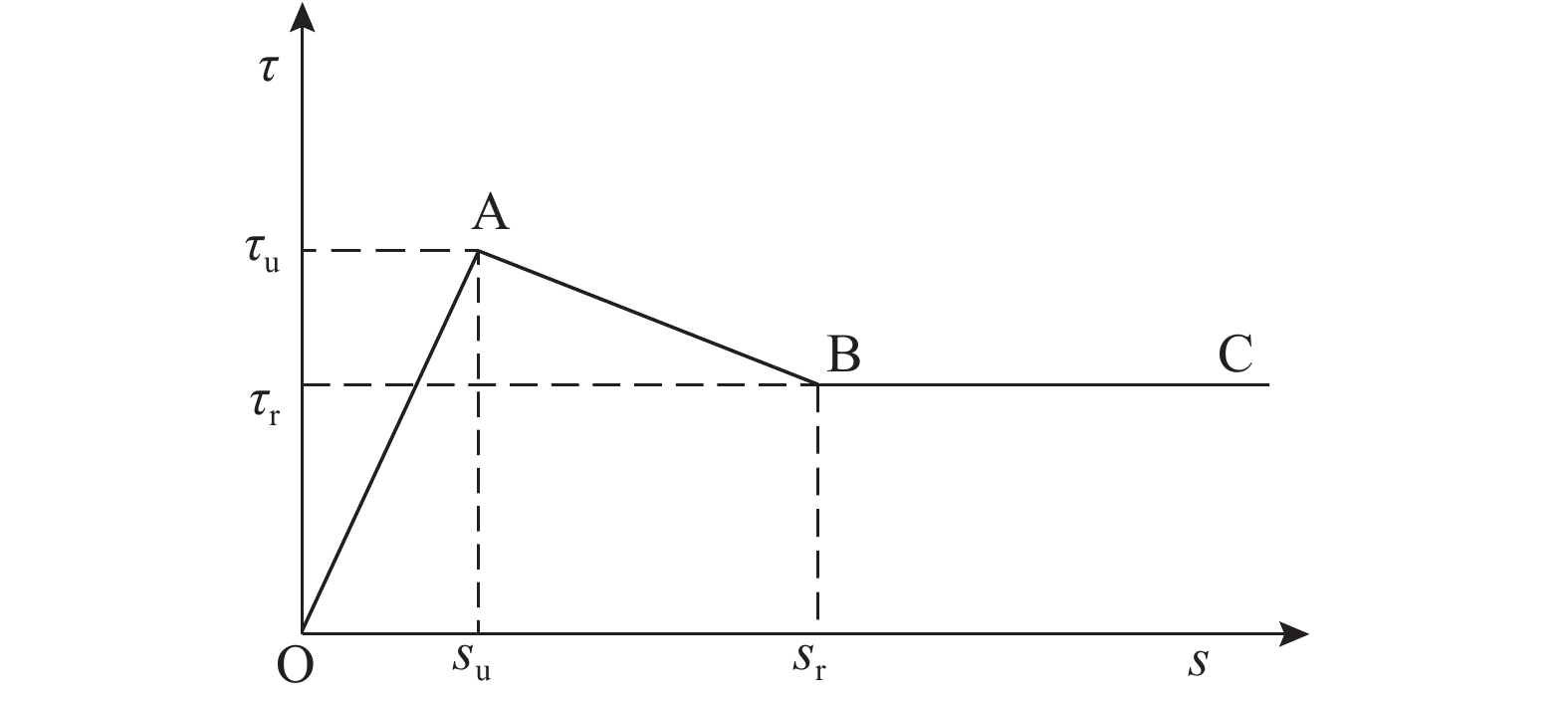
刘玉茜[22]通过对大量钢管混凝土考虑黏结滑移效应的推出试验结果进行分析,得到如式(3)~(5)所示的钢管混凝土黏结滑移曲线方程:
| $ \tau {\rm{ = }}\left\{ \begin{array}{l} 0.4s,\qquad\qquad\quad 0 < s \leqslant su;\\1.2{\tau _u} - 0.2\frac{{{\tau _u}}}{{{s_u}}}s,\quad {s_u} < s \leqslant {s_r};\\0.6{\tau _u},\qquad\qquad\;\;\, {s_r} < s.\end{array} \right. $ | (3) |
圆钢管混凝土:
| $ {\tau _{\rm{u}}} = 1.485\;7 - 0.021\;7\frac{d}{{{t_{\rm{s}}}}},\;\;d/{t_{\rm s}} \leqslant 68. $ | (4) |
方钢管混凝土:
| $ {\tau _{\rm{u}}} = 0.6\left( {1.485\;7 - 0.021\;7\frac{b}{{{t_{\rm{s}}}}}} \right),\;\;b/{t_{\rm s}} \leqslant 68. $ | (5) |
式中:τ为钢管与混凝土黏结滑移应力;s为滑移量;τu为黏结滑移峰值应力;su为与峰值应力对应的滑移值,su=2.5 τu;sr为水平段起点对应的滑移值,圆形截面为sr=3 su,方形截面为sr= 2.083 su;d为钢管直径;b为方钢管宽度;ts为壁厚.
曲线形状见图1,该曲线可较好地描述钢管混凝土的推出试验结果. 在钢管混凝土结构在徐变过程中,徐变次内力远小于推出试验过程中施加到核心混凝土上的内力,因此,滑移的变形范围主要集中在OA段.
|
图 1 钢管与混凝土之间的黏结滑移曲线 Fig. 1 Bond-slip curve between steel tube and core concrete |
在ANSYS程序中,用COMBIN39单元模拟钢管与混凝土之间的黏结滑移效应[22]. 弹簧刚度可通过输入的荷载—位移曲线自动计算. 荷载—位移曲线按下式计算:
| $ F = A \tau .$ | (6) |
式中:F为钢管轴力,A为每个弹簧对应的钢管侧面积.
在有限元建模时,钢管与核心混凝土采用相同的网格划分,以此保证接触面上的同一弹簧单元2个节点坐标相同. 并在2个节点之间采用3组不同方向的弹簧单元连接,3个方向分别代表轴向、径向和环向. 轴向单元模拟钢管与混凝土之间的黏结滑移. 径向和环向的弹簧单元刚度取轴向的1 000倍,可满足径向和环向完全黏结的要求[22].
3 计算分析方法验证 3.1 初始应力状态验证本文以文献[17]的试件为例验证1.1节给出的钢管初始应力模拟方法的正确性. 试件尺寸:长度l=560 mm;外径d=140 mm;壁厚ts=2.9 mm. 材料特性:混凝土弹性模量Ec=37.7×103 N/mm2;28 d混凝土轴心抗压强度fc28=57.1 N/mm2;泊松比µc=0.15;钢管弹性模量Es=212.7×103 N/mm2;屈服强度fy=264.7 N/mm2;泊松比µs=0.29;假定钢管初始应力为100 kN,均匀施加到钢管轴向截面.
按照1.1节方法建立如图2所示钢管混凝土有限元模型进行不同黏结滑移状态的钢管混凝土初始应力计算. 在未考虑钢管屈服时,钢管与混凝土均采用线弹性本构关系. 钢管轴向和径向的网格尺寸为0.040 和0.014 m. 表1给出了钢管与混凝土完全分离、考虑黏结滑移及完全黏结3种不同状态的钢管、混凝土应力与钢管顶端位移对比情况. 表中给出的应力和位移方向均为沿钢管轴线方向. 表中,Sc为钢管位移;σs为钢管应力;σc为钢管应力. 由表1可知,3种状态下钢管应力分布完全相同,且钢管顶端位移为0,仅完全黏结状态会产生最大为10−6 mm数量级的位移,完全可忽略不计. 钢管的初始应力计算会受到黏结滑移状态影响,因此不同黏结状态会对混凝土应力产生一定影响,随着黏结度增加,混凝土应力逐渐增大. 完全黏结状态下,混凝土最大应力仅为5 N/m2,也可忽略不计. 以上分析表明,本文的钢管初始应力模拟方法可适用于不同黏结状态下的钢管混凝土初始应力分析. 计算结果能满足钢管应力为设计值而管内混凝土无应力、截面无位移的目的.
| 表 1 不同黏结滑移状态的钢管混凝土位移和应力对比 Table 1 Comparison of initial stress results in CFST considering different bond-slip effect |

|
图 2 钢管混凝土(CFST)横截面的有限元网格划分 Fig. 2 Mesh of finite element model in cross-section of concrete filled steel tube (CFST) |
以文献[21]的YG8钢管混凝土推出试验为例,验证第2节采用COMBIN39单元模拟钢管混凝土黏结滑移效应方法的正确性. YG8试件尺寸:l=460 mm; d=115 mm; ts=4 mm;材料特性:fc28=32.3 N/mm2;fy=325 N/mm2;Ec=2.8×104 N/mm2,Es=2.06×105 N/mm2;µc=0.167,µs=0.3;t0=14 d;极限承载力Nu=165 kN;与峰值应力对应的滑移量su=2.487 mm.
图3给出了按照本文方法计算的荷载—滑移F-S曲线与试验结果的对比情况. 由图3可知,本文方法计算的钢管混凝土荷载滑移曲线与试验结果吻合较好,证明了本文用弹簧法模拟钢管与混凝土的黏结滑移效应的正确性.

|
图 3 荷载滑移曲线计算值与试验结果对比 Fig. 3 Comparison of load-slip curves between calculated and experimental results |
为研究黏结滑移效应对钢管混凝土收缩徐变的影响,Kwon等[17]进行了仅在核心混凝土施加320 kN轴向压力,且底部仅约束核心混凝土的钢管混凝土长期变形试验,试件尺寸和材料参数同3.1节. 与此同时,根据素混凝土收缩徐变试验得到了管内混凝土修正ACI209徐变模型[17].
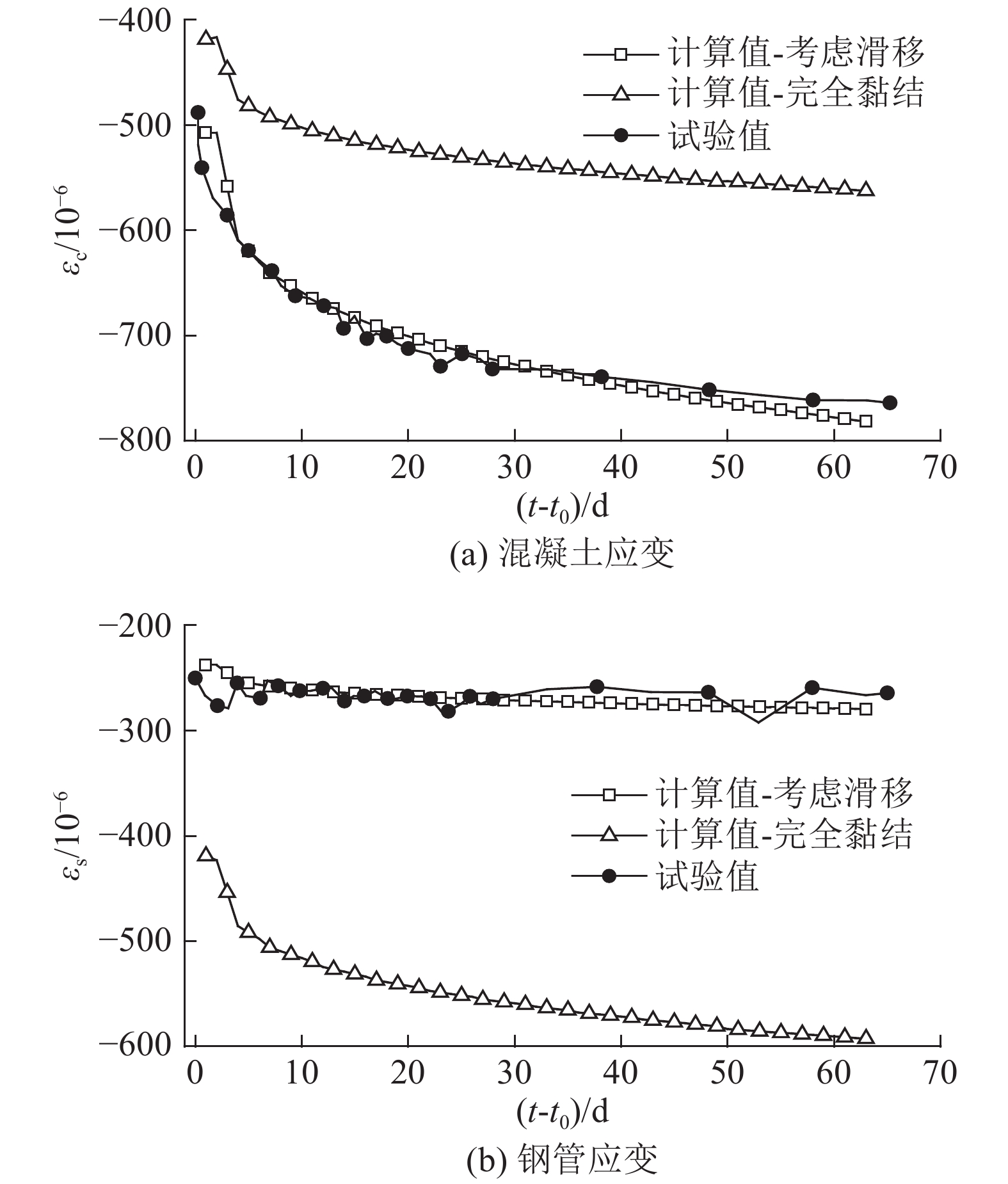
根据本文方法建立考虑黏结滑移效应的钢管混凝土收缩徐变有限元模型,徐变系数按文献[17]的修正ACI209模型取值,收缩按CEB90模型[25]计算,相对湿度取96 %. 混凝土应变εc和钢管应变εs计算结果与试验结果对比情况见图4. 图中,t-t0为持续荷载时间. 由图4可知,当考虑钢管与混凝土之间的黏结滑移效应时,钢管和混凝土应变的计算结果与试验结果吻合较好. 若计算时认为钢管与混凝土之间完全黏结,则提取的钢管应变比实测值大,而混凝土应变比实测值小,这明显与试验结果不符. 因此针对底部仅约束核心混凝土的钢管混凝土收缩徐变试件而言,考虑钢管与混凝土之间的黏结滑移效应更为合理. 不同约束条件和加载方式的钢管混凝土收缩徐变计算将在4.3节作深入分析.
|
图 4 考虑黏结滑移的钢管混凝土收缩徐变结果与试验结果对比 Fig. 4 Comparison between calculated and experimental shrinkage and creep results of CFST considering bond-slip |
第4.1和4.2节以Kwon等[17]进行的钢管混凝土收缩徐变试验试件为例分析钢管初始应力和屈服对混凝土长期变形和应力重分布效应的影响. 由于钢管混凝土底部约束条件为钢管与混凝土完全约束,考虑钢管与混凝土之间完全黏结.
第4.3节以Yamada等[19]的CR-40-4.5和CR-40-3.2方钢管混凝土徐变试件为例探讨黏结滑移效应对长期变形和应力重分布特征的影响. 试件尺寸:l=396 mm;ts=4.36 mm,3.12 mm;钢管宽度b=100.12 mm;fc28=13.57 N/mm2;Ec=17.12×103 N/mm2;fy=312.07 N/mm2;Es=184.96×103 N/mm2,t0=28 d,持续时间为100 d.
本节分析时,混凝土收缩徐变计算采用CEB90模型[25],t0=7 d,相对湿度取96 %. 按实际选取构件理论厚度和混凝土强度.
4.1 钢管初始应力参数分析时,钢管初始轴力分别为0、100、200、300 kN. 核心混凝土轴力恒为170 kN,将均布荷载均匀施加到钢管和混凝土截面,且假定钢管与混凝土均处于弹性工作阶段. 表2和3分别给出了不同初始应力下,考虑和不考虑黏结滑移的钢管应力随时间的变化情况. 表中φ为不同加载龄期的徐变系数. 由于核心混凝土的应力变化与钢管相同,表2和3仅列出了初始阶段及持荷21、65 d时的钢管轴向应力结果.
| 表 2 考虑黏结滑移效应的钢管应力 Table 2 Steel tube stress considering bond-slip |
| 表 3 不考虑黏结滑移的钢管应力 Table 3 Steel tube stress without considering bond-slip |
由表2和3可知,无论是否考虑钢管与混凝土的黏结滑移,随着钢管初始应力增加,均会增加相同大小的钢管应力,即钢管轴向内力每增加100 kN,钢管应力增加80.1 N/mm2,该应力不随时间变化而变化. 钢管初始应力对混凝土收缩徐变引起的截面应力重分布无影响,仅会增大钢管应力.
4.2 钢管屈服既有研究表明,受核心混凝土收缩徐变影响,钢管与混凝土之间会产生应力重分布,即钢管应力会随时间变化逐渐增大,混凝土应力随时间变化逐渐减小[3, 5-12]. 若初始阶段的钢管应力较大,则受混凝土收缩徐变的应力重分布影响,钢管应力较大并可能发生屈服,钢管屈服后的钢管混凝土收缩徐变性能是否会影响结构安全性也需要进一步分析. 下面将探讨钢管MISE屈服应力为264.7 N/mm2,管内混凝土轴力370 kN,钢管初始轴力为140、160、180、200、220 kN时的钢管混凝土收缩徐变效应. 钢管屈服分析时,钢管的本构关系取理想弹塑性本构模型.
图5给出了不同钢管初始应力下的钢管应力σs、管内混凝土应力σc、混凝土应变εc、钢管混凝土顶部变形Sc随持荷时间t−t0的变化情况. 由图5可知,当施加的钢管初始轴力为140和160 kN时,钢管的初始应力较小,且持荷65 d时,钢管也未发生屈服. 随着钢管初始轴力增加,施加160 kN时的钢管应力均比140 kN时的钢管应力大16 N/mm2,且此时管内混凝土的应力和应变变化均基本相同. 再次证明了若钢管在徐变后仍处于弹性阶段,钢管初始应力对钢管混凝土的应力重分布无影响.

|
图 5 考虑钢管屈服效应的钢管混凝土收缩徐变结果对比 Fig. 5 Comparison of shrinkage and creep results of CFST considering yield effect of steel tube |
当钢管初始轴力增大到180 kN时,在初始阶段钢管处于弹性工作阶段,钢管轴力对混凝土应力重分布无影响. 但随着时间变化,钢管会发生屈服,屈服后钢管应力基本维持不变,混凝土应力减小幅度也会相应减小. 当钢管轴力继续增大为200或220 kN后,刚加载时,钢管即发生屈曲,随着管内混凝土的收缩徐变,钢管应力和管内混凝土应力基本保持不变,但钢管施加的初始应力增大会引起管内混凝土的应力增大.
由图5(d)可知,当钢管初始轴力为140和160 kN时,钢管混凝土的顶部位移相同,初始轴力对钢管混凝土变形无影响. 但随着初始应力增大,钢管混凝土的顶部位移随时间变化增速加快. 与140 kN相比,当钢管轴力为180、200和220 kN时,持荷65 d时的钢管混凝土顶部位移增量分别为−0.006、−0.025、−0.049 mm.
以上分析表明:若钢管初始轴力较小,且发生徐变后,钢管仍未发生屈服,则初始应力对钢管混凝土的长期变形和应力重分布无影响,仅会增加钢管的轴向应力. 若钢管初始轴力较大,虽然在初始加载阶段钢管未发生屈服,但徐变后会发生屈服. 钢管屈服后,钢管与混凝土之间的应力重分布不再发生,但是截面上钢管或混凝土的位移变化速率会继续增大,且增加幅度较钢管未屈服时的位移大. 这说明钢管屈服会增加变形速率,进而影响结构安全性. 因此,对于大跨度桥梁而言,应控制初始阶段钢管轴力,给混凝土徐变后的钢管应力增长预留一定空间,防止钢管屈服引起影响结构正常使用的变形.
4.3 黏结滑移文献[19]给出了钢管和混凝土的轴力随时间变化的关系,且黏结滑移效应主要影响钢管与混凝土的应力重分布. 试验中钢管混凝土底部的钢管与混凝土完全约束. 图6给出了考虑和不考虑黏结滑移的钢管和混凝土应力计算结果与试验结果的对比情况. 由图6可知,钢管与混凝土之间完全黏结的计算结果与试验结果吻合较好,而考虑钢管与混凝土之间黏结滑移的曲线明显低估了钢管应力而高估了混凝土应力. 证明了按照现有钢管与混凝土之间完全黏结假定进行的钢管与混凝土的徐变分析对底部钢管与混凝土完全约束的构件是合理的.

|
图 6 考虑与不考虑黏结滑移效应下的钢管和混凝土应力随时间变化结果 Fig. 6 Stresses of steel tube and concrete with time considering or without considering bond-slip effect |
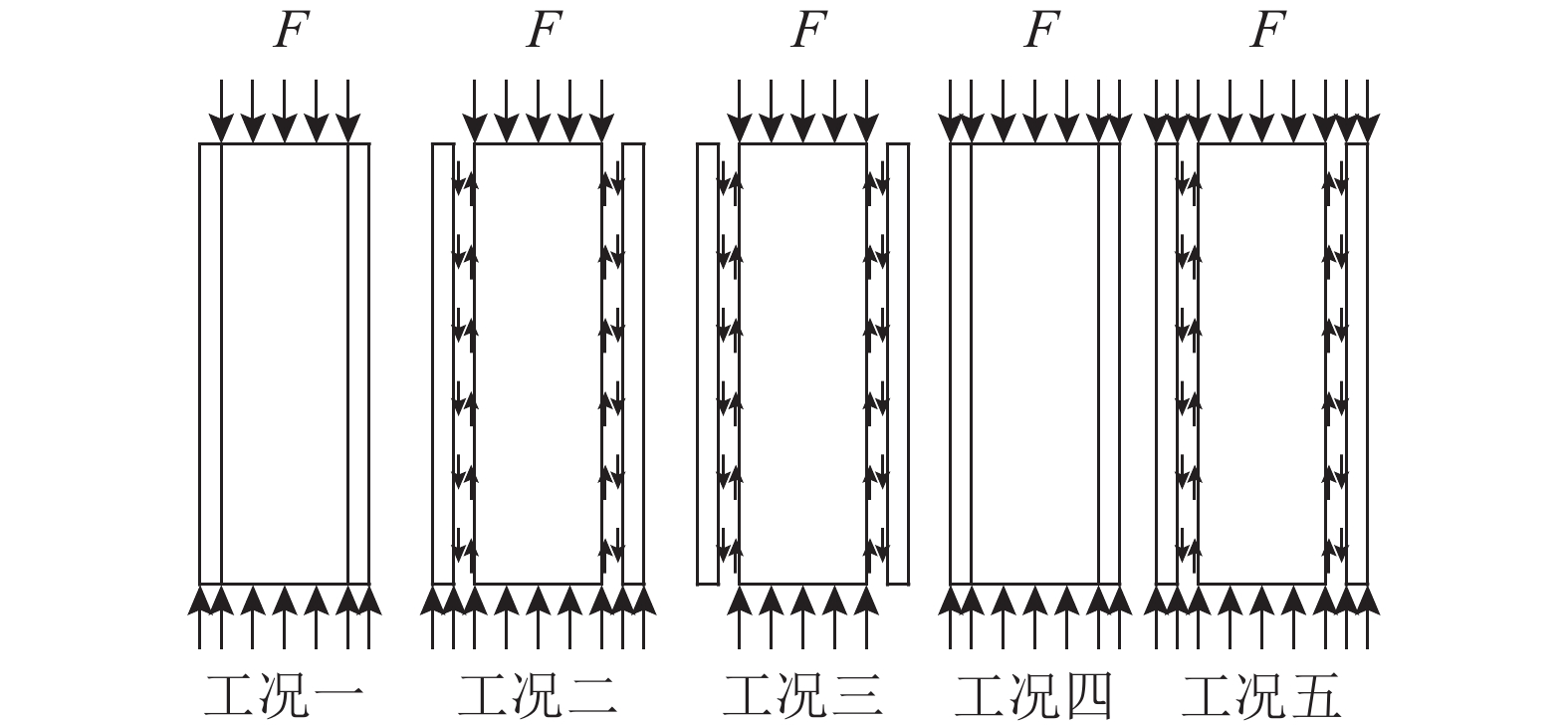
对比图4和图6可知:图4中仅约束核心混凝土时,考虑黏结滑移的有限元分析结果与试验结果吻合较好,但当同时约束底部钢管与混凝土(见图6)后,不考虑黏结滑移(即完全黏结)的有限元分析结果与试验吻合较好. 证明了不同约束和加载条件可能是影响考虑与不考虑黏结滑移效应的关键因素之一,因此下面将专门对不同约束和加载条件下(荷载工况如图7所示)的钢管混凝土试件进行收缩徐变效应分析.
|
图 7 钢管与混凝土黏结滑移及轴向荷载施加的工况分类 Fig. 7 Classification of axial load conditions and bong-slip effect between steel tube and core concrete |
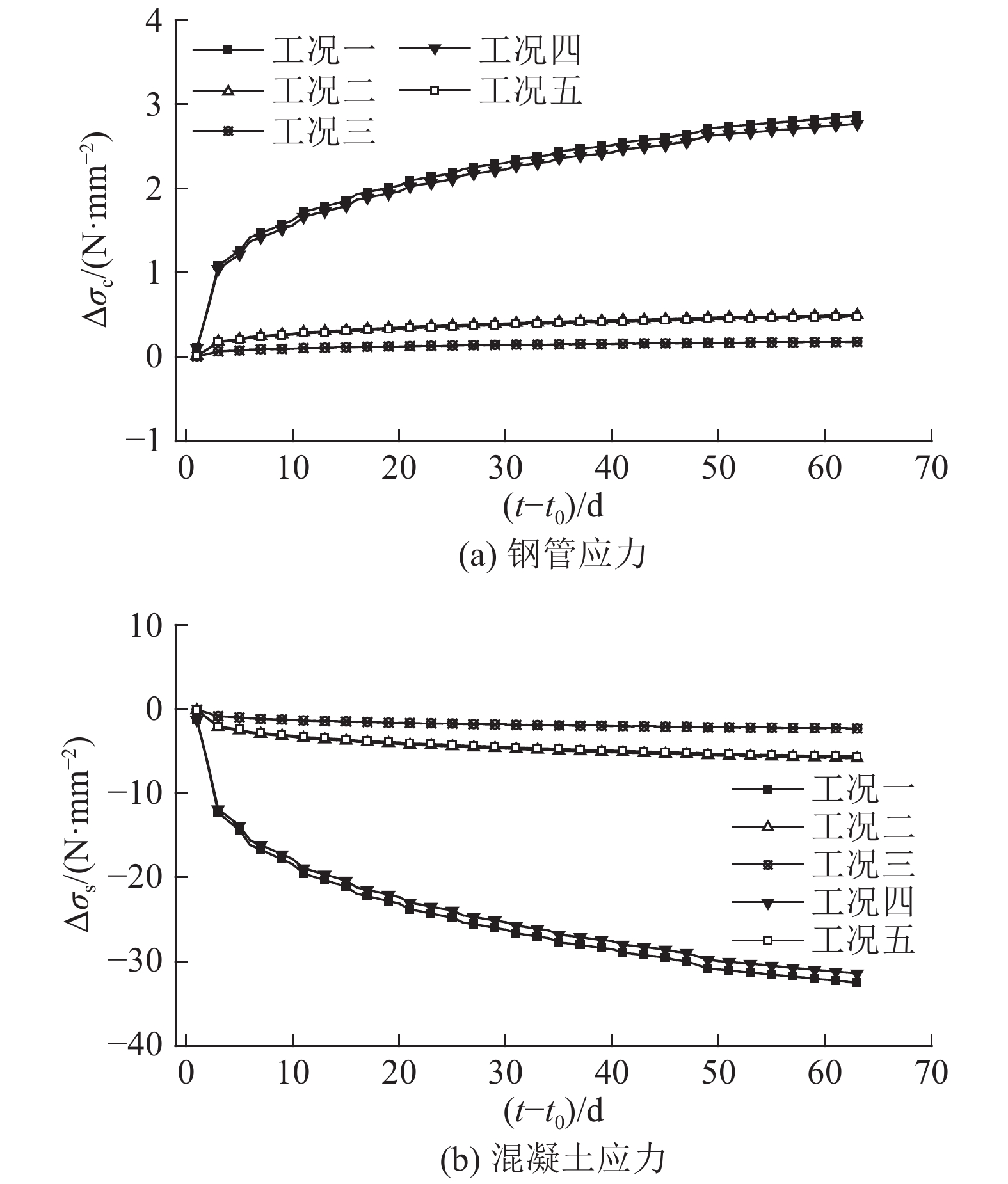
图8给出了不同边界和约束条件下的钢管和混凝土收缩徐变应力增量△σs和△σc随时间的变化关系. 图8中负值表示压应力增加,正值表示压应力减小. 由图8可知,工况一和工况四均为钢管与混凝土完全黏结,因此钢管与混凝土之间的应力重分布较大. 且由于工况一仅在核心混凝土上施加轴力,因此工况一的应力重分布大于工况四,工况一在持荷63 d后,混凝土和钢管的压应力增量可分别减小2.9 N/mm2和增加32.5 N/mm2,分别为初始阶段弹性应力的19.8 %和40.1 %. 与图6相似,工况二和工况五均考虑实际滑移效应,而同样也是仅施加到核心混凝土构件的应力重分布较大. 因此工况二计算得到的混凝土和钢管的压应力增量分别减小0.50 N/mm2和增大5.83 N/mm2,这表明考虑与不考虑黏结滑移效应对钢管与混凝土之间的应力重分布影响较大,且均匀施加到钢管与混凝土上的工况四和工况五与仅施加到核心混凝土上的工况一和工况二相比,可有效减小钢管与混凝土的应力重分布. 在所有的荷载工况中,当底部仅对核心混凝土约束时,钢管与混凝土之间的应力增量最小,说明即使是采用相同的黏结-滑移曲线,不同约束条件也会影响钢管与混凝土之间的应力重分布.
|
图 8 不同荷载工况下的钢管和混凝土应力增量随时间变化情况 Fig. 8 Stress increment of steel tube and concrete with time under different load conditions |
(1)本文采用的钢管初始应力及钢管与混凝土黏结滑移模拟方法可较为准确地模拟钢管混凝土的初始应力及黏结滑移效应,能满足本文计算需要;
(2)若混凝土徐变前后,钢管均处于线弹性工作阶段,则钢管初始应力不会对钢管混凝土应力重分布产生影响,发生徐变后的钢管混凝土中的钢管应力为初始应力与应力重分布应力增量之和;
(3)若混凝土徐变后,钢管发生屈服,则钢管初始应力会对钢管混凝土应力和变形产生较大影响. 主要表现为钢管屈服后,截面应力重分布效应不再发生,但是由此引起的钢管混凝土变形速率增加,显著影响结构的正常使用性能;
(4)考虑与不考虑钢管与混凝土之间的黏结滑移效应受钢管混凝土收缩徐变试块的约束条件影响较大. 在钢管混凝土构件的长期变形分析时,对于底部钢管与混凝土完全约束的构件,钢管与混凝土之间的完全黏结假定成立;但是对于仅约束钢管或混凝土的构件,需考虑钢管与混凝土之间的黏结滑移效应.
由于目前对不同约束和加载条件下的钢管混凝土长期变形试验研究较为欠缺,目前仍无法系统研究滑移效应与约束条件的关系,建议后续系统开展不同约束和加载条件下的钢管混凝土收缩徐变试验.
| [1] |
丁敏, 汪友弟, 代春辉, 等. 钢管混凝土轴心受压构件的徐变预测模型及其徐变性能分析[J]. 工程力学, 2017, 34(6): 166-177. DING Min, WANG You-di, DAI Chun-hui, et al. Creep calculation and behavior analysis of concrete-filled steel tubular member under axial compression[J]. Engineering Mechanics, 2017, 34(6): 166-177. |
| [2] |
CHEN B C, LAI Z C, VARMA A H, et al. Creep prediction models for concrete-filled steel tube arch bridges[J]. Journal of Bridge Engineering, 2017, 22(7): 1-15. |
| [3] |
王永宝. 自然环境条件下大跨度劲性骨架混凝土拱桥长期变形行为研究[D]. 成都: 西南交通大学, 2017. WANG Yong-bao. Study on long-term behavior of long span concrete arch bridge with stiffened concrete filled steel tube in natural environment [D]. Chengdu: Southwest Jiaotong University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10613-1017298579.htm |
| [4] |
张晓庆, 钟善桐, 闫善章, 等. 初应力对钢管混凝土偏压构件承载力影响的实验研究[J]. 哈尔滨建筑大学学报, 1997, 3(1): 50-56. ZHANG Xiao-qin, ZHONG Shan-tong, YAN Shan-zhang, et al. Experimental study about the effect of initial stress on bearing capacity of concrete filled steel tubular members under eccentric compression[J]. Journal of Harbin University of C.E. and Architecture, 1997, 3(1): 50-56. |
| [5] |
WANG Y Y, GENG Y, RANZI G, et al. Time-dependent behavior of expansive concrete-filled steel tubular columns[J]. Journal of Constructional Steel Research, 2011, 67(3): 471-483. DOI:10.1016/j.jcsr.2010.09.007 |
| [6] |
HAN L H, TAO Z, LIU W. Effects of sustained load on concrete-filled hollow structural steel columns[J]. Journal of Structural Engineering, 2004, 130(9): 1392-1404. DOI:10.1061/(ASCE)0733-9445(2004)130:9(1392) |
| [7] |
王玉银, 耿悦, 张素梅. 钢管微膨胀混凝土轴压短柱长期变形研究[J]. 中国公路学报, 2011, 24(6): 57-63. WANG Yu-yin, GENG Yue, ZHANG Su-mei. Research on long-term deformation of concrete-filled steel tubular stubs with expansive additive under axial loading[J]. China Journal of Highway and Transport, 2011, 24(6): 57-63. |
| [8] |
王永宝, 赵人达, 徐腾飞, 等. 钢管混凝土轴压构件徐变简化计算方法研究[J]. 公路交通科技, 2016, 33(1): 57-63. WANG Yong-bao, ZHAO Ren-da, XU Teng-fei, et al. Study on simplified creep calculation method of CFST members under axial loading[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 57-63. DOI:10.3969/j.issn.1002-0268.2016.01.009 |
| [9] |
赵金钢, 赵人达, 占玉林. 钢管混凝土轴向受压构件徐变计算方法及徐变模型对比分析[J]. 公路交通科技, 2013, 30(4): 46-52. ZHAO Jin-gang, ZHAO Ren-da, ZHAN Yu-lin. Comparative analysis of creep calculation methods and creep models for axially compressed CFST members[J]. Journal of Highway and Transportation Research and Development, 2013, 30(4): 46-52. DOI:10.3969/j.issn.1002-0268.2013.04.009 |
| [10] |
LIU H W, WANG Y, HE M. Strength and ductility performance of concrete-filled steel tubular columns after long-term service loading[J]. Engineering Structure, 2015, 100: 308-325. DOI:10.1016/j.engstruct.2015.06.024 |
| [11] |
MA Y S, WANG Y F. Creep of high strength concrete filled steel tube columns[J]. Thin Walled Structure, 2012, 53: 91-98. DOI:10.1016/j.tws.2011.12.012 |
| [12] |
NAGUIB W, MIRMIRAN A. Creep modeling for concrete-filled steel tubes[J]. Journal of Constructional Steel Research, 2003, 59(11): 1327-1344. DOI:10.1016/S0143-974X(03)00085-3 |
| [13] |
刘雪峰, 涂光亚, 易壮鹏. 钢管与核心混凝土之间的粘结单元及其应用[J]. 中外公路, 2012, 32(6): 184-189. LIU Xue-feng, TU Guang-ya, YI Zhuang-peng. Bonding element between steel tube and core concrete and its application[J]. Journal of China and Foreign Highway, 2012, 32(6): 184-189. DOI:10.3969/j.issn.1671-2579.2012.06.043 |
| [14] |
GENG Y, WANG Y Y, CHEN J. Time-dependent behavior of steel tubular columns filled with recycled coarse aggregate concrete[J]. Journal of Constructional Steel Research, 2016, 122: 455-468. DOI:10.1016/j.jcsr.2016.04.009 |
| [15] |
GENG Y, WANG Y Y, CHEN J. Time-dependent behavior of recycled aggregate concrete-filled steel tubular columns[J]. Journal of Structure Engineering, 2015, 141(10): 1-12. |
| [16] |
GENG Y, RANZI G, WANG Y Y, et al. Time- dependent behavior of concrete-filled steel tubular columns: analytical and comparative study[J]. Magazine of Concrete Research, 2012, 64(1): 55-69. DOI:10.1680/macr.2012.64.1.55 |
| [17] |
KWON S, KIM Y Y, KIM J K, et al. Long-term behavior under axial service loads of circular columns made from concrete filled steel tubes[J]. Magazine of Concrete Research, 2005, 57(2): 87-99. DOI:10.1680/macr.2005.57.2.87 |
| [18] |
ICHINOSE L, WATANABE E, NAKAI H, et al. An experimental study on creep of concrete filled steel pipes[J]. Journal of Constructional Steel Research, 2001, 57(4): 453-466. DOI:10.1016/S0143-974X(00)00021-3 |
| [19] |
YAMADA C, MORINO S, KAWAGUCHI J, et al. Creep behavior of concrete-filled steel tubular members[R]. Mie, Japan: Mie University, 1995.
|
| [20] |
张伟杰. 考虑初应力影响的钢管混凝土叠合柱在长期荷载作用下的力学性能研究[D]. 西安: 西北农林科技大学, 2016. ZHANG Wei-jie. Research on the behavior of concrete encased concrete filled steel tubular columns under long-term sustained load with preload effects considered [D]. Xi'an: Northwest Agriculture and Forestry University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10389-1016134072.htm |
| [21] |
池建军. 钢管混凝土界面抗剪粘结性能的试验研究与有限元分析[D]. 长沙: 长沙理工大学, 2004. CHI Jian-jun. Experimental study and FEA of the shear bond behavior at the interface of concrete of concrete filled steel tube [D]. Changsha: Changsha University of Science and Technology, 2004. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y611600 |
| [22] |
刘玉茜. 钢管混凝土粘结滑移性能的理论分析及ANSYS程序验证[D]. 西安: 西安建筑科技大学, 2006. LIU Yu-xi. Study on the basic theory of bond-slip between steel tube and concrete in CFT structures and numerical simulation by ANSYS program [D]. Xi'an: Xi'an University of Architecture and Technology, 2006. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y970679 |
| [23] |
ANSYS Help Release 15.0. SAS IP[CP/DK]. Inc Canonsburg, PA, ANSYS, 2013.
|
| [24] |
翁运新. 基于ANSYS二次开发的PC箱梁徐变效应分析[D]. 长沙: 中南大学, 2011. WENG Yun-xin. Analysis of creep effect of pc box girder based on two developments of ANSYS [D]. Changsha: Central South University, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1914730 |
| [25] |
COMITE EURO-INTERNATIONAL DU BETON. CEB-FIP Model Code 1990 [S]. Lausanne: Thomas Thelford, 1993: 53. https://ci.nii.ac.jp/naid/10004108525
|


