锈蚀是钢结构耐久性退化的典型形式,特别是沿海桥梁,钢材锈蚀是钢桥的主要病害. 钢材锈蚀不但影响钢板的有效截面积,锈蚀不但减少了钢板的有效截面积,而且产生蚀坑引起的应力集中使钢构件在车辆、地震等反复荷载作用下较早地萌生裂纹,从而减少了结构的使用寿命和超低周疲劳寿命. 迄今已有一些学者对锈蚀钢筋在单调拉伸以及反复荷载作用下的力学性能进行了试验研究[1-4],验证了钢筋的累计耗能性能、延性以及低周疲劳性能随着锈蚀程度增加而下降,认为锈蚀对钢筋承载能力和疲劳力学特性有不可忽视的影响.
1994年的美国Northridge地震和1995年的日本阪神地震的地震灾害表明,钢桥墩地震破坏主要表现为结构失稳和应变集中位置的超低周疲劳破坏[5-6]. 此后,不少学者对钢材的超低周疲劳破坏机理以及验算方法进行了一系列研究. 三木千寿等[7]根据塑性大应变对材料断裂韧性的影响分析了钢桥发生超低周疲劳的机理. 葛漢彬等[8-10]通过应变集中系数、Miner损伤累积准则以及Coffin-Manson公式提出了钢桥墩低周疲劳损伤计算方法. Hanji等[11-12]开发了钢材高应变幅超低周疲劳试验装置,通过包括焊缝、热影响区在内的钢材超低周疲劳试验研究提出了寿命预测模型. Kanvinde等[13-15]根据Rice的微空穴扩张理论提出了循环空穴扩张模型(cyclic void growth model,CVGM)用于预测钢材的超低周疲劳寿命. 石永久等[16]对钢框架梁柱节点进行了拉压循环试验并分析了不同参数对节点局部焊缝性能的影响. Zhou等[17]对全尺寸梁柱节点进行了循环荷载试验,验证了循环空穴扩张模型(CVGM)的有效性. 廖芳芳等[18]进行了钢管柱−梁焊接节点试件往复荷载试验以及有限元分析,证实已校准的微观断裂判据退化有效塑性应变模型(DSPS)与循环空穴扩张模型(CVGM)具有良好的精度,并发现损伤退化参数对断裂预测结果不敏感. 廖燕华等[19]对Q345钢材及其焊接接头的超低周疲劳性能进行了试验研究. 既有研究主要集中在焊缝、热影响区以及母材的低周疲劳破坏性能,而锈蚀对钢材低周疲劳性能的影响仍鲜有研究.
钢材腐蚀从形貌上可以分为均匀锈蚀和坑蚀2种形式[20]. 均匀锈蚀是金属在一个区域内厚度方向同程度减少;坑蚀是指在钢材表面集中腐蚀而引起的斑点状凹陷,即蚀坑. 相对均匀锈蚀而言,坑蚀引起局部应力集中,在地震作用下容易萌生裂纹,从而导致结构发生低周疲劳或超低周疲劳破坏. 因此,通过试验及理论分析2个方面研究蚀坑对低周疲劳性能的影响,对既有钢桥抗震性能评估以及加固设计都具有重要的参考意义.
为了研究锈蚀对钢材超低周疲劳强度的影响,本文以我国钢桥中广泛使用的Q345钢为研究对象,首先通过材料的低周疲劳试验,研究锈蚀对钢材抵抗低周疲劳破坏性能的影响. 在此基础上着眼于坑蚀对钢材低周疲劳性能的影响机理,通过精细的有限元分析,基于塑性损伤机制的循环空穴扩张模型建立低周疲劳性能与蚀坑参数的定量关系.
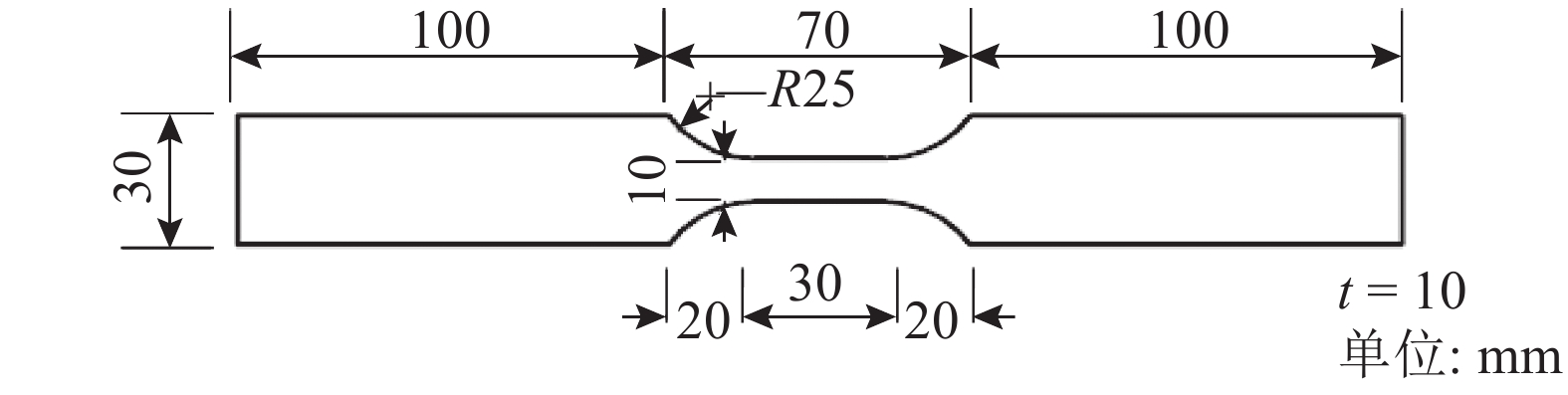
1 人工加速锈蚀试验 1.1 试验概况试验材料选择钢桥中较常用的Q345钢. 该类材料拉伸力学性能指标如表1所示,其中E为弹性模量,σs为屈服强度,σu为极限强度,δ为断后伸长率. 试样尺寸参照《金属材料轴向等幅低循环疲劳试验方法》(GB/T 15248-2008)[21],如图1所示,其中t为试样厚度.
| 表 1 Q345钢材拉伸性能 Table 1 Tensile properties of Q345 steel |
|
图 1 Q345钢试样尺寸示意图 Fig. 1 Schematic diagram of specimens Q345 steel |
腐蚀对疲劳的影响分为预腐蚀疲劳和腐蚀疲劳2个方面,前者不考虑腐蚀和疲劳的耦合作用,而后者则考虑两者的耦合影响. 本文以地震作用下锈蚀钢材的低周或超低周疲劳性能为对象,考虑到地震持续时间短,在数十秒的短时间内环境条件对疲劳损伤的影响忽略不计,因此,锈蚀试样采取预腐蚀方式制备.
钢材锈蚀采用大气中性盐雾人工加速腐蚀方法,盐雾为质量分数为5%的氯化钠溶液. 试样锈蚀后,采用稀盐酸酸洗的方法清除表面锈蚀物,浸泡后用氢氧化钙溶液进行中和,再用清水清洗并烘干,称重得到试样锈蚀后重量,并计算得到试样锈蚀率.
1.2 锈蚀试验结果与形貌锈蚀试样共6枚,锈蚀历时60 d. 锈蚀试样标记为A1~A6,质量损失率如表2所示. 表中Δm表示质量损失率. 由表中数据可知,锈蚀60 d的试样质量损失率为5.88%~6.56%. 图2为锈蚀前与锈蚀酸洗处理后试样试验段表面形貌对比,图中上方为未锈蚀试样,下方为锈蚀试样. 图3为使用LPX-600ds激光扫描仪得到的锈蚀试样试验段3D扫描图,可见锈蚀后试样试验段满布位置随机、大小不一的蚀坑. 经测量,最大的蚀坑深度约为0.47 mm,直径约为1.5 mm.
| 表 2 锈蚀试样质量损失率 Table 2 Mass loss rates of corroded specimens |

|
图 2 试样试验段锈蚀前与锈蚀酸洗后形貌对比 Fig. 2 Comparison between specimen before corrosion and corroded specimen after acid-washing |

|
图 3 锈蚀试验段3D扫描图 Fig. 3 3D scanning of corroded specimen |
为了比较坑蚀试样与未锈蚀试样超低周疲劳性能的差别,对2种试样进行大应变幅下的疲劳试验. 试验在常温环境下Instron 8802万能试验机上进行. 加载采用轴向应变控制,测量试验段应变的引伸计标距为25 mm,试验段施加的应变幅εa=1%,2.5%,应变比R=0,应变速率为0.5%/s. 应变范围属于低周及超低周范围. 试验现场如图4所示.

|
图 4 低周疲劳(LCF)试验装置 Fig. 4 Low cycle fatigue (LCF) test device |
试样包括锈蚀试样和未锈蚀试样各6枚,共计12枚. 未锈蚀试样标记为O1~O6,锈蚀试样标记为A1~A6,质量损失率约为6%. 试样分为2组:其中O1~O3与A1~A3加载的应变幅为1%,应变比R=0;O4~O6与A4~A6的加载的应变幅为2.5%,应变比R=0. 试样O3因试验机中途停机,试验结果无效.
2.2 试验结果与分析试验结果如表3所示. 其中,Nc为开裂循环次数,Nf为断裂循环次数,Et为发生疲劳断裂为止试样单位体积累计吸收的能量,根据滞回环围成的面积计算得到. 由于开裂位置难以预测,而且引伸计对观察有一定阻碍,开裂寿命近似取值为荷载峰值响应曲线的拐点. 由表3可知,未锈蚀试样在应变幅为1%和2.5%的循环荷载作用下平均寿命分别为666次和89次,而质量损失率为6%的试样为431次和68次,分别较未锈蚀试样下降35%与24%;未锈蚀试样在应变幅为1%和2.5%的作用下平均开裂寿命分别为566次和83次,而6%质量损失率的试样为333次和48次,分别较未锈蚀试样下降41%与42%. 这表明锈蚀使试样的低周疲劳寿命显著降低. 另外,锈蚀试样在1%和2.5%应变幅循环荷载作用下的平均单位体积吸收能量分别比未锈蚀钢材下降38%与34%.
| 表 3 锈蚀试样与未锈蚀试样的低周疲劳试验结果 Table 3 Results of LCF tests of corroded specimens and uncorroded specimens |
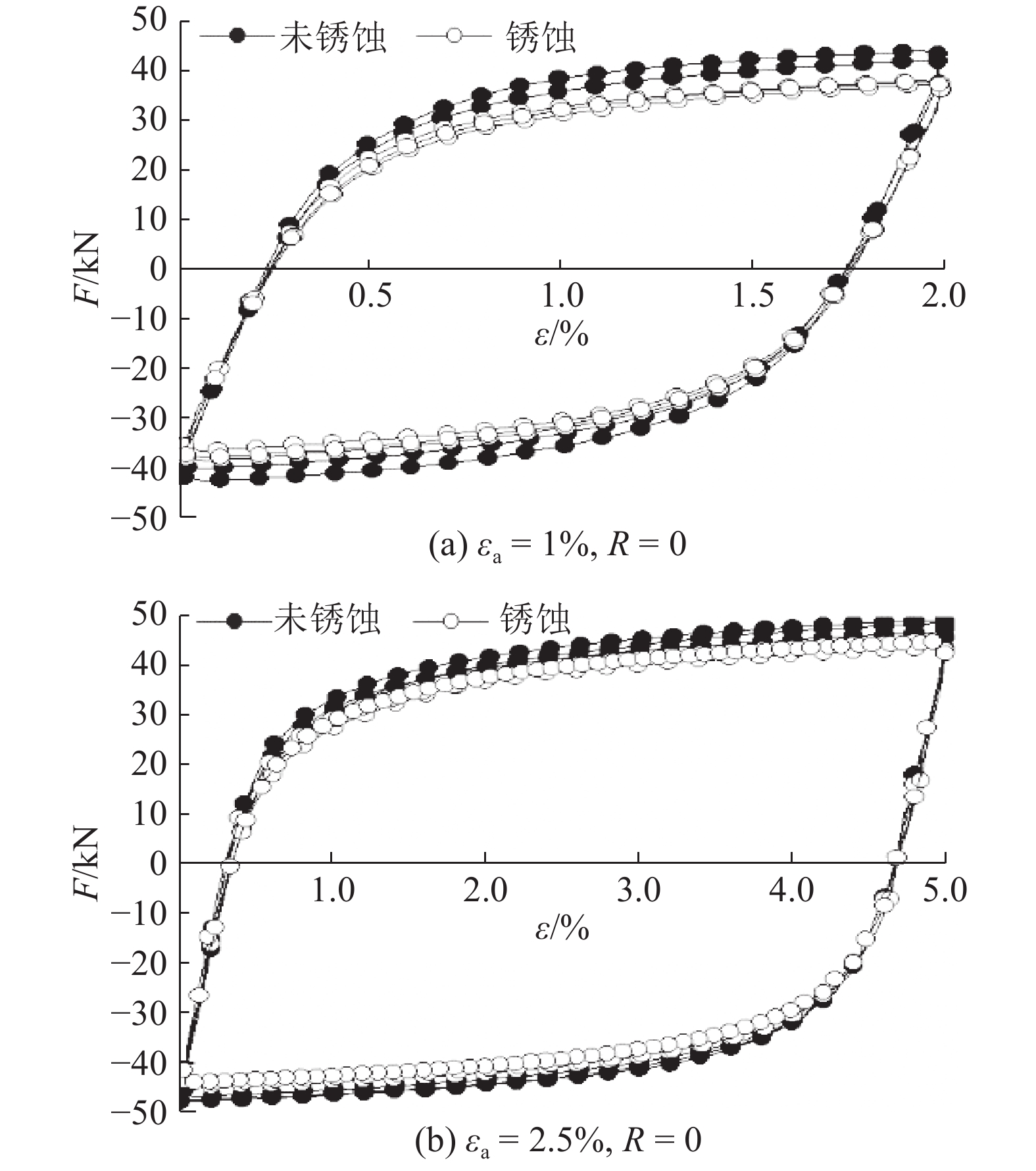
如图5所示为各试样试验过程中的稳定滞回曲线. 图中,F为循环荷载加载值,ε为试验段平均应变. 比较无锈蚀和锈蚀试样的滞回曲线可知,除了因为锈蚀引起试验段有效面积减小导致荷载峰值下降以外,在相同应变幅的情况下两者稳定状态的滞回环形状并无明显的差别.
|
图 5 各试样在1%与2.5%应变幅下荷载-应变稳定滞回曲线 Fig. 5 Stable load-strain hysteretic curve of specimens under 1% and 2.5% strain amplitude |
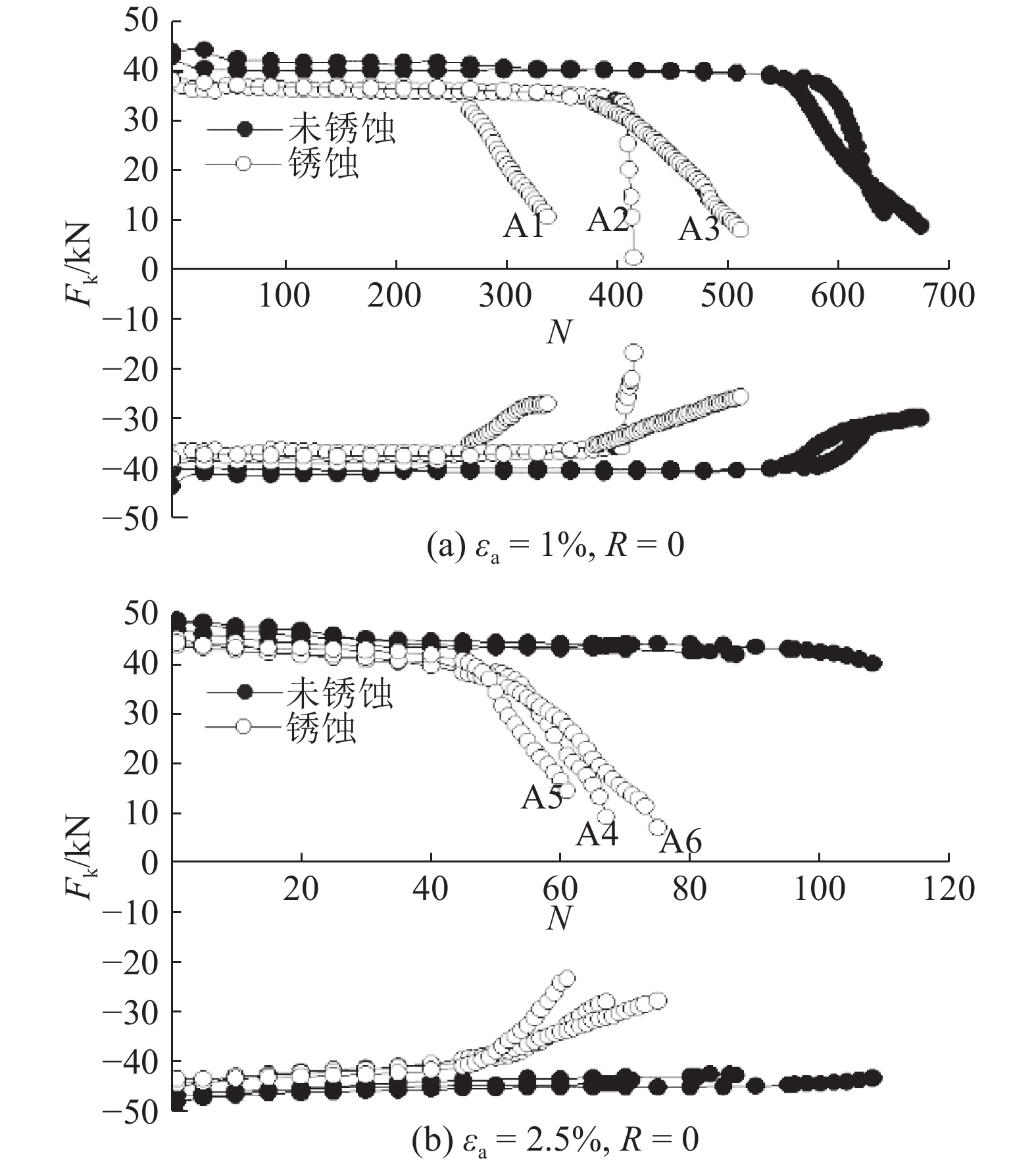
图6为各试样在循环过程中荷载峰值随循环次数的响应曲线比较结果. 图中Fk为循环荷载峰值,N为循环次数. 结果表明,在同应变幅条件下,未锈蚀试样与锈蚀试样在稳定状态的荷载峰值较相近,但是锈蚀试样的开裂寿命明显小于未锈蚀试样;在应变幅较小的情况下(如图6(a)所示),锈蚀试样与未锈蚀试样均有一定的荷载峰值衰减的现象,且衰减部分的斜率相近,说明两种试样在开裂之后的裂纹扩展过程相似;在应变幅较大的情况下(如图6(b)所示),未锈蚀试样最后没有明显的荷载峰值衰减现象,属于超低周疲劳破坏,而锈蚀试样则经历了一定荷载峰值衰减过程.
|
图 6 各试样在应变幅为1%与2.5%时的荷载峰值响应曲线 Fig. 6 Peak load response curve of specimens with strain amplitude of 1% and 2.5% |
如图7和8所示为2个不同应变幅的断口宏观特征. 在应变幅为1%时,疲劳裂纹多数源于四角(如图7(a)、(b)),但个别锈蚀试样在应变集中的蚀坑部位萌生初始裂纹,扩展区域呈现明显的贝纹弧线(如图7(c)所示);断裂面较平整,塑性残余变形小,没有明显的颈缩现象,同时因为循环加载过程中开裂面相互咬合摩擦,断裂后呈现光泽的金属面,为典型的低周疲劳破坏. 在应变幅为2.5%时,断裂面较崎岖,无锈蚀试样断裂后有明显的颈缩和残余塑性变形,表现为超低周疲劳破坏,而锈蚀试样残余变形相对不明显,断裂面呈剪切型破坏斜面.

|
图 7 应变幅为1%的部分试样断口形貌 Fig. 7 Fracture morphology of some specimens with strain amplitude of 1% |

|
图 8 应变幅为2.5%的部分试样断口形貌 Fig. 8 Fracture morphology of some specimens with strain amplitude of 2.5% |
上述结果表明,锈蚀对钢材力学性能的影响主要表现为促进蚀坑位置低周疲劳裂纹萌生,缩短了低周疲劳裂纹萌生寿命,而对钢材本身材料强度的影响不明显.
对部分试样断口进行SEM扫描以观测断口的微观特性. 图9(a)为试样A2疲劳源附近的形貌,从图中可以发现,试样在宽约590 μm、深约370 μm的蚀坑位置生成疲劳沟线,随后裂纹向周围扩展;图9(b)为试样O2扩展区域内的胎痕状花纹,显示了裂纹扩展的方向;图9(c)为O4试样的韧窝形貌,大量的韧窝形貌表明试样的最后断裂属于延性破坏.

|
图 9 试样断口SEM扫描图片 Fig. 9 SEM scanning of fracture sections |
锈蚀引起的坑蚀是促进低周疲劳裂纹萌生最主要的原因. 为了研究坑蚀对钢材抗低周疲劳性能的影响,对人工坑蚀试样进行低周疲劳试验.
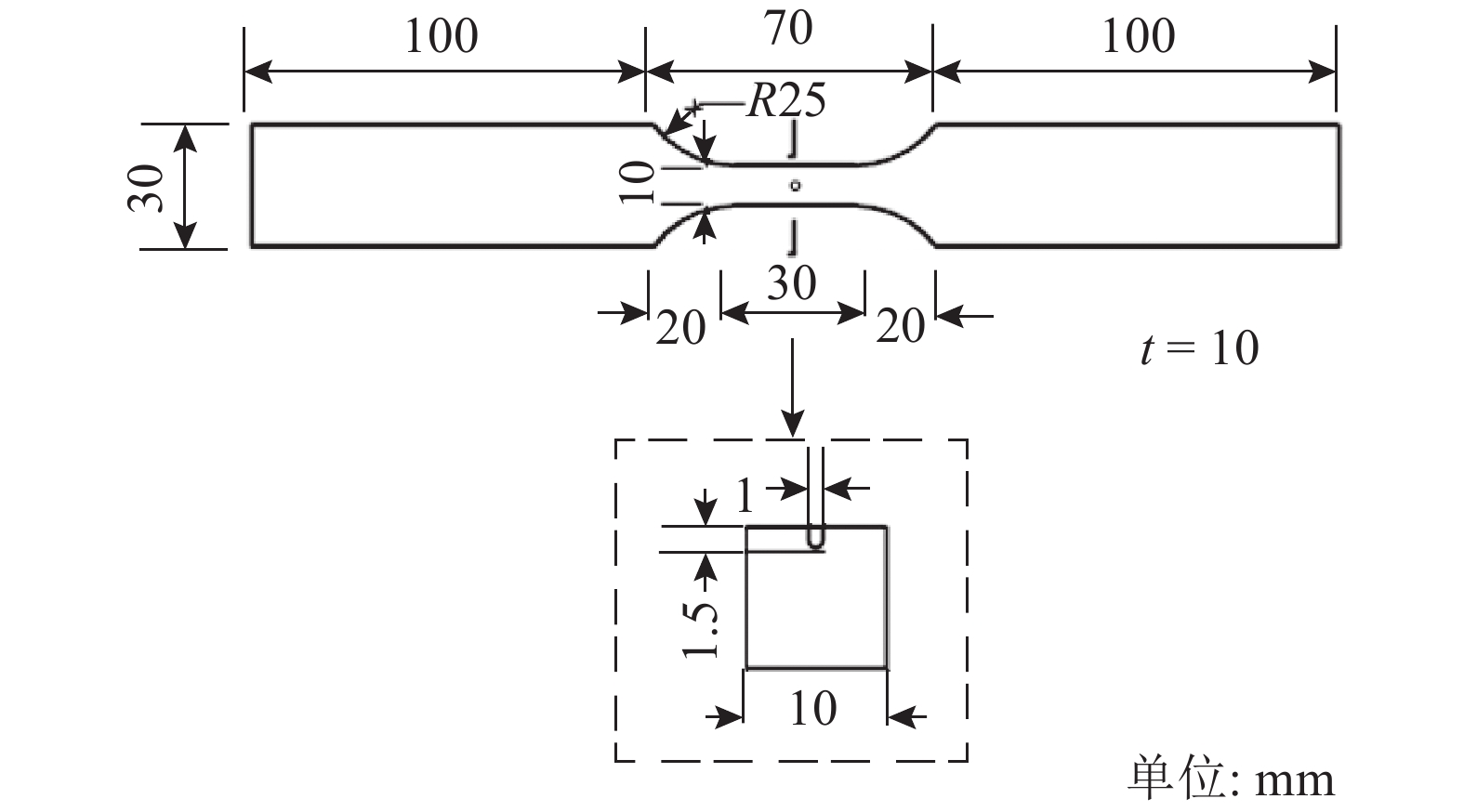
试样尺寸如图10所示,在试验段中心位置人工钻一小孔模拟坑蚀,小孔孔径为1 mm,深为1.5 mm. 实际加工后经过测量,试样小孔孔径为1.0~1.1 mm,深度为1.4~1.6 mm.
|
图 10 人工坑蚀尺寸示意图 Fig. 10 Dimension of artificial pit |
试验应变幅εa=1%,2%,应变比R=−1,应变速率为0.5%/s. 完好试样2枚,标记为NH1~NH2;人工坑蚀试样4枚,标记为H1~H4. 其中NH1、H1与H2加载的应变幅为1%,应变比R=−1;NH2、H3与H4加载的应变幅为2%,应变比R=−1. 对于人工坑蚀试样,试验中时刻观察孔周并记录明显裂纹生成时的循环次数.图11为人工坑蚀试样试验段照片.

|
图 11 人工坑蚀试样 Fig. 11 Specimen with artificial pit |
试验结果如表4所示. 结果表明,人工坑蚀试样在应变幅为1%和2%的循环荷载作用下的平均开裂寿命分别为96次与28次,较完好试样分别下降82%与84%;人工坑蚀试样在2种应变幅下的平均失效寿命分别为229次与46次,较完好试样分别下降68%与73%. 人工坑蚀试样的开裂寿命与失效寿命均远低于完好试样,表明蚀坑部位的应力集中导致锈蚀材料超低周疲劳寿命减小.
| 表 4 人工坑蚀试样低周疲劳试验结果 Table 4 Results of LCF tests of specimen with artificial pit |
如图12所示为人工坑蚀试样在2种应变幅循环作用下的断口宏观特征. 可以明显看到,疲劳裂纹均萌生于坑蚀附近. 在应变幅为1%时,扩展区域断面较为平整;而在应变幅为2%时,扩展区域存在较多台阶,说明在裂纹扩展过程中存在较多剪切破坏.

|
图 12 部分人工坑蚀试样断口形貌 Fig. 12 Fracture morphology of specimens with artificial pit |
为了评估蚀坑对钢材超低周疲劳断裂的影响,这里用基于微观机制的循环空穴扩张模型(cyclic void growth model,CVGM)进行分析.
Kanvinde等[13-15]采用空穴成长指数(void growth index,VGI)作为断裂预测的参数,提出以循环空穴扩张模型作为低周疲劳断裂判据. 该理论认为钢材延性断裂取决于内部空穴的扩张、收缩与聚合过程,其中VGI体现了空穴在拉、压循环中扩张、收缩的累积结果,循环加载过程中的 VGI 的表达式如下:
| $ \begin{split} {\text{VG}}{{\text{I}}_{{\text{cyc}}}} =& \sum\limits_{{\text{ten}}} {\int_{\varepsilon _{\text{1}}^{\text{p}}}^{\varepsilon _{\text{2}}^{\text{p}}} {\exp \left( {\left| {1.5T} \right|} \right){\text{d}}{\varepsilon _{\text{p}}}} } - \hfill \\ & \sum\limits_{{\text{com}}} {\int_{\varepsilon _{\text{1}}^{\text{p}}}^{\varepsilon _{\text{2}}^{\text{p}}} {\exp \left( {\left| {1.5T} \right|} \right){\text{d}}{\varepsilon _{\text{p}}}} } . \hfill\end{split} $ | (1) |
式中:dεp为受拉或受压循环中的等效塑性应变增量,T为应力三轴度.
VGIcyc由自身物理意义决定其非负性[13],因此当式(1)的计算结果出现负值时认为VGIcyc=0. 当循环进行至VGIcyc达到临界空穴成长指数
在循环荷载下,临界空穴成长指数会随塑性损伤的累积逐步下降:
| $ {\text{VGI}}_{{\text{cyc}}}^{{\text{cri}}} = {\text{VGI}}_{{\text{mono}}}^{{\text{cri}}}\exp\; \left( { - \lambda\, \varepsilon _{\text{p}}^{{\text{acc}}}} \right). $ | (2) |
式中:
由于延性断裂是材料的整体行为. 因此CVGM判据必须在特征长度l*上得到满足才能对延性断裂进行预测. 对于带坑蚀的钢材,由于蚀坑处的应力、应变梯度大,l*的大小对断裂预测结果有较大影响. l*值与材料微观结构有关,确定方法较复杂,一般仅能测得其上下限和均值[18]. Liao等[22]通过圆周平滑槽口试样循环加载试验校准了我国常用的Q345钢材的微观断裂判据参数,结果如表5所示.
| 表 5 Q345钢材循环空穴扩张模型(CVGM)微观断裂判据参数 Table 5 Cyclic void growth model (CVGM) parameters of micro mechanical fracture criteria of Q345 steel |
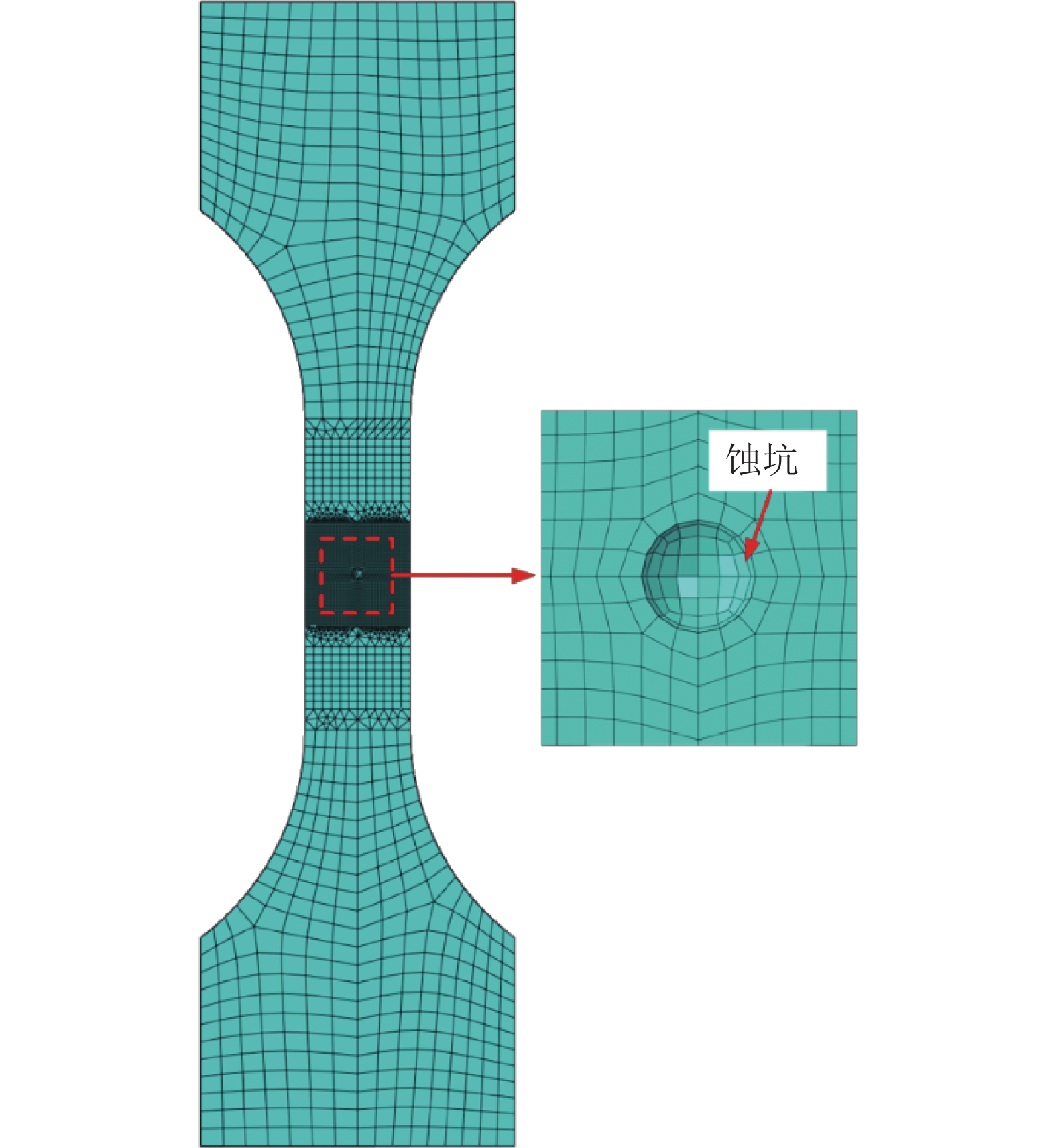
为了研究蚀坑对钢材低周疲劳性能的影响,以未锈蚀和含蚀坑的试样为对象进行分析. 图13为基于CVGM判据的有限元计算模型. 建模尺寸与实际试样相同,在试样的有效长度中点挖一个孔穴模拟蚀坑,蚀坑尺寸与人工坑蚀试样的孔穴尺寸相同. 为了反映蚀坑附近的应力应变梯度[23],同时匹配表5中的特征长度l*,关键区域单元尺寸为0.25 mm.
|
图 13 基于循环空穴扩张模型(CVGM)判据的人工蚀坑试样有限元计算模型 Fig. 13 FEM of specimen with artificial pit based on cyclic void growth model (CVGM) |
材料的滞回本构关系采用ABAQUS 6.10中的Lemaitre-Chaboche混合强化模型,以模拟材料的循环塑性流动. 相关参数通过材料的试验确定,具体如表6所示. 表中,σ|0为等效塑性应变为0时的应力;Q∞为屈服面大小的最大变化值;biso为屈服面随塑性应变发展变化的比率;Ckin为随动强化模量的初始值;γi(i=1,2,3,4)为塑性变形增加时随动强化模量减小的比率.
| 表 6 Q345钢材循环强化参数 Table 6 Cyclic hardening parameters of Q345 steel |
加载采用一端约束,另一端施加位移循环荷载的方式进行,使试验段轴向应变幅为1%与2%,应变比R=−1.
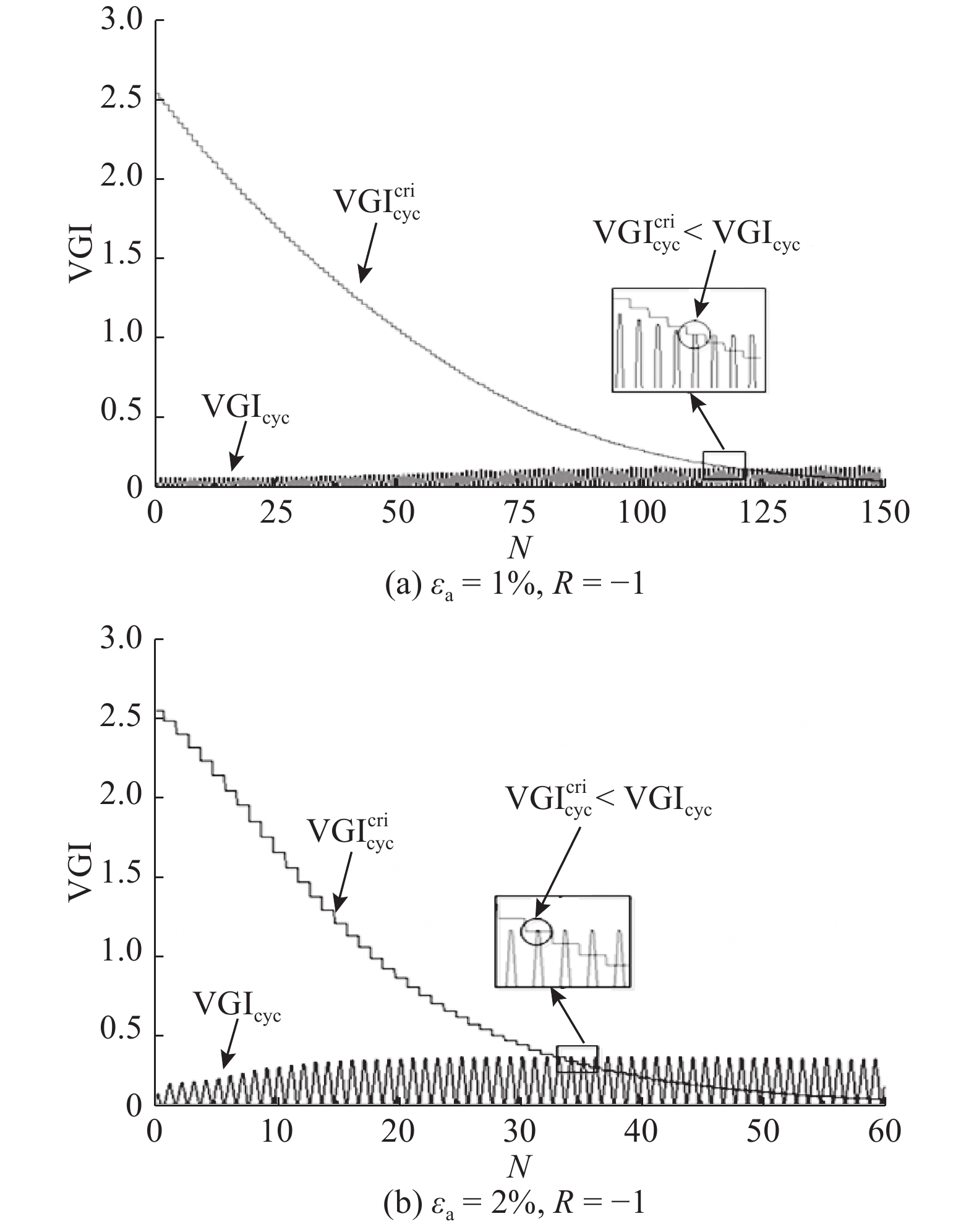
4.3 基于CVGM的单蚀坑试样延性开裂预测计算图14为基于CVGM的单蚀坑试样损伤演化过程,图中2条曲线交汇处表示蚀坑内等效塑性应变最大位置发生延性开裂. 由图可知,在应变幅为1%时,蚀坑内延性开裂的寿命为121次;在应变幅为2%时,蚀坑内延性开裂的寿命为34次. 与试验结果相比(应变幅为1%时,96次;应变幅为2%时,28次)计算结果偏大,但总体上较接近. 因此,CVGM对分析材料的超低周疲劳寿命有一定的参考意义.
|
图 14 蚀坑试样损伤演化过程 Fig. 14 Damage evolution of corroded specimens |
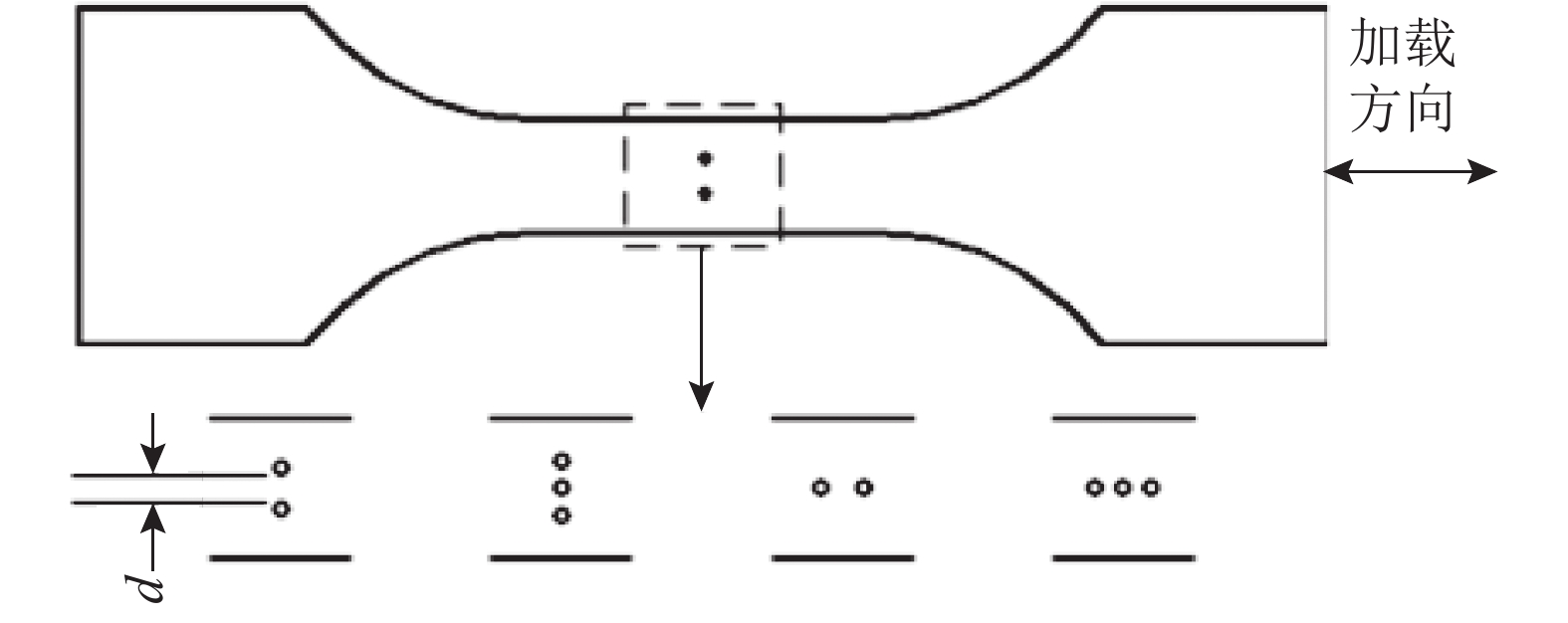
为了考察蚀坑分布对试样开裂寿命的影响,分别建立同一截面上存在2个或多个蚀坑的试样模型. 计算中蚀坑尺寸均与人工坑蚀试样中尺寸相同,即深为1.5 mm,坑口直径为1 mm. 如图15所示,坑的分布形式有4种,其中d为相邻孔缘间距. 为了保证相邻孔缘间距内有不少于2个单元,d的最小值设置为1倍孔穴半径(r),取值分别为r、2r和3r. 计算试验段轴向应变幅为2%,应变比R=−1.
|
图 15 多蚀坑计算模型的蚀坑分布示意图 Fig. 15 Schematic diagram of pits distribution of FEM model with multiple pits |
计算结果如表7所示. 由计算结果可知,垂直于加载方向分布的多蚀坑试样开裂寿命相对于单蚀坑明显降低,在相邻孔缘间距为r时降低了50%以上;孔缘间距引起的降低比蚀坑数量更明显. 平行于加载方向分布的多蚀坑相对于单蚀坑开裂寿命反而提高,其原因是轴向荷载作用下应力集中程度得到缓和. 因此,当钢材的蚀坑沿受力垂直方向分布比较密集时,其低周疲劳寿命进一步降低.
| 表 7 应变幅为2%时的多蚀坑模型LCF开裂寿命计算结果 Table 7 Calculation results of LCF cracking life of multiple pits models with strain amplitude of 2% |
(1)锈蚀后质量损失率约为6%的Q345钢材低周疲劳寿命大约下降30%,表明锈蚀有可能导致钢结构的抗震性能下降.
(2)在同应变幅情况下,完好试样与锈蚀试样在达到稳定状态时,滞回环形状几乎相同,应力峰值水平相近,表明锈蚀对钢材的强度影响较小.
(3)在应变幅为1%时,试样破坏现象为脆性的低周疲劳破坏;而应变幅为2.5%时的循环荷载下,未锈蚀试样发生延性的超低周疲劳破坏,锈蚀试样则表现出脆性断裂破坏的现象.
(4)根据带人工蚀坑的试样低周疲劳试验结果以及CVGM数值模型分析,可以推断出锈蚀引起钢材低周疲劳裂纹萌生寿命下降的主要原因是蚀坑位置的应变集中,且随着应变集中程度的增加,寿命下降程度增大.
| [1] |
DU Y G, CLARK L A, CHAN A H C. Residual capacity of corroded reinforcing bars[J]. Magazine of Concrete Research, 2005, 57(3): 135-147. DOI:10.1680/macr.2005.57.3.135 |
| [2] |
DU Y G, CLARK L A, CHAN A H C. Effect of corrosion on ductility of reinforcing bars[J]. Magazine of Concrete Research, 2005, 57(7): 407-419. DOI:10.1680/macr.2005.57.7.407 |
| [3] |
APOSTOLOPOULOS C A. Mechanical behavior of corroded reinforcing steel bars S500s tempcore under low cycle fatigue[J]. Construction and Building Materials, 2007, 21(7): 1447-1456. DOI:10.1016/j.conbuildmat.2006.07.008 |
| [4] |
HAWILEH R A, ABDALLA J A, TAMIMI A A, et al. Behavior of corroded steel reinforcing bars under monotonic and cyclic loadings[J]. Mechanics of Advanced Materials and Structures, 2011, 18(3): 218-224. DOI:10.1080/15376494.2010.499023 |
| [5] |
鋼構造委員会鋼構造震災調査特別小委員会. 阪神•淡路大震災における鋼構造物の震災の実態と分析[J]. 土木学会論文集, 2000, 647: 17-30. Subcommittee on Investigation of Seismic Damage of Steel Structure. Investigation of causes of damage to steel structure on Hanshin-Awaji earthquake disaster[J]. Proceedings of the Japan Society of Civil Engineers, 2000, 647: 17-30. |
| [6] |
MAHIN S A. Lessons from damage to steel building during the Northridge earthquake[J]. Engineering Structures, 1998, 20(4–6): 261-270. |
| [7] |
三木千寿, 四十沢利康, 穴見健吾. 鋼製橋脚ラーメン隅角部の地震時脆性破壊[J]. 土木学会論文集, 1998, 591: 273-281. MIKI Chitoshi, AIZAWA Toshiyasu, ANAMI Kengo. Brittle fracture at beam-to-column connection during earthquake[J]. Proceedings of the Japan Society of Civil Engineers, 1998, 591: 273-281. |
| [8] |
葛漢彬, 藤江渉, 田島僚. 鋼構造物の延性き裂発生の評価法の実験データによる検証[J]. 構造工学論文集A, 2009, 55: 617-628. GE Hai-bin, FUJIE Wataru, TAJIMA Ryo. Experimental verification of an evaluation method for predicting the ductile crack initiation in steel structures[J]. Journal of Structural Engineering, JSCE, 2009, 55: 617-628. |
| [9] |
GE H B, LUO X Q. A seismic performance evaluation method for steel structures against local buckling and extra-low cycle fatigue[J]. Journal of Earthquake and Tsunami, 2011, 5(2): 83-99. DOI:10.1142/S1793431111001005 |
| [10] |
GE H B, KANG L. Ductile crack initiation and propagation in steel bridge piers subjected to random cyclic loading[J]. Engineering Structures, 2014, 59: 809-820. DOI:10.1016/j.engstruct.2013.12.006 |
| [11] |
HANJI T, PARK J E, TATEISHI K. Low cycle fatigue assessments of corner welded joints based on local strain approach[J]. International Journal of Steel Structures, 2014, 14(3): 579-587. DOI:10.1007/s13296-014-3015-8 |
| [12] |
HANJI T, TATEISHI K, MINAMI K, et al. Extremely low cycle fatigue assessment for welded joints based on peak strain approach[J]. Journal of Japan Society of Civil Engineers Ser A1, 2006, 62(1): 101-109. |
| [13] |
KANVINDE A M, DEIERLEIN G G. Cyclic void growth model to assess ductile fracture initiation in structural steels due to ultra low cycle fatigue[J]. Journal of Engineering Mechanics, ASCE, 2007, 133(6): 701-712. DOI:10.1061/(ASCE)0733-9399(2007)133:6(701) |
| [14] |
KANVINDE A M, DEIERLEIN G G. Validation of cyclic void growth model for fracture initiation in blunt notch and dog-bone steel specimens[J]. Journal of Structural Engineering, 2008, 134(9): 1528-1537. DOI:10.1061/(ASCE)0733-9445(2008)134:9(1528) |
| [15] |
KANVINDE A M, DEIERLEIN G G. The void growth model and the stress modified critical strain model to predict ductile fracture in structural steels[J]. Journal of Structural Engineering, 2006, 132(12): 1907-1918. DOI:10.1061/(ASCE)0733-9445(2006)132:12(1907) |
| [16] |
石永久, 熊俊, 王元清. 钢框架梁柱节点焊缝损伤性能研究Ⅰ:试验研究[J]. 建筑结构学报, 2012, 33(3): 48-55. SHI Yong-jiu, XIONG Jun, WANG Yuan-qing. Study on damage behavior of weld of beam-to-column connection in steel frame I: experiment[J]. Journal of Building Structures, 2012, 33(3): 48-55. |
| [17] |
ZHOU H, WANG Y Q, SHI Y J, et al. Extremely low cycle fatigue prediction of steel beam-to-column connection by using a micro-mechanics based fracture model[J]. International Journal of Fatigue, 2013, 48(2): 90-100. |
| [18] |
廖芳芳, 王伟, 陈以一. 往复荷载下钢结构节点的超低周疲劳断裂预测[J]. 同济大学学报: 自然科学版, 2014, 42(4): 539-546. LIAO Fang-fang, WANG Wei, CHEN Yi-yi. Extremely low cycle fatigue fracture prediction of steel connections under cyclic loading[J]. Journal of Tongji University: Natural Science, 2014, 42(4): 539-546. |
| [19] |
廖燕华, 谢旭, 唐站站. Q345qC钢及焊接接头低周疲劳性能与断裂机理[J]. 浙江大学学报: 工学版, 2018, 52(1): 73-81. LIAO Yan-hua, XIE Xu, TANG Zhan-zhan. Low cycle fatigue properties and fracture mechanism of Q345qC steel and its welded joint[J]. Journal of Zhejiang University: Engineering Science, 2018, 52(1): 73-81. |
| [20] |
赵婷婷, 徐善华, 孔正义, 等. 碳钢人工加速腐蚀试验研究[J]. 水利与建筑工程学报, 2010, 8(2): 13-15. ZHAO Ting-ting, XU Shan-hua, KONG Zheng-yi, et al. Study on accelerated corrosion tests of carbon steel[J]. Journal of Water Resources and Architectural Engineering, 2010, 8(2): 13-15. DOI:10.3969/j.issn.1672-1144.2010.02.006 |
| [21] |
中国科学院金属研究所. GB/T15248-2008金属材料轴向等幅低循环疲劳试验方法[S]. 北京: 中国标准出版社, 2008. http://www.csres.com/detail/186365.html
|
| [22] |
LIAO F F, WANG W, CHEN Y Y. Parameter calibrations and application of micromechanical fracture models of structural steels[J]. Structural Engineering and Mechanics, 2012, 42(2): 153-174. DOI:10.12989/sem.2012.42.2.153 |
| [23] |
CHI W M. Prediction of steel connection failure using computational fracture mechanics[D]. California: Stanford University, 1999.
|



