2. 浙江大学 车辆工程研究所,浙江 杭州 310027
2. Institute of Vehicular Engineering, Zhejiang University, Hangzhou 310027, China
制动系统是汽车行驶安全的重要保障. 与传统制动系统相比,线控制动系统取消了真空助力器,具有结构简单、制动响应快、控制精度高等优点,制动力通过液压制动力及回馈制动力协调控制,可满足电动汽车及混合动力汽车的再生制动系统需求,具有很好的发展前景[1-3]. 线控制动系统可实现制动踏板与制动轮缸的解耦,但需要采用特定装置来模拟制动踏板感觉,保证给驾驶员传递制动反馈信息. 踏板模拟器作为关键部件之一,需要更真实地模拟传统制动踏板特性,因为驾驶员在长期的制动操作中,已形成使用这种带真空助力形式的制动踏板的习惯[4].
国内外厂商和科研机构对线控制动系统踏板模拟器进行了大量的分析研究,提出了多种类型的踏板模拟器设计思路,根据踏板力模拟方式可分为主动式和被动式. 主动式踏板模拟器可以对踏板行程−踏板力特性进行实时调整,一般设计有独立的信号反馈、控制系统及执行机构,结构复杂,多处于研究阶段. Ohtani等[5]对所设计的电子辅助制动系统进行了主动式踏板力补偿分析,对踏板感觉进行了优化. 金智林等[6]提出了一种踏板感觉可控的踏板模拟器,并通过实例仿真分析了踏板特性的影响参数. Pasquet[7]设计了利用高压蓄能器和气体弹簧共同调节模拟器内压力的制动踏板感觉模拟器. 王奎洋等[8]提出了一种基于磁流变液可控流变特性阻尼可调的制动踏板感觉模拟器. 被动式踏板模拟器踏板行程−踏板力特性多通过特殊的机械结构实现,一般不能实时调整和补偿,结构简单易于实现. 常见的形式有采用弹簧和橡胶体组合模拟传统非线性踏板感觉,采用两段或多段弹簧组合用分段线性模拟非线性踏板感觉,以及采用节流机构利用非线性液阻模拟非线性踏板感觉等[9-11].
踏板模拟器系统中各部件参数均可对踏板感觉即踏板行程−踏板力特性产生影响. Koizumi[12]分析了制动主缸活塞摩擦特性对制动踏板感觉的影响. Karlheinz等[13]在制动踏板感觉试验研究中,提出了影响制动踏板感觉的因素. 刘杨等[14]设计了一种组合弹簧式踏板感觉模拟器,仿真分析了活塞阻尼系数、推杆回位弹簧预紧力、电磁阀最大通流面积和助力比等参数对踏板力−行程曲线的影响. 以上研究多通过理论和仿真的方法验证模拟器设计,或是结合仿真与试验进行踏板感觉模拟影响因素分析,并未针对实际产品进行设计改进及验证. 特别地,将模拟器常闭电磁阀作为先导控制功能的阀控踏板模拟器研究未见报道.
本研究对自行设计的一种线控制动系统样机进行踏板行程−踏板力特性试验分析,针对因模拟器常闭电磁阀过流孔径偏小而造成的踏板行程−踏板力曲线随踏板速度偏移的问题,提出一种改进设计方案并通过仿真及试验验证其可行性.
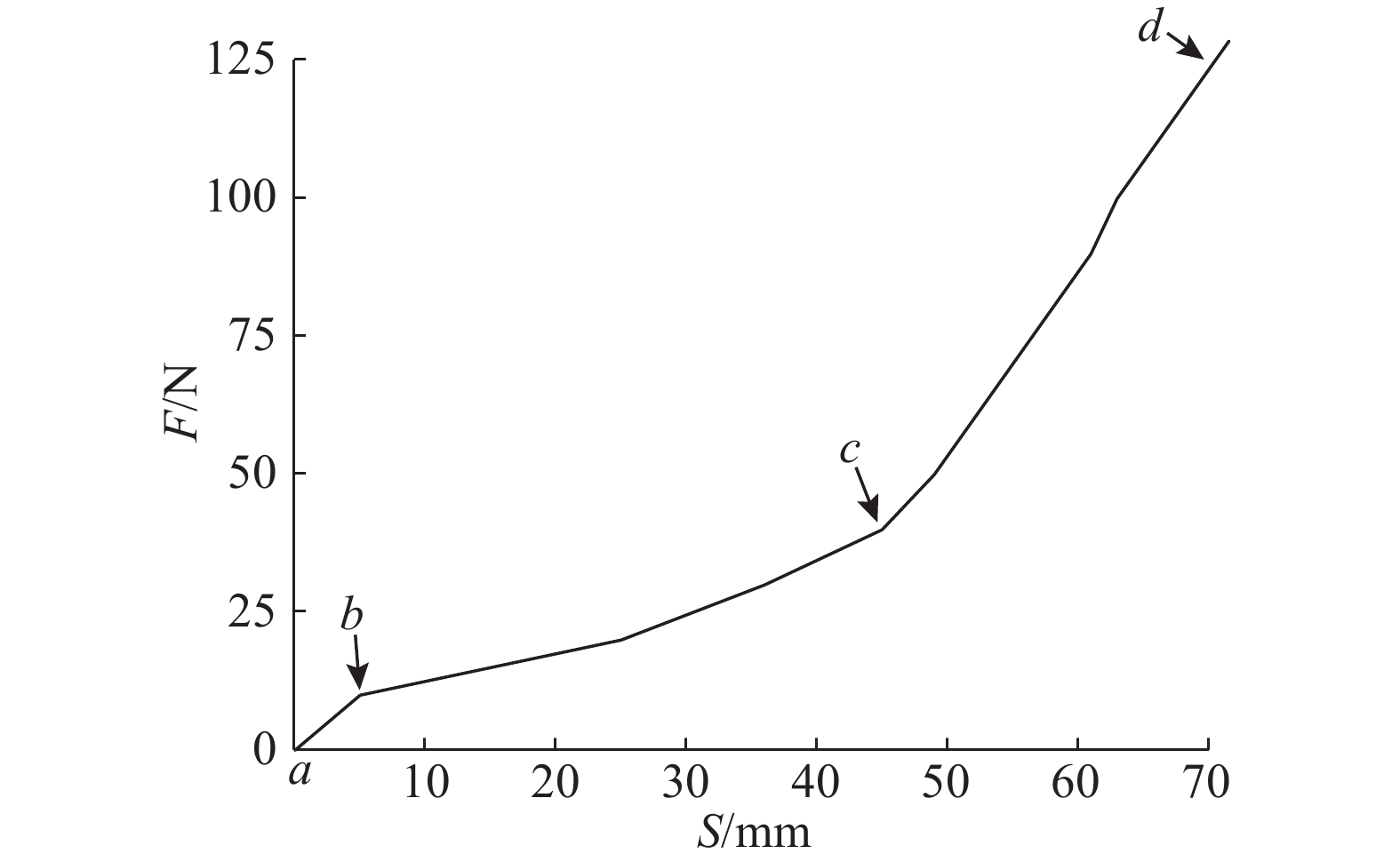
1 制动系统踏板力特性分析 1.1 传统制动系统踏板力特性传统液压制动系统踏板行程与踏板力的关系曲线如图1所示,图中S为踏板行程,F为踏板力. a-b段:主要消除踏板的自由行程,踏板位移较大,踏板压力没有明显增加;b-c段:真空助力装置起作用,踏板压力随踏板位移增加而变大;c-d段:真空助力比达到最大值并恒定,踏板压力随踏板位移变化较大. 在实际制动过程中,中小强度制动时,达到最大制动压力所需的踏板位移较大,即特性曲线斜率较小,踏板压力随踏板位移变化均匀,制动稳定舒适;紧急制动时,达到最大制动压力所需的踏板位移较小,即特性曲线斜率较大,踏板压力随踏板位移变化急剧增加,制动响应迅速.
|
图 1 传统液压制动系统踏板行程−力特性曲线 Fig. 1 Pedal stroke-force curve of traditional hydraulic brake system |
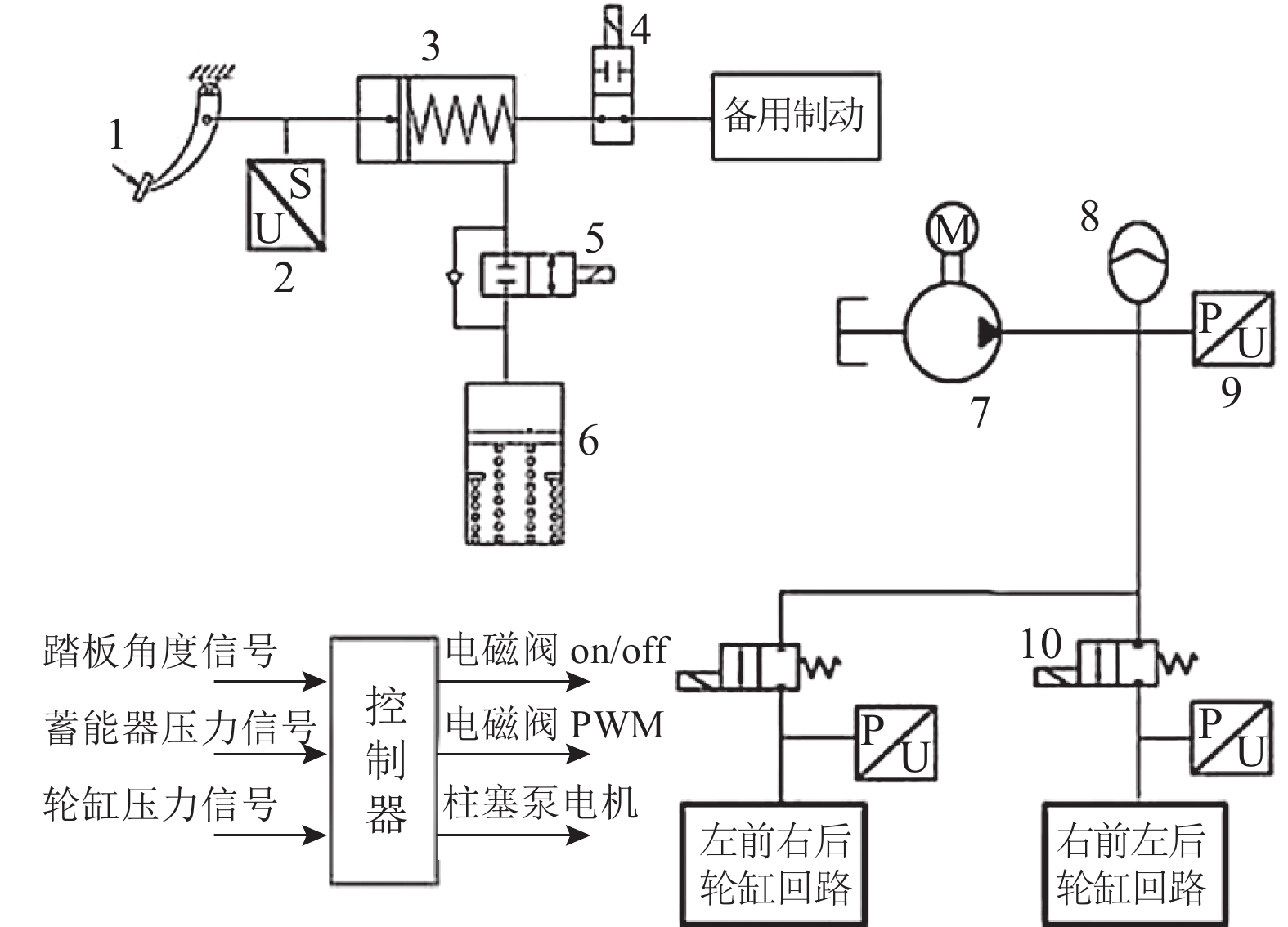
设计开发一种线控制动系统(wire brake system,WBS)踏板感觉模拟器[15],原理如图2所示.
|
1-制动踏板;2-踏板角度传感器;3-制动主缸;4-制动主缸隔离电磁阀;5-模拟器常闭电磁阀;6-模拟器主缸;7-柱塞泵;8-高压蓄能器;9-压力传感器;10-蓄能器隔离电磁阀 图 2 线控制动系统(WBS)踏板感觉模拟器液压原理图 Fig. 2 Hydraulic scheme of pedal feel emulator with wire brake system (WBS) |
常规制动工况下,驾驶员踩下制动踏板,控制器通过读取踏板角度信号确认车辆制动需求,常开型制动主缸隔离电磁阀上电关闭,模拟器常闭电磁阀上电打开,制动主缸油液通过模拟器常闭电磁阀进入模拟器主缸,并由制动主缸和模拟器主缸共同作用反馈合适的制动脚感. 线控制动系统的制动力源由电动柱塞泵提供,并由高压蓄能器储压,以减少油泵工作次数并提高系统压力速度响应. 控制器通过判断踏板角度传感器等信号,控制电磁阀开度及柱塞泵工作,按照控制逻辑控制线控制动系统输出相应制动力,此时制动踏板和制动力是完全解耦的;如果线控制动系统发生故障,进入备用制动状态,控制器控制制动主缸隔离电磁阀断电打开,模拟器常闭电磁阀断电关闭,模拟器停止工作. 此时制动油液通过制动主缸和制动主缸隔离电磁阀直接进入备用制动回路,提供车辆备用制动力.
如图2所示,在模拟器主缸中设置2段弹簧,分别模拟图1中b-c段和c-d段的踏板力特性. 不考虑空行程及制动过程中流体压力损失,制动主缸活塞及模拟器主缸活塞运动方程满足:
| $F\beta ={m_{\rm{c}}}\frac{1}{\beta }\ddot S +{F_{\rm{s}}}+{k_{\rm{c}}}\left( {{X_{{\rm{c}}0}}+S\frac{{\rm{1}}}{\beta }} \right)+{f_{\rm{c}}}{;}$ |
| ${\rm{}}{F_{\rm{s}}}{\rm{ = }}{m_{\rm{s}}}\frac{S}{\beta }{\left( {\frac{{{D_{\rm{c}}}}}{{{D_{\rm{s}}}}}} \right)^{\rm{2}}}\ddot S +{k_{\rm{A}}}\left( {{X_{{\rm{s0}}}}+\frac{S}{\beta }{{\left( {\frac{{{D_{\rm{c}}}}}{{{D_{\rm{s}}}}}} \right)}^{\rm{2}}}} \right)+{f_{{\rm{s }}}};$ |
| ${{{L}}_{{b}}}<S \leqslant {{{L}}_{{c}}};$ |
| $\begin{split}{F_{\rm{s}}}{\rm{ = }}&{m_{\rm{s}}}\frac{S}{\beta }{\left( {\frac{{{D_{\rm{c}}}}}{{{D_{\rm{s}}}}}} \right)^{\rm{2}}}\ddot S +{k_{\rm{A}}}\left( {{X_{{\rm{s0}}}}+\frac{S}{\beta }{{\left( {\frac{{{D_{\rm{c}}}}}{{{D_{\rm{s}}}}}} \right)}^{\rm{2}}}} \right)+{f_{\rm{s}}}+\\&{k_{\rm{B}}}\left( {\frac{S}{\beta }{{\left( {\frac{{{D_{\rm{c}}}}}{{{D_{\rm{s}}}}}} \right)}^{\rm{2}}}{\rm{ - }}\frac{{{{{L}}_{{{ab}}}}}}{\beta }{{\left( {\frac{{{D_{\rm{c}}}}}{{{D_{\rm{s}}}}}} \right)}^{\rm{2}}}} \right),\;{{{L}}_{{c}}}<S \leqslant {{{L}}_{{{d}}{.}}}\end{split}$ | (1) |
式中:β为制动踏板/制动主缸杠杆比,mc为制动主缸活塞及活塞杆质量,Fs为制动主缸液压力,kc为制动主缸弹簧刚度,Xc0为制动主缸弹簧预紧量,Xs0为模拟器主缸第一段弹簧预紧量,fc为制动主缸摩擦力,fs为模拟器主缸摩擦力,ms为模拟器主缸活塞及活塞杆质量,Dc为制动主缸内径,Ds为模拟器主缸内径,kA为模拟器第一段弹簧刚度,kB为模拟器第二段弹簧刚度,Lb为踏板空行程终点值,Lc为踏板第一段行程终点值,Ld为踏板第二段行程终点值,Lvab为从点a到点b的踏板行程增加值.
忽略主缸活塞及活塞杆惯量影响,目标踏板行程−踏板力曲线为
| $\left. \begin{array}{l}F{\rm{ = }}{a_{\rm{1}}}S + {b_{\rm{1}}},\;{L_{ b}} < S \leqslant {{{L}}_{{c}}};\\F{\rm{ = }}{a_{\rm{2}}}S + {b_{\rm{2}}},\;{L_{{c}}} < S \leqslant {L_{{d}}}.\end{array} \right\}$ | (2) |
式中:a1、a2、b1、b2为设定的S-F特性目标值. 联立式(1)、(2)可得模拟器弹簧刚度及预紧量:
| ${k_{\rm{A}}}{\rm{ = }}\left( {{{{a}}_{\rm{1}}}{\beta ^{\rm{2}}}{\rm{ - }}{k_{\rm{c}}}} \right){\left( {\frac{{{D_{\rm{c}}}}}{{{D_{\rm{s}}}}}} \right)^{\rm{2}}},$ |
| ${X_{{\rm{s0}}}}{\rm{ = }}\frac{{{{{b}}_{\rm{1}}}\beta {\rm{ - }}{k_{\rm{c}}}{X_{{\rm{c0}}}}{\rm{ - }}{f_{\rm{c}}}{\rm{ - }}{f_{\rm{s}}}}}{{{k_{\rm{A}}}}},$ |
| ${\rm{}}{k_{\rm{B}}}{\rm{ = }}\left( {{\beta ^{\rm{2}}}{{{a}}_{\rm{2}}}{\rm{ - }}{k_{\rm{c}}}} \right){\left( {\frac{{{D_{\rm{c}}}}}{{{D_{\rm{s}}}}}} \right)^{\rm{2}}}{\rm{ - }}{k_{\rm{A}}}.$ |
本研究试制的一种线控制动系统样机(WBS)构成如图3所示.

|
图 3 线控制动系统(WBS)样机 Fig. 3 Prototype of wire brake system (WBS) |
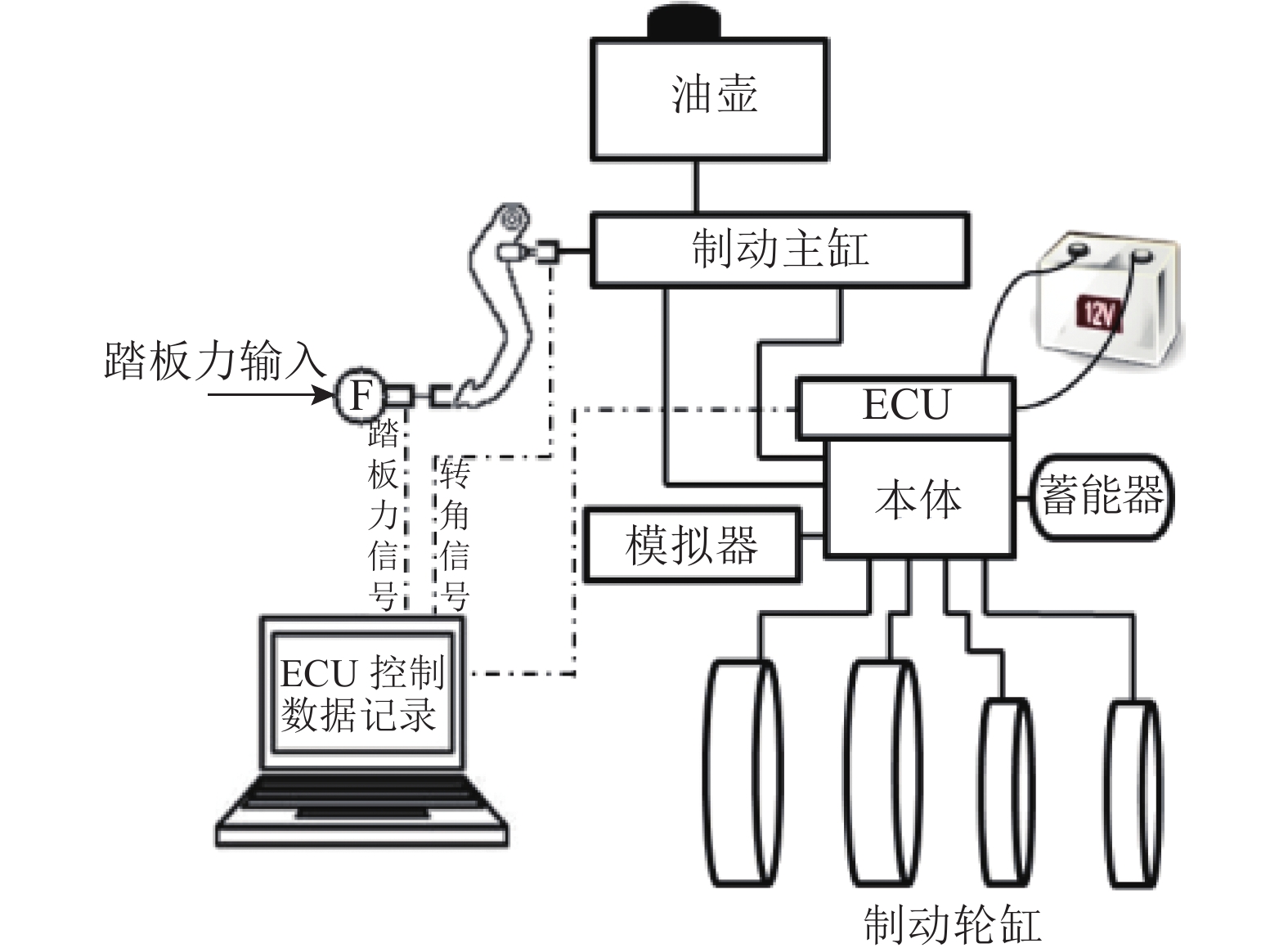
试验在万向WBS试验台架上展开,不考虑油温变化导致的油液黏度变化(室温条件下进行),台架测试原理如图4所示.
|
图 4 线控制动系统(WBS)试验台架 Fig. 4 Test bench of wire brake system(WBS) |
测试方法:模拟器常闭电磁阀通电,踏板力加载速率15~25 N/s.
记录数据:记录踏板转角传感器数据、踏板力传感器数据,每组试验记录3次.
由于空间布置、功率、发热量等实际要求,模拟器常闭电磁阀系列产品过流孔径存在限值,试验中采取2种不同的电磁阀规格以及短接导通(过流孔径为管路通径)进行对比试验,2种电磁阀的过流孔直径分别为Φ0.7和Φ1.0 mm,液压管路通径为Φ2.8 mm.
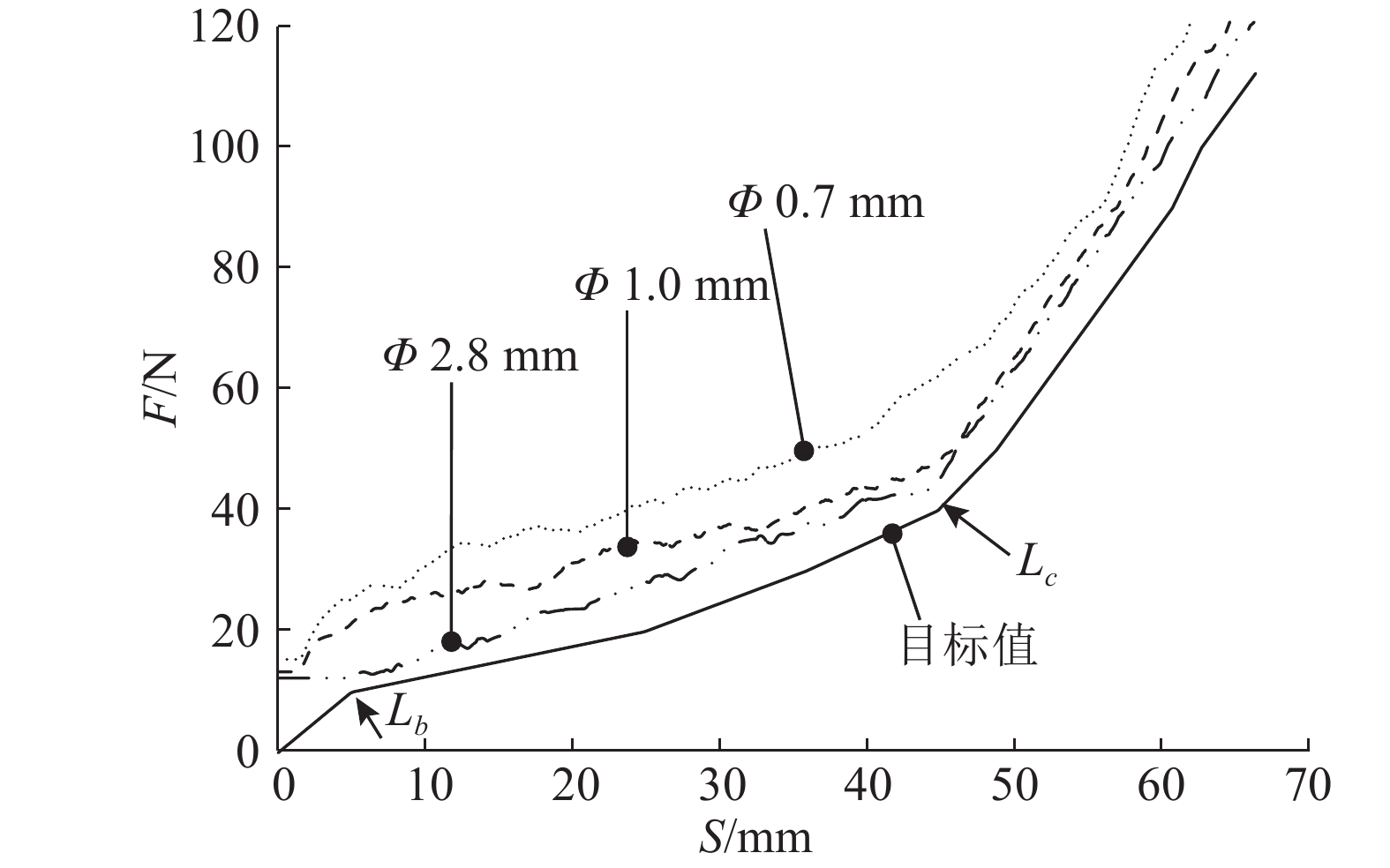
2.2 试验结果分析 2.2.1 踏板力加载速度为15 N/s的试验结果试验中踏板力加载速度为15 N/s,试验结果如图5所示. 试验中装配过流孔径分别为Φ0.7、Φ1.0 mm模拟器常闭电磁阀的样机第一段弹簧曲线均出现了偏移,踏板力偏大;而直接短接开闭电磁阀通路(孔径Φ2.8 mm)与目标值贴近较好;装配Φ0.7 mm孔径开闭电磁阀的样机曲线在第一段出现了明显了非线性特征.
|
图 5 踏板力加载速度为15 N/s时的踏板行程−力特性试验结果 Fig. 5 Test results of pedal stroke−force at pedal loading speed of 15 N/s |
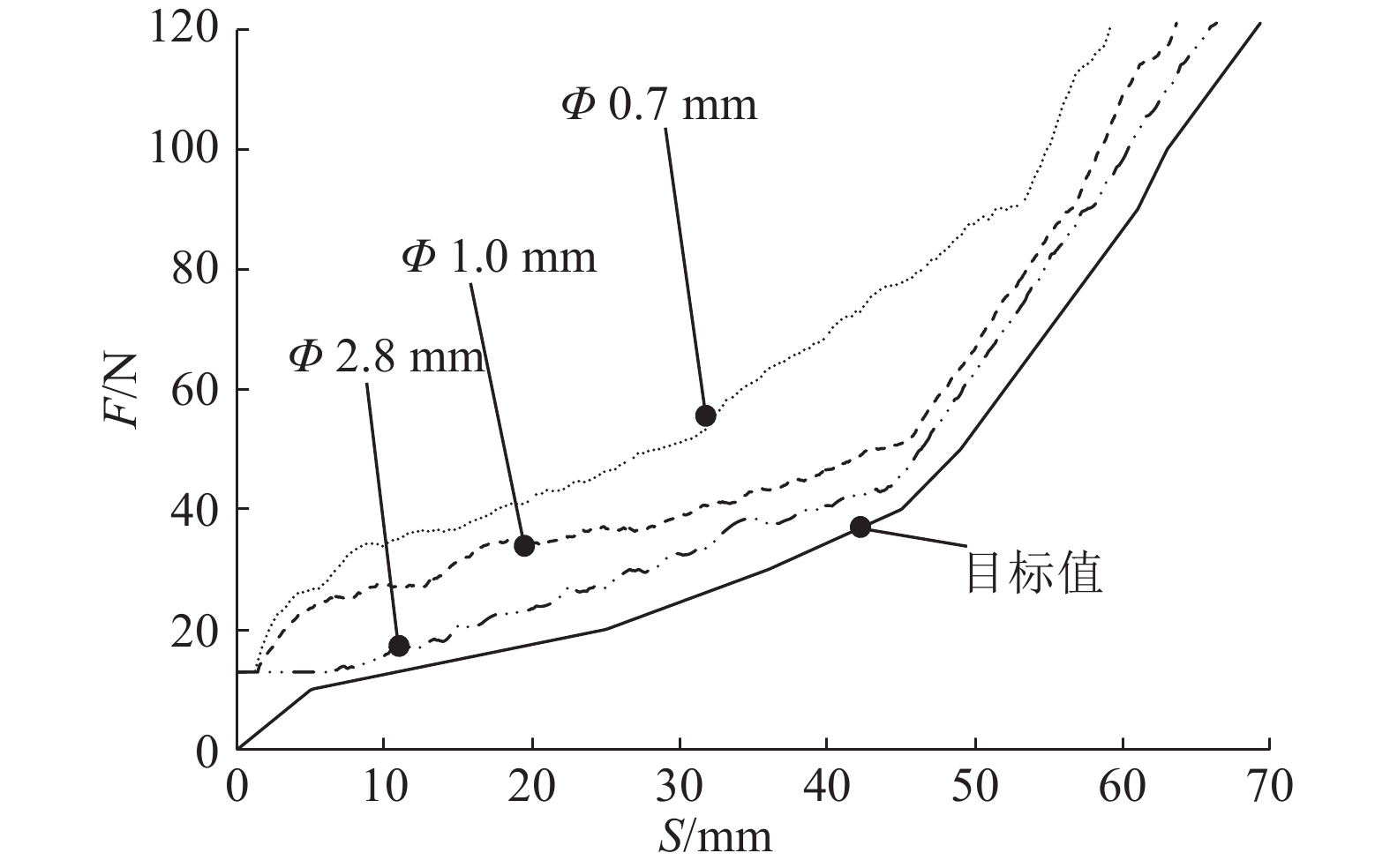
试验中踏板力加载速度为15 N/s,试验结果如图6所示。随着踏板加载速度加快:装配过流孔径分别为Φ0.7、Φ1.0 mm模拟器常闭电磁阀的样机第一段弹簧曲线偏移和非线性特性愈加明显,并且随着电磁阀过流孔径变小,偏移量和非线性化愈加明显;直接短接开闭电磁阀通路(孔径Φ2.8 mm)与目标值贴近较好,受踏板力加载速度影响小.
|
图 6 踏板力加载速度为25 N/s时的踏板行程−力特性试验结果 Fig. 6 Test results of pedal stroke-force at pedal loading speed of 25 N/s |
试验结果表明:模拟器常闭电磁阀过流孔径参数对踏板模拟器S-F试验结果影响显著,随着制动力加载速度提高,其液压阻尼力变大,踏板感变硬,影响制动舒适性;在紧急制动时,踏板不能及时踩下,导致控制器接收到的制动力请求不足,极大影响行车安全性.
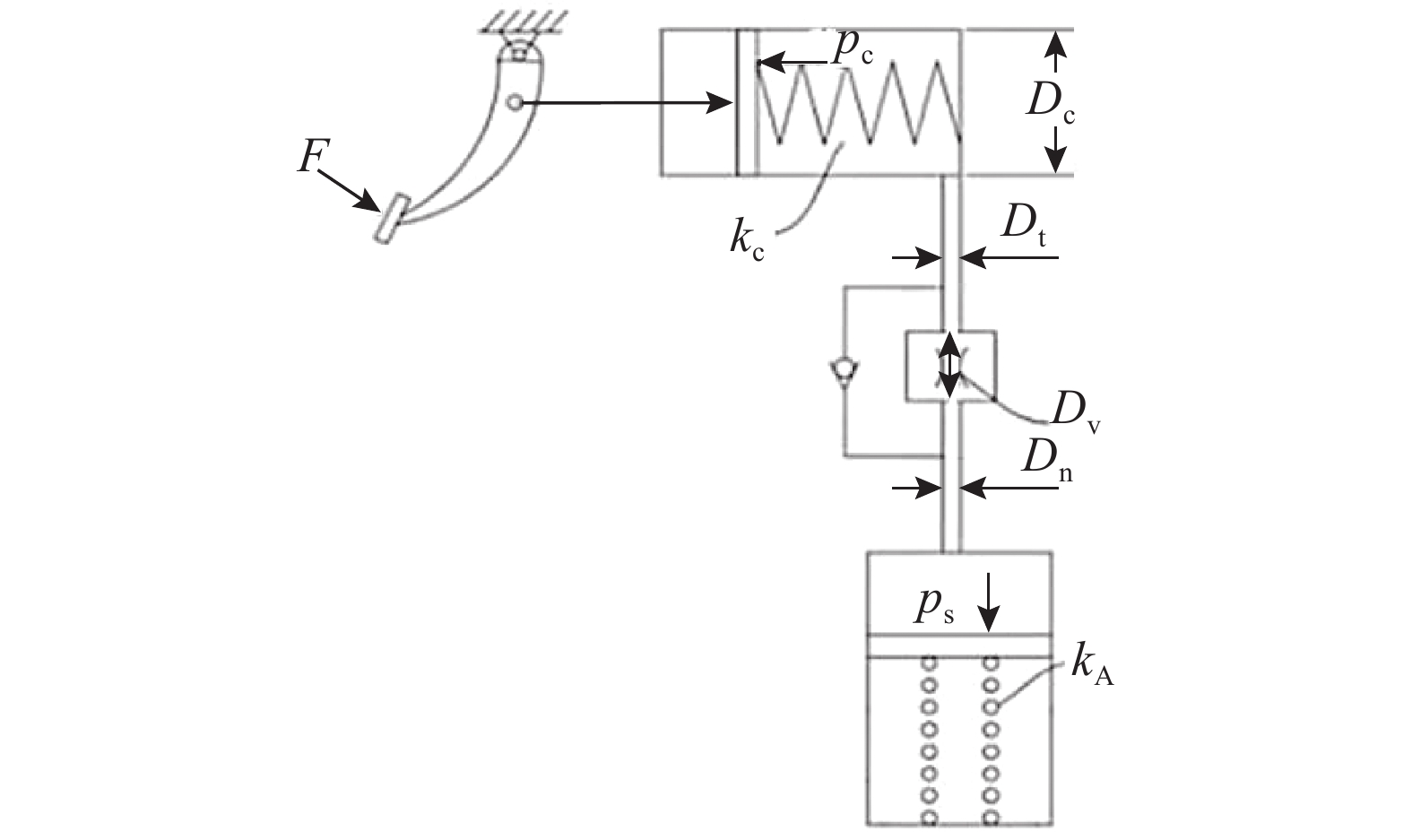
2.2.3 踏板特性影响因素理论分析由试验分析可知,当前模拟器开闭电磁阀过流孔所产生的液压损失不能忽略,应考虑过流孔径影响,建立如图7所示的踏板模拟器简化分析液路图.
|
图 7 线控制动系统踏板模拟器简化液路图 Fig. 7 Simplified hydraulic circuit of pedal feel emulator with wire brake system |
考虑管径突变及小孔节流产生的压力损失,根据伯努利定理和流量连续性方程,制动主缸油压pc与模拟器主缸油压ps的压力损失关系为
| ${p_{\rm{c}}}{\rm{ - }}{p_{\rm s}}{\rm{ = }}\frac{{{\rm{\rho }}D_{\rm{c}}^{\rm{4}}}}{{{\rm{2}}{\beta ^{\rm{2}}}}}\left( {\frac{{{\rm{1 + }}{k_{\rm{e}}}}}{{D_{\rm{t}}^{\rm{4}}}}+\frac{{\rm{1}}}{{C_{\rm{v}}^{\rm{2}}D_{\rm{v}}^{\rm{4}}}}{\rm{ - }}\frac{{{\rm{1 + }}k_{\rm{e}}'}}{{D_{\rm{n}}^{\rm{4}}}}} \right){\left( {\frac{{{\rm{d}}S}}{{{\rm{d}}t}}} \right)^{\rm{2}}}{.}$ | (3) |
式中:ρ为制动液密度,Dt为模拟器常闭电磁阀前管路内径,Cv为模拟器常闭电磁阀流量系数,Dv为模拟器常闭电磁阀阻尼孔直径,Dn为模拟器常闭电磁阀后管路内径,ke为Dt负相关系数,ke'为Dn负相关系数.
根据式(1),忽略惯量(mc、ms)以及摩擦力影响,根据牛顿第二定律得
| $F\beta = {p_{\rm{c}}}\frac{\pi }{{\rm{4}}}D_{\rm{c}}^{\rm{2}}+{k_{\rm{c}}}S{\rm{; }}\;{k_{\rm{A}}}S={p_{\rm{s}}}\frac{\pi }{{\rm{4}}}D_{\rm{c}}^{\rm{2}}.$ |
令
| $a{\rm{ = }}\displaystyle\frac{{{\rm{\rho \pi }}D_{\rm{c}}^{\rm{6}}}}{{{\rm{8}}{{\rm{\rho }}^{\rm{3}}}C_{\rm{v}}^{\rm{2}}}}\displaystyle\frac{{\rm{1}}}{{D_{\rm{v}}^{\rm{4}}}},\;b{\rm{ = }}\displaystyle\frac{{{k_{\rm{A}}}+{k_{\rm{c}}}}}{\beta },\;\lambda {\rm{ = }}\frac{F}{t}.$ |
代入式(3)并求导,可得踏板力加载时间t与踏板速度响应v的关系为
| $t=\frac{{{\rm{2}}a\beta }}{{{b^2}}}\left( {\lambda - bv - \alpha {\rm{ln}}\,\left| {\lambda - bv} \right| + {{C}}} \right).$ | (4) |
式中:C为常量.
无压力损失的模拟器系统,踏板力加载时间t与踏板速度响应v的关系为
| ${\rm{}}F\beta {\rm{ = }}{m_{\rm{c}}}\frac{1}{\beta }\ddot S +{F_{\rm{s}}}+{k_{\rm{c}}}\left( {{X_{{\rm{c0}}}}+S\frac{{\rm{1}}}{\beta }} \right)+{f_{\rm{c}}}.$ |
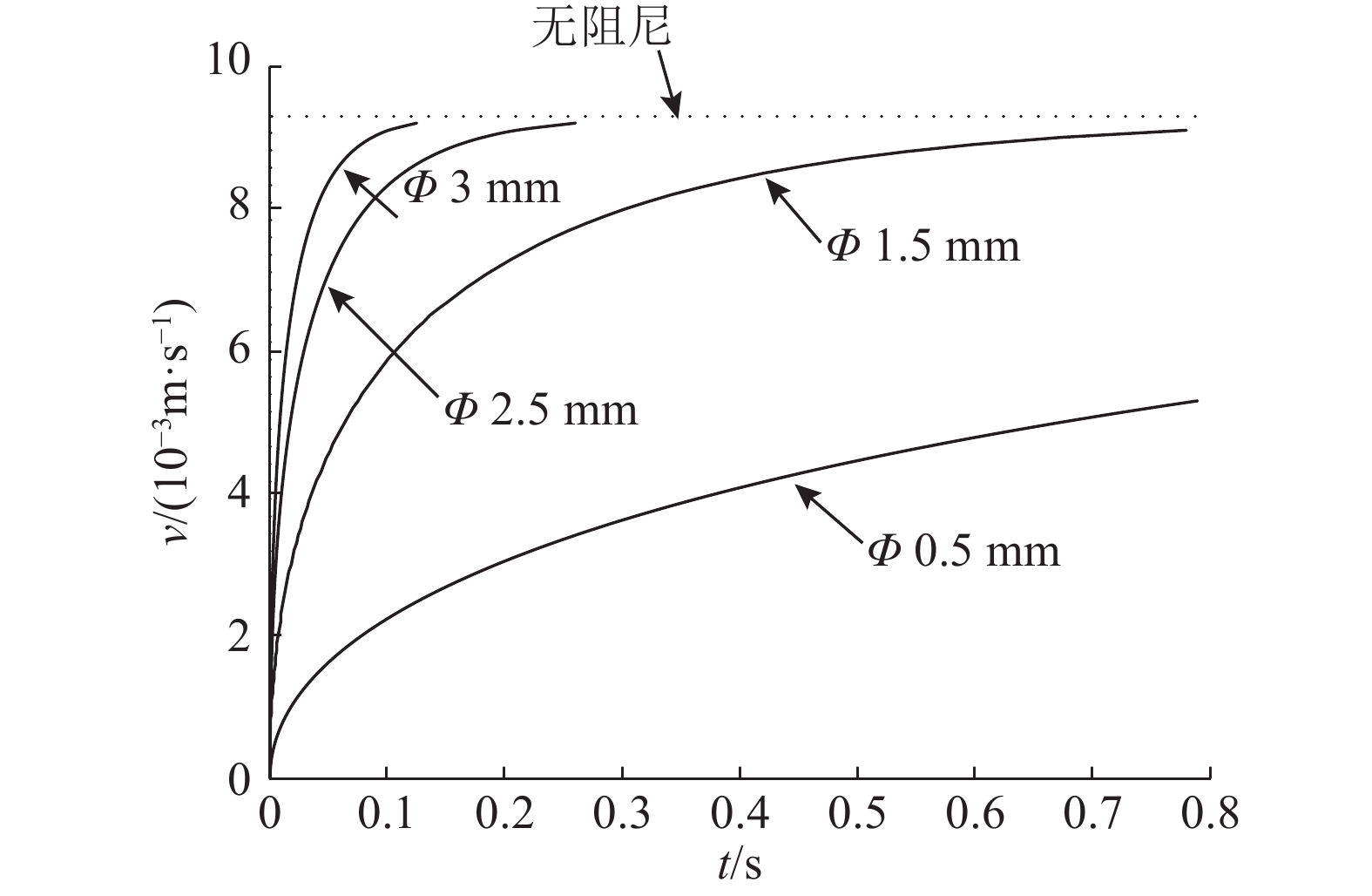
将当前设计参数代入式(4),并根据试验结果确定常量C的取值,用作图法可得到电磁阀阻尼孔径对踏板速度响应的影响曲线,如图8所示. 为提高踏板感模拟曲线精度,应提高实际系统到达理论无阻尼踏板速度的响应时间. 从图中可以看出,模拟器电磁阀阻尼孔径对速度响应具有高阶影响系数,增大电磁阀的阻尼孔径,即提高其过流面积,能显著提高踏板速度响应.
|
图 8 踏板力加载速度为25 N/s时的电磁阀阻尼孔径对踏板速度响应的影响 Fig. 8 Pedal velocity response at different holes at pedal loading speed of 25 N/s |
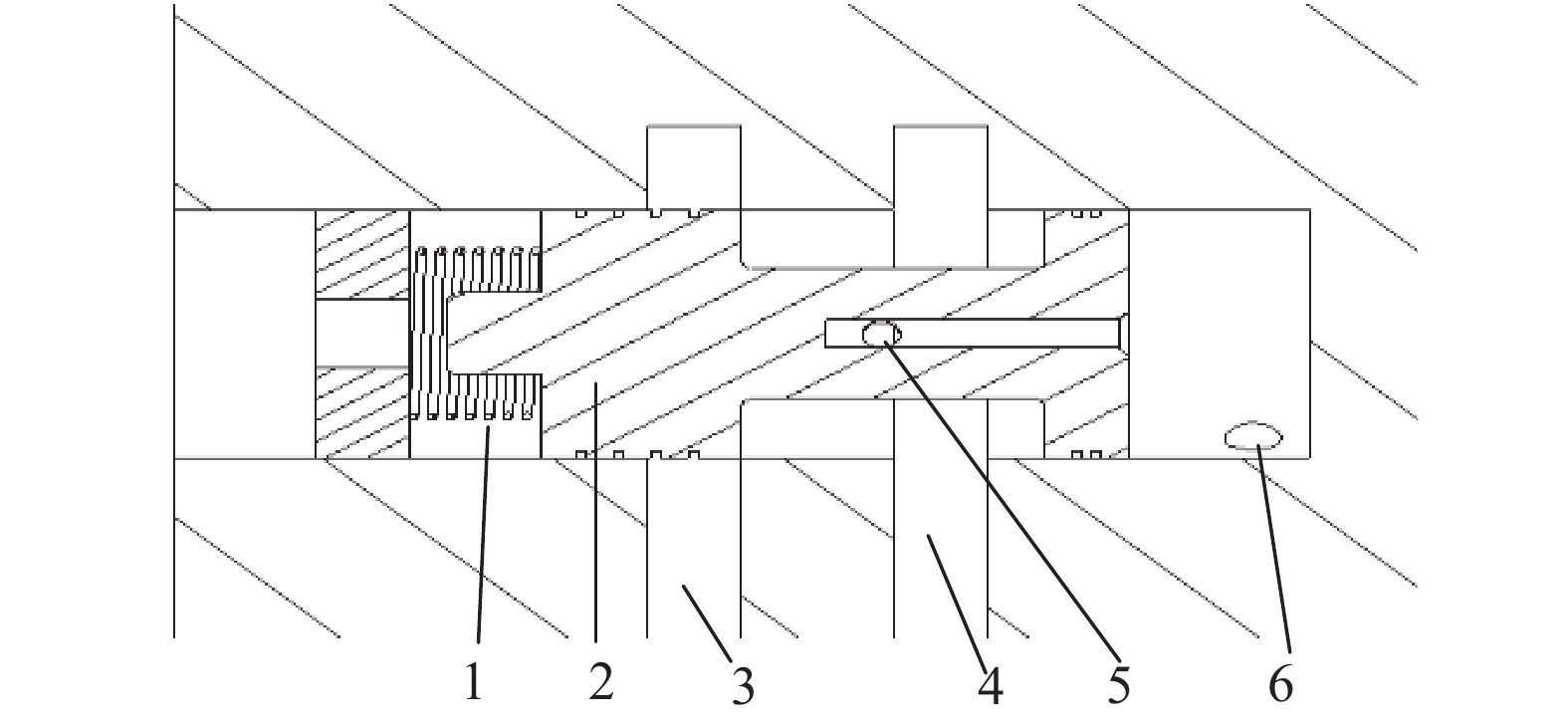
重新开发的满足要求的大过流孔径电磁阀理论上可消除上述试验问题. 但考虑到电磁阀产品开发周期较长,性能及可靠性短期内难以完成验证,同时需要与控制器、阀体重新匹配,是一个系统性问题,因此,考虑将当前电磁阀作为先导控制阀使用,充分利用当前开发成果. 改进设计方案原理如图9和10所示. 常规制动工况:模拟器常闭电磁阀通电打开,踩下制动踏板后制动油液通过电磁阀进入液控开闭阀控制口,油液首先通过回流排气孔进入模拟器主缸排气并推动模拟器主缸形成初始踏板力,当制动踏板力继续加大足以克服液控开关阀弹簧回复力时,主阀芯阀口打开,制动油液进入模拟器主缸. 松开踏板后,制动油液可通过主阀芯阀口和回流排气孔回制动主缸. 特别地,当踏板力超过一定小行程(足以克服液控开闭阀弹簧回复力打开主阀口)时,可关闭模拟器开闭电磁阀,因出油口压力与液控开关阀控制口连通,仍然能保证主阀口打开,这可在实际中降低模拟器开闭电磁阀通电工作时间,有利于控制电磁阀发热量并提高可靠性.

|
图 9 改进后的WBS踏板模拟器(PFE)液路原理图 Fig. 9 Improved hydraulic scheme of pedal feel emulator (PFE) with WBS |
|
1-回位弹簧;2-主阀芯;3-进油油路;4-排油油路;5-回流排气孔;6-电磁阀控制口 图 10 改进后的液控开闭阀结构图 Fig. 10 Improved structure of hydraulic control valve |
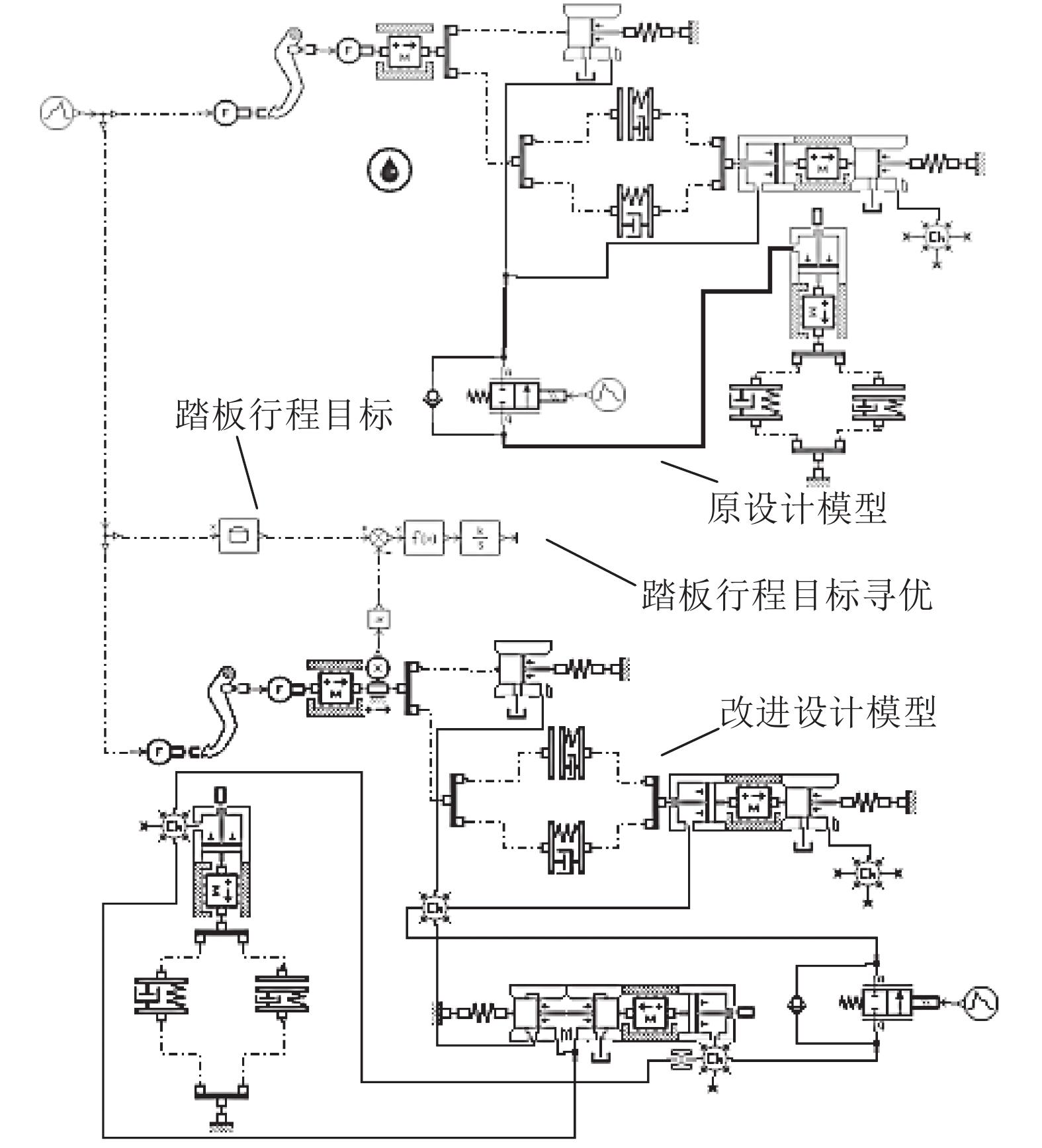
建立原设计及改进设计仿真模型如图11所示. 根据空间布置限制及工程设计经验确定液控开闭阀通径为Φ10 mm.
|
图 11 PFE回路原设计与改进设计AMEsim模型 Fig. 11 AMEsim models of original and improved designed PFE circuit |
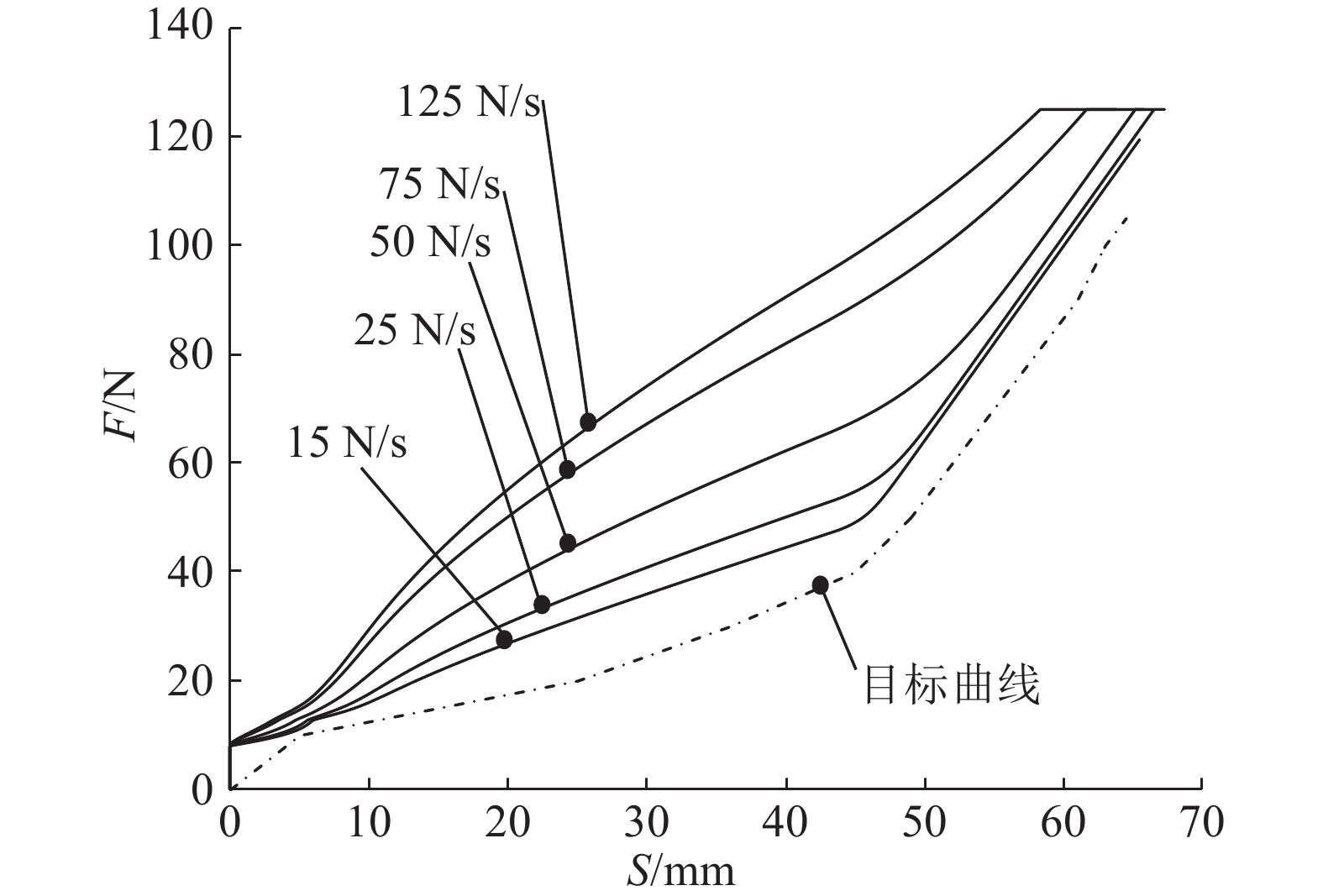
踏板模拟原设计仿真模型踏板行程-踏板力仿真结果如图12所示. 模型中模拟器常闭电磁阀过流孔径选定为Φ1.0 mm. 仿真结果表明:踏板力加载速度越快,曲线非线性特性越明显,这主要是由于电磁阀过流孔径过小,与之前试验结果趋势相同.
|
图 12 原设计的模拟器踏板行程−力特性仿真结果 Fig. 12 Pedal stroke-force simulation results of original designed pedal feel emulator |
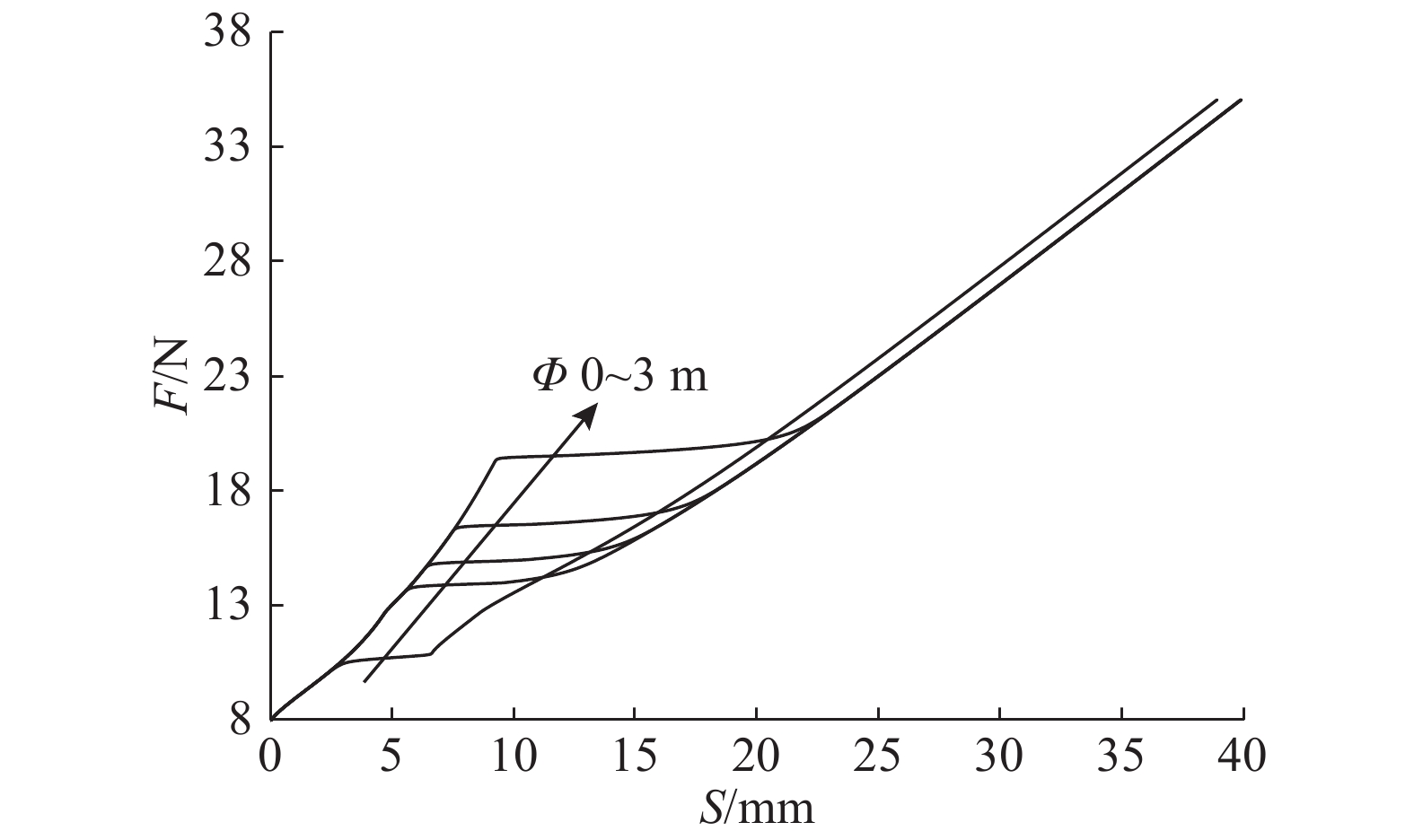
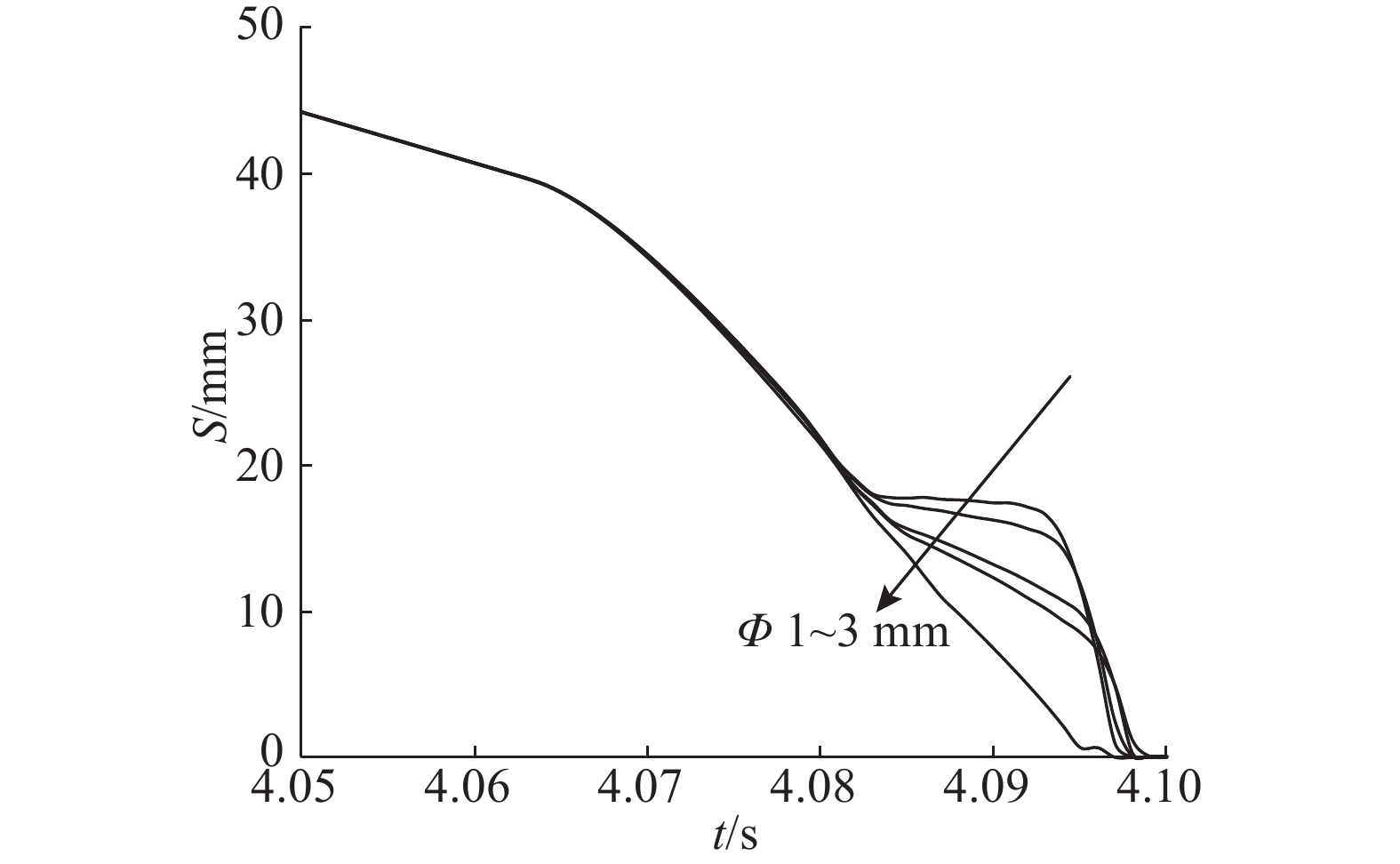
如图13所示为所设计的液控开闭阀主阀口初始密封量对踏板加载S-F特性曲线的影响:初始密封量过大会造成初段踏板力变大,并引起S-F特性曲线前段突变;如图14所示为回流排气孔径对踏板回程(踏板力为0)踏板行程的影响:在踏板回程后段,回流排气孔径过小,会造成后段踏板回程不够顺滑,但基本不影响踏板回程速度.
|
图 13 阀芯初始密封值影响 Fig. 13 Influence with initial underlap |
|
图 14 回流排气孔径影响 Fig. 14 Influence with back and exhaust hole diameters |
同时利用AMEsim-Optimus优化模块对所设计的液控开关阀进行参数寻优,并根据工程实际设定取值范围. 优化后该阀回复弹簧刚度选定为0.3 N/mm,预紧力为0.3 N,回流排气孔直径为Φ2.8 mm.
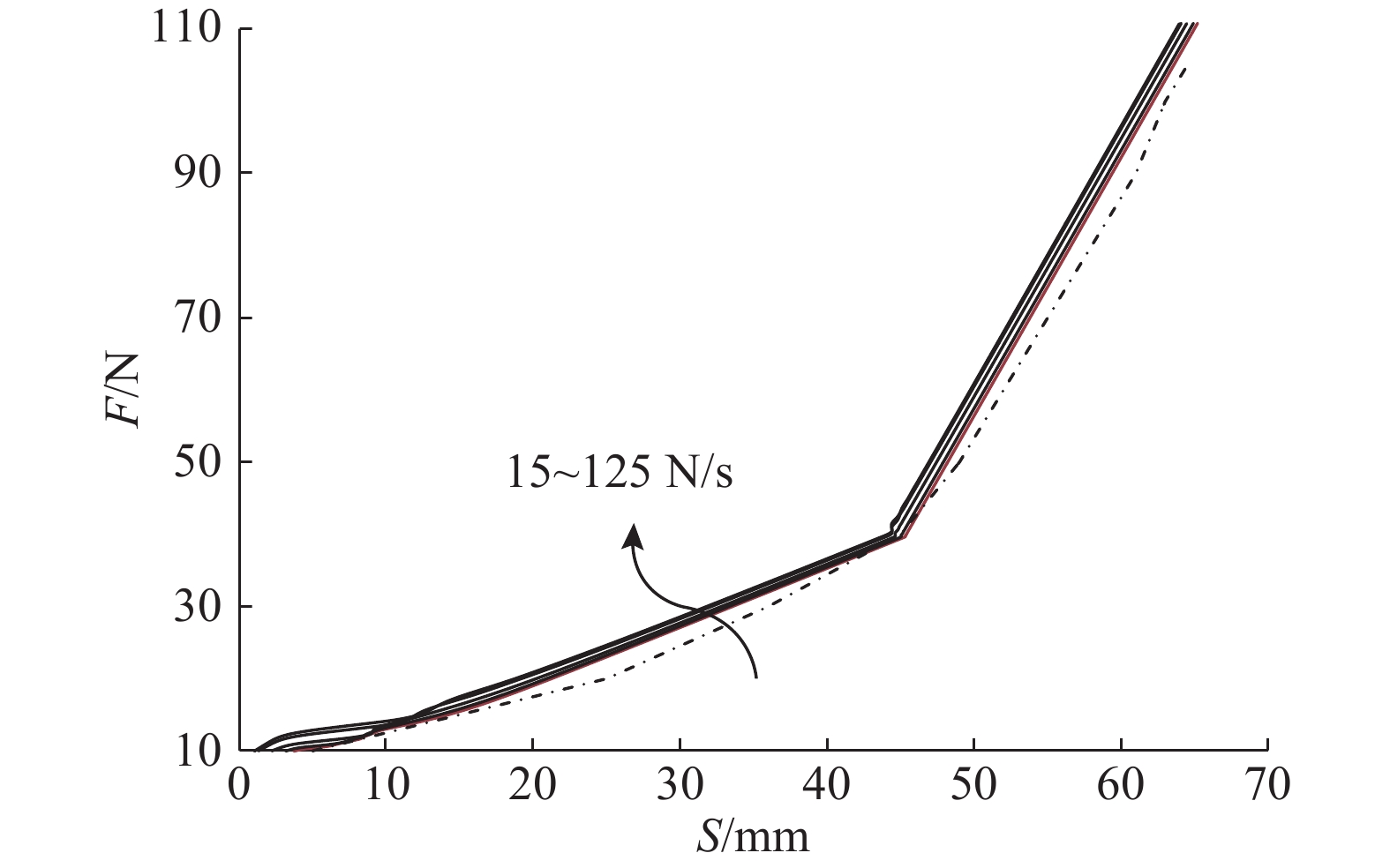
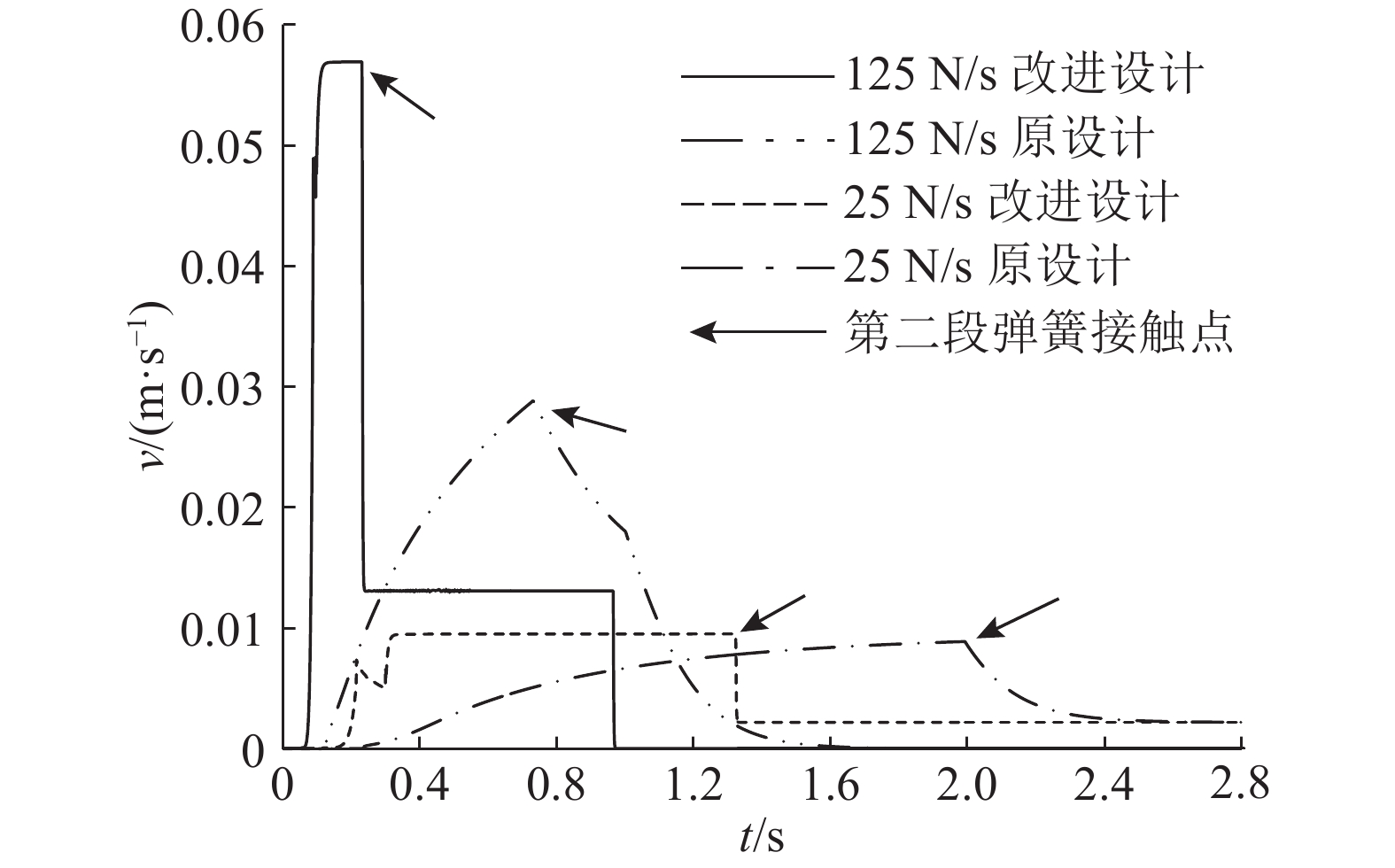
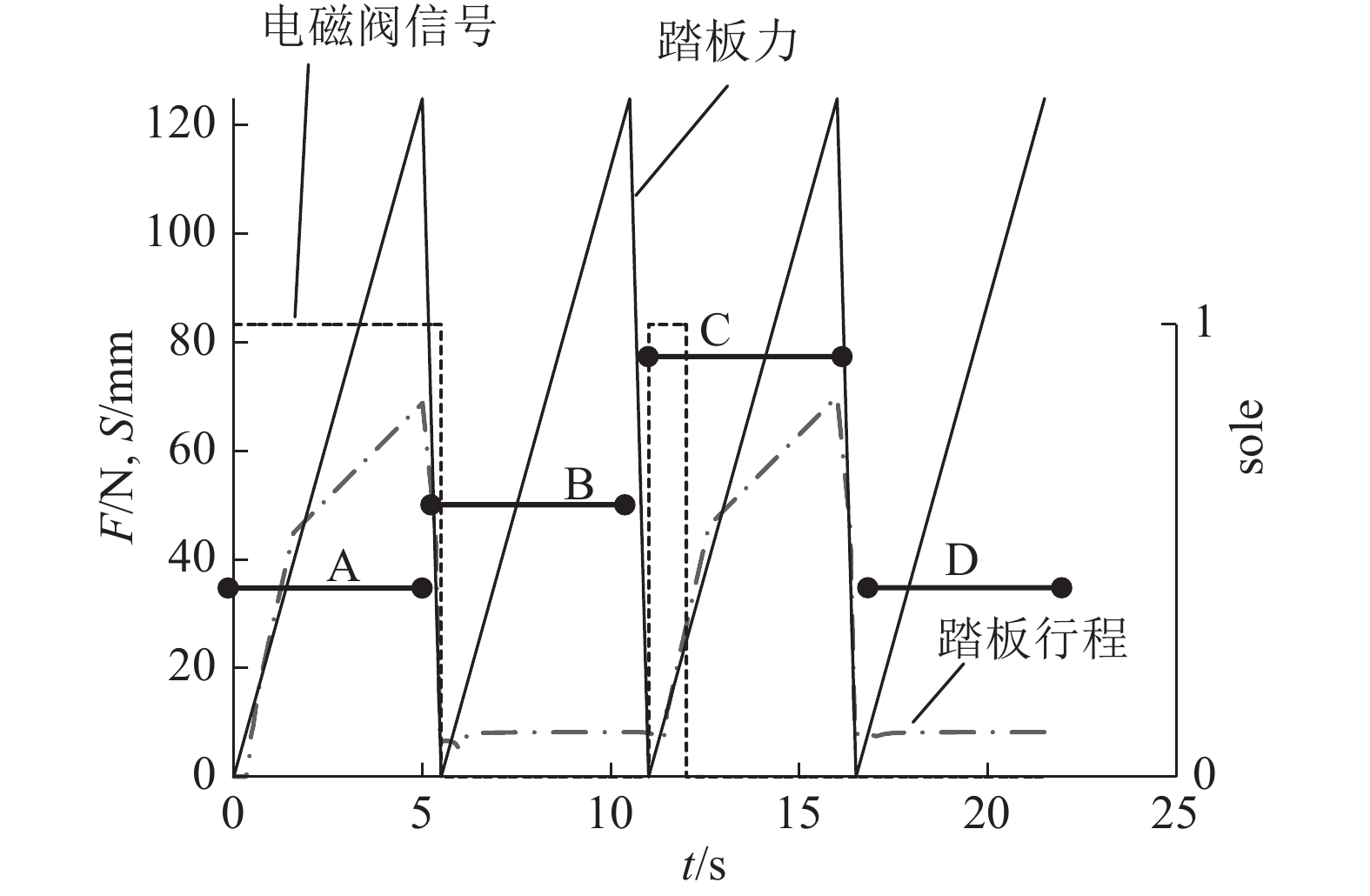
对参数优化后的改进仿真模型施加相同的踏板力,仿真结果曲线如图15所示. 仿真结果表明:改进设计仿真结果与目标曲线吻合度良好,受踏板力加载速度影响小,这主要是因为液控开闭阀有较强的通流能力,并可根据踏板力大小调节主阀口开度. 改进设计相比原设计,在不同踏板力加载时间下,踏板速度响应均有明显改善,如图16所示. 在踏板改进设计仿真模型中施加如图17所示周期性踏板力,sole表示电磁阀的开闭状态:0表示断电,1表示通电. 在A段周期内,模拟器常闭电磁阀上电打开,踏板模拟器正常工作;在B段周期内,模拟器常闭电磁阀断电关闭,模拟器停止工作,踏板仅输出固定空行程;在C段周期内,模拟器常闭电磁阀在前1 s内上电打开后关闭,踏板模拟器可依然保持正常工作. 这一特性可缩短开闭电磁阀工作时间,从而降低电磁阀负荷及发热量,提高了系统可靠性.
|
图 15 改进设计的踏板模拟器踏板行程-力特性仿真结果 Fig. 15 Pedal stroke-force simulation results of improved pedal feel emulator |
|
图 16 不同踏板力加载速度下的踏板速度响应仿真结果 Fig. 16 Simulation results of pedal velocity response at different pedal loading speed |
|
图 17 改进设计的模拟器通路断电保持特性 Fig. 17 Keeping open character of improved pedal feel emulator circuit with power off |
对采用改进方案设计的线控制动系统样机进行实车试验测试,试验情况如图18、19所示. 试验结果表明,该优化设计较好地实现了踏板行程−踏板力特性曲线跟随.

|
图 18 WBS改进方案实车测试 Fig. 18 Field test of improved pedal feel emulator with WBS |

|
图 19 改进设计的模拟器踏板行程-力特性试验结果 Fig. 19 Pedal stroke-force test results of improved pedal feel emulator |
改进前、后的踏板模拟器踏板行程−力特性进行了记录和对比如表1和2所示. 表中:Fori为改进前对应踏板位置的踏板力,Fimp为为改进后对应踏板位置的踏板力,Eori为改进前对应踏板位置的踏板力误差或误差百分比,Eimp改进后对应踏板位置的踏板力误差或误差百分比,Rori为改进前对应踏板位置的踏板力评价结果,Rimp为改进后对应踏板位置的踏板力评价结果:NG为不合格,OK为合格.
| 表 1 踏板加载速度为25 N/s时的踏板行程−力特性试验结果 Table 1 Pedal stroke-force test results at pedal loading speed of 25 N/s |
| 表 2 踏板加载速度为250 N/s(紧急制动)时的踏板行程−力特性试验结果 Table 2 Pedal stroke-force test results at pedal loading speed of 250 N/s (emergency braking) |
本研究对一种线控制动系统踏板感觉模拟器进行计算分析和试验验证,确定了模拟器常闭电磁阀过流孔径是影响踏板行程特性曲线偏离的主要因素. 重新设计了一种液控开闭阀,该阀由原踏板模拟器常闭电磁阀控制,所设计的液控开闭阀可提高踏板模拟器回路的通流能力. 利用AMEsim仿真模型完成参数选型并进行了装车试验,仿真及试验结果均表明该方案可获得良好的踏板感曲线精度,同时具备开发方便、降低电磁阀负荷的特点.
| [1] |
林志轩, 高晓杰. 制动踏板感觉研究现状[J]. 农业装备与车辆工程, 2007, 196(6): 4-7. LIN Zhi-xuan, GAO Xiao-jie. The research summarization of the brake pedal feeling[J]. Agricultural Equipment and Vehicle Engineering, 2007, 196(6): 4-7. DOI:10.3969/j.issn.1673-3142.2007.06.001 |
| [2] |
林逸, 沈沉, 王军, 等. 汽车线控制动技术及发展[J]. 汽车技术, 2005(12): 1-3. LIN Yi, SHEN Chen, WANG Jun, et al. Automotive by wire control technology and development[J]. Automobile Technology, 2005(12): 1-3. DOI:10.3969/j.issn.1000-3703.2005.12.001 |
| [3] |
潘宁, 于良耀, 张雷, 等. 电液复合制动系统防抱控制的舒适性[J]. 浙江大学学报: 工学版, 2017, 51(1): 9-11. PAN Ning, YU Liang-yao, ZHANG Lei, et al. Anti-lock b raking control in coordinated braking system considering braking comfort[J]. Journal of Zhejiang University: Engineering Science, 2017, 51(1): 9-11. |
| [4] |
裴晓飞, 董兴智, 张灿明, 等. 汽车制动踏板特性仿真及踏板感觉优化[J]. 汽车工程学报, 2017, 7(1): 052-060. PEI Xiao-fei, DONG Xing-zhi, ZHANG Can-ming, et al. Si mulation of brake pedal characteristic and optimization of brake pedal feel[J]. Chinese Journal of Automotive Engineering, 2017, 7(1): 052-060. |
| [5] |
OHTAIN Y, INNAMI T, OBATA T, et al. Development of an electrically-driven intelligent brake unit [C] // SAE Paper. Detroit: SAE World Congress, 2011: 2011-01-0572. http://www.doc88.com/p-202939857346.html
|
| [6] |
金智林, 郭立书, 赵又群, 等. 踏板感觉可控的汽车制动踏板模拟器研究[J]. 系统仿真学报, 2010, 22(12): 2795-2798. JIN Zhi-lin, GUO Li-shu, ZHAO You-qun, et al. Research on brake pedal emulator of vehicle with controllable pedal feeling[J]. Journal of System Simulation, 2010, 22(12): 2795-2798. |
| [7] |
Pasquet. Brake pedal simulator, master cylinder for a vehicle and method of operation of said simulator: EP, 1600347A1 [P]. 2005-05-23. http://www.freepatentsonline.com/EP1600347.html
|
| [8] |
王奎洋, 唐金花, 刘成晔, 等. 线控制动系统踏板感觉模拟器的分析与设计[J]. 机床与液压, 2011, 39(21): 108–111. WANG Kui-Yang, TANG Jin-hua, LIU Cheng-ye, et al. Aalysis and design on the pedal feeling simulator of brake-by-wire[J]. Machine Tool and Hydraulics, 2011, 39(21): 108–111. http://www.cnki.com.cn/Article/CJFDTotal-JCYY201121031.htm |
| [9] |
VON A C, KARNER J. Brake system for hybrid and electric vehicles [C] // SAE Paper. Detroit: SAE World Congress, 2009: 2009-01-1217.
|
| [10] |
NAKAURA E, SOGA M, SAKAI A, Et al. Development of electronically controlled brake system for hybrid vehicle [C] // SAE Paper. Detroit: SAE World Congress, 2002: 2002-01-0300.
|
| [11] |
丰田自动车株式会社. 用于产生制动踏板阻力的设备: 200810007052.6 [P]. 2008-01-25.
|
| [12] |
KOIZUMI N. Effect of phenolic brake piston tribology on brake pedal feel [C] // SAE Paper. Florida: SAE Annual Brake Colloquium. 2013: 2013-01-2051.
|
| [13] |
KARLHEINZ B, MARTIN S, BERT B. A new approach to investigate the vehicle interface driver/brake pedal under real road conditions in view of oncoming brake-by-wiresystems [C] // SAE Paper. Detroit: Future Transportation Technology Conference, 1999: 1999-01-2949.
|
| [14] |
刘杨, 孙泽昌, 冀文斌. 电液复合制动系统踏板感觉及其影响因素[J]. 吉林大学学报: 工学版, 2015, 45(4): 1049-1055. LIU Yang, SUN Ze-chang, JI Wen-bin. Brake pedal feel and its influencing factors for electro-hydraulic brake system[J]. Journal of Jilin University: Engineering and Technology Edition, 2015, 45(4): 1049-1055. |
| [15] |
万向集团公司. 车辆集成电控液压制动系统: 201510254642.9 [P]. 2015-08-26.
|


