2. 西安飞机工业(集团)有限责任公司,陕西 西安 710089
2. Xi'an Aircraft Industry Company Limited, Xi'an 710089, China
孔口倒角是飞机交点孔(孔径为Φ40~60 mm)加工过程中必不可少的一步工序,对加工一致性及可靠性要求很高[1]. 在飞机装配现场,飞机交点孔工装设备复杂,操作空间狭小,使得传统机床难以使用,只能依靠效率与质量难以保证的手动加工. 针对这种情况,在航空制造领域应用日益成熟的工业机器人[2-3]以其机动、灵活的特点,成为完成飞机交点孔倒角任务的理想选择.
试验发现,当机器人直接正向进给进行孔口倒角加工时,很容易产生振动. 科研工作者们在金属切削领域的振动形成机理、识别、监测和抑制等方面进行了大量科学研究,并取得了丰硕成果[4-6],但是这些几乎都是基于传统机床的研究,并不完全适用于串联式弱刚度机器人. 目前针对机器人切削振动的相关研究相对较少,一方面由于在切削领域中机器人应用较少,重视程度不够;另一方面由于机器人操作臂是一个多杆连接复杂动力学系统,实际测量和建模很难精确,加上外部干扰以及大量不确定因素存在,很难得到机器人实际精确和完整的运动模型,给加工振动研究带来了极大困难[7]. Pan等[8]分析了机器人铣削颤振问题,发现其颤振类型为模态耦合颤振,而不是传统机床上的再生颤振. Mejri等[9]研究发现通过调节机器人姿态可以显著提高机器人加工系统动态特性. Ozer等[10]对双连杆机械臂颤振问题进行了数值模拟研究,发现关节刚度对颤振抑制非常明显,为机器人颤振抑制设计提供了依据. Guo等[11]在忽略轴向力的情况下对机器人镗孔切削振动机理进行了研究,发现其是由径向力引起的具有位移反馈的强迫振动,并证实该类振动可以通过外加摩擦阻尼进行抑制. Hazel等[12]运用高速相机发现机器人磨削加工系统中刀具和工件之间存在反复冲击现象,指出再生颤振机理可能是磨削机器人加工颤振产生的原因,并通过仿真计算给出了机器人磨削加工的稳定区域. 关于机器人孔口倒角切削振动方面的研究目前仍鲜有报道.
本文通过构建机器人孔口倒角动力学模型,首先对机器人正向倒角切削振动成因进行分析,进而提出一种机器人反向倒角切削抑制振动方法,最后通过对比试验验证机器人反向倒角切削的可靠性.
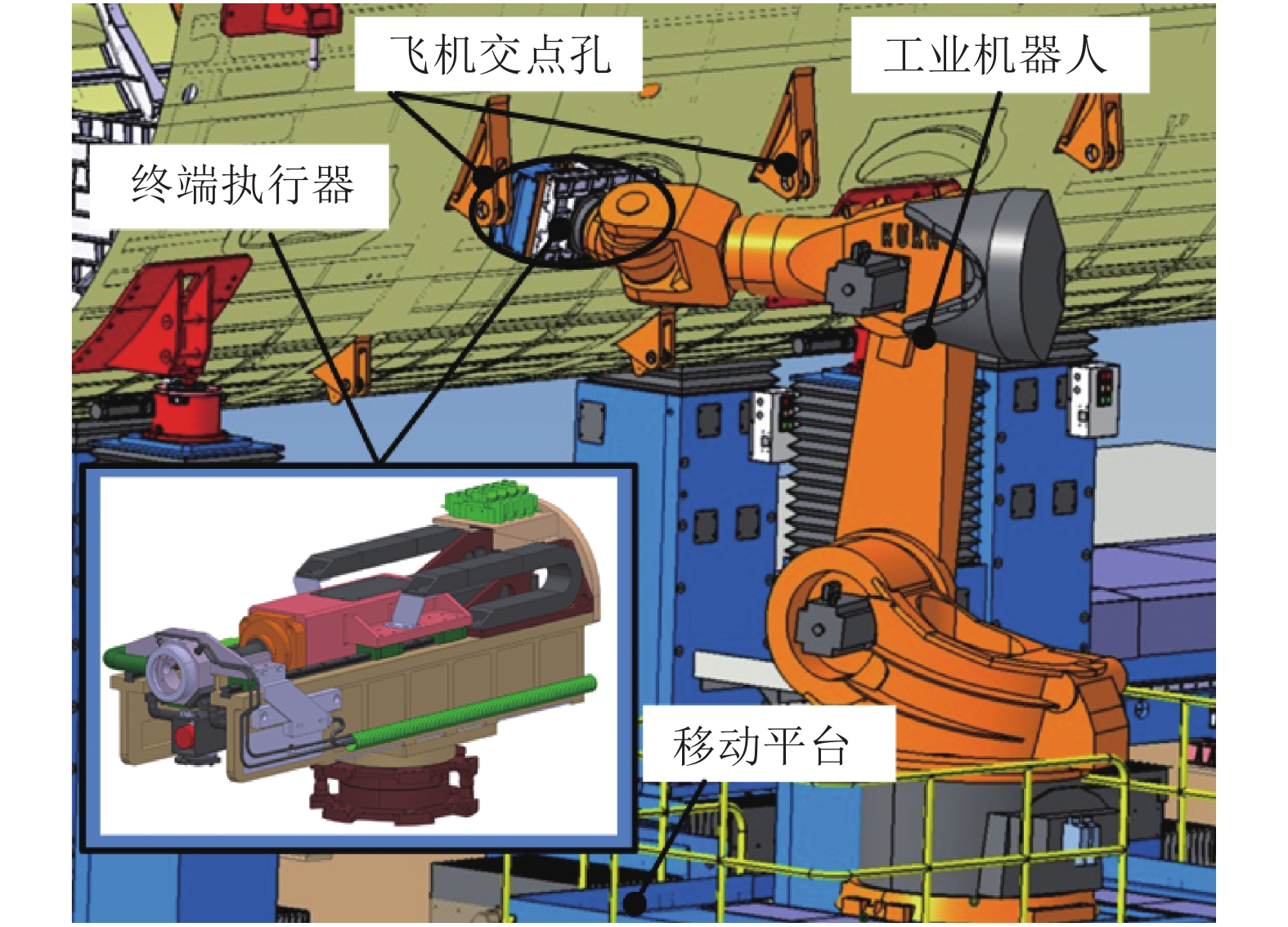
1 机器人倒角切削系统构建如图1所示为机器人倒角切削加工系统,终端执行器(如图2所示)通过快换法兰安装于工业机器人末端,是完成倒角切削的动力部件. 首先机器人沿移动平台移动到合适位置,然后携带终端执行器运动至交点孔孔位处,气缸推出压脚并压紧工件,最后主轴带动刀具旋转,并沿着直线进给实现切削运动,完成交点孔倒角加工.
|
图 1 机器人倒角加工系统图 Fig. 1 Schematic diagram of robotic chamfering hole |

|
图 2 机器人倒角终端执行器 Fig. 2 End-effector for robot chamfering hole |
机器人倒角切削具有如下特点:1)随着主轴进给,切削深度在逐渐变大,切削力也在逐渐增大;2)由于刀具旋转,切向力和径向力方向始终在周期性变化,易引起振动;3)机器人自身机械刚度较小,是切削系统中柔性的主要来源,这与机床切削加工存在明显不同.
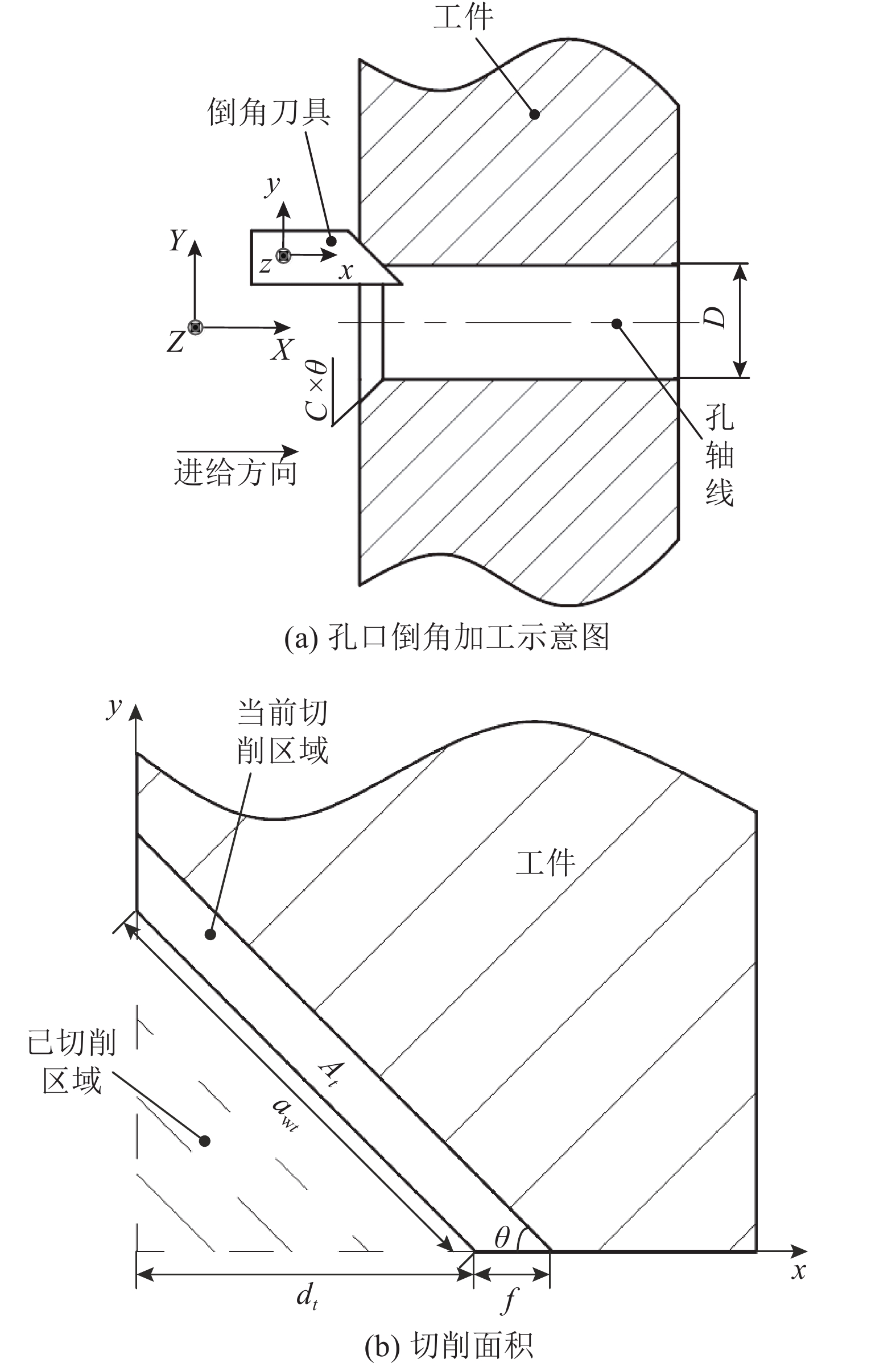
2 机器人倒角切削动力学建模 2.1 切削力建模机器人孔口倒角加工示意图如图3(a)所示,倒角深度C的取值与待倒角孔直径D相关,通常直径越大,倒角深度越大;倒角角度θ的取值与装配中倒角所起的作用相关[13],常见取值为45°. 为方便动力学建模,建立固定笛卡尔坐标系(X,Y,Z)和随主轴一起作旋转运动的旋转坐标系(x,y,z). 固定坐标系(X,Y,Z)的X轴、Y轴和Z轴方向固定,分别与进给方向、水平方向和垂直方向平行. 旋转坐标系(x,y,z)的x轴方向固定,沿着直线进给方向,而y轴和z轴方向始终在周期性改变(随主轴旋转),分别平行于孔截面圆半径方向.
|
图 3 机器人孔口倒角切削面积 Fig. 3 Cutting area of robotic chamfering hole |
在振动未发生时,倒角切削面积如图3(b)所示,在t时刻其大小与已切削深度dt、切削宽度awt、进给量f和倒角角度θ相关,切削面积At表达式为
| ${A_{{t}}} = \frac{{\rm{1}}}{2}\left( {\frac{{{d_{{t}}} + f}}{{\cos\; \theta }} + {a_{{{\rm{w}}t}}}} \right)f\sin \;\theta \cdot $ | (1) |
其中,已切削深度dt表达式为
| ${d_{{t}}} = \displaystyle\frac{{nf}}{{60}}t \cdot $ | (2) |
式中:n为主轴旋转速度.
待切削宽度awt表达式为
| ${a_{{\rm{w}}t}} = \frac{{nf}}{{60\cos\; \theta }}t \cdot $ | (3) |
基于单位面积切削力模型,得到在旋转坐标系(x,y,z)下倒角切削力表达式为
| ${F_x} = {K_{{\rm{fc}}}}{A_{{t}}},\;{F_y} = {K_{{\rm{rc}}}}{A_{{t}}},\;{F_z} = {K_{{\rm{tc}}}}{A_{{t}}}.$ | (4) |
式中:Fx、Fy和Fz分别为轴向、径向和切向分力,Kfc、Krc和Ktc分别为进给方向、径向和切向的切削力系数,大小取决于切削条件和工件-刀具材料性质等[14]. 对旋转坐标系(x,y,z)中的切削分力进行坐标转换,得到固定坐标系(X,Y,Z)中的切削力表达式为
| $\left\{ \begin{gathered} {F_X} \\ {F_Y} \\ {F_Z} \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos\;\, ({\omega _{{t}}}t)}&{ - \sin\;\, ({\omega _{{t}}}t)} \\ 0&{\sin\;\, ({\omega _{{t}}}t)}&{\cos\;\, ({\omega _{{t}}}t)} \end{array}} \right]\left\{ \begin{gathered} {F_x} \\ {F_y} \\ {F_z} \\ \end{gathered} \right\} \cdot $ | (5) |
式中:FX、FY和FZ是机器人倒角切削系统在固定坐标系X、Y和Z方向的作用力,ωt为主轴旋转频率.
2.2 考虑压脚作用的机器人倒角切削系统建模在某一固定位姿时,六自由度工业机器人笛卡尔刚度矩阵K(6×6)可表示4个3×3矩阵[15]:
| ${K} = \left[ {\begin{array}{*{20}{c}}{{{K}_{{\rm{fd}}}}}&{{{K}_{{\rm{f\delta }}}}}\\{{{K}_{{\rm{nd}}}}}&{{{K}_{{\rm{n\delta }}}}}\end{array}} \right].$ | (6) |
式中:Kfd为力−线位移刚度矩阵,Knd为力矩−线位移刚度矩阵,Kfδ为力−角位移刚度矩阵,Knδ为力矩−线位移刚度矩阵. 机器人倒角加工过程中,作用力f记为
| ${f} = {f_0} \cdot {{e}_{\rm f}} \cdot $ | (7) |
式中:ef为作用力方向,f0为作用力大小,记d为机器人末端位移变形矢量,则有
| ${f} = {{K}_{{\rm{fd}}}} \cdot {d} \cdot $ | (8) |
联立式(7)与式(8),可得
| ${d} = {{K}_{{\rm{fd}}}^{ - 1}}{f_0}{e}_{\rm f} \cdot $ | (9) |
将向量d投影至ef方向,利用向量投影点积运算规则,得到在力矢量f方向上发生的变形为
| ${d_f} = {{e}_{\rm f}} \cdot {d} \cdot $ | (10) |
由式(9)与式(10),根据刚度定义,可得在力矢量f上机器人单方向刚度为
| ${k_f} = \frac{1}{{{{e}^{\rm T}_{\rm f}}{{K}_{{\rm{fd}}}^{ - 1}}{e}_{\rm f}}}.$ | (11) |
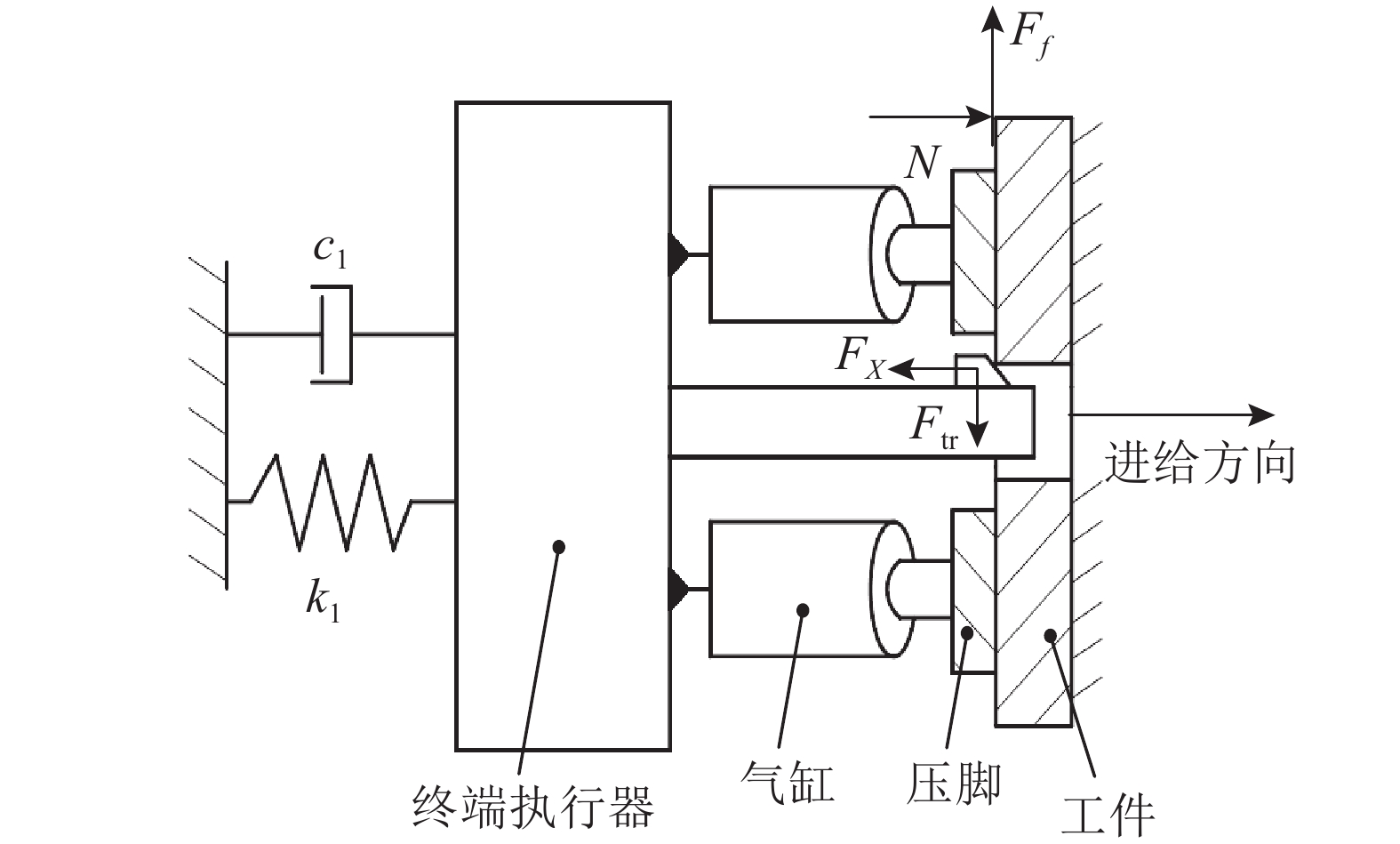
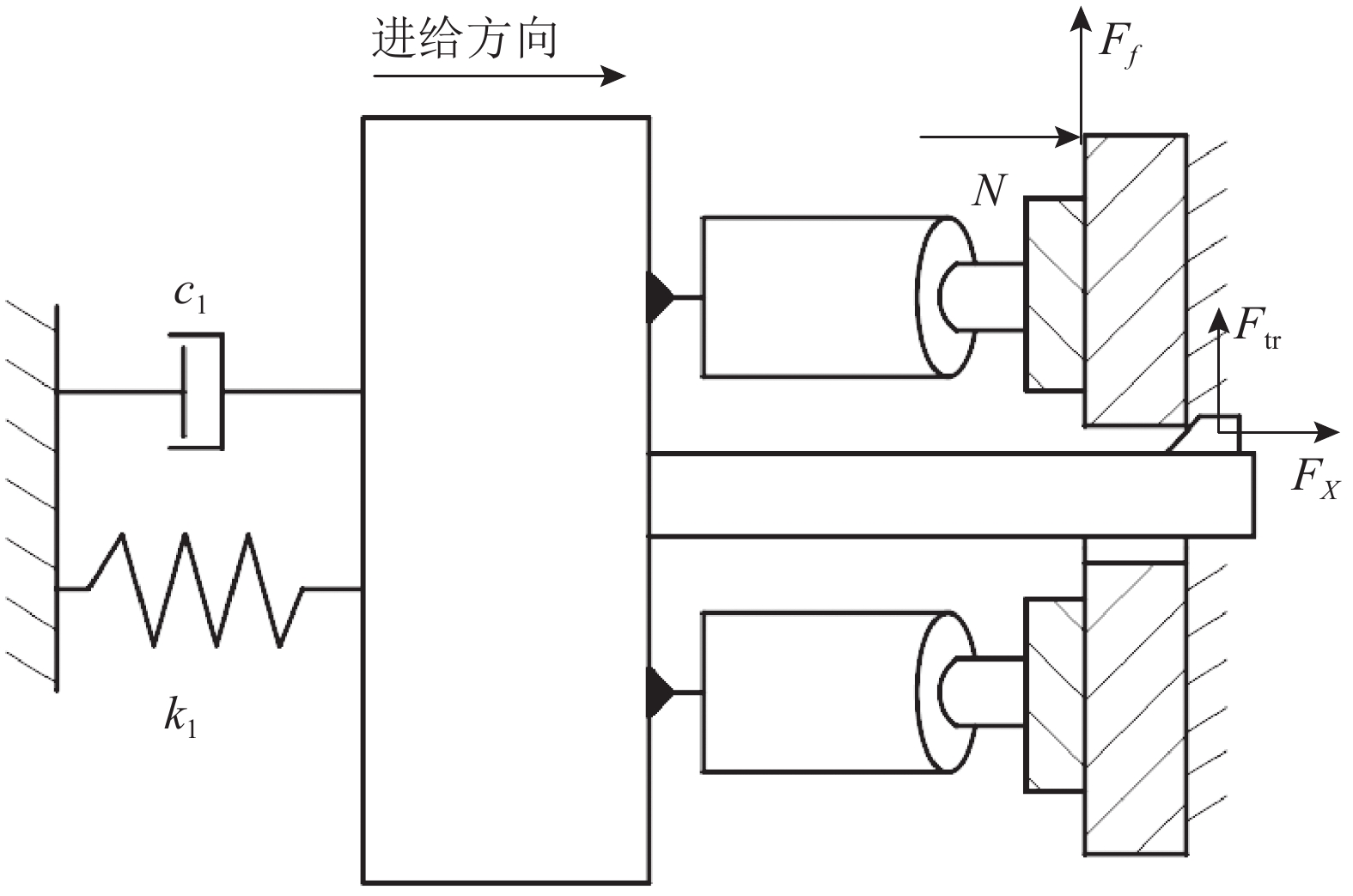
在机器人切削加工中通常都会使用压脚[16]. 压脚作用后,如图4所示,在XY平面内可以将系统简化为单自由度质量弹簧阻尼系统,X方向的动力学方程可表示为
|
图 4 压脚作用原理图 Fig. 4 Schematic diagram of the pressure foot |
| $m\ddot X + {c_1}\dot X + {k_1}X = {F_X} + 2{p_{{}_{\rm N}}}A \cdot $ | (12) |
式中:
假定在切削力作用下压脚与工件表面发生相对运动,此时两者间将产生滑动摩擦力Ff,大小为Ff=μN(μ为摩擦系数),方向与径向力和切向力合力Ftr方向相反. 采用能量方法将Ff简化为等效黏性阻尼以便于振动分析. Ff在一个周期内消耗能量为4Ff Xf,其中Xf为振动幅值. 根据文献[17]可知,等效黏性阻尼在一个周期内消耗能量为πceXf2ω,其中,ω为振动频率. 于是可得Ff的等效黏性阻尼系数为
| ${c_{\rm e}} = \frac{{4{F_f}}}{{\pi \omega {X_f}}} \cdot $ | (13) |
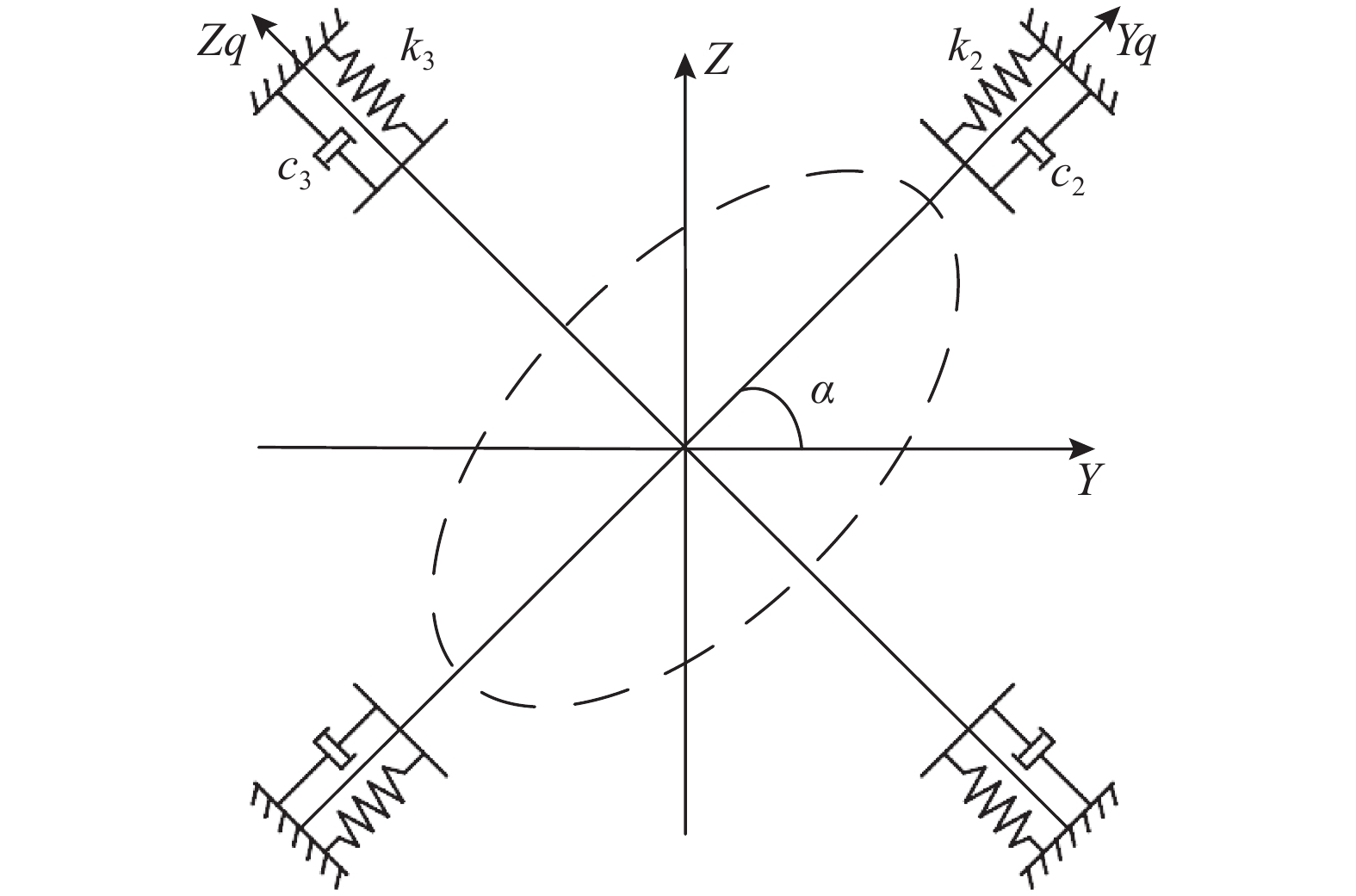
由文献[18]可知,机器人在某一位姿时,其刚度模型在二维空间中的几何模型是一个椭圆,椭圆半轴方向对应的刚度矩阵为对角矩阵. 因此将机器人倒角加工系统按椭圆半轴方向Yq和Zq建立主刚度坐标系以消除耦合性,如图5所示. 其中α为Yq(Zq)与固定坐标系Y(Z)方向之间的夹角,c2、c3和k2、k3分别为阻尼系数和刚度值.
|
图 5 机器人倒角系统模型 Fig. 5 Schematic diagram of robot machining chamfer system |
压上压脚后,振动未发生时,包括压脚机构的系统动力学方程可以表示为
| $\left. \begin{gathered} m\ddot Yq + \left({c_2} + {c_{{\rm e}Yq}}\right)\dot Yq + {k_2}Yq = {F_{Yq}}, \\ m\ddot Zq + \left({c_3} + {c_{{\rm e}Zq}}\right)\dot Zq + {k_3}Zq = {F_{Zq}}. \end{gathered} \right\}$ | (14) |
式中:FYq、FZq和ceYq、ceZq分别是主刚度坐标系Yq和Zq方向的作用力和等效黏性阻尼系数. 主刚度坐标系下切削力与固定坐标系下关系为
| $\left\{ \begin{gathered} {F_{Yq}} \\ {F_{Zq}} \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}{c}} {\cos\, \alpha }&{\sin\, \alpha } \\ { - \sin\, \alpha }&{\cos\, \alpha } \end{array}} \right]\left\{ \begin{gathered} {F_Y} \\ {F_Z} \\ \end{gathered} \right\} \cdot $ | (15) |
由式(1)~(5)以及式(15)得
| $\left. \begin{aligned} {F_{Yq}} = {{ K}_{{\rm{rt}}}}\left(\displaystyle\frac{{nft}}{{60}} + \frac{1}{2}f\right)f\tan\, \theta \;{\rm{sin}}\,\left({\omega _{{t}}}t - \alpha - \beta - \pi \right), \\ {F_{Zq}} = {{ K}_{{\rm{rt}}}}\left(\displaystyle\frac{{nft}}{{60}} + \displaystyle\frac{1}{2}f\right)f\tan\, \theta \;{\rm{sin}}\,\left({\omega _{{t}}}t - \alpha - \beta - \displaystyle\frac{\pi }{2}\right). \\ \end{aligned} \right\}$ | (16) |
式中:
将式(16)代入式(14)得动力学方程表达式:
| $\left. \begin{aligned}& \ddot Yq + \left(2{\xi _Y}{\omega _{{\rm n}Yq}} + \displaystyle\frac{{{c_{{\rm e}Yq}}}}{m}\right)\dot Yq + {\omega _{{\rm n}Yq}}^2Yq = \\& \displaystyle\frac{1}{m}\left({K_{{\rm{rt}}}}\left(\frac{{nft}}{{60}} + \displaystyle\frac{1}{2}f\right)f\tan\, \theta\; {\rm{sin}}\,\left({\omega _{{t}}}t - \alpha - \beta - \pi \right)\right), \\& \ddot Zq +\left (2{\xi _Z}{\omega _{{\rm n}Zq}} + \displaystyle\frac{{{c_{{\rm e}Zq}}}}{m}\right)\dot Zq + {\omega _{{\rm n}Zq}}^2Zq = \\& \displaystyle\frac{1}{m}\left({K_{{\rm{rt}}}}\left(\frac{{nft}}{{60}} + \displaystyle\frac{1}{2}f\right)f\tan\, \theta\; {\rm{sin}}\,\left({\omega _{{t}}}t - \alpha - \beta - \displaystyle\frac{\pi }{2}\right)\right). \\ \end{aligned} \right\} $ | (17) |
式中:f为进给量,ζYq、ζZq为系统在Yq和Zq方向上的阻尼比,ωnYq、ωnZq为系统在Yq和Zq方向上固有频率分量,表达式分别为
| $\left.\begin{gathered} {\xi _{Yq}} = \displaystyle\frac{{{c_2}}}{{2\sqrt {m{k_2}} }},\;{\xi _{Zq}} = {\displaystyle\frac{{{c_3}}}{{2\sqrt {m{k_3}}}}}, \\ {\omega _{{\rm n}Yq}} = \sqrt {\displaystyle\frac{{{k_2}}}{m}},\;{\omega _{{\rm n}Zq}} = \sqrt {\displaystyle\frac{{{k_3}}}{m}}. \\ \end{gathered} \right\}$ | (18) |
机器人自身刚度相比机床小得多,使其成为机器人倒角切削系统的主要柔性来源,这与机床切削存在明显不同,因此本节针对机器人倒角自身特点,对其进行振动分析.
首先,对试验用ABB-IRB6600-175/2.5型机器人进行刚度辨识. 由六自由度机器人关节刚度辨识方法[19],辨识出机器人在试验现场优化位姿下(α1=−48.38°,α2=54.82°,α3=6.86°,α4=54.16°,α5=107.43°,α6=−21.95°)的各关节刚度值,计算得到机器人力−线位移刚度矩阵Kfd. 根据式(6)~(11),再由k2和k3是YZ平面极大值和极小值得到k1、k2、k3分别为8.646×102、1.078×103、1.394×103 N/mm,刚度k3对应方向与Y轴夹角α=13.2°. 等效质量m通过下式确定:
| $m = \frac{{\left| {{{ K}_{{\rm{fd}}}}} \right|}}{{{\omega _{\rm n}}^2}} \cdot $ | (19) |
式中:|Kfd|为Kfd的欧几里德范数.
为了获得切削姿态下的机器人倒角加工系统固有频率,对系统进行模态测试试验. 将多个加速度传感器均匀分布安装在机器人本体上,用力锤敲打加速度传感器安装附近位置,通过B&K 3053-B-12数据采集卡和B&K PULSE测试软件包进行分析. 选取模态试验分析中常用的复模态指示函数(complex mode indicator function, CMIF)法对测试所得信号的主模态进行识别,利用Polyreference time参数估计法对CMIF方法处理后的数据作曲线拟合,这样便得到固定姿态下机器人倒角加工系统的系统频率响应,如图6所示. 图中,RF为频率响应,fv为频率. 得到前5阶固有频率以及阻尼比数据如表1所示,表中ζ为阻尼比.
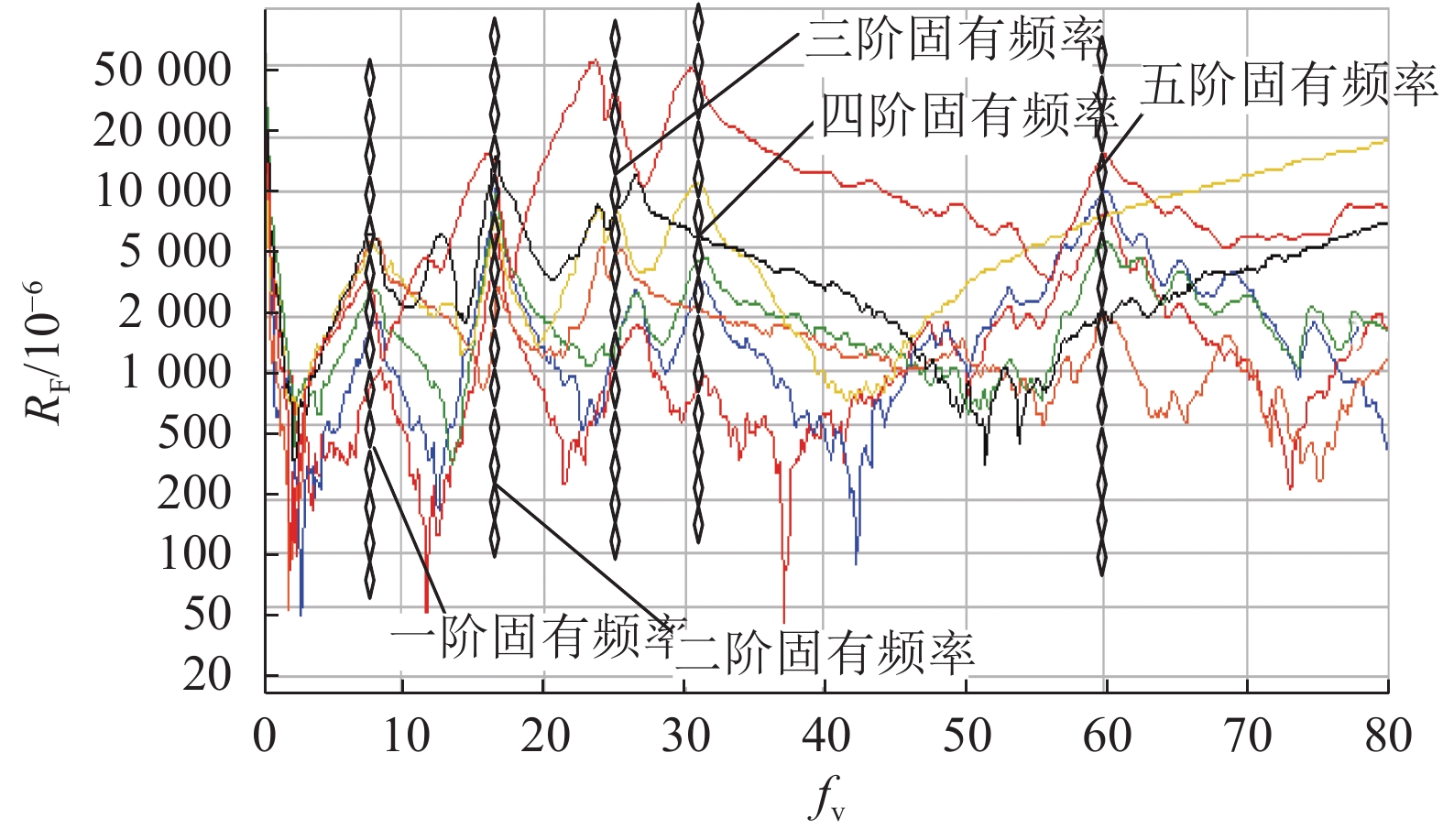
|
图 6 机器人倒角加工系统频率响应 Fig. 6 Frequency response of robotic machining chamfering |
| 表 1 机器人倒角加工系统模态试验结果 Table 1 Modal experiment results of robotic machining chamfering |
借助机器人倒角试验,对Kistler9257B测力仪所测数据进行拟合计算,试验所用工件为45钢,直径为42 mm. 得到加工工件切削力系数Kfc和Krt分别为1.96×103和2.14×103 N/mm2. 在未振动情况下,得到测力仪所得结果与预测模型幅值和频率吻合,这同时证明了切削力模型的准确性.
记初始位移和初始加速度为0,倒角深度C=1 mm,倒角角度θ=45°,进给量f=0.05 mm/r,旋转速度n=300 r/min,压脚压力pN=0.3 MPa,采用四阶龙格库塔(Runge-Kutta)法求解机器人倒角切削动力学微分方程,其X方向结果如图7(a)所示. 图中AX为机器人X方向位移.
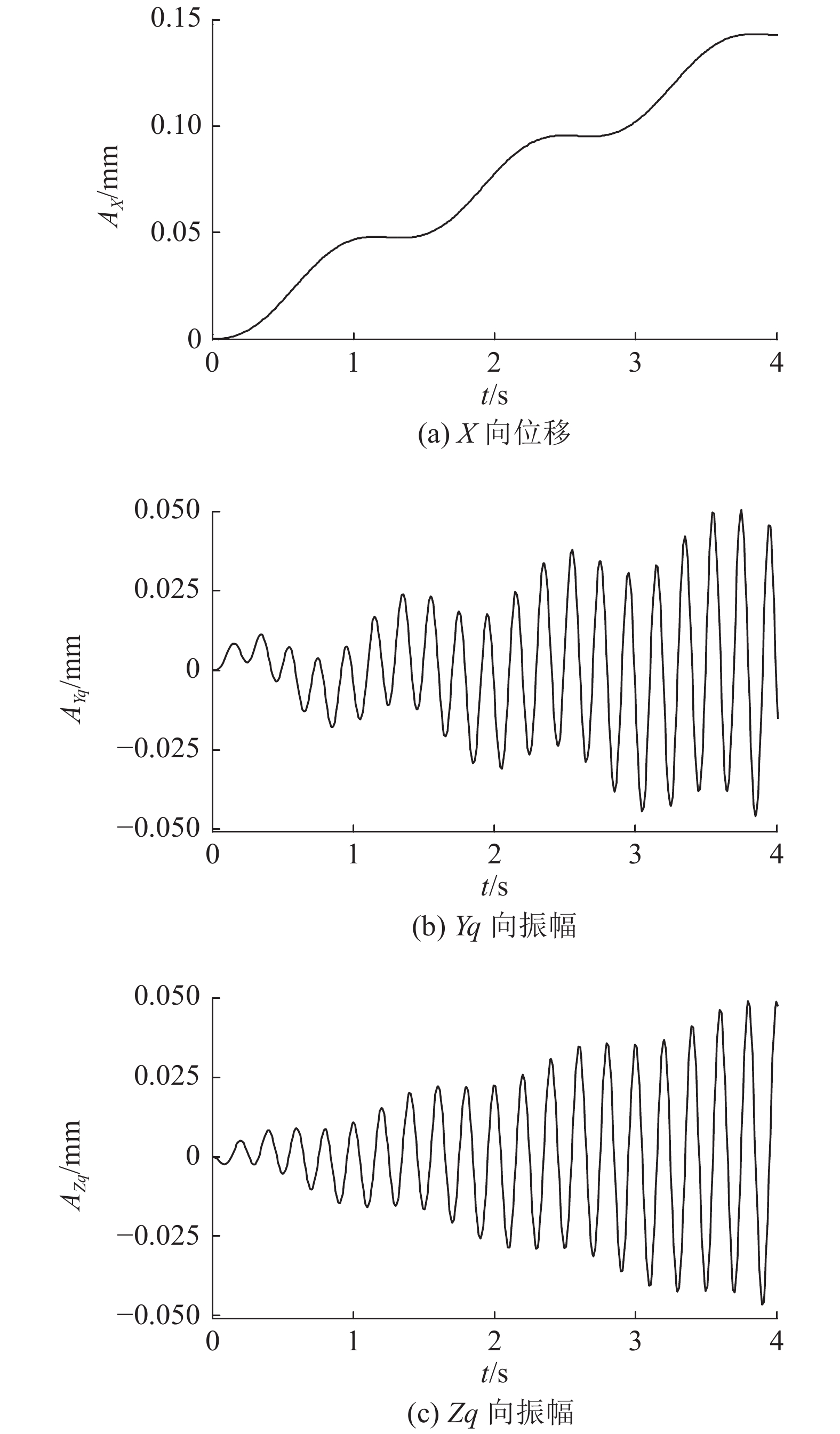
|
图 7 机器人X向位移及Yq和Zq向振幅 Fig. 7 Robot placement in X direction and vibration amplitude in Yq and Zq direction |
从图7(a)中可以看出在X方向机器人发生明显变形,且随着加工进行变形愈来愈大. 与一般变形不同的是,机器人倒角加工过程中产生的变形将会引起切削深度的明显变化,进而产生切削力变化反作用于系统,进一步引起动态变形. 根据文献[20]可知,在机器人制孔系统中,为消除轴向力影响,须施加外力与轴向力耦合使机器人受力始终为恒力,以此保证加工系统的稳定性.
假设由于X方向动态变形使得压脚瞬间脱离工件表面,此时压脚产生的等效黏性阻尼系数ceYq、ceZq将为0. 如图7(b)、(c)所示是ceYq和ceZq都为0时Yq和Zq方向振幅曲线(切削参数条件同上),图中AYq和AZq为振幅. 可见曲线呈现明显周期性,并且幅值愈来愈大,曲线单位时间内波峰数目等于主轴旋转周期频率数,因此判定由强迫振动导致,来源于周期性切削力. 此外,当主轴旋转频率与机器人固有频率相近时,机器人易产生共振,对加工系统造成严重伤害.
如图8所示为机器人正向倒角试验加工质量,从图中可以看出,由于机器人振动,倒角表面存在明显振痕和偏斜.

|
图 8 机器人正向倒角孔口质量图 Fig. 8 Surface quality of robotic forward chamfering hole |
由上可知,在机器人倒角切削过程中,X方向动态变形明显,易引起机器人振动,严重破坏系统稳定性;而当压脚与工件间阻尼效应消失或较小时,机器人在Yq和Zq方向上则会发生明显强迫振动,严重影响倒角质量. 针对这种情况,本文提出一种机器人反向倒角切削方法,以抵消轴向力对机器人的作用,并通过合理选取压脚压力抑制径向与切向强迫振动的发生.
3.2 反向倒角抑制振动原理反向倒角时,机器人倒角系统在进给方向简化模型如图9所示. 由图可知,反向倒角的轴向力方向与正向倒角时相反,对机器人起到的是“拉力”作用. 由于压脚气缸相当于一个刚度和阻尼极大的“气动弹簧”,“拉力”作用通过压脚使机器人进一步压紧在工件上,起到了增大压脚压力、提高系统稳定性的作用,这与正向倒角轴向力作用正好相反. 此外,由于摩擦力方向总是与切向力与径向力合力方向相反,显然会抵消其对机器人的作用,从而使机器人在YZ平面所受合力为0,抑制振动发生. 下面将分析为完全抑制振动的发生,压脚压力需要满足的条件.
|
图 9 机器人反向倒角图 Fig. 9 Schematic diagram of robot chamfering hole backward |
对于待倒角孔,其倒角深度C为定值,当满足倒角深度为C时的摩擦力大于径向力与切向力时,即可抑制整个加工过程中振动的发生. 由于等效黏性阻尼系数ceYq、ceZq较机器人阻尼c2、c3大得多,因此将压脚作用下的机器人反向倒角切削系统在倒角深度为C时Yq和Zq方向的运动微分方程表示为
| $\left. \begin{gathered} m\ddot Yq + {c_{{\rm e}Yq}}\dot Yq + {k_2}Yq = \\ {K_{{\rm{rt}}}}\left(C + \displaystyle\frac{1}{2}f\right)f\tan\, \theta \;{\rm{sin}}\,({\omega _{{t}}}t - \alpha - \beta - \pi ), \\ m\ddot Zq + {c_{{\rm e}Zq}}\dot Zq + {k_3}Zq = \\ {K_{{\rm{rt}}}}\left(C + \displaystyle\frac{1}{2}f\right)f\tan\, \theta \;{\rm{sin}}\,\left({\omega _{{t}}}t - \alpha - \beta - \displaystyle\frac{\pi }{2}\right). \\ \end{gathered} \right\} $ | (20) |
根据振动力学可得机器人在Yq和Zq方向强迫振动响应为
| $\left. \begin{gathered} Yq = {Y_{\rm{m}}}\sin\, \left( {{\omega _{{t}}}t - \alpha - \beta - \pi - {\varphi _2}} \right), \\ Zq = {Z_{\rm{m}}}\sin\, \left( {{\omega _{{t}}}t - \alpha - \beta - \frac{\pi }{2} - {\varphi _3}} \right). \\ \end{gathered} \right\}$ | (21) |
式中:φ2和φ3为相位差,Ym和Zm为振幅,分别可以表示为
| $\left.\begin{aligned}& {Y_{\rm{m}}} = \displaystyle\frac{{{M}}}{{\sqrt {{{({k_2} - m{\omega _{{t}}}^2)}^2} + {{({c_{{\rm e}Yq}}{\omega _{{t}}})}^2}}}}, \\& {Z_{\rm{m}}} = \displaystyle\frac{{{M}}}{{\sqrt {{{({k_3} - m{\omega _{{t}}}^2)}^2} + {{({c_{{\rm e}Zq}}{\omega _{{t}}})}^2}} }}, \\& {{M}} = {K_{{\rm{rt}}}}\left(C + \displaystyle\frac{1}{2}f\right)f{\rm tan}\,\theta . \\ \end{aligned} \right\}$ | (22) |
由分析知,反向倒角时,工件表面上的压力是压脚压力与轴向力的和,摩擦力Ff表达式为
| ${F_f} = \mu (2{p_{{}_{\rm N}}}A + {F_X}) \cdot $ | (23) |
将式(23)代入到式(13)中,得在Yq和Zq方向上等效黏性阻尼系数表达式为
| ${c_{{\rm e}Yq}} = \frac{{4\mu (2{p_{{}_{\rm N}}}A + {F_X})}}{{\pi {\omega _{{t}}}{Y_{\rm{m}}}}},\;{c_{{\rm e}Zq}} = \frac{{4\mu (2{p_{{}_{\rm N}}}A + {F_X})}}{{\pi {\omega _{{t}}}{Z_{\rm m}}}} \cdot $ | (24) |
再将式(24)代入式(22)得
| $\left.\begin{gathered} \begin{gathered} {Y_{\rm{m}}} = \displaystyle\frac{{{Q}}}{{{k_2} - m{\omega _{{t}}}^2}},\;{Z_{\rm{m}}} = \displaystyle\frac{{{Q}}}{{{k_3} - m{\omega _{{t}}}^2}} \\ \end{gathered}, \quad\quad\quad\quad\;\,\\{{Q}} = {K_{{\rm{rt}}}}\left( {C + f/2} \right)f{\rm tan}\,\theta \; \times \quad\quad\quad\quad\quad\quad\quad\quad \\{\left[ {1 - {{\left( {\displaystyle\frac{{4\mu \left( {2{p_{{}_{\rm N}}}A + {K_{{\rm{fc}}}}\left(C + f/2\right)f{\rm tan}\,\theta } \right)}}{{\pi {K_{{\rm{rt}}}}\left( {C +f/2} \right)f{\rm tan}\,\theta }}} \right)}^2}} \right]^{{\rm{1/2}}}}. \\ \end{gathered} \right\}$ | (25) |
其中,当满足
| $4\mu \left[ {2{p_{{}_{\rm N}}}A + {K_{{\rm{fc}}}}(C + \frac{1}{2}f)f{\rm tan}\,\theta } \right] > \pi {K_{{\rm{rt}}}}\left( {C + \frac{1}{2}f} \right)f{\rm tan}\,\theta $ |
时,振幅在实数范围内没有意义,即振幅不存在. 进一步化简可得
| ${p_{{}_{\rm N}}} > \frac{1}{{2A}}\left( {\frac{{\pi {K_{{\rm{rt}}}}}}{{4\mu }} - {K_{{\rm{f}}{\rm c}}}} \right)\left(\frac{1}{2}{f^2} + Cf\right){\rm tan}\,\theta \cdot $ | (27) |
因此,当压脚压力满足式(26)条件时,径向力与切向力将始终被摩擦力抵消,不会产生振动.
4 试验验证与分析试验系统由ABB-IRB6600-175/2.55机器人与终端执行器组成,如图10所示. 为验证振动抑制方法的有效性及振动分析的正确性,将切削参数设置在如下范围内:进给量为0.01~0.05 mm/r,主轴转速为200~800 r/min,压脚压力为0~0.5 MPa. 在压脚压紧工件表面的情况下,测力仪所测Y向和Z向分力的合力对应切向力、径向力以及压脚摩擦力的合力,X向分力对应于轴向力与压脚压力的合力. 本节将由测力仪所测Y向和Z向切削力信号及其FFT结果以及倒角质量作为振动是否发生的评判依据.

|
图 10 机器人倒角切削试验系统 Fig. 10 Robotic machining chamfering experiment system |
压上压脚后,先进行镗孔切削加工对刀,当实现镗刀片与孔壁四周完全接触后,在不松开压脚情况下将镗刀片替换为倒角刀片,以此保证刀具定位准确. 选取表2中具有代表性的2组正向倒角试验对振动分析正确性进行验证. 试验中发现:试验A在前半段振动不明显,而在后半段机器人振动强烈;试验B在加工开始后便出现振动,加工过程中机器人振动幅度明显,对系统造成损害. 试验A与试验B测力仪所测Y向和Z向切削力结果及其FFT结果如图11和图12所示,图中RA表示相对振幅,FYm和FZm分别为测力仪所测Y向和Z向切削力. 由图可见,试验A、B在压脚作用下的切削力幅值最大可达到数百牛顿,这说明机器人发生了明显的振动(未振动情况下应接近于0);此外,试验A、B切削力的基频分别为5.02和6.76 Hz,分别与主轴旋转频率相等(5.00和6.67 Hz),并且在试验B中观察到机器人振动幅度异常明显,这是由于试验B主轴旋转频率与机器人一阶固有频率接近,导致了机器人共振的发生. 因此机器人正向倒角切削中发生了由切削力引起的明显强迫振动,很难得到满足要求的倒角质量(如图8所示).
| 表 2 试验A和试验B的参数条件 Table 2 Cutting conditions for Test A and Test B |
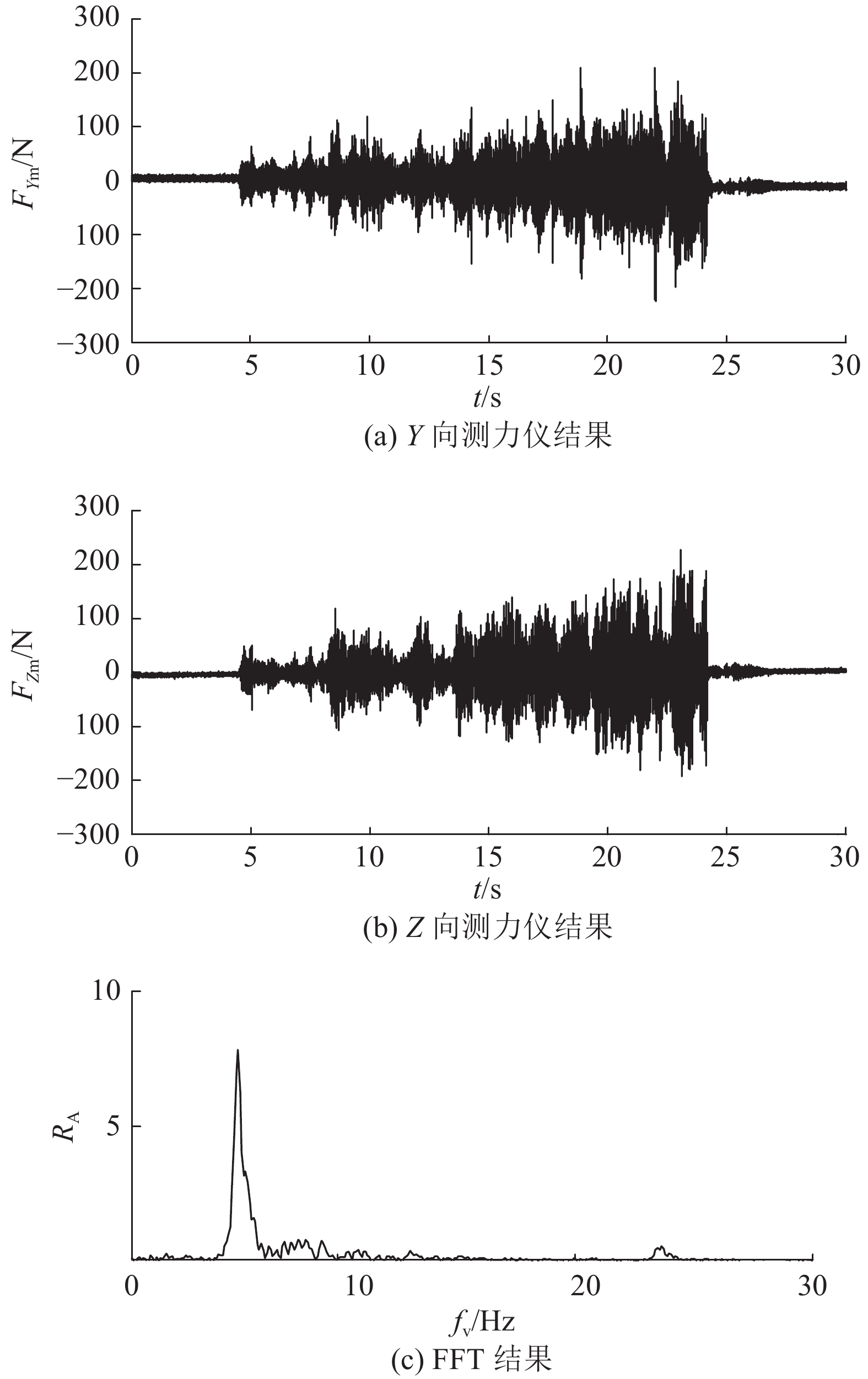
|
图 11 试验A测力仪结果及其快速傅里叶变换 Fig. 11 Cutting force values and fast Fourier transformation for Test A |

|
图 12 试验B测力仪结果及其快速傅里叶变换 Fig. 12 Cutting force values and fast Fourier transformation for Test B |
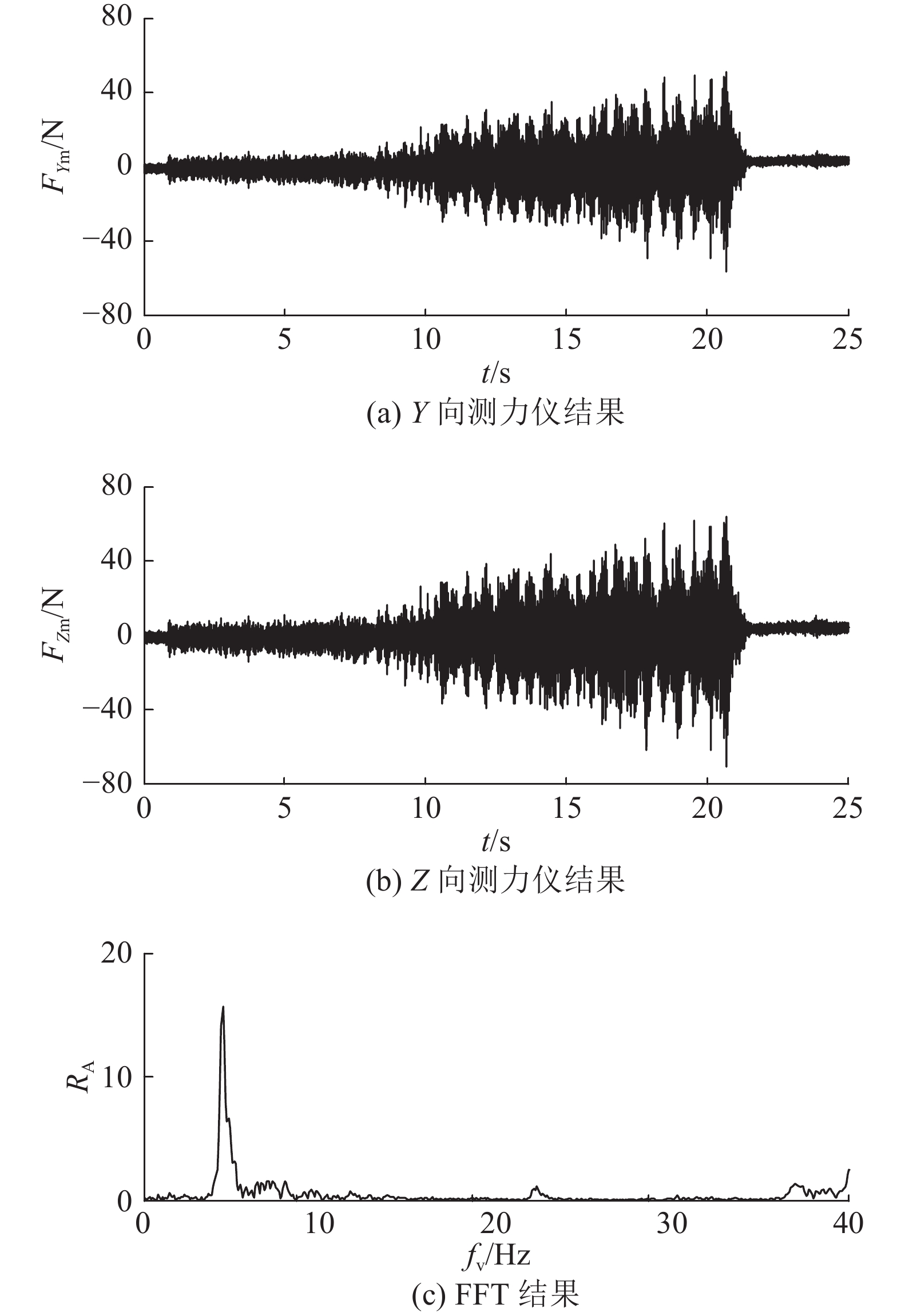
在镗孔对刀完成之后,在不退回情况下直接装上倒角刀以表3参数反向进给加工,试验C测力仪及其FFT结果如图13所示. 可见其前半段所受合力很小,未发生振动,但随着主轴进给,切削力在逐渐增大,压脚压力产生的摩擦力不足以抵消切削力,从而导致机器人在径向和切向所受合力越来越大,无法有效抑制机器人振动.
| 表 3 试验C、D及E的反向倒角参数条件 Table 3 Cutting conditions for Test C, D and E |
|
图 13 试验C测力仪结果及其快速傅里叶变换 Fig. 13 Cutting force values and fast Fourier transformation for Test C |
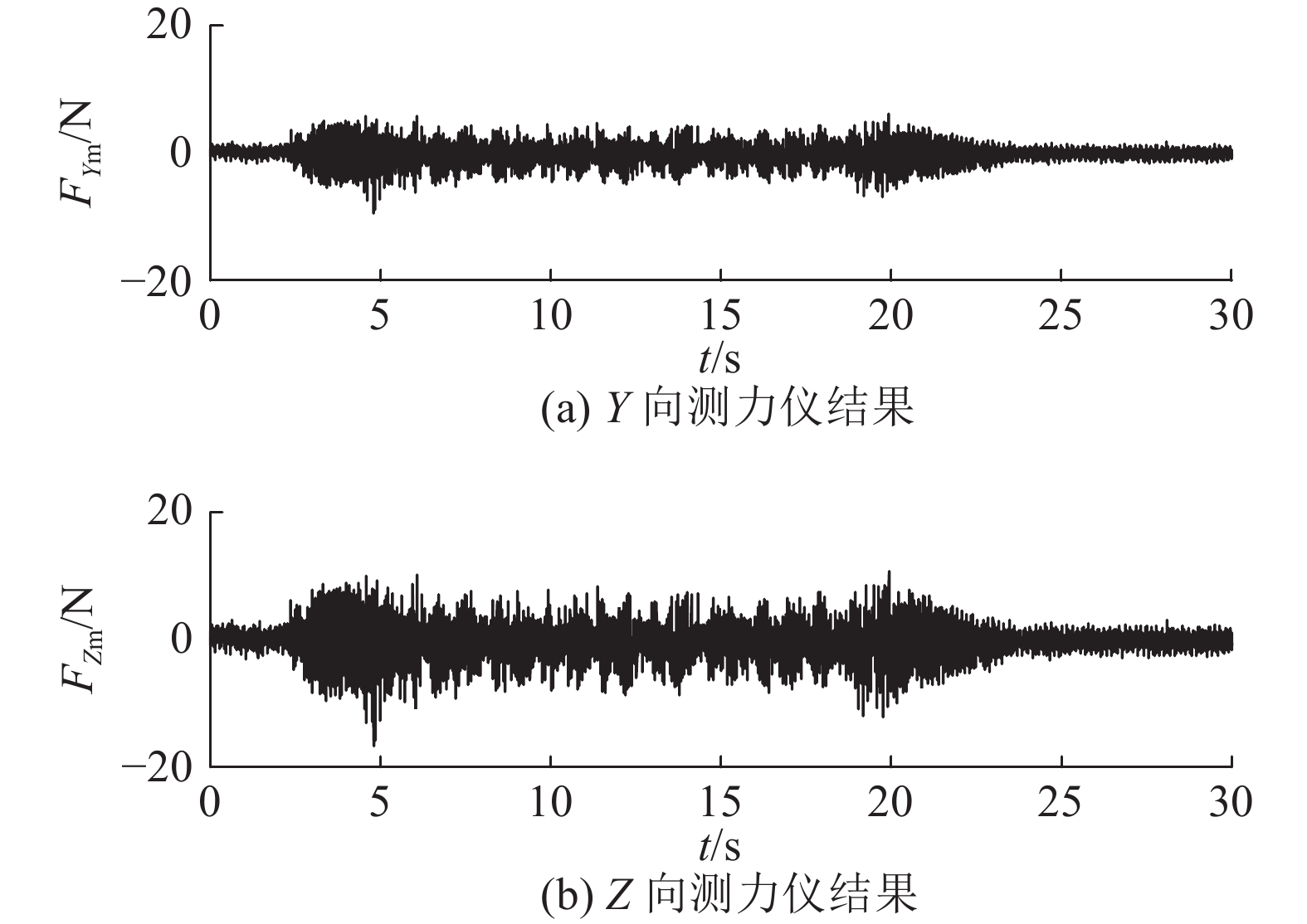
与试验C以及表2中试验机器人产生强烈振动不同的是,表3中试验D与试验E机器人所受合力很小,切削过程非常稳定,如图14所示是试验E测力仪所测切削力结果. 可见,在机器人反向倒角加工过程中,轴向力使压脚保持压紧在工件表面上,在压脚压力较大时,工件与压脚间产生的摩擦力能够抵消径向力和切向力,抑制振动发生. 反向倒角加工质量如图15所示,其表面粗糙度可达Ra1.6 μm. 采用Nscing Es倒角游标卡尺对孔口倒角多方位尺寸进行测量,测得最大孔口宽度差为0.05 mm.
|
图 14 振动被抑制的试验E测力仪结果 Fig. 14 Cutting force values for Test E with vibration suppressed |

|
图 15 机器人反向倒角质量 Fig. 15 Surface quality of robot backward chamfering hole |
(1)机器人正向倒角切削过程中易发生由轴向力引起的机器人动态变形以及由切向力及径向力引起的机器人强迫振动,并且当主轴旋转频率与机器人固有频率接近时,共振发生.
(2)机器人反向倒角切削对振动有明显抑制作用:轴向力通过压脚气缸作用使机器人进一步压紧在工件上,而不会产生动态变形;压脚与工件间产生的摩擦力能够完全抵消径向力与切向力作用,抑制强迫振动发生.
(3)机器人反向倒角孔口倒角表面粗糙度小于Ra1.6 μm,最大孔口宽度差为0.05 mm.
| [1] |
TEUN V A, JAN W V I. MEP倒角刀在航空零件中的应用[J]. 工具技术, 2014(10): 7-9. TEUN V A, JAN W V I. MEP chamfering tool used in aviation parts[J]. Tool Engineering, 2014(10): 7-9. DOI:10.3969/j.issn.1000-7008.2014.10.041 |
| [2] |
HARTMANN J, MEEKER C, MINSHULL A, et al. Automated wing panel assembly for the A340-600[J]. SAE Transactions, 2000, 7(1): 44-47. |
| [3] |
毕树生, 梁杰, 战强, 等. 机器人技术在航空工业中的应用[J]. 航空制造技术, 2009(4): 34-39. BI Shu-sheng, LIANG Jie, ZHAN Qiang, et al. Robot technology and aerospace manufacturing[J]. Robot Technique and Application, 2009(4): 34-39. DOI:10.3969/j.issn.1671-833X.2009.04.001 |
| [4] |
ALTINTAS Y. Manufacturing automation: metal cutting mechanics, machine tool vibrations, and CNC design [M]. Cambridge: Cambridge University Press, 2000.
|
| [5] |
KILIC Z M, ALTINTAS Y. Generalized mechanics and dynamics of metal cutting operations for unified simulations[J]. International Journal of Machine Tools and Manufacture, 2016, 104: 1-13. DOI:10.1016/j.ijmachtools.2016.01.006 |
| [6] |
YANG Y, ZHANG W H, MA Y C, et al. Chatter prediction for the peripheral milling of thin-walled workpieces with curved surfaces[J]. International Journal of Machine Tools and Manufacture, 2016, 109: 36-48. DOI:10.1016/j.ijmachtools.2016.07.002 |
| [7] |
CHEN Y, DONG F. Robot machining: recent development and future research issues[J]. International Journal of Advanced Manufacturing Technology, 2013, 66(9-12): 1489-1497. DOI:10.1007/s00170-012-4433-4 |
| [8] |
PAN Z, ZHANG H, ZHU Z, et al. Chatter analysis of robotic machining process[J]. Journal of Materials Processing Technology, 2006, 173(3): 301-309. DOI:10.1016/j.jmatprotec.2005.11.033 |
| [9] |
MEJRI S, GAGNOL V, LE T P, et al. Dynamic characterization of machining robot and stability analysis[J]. International Journal of Advanced Manufacturing Technology, 2016, 82(1-4): 351-359. DOI:10.1007/s00170-015-7336-3 |
| [10] |
OZER A, SEMERCIGIL S E, KUMAR R P, et al. Tool chatter in turning with a two-link robotic arm[J]. Journal of Sound and Vibration, 2013, 332(6): 1405-1417. DOI:10.1016/j.jsv.2012.08.006 |
| [11] |
GUO Y, DONG H, WANG G, et al. Vibration analysis and suppression in robotic boring process[J]. International Journal of Machine Tools and Manufacture, 2016, 101: 102-110. DOI:10.1016/j.ijmachtools.2015.11.011 |
| [12] |
HAZEL B, RAFIEIAN F, LIU Z. Impact-cutting and regenerative chatter in robotic grinding [C] // ASME International Mechanical Engineering Congress and Exposition (IMECE). Denver: ASME. 2011: 349–359.
|
| [13] |
于学全, 邵大鹏, 倪红军, 等. 孔口倒角工艺及刀具研究[J]. 铁道机车车辆, 2011, 31(增1): 374-378. YU Xue-quan, SHAO Da-peng, NI Hong-jun, et al. Orifice chamfering technique and tools research[J]. Railway Locomotive and CAR, 2011, 31(增1): 374-378. |
| [14] |
KAYMAKCI M, KILIC Z M, ALTINTAS Y. Unified cutting force model for turning, boring, drilling and milling operations[J]. International Journal of Machine Tools and Manufacture, 2012, 5455(3): 34-45. |
| [15] |
ANGELES, JORGE. On the nature of the cartesian stiffness matrix[J]. Ingeniería Mecánica Tecnología Y Desarrollo, 2010, 3(5): 163-170. |
| [16] |
OLSSON T, ROBERTSSON A, JOHANSSON R. Flexible force control for accurate low-cost robot drilling [C] // IEEE International Conference on Robotics and Automation (ICRA). Rome: IEEE, 2007: 4770–4775.
|
| [17] |
THOMSON W T, DAHLEH M D. Theory of vibration with applications [M]. 5th ed. New Jersey: Prentice Hall, 1997.
|
| [18] |
GUO Y, DONG H, KE Y. Stiffness-oriented posture optimization in robotic machining applications[J]. Robotics and Computer-Integrated Manufacturing, 2015, 35(C): 69-76. |
| [19] |
曲巍崴, 侯鹏辉, 杨根军, 等. 机器人加工系统刚度性能优化研究[J]. 航空学报, 2013, 34(12): 2823-2832. QU Wei-wei, HOU Peng-hui, YANG Gen-jun, et al. Research on the stiffness performance for robot maching systems[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(12): 2823-2832. |
| [20] |
BI S, LIANG J. Robotic drilling system for titanium structures[J]. International Journal of Advanced Manufacturing Technology, 2011, 54(5-8): 767-774. DOI:10.1007/s00170-010-2962-2 |



