图像超分辨率技术是指由一幅或多幅低分辨率图像重建高分辨图像的技术. 硬件采样得到的图像分辨率有限,通过增加传感器数量提高图像分辨率的方式在成本和技术上都存在局限性,因此寻求低成本、高效率的图像超分辨率实现方法十分必要. 如今超分辨率技术已经被广泛应用于生物医学成像、安全监控、视频处理、卫星图像处理等领域[1-3].
图像超分辨率技术可以分为3大类,基于插值、基于重建模型和基于学习的方法. 基于插值的算法是依据低分辨率图像本身像素进行插值得到高分辨率图像;基于重建模型的算法是通过获取先验模型的相关约束条件,完成对超分辨率重建过程的建模;基于学习的方法是通过学习大量样本得到低分辨率图像与高分辨率图像之间的联系重建超分辨率图像[4-10]. 广泛使用的基于插值的算法只依靠低分辨率图像本身得到高分辨率图像,计算复杂度是3类超分辨率算法中最低的. 传统的插值算法包括最近邻插值、双线性插值、双立方插值,硬件实现方案比较简单. 邓亚斌等[11]结合双线性插值和图像自相似原理,在现场可编程门阵列(filed programmable gate array, FPGA)上实现了实时视频超分辨率处理;钟雪燕等[12]提出循环调度机制,设计了双线性插值的FPGA实现方案;Nuno-Maganda等[13]基于双立方插值算法,提出可替换算法内核的三段式硬件架构. 但是在不同区域内都采用相同的插值方法,会造成图像高频细节丢失,在边缘区域出现锯齿状模糊等情况. 为了克服这些不足,Li等[14]根据高分辨率图像和低分辨率图像局部协方差之间的几何对偶性提出新边缘指导插值(new edge-directed interpolation,NEDI)算法. NEDI算法可以有效解决传统插值算法在图像边缘区域出现模糊边缘的情况. 但是由于NEDI算法涉及大量矩阵乘法和矩阵求逆运算,计算复杂度较高,所需要的软件处理时间较长.
根据NEDI算法中矩阵的对称性,引入Cholesky分解方法简化算法的计算过程,基于Goldschmidt算法[15-16]设计低延时的定点数除法器,设计NEDI算法的核心计算硬件模块,并且提出适用于不同大小窗口的硬件扩展方案.
1 NEDI图像插值算法NEDI算法的基本原理是基于低分辨率图像和高分辨率图像在对应像素点区域的局部协方差具有几何对偶性,通过低分辨率图像的局部协方差系数推导出相应的插值系数,对该像素点进行插值. 将一幅分辨率为
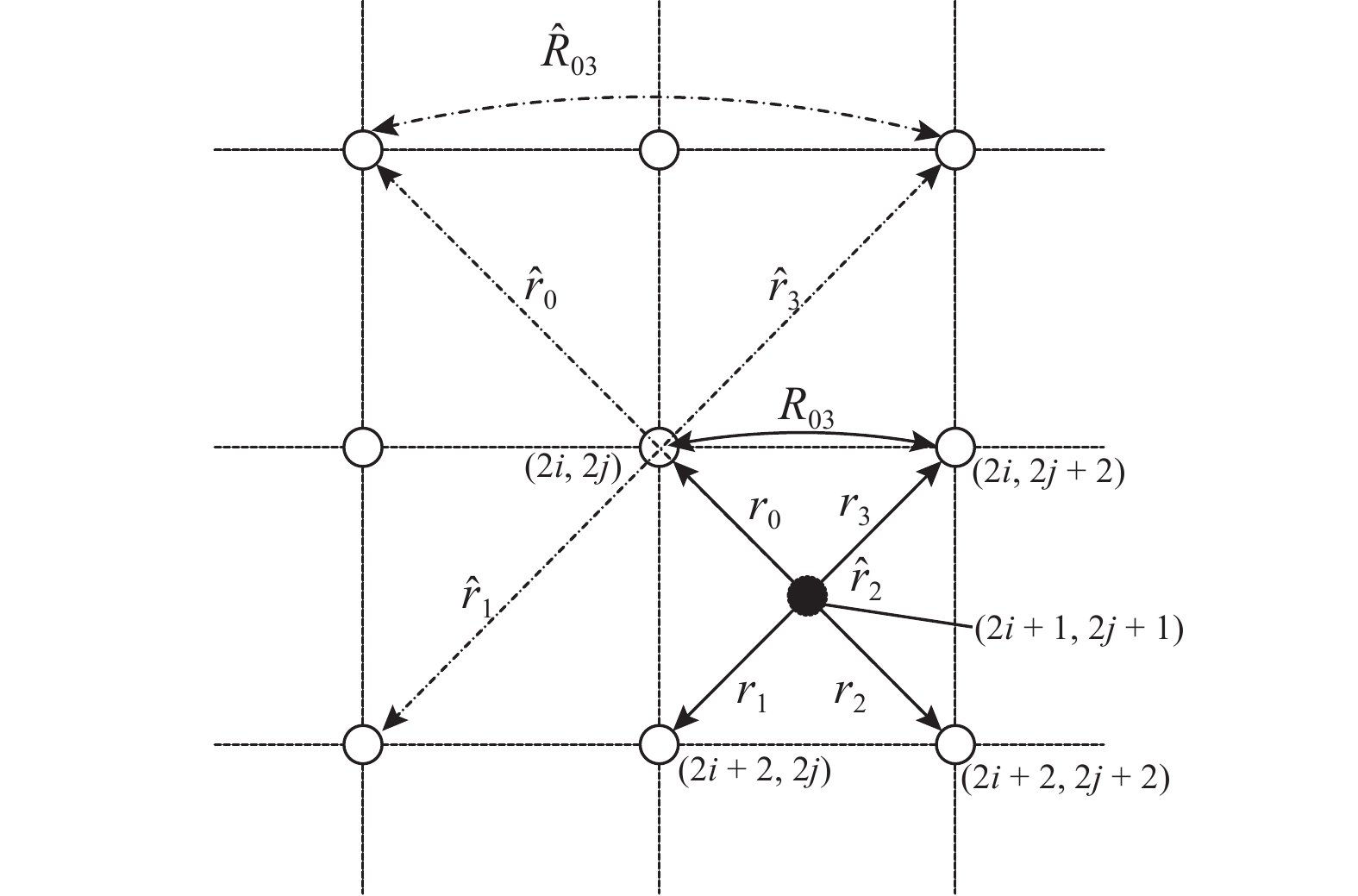
|
图 1 图像G中(2i+1,2j+1)处像素的几何对偶性 Fig. 1 Geometric duality of pixel (2i+1,2j+1) in image G |
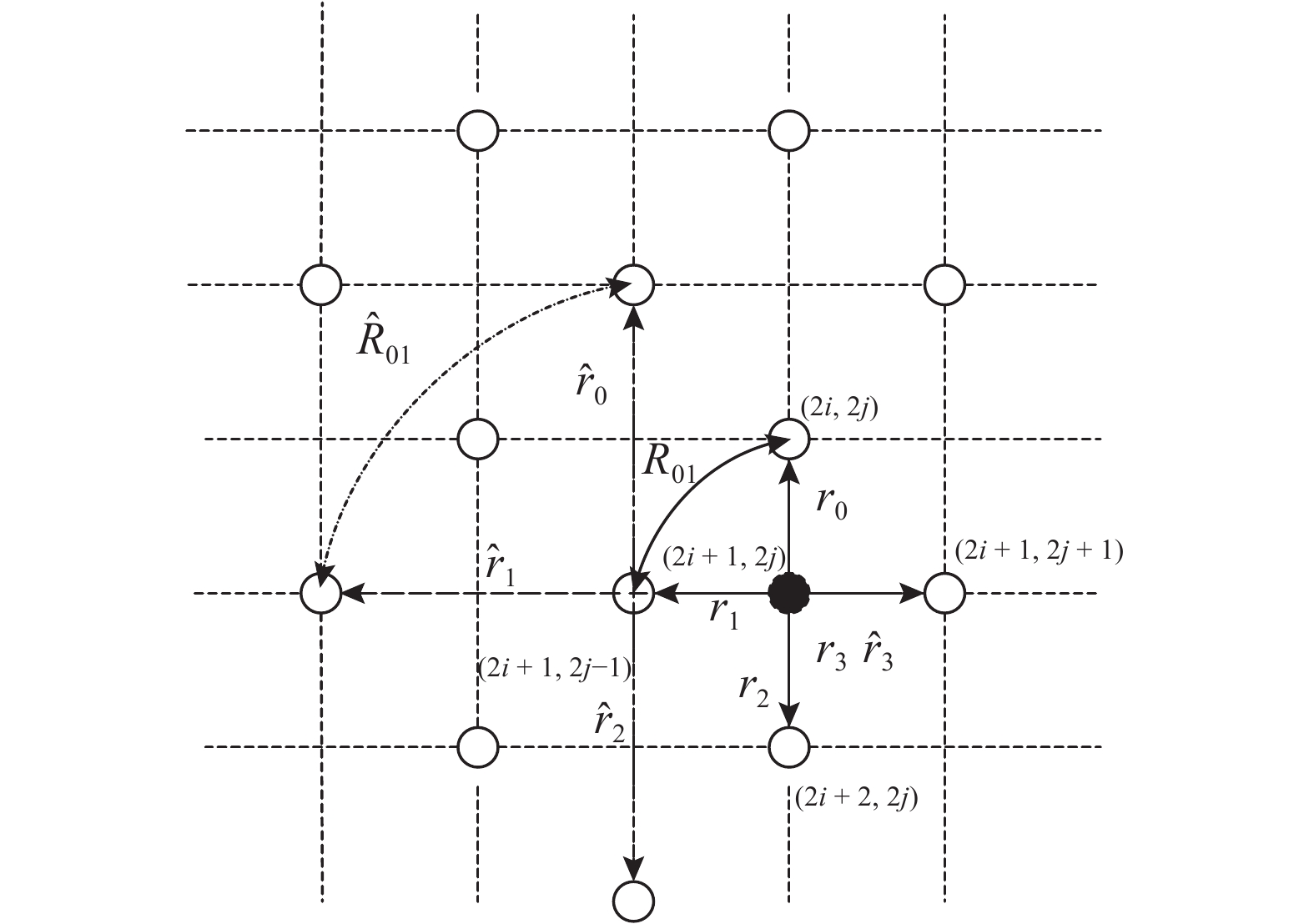
|
图 2 图像G中(2i+1,2j)处像素的几何对偶性 Fig. 2 Geometric duality of pixel (2i+1,2j) in image G |
以第1步插值过程为例,将NEDI插值算法表示为
| $G\;(2i + 1,2j + 1) = \sum\limits_{q = 0}^1 {\sum\limits_{l = 0}^1 {\Big({\alpha _{2q + l}} } } \;G\;(2(i + q),\;2(j + l))\Big). $ | (1) |
式中:i、j分别为图像P中像素的横、纵坐标,q、l分别为用于插值的4个像素点与像素点(i,j)的坐标偏移量,α2q+l为用于插值的像素点(i+q,j+l)的插值系数.
假设自然图像为局部平稳高斯过程,根据Wiener滤波理论,最优最小均方误差的线性插值系数为
| ${{\alpha}} = {{{R}}^{ - 1}}{{r}}.$ | (2) |
式中:R、r分别为高分辨率图像的局部协方差. 根据几何对偶性,使用低分辨率图像的局部协方差
| $\left.\begin{split}&\hat {{R}} = \frac{1}{{{M^2}}}{{C}}{{{C}}^{\rm{T}}}, \\&\hat {{r}} = \frac{1}{{{M^2}}}{{Ch}}. \end{split}\right\}$ | (3) |
式中:M为所选取正方形窗口的大小,h为由该窗口包含的M2个像素构成的列向量;C为4×M2矩阵,每一列由窗口内像素点的对角线方向上的4个像素值构成. 将式(3)代入式(2),得到插值系数向量为
| ${{\alpha}} {\rm{ = }}{\left( {{{C}}{{{C}}^{\rm{T}}}} \right)^{ - 1}}\left( {{{Ch}}} \right). $ | (4) |
如式(4)所示,NEDI算法的计算复杂度较高,整幅图片全部采用NEDI算法插值需要的时间较长. 由于NEDI算法的主要目的是解决传统插值算法导致的图片边缘区域模糊的问题,采用混合插值的方法减少计算量,即边缘区域采用NEDI算法插值,平坦区域采用双线性插值.
2 硬件电路设计 2.1 NEDI算法计算简化NEDI算法的计算复杂度主要来自于矩阵求逆运算量和较大窗口下矩阵乘法的运算量. 由于CCT是对称矩阵,采用Cholesky分解方法简化矩阵求逆运算的过程. Cholesky分解将正定对称矩阵A分解为三角矩阵乘积的形式:
| $ {{A}} = {{B}}{{{B}}^{\rm{H}}} \;{\text{或}}\;{{A}} = {{LD}}{{{L}}^{\rm{H}}} . $ | (5) |
式中:B是下三角矩阵,L是对角线上值均为1的下三角矩阵,D是对角矩阵,BH、LH分别为B和L的共轭转置矩阵.
记CCT的计算结果为4阶矩阵A,采用Cholesky方法分解A:
| $\begin{gathered} \hfill \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}&{{a_{14}}} \\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}&{{a_{24}}} \\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}}&{{a_{34}}} \\ {{a_{41}}}&{{a_{42}}}&{{a_{43}}}&{{a_{44}}} \end{array}} \right]{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\rm{1}}&{}&{}&{} \\ {{l_{21}}}&{\rm{1}}&{}&{} \\ {{l_{31}}}&{{l_{32}}}&{\rm{1}}&{} \\ {{l_{41}}}&{{l_{42}}}&{{l_{43}}}&{\rm{1}} \end{array}} \right] \times \\ \hfill \left[ {\begin{array}{*{20}{c}} {{d_1}}&{}&{} \\ {}& \ddots &{} \\ {}&{}&{{d_4}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} 1&{{l_{21}}}&{{l_{31}}}&{{l_{41}}} \\ {}&1&{{l_{32}}}&{{l_{42}}} \\ {}&{}&1&{{l_{43}}} \\ {}&{}&{}&1 \end{array}} \right]\\ \end{gathered}. $ | (6) |
式(6)中元素的计算方法为
| $ \left. \begin{array}{l}{d_m} = {a_{mm}} - \displaystyle\sum\limits_{p = 1}^{m - 1} {{d_p}{l_{mp}}^2}, \\{d_t}{l_{mt}} = {a_{mt}} - \displaystyle\sum\limits_{p = 1}^{t - 1} {{d_p}{l_{mp}}{l_{tp}}} ;\quad m > t. \end{array} \right\} $ | (7) |
式中:dm为式(5)中对角矩阵D第m行、m列上的值,amm为式(5)中矩阵A第m行、m列上的值,dp为式(5)中对角矩阵D第p行、p列上的值,lmp为式(5)中矩阵L第m行,p列上的值,lmt为式(5)中矩阵L第m行,t列上的值,amt为式(5)中矩阵A第m行,t列上的值,ltp为式(5)中矩阵L第t行,p列上的值. 基本结构dtlmt同时存在于等式的两端,可以将dtlmt的结果作为中间值在后续计算中使用. 通过增加额外存储空间的方法,能够减少一半的乘法次数,提高运算速度,减少lmt对结果精度的影响. 同时保存4阶矩阵中的2个中间值,以保证运算过程的完整性. 对式(5)两边求逆,得到A的逆矩阵为
| $ {{{A}}^{{-1}}} = {({{{B}}^{{-1}}})^{\rm{H}}}{{{B}}^{ - 1}} \;{\text{或}}\;{{{A}}^{ - 1}} = {({{{L}}^{ - 1}})^{\rm{H}}}{{{D}}^{ - 1}}{{{L}}^{ - 1}}. $ | (8) |
将式(8)、(4)代入式(1),得到(2i+1,2j+1)上的插值结果为
| $G\;(2i + 1,2j + 1) = {{{G}}_z}{{\alpha}} = {{{G}}_z}{({{{L}}^{ - 1}})^{\rm{T}}}{{{D}}^{ - 1}}{{{L}}^{ - 1}}{{Ch}}. $ | (9) |
式中:Gz为由待插值点对角线上4个点构成的行向量. 根据矩阵相乘的特点,通过调整矩阵相乘的顺序减少所需乘法的次数. Gz和h都是向量,两者同时向中间结合计算可以减少乘法次数. 使用除以D中元素的方式代替与D−1相乘的过程. 经过调整后的计算方法比顺序相乘减少了M2−4次乘法计算,并且填补了Cholesky分解过程中因等待相关数据出现的计算空缺. 采用Cholesky分解方法求逆矩阵只需要计算1个三角矩阵及逆矩阵,与常用的LU分解求逆方法相比,减少了近一半的计算量和存储空间.
2.2 低延时定点数除法器由于数据之间存在关联,NEDI算法中除法的计算是有顺序的,无法使用多个除法器并行计算提高整体的计算速度. 虽然NEDI算法中除法运算的次数较少,但是仍然是限制计算速度的瓶颈. 采用低延时除法器可以缩短计算周期,提高处理速度. 采用乘法代替除法运算的方式设计低延时定点数除法器.
常用的乘法代替除法的方法是牛顿法. 假设除法器输入的被除数和除数分别为y和x,使用牛顿迭代法计算出1/x,将结果和y做一次乘法得到除法器的结果. 构造函数f(z)=x−1/z,f(z)=0的根是1/x的值,采用牛顿迭代法得到z的递推式:
| ${z_{s + 1}} = {z_s}(2 - {z_s}x). $ | (10) |
式中:s为迭代次数,zs为f(z)=0的近似根. 牛顿法在根邻近区域是平方收敛的,只需要几次迭代,zs的值就能达到较高的精度要求.
另一种方法是Goldschmidt算法. 计算y/x时,y和x同时乘以系数fk,将x转化为接近1的值xk+1,对应的yk+1就是除法的近似商. 具体过程可以表示为
| $\frac{{{y_{k + 1}}}}{{{x_{k + 1}}}}{\rm{ = }}\displaystyle\frac{{{y_k}}}{{{x_k}}} \cdot \displaystyle\frac{{{f_k}}}{{{f_k}}} = \cdot \cdot \cdot = \displaystyle\frac{y}{x}. $ | (11) |
采用类似牛顿法的迭代式构造递推公式:
| $\left. \begin{array}{l}{x_{k + 1}} = {x_k}(2 - {x_k}),\\{y_{k + 1}} = {y_k}(2 - {x_k}). \end{array} \right\}$ | (12) |
式中:数列xk收敛于1,yk收敛于y/x,确定系数fk=2-xk. Goldschmidt算法也是平方收敛的,和牛顿法的收敛速度相似.
牛顿法所需迭代次数以及计算结果的精度和初值选取有关,选取靠近根的初值可以减少迭代次数,但是选取初值较差时可能会出现无法收敛的情况. 通过预处理方法选择合理的初值可以减少迭代次数,但是会增加资源消耗;并且牛顿法每次迭代所需的2次乘法无法并行计算,迭代周期较长. Goldschmidt算法的迭代初值是x,完成1次迭代也需要2次乘法,但是2次乘法可以并行计算,迭代结果yk+1就是除法的结果. 和牛顿迭代法相比,Goldschmidt算法的硬件设计简单、可以采用并行计算方法,但是无法通过选取初值等方式减少迭代次数.
考虑到硬件设计的复杂度,使用Goldschmidt算法设计低延时除法器,并且采用定点数代替浮点数运算来加快计算速度. 定点数Goldschmidt算法的递推式为
| ${x_{k + 1}} = ({2^{n + 1}} - {x_k}){x_k}/{2^n}. $ | (13) |
式中:n为定点数小数部分的位数. 求解递推式(13),
得到x迭代k次的表达式为
| ${x_{k + 1}} = N - N{(\frac{{N - x}}{N})^{{2^k}}};\;x < N = {2^n}. $ | (14) |
x越接近N,所需要的迭代次数越少. 当x=N/2时,经过log n次迭代就可以将x转化为N−1. 对y和x进行移位,将分母x统一到N/2与N−1之间,保证除法运算所需的迭代次数基本一致.n的取值为16,经过移位后x的最小值为32 768,最多经过4次迭代能够完成1次除法计算.
使用
除法器模块数据传输如图3所示,y、x分别为被除数和除数,Valid为输入数据有效信号,out为运算结果,done为运算结束信号. div_cnt为迭代计数器,用于记录迭代次数. xk为每次迭代得到的除数,sel为控制模块产生的数据选择信号.
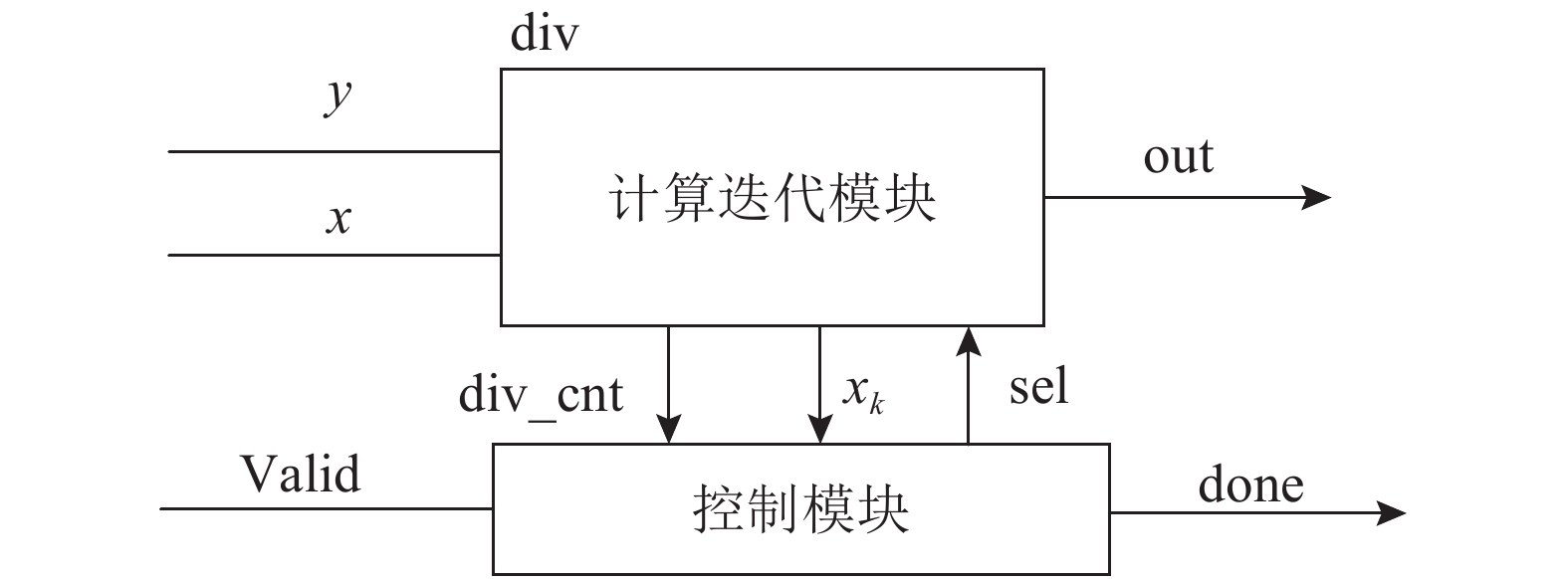
|
图 3 低延时定点数除法器模块数据传输图 Fig. 3 Dataflow of low latency fixed-point divider module |
除法器的计算迭代模块如图4所示,SIGN_i模块将y转化为无符号数,SIGN_o模块将输出转化为有符号数,s1和s2为右移16位的移位模块,Not是按位取反计算模块,Re模块将除数移位到指定区间,div_cnt是以sel1为复位信号的2个DFF触发器构成的2 bit计数器,Mux1、Mux2、Mux3为两路数据选择器. 通过sel信号控制输入值和迭代值的切换,保证除法器计算能够连续、有效地运行. 当完成4次迭代或者xk的值为65 534时,除法计算结束,s1的输出值为无符号数除法的结果. 单次除法计算需要5个时钟周期,连续的除法计算每4个时钟周期完成1次有效运算.

|
图 4 低延时定点数除法器的硬件结构 Fig. 4 Hardware structure of low latency fixed-point divider |
控制模块根据div_cnt、xk、valid改变除法器的状态以及sel和done信号. 较低的除法器延时能够加快算法计算速度,减少其余硬件的空闲时间,提高硬件的利用率.
2.3 可扩展NEDI硬件电路由式(4)、(9)可知,除了计算矩阵A和矩阵Ch之外,不同大小窗口的NEDI算法的计算过程是一致的. 为了实现不同大小窗口的NEDI算法,降低设计的复杂度,减少硬件资源的使用,将NEDI划分为核心计算模块和扩展模块2部分. 核心计算模块采用固定的硬件资源完成算法中不变的计算流程,包含矩阵A求逆和之后的所有计算;扩展模块采用较少的可变资源完成矩阵A和矩阵Ch的一部分计算. 硬件设计如图5所示,虚线框内的部分为核心计算模块,余下部分除Ram外构成扩展模块.

|
图 5 边缘指导插值算法的硬件结构 Fig. 5 Hardware structure of new edge-directed interpolation algorithm |
核心计算模块是完整的
扩展模块只完成大于
采用可扩展的硬件电路设计减少重复设计,提高硬件的利用率,减少不必要的硬件消耗,保证不同窗口NEDI算法的计算时间一致. 使用硬件电路处理单通道的灰度图片,使用3个相同的模块分别处理3个通道得到彩色图片.
3 实验结果与分析采用Matlab设计基于Cholesky分解的NEDI算法,对90张灰度图和彩色图进行超分辨率处理的仿真,确认算法的可行性. 通过双立方插值方法降采样得到低分辨率图片,使用sobel算子进行边缘检测,对边缘区域的像素采用NEDI算法进行插值,对平坦区域采用双线性插值计算. Lena图的实验结果如图6所示,图6(a)为降采样得到的

|
图 6 Lena图的双线性插值与NEDI算法插值结果比较 Fig. 6 Comparison of results to Lena between bilinear interpolation and NEDI algorithm |
使用Mentor公司的ModelSim工具对设计的硬件电路进行时序仿真,并分析硬件计算结果的准确性. 硬件电路的计算误差由除法计算产生,主要出现在矩阵A分解为矩阵L的过程中. 选取测试的90张图片的边缘区域的像素值,得到共200 000组数据进行仿真,其中一组数据的矩阵分解结果如表1所示. 表中的计算值是由Matlab计算并放大65 536倍之后的值. 定点数除法结果的最大误差出现在L43上. 这是由于L43的计算需要使用矩阵L中的其他值,因此误差被积累放大,在L43上呈现为最大误差. 硬件仿真得到的该组数据最终插值的像素值为12 626 526,Matlab处理该组数据的计算结果为12 625 730.598,误差为
| 表 1 除法器仿真结果与软件计算结果比较 Table 1 Comparison of divider’s simulation results and software’s calculation results |
在测试的200 000组数据中,174 622组数据的结果与Matlab的计算结果一致,20 981组数据的结果与Matlab的计算结果相差1,其余的误差不大于6,最大相对误差为6.8%,平均误差为0.1%. 这说明设计的硬件电路可以实现NEDI算法.
在Xilinx的virtex-7系列xc7vx330tffg1157-3芯片上实现硬件电路. 经过Vivado综合布线之后,时序报告显示采用100 MHz的时钟频率时,最长路径延时为7.007 ns. 芯片资源使用情况如表2所示,核心电路模块一共使用了13个乘法器,9个用于基本的乘法运算,4个用于构成2个除法器,乘法器由芯片上的DSP48E1综合得到,总共占用了3.75%的DSP资源. 核心电路模块消耗FPGA芯片内3%左右的LUT和register资源,为图像处理的其他模块如滤波、边缘检测等提供了足够空间。
| 表 2 NEDI算法FPGA资源使用情况 Table 2 FPGA resource consumption of NEDI algorithm |
在配置为i5-2400、主频为3.1 GHz、内存为4 GB的PC上采用Matlab计算一幅
分析了NEDI算法中矩阵的正定对称性,使用Cholesky分解和Goldschmidt定点数除法器加速矩阵运算过程. 设计了NEDI算法的核心计算电路,对不同大小窗口的算法提出了扩展方案,充分提高了硬件资源的利用率和设计的灵活性. 实验表明,设计的电路能够在频率为100 MHz时工作,计算速度比使用软件计算快51倍. 目前需要使用软件对图片进行边缘检测的预处理,但是由于硬件电路占用FPGA芯片上较少资源,下一步可以将滤波、边缘检测等模块硬件化,并且增加时序关系调整模块以满足对视频超分辨率的处理.
| [1] |
AKHTAR P, AZHAR F. A single image interpolation scheme for enhanced super resolution in bio-medical imaging [C] // International Conference on Bioinformatics and Biomedical Engineering. Chengdu: IEEE, 2010: 1–5. http://www.mendeley.com/research/single-image-interpolation-scheme-enhanced-super-resolution-biomedical-imaging/
|
| [2] |
PARK S C, MIN K P, KANG M G. Super-resolution image reconstruction: a technical overview[J]. IEEE Signal Processing Magazine, 2003, 20(3): 21-36. DOI:10.1109/MSP.2003.1203207 |
| [3] |
YANG J, WRIGHT J, HUANG T S, et al. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 2010, 19(11): 2861-2873. DOI:10.1109/TIP.2010.2050625 |
| [4] |
GLASNER D, BAGON S, IRANI M. Super-resolution from a single image [C] // 12th International Conference on Computer Vision. Kyoto: IEEE, 2009: 349–356. http://www.researchgate.net/publication/224135979_Super-resolution_from_a_single_image?ev=auth_pub
|
| [5] |
TAI Y W, LIU S, BROWN M S, et al. Super resolution using edge prior and single image detail synthesis [C] // Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010: 2400–2407. http://www.researchgate.net/publication/224164286_Super_resolution_using_edge_prior_and_single_image_detail_synthesis
|
| [6] |
BAKER S, KANADE T. Limits on super-resolution and how to break them[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(9): 1167-1183. DOI:10.1109/TPAMI.2002.1033210 |
| [7] |
CHANG H, YEUNG D Y, XIONG Y. Super-resolution through neighbor embedding [C] // Computer Society Conference on Computer Vision and Pattern Recognition. Washington DC: IEEE, 2004: 275–282 http://www.researchgate.net/publication/4082219_Super-resolution_through_neighbor_embedding
|
| [8] |
DONG C, CHEN C L, HE K, et al. Learning a deep convolutional network for image super-resolution [C] // European Conference on Computer Vision. Zurich: ECCV, 2014: 184–199. http://rd.springer.com/chapter/10.1007/978-3-319-10593-2_13
|
| [9] |
PROTTER M, ELAD M, TAKEDA H, et al. Generalizing the nonlocal-means to super-resolution reconstruction[J]. IEEE Transactions on Image Processing a Publication of the IEEE Signal Processing Society, 2009, 18(1): 36-51. DOI:10.1109/TIP.2008.2008067 |
| [10] |
KIM K I, KWON Y. Single-image super-resolution using sparse regression and natural image prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(6): 1127. DOI:10.1109/TPAMI.2010.25 |
| [11] |
邓亚斌, 陈立, 方志宏, 等. 基于FPGA的图像超分辨率算法的实现[J]. 电视技术, 2015, 39(23): 5-8. DENG Ya-bin, CHEN Li, FANG Zhi-hong, et al. FPGA implementation of LSE scale algorithm[J]. Video Engineering, 2015, 39(23): 5-8. |
| [12] |
钟雪燕, 夏前亮, 陈智军. 基于FPGA的图像超分辨率的硬件化实现[J]. 现代电子技术, 2017, 40(17): 44-46. ZHONG Xue-yan, XIA Qian-liang, CHEN Zhi-jun. FPGA-based hardware implementation of image super-resolution[J]. Modern Electronics Technique, 2017, 40(17): 44-46. |
| [13] |
NUNO-MAGANDA M A, ARIAS-ESTRADA M O. Real-time FPGA-based architecture for bicubic interpolation: an application for digital image scaling [C] // International Conference on Reconfigurable Computing and FPGAs. Puebla: IEEE, 2005: 1–8. http://dl.acm.org/citation.cfm?id=1115246
|
| [14] |
LI X, ORCHARD M T. New edge-directed interpolation[J]. IEEE Transactions on Image Processing: A Publication of the IEEE Signal Processing Society, 2001, 10(10): 1521. DOI:10.1109/83.951537 |
| [15] |
GOLDSCHMIDT R E. Applications of division by convergence [D]. Boston: Massachusetts Institute of Technology, 1964: 7–14.
|
| [16] |
ANDERSON S F, EARLE J G, GOLDSCHMIDT R E, et al. The IBM system/360 model 91: floating-point execution unit[J]. IBM Journal of Research and Development, 1967, 11(1): 34-53. DOI:10.1147/rd.111.0034 |



