局部维度改进的教与学优化算法

引用本文 [复制中英文]

何杰光, 彭志平, 崔得龙, 李启锐. 局部维度改进的教与学优化算法[J]. 浙江大学学报(工学版), 2018, 52(11): 2159-2170.
dx.doi.org/10.3785/j.issn.1008-973X.2018.11.015

[复制中文]

HE Jie-guang, PENG Zhi-ping, CUI De-long, LI Qi-rui. Teaching-learning-based optimization algorithm with local dimension improvement[J]. Journal of Zhejiang University(Engineering Science), 2018, 52(11): 2159-2170.
dx.doi.org/10.3785/j.issn.1008-973X.2018.11.015

[复制英文]

基金项目

国家自然科学基金资助项目（61772145，61672174）；茂名市科技计划资助项目（2017287）；广东石油化工学院人才引进项目（2016rc02）

作者简介

何杰光（1981—），男，讲师. 从事云计算、机器学习、智能优化算法研究.
orcid.org/0000-0003-2321-1022.
E-mail：hubice@163.com.

文章历史

收稿日期：2018-03-03

Contents Abstract Full text Figures/Tables PDF

局部维度改进的教与学优化算法

何杰光, 彭志平, 崔得龙, 李启锐

广东石油化工学院计算机与电子信息学院，广东茂名 525000

收稿日期：2018-03-03

基金项目：国家自然科学基金资助项目（61772145，61672174）；茂名市科技计划资助项目（2017287）；广东石油化工学院人才引进项目（2016rc02）

作者简介：何杰光（1981—），男，讲师. 从事云计算、机器学习、智能优化算法研究.
orcid.org/0000-0003-2321-1022.
E-mail：hubice@163.com.

摘要: 针对原始教与学优化算法局部搜索能力不强和进化后期容易陷入局部最优的问题，提出基于局部维度改进和自学习扰动的教与学优化算法. 将局部维度改进融入教和学2个阶段，将个体的高质量维度变量保留到下一代，不断改善低质量维度变量，提高算法的细粒度搜索能力. 提出一种混合全局维度改进和局部维度改进的个体更新方式，通过2种改进权重的逐代变化实现算法早期全局搜索和后期局部探测的平衡. 在新算法中增加基于个体最优位置和搜索边界信息的自学习阶段，使种群在进化后期仍能向最优解方向搜索，避免算法过早陷入局部最优. 基于标准测试函数的仿真结果表明，相比于原始的教与学优化算法和当前其他优秀的改进版本，局部维度改进的教与学优化算法的收敛精度平均提高了10²~10⁵倍，收敛速度平均提高了2~3倍.

关键词: 教与学优化算法局部维度改进自学习扰动混合策略

Teaching-learning-based optimization algorithm with local dimension improvement

HE Jie-guang , PENG Zhi-ping , CUI De-long , LI Qi-rui

College of Computer and Electronic Information, Guangdong University of Petrochemical Technology, Maoming 525000, China

Abstract: A local-dimension-improved teaching-learning-based optimization (LDimTLBO) algorithm based on local dimension improvement and self-learning disturbance was proposed, aiming at the problem of weak local search ability and easy to fall into local optimum during the anaphase of evolution in the original teaching-learning-based optimization (TLBO) algorithm. The local dimension improvement strategy was integrated into the teaching and learning phases, which passed the high-quality dimension variables down to the next generation, improved the low-quality ones, and enhanced the fine-grained search capability of the proposed algorithm. A new individual update mode combining global and local dimension improvements was designed. Through the generational change of these two improvements’ weights, the global exploration at early stage and local exploitation at late stage was balanced in the hybrid update mode. A self-learning phase based on individual so-far-best position and search boundary information was also added into the search process, which made the population search towards the optimum even in the later stage of the evolution, thus, the algorithm escaped from getting into the local optimum in the early stage. The simulation results based on testing on benchmark functions demonstrated that in contrast to results of TLBO and other improved variants, the convergence accuracy of LDimTLBO was 10² to 10⁵ times higher, and the convergence speed was 2 to 3 times faster.

Key words: teaching-learning-based optimization (TLBO) algorithm local dimension improvement self-learning disturbance hybrid strategy

教与学优化（teaching-learning-based optimization，TLBO）算法是由Rao等^[1]在2011年首次提出的群智能优化算法，通过教学过程中的教师教学与学生学习2个过程来实现. 与遗传算法、粒子群优化算法、模拟退火算法、禁忌搜索等传统的进化算法相比，TLBO算法具有实现简单、参数设置少、并行度高、收敛稳定等优点，一经提出就受到学者的普遍关注，并且在函数优化^[2-3]、工程优化^[4-5]和多目标优化^[6-7]等领域得到了广泛的应用.

TLBO算法虽然在求解低维单峰值问题时表现出很好的求解效率和性能，但是在求解高维多峰复杂问题时同样容易陷入局部最优，算法的收敛速度和精度都不理想. 许多学者进行了改进TLBO算法的研究. Rao等^[8]在TLBO算法中加入精英机制，提出精英TLBO算法，增强了算法的寻优能力. Satapathy等^[9]在TLBO算法的教师和学生阶段加入随进化呈代数线性变化的权重因子，平衡了算法的全局搜索和局部探测能力. Chen等^[10]将发现-搜索模型与TLBO算法相结合，有效地降低了原始TLBO算法的计算成本，取得了较好的求解效果. Zhang等^[11]在TLBO算法中融合了单纯形算法的局部优化思想，通过反射、扩展、收缩和缩减运算符迭代寻优，提高了算法的收敛精度. 毕晓君等^[12]在TLBO算法的学习阶段融合了差分进化算法的变异策略，在进化后期加入了个体扰动，提高了算法的优化性能. Zou等^[13]提出基于局部学习和排斥学习的教与学优化算法，在算法中加入结合历史信息的自学习方法和每隔一定代数后的种群再分组操作. 童楠等^[14]提出基于反思的教与学优化算法，即在教学和学习阶段都加入个体的反思机制，提高了算法的寻优性能. 于坤杰等^[15]在精英教学优化算法的基础上，提出反馈精英教学优化算法，通过在学习阶段之后加入反馈阶段，增加了种群的多样性，提高了算法的全局搜索能力. Yu等^[16]将学习反馈、差分进化算法的变异交叉操作和混沌扰动机制融入TLBO算法，提出了改进的教与学优化算法. Yu等^[17]提出解决约束优化问题的改进约束教与学优化算法，在教学阶段将种群划分为若干个子种群，子种群通过自身的均值个体和最优个体来引导进化，子种群间的信息交互能够有效抑制早熟收敛，并且在学习阶段提出了新的学习策略来改进种群的多样性.

进化过程中陷入局部最优仍然是TLBO算法和改进TLBO算法面临的主要问题，虽然当前的改进方法在一定程度上提高了算法的收敛性能，但是与非TLBO的进化算法和变体相比，TLBO算法仍需要较大的改进^[12,18]. 目前原始TLBO算法和改进TLBO算法集中于对种群个体进行全维度变量的更新，几乎没有关于局部维度变量更新的研究. 实际上，在算法进化的前期，进行个体的全维度更新有利于算法的全局搜索，但是在进化的后期，个体的局部维度更新更有利于算法的局部探测，加速算法的收敛速度和精度. 增加种群的多样性是TLBO算法跳出局部最优的有效方法，但是当前增加种群多样性的改进方法主要有个体邻域重组^[13,18-19]、混合其他搜索模型^{[10,16,20-21]}、个体扰动^[12]等方式，用到的信息依然来自于种群内部，在进化后期种群的个体大量趋同时，对种群多样性的改进较少，削弱了算法跳出局部最优的能力.

提出基于个体局部维度改进的教与学优化（local-dimension-improved TLBO，LDimTLBO）算法. 在教学和学习阶段，在原有的个体更新公式上加入更新个体局部维度的操作，保证算法在进化的后期进行更加细致的局部搜索，提高算法的收敛速度和精度. 在教和学的基础上，增加个体的自学习阶段，使用个体历史最优位置和搜索边界信息指导自学习，增加种群的多样性，提升算法跳出局部最优的能力.

1 教与学优化算法 1.1 教学阶段

1个班级为1个种群，种群中的最优个体为教师，剩余个体为学生. 教师根据班级的平均水平采对学生进行教学:

${{X}}_i^{{\rm{new}}} = {{{X}}_i} + {r_i}({{ X}_{{\rm{teacher}}}} - {T_{\rm{F}}}{{ X}_{{\rm{mean}}}}),$

(1)

${T_{\rm{F}}} = {\rm round}\;(1 + {\rm rand}\;(0,1)). $

(2)

式中： ${{{X}}_i} = ({x_{i1}},{x_{i2}}, \cdots ,{x_{ij}},\cdots,{x_{iD}})$ 为班级中的第i个学生， ${x_{ij}} $ 为该个体的第j维变量值. ${{X}}_i^{{\rm{new}}}$ 表示由 ${{{X}}_i}$ 产生的新个体，D为问题空间的维度， ${r_i}$ 为[0，1.0]的随机数， ${{ X}_{{\rm{teacher}}}}$ 为教师个体， ${{ X}_{{\rm{mean}}}}$ 为均值个体， ${{ X}_{{\rm{mean}}}} =\displaystyle \frac{1}{n}\sum\nolimits_{i = 1}^n {{{{X}}_i}} $ ，n为种群规模， ${T_{\rm{F}}}$ 为教学因子，round为四舍五入取整. 如果 ${{X}}_i^{{\rm{new}}}$ 优于 ${{{X}}_i}$ ，接受 ${{X}}_i^{{\rm{new}}}$ ，即 ${{{X}}_i} = {{X}}_i^{{\rm{new}}}$ ，否则，保持 ${{{X}}_i}$ 不变. 以个体的目标函数值 $f({ X}_i) $ 衡量个体的优劣，由于众多的无约束函数优化问题都以求解目标函数的最小值为优化目标，个体的函数值越小，质量越优，反之质量越差.

1.2 学习阶段

学习阶段即班级中的学生互相学习的过程：

$\begin{array}{l}{{X}}_i^{{\rm{new}}} = \left\{ \begin{array}{l}{{{X}}_i} + {r_i}({{{X}}_i} - {{{X}}_j}),\;f({{{X}}_i}) < f({X_j}),\;i\ne j;\\{{{X}}_i} + {r_i}({{{X}}_j} - {{{X}}_i}),\;f({{{X}}_i}) > f({X_j}),\;i \ne j.\end{array} \right.\;\;\\\end{array}$

(3)

式中： ${{ X}_j}$ 为种群中异于 ${{{X}}_i}$ 的任一学生，通过随机方式选择. 求得 ${{X}}_i^{{\rm{new}}}$ 后，按照1.1节中的方式更新 ${{{X}}_i}$ .

2 局部维度改进的教与学优化算法 2.1 局部维度改进策略

从原始TLBO和变体算法中可以看出，无论是在教学阶段还是学习阶段，个体的更新都是全维度进行的，这使得一些高质量连续维度变量在进化的过程中遭受破坏，无法保留到下一代种群中，降低了算法局部搜索的精确度. 在进化的后期，全维度进行的个体更新对准确查找最优解的影响更为明显. 此时大量个体的高质量局部维度的值已经非常接近甚至等于最优解相应维度的值，即使是对局部维度的细微修改也会使得更新后的函数值与最优值产生10倍以上的偏离，出现进化停滞的现象，即种群中的最好解总是在问题的最优解或局部最优解附近来回跳跃，无法找到最优解或是更好的局部最优解. 在进化的过程中，个体的一些高质量连续局部维度值应该保留到下一代个体中，当前代只对质量较差的局部维度值进行更新.

局部维度改进策略的实现步骤如下. 随机产生整数 $L({c_1}D \leqslant L \leqslant {c_2}D)$ ， ${c_1}$ 为最小长度因子， ${c_2}$ 为最大长度因子， ${c_1},{c_2} \in [0,1.0].$ 在个体 ${{{X}}_i} $ 中查找函数值最大（质量最差）、维度为 $L$ 的子向量 ${{X}}_i^{{\rm{sub}}} = ({x_{i{q_1}}}, $ ${x_{i{q_2}}},\cdots,{x_{i{q_j}}},\cdots,{x_{i{q_L}}})$ ， ${{X}}_i^{{\rm{sub}}}$ 中第 $j$ 维的变量值实际上是 ${{{X}}_i}$ 中第 ${q_j}$ 维的变量值，例如，若 ${q_2} = 5$ ，表示 ${{X}}_i^{{\rm{sub}}}$ 中第2维的变量值实际上是 ${{{X}}_i}$ 中第5维的变量值，同时可知 ${q_1} = 4$ ， ${q_3} = 6$ . 更新 ${{{X}}_i}$ 时只更新局部维度质量最差的子向量 ${{X}}_i^{{\rm{sub}}}$ ，不更新首尾两部分的高质量的局部维度子向量 ${{X}}_i^{{\rm{su}}{{\rm{b}}_{\rm{1}}}} = ({x_{i1}}, $ ${x_{i2}}, \cdots ,{x_{i{q_1}{\rm{ - }}1}})$ 和 ${{X}}_i^{{\rm{su}}{{\rm{b}}_{\rm{2}}}} =({x_{i{q_L} + 1}},{x_{i{q_L} + 2}}, \cdots ,{x_{iD}})$ ， ${{X}}_i^{{\rm{sub}}}$ 的具体更新方法见2.2节和2.3节.

查找个体 ${{{X}}_i}$ 中局部维度质量最差的子向量 ${{X}}_i^{{\rm{sub}}}$ 的具体步骤如下.

1）令 ${q_1} = 1$ ，maxFun=−Q，Q为一个足够大的数.

2）在 ${{{X}}_i}$ 中取维度连续的子向量 ${{X}}_i^{{\rm{sub}}} = ({x_{i{q_1}}},$ ${x_{i{q_2}}},\; \cdots ,\;{x_{i{q_L}}}),\;{\text{其中}}\;{q_2}\; =\; {q_1} + 1,\;{q_3} \;=\;{q_1} + 2,\; \cdots,\;{q_L}\; = $ ${q_1} +$ L−1.

3）计算 ${{X}}_i^{{\rm{sub}}}$ 的函数值 $f({{X}}_i^{{\rm{sub}}})$ ，如果 $f({{X}}_i^{{\rm{sub}}}) >$ $ \max {\rm{Fun}}$ ，设置 ${\rm{maxFun}} = f({{X}}_i^{{\rm{sub}}})$ .

4）如果 ${q_1} + L - 1 < D$ ，设置 ${q_1} = {q_1} + 1$ ，转到步骤2），否则转到步骤5）.

5）返回 ${{X}}_i^{{\rm{sub}}}$ 和maxFun..

显然，该操作的时间复杂度为 ${\rm O}\;(D - L + 1)$ .

2.2 基于局部维度改进的教学阶段

基于局部维度改进策略，提出混合教学方法：

${{X}}_i^{{\rm{new}}} = \eta (1 - {t / {{T_{\max }}}}){{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{1}}}} + ({t / {{T_{\max }}}}){{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{2}}}}. $

(4)

式中： $\eta $ 为折扣因子， $\eta \in [0,1.0]$ ， $t$ 为当前迭代次数， ${T_{\max }}$ 为最大迭代次数， ${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{1}}}}$ 为使用原始TLBO教学阶段个体更新方式求得的新个体，如式（1）所示， ${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{2}}}}$ 为教学阶段使用局部维度改进方法求得的新个体，求解方法如下：

${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{2}}}{\rm{sub}}} = {{X}}_i^{{\rm{sub}}} + r({{X}}_{{\rm{firstteacher}}}^{{\rm{sub}}} - {{X}}_i^{{\rm{sub}}}),$

(5)

${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{2}}}} = {{X}}_i^{{\rm{su}}{{\rm{b}}_{\rm{1}}}} \cup {{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{2}}}{\rm{sub}}} \cup {{X}}_i^{{\rm{su}}{{\rm{b}}_{\rm{2}}}}. $

(6)

式中： $r$ 为[0，1.0]的随机数， ${{X}}_{{\rm{firstteacher}}}^{{\rm{sub}}}$ 为第一教师子向量，其分量的下标与 ${{X}}_i^{{\rm{sub}}}$ 的一致. 将种群中的个体按函数值降序排列，如果第1个个体（ ${ X_{{\rm first}}} $ ）的子向量 ${{X}}_{{\rm{first}}}^{{\rm{sub}}}$ 的函数值小于 ${{X}}_i^{{\rm{sub}}}$ 的函数值，取该子向量为 ${{X}}_{{\rm{firstteacher}}}^{{\rm{sub}}}$ ，否则继续考察剩余个体的子向量，直到找到第1个符合上述要求的个体为止. 式（6）表示将 ${{X}}_i $ 更新后的子向量 ${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{2}}}{\rm{sub}}}$ 与原来首尾的子向量合并成新的个体 ${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{2}}}}$ .

由式（4）可知，在算法迭代的早期， $t$ 值较小， ${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{1}}}}$ 前的系数 $(1 - t/{T_{\max }})$ 较大，说明原始TLBO算法中教学阶段的个体更新方式所占的比重较大. 由式（1）可知，原始的教学方法侧重于提高整个班级的平均水平，说明LDimTLBO算法的早期更注重全局搜索，有利于找到更多的局部最优解；在算法迭代的后期， $t$ 值逐渐增大， ${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{2}}}}$ 前的系数 $t/{T_{\max }}$ 也逐渐增大并且趋向于1，说明基于局部维度改进的教学方法起主导作用. 由式（5）可知， ${ X}_{\rm{i}}^{{\rm ne{w}_2}} $ 是在 ${ X}_{{\rm{firstteacher}}} $ 指导下的搜索，有利于在当前的最好解附近找到更好的局部最优解，基于局部维度改进的更新方式有利于进行更小粒度的局部搜索，提高收敛速度和精度. 折扣因子 $\eta $ 在式（4）中是 ${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{1}}}}$ 的因子，可用于抑制原始TLBO中教学阶段个体更新方式的作用，合适的 $\eta $ 可以平衡算法的收敛速度和精度.

基于局部维度改进的混合教学方法兼顾了算法早期的全局搜索和后期的局部探测，既保证了算法大范围的广度搜索（跳出局部最优），又保证了算法小范围的精细探测（更接近全局最优）.

2.3 基于局部维度改进的学习阶段

基于局部维度改进策略，提出混合的学习方式：

${{X}}_i^{{\rm{new}}} = \eta (1 - {t / {{T_{\max }}}}){{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{3}}}} + ({t / {{T_{\max }}}}){{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{4}}}}. $

(7)

式中： ${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{3}}}}$ 为使用原始TLBO学习阶段个体更新方式求得的新个体，如式（3）所示， ${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{4}}}}$ 为学习阶段使用局部维度改进方法求得的新个体，由式（8）、（9）产生，其中式（8）中 ${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{4}}}{\rm{sub}}}$ 表示使用局部维度更新方式求得的 ${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{4}}}}$ 中的子向量，式（9）的求解方式类同式（6）.

${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{4}}}{\rm{sub}}} = \left\{ \begin{array}{l}{{X}}_i^{{\rm{sub}}} + {r_1} ({{X}}_{{\rm{teacher}}}^{{\rm{sub}}} - {{X}}_i^{{\rm{sub}}}) + {r_2}({{X}}_{{\rm{mean}}}^{{\rm{sub}}} - {{X}}_i^{{\rm{sub}}}),\\\qquad f({{X}}_{{\rm{teacher}}}^{{\rm{sub}}}) < f({{X}}_i^{{\rm{sub}}});\\{{X}}_i^{{\rm{sub}}} + {r_1}({{X}}_i^{{\rm{sub}}} - {{X}}_{{\rm{teacher}}}^{{\rm{sub}}}) +{r_2}({{X}}_i^{{\rm{sub}}} - {{X}}_{{\rm{mean}}}^{{\rm{sub}}}), \\\qquad f({{X}}_{{\rm{teacher}}}^{{\rm{sub}}}) > f({{X}}_i^{{\rm{sub}}}),\end{array} \right.$

(8)

${{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{4}}}} = {{X}}_i^{{\rm{su}}{{\rm{b}}_{\rm{1}}}} \cup {{X}}_i^{{\rm{ne}}{{\rm{w}}_{\rm{4}}}{\rm{sub}}} \cup {{X}}_i^{{\rm{su}}{{\rm{b}}_{\rm{2}}}}. $

(9)

式中：r₁为[0,1.0]的随机数，r₂为[−1.0，1.0]的随机数， ${ X}_{\rm teacher}^{\rm sub}$ 、 $ { X}_{\rm mean}^{\rm sub}$ 分别为教师和均值个体子向量.

式（7）的构建方式与式（4）相同，寻优方式的原理与2.2节中相同. 由式（8）可知， ${{X}}_i $ 进行局部维度更新时除了使用 ${{X}}_{{\rm{teacher}}} $ 作为指导信息，还使用了 ${{{X}}_{{\rm{mean}}}}$ ，这是为了避免个体过快趋向于 ${{X}}_{{\rm{teacher}}}, $ 增加种群的多样性. 基于局部维度改进的混合学习方法实现了算法早期的全局搜索和后期的局部探测的均衡.

2.4 自学习阶段

虽然前2个阶段在一定程度上增加了种群的多样性，但是在种群进化的后期仍然会出现个体大量趋同的情况，为了增加种群的多样性、跳出局部最优，提出基于个体历史最优位置和搜索边界的个体扰动方式，增加自学习阶段.

${{X}}_i^{{\rm{new}}} = \left\{ \begin{array}{l}{{{X}}_i} + {r_1}({{X}}_i^{{\rm{sofarbest}}} - {{{X}}_i}) +{r_2}({{{X}}_i} - {{L}}),\;{r_2} < 0;\\{{{X}}_i} + {r_1}({{X}}_i^{{\rm{sofarbest}}} - {{{X}}_i}) +{r_2}({{U}} - {{{X}}_i}),\;{r_2} > 0 .\end{array} \right.$

(10)

式中： ${{X}}_i^{{\rm{sofarbest}}}$ 为 ${{{X}}_i}$ 的历史最优位置， ${{L}}$ 为各维变量下界构成的向量， ${{L}} = ({l_1},{l_2},\cdots,{l_D})$ ， ${{U}}$ 为各维变量上界构成的向量， ${{U}} = ({u_1},{u_2},\cdots,{u_D})$ .

由式（10）可知，个体的自学习完全不依赖种群中其他个体的信息， ${{X}}_i^{{\rm{sofarbest}}}$ 信息的加入可以避免随机搜索过于盲目，使个体朝好的方向进化，上下界信息的加入可以有效地增加种群的多样性，避免算法过早陷入局部最优，即使在进化的后期也有可能找到更好的解. 实质上，式（10）也是一种算法收敛精度（较好的种群多样性）和速度（避免盲目搜索，加快收敛）的平衡.

2.5 域约束

在学生个体的更新过程中，经常会出现某些维度变量的值超出可行域的情况，必须对个体进行域约束操作. 当前约束域主要采取直接将超出边界值的维度变量设置为边界值的方式，许多维度的变量值可能无法反映出公式计算后值的变化趋势，丢失种群进化过程中的有用信息. 提出基于循环重置的域约束操作方法：

${x_{ij}} = \left\{ \begin{gathered} {x_{ij}} + \left\lfloor {\frac{{{m_j} - {x_{ij}}}}{{{a_j}}}} \right\rfloor {l_j},\;\;{x_{ij}} < {l_j}; \hfill \\ {x_{ij}} - \left\lfloor {\frac{{{x_{ij}} - {m_j}}}{{{a_j}}}} \right\rfloor {l_j},\;\;{x_{ij}} > {u_j}. \hfill \\ \end{gathered} \right.$

(11)

式中： $j = 1,2, \cdots ,D,$ ${m_j} = ({l_j} + {u_j})/2,\;{a_j} = ({u_j} - {l_j})/2$ . ${x_{ij}}$ 重置后依然能反映出更新后的变化趋势，保留了个体更新操作的有用信息，有利于增加种群的多样性.

2.6 LDimTLBO算法实现流程

LDimTLBO算法的实现流程如图1所示.

图 1 局部维度改进的教与学优化算法流程图 Fig. 1 Flowchart of local-dimension-improved teaching-learning-based optimization algorithm

3 仿真实验与结果分析 3.1 测试环境与参数设置

使用Java编程实现LDimTLBO，测试机CPU的主频为3.0 G，内存为4 GB，操作系统为Windows 7. 为了验证算法的有效性，分别对10个通用的标准Benchmark函数进行仿真测试，与原始TLBO算法以及最近新提出的改进效果较好的RTLBO算法^[14]、DSTLBO算法^[12]、DRLTLBO算法^[13]和非TLBO的SaDE^[22]算法进行对比. Benchmark函数的表达式和搜索范围如表1所示. 为了更好地检测算法的全局搜索性能，将函数f₄~f₇的搜索范围扩展到[−100,100]，f₁~f₅是单峰函数，f₆~f₁₀是多峰函数，这些函数具有不同的特点，都能从收敛精度和收敛速度方面测试不同算法的性能，具有很好的普遍性.

表 1 Benchmark函数的表达式和搜索范围 Table 1 Formulas and ranges of Beanchmark functions

函数	公式	范围
f₁ （Sphere）	\setlength{\voffset}{0pt}${f_1}(x) = \displaystyle\sum\limits_{i = 1}^D {} {x_i^2} $	[−100，100]
f₂ （Quadric）	\setlength{\voffset}{0pt}${f_2}(x) = \displaystyle\displaystyle\sum\limits_{i = 1}^D {} \left({{{\displaystyle\sum\limits_{j = 1}^i {} {{x_j}}^2}}}\right) $	[−100，100]
f₃ （Sum Square）	\setlength{\voffset}{0pt}${f_3}(x) = \displaystyle\displaystyle\sum\limits_{i = 1}^D {} {ix_i^2} $	[−100，100]
f₄ （Zakharov）	\setlength{\voffset}{0pt}${f_4}(x) = \displaystyle\displaystyle\sum\limits_{i = 1}^D {} {x_i^2} + {\left(\displaystyle\sum\limits_{i = 1}^D {} {0.5i{x_i}}\right)^2} + {\left(\displaystyle\sum\limits_{i = 1}^D {} {0.5i{x_i}} \right)^4}$	[−100，100]
f₅（Rosenbrock）	\setlength{\voffset}{0pt}${f_5}(x) = \displaystyle\sum\limits_{i = 1}^{D-1}{\Big[100{{\big(x_i^2 - {x_{i + 1}}\big)}^2} + {{\big({x_i} - 1\big)}^2}\Big]} $	[−100，100]
f₆ （Ackley）	\setlength{\voffset}{0pt}$\begin{aligned} {f_6}(x) =20 - 20\exp {\kern 1pt} \left( {{\rm{ - 0}}{\rm{.2}}{{\left( {\sum\limits_{{{i}} = 1}^D {x_i^2/D} } \right)}^{1/2}}} \right)-\exp {\kern 1pt} \left( { \left({\sum\limits_{i = 1}^D {\cos \;(2{\text{π}} {x_i})} }\right) /D} \right) + {\rm{e}}\end{aligned} $	[−100，100]
f₇ （Rastrigin）	\setlength{\voffset}{0pt}${f_7}(x) = \displaystyle\displaystyle\sum\limits_{i = 1}^D {} {\Big(x_i^2 - 10\cos\;(2{\text{π}} {x_i}) + 10\Big)} $	[−100，100]
f₈ （Weierstrass）	\setlength{\voffset}{0pt}$\begin{aligned} {f_8}(x) =& \displaystyle\sum\limits_{i = 1}^D {} {\left(\displaystyle\sum\limits_{k = 0}^{k_{\rm max}} {} {\left[{a^k}\cos\; \left(2{\rm{{\text{π}} }}{b^k}({x_i} + 0.5)\right)\right]} \right)}- D\displaystyle\sum\limits_{k = 0}^{k_{\rm max}} {} {\Big[{a^k}\cos\;(2{\rm{{\text{π}} }}{b^k} \times 0.5)\Big]} \hfill \\ &(a = 0.5,\;b = 3,\;{k_{\rm max}} = 20) \end{aligned} $	[−0.5，0.5]
f₉ （Griewank）	\setlength{\voffset}{0pt}${f_9}(x) =\displaystyle\sum\limits_{i = 1}^D {} {x_i^2}/4\;000 - \prod\limits_{i = 1}^D {\cos\;{x_i}{i^{-1/2}}} + 1$	[−600，600]
f₁₀ （Schwefel）	\setlength{\voffset}{0pt}${f_{10}}(x) = 418.982\;9D + \displaystyle\displaystyle\sum\limits_{i = 1}^D {} {( - {x_i}\sin \sqrt {\left\| {{{x_i}}} \right\|)}} $	[−500，500]

表 1 Benchmark函数的表达式和搜索范围 Table 1 Formulas and ranges of Beanchmark functions

除了3.2节的实验，后续所有的测试实验中的算法的种群大小设置为50，决策变量的维度设置为50，LDimTLBO算法的参数 $ \eta = 0.5,{c_1} = 0.25,$ ${c_2} = 0.6$ . 对比算法中涉及到的参数均与相应的文献中相同. 使用函数评价次数（function evaluations，FEs）^[13]作为各个算法迭代终止的判断条件，最大FEs（maxFEs）设置为100 000. 在LDimTLBO算法中，由于在式（4）、（7）中需使用到参数 ${T_{\max }}$ ，设置 ${T_{\max }} = 666$ （相当于maxFEs=99 900）.

3.2 局部维度改进策略有效性验证

从局部维度质量改变与全局维度质量改变的相关性、相关性与算法收敛精度和速度的关系、折扣因子 $\eta $ 对相关性的影响3个方面验证和分析局部维度改进策略的有效性.

为了说明局部维度质量（函数值）改变与全局维度质量改变的相关性，设置衡量指标为PCwPCh（正相关且积极改变）、PCwNCh（正相关但消极改变）、NCwPCh（负相关且积极改变）、NCwNCh（负相关但消极改变）、UCwPCh（不相关且积极改变）、UCwNCh（不相关但消极改变）、UCwUCh（不相关且无改变）等相关性出现次数的百分比，用 $\varphi $ （_）表示，（_）为对应相关性符号. 其中，正相关指局部维度质量与全局维度质量的改变方向相同；负相关指局部维度质量与全局维度质量的改变方向相反；不相关指局部维度质量和全局维度质量至少有一方未发生改变，这种情况通常出现在算法进化的后期当所求的最优值非常接近理论最优值时. 积极改变指全局维度质量变好（改进），消极改变指全局维度质量变差. 选用f₂（Quadric）和f₅（Rosenbrock）作为测试函数，因为Quadric和Rosenbrock函数（特别是Rosenbrock）的最优值比其他函数更难求得. LDimTLBO的种群规模设置为10，测试函数的维度设置为10，按照表2设置式（4）、（7）中的折扣因子 $\eta $ ，迭代终止条件设置为 ${T_{\max }} = 250$ （相当于maxFEs=10 000）. 对2个测试函数分别进行20次独立测试，统计各种相关性出现次数的百分比，计算各个衡量指标的平均值，分别汇总正相关、负相关和不相关关系出现次数的百分比（ $\varphi ({{\rm PC}_{\rm total}}) $ 、 $\varphi ({{\rm NC}_{\rm total}}) $ 、 $\varphi ({{\rm UC}_{\rm total}}) $ ）. 结果如表2所示. 函数的均值和标准差列如表3所示，函数的平均收敛曲线如图2所示，图中的lg f为求得的函数值的以10为底的对数，Fes为函数评价次数.

表 2 局部维度质量改变与全局维度质量改变的相关性 Table 2 Correlation between local dimension quality change and global dimension quality change

函数	η	$\varphi$
函数	η	${{\rm PCwPCh}}$	${{\rm PCwNCh}}$	${{\rm PC_{total}}}$	${{\rm NCwPCh}}$	${{\rm NCwNCh}}$	${{\rm NC_{total}}}$	${{\rm UCwPCh}}$	${{\rm UCwNCh}}$	${{\rm UCwUCh}}$	${{\rm UC_{total}}}$
f₂	0.01	23.04	0.16	23.20	0.00	12.92	12.92	0.00	0.20	63.68	63.88
	0.03	27.24	0.44	27.68	0.08	23.12	23.20	0.04	3.20	45.88	49.12
	0.05	30.32	10.16	40.48	0.00	55.08	55.08	0.00	1.72	2.72	4.44
	0.07	32.88	2.52	35.40	0.00	64.60	64.60	0.00	0.00	0.00	0.00
	0.09	28.56	4.92	33.48	0.04	66.48	66.52	0.00	0.00	0.00	0.00
	0.11	15.20	6.56	21.76	0.00	78.24	78.24	0.00	0.00	0.00	0.00
f₅	0.4	42.97	45.15	88.12	0.40	11.39	11.79	0.00	0.00	0.09	0.09
	0.5	35.01	53.07	88.08	0.37	11.28	11.65	0.00	0.00	0.28	0.28
	0.6	34.29	53.87	88.16	0.28	11.21	11.49	0.00	0.00	0.35	0.35
	0.7	33.26	55.81	89.07	0.30	10.45	10.75	0.00	0.00	0.18	0.18
	0.8	32.70	55.97	88.67	0.20	10.65	10.85	0.00	0.00	0.00	0.48
	0.9	41.32	46.13	87.45	0.40	11.66	12.06	0.00	0.00	0.00	0.49

表 2 局部维度质量改变与全局维度质量改变的相关性 Table 2 Correlation between local dimension quality change and global dimension quality change

表 3 不同 $\eta $ 取值下函数的均值和标准差 Table 3 Mean and standard deviation of different functions with different $\eta $ values

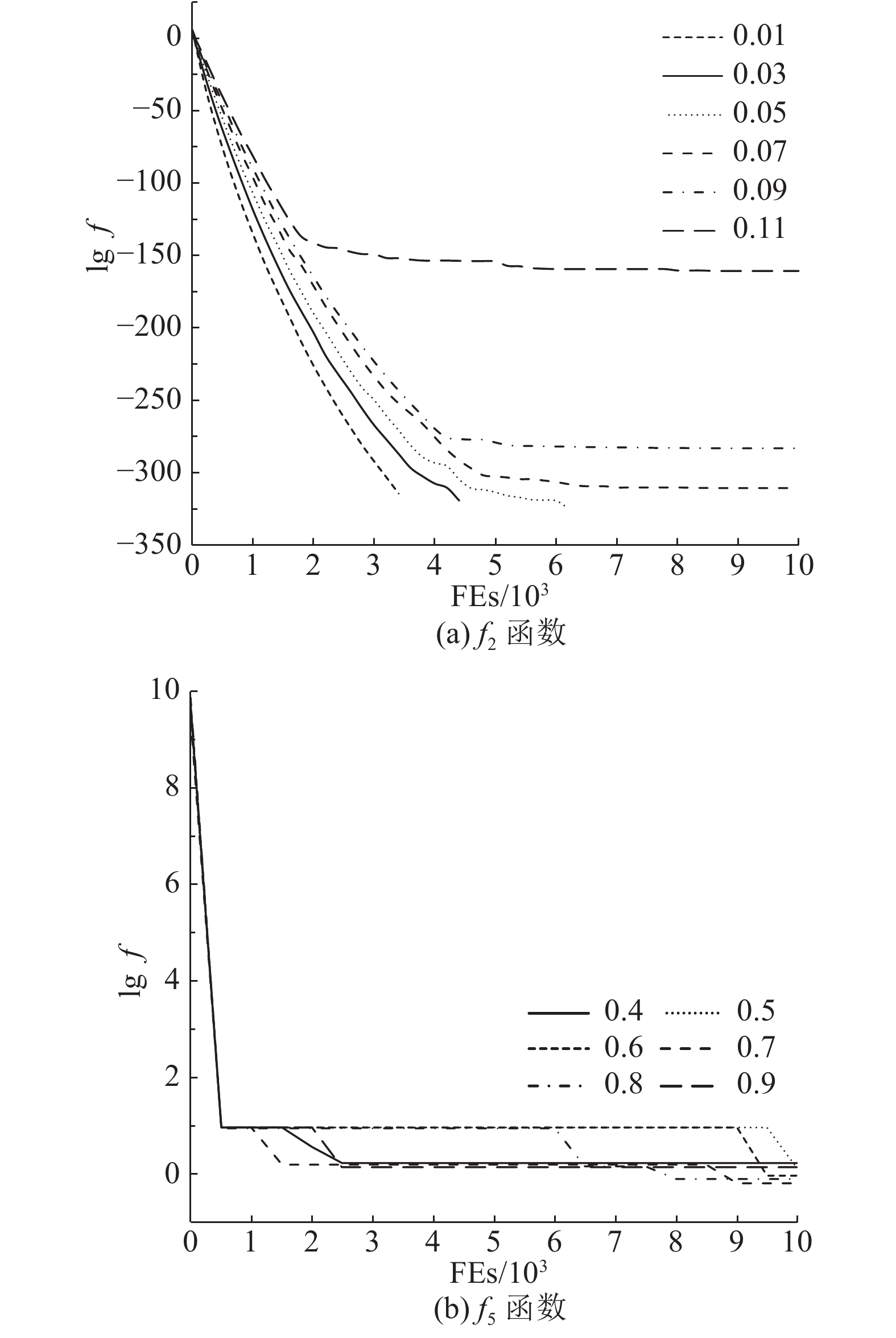
图 2 $\eta $ 取值不同时不同函数的收敛曲线 Fig. 2 Convergence curves of different functions with different $\eta $ values

分析表2、3中的数据和函数收敛曲线，得出如下结论.

1）如表2所示，各列中都存在不为0的值，表明局部维度质量的改变与全局维度质量的改变存在不同的相关性，这是因为局部维度变量值改变后，局部维度和全局维度质量的变化情况由变量值改变的情况和函数表达式决定. 因此，当局部维度质量改进后，全局维度质量不一定会改进，甚至会变差（如表2中的 $\varphi $ (NCwNCh)）；当局部维度质量没有改进时，全局维度质量也可能改进（这种情况极少，如表2中的 $\varphi $ (UCwPCh)）或不变（如表2中的 $ \varphi$ (UCwUCh)）；当局部维度质量变差时，全局维度质量也可能改进（这种情况较少，如表2中的NCwPCh）.

2）当算法迭代次数固定，局部维度质量和全局维度质量的相关性主要表现为非负相关（即负相关的比例较小）时，这种情况能够有效地提高算法的收敛速度和精度. f₂函数的求解过程反映了这种情况，当 $\eta = 0.01$ 时，非负相关所占的比例为87.08%（表2中 $ \varphi$ (PC_total)+ $ \varphi$ (UC_total)），负相关所占比例为12.92%（表2中 $ \varphi$ (NC_total)），是不同 $\eta $ 取值情况下负相关所占比例的最小值，算法的收敛精度和收敛速度最好；随着 $\eta $ 的增大，负相关所占比例逐渐增大，算法的收敛精度和速度都逐渐变差. f₅函数的求解过程也反映了这种情况，当 $\eta $ 改变时，负相关所占比例的变化不大，算法的收敛精度和速度在各种不同 $\eta $ 取值下的差异较小；当负相关的值最小时，算法的收敛精度和速度还是最优的. 当负相关比例较大时，会出现局部维度质量改进但是全局维度质量变差的情况（表2中 $ \varphi$ (NC_total)与 $ \varphi$ (NCwNCh)相差较小）. 由于局部维度对应的质量已经得到了改善，维度的变量值在进化中被改进的概率降低，但是实际上质量的改善对全局维度的质量的改变却是消极的，降低了算法的收敛精度和速度.

3）合适的 $\eta $ 取值能获得较低的负相关占比，提升算法的收敛精度和速度. 由式（4）、（7）可知，折扣因子 $\eta $ 用于抑制原始TLBO中教学和学习阶段的个体更新方式，原始TLBO中教学和学习阶段的个体更新方式有利于算法的全局搜索，局部维度改进策略有利于更小粒度的局部搜索，控制 $\eta $ 的取值能够有效提高算法的收敛精度和速度. f₂函数的理论最优值较容易查找，搜索空间较小，选择较小的 $\eta $ 值能够加强算法的局部搜索能力，算法在全局最优解的附近进行更精细的搜索，提升算法的收敛精度和速度. 同理当 $\eta $ 取最小值0.01时，算法能够获得最好的收敛精度和速度. f₅函数的搜索空间较大，全局最优解在一条狭长而平滑的抛物线山谷中，难以搜索^[13-14,23]，算法很容易陷入局部最优，选择较大的 $\eta $ 值能够加强算法的全局搜索能力，利于算法跳出局部最优. 局部维度改进策略有利于进一步改善局部最优解，在测试中虽然所有不同的 $\eta $ 取值都没有求得函数的理论最优值，但是当 $\eta = 0.7$ 时，可以较好地实现算法全局搜索和局部搜索的平衡，获得最好的搜索精度和速度. 需要说明的是，3.1节中 $\eta $ =0.5也是通过这种方法获得的（函数维度为50，maxFEs=99 900）.

3.3 自学习策略有效性验证

从两方面验证提出的自学习策略的有效性：比较使用和未使用自学习策略的LDimTLBO算法；将自学习策略用于其他算法，比较使用前后的效果. 选用TLBO作为对比算法，构造4种不同的算法进行比较：LDimTLBO、LDimTLBO-SL（不使用自学习策略）、TLBO、TLBO+SL（使用自学习策略）. 选用函数f₅（Rosenbrock）作为测试函数，Rosenbrock是一种典型的病态非凸单峰函数，极难搜索全局最优解，非常适用于测试算法的收敛性能. 使用4种算法分别对Rosenbrock函数进行20次独立测试，计算出函数最优值的平均值和标准差，结果如表4所示. 绘制出算法的平均收敛曲线，如图3所示.

表 4 自学习策略对LDimTLBO、LDimTLBO-SL、TLBO、TLBO+SL算法收敛结果的影响 Table 4 Influence of self-learning strategy on convergence results of LDimTLBO，LDimTLBO-S，TLBO and TLBO+SL

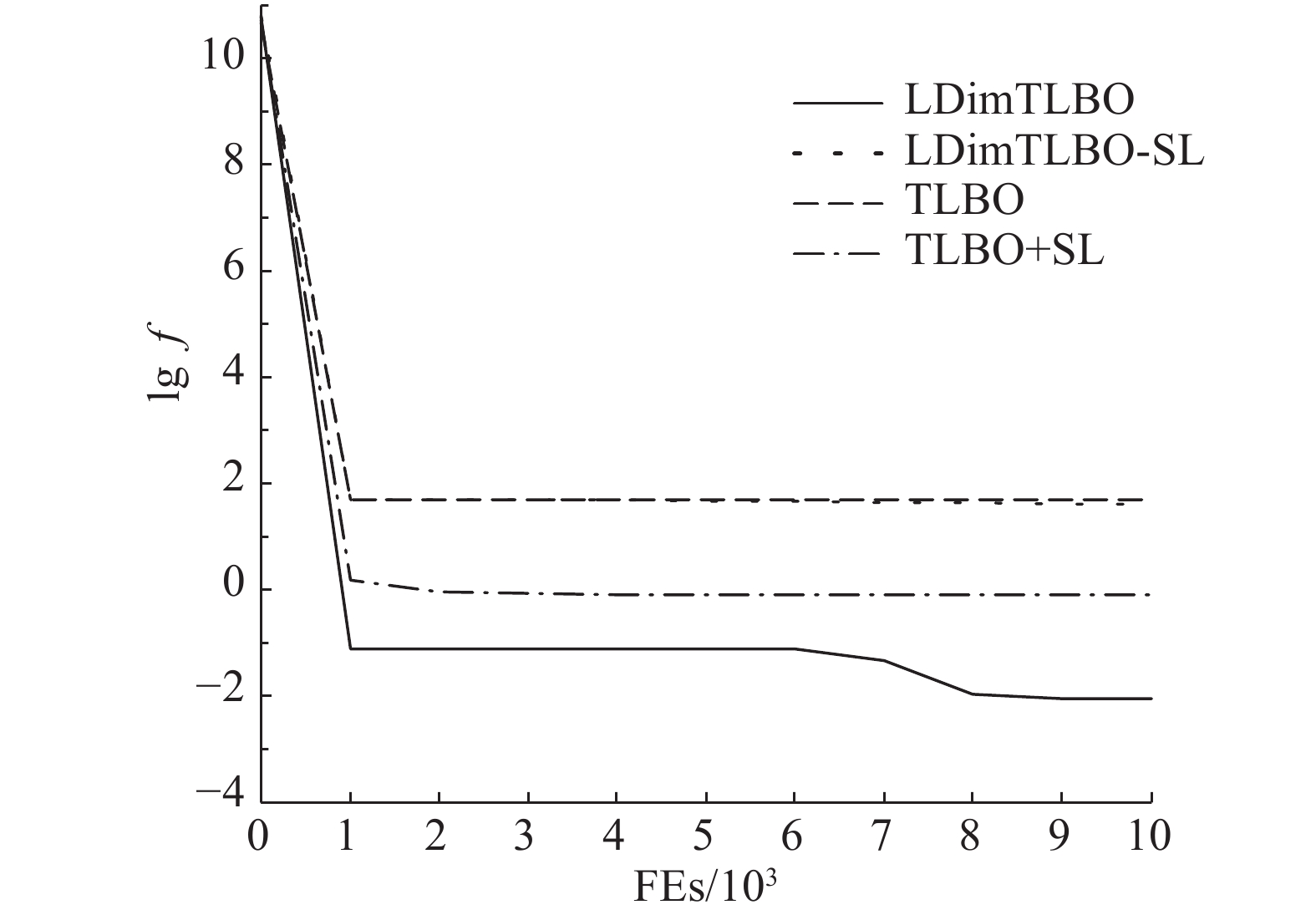
图 3 自学习策略对算法收敛过程的影响 Fig. 3 Influence of self-learning strategy on convergence process

由表4可知，使用了自学习策略的算法LDimTLBO和TLBO+SL的函数值更小，收敛结果明显优于未使用自学习策略的算法LDimTLBO-SL和TLBO，说明自学习策略有利于提高种群的多样性，提高算法的收敛精度. 由图3可知，未使用自学习策略的TLBO和LDimTLBO-SL算法出现了早熟收敛的情况，进行10 000次函数评价后，算法已经陷入了局部最优，之后求得的函数最优值没有变化，使用了自学习策略的LDimTLBO和TLBO+SL在进化到EFs=10 000时，已经收敛到精度较高的函数值，说明自学习策略有利于加速算法的收敛. 在进一步的进化过程中，TLBO+SL获得的最优值只出现了细微的改善，LDimTLBO仍然可以使种群获得进一步的进化，求得更好的最优解. 这是因为局部维度改进策略有利于算法进行更加细粒度的搜索，与自学习策略的综合作用可以更好地平衡算法的全局搜索和局部探测能力. 自学习策略是有效的，可以增加种群的多样性，使算法跳出局部最优，提高算法的收敛速度和精度.

3.4 LDimTLBO算法整体性能验证

使用LDimTLBO算法、TLBO算法、RTLBO算法、DSTLBO算法、DRLTLBO算法分别独立运行测试函数20次，所得的平均函数最优值、标准差和平均运行时间如表5所示，绘制出算法的平均收敛曲线图，如图4所示.

表 5 LDimTLBO、TLBO、RTLBO、DSTLBO、DRLTLBO、SaDE算法的收敛结果对比 Table 5 Comparison of convergence results of LDimTLBO，TLBO，RTLBO，DSTLBO，DRLTLBO and SaDE

函数	算法	均值	标准差	运行时间/s	函数	算法	均值	标准差	运行时间/s
f₁	TLBO	6.60×10⁻²⁴⁰	0	0.162	f₆	TLBO	4.00×10⁻¹⁵	0	0.458
f₁	RTLBO	1.45×10⁻¹¹⁷	1.57×10⁻¹¹⁷	0.577	f₆	RTLBO	4.00×10⁻¹⁵	0	0.735
f₁	DSTLBO	3.13×10⁻¹⁸⁷	0	0.251	f₆	DSTLBO	4.00×10⁻¹⁵	0	0.560
f₁	DRLTLBO	2.57×10⁻³¹⁴	0	0.472	f₆	DRLTLBO	3.82×10⁻¹⁵	7.74×10⁻¹⁶	0.830
f₁	LDimTLBO	0	0	2.113	f₆	LDimTLBO	4.44×10⁻¹⁶	0	5.060
f₁	SaDE	6.91×10⁻¹²³	1.08×10⁻¹²²	0.612	f₆	SaDE	5.87×10⁻¹⁵	0	0.813
f₂	TLBO	1.39×10⁻²³⁷	0	0.322	f₇	TLBO	0	0	0.527
f₂	RTLBO	6.06×10⁻¹¹⁵	1.44×10⁻¹¹⁴	0.738	f₇	RTLBO	0	0	0.723
f₂	DSTLBO	3.22×10⁻¹⁸⁵	0	0.375	f₇	DSTLBO	0	0	0.563
f₂	DRLTLBO	4.31×10⁻³¹⁵	0	0.638	f₇	DRLTLBO	3.78	1.65×10	0.812
f₂	LDimTLBO	0	0	3.064	f₇	LDimTLBO	0	0	2.669
f₂	SaDE	3.02×10⁻⁷	3.88×10⁻⁸	0.792	f₇	SaDE	0	0	0.842
f₃	TLBO	6.35×10⁻²³⁸	0	0.191	f₈	TLBO	0	0	47.972
f₃	RTLBO	1.60×10⁻¹¹⁵	3.31×10⁻¹¹⁵	0.612	f₈	RTLBO	0	0	47.161
f₃	DSTLBO	1.76×10⁻¹⁸⁴	0	0.238	f₈	DSTLBO	0	0	44.983
f₃	DRLTLBO	6.06×10⁻³¹⁶	0	0.560	f₈	DRLTLBO	0	0	67.355
f₃	LDimTLBO	0	0	2.294	f₈	LDimTLBO	0	0	459.346
f₃	SaDE	1.32×10⁻¹²⁴	2.27×10⁻¹²⁴	0.714	f₈	SaDE	0	0	50.145
f₄	TLBO	1.47×10⁻²³⁷	0	0.206	f₉	TLBO	0	0	0.460
f₄	RTLBO	4.70×10⁻¹¹⁶	8.48×10⁻¹¹⁶	0.477	f₉	RTLBO	0	0	0.690
f₄	DSTLBO	6.94×10⁻¹⁸⁶	0	0.257	f₉	DSTLBO	0	0	0.501
f₄	DRLTLBO	2.18×10⁻³¹⁷	0	0.455	f₉	DRLTLBO	0	0	0.935
f₄	LDimTLBO	0	0	3.073	f₉	LDimTLBO	0	0	2.987
f₄	SaDE	9.00×10⁻¹¹	4.33×10⁻¹¹	0.501	f₉	SaDE	0	0	0.547
f₅	TLBO	4.89×10	4.00×10⁻²	0.186	f₁₀	TLBO	1.40×10⁴	8.71×10²	0.517
f₅	RTLBO	4.79×10	3.30×10⁻²	0.949	f₁₀	RTLBO	9.09×10³	8.37×10²	0.719
f₅	DSTLBO	4.89×10	4.00×10⁻²	0.246	f₁₀	DSTLBO	1.37×10⁴	6.02×10²	0.515
f₅	DRLTLBO	4.83×10	3.22×10⁻¹	0.540	f₁₀	DRLTLBO	8.01×10³	2.26×10²	0.836
f₅	LDimTLBO	9.00×10⁻³	8.93×10⁻³	0.613	f₁₀	LDimTLBO	5.00×10⁻²	5.20×10⁻²	3.161
f₅	SaDE	3.89×10	1.02	0.842	f₁₀	SaDE	9.76	8.07	0.768

表 5 LDimTLBO、TLBO、RTLBO、DSTLBO、DRLTLBO、SaDE算法的收敛结果对比 Table 5 Comparison of convergence results of LDimTLBO，TLBO，RTLBO，DSTLBO，DRLTLBO and SaDE

图 4 LDimTLBO、TLBO、RTLBO、DSTLBO、DRLTLBO、SaDE算法的收敛曲线 Fig. 4 Convergence curves of LDimTLBO, TLBO, RTLBO, DSTLBO, DRLTLBO and SaDE

从收敛精度、收敛速度、运行时间3个方面分析各算法的收敛性能.

1）收敛精度. 由表5可知，LDimTLBO对单峰函数f₁~f₄都能求得函数的理论最优值，并且标准差为0，具有较好的鲁棒性；其他5种算法都没有求得函数的最优值，说明LDimTLBO的收敛精度和稳定性更好. 单峰函数f₅的全局最优解极难搜索，TLBO、RTLBO、DSTLBO、DRLTLBO和SaDE都陷入了局部最优，求解精度不高，LDimTLBO虽然没有求得到函数的理论最优值，但是求解精度明显高于其他5种算法，这主要得益于基于个体局部最优和搜索边界的自学习策略的扰动作用. LDimTLBO对多峰函数f₇~f₉都求得了函数的理论最优值. 对于存在大量局部极值点的多峰函数f₆和f₁₀，LDimTLBO的求解质量和稳定性明显优于其他5种算法，其他5种算法对f₁₀函数都过早陷入了局部最优. 观察各算法最终求得的解，发现TLBO、RTLBO、DSTLBO、DRLTLBO这4种算法的解普遍存在维度变量值严重偏离最优解相应维度的值的情况，SaDE求得的维度值偏差较小，LDimTLBO求得的维度值偏差最小，求解精度至少提高了10²~10⁵倍，说明LDimTLBO明显优于其他5种算法. 局部维度改进策略使得高质量的维度值在进化的过程中得以保留，质量较差的维度值不断得到改进，自学习策略的扰动作用使得LDimTLBO在进化的后期也能朝最优解的方向变化.

2）收敛速度. 由图4可知，与其他5种算法相比，LDimTLBO的收敛速度有较大幅度的提升，FEs<10 000这一段的收敛曲线的斜率更大. 对于函数f₁~f₄，LDimTLBO在EFs>35 000时已经收敛到函数的理论最优值；对于函数f₅、f₁₀，LDimTLBO在EFs=20 000时求得了优于其他算法的精度较高的值，并且在EFs>20 000的进化后期还能进一步找到更好的解；对于函数f₆，LDimTLBO在EFs=10 000求得的函数精度已经高于其他算法，不过在进化的后期出现了停滞的情况；对于函数f₇~f₉，LDimTLBO在EFs $\leqslant $ 2 000时就求得了函数的理论最优值，收敛速度明显快于其他算法. 由此可见，在局部维度改进策略和自学习策略的综合作用下，LDimTLBO很好地兼顾了收敛精度和收敛速度.

3）运行时间. 根据“无免费午餐”理论^[24]，1个算法不可能在所有指标或每个求解问题上都优于其他算法，同样LDimTLBO也存在这种情况. 虽然LDimTLBO在收敛精度和速度上都表现出较大的优势，但是平均运行时间明显多于其他算法. 因为在LDimTLBO的教与学2个阶段都融入了局部维度改进策略，在每个个体中查找函数值最大的子向量，需要较多的计算时间. 在一次迭代中，LDimTLBO的时间复杂度为 ${\text{O}}\,(2{{N_{\rm p}}}$ $(D - L + 1))$ ，查找某个个体的函数值最大的子向量的时间复杂度为 ${\rm O}\,(D - L + 1)$ ，在一次迭代过程中，教与学2个阶段都使用了局部维度改进策略，对于规模为N_p的整个种群来说，总的查找子向量的时间复杂度为 ${\rm O}(2{{N_{\rm p}}}(D - L + 1))$ .

但是，LDimTLBO具有较好的收敛精度和速度，并不需要在EFs达到最大值时才停止搜索. 由图4可知，当EFs达到maxEFs的一半时，LDimTLBO已经收敛稳定，在保证收敛精度的前提下，可以通过减少算法的迭代次数缩短运行时间. 除了使用最大函数评价次数或迭代次数作为算法的终止条件外，当最优个体（即求得的函数精度）连续多代都没有改进时，也可终止算法运行.

4 结　语

提出了局部维度改进的教与学优化算法（LDimTLBO）. 局部维度改进是比当前已有局部搜索方法更加细粒度的一种局部搜索策略，不断在后代中扩散高质量的局部维度信息，不断改善低质量的局部维度信息. 将局部维度改进策略融入原有的教与学阶段，平衡了算法早期的全局搜索能力和后期的局部探测能力. 提出了基于个体最优位置和搜索边界信息的自学习扰动策略，作为自学习阶段加入LDimTLBO中. 自学习策略对复杂的单、双峰函数的测试结果表明，自学习策略能够有效增加种群的多样性，算法在搜索的后期仍有机会找到更好的解. 自学习策略也适用于TLBO和变体算法，多种策略的综合作用使得LDimTLBO无论在收敛精度还是速度上都明显优于其他的优秀的改进TLBO算法. 下一步的工作将研究LDimTLBO在实际的工程优化问题，特别是组合优化问题上的有效性.

参考文献

[1]	RAO R V, VSAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: a novel method for constrained mechanical design optimization problem[J]. Computer-Aided Design, 2011, 43(3): 303-315. DOI:10.1016/j.cad.2010.12.015
[2]	RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization: an optimization method for continuous non-linear large scale problems[J]. Information Sciences, 2012, 183(1): 1-15. DOI:10.1016/j.ins.2011.08.006
[3]	RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization algorithm for unconstrained and constrained real-parameter optimization problems[J]. Engineering Optimization, 2011, 44(12): 1447-1462.
[4]	RAO R V, KALYANKAR V D. Parameter optimization of modern machining processes using teaching-learning-based optimization algorithm[J]. Engineering Applications of Artificial Intelligence, 2013, 26(1): 524-531. DOI:10.1016/j.engappai.2012.06.007
[5]	DEGERTEKIN S O, HAYALIOGLU M S. Sizing truss structures using teaching-learning-based optimization[J]. Computers and Structures, 2013, 119: 177-188. DOI:10.1016/j.compstruc.2012.12.011
[6]	NIKNAM T, GOLESTANEH F, SADEGHI M S. θ-multi-objective teaching-learning-based optimization for dynamic economic emission dispatch[J]. IEEE Systems Journal, 2012, 6(2): 341-352. DOI:10.1109/JSYST.2012.2183276
[7]	PATEL V K, SAVSANI V J. A multi-objective improved teaching-learning based optimization algorithm (MO-ITLBO)[J]. Information Sciences, 2016, 357: 182-200. DOI:10.1016/j.ins.2014.05.049
[8]	RAO RV, PATEL V. An elitist teaching-learning-based optimization algorithm for solving complex constrained optimization problems[J]. International Journal of Industrial Engineering Computations, 2012, 3(4): 535-560. DOI:10.5267/j.ijiec
[9]	SATAPATHY S C, NAIK A, PARVATHI K. Weighted teaching-learning-based optimization for global function optimization[J]. Applied Mathematics, 2013, 4(3): 429-439. DOI:10.4236/am.2013.43064
[10]	CHEN D B, ZOU F, WANG J, et al. A teaching-learning-based optimization algorithm with producer-scrounger model for global optimization[J]. Soft Computing, 2015, 19(3): 745-762. DOI:10.1007/s00500-014-1298-5
[11]	ZHANG H, LI B, ZHANG J, et al. Parameter estimation of nonlinear chaotic system by improved TLBO strategy[J]. Soft Computing, 2016, 20(12): 4965-4980. DOI:10.1007/s00500-015-1786-2
[12]	毕晓君, 王佳荟. 基于混合学习策略的教与学优化算法[J]. 浙江大学学报: 工学版, 2017, 51(5): 1024-1031. BI Xiao-jun, WANG Jia-hui. Teaching-learning-based optimization algorithm with hybrid learning strategy[J]. Journal of Zhejiang University: Engineering Science, 2017, 51(5): 1024-1031.
[13]	ZOU F, CHEN D, LU R, et al. Teaching-learning-based optimization with differential and repulsion learning for global optimization and nonlinear modeling[J]. Soft Computing, 2018, 22(21): 7177-7205. DOI:10.1007/s00500-017-2722-4
[14]	童楠, 符强, 钟才明. 一种基于反思机制的教与学优化算法[J]. 计算机应用研究, 2018(12): 1-6. TONG Nan, FU Qiang, ZHONG Cai-ming. Improved TLBO algorithm based on reflection mechanism[J]. Application Research of Computers, 2018(12): 1-6.
[15]	于坤杰, 王昕, 王振雷. 基于反馈的精英教学优化算法[J]. 自动化学报, 2014, 40(9): 1976-1983. YU Kun-jie, WANG Xin, WANG Zhen-lei. Elitist teaching-learning-based optimization algorithm based on feedback[J]. Acta Automatica Sinica, 2014, 40(9): 1976-1983.
[16]	YU K J, WANG X, WANG Z L. An improved teaching-learning-based optimization algorithm for numerical and engineering optimization problems[J]. Journal of Intelligent Manufacturing, 2016, 27(4): 831-843. DOI:10.1007/s10845-014-0918-3
[17]	YU K J, WANG X, WANG Z L. Constrained optimization based on improved teaching-learning-based optimization algorithm[J]. Information Sciences, 2016, 352: 61-78.
[18]	CHEN D B, ZOU F, LI Z, et al. An improved teaching-learning-based optimization algorithm for solving global optimization problem[J]. Information Sciences, 2015, 297: 171-190. DOI:10.1016/j.ins.2014.11.001
[19]	ZOU F, WANG L, HEI X H, et al. Teaching-learning-based optimization with dynamic group strategy for global optimization[J]. Information Sciences, 2014, 273: 112-131. DOI:10.1016/j.ins.2014.03.038
[20]	ZOU F, CHEN D, WANG J T. An improved teaching-learning-based optimization with the social character of PSO for global optimization[J]. Computational Intelligence and Neuroscience, 2016, 2016(2): 1-10.
[21]	WANG L, ZOU F, HEI X H, et al. A hybridization of teaching-learning-based optimization and differential evolution for chaotic time series prediction[J]. Neural Computing and Applications, 2014, 25(6): 1407-1422. DOI:10.1007/s00521-014-1627-8
[22]	QIN A K, HUANG V L, SUGANTHAN P N. Differential evolution algorithm with strategy adaptation for global numerical optimization[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(2): 398-417. DOI:10.1109/TEVC.2008.927706
[23]	赵乃刚. 求解无约束优化问题的改进教与学优化算法[J]. 小型微型计算机系统, 2017, 38(9): 2107-2112. ZHAO Nai-gang. Improved teaching-learning-based optimization algorithm for unconstrained optimization problems[J]. Journal of Chinese Computer Systems, 2017, 38(9): 2107-2112. DOI:10.3969/j.issn.1000-1220.2017.09.035
[24]	WOLPERT D H, MACREADY W G. No free lunch theorems for optimization[J]. IEEE Transactions on Evolutionary Computation, 1997, 1(1): 67-82. DOI:10.1109/4235.585893