由于加工、装配、工作环境等因素,机械臂的实际结构参数与理论值存在一定偏差,使得机械臂运动学模型并不准确,从而影响机械臂定位精度. 机械臂标定就是应用先进的测量手段和基于模型的参数识别方法辨识出机械臂模型的准确参数,从而提高机械臂绝对定位精度[1],标定的结果是一组被识别的机械臂参数. Judd等[2]的标定实验研究表明,运动学参数误差对机械臂定位精度的影响占所有因素的90%左右. 目前,国内外常用的运动学标定方法主要分为2种:运动学回路法和轴线测量法[3]. 运动学回路法根据是否利用外界测量设备又可分为开环法和闭环法2类[4]. Stone等[5-6]利用轴线测量法建立各关节轴线的空间方程,轴线的相对位置即真实的运动学参数;Newman等[7-9]分别利用激光跟踪仪、OPTOTRAK- CERTUSTM和Vxtrack测量得到机械臂实际末端位姿数据,都属于开环法. 上述方法都需要借助于外界先进的测量设备,成本高,且测量过程复杂,需要专业人员进行较长时间操作,因此比较适用于实验室环境下的标定而不适用于现场标定[10]. 为了降低成本,许多学者提出闭环标定法(也称自标定),通过施加物理约束如点、线、面等,限制机器人末端执行器的运行空间,从各个关节编码器获得关节角度并通过正运动学得到末端位姿. 点约束对操作者要求较高,需低速点动操作机器人,以保证末端测头与孔或球契合[11-12],或者需要借助激光装置,从而增加标定成本与复杂度[13]. 相比之下平面约束操作简单且成本低[14-16]. Ikits等[17]指出,在基于平面约束的机械臂标定中,根据机械臂末端各工具中心点(tool center point, TCP)位置数据拟合出的平面与实际约束平面往往存在一定偏差(点、线约束也存在此偏差),该偏差会直接影响标定精度. 虽然可以通过修正误差模型减小该偏差,但建立的误差模型复杂,且不能从根本上消除该偏差[16, 18].
针对上述情况,研究发现出现偏差的根本原因在于理论平面(即拟合平面)是利用机械臂在各位形下的TCP空间位置数据拟合得到的. 拟合必然存在偏差,如果存在某种方法,能够避免拟合过程而得到约束平面准确的空间方程,即可避免平面出现偏移现象. 因此提出一种方法,在实际约束平面上建立平面坐标系(planar coordinate system, PCS),即可得到约束平面在PCS中的准确方程,将TCP在基坐标系(base coordinate system, BCS)中的理论位置转换到PCS,并通过接触式测量头对约束平面进行接触式测量,得到TCP在PCS中的实际位置. 该方法由于PCS、机械臂末端工具坐标系(tool coordinate system, TCS)的存在,引入了冗余参数,因此将建立最小完整连续运动学模型,以减小冗余参数的影响. 为了实现自动化测量,提高标定效率,利用双目视觉定位约束平面并规划理论测量点位置,并利用改进的最小二乘法对参数误差进行辨识.
1 机械臂运动学误差模型 1.1 平面约束误差模型基于平面约束的机械臂闭环标定,其原理是通过在机械臂工作空间内施加一个或多个物理约束平面,限制机械臂末端接触式测量头的运行空间,从各个关节编码器获得关节角度并通过正运动学得到机械臂在各个位形下TCP在BCS中的位置数据,这一系列名义TCP位置坐标在理想情况下都应满足平面方程:
| $ax_{\rm N}^i + by_{\rm N}^i + cz_{\rm N}^i = [a,b,c]{{p}}_{\rm N}^i = 1.$ | (1) |
式中:
由于各连杆参数均存在误差,各名义TCP不在式(1)的平面上,与平面存在一定偏差:
| $S = \sum\limits_{i = 1}^n {{{([a,b,c]{{p}}_{\rm N}^i - 1)}^2}\;} .$ | (2) |
| $[a,b,c]{ p}_{\rm N}^i{\rm{ = }}F(a,b,c,{{\phi}} ).$ | (3) |
式中:
| $S = \sum\limits_{i = 1}^n {{{[F(a,b,c,{{\phi}} ) - 1]}^2}\;} .$ | (4) |
当
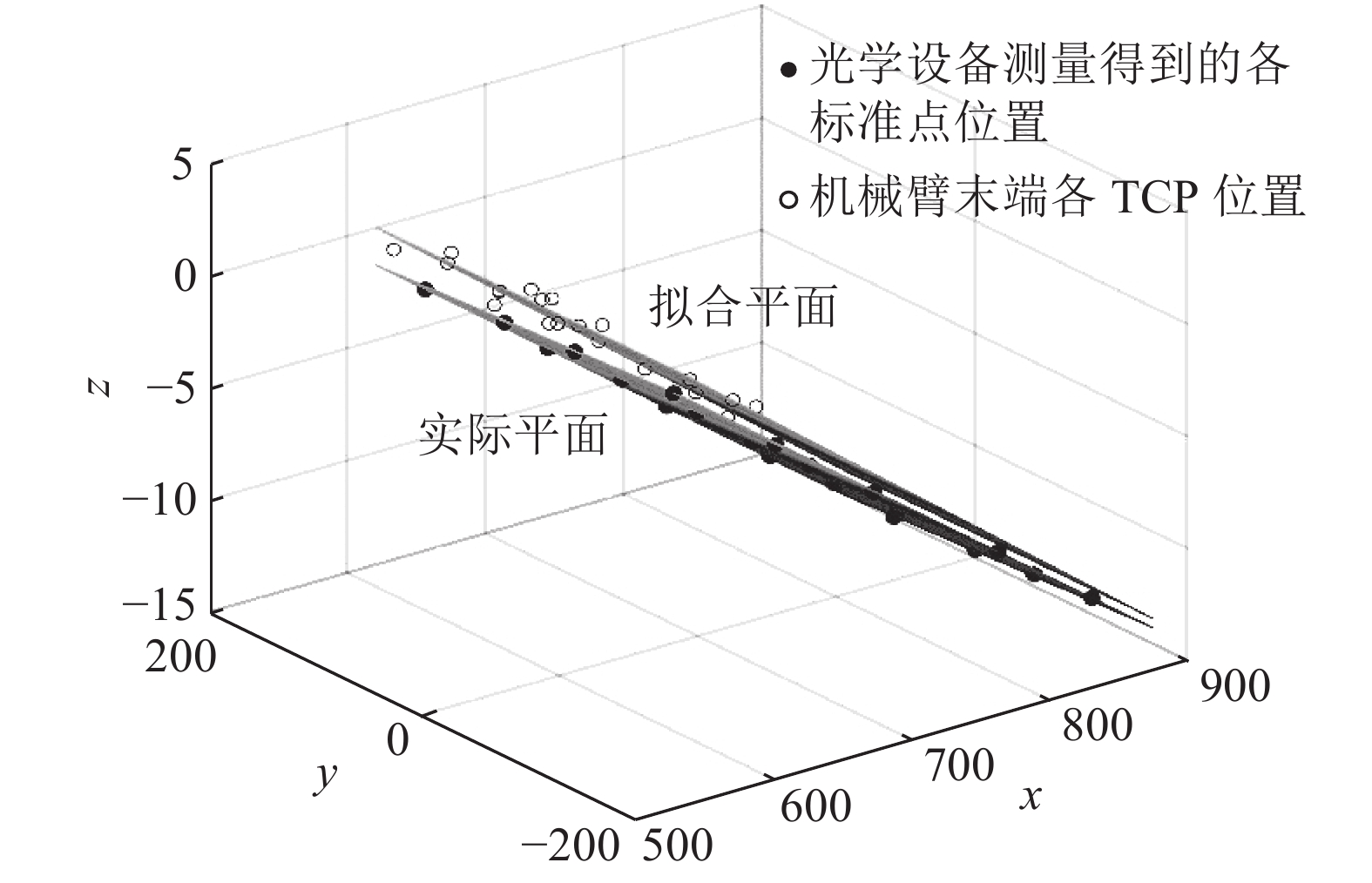
|
图 1 拟合平面与实际平面偏差图 Fig. 1 Error between fitting plane and real plane |
如果存在某种方法,能够避免拟合过程而得到约束平面准确的空间方程,这将避免偏移现象. 如图2所示,在实际平面上建立PCS,
| ${P_z} = 0,$ | (5) |
则
| ${P_z} - {P_{{\rm N}z}} = - {P_{{\rm N}z}} = \Delta {P_z} = {{{J}}_z}\Delta {{X}}.$ | (6) |
式中:
建立合适、完整、准确的机械臂运动学模型是标定过程中首要的一步,根据该模型可以得知机械臂末端位姿与各运动学参数之间的函数关系,而要建立机械臂运动学模型,首先要确定各连杆坐标系. 目前,常用的连杆坐标系建立方法有2种[19]:Paul法(标准D-H)和Craig法(改进D-H),都是在Denavit和Hartenberg提出的连杆参数(运动学参数)基础上提出或改进的,前者将坐标系建立在连杆的末端,后者建立在连杆首端,本研究使用Craig方法建立连杆坐标系. 研究对象是一般串联工业机械臂,根据Craig法建立的D-H坐标系如图3所示,其中4、5两连杆坐标系原点重合.
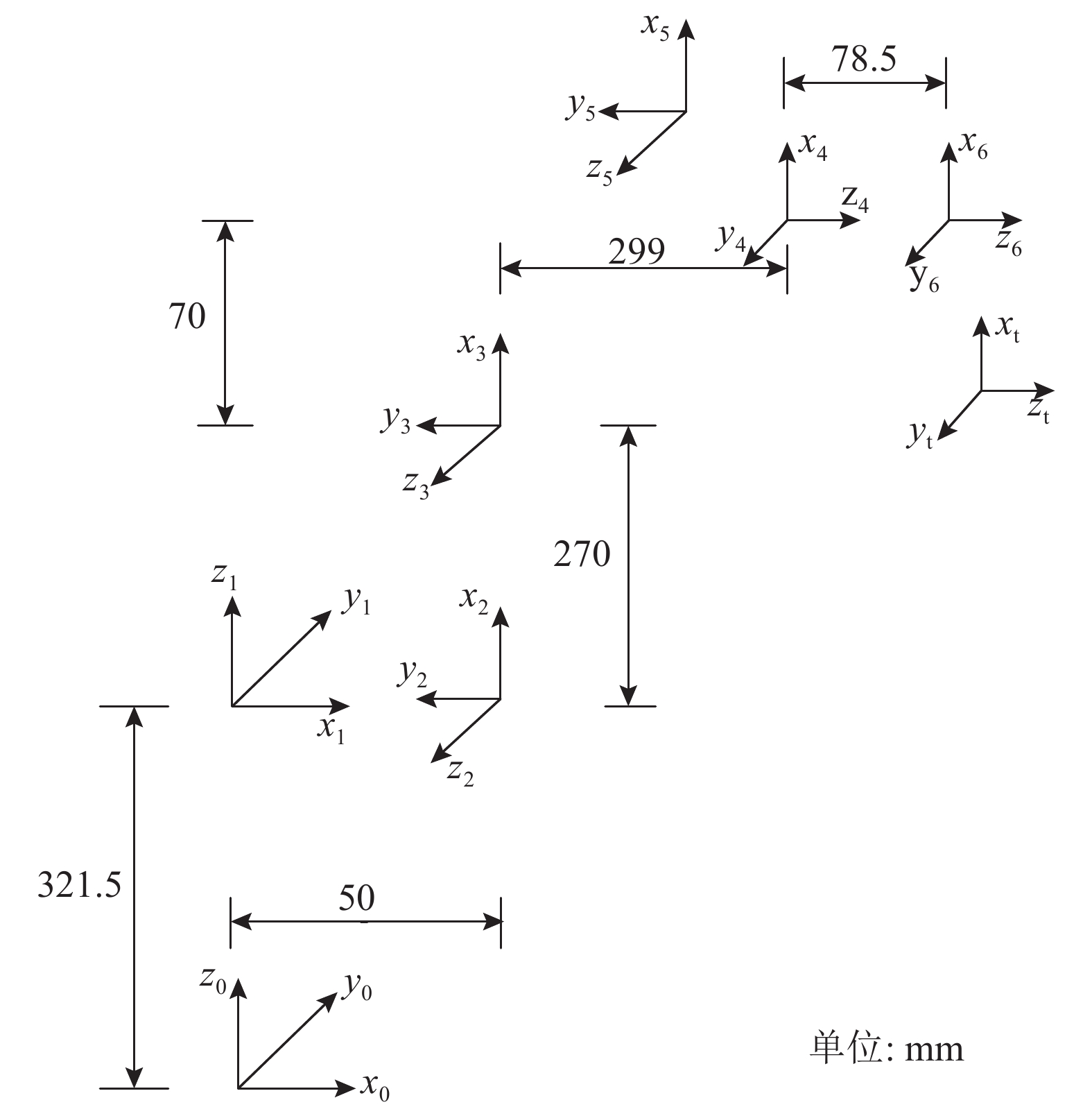
|
图 3 机械臂连杆坐标系 Fig. 3 Link coordinate frames of robot |
相邻两连杆坐标系
| $\begin{split}{{{A}}_i} = {{{R}}_{{x_{i - 1}}}}({\alpha _{i - 1}}){{{T}}_{{x_{i - 1}}}}({a_{i - 1}}){{{T}}_{{z_{i - 1}}}}({d_i}){{{R}}_{{z_{i - 1}}}}({\theta _i})=\quad\quad\quad\quad\quad\quad\\\left[\!\! {\begin{array}{*{20}{c}} {{\rm cos}\;{\theta _i}} &\!\! { - {\rm sin}\;{\theta _i}} &\!\! 0 &\!\! {{a_{i - 1}}}\\ {{\rm sin}\;{\theta _i}\;{\rm cos}\;{\alpha _{i - 1}}} &\!\!\!\! {{\rm cos}\;{\theta _i}\;{\rm cos}\;\,{\alpha _{i - 1}}} &\!\!\!\! { - {\rm sin}\;{\alpha _{i - 1}}} &\!\!\!\! { - {d_i}\;{\rm sin}\;{\alpha _{i - 1}}}\\{{\rm sin}\;{\theta _i}\;{\rm sin}\;{\alpha _{i - 1}}} &\!\!\!\! {{\rm cos}\;{\theta _i}\;{\rm sin}\;{\alpha _{i - 1}}} &\!\!\!\! {{\rm cos}\;{\alpha _{i - 1}}} &\!\!\!\! {{d_i}\;{\rm cos}\;{\alpha _{i - 1}}}\\0 &\!\!\!\! 0 &\!\! 0 &\!\! 1 \end{array}} \!\!\right]. \;\;\;\;\end{split}$ | (6) |
式中:
对于机械臂标定研究,各连杆之间不能视作完全平行或垂直,因此相关理论参数值存在微小偏差;在考虑相邻关节轴线近似平行(2、3关节)时,微小的不平行度会引起参数突变,式(7)所表示的4参数模型不再适用,需要增加绕
| ${{{A}}_i} = {{{R}}_{{x_{i - 1}}}}({\alpha _{i - 1}}){{{T}}_{{x_{i - 1}}}}({a_{i - 1}}){{{R}}_{{y_{i - 1}}}}({\beta _i}){{{T}}_{{z_{i - 1}}}}({d_i}){{{R}}_{{z_{i - 1}}}}({\theta _i}).$ | (8) |
式中:
由于PCS与机械臂BCS之间不遵循上述D-H参数建立规则,两坐标系之间的齐次矩阵可表示为
| $\begin{split}{}^{\rm{p}}{{ A}_0} = {{ T}_{{x_{\rm{p}}}}}({d_{{x_{\rm{p}}}}}){{ T}_{{y_{\rm{p}}}}}({d_{{y_{\rm{p}}}}}){{ T}_{{z_{\rm{p}}}}}({d_{{z_{\rm{p}}}}}) {{ R}_{{x_{\rm{p}}}}}({\delta _{{x_{\rm{p}}}}}){{ R}_{{y_{\rm{p}}}}}({\delta _{{y_{\rm{p}}}}}){{ R}_{{z_{\rm{p}}}}}({\delta _{{z_{\rm{p}}}}}).\end{split}$ | (9) |
同样地,第6连杆坐标系与TCS之间的坐标变换矩阵表示如下:
| $\begin{split}{}^6{{ A}_{\rm t}} = {{ T}_{{x_6}}}({d_{{x_6}}}){{ T}_{{y_6}}}({d_{{y_6}}}){{ T}_{{z_6}}}({d_{{z_6}}}) {{ R}_{{x_6}}}({\delta _{{x_6}}}){{ R}_{{y_6}}}({\delta _{{y_6}}}){{ R}_{{z_6}}}({\delta _{{z_6}}}).\end{split}$ | (10) |
式中:
Schröer等[20]指出,机械臂的D-H参数完整表达姿态最小个数为
首先讨论从PCS到第1连杆坐标系的冗余参数,由式(8)、(9)结合图2、3分析可知,从PCS到BCS中,沿
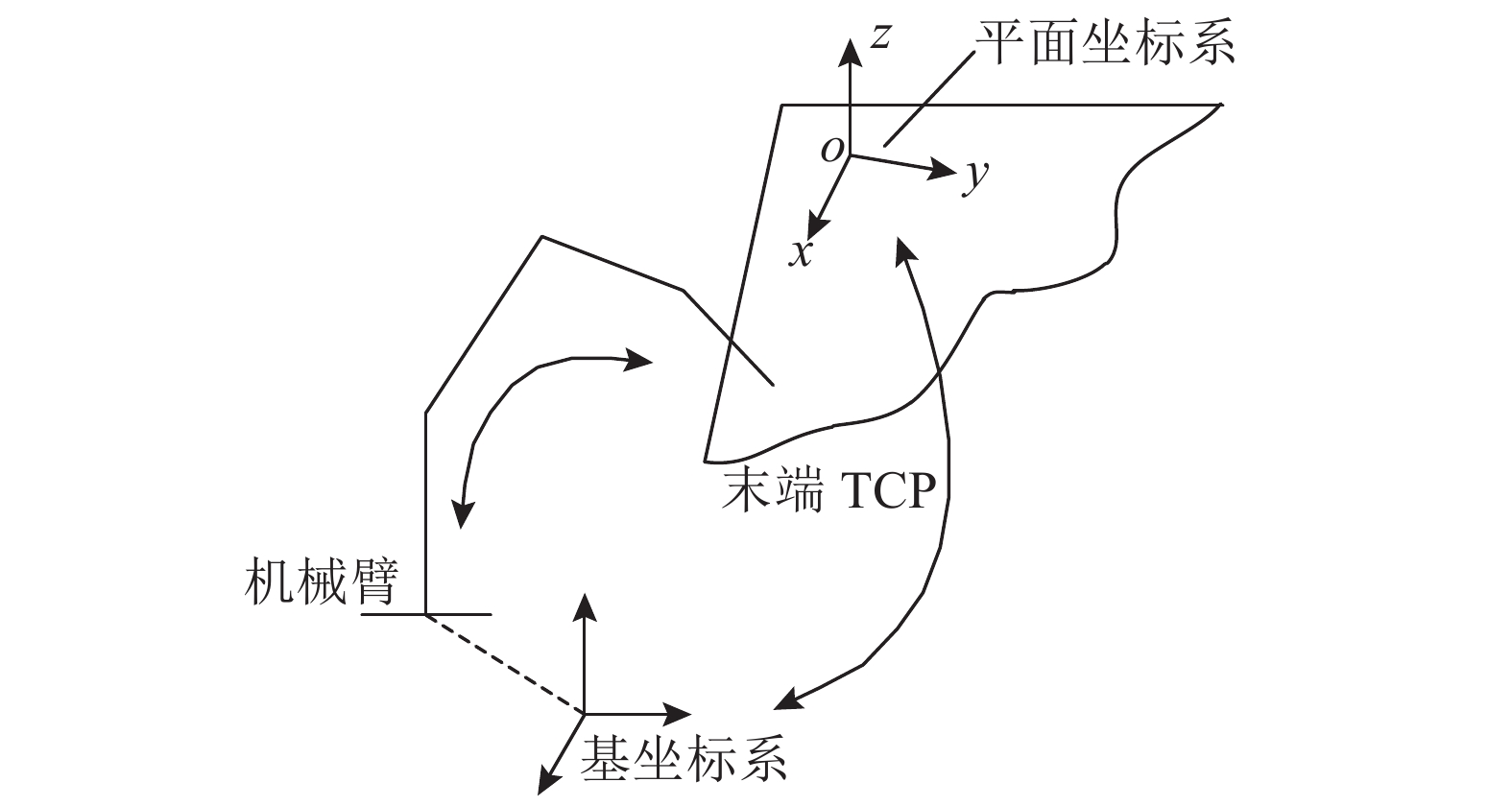
|
图 2 消除平面偏移原理图 Fig. 2 Principle of eliminating plane wandering |
| ${}^{\rm{p}}{{ A}_0} = {{ T}_{{x_{\rm{p}}}}}({d_{{x_{\rm{p}}}}}){{ T}_{{y_{\rm{p}}}}}({d_{{y_{\rm{p}}}}}){{ R}_{{x_{\rm{p}}}}}({\delta _{{x_{\rm{p}}}}}){{ R}_{{y_{\rm{p}}}}}({\delta _{{y_{\rm{p}}}}})\;.$ | (11) |
其次讨论从第5连杆坐标系到TCS的冗余参数,由于工具是固定安装在末端法兰上的,不存在自由度,通常认为TCS的姿态与第6连杆坐标系保持一致. 从第6连杆坐标系到TCS中,沿
| ${}^6{{ A}_{\rm{t}}} = {{ T}_{{x_6}}}({d_{{x_6}}}){{ T}_{{y_6}}}({d_{{y_6}}})\;.$ | (12) |
综上所述,从PCS到TCS共有30(
| $\begin{array}{l}\!\!\!\!\!\!\!\!\!{{ T}_{\rm{t}}} ={}^{\rm{p}}{{ A}_0}{{ A}_1} \cdots {{ A}_n}{}= \\\;\;{ f}_0^{\rm{p}}({b_1}, \cdots ,{b_4}){ f}_6^0({b_5}, \cdots ,{b_{28}}){ f}_{\rm{7}}^6({b_{29}},{b_{30}});\;n=7.\end{array}$ | (13) |
式中:
| $\left. \begin{split}d_1'&= {d_1} + {d_{{z_{\rm{p}}}}},\\{\theta _1'}&= {\theta _1} + {\delta _{{z_{\rm{p}}}}},\\d_6'&= {d_6} + {d_{{z_6}}}.\;\end{split} \right\}$ | (14) |
由于运动学参数名义值存在误差,相邻两连杆间的实际坐标变换矩阵
| ${\rm d}{{{A}}_i} = {{A}}_i^{\rm R} - {{{A}}_i} = {{{A}}_i}{{{\varDelta}} _i}\;.$ | (15) |
式中:
对
| $\begin{split}{\rm d}{{{A}}_i} =& \displaystyle\frac{{\partial {{{A}}_i}}}{{\partial {\alpha _{i{\rm{ - }}1}}}}\Delta {\alpha _{i{\rm{ - }}1}} + \displaystyle\frac{{\partial {{{A}}_i}}}{{\partial {a_{i{\rm{ - }}1}}}}\Delta {a_{i{\rm{ - }}1}} + \displaystyle\frac{{\partial {{{A}}_i}}}{{\partial {\theta _i}}}\Delta {\theta _i} + \\&\displaystyle\frac{{\partial {{{A}}_i}}}{{\partial {d_i}}}\Delta {d_i} + \displaystyle\frac{{\partial {{{A}}_i}}}{{\partial {\beta _i}}}\Delta {\beta _i};\quad i = 1, \cdots ,6\;.\end{split}$ | (16) |
可以得到
| ${{ e}_i} = {[{d_{{x_i}}},{d_{{y_i}}},{d_{{z_i}}},{\delta _{{x_i}}},{\delta _{{y_i}}},{\delta _{{z_i}}}]^{\rm{T}}}.$ | (17) |
式中:前3个元素为位置误差,后3个元素为姿态误差. 将ei表示成运动学参数误差的形式:
| ${{{e}}_i} = {{{G}}_i}\Delta {{{X}}_i}\;.$ | (18) |
式中:
| ${{e}}_i^{\rm t} = {{J}}_i^{\rm t}{{{e}}_i};\;\;i = 0,\; \cdots,\; 7.$ | (19) |
式中:
机械臂末端位姿误差
| ${{{e}}_{\rm T}} = \sum\limits_{i = 0}^{\rm 7} {{{J}}_i^{\rm t}{{{G}}_i}} \Delta {{{X}}_i}.$ | (20) |
表示成矩阵形式为
| ${{{e}}_{\rm T}} = [{{J}}_0^{\rm t}{{{G}}_0} ,\cdots ,{{J}}_{\rm 7}^{\rm t}{{{G}}_{\rm 7}}]\left[ {\begin{array}{*{20}{c}}{{b_1}}\\ \vdots \\{{b_{30}}}\end{array}} \right] = {{{J}}^{\rm t}}\Delta {{X}}\;.$ | (21) |
式中:
可对式(6)作相关说明,取
| $\Delta{{{P}}_z}={{ J}_z}\Delta {{X}},$ | (22) |
则
| $ - {{ P}_{{\rm N}z}} = {{{J}}_z}\Delta {{X}}\;.$ | (23) |
测量获得
| ${{H}}\Delta {{X}} = {{S}}\;.$ | (24) |
式中:
一般的平面约束标定方法,数据测量通过手动示教完成,本研究采用双目视觉系统定位约束平面基准,实现自动化测量. 由于双目视觉公共视场范围狭小,在约束平面上粘贴3个靶点,如图4所示,由此对约束平面的定位即可等效成对靶点的定位.
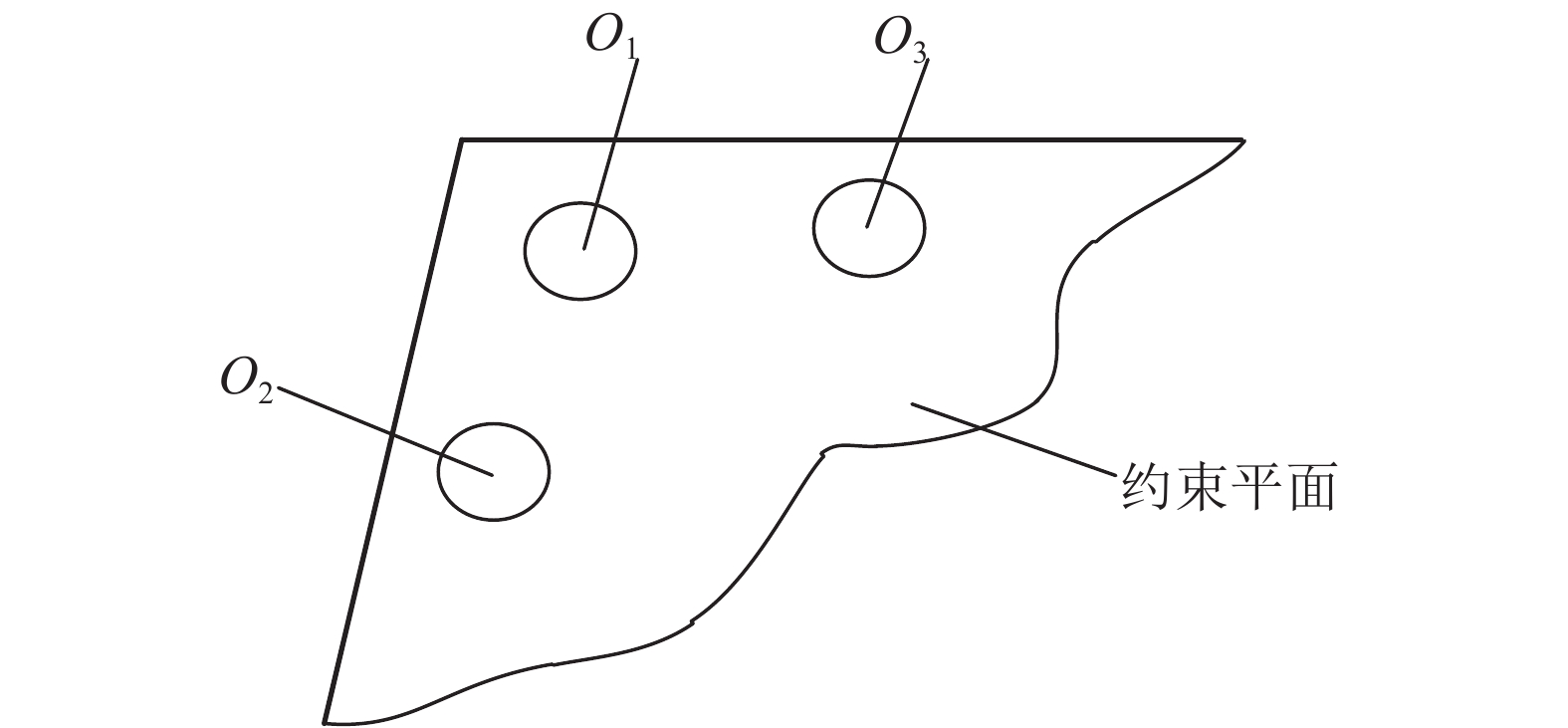
|
图 4 靶点粘贴示意图 Fig. 4 Sketch of attaching target spots |
利用张正友标定法对左右2个相机分别进行内参标定,得到4参数内参矩阵:
| ${{{M}}_j} = \left[ {\begin{array}{*{20}{c}} {{f_{xj}}}&0&{{u_{j0}}}&0 \\ 0&{{f_{yj}}}&{{v_{j0}}}&0 \\ 0&0&1&0 \end{array}} \right].$ | (25) |
式中:
对左右2个相机分别进行手眼标定,即确定摄像机坐标系相对于第6连杆坐标系的变换矩阵,利用传统手眼标定方法
| $\left. {\begin{array}{*{20}{l}}{{ L} = \left[ {\begin{array}{*{20}{c}}{{l_{11}}}&\;{{l_{12}}}&\;{{l_{13}}}&\;{{l_{14}}}\\{{l_{21}}}&\;{{l_{22}}}&\;{{l_{23}}}&\;{{l_{24}}}\\{{l_{31}}}&\;{{l_{32}}}&\;{{l_{33}}}&\;{{l_{34}}}\end{array}} \right],}\\{{ R} = \left[ {\begin{array}{*{20}{c}}{{r_{11}}}&{{r_{12}}}&{{r_{13}}}&{{r_{14}}}\\{{r_{21}}}&{{r_{22}}}&{{r_{23}}}&{{r_{24}}}\\{{r_{31}}}&{{r_{32}}}&{{r_{33}}}&{{r_{34}}}\end{array}} \right].}\end{array}} \right\}$ | (26) |
设目标点在第6连杆坐标系(世界坐标系)中的三维位置坐标为
| $Z_{{i}}^{ {\rm l}}\left[ {\begin{array}{*{20}{c}} u_{{i}}^{\rm l} \\ v_{{i}}^{\rm l} \\ 1\end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{l_{11}}}&{{l_{12}}}&{{l_{13}}}&{{l_{14}}} \\ {{l_{21}}}&{{l_{22}}}&{{l_{23}}}&{{l_{24}}} \\ {{l_{31}}}&{{l_{32}}}&{{l_{33}}}&{{l_{34}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_i}} \\ {{y_i}} \\ {{z_i}} \\ 1\end{array}} \right],$ | (27) |
| $Z_{{i}}^{\rm r}\left[ {\begin{array}{*{20}{c}} u_{{i}}^{\rm r} \\ v_{{i}}^{\rm r} \\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}&{{r_{14}}} \\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}&{{r_{24}}} \\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}}&{{r_{34}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_i}} \\ {{y_i}} \\ {{z_i}} \\ 1 \end{array}} \right].$ | (28) |
式中:
| $\left. \begin{array}{l}\!\!\!\!(u_i^{\rm{l}}{l_{31}} - {l_{11}}){x_i} + (u_i^{\rm{l}}{l_{32}} - {l_{12}}){y_i} + (u_i^{\rm{l}}{l_{33}} - {l_{13}}){z_i} = {l_{14}} - u_i^{\rm{l}}{l_{34}},\\\!\!\!\!(v_i^{\rm{l}}{l_{31}} - {l_{21}}){x_i} + (v_i^{\rm{l}}{l_{32}} - {l_{22}}){y_i} + (v_i^{\rm{l}}{l_{33}} - {l_{23}}){z_i} = {l_{24}} - v_i^{\rm{l}}{l_{34}},\\\!\!\!\!(u_i^{\rm{r}}{r_{31}} \!-\! {r_{11}}){x_i} \!+\! (u_i^{\rm{r}}{r_{32}} \!-\! {r_{12}}){y_i} \!+\! (u_i^{\rm{r}}{r_{33}} \!-\! {r_{13}}){z_i} \!=\! {r_{14}} \!-\! u_i^{\rm{r}}{r_{34}},\\\!\!\!\!(v_i^{\rm{r}}{r_{31}} \!-\! {r_{21}}){x_i} \!+\! (v_i^{\rm{r}}{r_{32}} \!-\! {r_{12}}){y_i} \!+\! (v_i^{\rm{r}}{r_{33}} - {r_{23}}){z_i} \!=\! {r_{24}} - v_i^{\rm{r}}{r_{34}}.\end{array}\!\!\!\! \right\}$ | (29) |
式中:
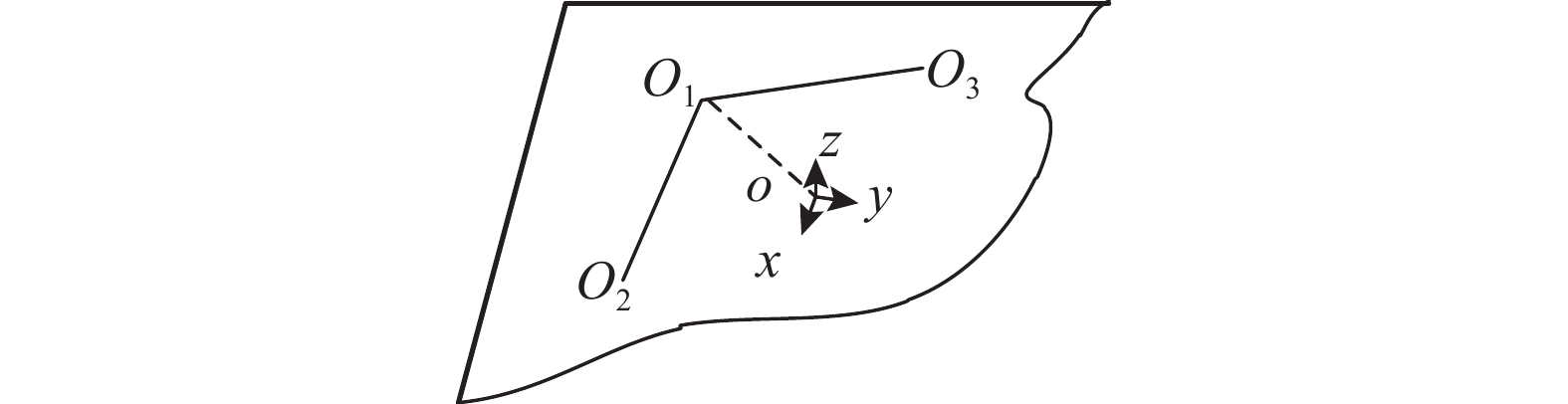
PCS原点取在
| ${{x}} = \frac{{({x_2} - {x_1},{y_2} - {y_1},{z_2} - {z_1})}}{{\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} }}.$ | (30) |
同理,取
|
图 5 平面坐标系示意图 Fig. 5 Sketch of planar coordinate system |
平面上的所有点在BCS下的三维位置都可以通过BCS的原点以及
| ${{P}} = { o}({x_1},{y_1},{z_1}) + a{{x}} + b{{y}}.$ | (31) |
式中:
然而,由于双目视觉定位、机械臂等都存在一定量的误差,在实际测量过程中,测量头不能到达由式(31)所规划的理论坐标值,甚至会出现测量头已经接触实际约束平面,而控制器仍然控制其运动到理论约束点的情况. 因此,考虑实际因素,对式(31)进行如下修正:
| ${{P}} = { o}({x_1},{y_1},{z_1}) + a{{x}} + b{{y}} + c{{z}}\;.$ | (32) |
式中:
实验对象为埃夫特ER3C-C60本体,采用课题组自主研发的6R型串联工业机械臂控制系统;双目摄像机选用德国IMAGING工业相机;接触式测量头选用英国RENISHAW公司生产的MCP型测量头,在测量的5个方向上精度均达到 0.75 μm;大理石各表面(除底面外)的平面度均为3.5 μm,满足标定所需要的约束要求. 整个标定实验系统如图6所示.

|
图 6 标定系统实验现场 Fig. 6 Experiment site of calibration system |
通过Matlab相机标定工具箱,分别得到左右相机的4个内参数;通过

|
图 7 各靶点圆心坐标 Fig. 7 Circle center of each target spot |
依次取
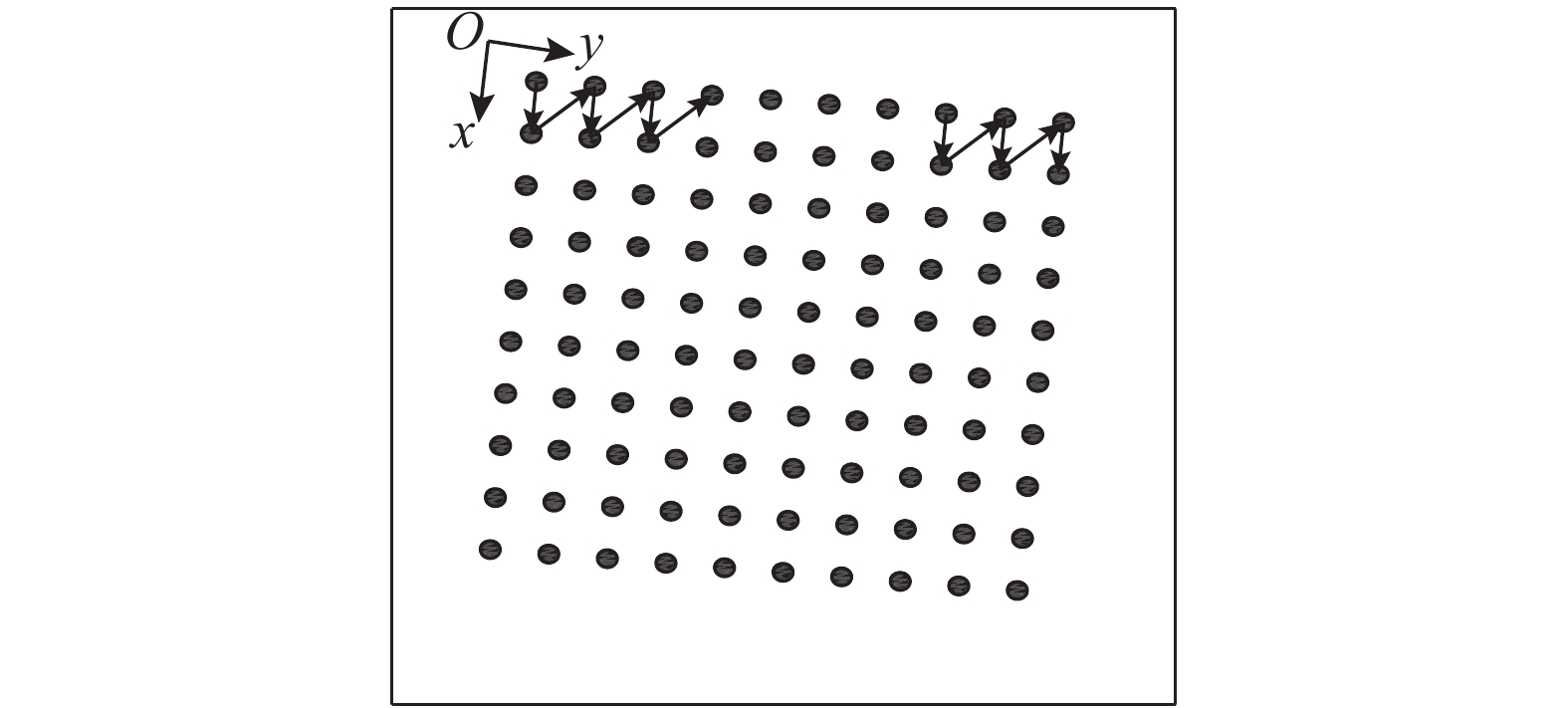
|
图 8 按矩形阵列分布的约束点 Fig. 8 Rectangular array distribution of constraint points |
| $\Delta { X} = {({{ H}^{\rm T}}{ H} + \mu { I})^{ - 1}}{{ H}^{\rm T}}{ S}.$ | (33) |
式中:
最终参数误差辨识结果如表1所示. 另外,由于构建了PCS及TCS而引入的其他运动学参数如下,
| 表 1 参数误差辨识结果 Table 1 Results of parameter error identification |
控制器使机械臂任意运动到50个位形,通过加拿大Creaform公司精度可达22 μm的光学测量设备Vxtrack380,测量得到每个位形的实际位置数据,同时记录下对应的关节角度值;通过理论运动学参数及修正后的运动学参数,分别计算得到机械臂末端对应的名义位置值及修正位置值;以测量得到的实际位置数据为基准,计算修正运动学参数前、采用基于一般平面约束误差模型修正后(修正1)、采用本研究提出的误差模型修正后(修正2)的机械臂在

|
图 9 修正前后各位置误差比较 Fig. 9 Comparison of position crrors before and after modification |
| 表 2 一般标定方法修正前后位置值(在BCS中) Table 2 Positions before and after modification using common calibration method (in BCS) |
| 表 3 所提标定方法修正前后位置值(在PCS中) Table 3 Positions before and after modification using proposed calibration method (in PCS) |
对于位置误差,计算公式如下:
| $\Delta p = \sqrt {{{(x - {x_{\rm r}})}^2} + {{(y - {y_{\rm r}})}^2} + {{(z - {z_{\rm r}})}^2}} .$ | (34) |
如图9所示,修正运动学参数后,机械臂在
(1)与一般平面约束标定方法不同,需要构建PCS,引入了PCS与BCS之间的参数误差,不过系统对该参数误差也进行了辨识,尽可能减小此误差对标定精度的影响,而由图9可知,平面偏移误差比坐标系间的转换误差对标定精度的影响更大. 通过双目视觉构建了PCS,但完全可以通过其他方式建立,比如控制机械臂末端运动至平面上不共线的3个点,获取各个点在BCS中的位置,从而建立PCS. 应用双目视觉是为了辅助定位约束平面,实现自动化测量数据,这为机械臂生产厂家对机械臂实现批量标定提供了思路. 使用视觉的另一个好处是可以规划测量点的位置,使其按一定规律有序分布(如图8所示),这为研究机械臂标定位形对参数辨识的影响奠定了基础.
(2)构建PCS时只对其
(3)目前很多标定方法虽然提高了机械臂绝对定位精度,但是大多需要使用先进的测量设备,操作复杂,比较适用于在实验室环境下由专业人员进行标定,并不适用于工业现场标定. 但在工业现场使用中,机械臂在受到碰撞或者使用一段时间后疲劳磨损,往往需要重新标定. 本研究提出的标定方法,成本低,只需要一个精度相对较高的平面即可完成,只要在机械臂工作空间内,可任意摆放平面位置,如果有双目视觉辅助定位,可以实现自动化标定并补偿,减轻了机械臂后期的维护工作.
5 结 语基于平面约束,提出一种工业机械臂的闭环标定方法及其误差模型,消除了一般平面约束标定方法拟合平面与实际约束平面之间的偏差;为了避免冗余参数对参数辨识造成影响,建立了最小连续完整运动学模型;为了提高标定效率,应用双目视觉辅助定位约束平面,实现自动化测量数据;最终通过改进的最小二乘法辨识出了真实的运动学参数误差. 实验结果表明,修正运动学参数后,机械臂的绝对定位精度由1.234 mm提高到0.405 mm.
| [1] |
张永贵, 黄玉美, 高峰. 基于遗传算法的机器人运动学参数误差识别[J]. 农业机械学报, 2008, 39(9): 153-157. ZHANG Yong-gui, HUANG Yu-mei, GAO Feng. Robotics kinematics parameters error identification based on geneticalgorithm[J]. Transactions of the Chinese Society of Agricultural Machinery, 2008, 39(9): 153-157. |
| [2] |
JUDD R P, KNASINSKI A B. A technique to calibrate industrial robots with experimental verification[J]. IEEE Transactions on Robotics and Automation, 1990, 6(1): 20-30. DOI:10.1109/70.88114 |
| [3] |
解则晓, 辛少辉, 李绪勇, 等. 基于单目视觉的机器人标定方法[J]. 机械工程学报, 2011, 47(5): 35-39. XIE Ze-xiao, XING Shao-hui, LI Xu-yong, et al. Method of robot calibration based on monocular vision[J]. Journal of Mechanical Engineering, 2011, 47(5): 35-39. |
| [4] |
HOLLERBACH J M, WAMPLER C W. The calibration index and taxonomy for robot kinematic calibration methods[J]. The International Journal of Robotics Research, 1996, 15(6): 573-591. DOI:10.1177/027836499601500604 |
| [5] |
STONE H, SANDERSON A. A prototype arm signature identification system [C] // Proceedings of the IEEE International Conference on Robotics and Automation. Raleigh, IEEE, 1987: 175–182. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1087835
|
| [6] |
叶声华, 王一, 任永杰, 等. 基于激光跟踪仪的机器人运动学 参数标定方法[J]. 天津大学学报, 2007, 40(2): 202-205. YE Sheng-hua, WANG Yi, REN Yong-jie, et al. A robot kinematic calibration method based on laser tracker[J]. Journal of Tianjin University, 2007, 40(2): 202-205. DOI:10.3969/j.issn.0493-2137.2007.02.014 |
| [7] |
NEWMAN W S, BIRKHIMER C E, HORNING R J, et al. Calibration of a Motoman P8 robot based on laser tracking [C] // Proceedings of the IEEE International Conference on Robotics and Automation. San Francisco: IEEE, 2000, 4: 3597–3602. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=845292
|
| [8] |
王琨, 骆敏舟, 曹毅, 等. 基于遗传算法的串联机械臂运动学 参数标定[J]. 系统科学与数学, 2015(1): 19-30. WANG Kun, LUO Min-zhou, CAO Yi, et al. Kinematic parameter calibration of a serial manipulator based on genetic algorithm[J]. Journal of Systems Science and Mathematical Sciences, 2015(1): 19-30. |
| [9] |
刘洁, 平雪良, 齐飞, 等. 基于视觉跟踪的机器人测量方法与实现[J]. 应用光学, 2016, 37(5): 686-692. LIU Jie, PING Xue-liang, QI Fei, et al. A robot measurement method based on vision tracking[J]. Journal of Applied Optics, 2016, 37(5): 686-692. |
| [10] |
任永杰, 邾继贵, 杨学友, 等. 利用激光跟踪仪对机器人进行标定的方法[J]. 机械工程学报, 2007, 43(9): 195-200. REN Yong-jie, ZHU Ji-gui, YANG Xue-you, et al. Method of robot calibration based on laser tracker[J]. Journal of Mechanical Engineering, 2007, 43(9): 195-200. DOI:10.3321/j.issn:0577-6686.2007.09.038 |
| [11] |
刘振宇, 陈英林, 曲道奎, 等. 机器人标定技术研究[J]. 机器人, 2002, 24(5): 447-450. LIU Zhen-yu, CHEN Ying-lin, QU Dao-kui, et al. Research on robot calibration[J]. Robot, 2002, 24(5): 447-450. DOI:10.3321/j.issn:1002-0446.2002.05.014 |
| [12] |
南小海. 6R型工业机器人标定算法与实验研究[D]. 武汉: 华中科技大学, 2008: 33-37. NAN Xiao-hai. Research on 6R industrial robot calibration algorithm and experimental verification [D]. Wuhan: Huazhong University of Science and Technology, 2008: 33-37. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D063691 |
| [13] |
时定兵. 基于点约束的机器人运动学参数标定技术研究[D]. 南京: 南京理工大学, 2014: 12-18. SHI Ding-bing. Research on robot kinematic parameters calibration based on point constraints [D]. Nanjing: Nanjing University of Science and Technology, 2014: 12-18. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2521941 |
| [14] |
ZHONG X L, LEWIS J M. A new method for autonomous robot calibration [C] // Proceedings of the IEEE International Conference on Robotics and Automation, 1995. Nagoya: IEEE, 1995: 1790–1795.
|
| [15] |
JOUBAIR A, BONEV I A. Non-kinematic calibration of a six-axis serial robot using planar constraints[J]. Precision Engineering, 2015, 40: 325–333. https://www.researchgate.net/publication/269103378_Non-kinematic_calibration_of_a_six-axis_serial_robot_using_planar_constraints
|
| [16] |
齐飞. 基于平面约束的工业机器人误差补偿技术研究[D]. 无锡: 江南大学, 2016: 37-53. QI Fei. Research on error compensation technology of industrial robot based on planar constraints [D]. Wuxi: Jiangnan University, 2016: 37-53. http://d.wanfangdata.com.cn/Thesis/D589238 |
| [17] |
IKITS M, HOLLERBACH J M. Kinematic calibration using a plane constraint [C] // Proceedings of the IEEE International Conference on Robotics and Automation. Albuquerque: IEEE, 1997, 4: 3191–3196.
|
| [18] |
董慧颖, 李文广. 一种基于平面精度的机器人标定方法及仿真[J]. 中国机械工程, 2011, 22(17): 2039-2042. DONG Hui-ying, LI Wen-guang. Robot calibration simulation based on planar precision[J]. China Mechanical Engineering, 2011, 22(17): 2039-2042. |
| [19] |
谭民, 徐德, 侯增广, 等. 先进机器人控制[M]. 北京: 高等教育出版社, 2007: 39-46. http://www.bookask.com/book/1595702.html
|
| [20] |
SCHRÖER K, ALBRIGHT S L, Grethlein M. Complete, minimal and model-continuous kinematic models for robot calibration[J]. Robotics and Computer-Integrated Manufacturing, 1997, 13(1): 73–85. https://www.researchgate.net/publication/222169921_Complete_minimal_and_model-continuous_kinematic_models_for_robot_calibration
|
| [21] |
卢钰庭. 基于视觉的机器人标定的研究 [D]. 广州: 华南理工大学, 2013. LU Yu-ying. Research on robot calibration based on vision [D]. Guangzhou: South China University of Technology, 2013. |



