旋转向量(rotate vector, RV)减速器作为工业机器人传动系统的最重要的机械部件,主要安装在机座、大臂、肩部等重载位置的驱动减速装置中,其工作性能直接影响机器人后续性能发挥. 建立合理精确的RV减速器动力学模型,研究传动中重要非线性因素的影响,提出合理有效的控制方案,能够有效减少RV减速器运行过程中的振动和冲击,保证传动的平稳性和精确性. Hidaka等[1-2]用弹簧代替K-H-V型摆线针轮减速器中各要素之间的游隙,建立质量弹簧的等价模型,奠定RV减速器动力学分析的基础. 何卫东等[3-5]建立RV减速器的等效扭转刚度模型,以RV-40E为例进行计算,建立基于Admas的有限元刚柔耦合模型. 张大卫等[6]建立了扭转刚度模型,分析了各参数对扭转刚度的影响,搭建了RV-6AⅡ减速器运动特性实验台. 杨玉虎等[7-8]建立了RV减速器的几何和有限元模型,研究了曲柄轴中转角和整机扭转刚度之间的变化规律,发现轴承刚度是影响整机扭转刚度的重要因素,搭建RV减速器扭转刚度实验台,分析RV减速器的振动模态. Han等[9]对RV减速器进行灵敏度分析. Sun等[10]搭建RV减速器故障树模型. 吕明帅[11]搭建RV减速器扭转刚度测试台和传动精度实验台. 上述文献表明,RV减速器理论研究主要针对简化的扭转刚度模型,对动力学的分析较少,基本没有研究对RV减速器系统的非线性动力学特性进行分析. 实验研究主要针对RV减速器的扭转刚度,对传动精度以及其他动力性能参数的研究较少,并且实验台功能单一,缺少能够同时测量多项指标的综合实验平台.
采用相对位移思想,根据力平衡和力矩平衡的达朗贝尔原理[12]建立5自由度的纯扭转动力学模型,对模型进行坐标变换消除系统的刚性位移;对系统进行无量纲化处理[13],使用数值法求解动力学方程,得到系统在启动过程中和稳定运行状态中的动态响应曲线. 搭建RV减速器动力性能综合检测实验平台,通过更换机械接口实时测量多个动力参数,并且将实验结果与理论结果进行对比分析.
1 RV减速器纯扭转动力学模型建立 1.1 模型假设条件影响RV减速器系统运行的因素众多,需要简化系统,提出理想假设,排除可能存在的次要影响因素,分析主要动力特性. 采用集中质量法建立齿轮-转子系统的多自由度扭转振动模型[14],考虑输入轴的扭转刚度,并且由于模型中曲柄轴的扭转刚度和弯曲刚度较大,不考虑曲柄轴的扭转和弯曲变形. 在建模过程中,同时假设以下条件. 1)研究重点是RV减速器系统内部非线性特性,不考虑输入速度波动和负载转矩波动等外界非线性特性. 2)为了保证模型中齿轮啮合的稳定性,假设在传动过程中,两构件的作用线固定不变,即齿轮啮合作用力一直在两者的啮合线上. 在动力学模型中考虑齿轮啮合处的摩擦力能够让模型更加接近实际情况,但是在运动过程中,摩擦力的方向大小会随着啮合状态变化,模型较为复杂. 在纯扭转模型中忽略齿轮啮合处摩擦力的作用,只考虑理想状态下的齿轮啮合,各部件在径向平面内转动,不承受轴向荷载. 3)建模过程中,不考虑齿轮在齿宽方向上的加工误差以及曲柄轴的弯曲造成的倾角等,即不考虑在系统轴向上的受力和变形,只考虑各要素在垂直平面内的运动.
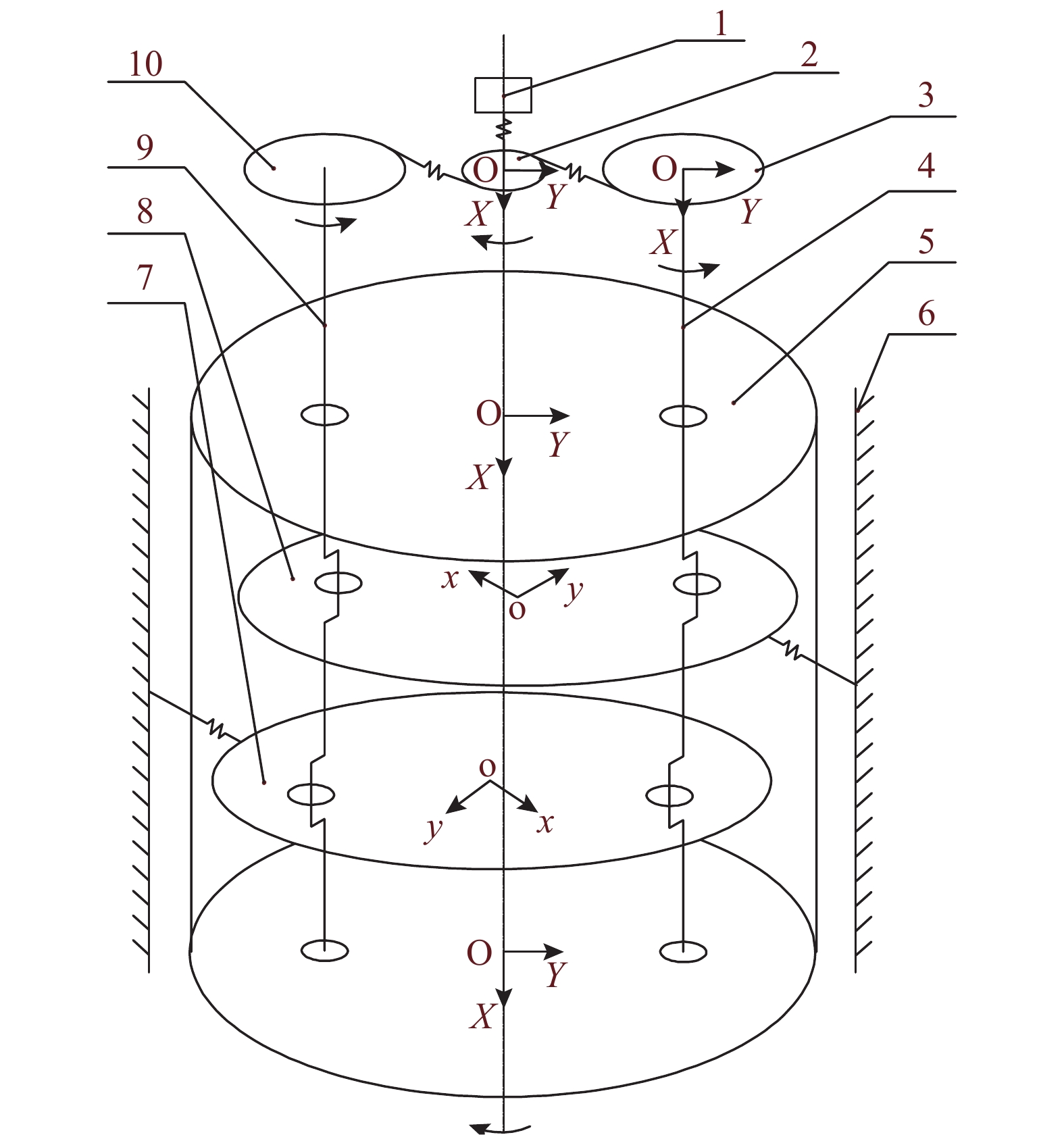
1.2 纯扭转振动模型建立 1.2.1 RV减速器动力学模型图以固定针轮中心为原点,在轴线的垂面上建立静坐标系OXY,方向如图1所示. 以摆线轮中心为原点,建立动坐标系oxy,偏心距的方向为y方向,沿摆线轮公转方向转动90°为x方向,动坐标系的y方向在初始位置时和固定坐标系的Y方向相同. 动坐标系不仅绕动坐标系原点随着曲柄轴的转动而转动,同时随着曲柄轴绕固定坐标系原点转动.
|
1 输入轴;2 太阳轮;3 行星轮;4 曲柄轴;5 行星架;6 针轮;7 摆线轮;8 摆线轮;9 曲柄轴;10行星轮 图 1 两曲柄轴旋转向量减速器模型简图 Fig. 1 Diagram of RV reducer model with two crankshafts |
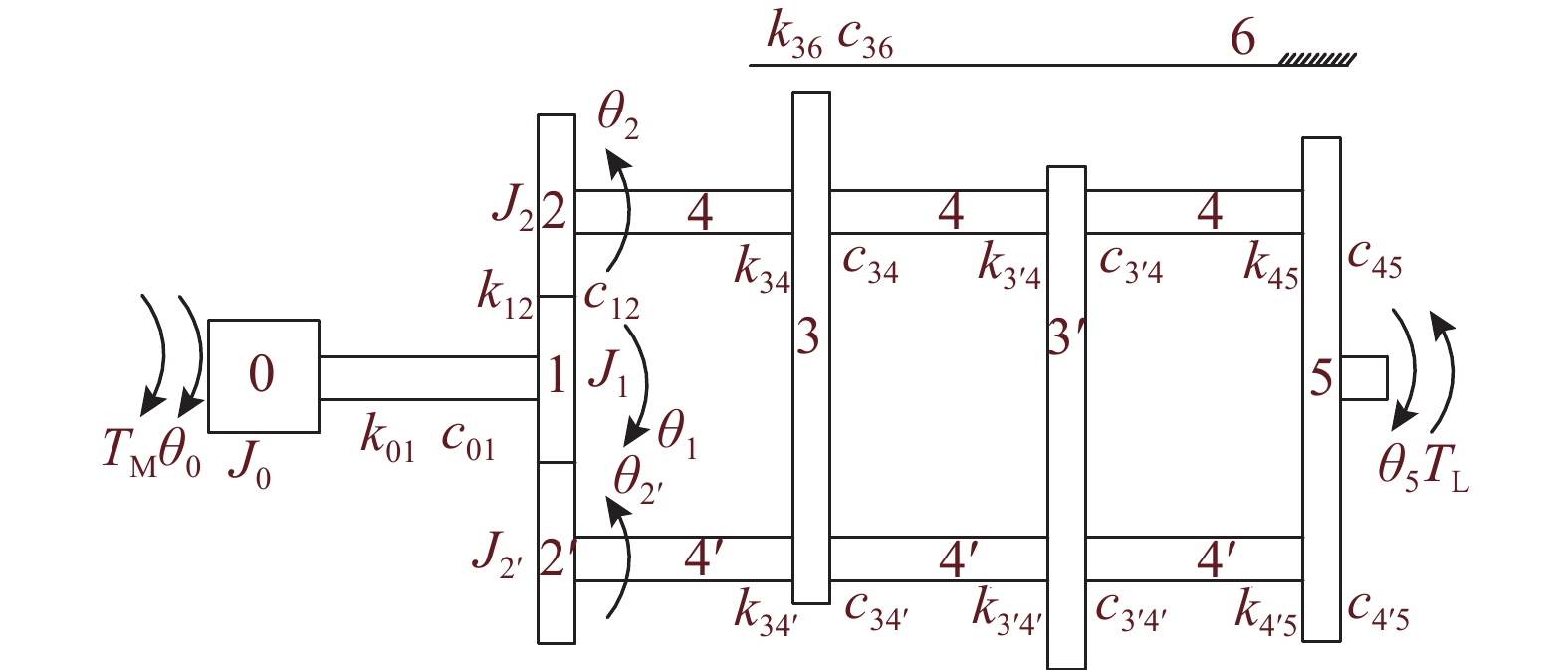
采用动态子结构法[15]将RV系统分为5个子结构:原动机、太阳轮、行星轮与曲柄轴、摆线轮与针轮、行星架. 两曲柄轴的RV减速器总共有7个部件和7个转动自由度,即原动机的1个转动自由度,太阳轮的1个转动自由度,2个行星轮的2个转动自由度,2个摆线轮的2个转动自由度,行星架的1个转动自由度. RV减速器传动如图2所示.
|
图 2 两曲柄轴RV减速器动力学模型 Fig. 2 RV reducer dynamic model with two crankshafts |
根据扭矩平衡条件,可知
| ${J_0}{\ddot \theta _0} = {T_{\rm M}} - {k_{01}}\left( {{\theta _0} - {\theta _1}} \right) - {c_{01}}\left( {{{\dot \theta }_0} - {{\dot \theta }_1}} \right).$ | (1) |
式中:
太阳轮和行星轮之间的啮合相对位移为
| ${x_{12}}_i = {r_1}{\theta _1} - {r_2}{\theta _{2i}}.$ | (2) |
式中:
假设啮合重合对小于2,啮合齿对在啮合线上的综合变形为
| ${\delta _{12i}} = {x_{12i}} - {\zeta _{12i}}.$ | (3) |
式中:
齿轮动态法向啮合力为
| ${F_{12i}} = {k_{12}}{\delta _{12i}} + {c_{12}}{\dot \delta _{12i}}.$ | (4) |
式中:
根据扭矩平衡条件,可知
| ${J_1}{\ddot \theta _1} = {k_{01}}\left( {{\theta _0} - {\theta _1}} \right) + {c_{01}}\left( {{{\dot \theta }_0} - {{\dot \theta }_1}} \right) - \mathop \sum \limits_{i = 0}^1 {r_1}{F_{12i}}.$ | (5) |
式中:
考虑曲柄轴扭转刚度和弯曲刚度时,行星轮和曲柄轴通过花键固结在一起,具有相同的转角和位移,将两者作为整体进行分析.
曲柄轴自转角度误差在Y、X方向上产生的等价位移分别为
| ${\sigma _{2i3jY}} = {e_{\rm c}}\left( {{\theta _{2i}} - {\theta _{\rm c}}} \right){\rm{sin }}\;({\theta _{\rm c}} + {\text{π}}j),$ | (6) |
| ${\sigma _{2i3jX}} = {e_{\rm c}}\left( {{\theta _{2i}} - {\theta _{\rm c}}} \right){\rm{cos }}\;({\theta _{\rm c}} + {\text{π}}j). $ | (7) |
式中:θc为曲柄轴的理论自转角度,
摆线轮公转误差和自转角度误差的总和在Y、X方向上产生的等价位移分别为
| $\begin{split}&{\tau _{3j4iY}} = {e_{\rm c}}\left( {{\theta _{3{\rm c}j}} - {\theta _{\rm c}}} \right){\rm{sin}}\;({\theta _{\rm c}} + {\text{π}}j) + \\ &\quad\quad\quad\;{a_0}\left( {{\theta _{3j}} - {\theta _{\rm g}}} \right){\rm{sin}}\;({\theta _{\rm g}} + {\text{π}}i),\end{split}$ | (8) |
| $\begin{split}&{\tau _{3j4iX}} = {e_{\rm c}}\left( {{\theta _{3{\rm{c}}j}} - {\theta _{\rm{c}}}} \right){\rm{cos }}\;({\theta _{\rm{c}}} + {\text{π}}j) - \\ &\quad\quad\quad\;{a_0}\left( {{\theta _{3j}} - {\theta _{\rm g}}} \right){\rm{cos}}\;({\theta _{\rm g}} + {\text{π}}i).\end{split}$ | (9) |
式中:
摆线轮和曲柄轴孔处Y、X方向上的综合变形分别为
| ${\delta _{3j4iY}} = {\sigma _{2i3jY}} - {\tau _{3j4iY}} - {\zeta _{3j4iY}},$ | (10) |
| ${\delta _{3j4iX}} = {\sigma _{2i3jX}} - {\tau _{3j4iX}} - {\zeta _{3j4iX}}.$ | (11) |
式中:
摆线轮和曲柄轴在转臂轴承处的作用力分别为
| ${F_{3j4iY}} = {k_{34}}{\delta _{3j4iY}} + {c_{34}}{\dot \delta _{3j4iY}},$ | (12) |
| ${F_{3j4iX}} = {k_{34}}{\delta _{3j4iX}} + {c_{34}}{\dot \delta _{3j4iX}}.$ | (13) |
式中:
根据扭矩平衡条件,可知
| $\begin{split}{J_2}{{\ddot \theta }_{2i}} = & {r_2} {F_{12i}} - ({F_{3j4iY(j = 0)}} - {F_{3j4iY(j = 1)}}){e_{\rm c}} {\rm{sin}}\;{\theta _{\rm c}} -\\ & ({F_{3j4iX(j = 0)}} - {F_{3j4iX(j = 1)}}) {e_{\rm c}} {\rm{cos}}\;{\theta _{\rm c}}.\end{split}$ | (14) |
式中:
摆线轮各齿与针轮啮合,需要计算各个啮合刚度和阻尼,得到总刚度、总阻尼. 采用简化算法把各齿啮合力合成为总的啮合力,计算总刚度和总阻尼,而不单独计算各齿的刚度和阻尼.
摆线轮和针轮啮合方向上的弹性变形所产生的等价位移为
| ${\tau _{3j6}} = - {r_{\rm c}}'\left( {{\theta _{3j}} - {\theta _{\rm g}}} \right){\rm{sin}}\;{\alpha _{\rm k}} + {e_{\rm c}}({\theta _{3{\rm c}j}} - {\theta _{\rm c}}){\rm{sin}}\;{\alpha _{\rm k}},$ | (15) |
| ${r_{\rm c}}' = {e_{\rm c}}{z_{\rm c}},$ | (16) |
| ${\alpha _{\rm k}} = {\text{π}}/2 - {\alpha _{\rm c}} + {\text{π}}j.$ | (17) |
式中:
摆线轮和针轮在啮合线方向上的综合变形为
| ${\delta _{3j6}} = {\tau _{3j6}} - {\zeta _{3j6}}.$ | (18) |
式中:
| ${F_{63j}} = {k_{36}}{\delta _{3j6}} + {c_{36}}{\dot \delta _{3j6}}.$ | (19) |
式中:
根据扭矩平衡条件,可知
| $\begin{split}{J_3}{{\ddot \theta }_{3j}} = & {F_{63j}}{r_{\rm c}}'{\rm{cos }}\;{\alpha _{\rm c}} - {F_{3j4iX(i = 0)}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + \\ &{F_{3j4iX(i = 1)}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + {F_{3j4iY(i = 0)}}{a_0}{\rm{sin }}\;{\theta _{\rm g}} - \\ &{F_{3j4iY(i = 1)}}{a_0}{\rm{sin }}\;{\theta _{\rm g}}.\end{split}$ | (20) |
式中:
行星架自转角度误差在Y、X方向上产生的等价位移分别为
| ${\tau _{54iY}} = {a_0}\left( {{\theta _5} - {\theta _{\rm g}}} \right){\rm{sin}}\;({\theta _{\rm g}} + {\text{π}}i),$ | (21) |
| ${\tau _{54iX}} = - {a_0}\left( {{\theta _5} - {\theta _{\rm g}}} \right){\rm{cos }}\;({\theta _{\rm g}} + {\text{π}}i).$ | (22) |
式中:
行星架和曲柄轴孔处Y、X方向上的综合变形分别为
| ${\delta _{54iY}} = - {\tau _{54iY}} - {\zeta _{4i5Y}},$ | (23) |
| ${\delta _{54iX}} = - {\tau _{54iX}} - {\zeta _{4i5X}}.$ | (24) |
式中:
行星架和曲柄轴在转臂轴承处的作用力分别为
| ${F_{54iY}} = {k_{54}}{\delta _{54iY}} + {c_{54}}{\dot \delta _{54iY}},$ | (25) |
| ${F_{54iX}} = {k_{54}}{\delta _{54iX}} + {c_{54}}{\dot \delta _{54iX}}.$ | (26) |
式中:
| $\begin{split}{J_5}{{\ddot \theta }_5} = & \mathop \sum \limits_{i = 0}^1 - {F_{54iX}}{\rm{cos}}\;({\theta _{\rm g}} + {\text{π}}i){a_0} + \\ &\mathop \sum \limits_{i = 0}^1 {F_{54iY}}{\rm{sin}}\;({\theta _{\rm g}} + {\text{π}}i){a_0} - {T_{\rm L}}.\end{split}$ | (27) |
式中:
由式(14)、(20)可知,同一名称的部件只建立了1个通用的方程,式(1)、(5)、(14)、(20)、(27)列出的分别是以
系统有5个回转自由度,θ0、θ1、θ2i、θ3j、θ5为原始广义坐标. 系统是半正定、变参数的非线性方程,存在刚性位移[16],总共有6个构件,取2个构件之间的相对位移为新的广义坐标.
| ${x_{01}} = {\theta _0} - {\theta _1},$ | (28) |
| ${x_{12i}} = {r_1}{\theta _1} - {r_2}{\theta _{2i}},$ | (29) |
| ${x_{2i3j}} = {\theta _{2i}} - {\theta _{3j}},$ | (30) |
| ${x_{3j6}} = {\theta _{3j}},$ | (31) |
| ${x_{2i5}} = {\theta _{2i}} - {\theta _5}.$ | (32) |
式中:
| $\begin{split}{J_0}{{\ddot x}_{01}} = & {T_{\rm M}} - {k_{01}}{x_{01}} - {c_{01}}{{\dot x}_{01}} - \\ &({J_0}/{J_1})[{k_{01}}{x_{01}} + {c_{01}}{{\dot x}_{01}} - {r_1}{f_{12}} - {r_1}{f_{12'}}],\end{split}$ | (33) |
| $\begin{split}({J_1}/{r_1}) {{\ddot x}_{12}} = &{k_{01}}{x_{01}} + {c_{01}}{{\dot x}_{01}} - {r_1}{f_{12}} - {r_1}{f_{12'}} - \\ & ({J_1}{r_2}/{J_2}{r_1})[{r_2}{f_{12}} - ({F_{34Y}} - {F_{3'4Y}}){e_{\rm c}}{\rm{sin}}\;{\theta _{\rm c}} - \\ & ({F_{34X}} - {F_{3'4X}}){e_{\rm c}}{\rm cos} \;{\theta _{\rm c}}],\end{split}$ | (34) |
| $\begin{split}({J_1}/{r_1}){{\ddot x}_{12'}} = & {k_{01}}{x_{01}} + {c_{01}}{{\dot x}_{01}} - {r_1}{f_{12}} - {r_1}{f_{12'}} - \\ & ({J_1}{r_2}/{J_2}{r_1})[{r_2}{f_{12'}} - ({F_{34'Y}} - {F_{3'4'Y}}){e_{\rm c}}{\rm{sin}}\;{\theta _{\rm c}} - \\ & ({F_{34'X}} - {F_{3'4'X}}){e_{\rm c}}\cos\; {\theta _{\rm c}}],\end{split}$ | (35) |
| $\begin{split}{J_2}{{\ddot x}_{23}} = & {r_2}{f_{12}} - \left( {{F_{34Y}} - {F_{3'4Y}}} \right){e_{\rm c}}{\rm{sin }}\;{\theta _{\rm c}} - \\ &\left( {{F_{34X}} - {F_{3'4X}}} \right){e_{\rm c}}{\rm{cos }}\;{\theta _{\rm c}} - ({J_2}/{J_3})[{F_{63}}{r_{\rm c}}'{\rm{cos }}\;{\alpha _{\rm c}} - \\ &{F_{34X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + {F_{34'X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + \\ &{F_{34Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}} - {F_{34'Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}}],\quad\quad\quad\quad\quad\quad\quad(36)\end{split}$ |
| $\begin{split}{J_2}{{\ddot x}_{23'}} =& {r_2}{f_{12}} - \left( {{F_{34Y}} - {F_{3'4Y}}} \right){e_{\rm c}}{\rm{sin }}\;{\theta _{\rm c}} - \\&\left( {{F_{34X}} - {F_{3'4X}}} \right){e_{\rm c}}{\rm{cos }}\;{\theta _{\rm c}} - ({J_2}/{J_3})[{F_{63{\rm{'}}}}{r_{\rm c}}'{\rm{cos }}\;{\alpha _{\rm c}} - \\&{F_{3'4X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + {F_{3'4'X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + \\&{F_{3'4Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}} - {F_{3'4'Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}}],\quad\quad\quad\quad\quad\quad(37)\end{split}$ | (37) |
| $\begin{split}{J_2}{{\ddot x}_{2'3}} = &{r_2}{f_{12'}} - \left( {{F_{34'Y}} - {F_{3'4'Y}}} \right){e_{\rm c}}{\rm{sin }}\;{\theta _{\rm c}} - \\&\left( {{F_{34'X}} - {F_{3'4'X}}} \right){e_{\rm c}}{\rm{cos }}\;{\theta _{\rm c}} - ({J_2}/{J_3})[{F_{63}}{r_{\rm c}}'{\rm{cos }}\;{\alpha _{\rm c}} - \\&{F_{34X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + {F_{34'X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + \\&{F_{34Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}} - {F_{34'Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}}],\quad\quad\quad\quad\quad\quad(38)\end{split}$ | (38) |
| $\begin{split}{J_2}{{\ddot x}_{2'3'}} = &{r_2}{f_{12'}} - \left( {{F_{34'Y}} - {F_{3'4'Y}}} \right){e_{\rm c}}{\rm{sin }}\;{\theta _{\rm c}} - \\&\left( {{F_{34'X}} - {F_{3'4'X}}} \right){e_{\rm c}}{\rm{cos }}\;{\theta _{\rm c}} - ({J_2}/{J_3})[{F_{63{\rm{'}}}}{r_{\rm c}}'{\rm{cos }}\;{\alpha _{\rm c}} - \\&{F_{3'4X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + {F_{3'4'X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + \\&{F_{3'4Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}} - {F_{3'4'Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}}],\quad\quad\quad\quad\quad(39)\end{split}$ | (39) |
| $\begin{split}{J_3}{{\ddot x}_{36}} =& {F_{63}}{r_{\rm c}}'{\rm{cos }}\;{\alpha _{\rm c}} - {F_{34X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} +{F_{34'X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + \\& {F_{34Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}} - {F_{34'Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}},\quad\quad\quad\quad\quad\quad\;(40)\end{split}$ | (40) |
| $\begin{split}{J_3}{{\ddot x}_{3'6}} =& {F_{63{\rm{'}}}}{r_{\rm c}}'{\rm{cos }}\;{\alpha _{\rm c}} - {F_{3'4X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} +{F_{3'4'X}}{a_0}{\rm{cos }}\;{\theta _{\rm g}} + \\ & {F_{3'4Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}} -{F_{3'4'Y}}{a_0}{\rm{sin }}\;{\theta _{\rm g}},\end{split}$ | (41) |
| $\begin{split}{J_5}{{\ddot x}_{25}} =& - \left( {{F_{54'X}} - {F_{54X}}} \right){a_0}{\rm{cos }}\;{\theta _{\rm g}} \!-\!\left( {{F_{54Y}} - {F_{54'Y}}} \right){a_0}{\rm{sin }}\;{\theta _{\rm g}} + \\& {T_{\rm L}} +({J_5}/{J_2})\Big[{r_2}{f_{12}} - ({F_{34Y}} - {F_{3'4Y}}){e_{\rm c}}{\rm{sin }}\;{\theta _{\rm c}} - \\& ({F_{34X}} - {F_{3'4X}}){e_{\rm c}}{\rm{cos }}\;{\theta _{\rm c}}\Big],\quad\quad\quad\quad\quad\quad\quad\quad\quad(42)\end{split}$ | (42) |
| $\begin{split}{J_5}{{\ddot x}_{2'5}} =& - \left( {{F_{54'X}} - {F_{54X}}} \right){a_0}{\rm{cos }}\;{\theta _{\rm g}} - \left( {{F_{54Y}} - {F_{54'Y}}} \right){a_0} \cdot \\& {\rm{sin }}\;{\theta _{\rm g}} +{T_{\rm L}} + ({J_5}/{J_2})\Big[{r_2}{f_{12'}} - ({F_{34'Y}} - {F_{3'4'Y}}){e_{\rm c}}\cdot \\& {\rm{sin }}\;{\theta _{\rm c}} -({F_{34'X}} - {F_{3'4'X}}){e_{\rm c}}{\rm{cos }}\;{\theta _{\rm c}}\Big].\quad\quad\quad\quad\quad\quad(43)\end{split}$ | (43) |
由于系统中刚度、阻尼和质量参数不处于同一量级上,需要对转换后的方程进行无量纲化处理,才能保证方程求解正确[17-18].
2.2 系统动力学参数 2.2.1 输入轴参数计算以输入轴为阶梯轴,两端面之间的扭转角为各端面扭转角之和:
| $\mathop \sum \nolimits \phi_u = \mathop \sum \limits_{u = 1}^3 \frac{{T{l_u}}}{{G{I_u}}} = \mathop \sum \limits_{u = 1}^3 \frac{{32T{l_u}}}{{G{\text{π}}{{\left( {2{r_u}} \right)}^4}}}\,. $ | (44) |
式中:
输入轴的扭转刚度为
| ${k_{01}} = \frac{T}{\mathop \sum \nolimits {\phi_u} . }$ | (45) |
输入轴的扭转阻尼系数[19]为
| ${c_{01}} = 2\xi \bigg[{{{{k_{01}}}}/\Big({{{\rm{1/}}{J_{\rm{0}}} + {\rm{1/}}{J_{\rm{1}}}}}}\Big)\bigg]^{1/2} .$ | (46) |
式中:
单齿刚度为
| $c' = 1/s.$ | (47) |
式中:
根据文献[20]可知,当
| $\begin{array}{l}s = 0.047 \; 23 + {{0.155 \; 51} / {{z_1}}} + {{0.257 \; 91} / {{z_2}}} - 0.006 \; 35{\gamma _1}\;\\\quad\;\; - 0.116 \; 54{{{\gamma _1}} / {{z_1}}} - 0.001 \; 93{\gamma _2} - 0.241 \; 88{{{\gamma _2}} / {{z_2}}} + \\\quad\;\; 0.005 \; 29\gamma _1^2 + 0.001 \; 82\gamma _2^2.\end{array}$ | (48) |
式中:
齿轮的啮合刚度为
| ${k_{\rm{r}}} = (0.75{\varepsilon _{\rm a}} + 0.25)c'. $ | (49) |
式中:
| ${\varepsilon _{\rm a}} = [{z_1}(\tan\; {\alpha _{{\alpha _1}}} - \tan\; \alpha ) + {z_2}(\tan\; {\alpha _{{\alpha _2}}} - \tan\; \alpha ){\rm J}/2{\text{π}}. $ | (50) |
式中:
齿轮的总啮合刚度为
| ${k_{12}} = {k_{\rm{r}}} b \times {10^6}. $ | (51) |
式中:
齿轮啮合阻尼为
| ${c_{12}} = 2{\xi _{{\rm{12}}}} \bigg[{{k_{12}}{{r_1^2r_2^2{J_1}{J_2}}}/\Big( {{r_1^2{J_1} + r_2^2{J_2}}}}\Big)\bigg] ^{1/2}. $ | (52) |
式中:
摆线轮各齿和滚针之间的啮合刚度表达式为
| ${k_\nu } = \frac{{{\text{π}}bE{\rho _{\nu {\rm r}}}{\rho _{\rm c}}}}{{4(1 - {\mu ^2})({\rho _{\nu {\rm r}}} + {\rho _{\rm c}}){\rho _\nu }}}. $ | (53) |
式中:
| ${\rho _{\nu {\rm{r}}}} = \frac{{\left( {{r_{\rm{z}}} + {\varOmega _1}} \right){{\left( {1 + {k^2} - 2k{\rm{cos }}\;{\varphi _\nu }} \right)}^{3/2}}}}{{k\left( {{z_{\rm{p}}} + 1} \right){\rm{cos }}\;{\varphi _\nu } - \left( {1 + {z_{\rm{p}}}{k^2}} \right)}} + \left( {{r_{\rm rp}} + {\varOmega _2}} \right),$ | (54) |
| ${\rho _c} = {r_{\rm rp}},$ | (55) |
| ${\rho _\nu } = \frac{{{\rho _{\nu {\rm{r}}}}{\rho _{\rm{c}}}}}{{{\rho _{\nu {\rm{r}}}} + {\rho _{\rm{c}}}}}. $ | (56) |
式中:
| ${k_{36}} = \sum\limits_{\nu = n}^m {{k_\nu }l_{{\rm o}v}^2}, $ | (57) |
| ${l_{{\rm o}\nu }} = {r_{\rm c}}'{{({\rm{sin}}\;{\varphi _\nu })}}/({{{1 + {k^2} - 2k{\rm{cos}}\;{\varphi _\nu }}}})^{1/2}. $ | (58) |
式中:
摆线轮和针轮的啮合阻尼
| ${c_\nu } = 2{\xi _{{\rm{36}}}}\left({{{{{k_\nu }r_{\rm c}}{'^2}{r_{{\rm{rp}}}}^2{J_3}{J_6}}}/\big({{{r_{\rm c}}{'^2}{J_3} + {r_{{\rm{rp}}}}^2{J_6}}}}\big)\right)^{1/2}. $ | (59) |
式中:
| ${c_{36}} = \sum\limits_{\nu = n}^m {{c_\nu }} . $ | (60) |
将各部件都简化为轴式、盘式或者轴式和盘式叠加的形式,计算各部件的转动惯量,轴式和盘式部件转动惯量分别为
| ${m_{\bar \omega} } = {\rho _{{\bar \omega}}}{\text{π }}{r_{\bar \omega}}^2{l_{\bar \omega} },$ | (61) |
| ${J_{\bar \omega}} = {\rho _{{\bar \omega}}}{\text{π}}{r_{\bar \omega}}^4{l_{\bar \omega}}/2. $ | (62) |
式中:
输入轴扭转刚度
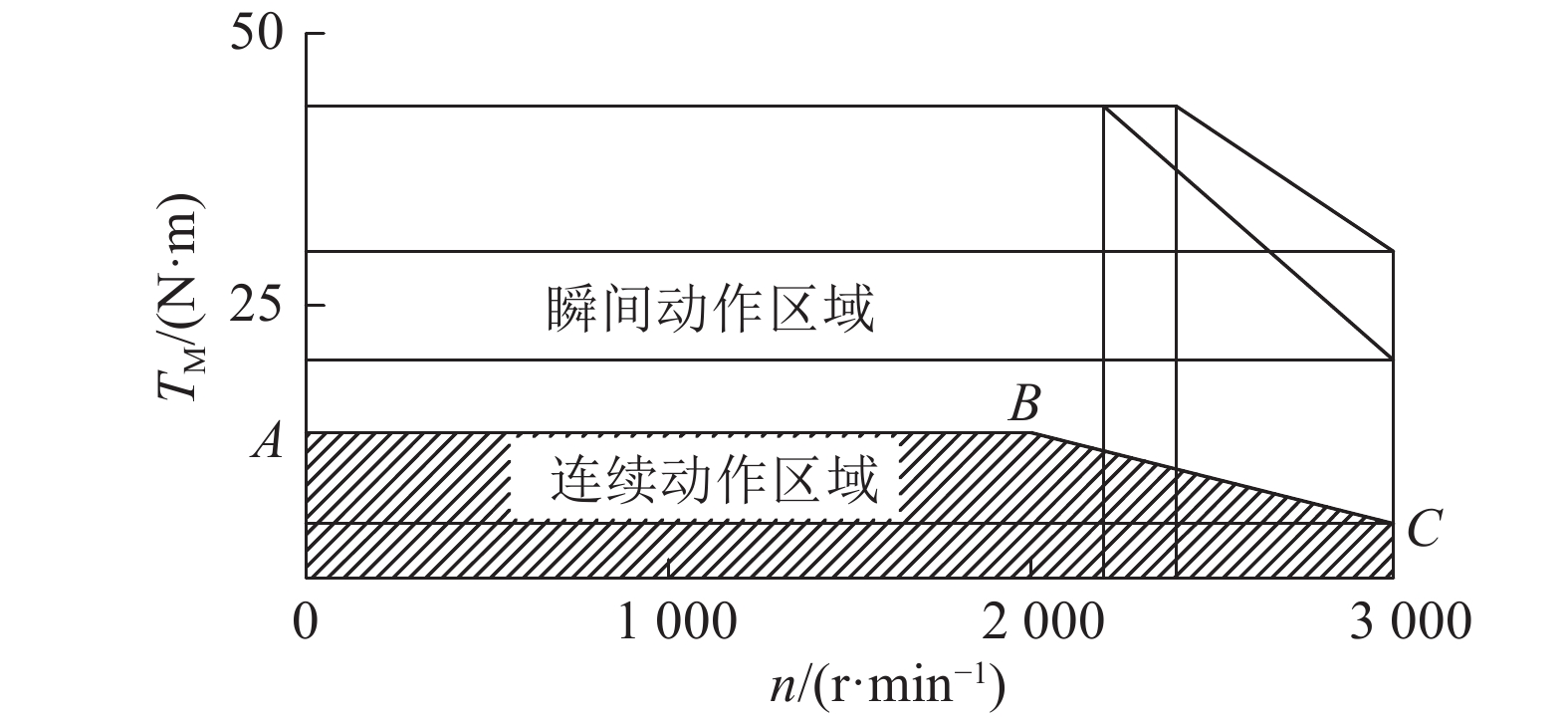
RV减速器驱动电机的启动机械特性曲线如图3所示. 连续动作区域是指电机连续不间断的工作方式,并且不受时间和发热的限制. 瞬间动作区域是指短时间断工作方式,如点动启停. 考察RV减速器运动特性是在连续动作区域中进行,即在图3中ABC曲线的下方区域中进行.
|
图 3 电机驱动机械特性曲线 Fig. 3 Mechanical characteristic curve of motor driver |
根据电动机铭牌可知,电动机额定功率为3 kW,额定转速为2 000 r/min,额定驱动转矩为14.3 N·m,同步转速为3 000 r/min.
采用直线形式的机械特性曲线,设
| ${T_{\rm M}} = {\partial _1} + {\partial _2}\omega . $ | (63) |
额定角速度为
| ${\omega _{\rm H}} = {n_{\rm H}}{\text{π}}/30.$ | (64) |
式中:
同步角速度为
| ${\omega _0} = {n_{\rm 0}}{\text{π}}/30.$ | (65) |
式中:
如图3所示,B、C两点坐标分别为(
| ${T_{\rm M}} = 23.9 - 0.045\;86\omega .$ | (66) |
AB段力矩恒为14.3 N·m,超过BC段的驱动力矩为0 N·m.
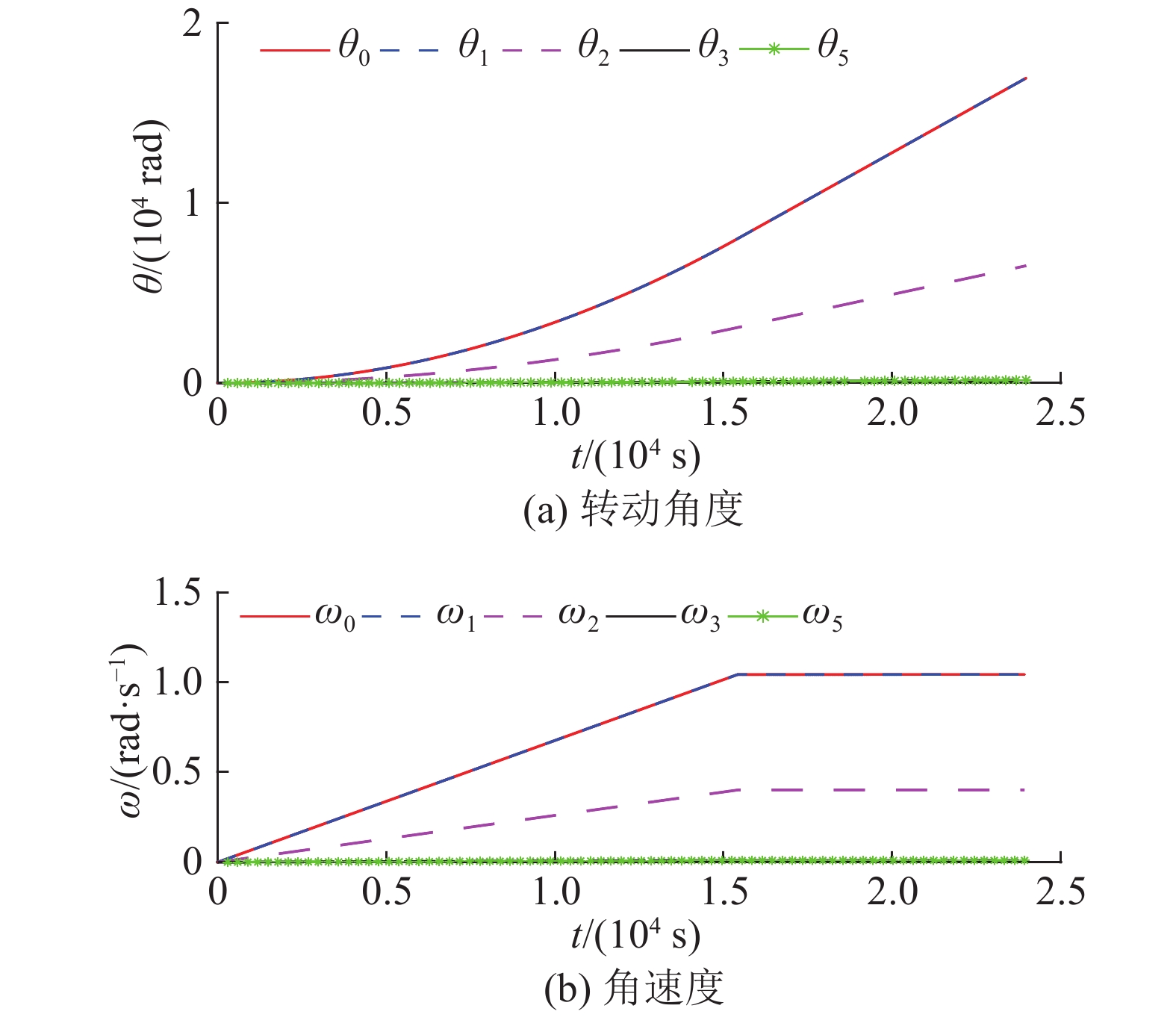
2.3.2 加速到稳定状态中的系统动态响应当输入轴转速小于10 r/min时,
|
图 4 RV减速器各部件的转动角、转动角速度关系 Fig. 4 Rotational angle and rotational angular velocity relationship between various components of RV reducer |
由图5(a)可以看出,模型在加速过程中输入轴和太阳轮之间的相对位移
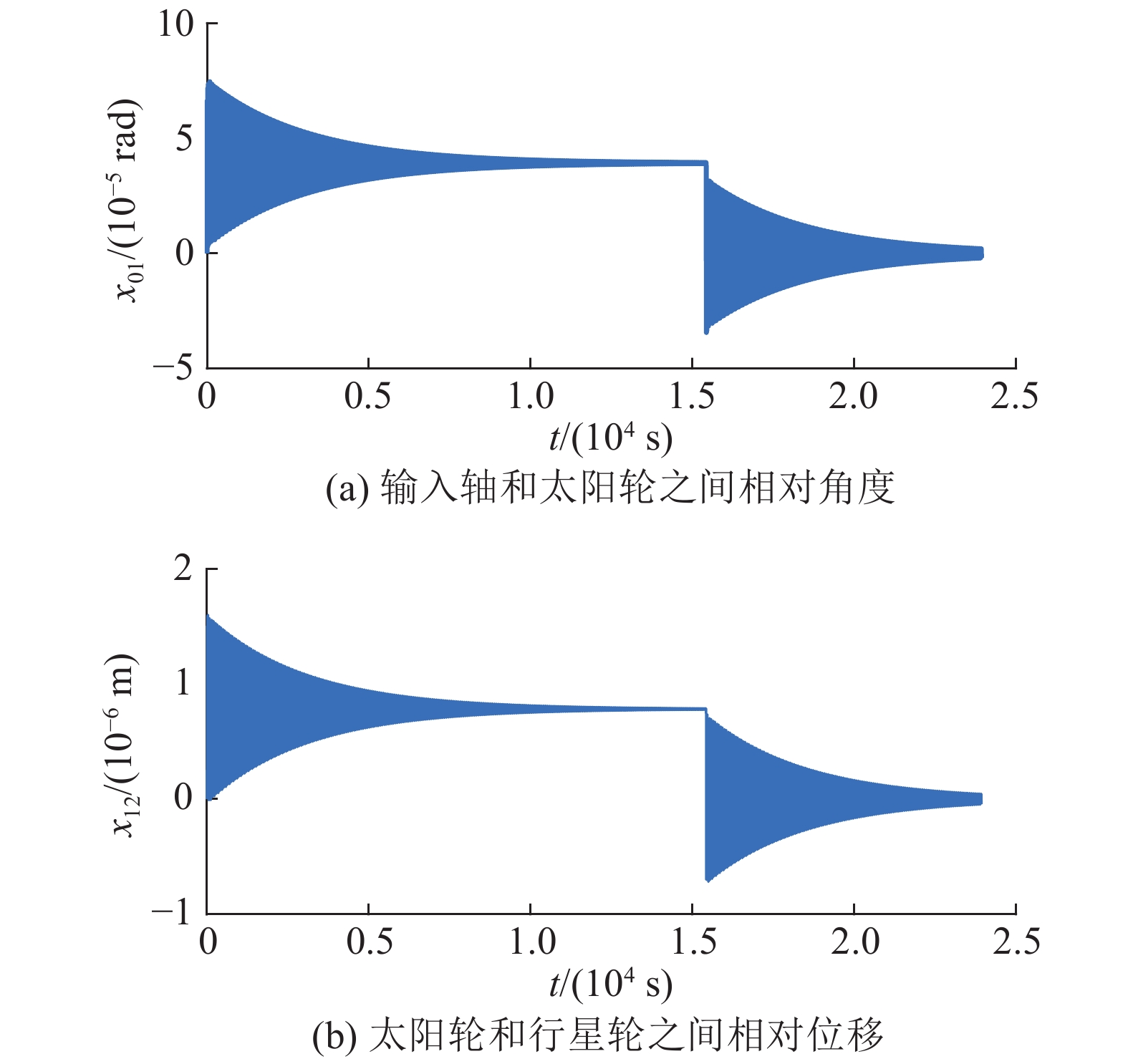
|
图 5 RV减速器第1级传动部分传动误差 Fig. 5 Transmission error of first transmission part of RV reducer |
摆线轮转角和行星架转角之间具有一定的传动误差
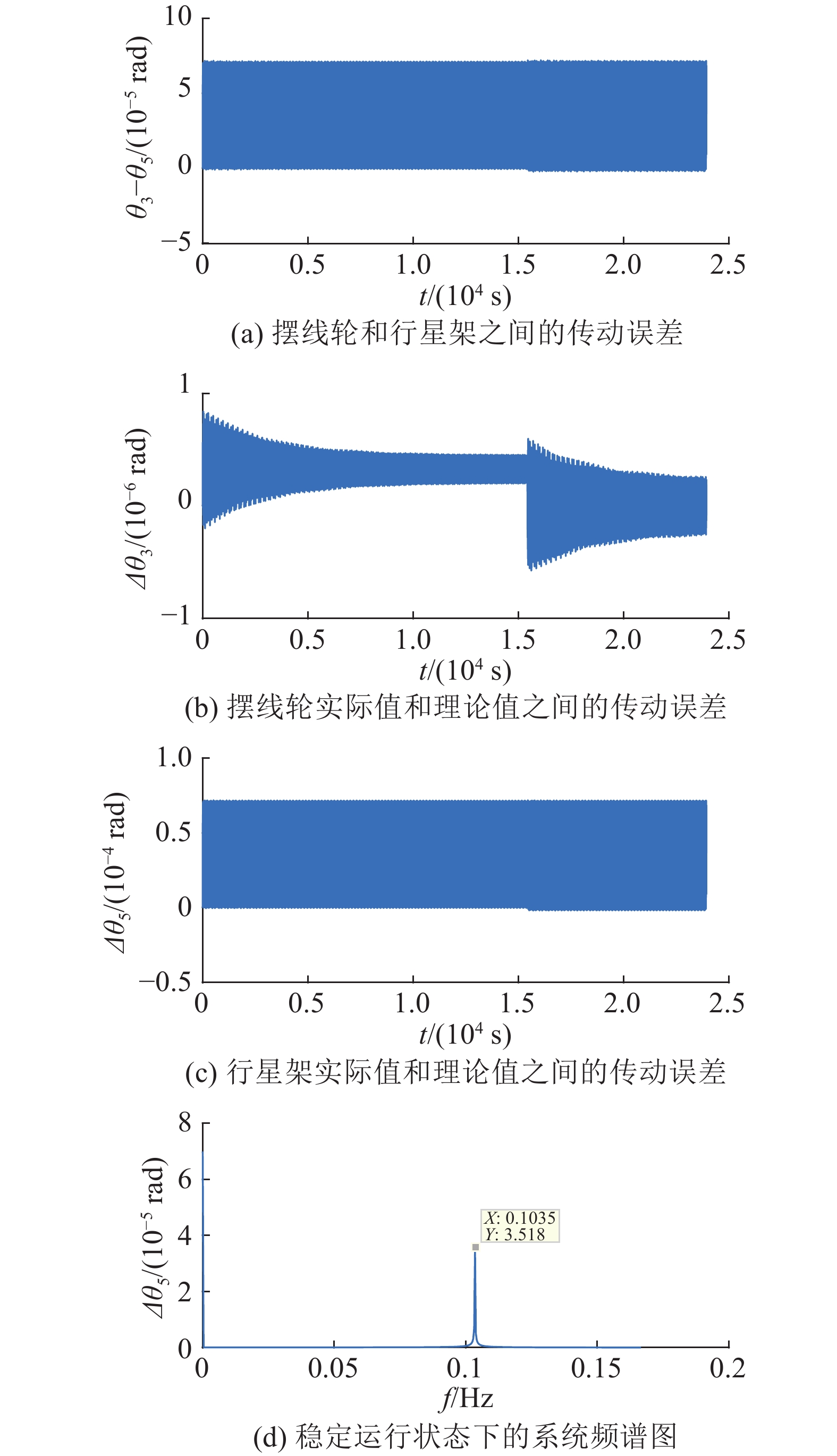
|
图 6 RV减速器第2级传动部分传动误差 Fig. 6 Transmission error of second transmission part of RV reducer |
分析直齿轮传动非线性特性时,主要考虑时变啮合刚度、啮合误差和啮合间隙对系统动力学特性的影响[23-24]. 分析RV减速器第1级直齿轮传动非线性特性时,也主要考虑这3个因素.
考虑时变啮合刚度、啮合误差和啮合间隙时,齿轮之间的啮合力可以表示为
| ${F_{12t}}{\rm{ = }}{c_{{\rm{12}}}}\dot x(t) + {k_{12}}tx(t). $ | (67) |
式中:
| $x(t) = \left\{ {\begin{array}{*{20}{c}}{{x_\beta } - \eta ,\;\;\;\;\;\;\;\;\;\;{x_\beta } > \eta };\\{\;\;\;\;0,\;\;\;\;\;\; - \eta \leqslant {x_\beta } \leqslant \eta \;};\\{{x_\beta }{\rm{ + }}\eta ,\;\;\;\;\;\;\;\;\;{x_\beta } < - \eta ,\;}\end{array}} \right.$ | (68) |
| ${x_\beta } = {x_{12}} - \varsigma (t). $ | (69) |
式中:
| $\varsigma (t) =\sum\limits_{{q_1} = 1}^{{{{x }}_1}}{{\varsigma _{q_1}}\sin\; ({q_1}{\omega _{\rm m}}t + {\psi _{{\varsigma }{q_1}}})} . $ | (70) |
式中:
直齿轮外啮合时变刚度为均值和随时间变动量的叠加:
| ${k_{12}}(t) = {k_{12}} + \Delta {k_{12}}(t),$ | (71) |
| $\Delta {k_{12}}(t) =\sum\limits_{{q_2} = 1}^{{{{x }}_2}}{{k_{12}}_{q_2}\cos\; (q{\omega _{\rm m}}t + {\psi _{{k}{q_2}}})} . $ | (72) |
式中:
如图7(a)所示,没有考虑原系统响应曲线,仅考虑第1级直齿轮时变啮合刚度、啮合误差和啮合间隙. 由图7(a)可知,第1级直齿轮时变啮合刚度对刚开始的输入轴转角误差运动影响较明显,但是误差衰减很快,能够有效抑制输入轴的转角误差. 由图7(b)可知,时变刚度能够明显降低第1级直齿轮啮合的线性传动误差,第1级直齿轮啮合误差对输入轴转角误差、第1级直齿轮线性传递误差和第2级摆线轮传动误差都有明显的影响,如图7(a)、(c)、(d)所示,误差幅值明显增加. 第1级直齿轮啮合间隙能够明显降低输入轴的扭转误差,但是会导致齿轮线性传动误差和第2级摆线轮传动误差呈直线增加. 由图7(e)可知,虽然第1级直齿轮啮合间隙使整机传动误差略微增加,3种非线性因素对整机传动误差的影响较小.

|
图 7 第1级传动部分非线性因素对RV减速器系统动力特性的影响 Fig. 7 Effects of nonlinear factors of first transmission part on system dynamic characteristics of RV reducer |
在第2级摆线针轮传动中,摆线轮对每个针齿具有初始啮合间隙,并且间隙在同一时刻并不相同,非线性间隙导致初始间隙发生变化,直接影响啮合齿数和啮合稳定性. 摆线轮与针轮之间的等效啮合刚度通过摆线轮和各个齿之间的啮合刚度叠加而成. 初始间隙的变化直接导致参与刚度计算的齿数减小,摆线轮和针轮之间的等效啮合刚度减小. 等效后的啮合刚度周期性变化[25-26],不是一个固定的值,摆线轮和针轮之间的时变啮合刚度为
| ${k'_{36}}(t) = {k'_{36}} + \Delta {k'_{36}}(t). $ | (73) |
式中:
摆线轮和针轮之间的啮合误差会影响齿间作用力和啮合稳定性,在摆线轮啮合中,单齿误差会产生叠加作用,严重影响整体的啮合稳定性.
第2级摆线轮非线性因素影响如图8所示. 由图8(a)、(b)可知,二级非线性因素对一级直齿轮输入轴转角误差和第1级直齿轮线性传动误差影响不明显,对第2级摆线轮传动误差影响显著. 如图8(c)所示,二级摆线轮啮合时变刚度能够显著降低摆线轮的传动误差,啮合误差能够显著增大摆线轮的传动误差,啮合间隙只会略微增加摆线轮的传动误差. 但是由图8(d)可知,第2级非线性因素对系统整体传动误差影响也不显著,各因素略微降低系统的传动精度.
综上可知,RV减速器传动稳定性非常高,非线性因素对传动精度影响较小,但是第1级直齿轮传动中的齿轮啮合误差和啮合间隙以及第2级摆线轮传动中啮合误差能够明显影响部分部件的传动误差,应该给予重视和控制.
4 RV减速器综合检测实验平台 4.1 搭建实验台采用驱动系统、被测件系统、负载系统组合模块的方式,结合机械工装和滑轨将模块组装为单台面模式,搭建可以在不同的工作状态下运行的高精度RV减速器综合性能检测实验平台. 平台能够对被测件的传递扭矩、转速、功率、效率、传动误差、刚度、背隙、启动力矩、寿命、温升、振动、噪声等指标进行测量与计算. 实验台设计思路和示意图如图9所示.
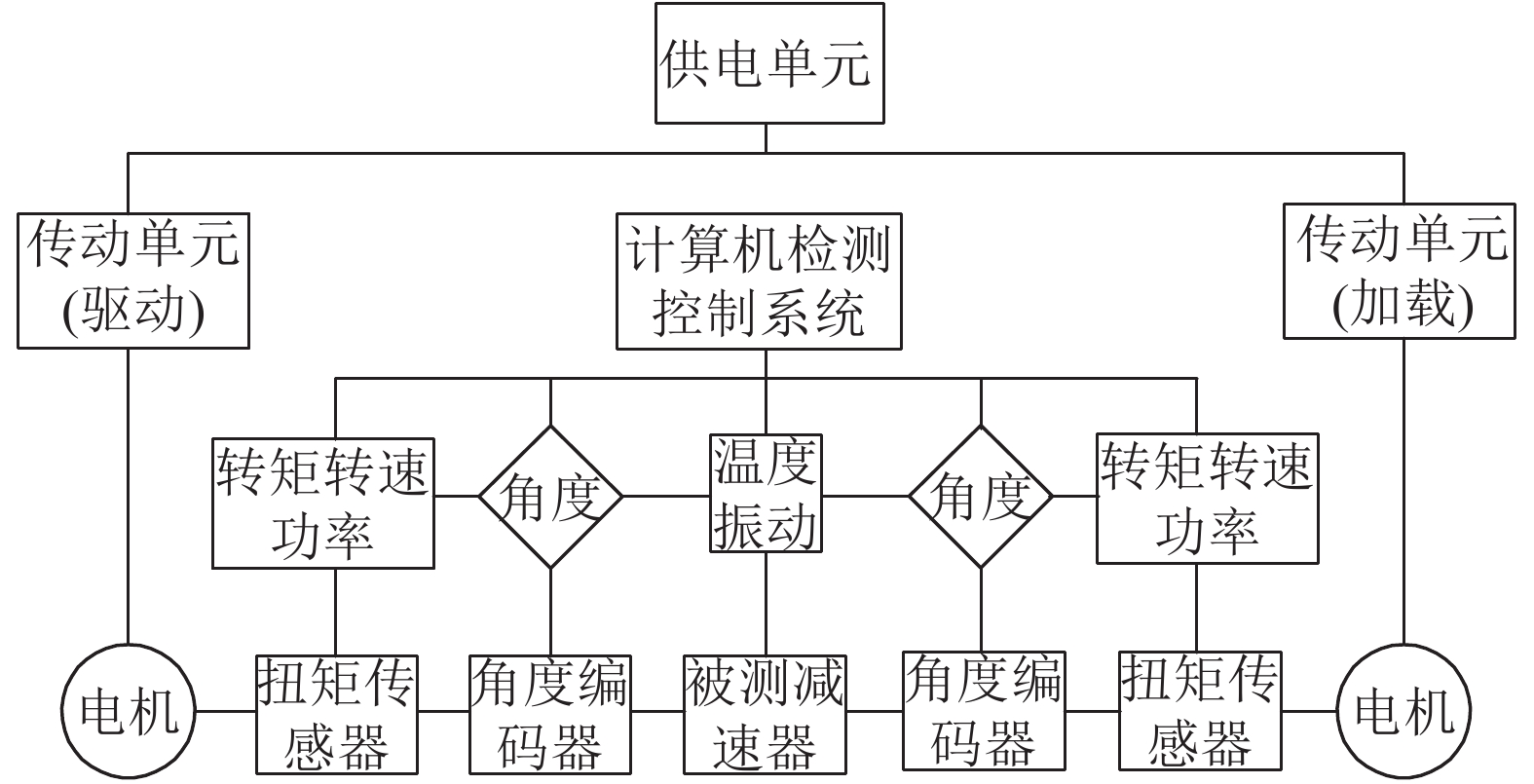
|
图 9 RV减速器动力性能综合检测实验平台示意图 Fig. 9 Sketch map of experimental platform for comprehensive testing of dynamic performance of RV reducer |
通过设备选型,确定RV减速器实验台的工作范围,如表1所示. 如图10所示为实验台整体图. 图10(a)中从右到左依次为驱动电机、输入扭矩传感器、RV减速器、输出扭矩传感器、增速器和负载电机;如图10(b)所示,实验台还配备了角度编码器、振动加速度传感器、温度传感器和电子千分表.
| 表 1 RV减速器动力性能综合检测实验平台工作范围 Table 1 Working range of comprehensive experimental platform for dynamic performance of RV reducer |

|
图 10 RV减速器动力性能综合检测实验平台 Fig. 10 Comprehensive experimental platform for dynamic performance of RV reducer |
对比传动误差和振动噪声的实验台运行结果与理论值.设置实验条件和理论分析中的参数一致,即输入轴加速到10 r/min后保持恒定,运行负载恒定为30 N·m. 为保持此条件,施加的负载扭矩
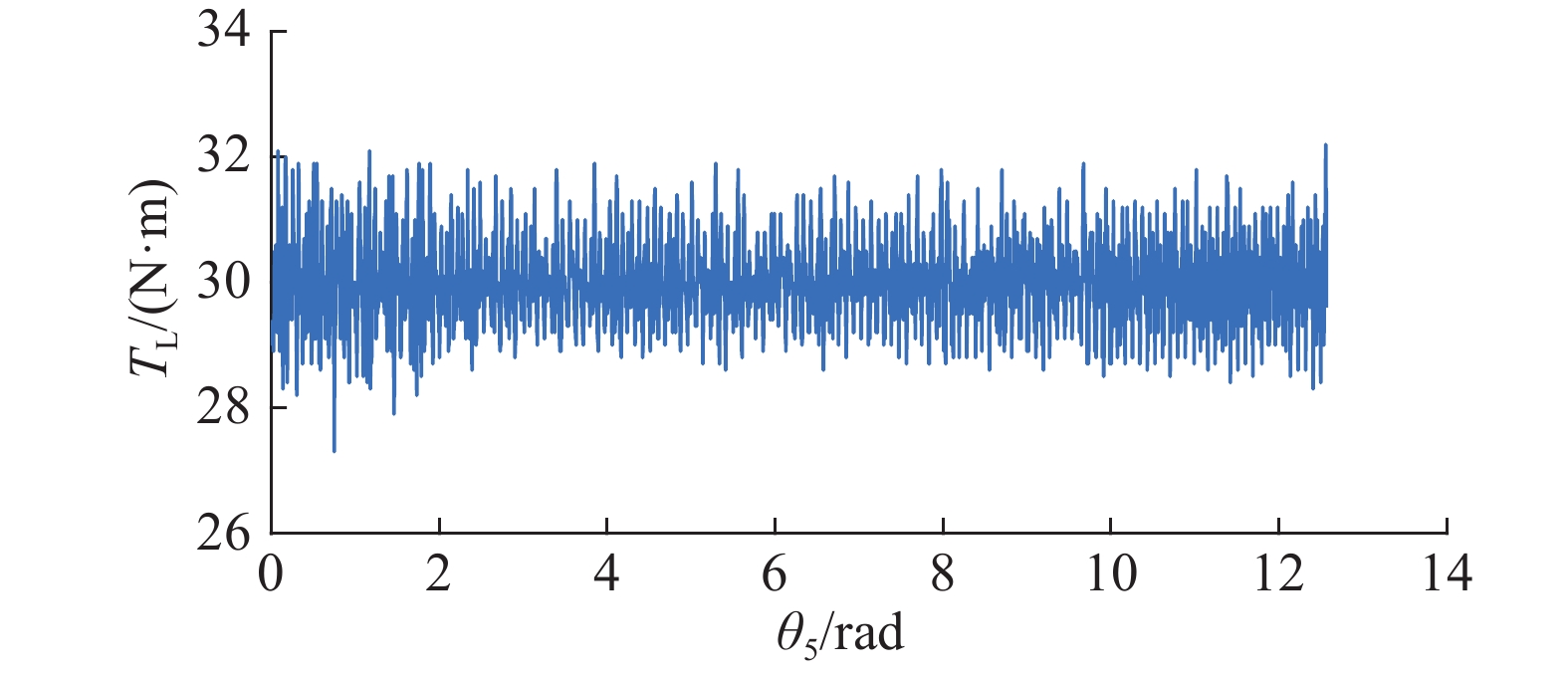
|
图 11 RV减速器负载扭矩 Fig. 11 Load torque of RV reducer |
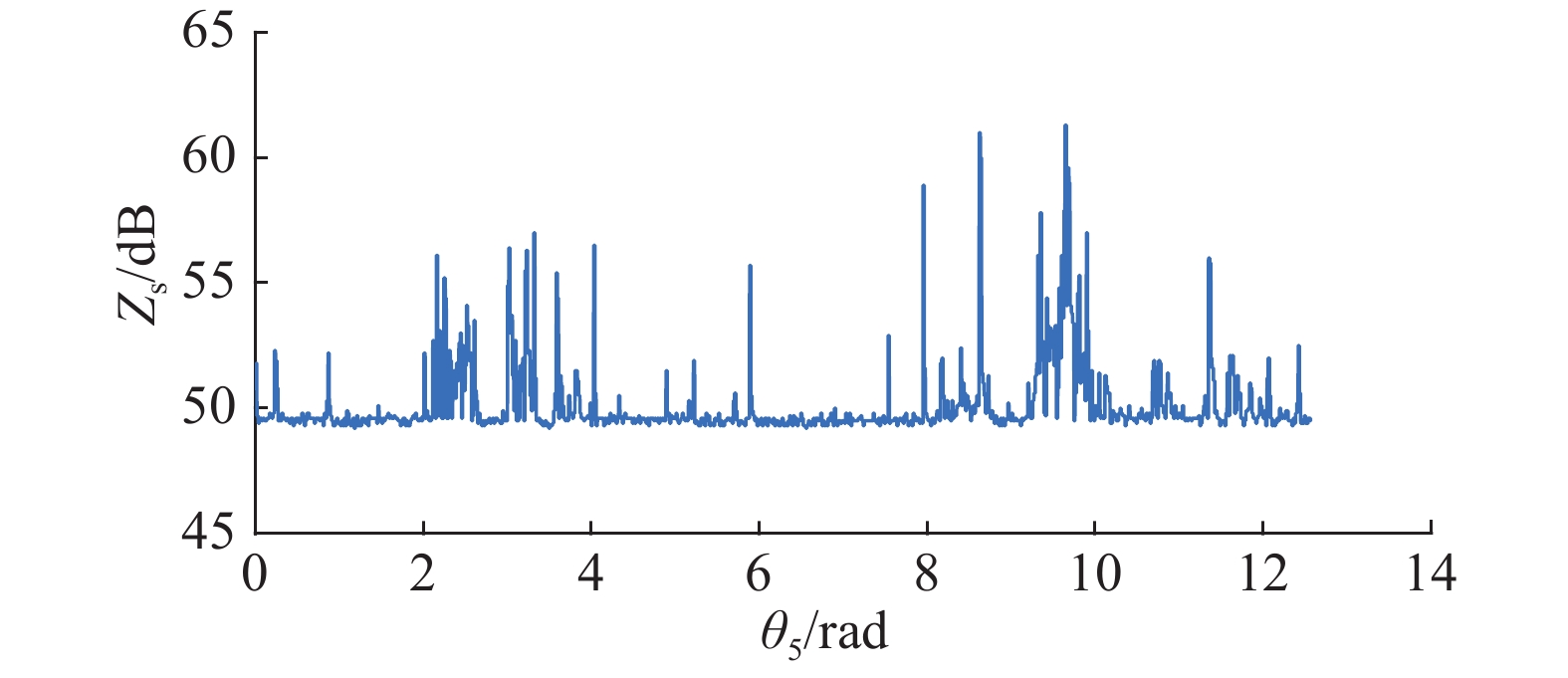
振动产生噪声,所以噪声能在一定程度上反映RV减速器在运行过程中产生的振动. 由图12可知,运行过程中产生的噪声
|
图 12 RV减速器运行过程中的噪声 Fig. 12 RV reducer’s noise during operation |
传动误差测量实验使用增量式角度编码器通过计算脉冲数计算角度. 角度大小跟计数的起始位置和中间过程都有关系,第1圈中传感器受到的干扰会直接累加进第2圈;误差曲线跟角度编码器的精度有关,精度越高,干扰产生的误差越小. 实验台传感器精度为5万线,4倍频后为20万细分,一圈为1 296 000″,每个脉冲的角度为6.48″,干扰会产生非常大的误差,所以在实验过程中要尽量消除角度检测系统中通信信号的干扰. 角度编码器分辨率越高,对安装精度的要求也越高,安装中出现的偏心或者垂直度不够等问题会严重影响结果. 有时在旋转轴旋转一周的过程中,某个区域的测量误差明显偏大,导致转角测量中存在周期性波动,因此需要严格保证高精度角度编码器与RV减速器输入端和输出端的安装精度.
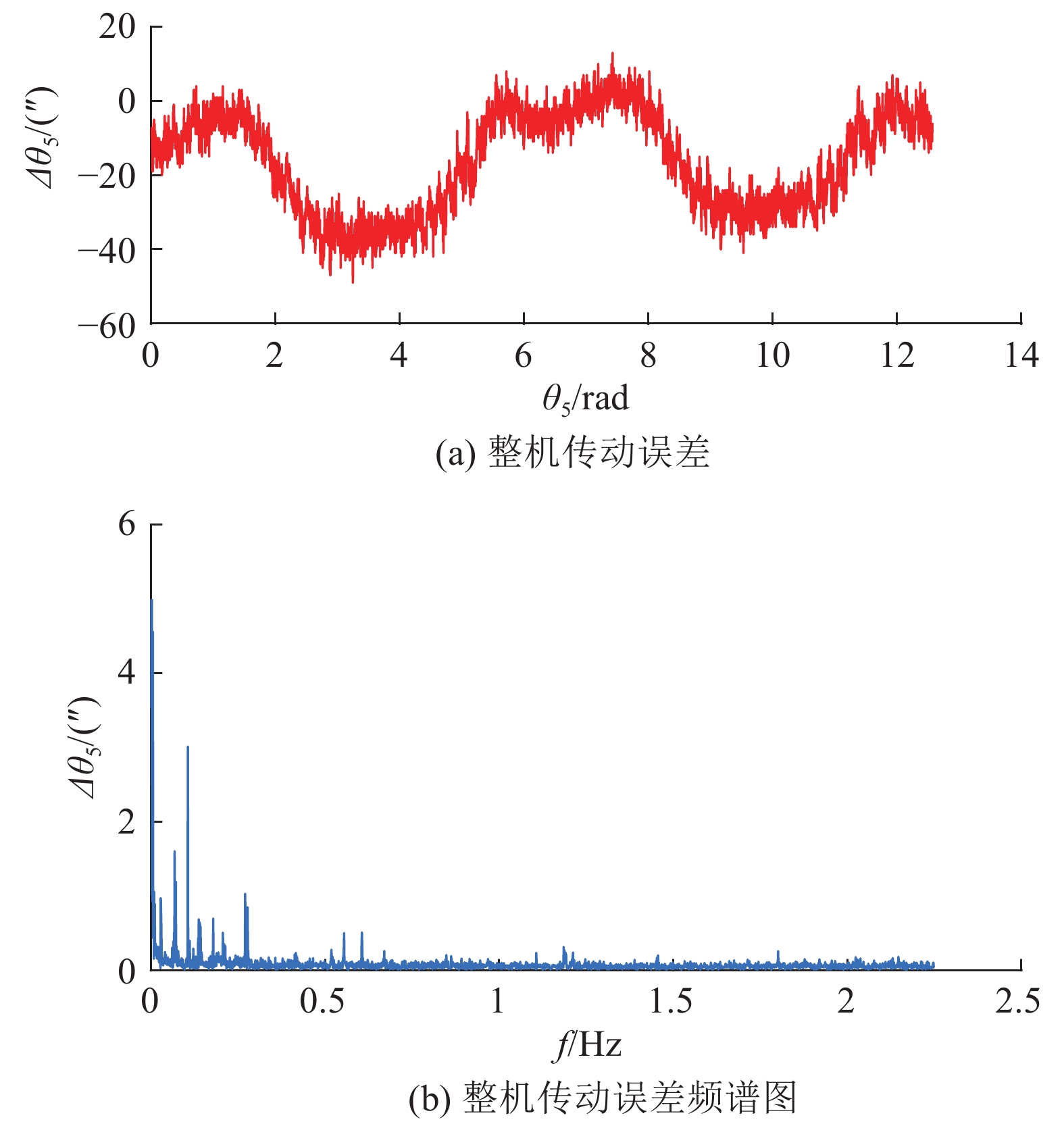
RV减速器的传动误差是指在个周期内传动误差的最大数值和最小数值之间的差值. 被测减速器的传动角度误差曲线如图13(a)所示. 图13(a)为输出轴旋转2圈得到的结果,0~2π rad为第1周期,2π~4π rad为第2周期,分别分析每个周期. 在0~2π rad中,分析最大和最小传动误差的差值,在2π~4π rad中,再次分析最大和最小传动误差的差值. 起点不同的2组实验得到的传动误差数值不同,但是2次数据的整体变化趋势相同,并且第1周期和第2周期变化趋势相同. 被测RV减速器在第1组数据的第1个周期内的最大传动误差为53″,第1组数据的第2个周期内的最大传动误差为54″,第2组数据的第1个周期内的最大传动误差为52″,第2组数据的第2个周期内的最大传动误差为50″,说明实验在2个周期内运行平稳,没有出现周期性干扰或者误差. 实验数据与图6(c)中不考虑时变刚度、啮合间隙和啮合误差时的最大传动误差18″和图7(f)、8(d)中考虑非线性因素时的最大传动误差26″较接近,说明理论模型的计算精度较高. 但是实验和理论计算之间仍有一定的差异,主要是因为理论模型是建立在一定假设条件下的理想模型,考虑的影响因素较少,实际中的传动系统中的影响因素众多,传动误差大于理论计算结果是可以接受的. 如图13(b)所示为整机传动误差的频谱图. 系统在0.000 86、0.002 772、0.067 58、0.105 7、0.136 9、0.178 5、0.206 2、0.270 3、0.554 5、0.605 6、1.185、1.456、1.801 Hz等处都出现了明显的峰值,其中在0.000 86、0.067 58、0.105 7 Hz处峰值最大,0.107 5 Hz与理论计算中的0.103 5 Hz非常接近,进一步说明理论计算和实验结果较吻合. 实验中的多峰值频率主要是由系统中的不稳定输入和输出引起其他频谱.
|
图 13 RV减速器运行过程中的整机传动误差 Fig. 13 RV reducer’s transmission error during operation |

|
图 8 第2级非线性因素对RV减速器系统动力特性影响 Fig. 8 Effects of nonlinear factors of second transmission part on system dynamic characteristics of RV reducer |
建立了5自由度纯扭转模型,为利用数值求解建立RV减速器动力学仿真奠定了基础. 计算得到的理论模型传动比为105,与实际值完全吻合,并且理论数据和实验数据都满足RV减速器最大传动误差不大于60″的要求. 理论和实验结果的峰值都在0.1 Hz附近出现,证明了理论模型的正确性. 计算得到的动态响应曲线和非线性因素分析,为RV减速器动力学特性的研究提供了分析方法,促进了RV减速器的研究和发展. 搭建的RV减速器实验平台能够实现多项动力指标测试,节约实验成本,同时也可以作为各种RV减速器之间的性能对比的实验平台.
后续研究将在纯扭转模型的基础上增加轴向和径向等自由度,构建多因素复杂耦合动力学模型,以更加准确地模拟RV减速器的实时运动状态.
| [1] |
HIDAKA T, WANG H, ISHIDA T, et al. Rotational transmission error of K-H-V plantary gears with cycloid gear (1st report, analytical method of the rotational transmission error) [J]. JSME International Journal: Serises C, 1994, 60(570): 645–653.
|
| [2] |
ISHIDA T, WANG H, HIDAKA T, et al. Rotational transmission error of K-H-V planetary gears with cycloid gear (2nd report, effects of manufacturing and assembly error)[J]. JSME International Journal: Serises C, 1994, 60(578): 278-285. |
| [3] |
何卫东, 陆岩, 吴鑫辉. 基于等价模型的RV减速器扭转刚度计算[J]. 机械传动, 2013, 37(9): 38-41. HE Wei-dong, LU Yan, WU Xin-hui. Torsional rigidity calculation of RV reducer based on equivalent model[J]. Journal of Mechanical Transmission, 2013, 37(9): 38-41. |
| [4] |
SHAN L J, LIU Y T, HE W D. Analysis of nonlinear dynamic accuracy on RV transmission system[J]. Advanced Materials Research, 2012, 510: 529-535. DOI:10.4028/www.scientific.net/AMR.510 |
| [5] |
ZHANG Y H, CHEN Z, HE W D. Virtual prototype simulation and transmission error analysis for RV reducer[J]. Applied Mechanics and Materials, 2015, 789: 226-230. |
| [6] |
张大卫, 王刚, 黄田, 等. RV减速机动力学建模与结构参数分析[J]. 机械工程学报, 2001, 37(1): 69-73. ZHANG Da-wei, WANG Gang, HUANG Tian, et al. Dynamic formulation of RV reducer and analsis of structural parameters[J]. Chinese Journal of Mechanical Engineering, 2001, 37(1): 69-73. DOI:10.3321/j.issn:0577-6686.2001.01.016 |
| [7] |
杨玉虎, 朱临宇, 陈振宇, 等. RV减速器扭转刚度特性分析[J]. 天津大学学报: 自然科学与工程技术版, 2015, 48(2): 111-117. YANG Yu-hu, ZHU Lin-yu, CHEN Zhen-yu, et al. Characteristic analysis of torsional stiffness of RV reducer[J]. Journal of Tianjin University: Science Technology, 2015, 48(2): 111-117. |
| [8] |
CHEN C, YANG Y H. Structural characteristics of rotate vector reducer free vibration[J]. Shock and Vibration, 2017, 2017: 4214-4370. |
| [9] |
HAN L S , GUO F. Global sensitivity analysis of transmission accuracy for RV-type cycloid-pin drive[J]. Journal of Mechanical Science and Technology, 2016, 30(3): 1225-1231. DOI:10.1007/s12206-016-0226-2 |
| [10] |
SUN Y G, YU G B, ZHANG J, et al. Reliability prediction of RV reducer based on fault tree and Monte-Carlo simulation[J]. Applied Mechanics and Materials, 2013, 274: 663-666. DOI:10.4028/www.scientific.net/AMM.274 |
| [11] |
吕明帅. RV减速器传动特性的仿真与实验研究 [D]. 哈尔滨: 哈尔滨工业大学, 2016: 31–54. LV Ming-shuai. Simulation and experimental study of transmision characteriestic of RV reducer [D]. Harbin: Harbin Institute of Technology, 2016: 31–54. http://cdmd.cnki.com.cn/Article/CDMD-10213-1016914462.htm |
| [12] |
VAREDI-KOULAEI S M, DANIALI H M, FARAJTABAR M, et al. Reducing the undesirable effects of joints clearance on the behavior of the planar 3-RRR parallel manipu-lators[J]. Nonlinear Dynamics, 2016, 86: 1007-1022. DOI:10.1007/s11071-016-2942-7 |
| [13] |
李同杰, 朱如鹏, 鲍和云, 等. 行星齿轮系扭转非线性振动建模与运动分岔特性研究[J]. 机械工程学报, 2011, 47(21): 76-83. LI Tong-jie, ZHU Ru-peng, BAO He-yun, et al. Nonlinear torsional vibration Modeling and Bifurcation characteristic study of a planetary gear train[J]. Journal of Mechanical Mngineering, 2011, 47(21): 76-83. |
| [14] |
KHABOU M T, BOUCHAALA N, CHAARI F, et al. Study of a spur gear dynamic behavior in transient regime[J]. Mechanical Systems and Signal Processing, 2011, 25(8): 3089-3091. DOI:10.1016/j.ymssp.2011.04.018 |
| [15] |
LEI D C, TANG J Y, TANG J J. Gear dynamic transmission error testing[J]. Advanced Materials Research, 2014, 871: 352-357. |
| [16] |
李瑰贤, 于广滨, 温建民, 等. 求解齿轮系统非线性动力学微分方程的多尺度方法[J]. 吉林大学学报: 工学版, 2008, 38(1): 75-79. LI Gui-xian, YU Guang-bin, WEN Jian-min, et al. Nonlinear torsional vibration modeling and bifurcation characteristic study of a planetary gear train[J]. Journal of Jilin University: Engineering and Technology Edition, 2008, 38(1): 75-79. |
| [17] |
刘振皓. 车辆复合行星传动系统动力学特性研究 [D]. 武汉: 武汉大学, 2012: 18–30. LIU Zhen-hao. Research on dynamic characteristics of vehicle compound planetary gear train sets [D]. Wuhan: Wuhan University, 2012: 18–30. http://cdmd.cnki.com.cn/Article/CDMD-10486-1012029516.htm |
| [18] |
GUO Y, PARKER R G. Purely rotational model and vibration modes of compound planetary gears [J]. Mechanism and Machine Theory, 2010, 45(3): 365–377.
|
| [19] |
李一民, 郝志勇, 叶慧飞. 柴油机正时齿轮系动力学特性分析[J]. 浙江大学学报: 工学版, 2012, 46(8): 1472-1477. LI Yi-min, HAO Zhi-yong, YE Hui-fei. Dynamic characteristic analysis of diesel timing gear trains[J]. Journal of Zhejiang University: Engineering Science, 2012, 46(8): 1472-1477. |
| [20] |
FARSHIDIANFAR A, SAGHAFI A. Identification and control of chaos in nonlinear gear dynamic systems using Melnikov analysis[J]. Physics Letters A, 2014, 378(46): 3457-3463. DOI:10.1016/j.physleta.2014.09.060 |
| [21] |
刘文, 李锐, 张晋红, 等. 斜齿轮时变啮合刚度算法修正及影响因素研究[J]. 湖南大学学报: 自然科学版, 2018, 45(2): 1-10. LIU Wen, LI Rui, ZHANG Jin-hong, et al. Study on correction algorithm of time-varying meshing stiffness of helical gears and its influencing factors[J]. Journal of Hunan University: Natural Sciences, 2018, 45(2): 1-10. |
| [22] |
LI Z, WANG J, ZHU R. Influence comparisons of two version tooth profile modifications on face gear dynamic behaviors[J]. Journal of Vibroengineering, 2016, 18(6): 3499-3511. DOI:10.21595/jve.2016.17025 |
| [23] |
GUILBAULT R, LALONDE S, THOMAS M. Nonlinear damping calculation in cylindrical gear dynamic modeling[J]. Journal of Sound and Vibration, 2012, 331(9): 2110-2128. DOI:10.1016/j.jsv.2011.12.025 |
| [24] |
WU L, TANG J, CHEN S. Effect of nonlinear impact damping with non-integer compliance exponent on gear dynamic characteristics[J]. Journal of Central South University: Science and Technology of Mining and Metallurgy, 2014, 21(10): 3713-3721. |
| [25] |
曾庆峰, 安子军. 无隙摆线钢球传动啮合副啮合刚度系数分析[J]. 机械设计, 2017, 34(4): 24-28. ZENG Qing-feng, AN Zi-jun. Analysis of meshing stiffness coefficient for no clearance cycloid ball transmission meshing pair[J]. Journal of Machine Design, 2017, 34(4): 24-28. |
| [26] |
陈忠敏, 侯力, 段阳, 等. 新型摆线针轮行星减速器传动系统的振动 [J]. 吉林大学学报: 工学版, 2018, 48 (1): 174–185. CHEN Zhong-min, HOU Li, DUAN Yang, et al. Vibration characteristics analysis of the new pin-cycloid speed reducer [J]. Journal of Jilin University: Engineering and Technology Edition, 2018, 48 (1): 174–185. http://www.cnki.com.cn/Article/CJFDTotal-JLGY201801021.htm |



