20世纪50年代以来，随着科技的发展和海洋开发的需要，在船舶和海洋建筑物的研究中越来越多地涉及到流固耦合问题^[1-5]，其中对结构物入水冲击问题的研究非常复杂，且具有实际意义. 结构物入水问题广泛存在于船舶工业与海洋工程中. 当船舶在恶劣的海况下行驶时，经常会发生入水冲击现象，该现象会产生巨大的冲击压力，使船体产生变形，对受到冲击的部位造成损伤，甚至导致船体结构失效折断. 由于冲击问题具有非定常性，难以准确地预报船舶受到的冲击压力. 传统的数值方法在处理结构物入水冲击的流固耦合问题时，遇到了相当大的困难. 例如在利用有限元法(finite element method，FEM)处理结构入水问题时，由于流固耦合交界面网格变形过大，计算经常失败. 在利用有限体积法(finite volume method，FVM)处理流固耦合问题时，流固耦合交界面的处理过程非常繁琐.

无网格法^[5-7]的基本思想是将流体(或固体)离散成相互作用的拉格朗日粒子，用一系列的节点来代替网格结构. 每个粒子上承载各自的物理量，如质量、速度、加速度等，粒子之间的相互作用通过“核函数”实现. 在数值计算过程中摆脱了单元或者网格的概念，完全抛开了网格重构，在处理船舶冲击入水、结构大变形以及破坏失效等不连续问题时具有明显的优势. 移动粒子半隐式（moving-particle semi-implicit，MPS）法是一种全新的拉格朗日粒子法，最早由Koshizuka等^[8]于1996年提出，被广泛运用于许多研究领域. 潘徐杰等^[9]研究MPS法所存在的主要问题，利用MPS法模拟液舱横摇晃荡现象. Shibata等^[10]对于如何缓解压力振荡问题做了大量研究. Yu等^[11]基于MPS-les法模拟楔形体入水冲击问题. Gotoh等^[12]采用MPS法模拟波浪的传播问题. Tang等^[13]提出基于无网格节点的光滑点插值法（NS-PIM）,该方法在计算复杂几何结构时相对较为简单。Chen等^[14]对平底结构的进水问题进行研究，并对冲击产生的压力峰值进行分析。Tang等^[15]提出新的光滑点插值方法（ES-PIM）用于二维和三维弹性问题的分析计算，得到了较好的计算效果。He等^[16]提出全新的ES-FEM/BEM方法，分析计算流固耦合相互作用问题。在MPS法早期发展过程中，主要侧重于流体方面的模拟研究，对于流固耦合方面的研究相对较少，这是由于流固耦合交界面处理的难度较大，常常由于交界面处理不好而导致计算无法进行. 并且MPS法在计算流固耦合问题时经常发生流体粒子穿越固体边界的现象，极大地影响了数值计算结果的精度. MPS法与另一种无网格方法——光滑粒子流体力学（smoothed particle hydrodynamics，SPH）法的共同缺点是压力振荡性太大，特别是在处理高速冲击入水的流固耦合问题时，由于算法本身的压力震荡问题，在流固耦合交界面处会产生压力畸变，导致计算结果发散. 在流固耦合交界面如何减小压力振荡提高计算精度一直是研究难点.

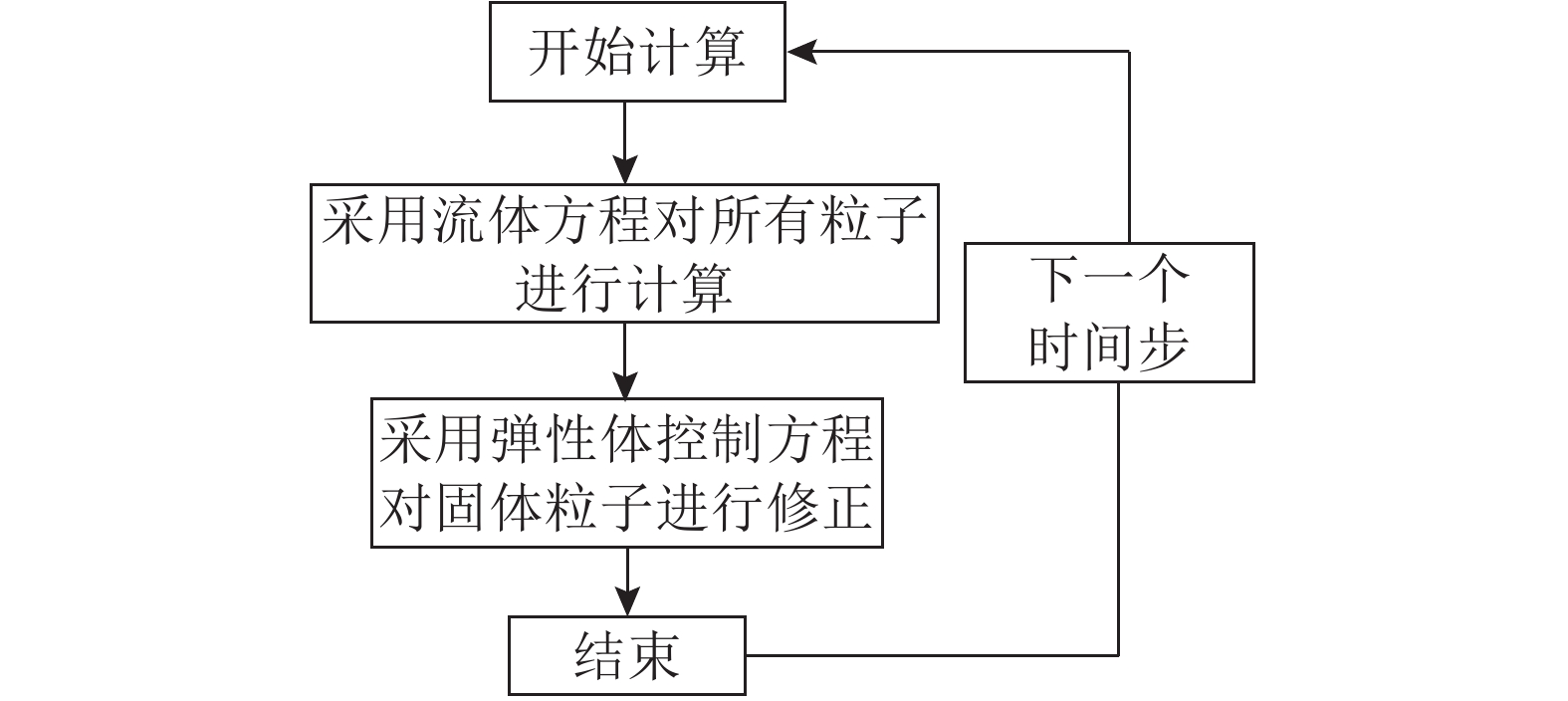
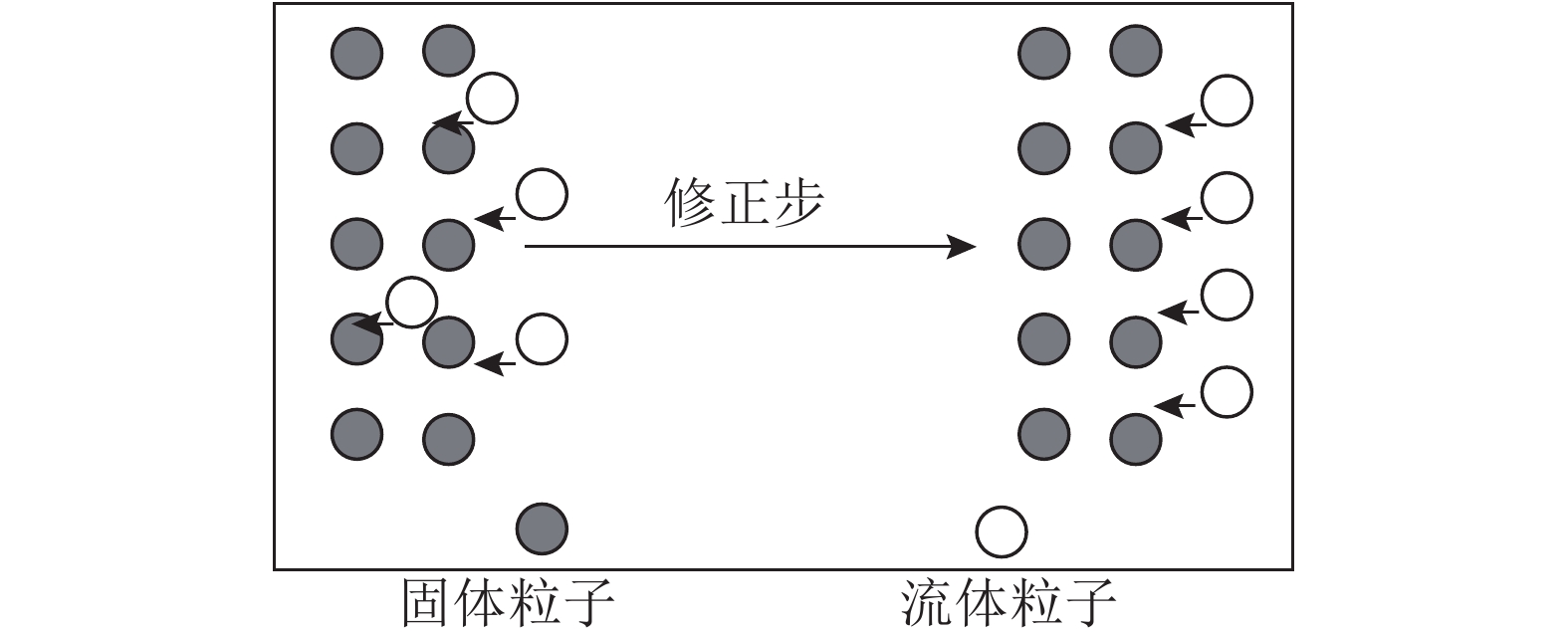
采用全新的流固耦合计算流程，使用流体控制方程计算所有粒子（流体粒子和固体粒子）的速度和位移；采用弹性体控制方程对固体粒子的速度和位移进行修正. 不需要对流固耦合交界面做单独处理，极大地简化处理程序. 为了防止产生粒子穿越现象，影响计算精度，编写防止粒子在边界处发生穿越的附加程序. 根据MPS法的计算流程特性，采用新的压力迭代方法求解压力泊松方程，可以防止压力发生畸变，保证模拟顺利进行. 将MPS法应用于入水冲击流固耦合数值模拟，对模拟结果和实验结果进行对比分析，证明MPS法适用于平板冲击入水、大变形等不连续问题的模拟计算.

1 移动粒子半隐式法 1.1 流体控制方程

MPS法采用Navier-Stokes方程作为控制方程. 连续方程为

$\nabla \cdot {{u}} = 0.$

(1)

Navier-Stokes方程为

$\frac{{{\rm d}{{u}}}}{{{\rm d}t}} = - \frac{1}{\rho }\nabla P + \nu {\nabla ^2}{{u}} + {{F}}.$

(2)

式中： $\rho $ 为流体的密度, ${{u}}$ 为速度矢量， $t$ 为时间， ${{F}}$ 为体积力， $P$ 为压力， $ \nu $ 为运动黏度.

MPS法中粒子之间的相互影响通过核函数实现，核函数是MPS法中的基本函数，承于SHP法，采用的核函数方程为

$w(r) = \left\{ \begin{aligned}& {r_{\rm{e}}}/r - 1,\;\;\;0 \leqslant r < {r_{\rm{e}}}{\text{；}}\\ & 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;r \geqslant{r_{\rm{e}}} .\end{aligned} \right.$

(3)

式中： ${r_{\rm{e}}}$ 为决定MPS法中粒子的作用范围的参数， $r$ 为2个粒子之间的距离. 2个粒子的距离越近，核函数的值越大. 粒子数密度为

${n_i} = \sum\limits_{j \ne i} {w\Big(\left| {{{{r}}_{i}} - {{{r}}_{j}}} \right|\Big)} .$

(4)

式中： ${{{r}}_{i}}$ 、 ${{{r}}_{j}}$ 分别为粒子 $i$ 和粒子 $j$ 的坐标. 粒子数密度是粒子同它的作用范围内其他粒子之间核函数之和，粒子 $i$ 同自身的作用不考虑.

MPS法采用梯度模型与拉普拉斯模型来取代控制方程的某些项，2个模型与式(3)类似，只在给定的范围 ${\;r_{\rm{e}}}\;$ 内起作用. 梯度模型为

$ < \nabla f{ > _i} = \frac{d}{{{n_0}}}\sum\limits_{j \ne i} {\left[ {\frac{{{f_j} - {f_i}}}{{{{\left| {{{{r}}_{j}} - {{{r}}_{i}}} \right|}^2}}}\Big( {{{{r}}_{i}} - {{{r}}_{j}}} \Big)w\Big(\left| {{{{r}}_{i}} - {{{r}}_{j}}} \right|\Big)} \right]} .$

(5)

式中：d为空间的维数， ${n_0}$ 为初始粒子数密度，f_i为粒子i的物理量，f_j为邻居粒子j的物理量. 拉普拉斯模型为

$ < {\nabla ^2}f{ > _i} = \frac{d}{{\lambda {n_0}}}\sum\limits_{j \ne i} {\left[ {\left( {{f_j} - {f_i}} \right)w\left( {\left| {{{{r}}_i} - {{{r}}_{j}}} \right|} \right)} \right]} .$

(6)

式中：

$\lambda = \frac{{\sum\limits_{j \ne i} {w\left( {\left| {{{{r}}_{i}} - {{{r}}_{j}}} \right|} \right){{\left| {{{{r}}_{i}} - {{{r}}_{j}}} \right|}^2}} }}{{w\left( {\left| {{{{r}}_{i}} - {{{r}}_{j}}} \right|} \right)}}.$

(7)

针对压力振荡作出改进，利用船舶计算流体力学里的差分法将压力泊松方程差分，将隐式速度修正中的压力与速度关系一同代入压力泊松方程中，在每一步中对压力方程进行平均，对压力振荡现象进行修正. 根据液体不可压缩性，速度的修正值和隐式压力梯度项之间的关系为

$\Delta {{u}}' = - \frac{{\Delta t}}{\rho }\nabla {P^{n + 1}}.$

(8)

式中：P^{n + 1}为隐式压力. 转化式（8）可得

$< {\nabla ^2}{P^{n + 1}} > = - \frac{\rho }{{\Delta {t}}}\nabla \cdot{{u}}.$

(9)

合并式（9）与原压力泊松方程，在原泊松方程中加系数 $\gamma $ ，得到新的压力泊松方程：

$< {\nabla ^2}{P^{n + 1}} > = \frac{\rho }{{\Delta {t}}} {\nabla \cdot{{u}} - \gamma \frac{\rho}{{{\Delta t^2}}} \cdot \frac{{ < {n^*}{ > _i} - {n^0}}}{{{n^0}}}} .$

(10)

式中：n*为第1次显式修正后的粒子数密度；经过反复验证，当γ=0.01 时，压力结果最好，因此在计算中，取γ=0.01。通过解压力泊松方程，得到下一个时间步的压力，并且通过式（11）求得第2次速度修正量：

${ u}_i' = - \frac{{\Delta t}}{\rho }\nabla P_i^{n + 1}.$

(11)

根据第2次速度的修正量可知，下一个时间步的速度 ${ u}_i^{n + 1}$ 和位置 ${ r}_i^{n + 1}$ 为

${{ u}_i^{n + 1}} = { u}_i^* + { u}_i'{\text{，}}$

(12)

${{ r}_i^{n + 1}} = { r}_i^* + { u}_i' \Delta t.$

(13)

式中： ${ u}_i^*$ 、 ${ r}_i^*$ 分别为第1次显式修正后的速度和位置.

1.2 弹性体控制方程

弹性体的控制方程为

${\rho _{\rm{s}}}\frac{{{\rm d}{{{v}}_{l,s}}}}{{{\rm d}t}} = \frac{\partial }{{\partial x_m}}\left( {{\lambda _{\rm s}}{\varepsilon _{{\rm rr}}}{{{\delta}} _{lm}} + 2{\mu _{\rm s}}{{{\varepsilon}} _{lm}}} \right){\text{，}}$

(14)

${{{\varepsilon}} _{lm}} = \frac{1}{2}\left( {\frac{{\partial {{ u}_l}}}{{\partial {{ x}_m}}} + \frac{{\partial {{ u}_m}}}{{\partial {{ x}_l}}}} \right){\text{，}}$

(15)

${\lambda _{\rm s}} = \frac{{E\mu }}{{(1 + \mu )(1 - 2\mu )}}{\text{，}}$

(16)

${\mu _{\rm s}} = \frac{E}{{2(1 + \mu )}}.$

(17)

式中： $\rho_{\rm s}$ 为材料密度， $ v_{l,s}$ 为速度矢量的坐标形式， $ {{\varepsilon}}_{lm}$ 为应变率张量， $\varepsilon_ {\rm rr}$ 为单位体积的体积变化率， $\lambda _{\rm s}$ 、 $\mu _{\rm s}$ 为拉梅常数， $E$ 为弹性模量， $\mu $ 为泊松比.

粒子间各项力产生的加速度为

${\left[ {\frac{{\partial {{ v}_i}}}{{\partial t}}} \right]_n} = \frac{{2d}}{{{\rho _i}{n^0}}}\sum\limits_{j \ne i} {\frac{{{{{\sigma}} _{ij}}}}{{\left| {{ r}_{ij}^0} \right|}}} w\left( {\left| {{ r}_{ij}^0} \right|} \right){\text{，}}$

(18)

${\left[ {\frac{{\partial {{{v}}_i}}}{{\partial t}}} \right]_t} = \frac{{2d}}{{{\rho _i}{n^0}}}\sum\limits_{j \ne i} {\frac{{{{{\tau}} _{ij}}}}{{\left| {{{r}}_{ij}^0} \right|}}} w\left( {\left| {{{r}}_{ij}^0} \right|} \right),$

(19)

${\left[ {\frac{{\partial {{{v}}_i}}}{{\partial t}}} \right]_p} = - \frac{d}{{{\rho _i}{n^0}}}\sum\limits_{j \ne i} {\frac{{\left( {{p_i} + {p_j}} \right){{{r}}_{ij}}}}{{\left| {{{r}}_{ij}^0} \right|\left| {{{r}}_{ij}^{}} \right|}}} w\left( {\left| {{{r}}_{ij}^0} \right|} \right).$

(20)

式中：σ_ij、τ_ij为粒子的正应力和切应力，n、t表示粒子i、j之间的法向和切向，p代表粒子i、j的压力方向， ${ r}_{ij}^0$ 为初始粒子间距，α为维度.

粒子的速度和坐标位置被修正为

${ v}_i^{n + 1} = { v}_i^n + \Delta t{\left[ {\frac{{\partial {{ v}_i}}}{{\partial t}}} \right]^n}{\text{，}}$

(22)

${ r}_i^{n + 1} = { r}_i^n + \Delta t{ v}_i^{n + 1}.$

(23)

1.3 数值模拟流程

当采用MPS法处理流固耦合问题时，忽略固体粒子本身的属性，将固体粒子视为流体粒子，与流体粒子一起进行模拟计算. 固体粒子之间的相对位置会产生变化，引起粒子间应力的变化. 根据固体粒子之间的应力考虑固体弹性模量 $E$ 以及泊松比 $\mu $ ，对固体粒子的速度与位置进行修正. 不需要对流固耦合交界面进行特殊处理，既保证精度又简洁. 具体的模拟过程如图1所示. 在计算时，当流体粒子距离固体粒子过近（ ${r_{ij}} < 0.25l_0^2$ ， $l_0^{}$ 为粒子的初始间距）时，通过附加修正步对流体粒子位置进行修正. 考虑到对粒子速度的修正过大可能会影响计算，修正值取该粒子与其邻居粒子速度差值的和，如图2所示，在实际应用中效果较好.

2 数值模拟结果

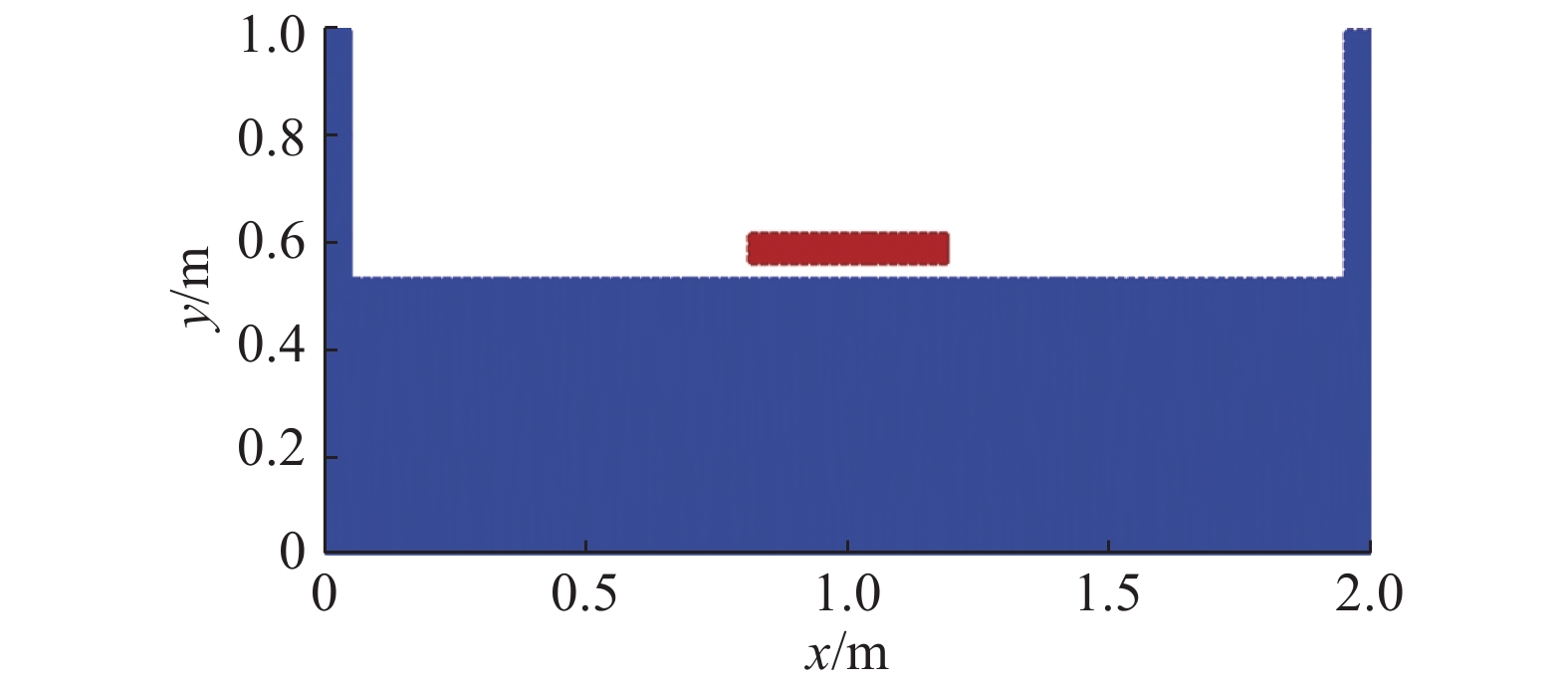
利用MPS法对弹性体入水的流固耦合问题进行模拟计算. 弹性平板冲击入水模型如图3所示，平板尺寸为0.4 m×0.2 m，平板密度为7 800 kg/m³，弹性模量为2.1 × 10¹¹ Pa，泊松比为0.3，入水速度为6.28 m/s. 粒子间距为0.01 m，时间步长为2.0×10⁻⁶ s.

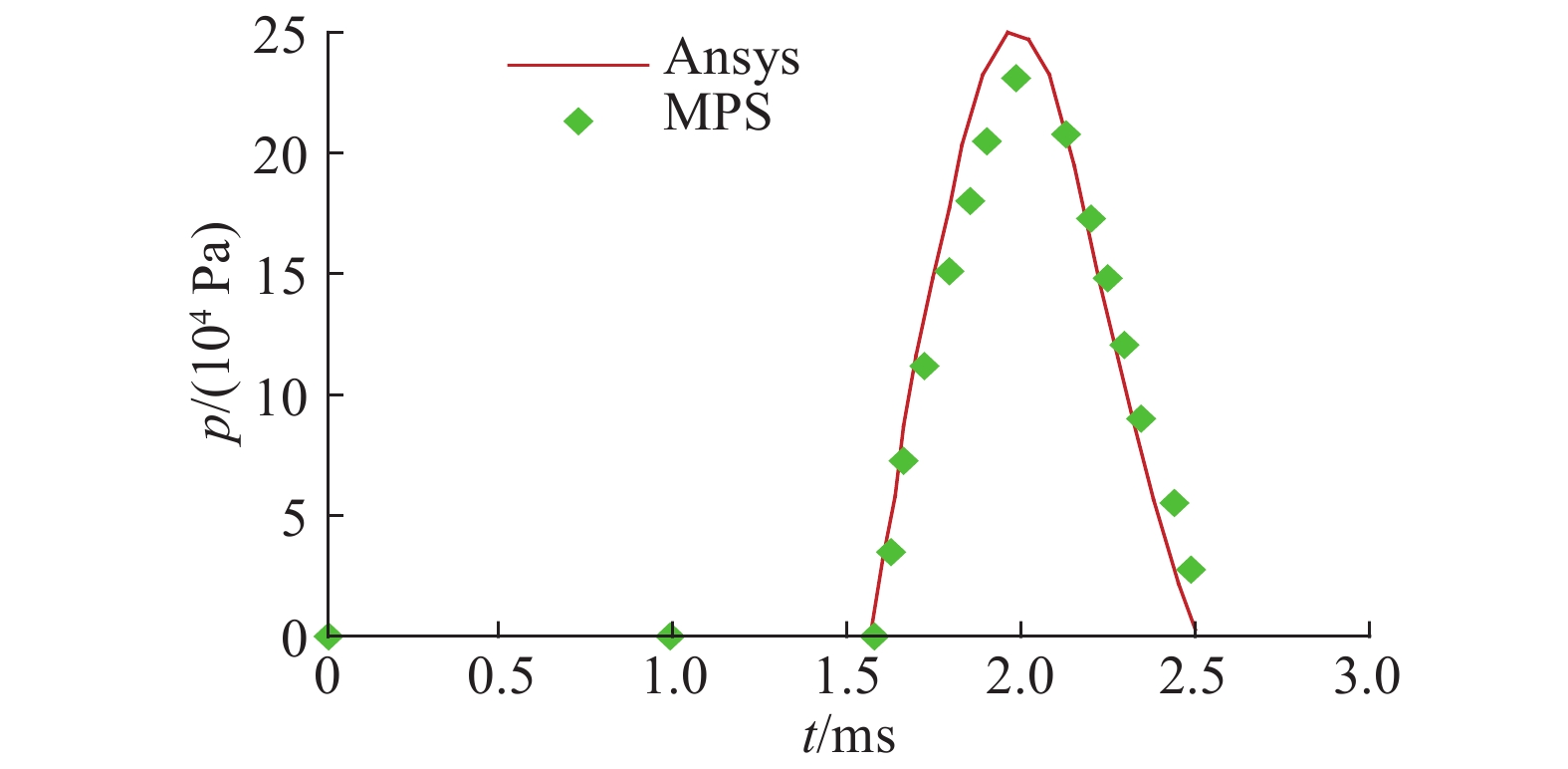
如图4所示为基于Ansys法和MPS法模拟平板入水的过程. Ansys法由于受到网格限制，只能模拟自由液面的变形轮廓，MPS法能够精确模拟水粒子的飞溅现象. 采用Ansys法模拟时，既要设置动网格又牵涉到流固耦合交界面的处理，对网格质量的要求非常高，前处理繁琐，在计算过程中常常由于网格扭曲导致计算终止. 且传统网格法Ansys法需要进行网格重构，导致计算效率较低，在相同工况下计算模型入水流固耦合问题时，MPS法所需的时间约为Ansys法的一半. 如图5所示为MPS法和Ansys法计算的平板中心压力p历时曲线图. 在弹性平板入水过程中，平板中心的冲击压力和变形最大. 结构物接触到水面的瞬间，平板底部中心处遭受的压力载荷迅速上升，之后在极短的时间内冲击压力达到峰值，又迅速衰减. 如图6所示，对于弹性平板，流体作用在结构物上的冲击载荷使结构产生相应的变形D，平板在冲击压力的作用下变形达到最大，之后随冲击压力的减小而减小. MPS法和Ansys法数值模拟的计算结果一致.

压力峰值的大小是平板结构是否会发生破坏或失效的决定性因素. 如表1所示为平板中心冲击压力峰值的实验结果与采用MPS法的计算结果的对比，结构入水的冲击压力的实验值与计算值相近. 实验值与计算值的变化趋势也一致，冲击压力峰值随着入水速度的增大相应增大. MPS法适用于计算弹性平板冲击入水的流固耦合问题，计算结果较精确. 进一步对和船体相似的盒式结构进行计算分析. 如图7所示，平底结构长和高分别为0.3 m和0.08 m，底部平板密度为7 800 kg/m³，弹性模量为2.1 × 10¹¹ Pa，泊松比为0.3. 弹性平底和周围框架刚性连接.盒式结构平底中心的冲击压力峰值极大地影响结构的局部强度，压力峰值的大小是盒式结构是否会发生破坏或失效的决定性因素.

如表2所示为模型分别以3种不同速度v入水的冲击压力峰值，MPS法与MSC.Dytran法^[17]的计算结果较接近. 且2种计算结果的变化趋势一致，压力峰值随着入水速度的增大而增大.

流体作用在盒式结构物上的冲击载荷会使结构产生相应的变形. 如图8所示，当结构接触水面时，由于冲击压力的作用，盒式平底结构变形瞬间达到最大，之后随着模拟的进行逐渐减小. 采用MPS法与MSC.Dytran法^[17]计算的数值曲线吻合度较高，所以利用MPS法计算盒式结构的结果真实可信.

3 结　语

传统的网格法如有限元法、有限差分法在模拟爆炸、冲击、大变形、大梯度、移动材料界面和自由表面等问题时，需要不断地重新划分网格，计算量大，计算精度不高，在解决流固耦合问题时存在较大的局限性. MPS法摆脱计算网格的约束，抛开网格重构，在处理流固耦合交界面等不连续问题时具有明显优势. 采用MPS法模拟平底结构冲击入水问题，能够准确模拟出流体大变形自由表面以及弹性结构在流体冲击作用下发生弹性变形的情况. 数值模拟的计算结果和采用其他方法得出的实验结果接近，MPS法能够较好地处理流固耦合大变形问题. MPS法从提出至今只有二十余年，尚不成熟，需要进一步改善的方面有，MPS法的内核是基于均布粒子展开的，要实现粒子的不均匀布置对MPS法来说是一个巨大的挑战；从目前的研究看，MPS法相当耗资源，提高MPS法的计算效率首先可以从编程自身挖掘，例如编写更合理的代码以及实现并行计算等.