随着现代结构产品功能和复杂性的增加,结构的可靠性越来越受到人们的重视. 实际工程结构的极限状态函数(limit state function,LSF)通常无法显式表达,为了精确评估失效概率,所需计算量太大,从而限制了大多数可靠性分析方法在实际工程结构中的应用. 代理模型也称为元模型或近似模型,是提高实际工程结构优化与分析效率的重要方法[1]. 常用的代理模型方法有响应面法、径向基函数方法、Kriging模型、神经网络法和支持向量机方法等. 其中支持向量机因其具有较强的小样本学习能力和泛化能力,已广泛应用于工程结构可靠性分析中[2].
结构可靠性分析主要通过判断结构系统的极限状态函数是否超过许用值来评估结构的失效概率. 小于许用值则认为结构处于安全域,反之则认为结构处于失效域[3]. 代理模型方法通常利用少量样本点来建立精度较高的显式或者近似极限状态函数. 不同的试验设计方法对代理模型精度有显著影响. Jin等[4]指出对于确定性的试验设计方法,样本点应分布在整个参数空间内,同时表明在相同的样本量与代理模型方法下,样本点分布越均匀,模型精度越高. 拉丁超立方抽样方法(Latin hypercube sampling,LHS)是一种广泛应用的试验设计方法. 虽然能够同时考虑可行域与不可行域,但难以保证训练样本的空间均匀性. 近年发展起来的质心Voronoi网格试验设计方法[5-8](centroidal Voronoi tessellation,CVT)和拉丁质心Voronoi网格试验设计方法[9-10](Latinized centroidal Voronoi tessellation,LCVT)较其他试验设计方法有更好的均匀性.
本文结合支持向量机回归方法与拉丁质心Voronoi网格试验设计方法,并将该方法应用于结构可靠性分析领域. 与其他抽样方法进行对比,在相同数量的训练样本集下,获取更多的设计变量空间信息,以建立更高精度的结构极限状态函数代理模型. 利用1个数值算例及2个工程算例,验证所提方法的计算性能和可行性.
1 质心Voronoi网格给定一个开区域为
| $\left.\begin{aligned} {v_i} = \left\{ {y \in \varOmega \left| {{{\left\| {y - {z_i}} \right\|}_2} < {{\left\| {y - {z_j}} \right\|}_2}} \right.} \right\}{\text{ }}{\text{;}} \\ j = 1,2,\,\cdots\,,n,\;j \ne i. \end{aligned}\right\}$ | (1) |
式中:
| $z_i^ * = \frac{{\int\limits_v {y\rho \left( y \right){\rm d}y} }}{{\rho \left( y \right){\rm d}y}}{\text{ }}.$ | (2) |
当
| $F\left( {{z_i},{v_i}} \right) = \sum\limits_{i = 1}^n {\int\limits_{y \in {v_i}} {\rho \left( y \right)} } {\left\| {y - {z_i}} \right\|^2}{\rm d}y{\text{ }}{\text{.}}$ | (3) |
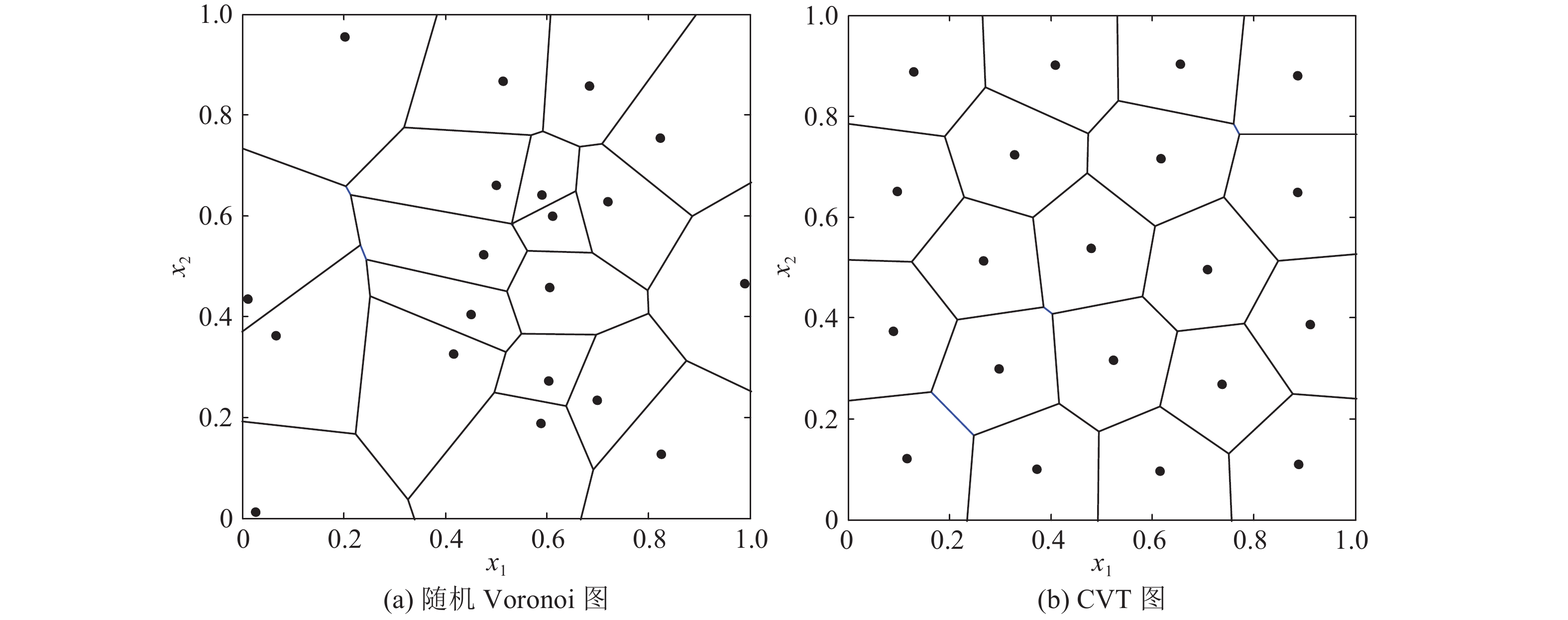
如图1所示为样本点数为20的随机 Voronoi 图和 CVT 图.
|
图 1 随机Voronoi图和CVT图 Fig. 1 Random Voronoi diagram and CVT diagram |
CVT抽样方法是在质心Voronoi网格(CVT)的基础上发展出来的一种试验设计方法[5-6]. Voronoi网格是对区域按空间距离进行的一个划分,CVT抽样方法是寻找一种最优的Voronoi划分,使得CVT抽样样本点为质心Voronoi网格中的质心点. CVT抽样方法具有良好的稳定性,在确定采样点之后,对应的质心Voronoi网格也确定了. Saka等[9]结合LHS方法和CVT抽样方法,提出新的抽样方法,称为拉丁质心Voronoi网格抽样方法. 对质心Voronoi网格进行特殊处理,使其具有拉丁超立方体的性质.
若LHS的样本量为
| $\left.\begin{aligned} {z_i}\left( j \right) = \frac{{{P_j}\left( i \right) - {U_{ji}}}}{n}{\text{ }}; \hfill \\ {\text{ }}i = 1,2,\,\cdots\,,n{\text{ }},\;j = 1,2,\,\cdots\,,d{\text{ }}{\text{.}} \hfill \\ \end{aligned} \right\}$ | (4) |
式中:
| $\begin{gathered} {z_i}\left( j \right) = \frac{{{P_j}\left( i \right) - 0.5}}{n}; \; i = 1,2,\,\cdots\,,d,\;j = 1,2,\,\cdots\,,n{\text{ }}{\text{.}} \hfill \\ \end{gathered} $ | (5) |
经过转换后,将非拉丁超立方体的抽样点调整为拉丁超立方体的抽样点,该调整称为拉丁化. 具体步骤如下:首先定义一个抽样点集
1)第
| $\begin{aligned} {S_k}{z_i}\left( j \right) = \left\{ {\begin{aligned} &{{z_i}\left( j \right),{\text{ }}{\text{ }}j \ne k}; \\ &{\displaystyle\frac{{i - {U_{ji}}}}{n},{\text{ }}{\text{ }}j = k}. \end{aligned}} \right.\end{aligned}$ | (6) |
2)第
3)对于任意一个抽样点集
| ${{\rm L{z}}_i} = \left( {\displaystyle\Pi _{k = 1}^d\left( {{S_k}{R_k}} \right)} \right){z_i}{\text{ }}{\text{.}}$ | (7) |
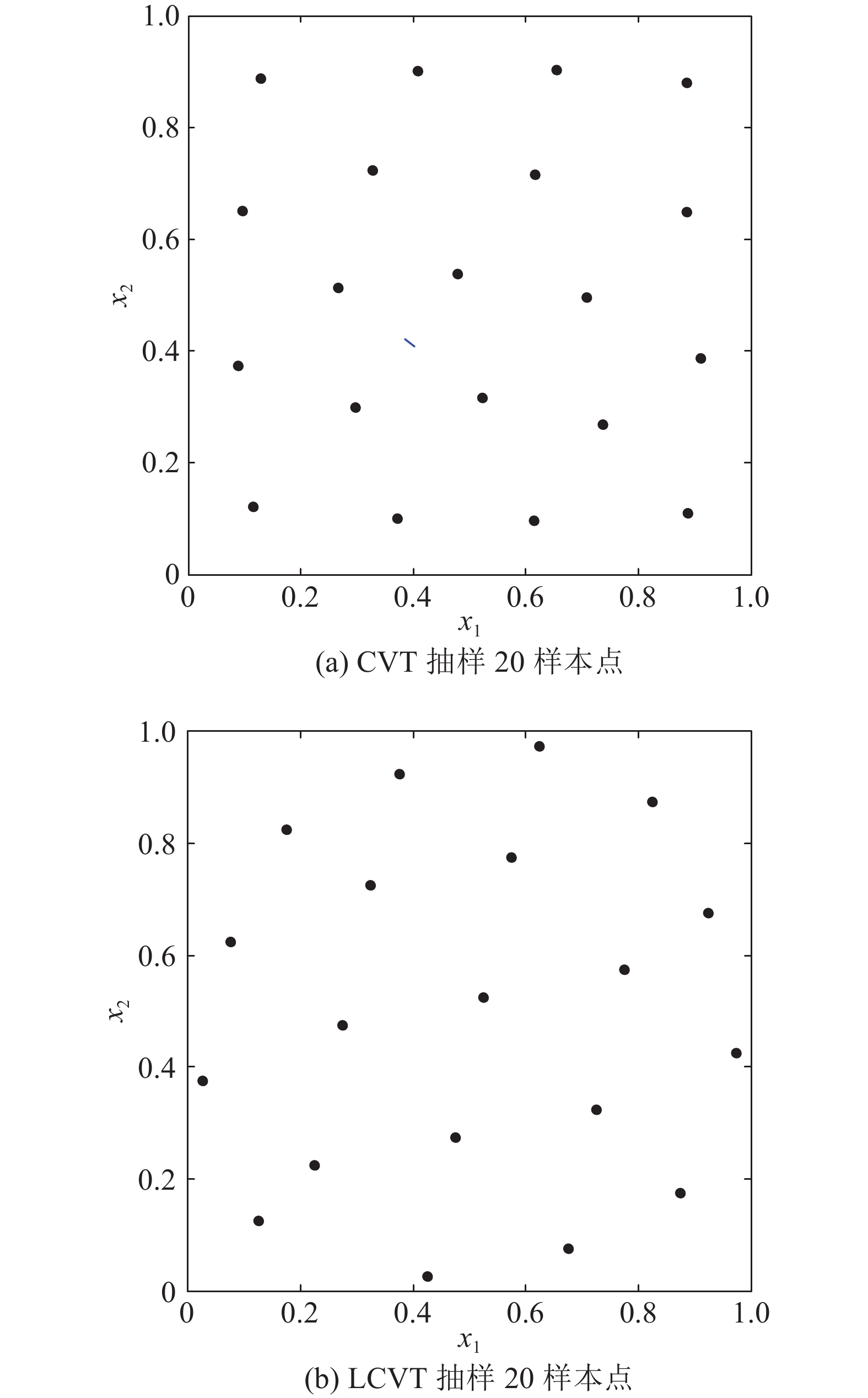
对质心Voronoi网格进行拉丁化,获得的新方法称为拉丁质心Voronoi网格. 如图2所示为CVT抽样点与LCVT抽样点.
|
图 2 CVT抽样与LCVT抽样比较 Fig. 2 Comparison of CVT sampling and LCVT sampling |
支持向量机方法(support vector machine,SVM)是建立在结构风险最小化原则和统计学习理论的VC维理论基础上的一种机器学习方法,可以用于分类问题与回归估计. 当SVM应用于回归估计的时候称为支持向量机回归(support vector regression,SVR). 利用SVR进行回归估计.
给定训练样本集:
| $\begin{gathered} S = \left\{ {{{\left( {{{{x}}_i},{{{y}}_i}} \right)}^l}} \right\};\; {{{x}}_i} \in {{\bf R}^n}\,,\;{{{y}}_i} \in {{\bf R}^m}\,,\; i = 1,2, \,\cdots\, ,m{\text{ }}{\text{.}} \hfill \\ \end{gathered} $ | (8) |
式中:
| $f({{x}}) = ({{w}} \cdot {{x}}) + {w_0}{\text{ }}{\text{.}}$ | (9) |
根据结构风险最小化原则,对式(9)的求解转化为优化问题:
| $\left.\begin{gathered} \left\| {{{ w}^2}} \right\| = {{\left( {{{w}} \cdot {{w}}} \right)} / 2}; \hfill \\ {\text{s}}{\text{.t}}{\text{. }}\left| {{y_i} - \left( {{{w}} \cdot {{{x}}_i}} \right) + {w_0}} \right| \leqslant \varepsilon ,i = 1,2,\cdots\,,m{\text{ }}{\text{.}} \hfill \\ \end{gathered} \right\}$ | (10) |
式中:
当约束条件不满足时,引入松弛变量
| $\begin{split} \min &{\text{ }}\frac{1}{2}\sum\limits_{i,j}^m {\left( {{\alpha _i} - \alpha _i^*} \right)} \left( {{\alpha _i} - \alpha _j^*} \right)\left( {{{{x}}_i} \cdot {{{x}}_j}} \right) +\\ &\varepsilon \sum\limits_{i = 1}^m {\left( {{\alpha _i} + \alpha _i^*} \right)} - \sum\limits_{i = 1}^m {{y_i}\left( {{\alpha _i} - \alpha _i^*} \right)} {\text{ }}{\text{.}} \end{split} $ | (11) |
式中:
约束条件为
| $\left.\begin{aligned} {\text{s}}{\text{.t}}{\text{. }}\sum\limits_{i = 1}^m {\left( {{\alpha _i} - \alpha _i^*} \right)} = 0;{\text{ }} \hfill \\ {\text{ 0}} \leqslant {\alpha _i},\;{\text{ }}\alpha _i^* \leqslant c{\text{ }}\left( {i = 1,2,\,\cdots\,,m} \right){\text{ }}{\text{.}} \hfill \\ \end{aligned} \right\}$ | (12) |
求得最优回归函数:
| $f\left( x \right) = \sum\limits_{{x_i} \in { S}_{\rm V}} {\left( {{\alpha _i} - \alpha _i^*} \right)} \left( {{{{x}}_i} \cdot {{{x}}_j}} \right) + {w_0}{\text{ }}{\text{.}}$ | (13) |
式中:
对于非线性训练样本,通过非线性变换
| $f\left( {{x}} \right) = \sum\limits_{{x_i} \in SV} {\left( {{\alpha _i} - \alpha _i^*} \right)} K\left( {{{{x}}_i},{{{x}}_j}} \right) + {w_0}{\text{ }}{\text{.}}$ | (14) |
在结构可靠性分析中,各随机变量通常服从某一种概率分布. 逆变换法是目前应用最广泛的随机变量产生方法. 令随机变量
| ${{{x}}_i} = {F^{ - 1}}\left( {{u_i}} \right){\text{ }}{\text{.}}$ | (15) |
对于SVR代理模型,训练样本的均匀性和覆盖性是至关重要的. 对于小失效概率的结构极限状态函数,上述简单随机抽样方法可能经过多次抽样不出现失效点,不宜作为SVR的训练样本. 参考文献[11],采用LCVT抽样方法在
对于
结构可靠性分析的LCVT-SVR方法的实现步骤如下.
1)确定结构输入变量数目
2)随机生成样本
3)根据式(7)不断调整
4)根据各随机变量的概率分布,由抽样策略将LCVT抽样的样本点转换为SVR的训练样本
5)对
| ${{x}}_i^* = \frac{{2\left( {{{{x}}_i} - {{{x}}_{i{\min }}}} \right)}}{{{{{x}}_{i{\max }}} - {{{x}}_{i{\min }}}}} - {\bf 1}{\text{ }}{\text{.}}$ | (16) |
式中:xi为归一化前的数据,xi*为归一化后的数据,ximax和ximin分别为归一化前数据的最大值和最小值.
6)通过
7)根据得到的SVR代理模型,运用蒙特卡罗方法计算失效概率:
| ${P_{\rm f}} = P\left( {g\left( {{x}} \right) \leqslant 0} \right) \approx P\left( {f\left( {{x}} \right) \leqslant 0} \right) = \frac{{{N_{\rm f}}}}{N}{\text{ }}{\text{.}}$ | (17) |
式中:
分别采用1个数值算例和2个工程算例,研究所提方法在结构可靠性中的应用,考察计算精度. SVR代理模型基于LIBSVM[12]工具箱建立.
4.1 算例1考察4次极限状态函数的可靠性分析,通过蒙特卡罗计算,得到失效概率为0.001 84[13].
| $g\left( {{x}} \right) = 2 + \exp \left( { - \frac{{x_1^2}}{{10}}} \right) + {\left( {\frac{{x_1^2}}{5}} \right)^4} - {x_2}{\text{ }}{\text{.}}$ | (18) |
式中:
对于常用的抽样方法,如简单随机抽样(simple random sampling,SRS)、LHS抽样、CVT抽样、LCVT抽样、均匀抽样(uniform sampling,US)以及Sobol、Halton、Hammersley等序列抽样方法,分别生成20个样本点,并构建SVR代理模型. 随机采样10 000个点作为测试样本. 其中
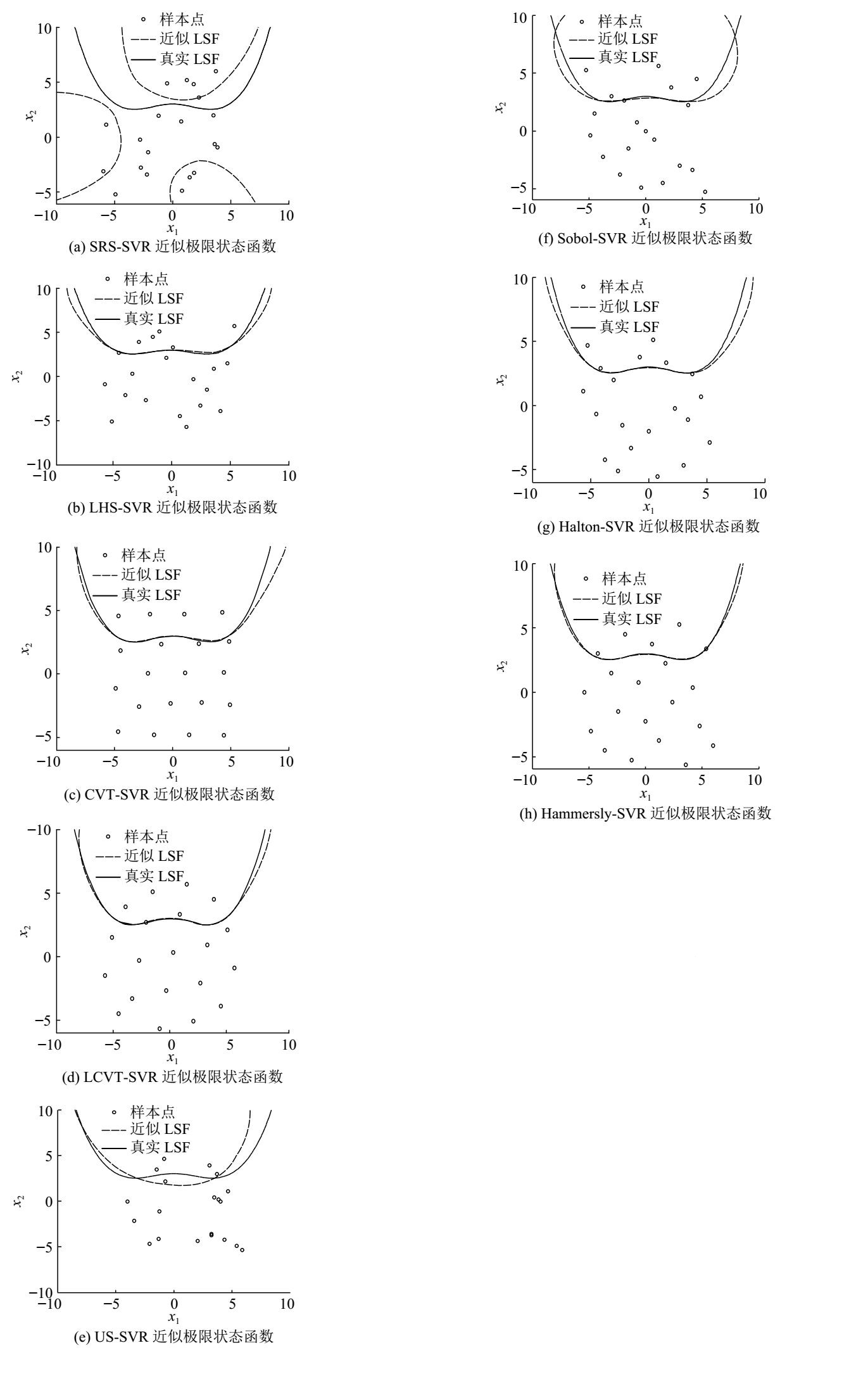
图3给出不同抽样方法下LSF的近似情况. 可以看出,SRS抽样与US抽样方法LSF的近似情况较差,其他抽样方法的近似情况较好. 表1给出不同抽样方法的计算结果. 表中,
|
图 3 不同抽样方法SVR模型近似极限状态函数 Fig. 3 Approximated LSFs of SVR model with different sampling methods |
| 表 1 不同抽样方法SVR模型的评价指标与计算结果 Table 1 Measure indices and computational results of SVR model with different sampling methods |
由表2可知,SRS和US抽样的SD和COV较大,表明SRS-SVR和US-SVR计算结果不稳定,计算精度不高,鲁棒性较差,这与图1和表1的结果相互验证. LCVT抽样均值更加接近理论值,同时SD较小,表明LCVT-SVR计算结果稳定,同时精度较高,鲁棒性较好,可以认为计算结果是可靠的.
| 表 2 不同抽样方法SVR模型统计学性能 Table 2 Statistical performance of SVR model with different sampling methods |
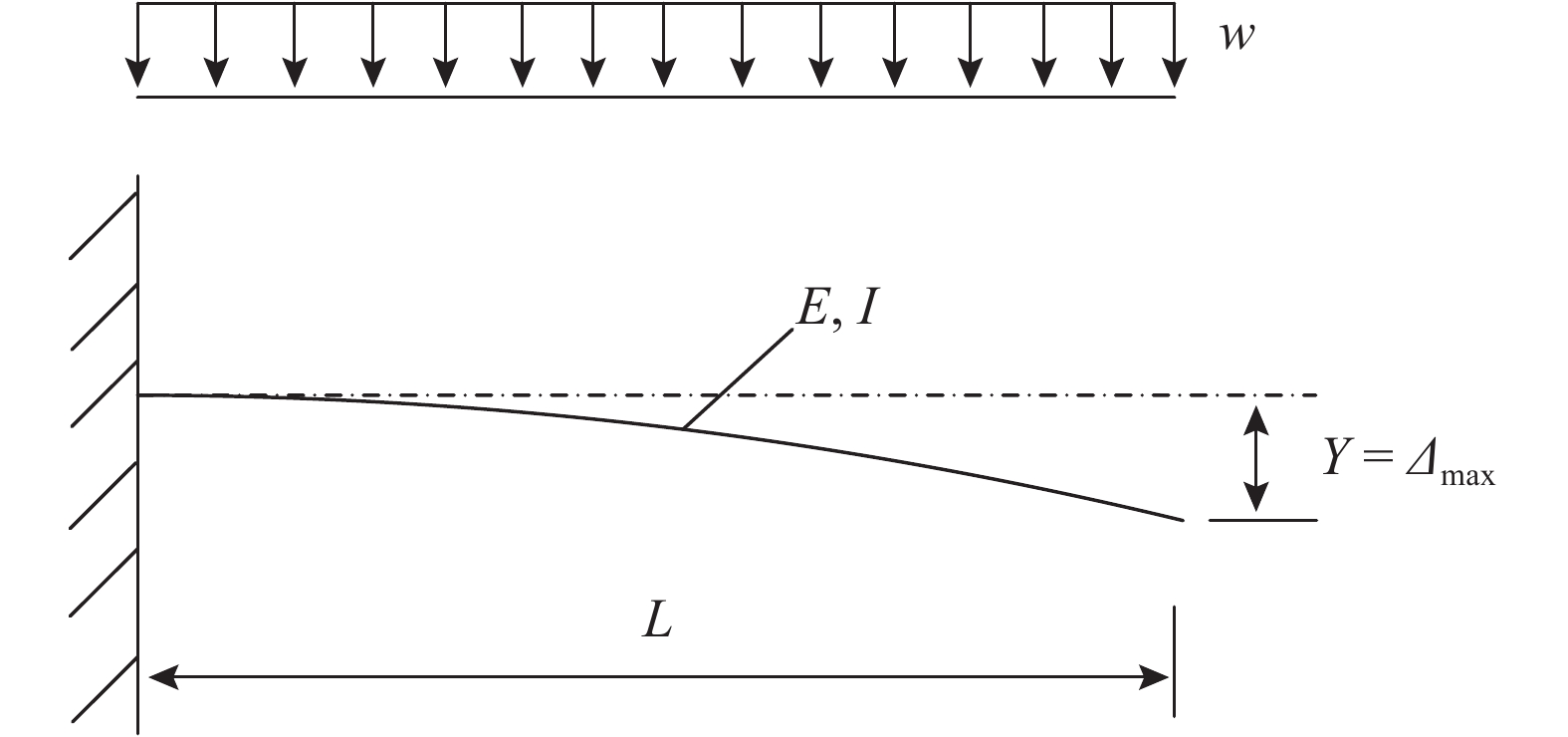
如图4所示为各向异性的悬臂梁结构[14],可以建立如下的极限状态函数:
| $g = g\left( {{{w}},{{L}},{{E}},{{I}}} \right) = {\varDelta _{\max }} - \frac{{w{L^4}}}{{8EI}}.$ | (19) |
式中:
|
图 4 悬臂梁结构示意图 Fig. 4 Cantilever beam structure diagram |
| 表 3 悬臂梁的输入随机变量 Table 3 Input random variables of cantilever beam |
采用本文方法,取均匀映射参数
| 表 4 悬臂梁失效概率 Table 4 Failure probabilities for cantilever beam |
从表4可以看出,LCVT方法的计算结果与文献[15]的理论值接近,尤其是在小失效概率区域能够更好地拟合结构极限状态函数.
4.3 算例3算例来自文献[15],如图5所示为九盒段机翼翼盒,该结构由64个杆单元和42个板单元组成. 由设计准则可以建立如下的极限状态函数:
| $g = g\left( {{{L}},{{A}},{{E}},{{P}},{{H}}} \right) = {\varDelta _{\max }} - {\varDelta _y}{\text{ }}{\text{.}}$ | (20) |
式中:
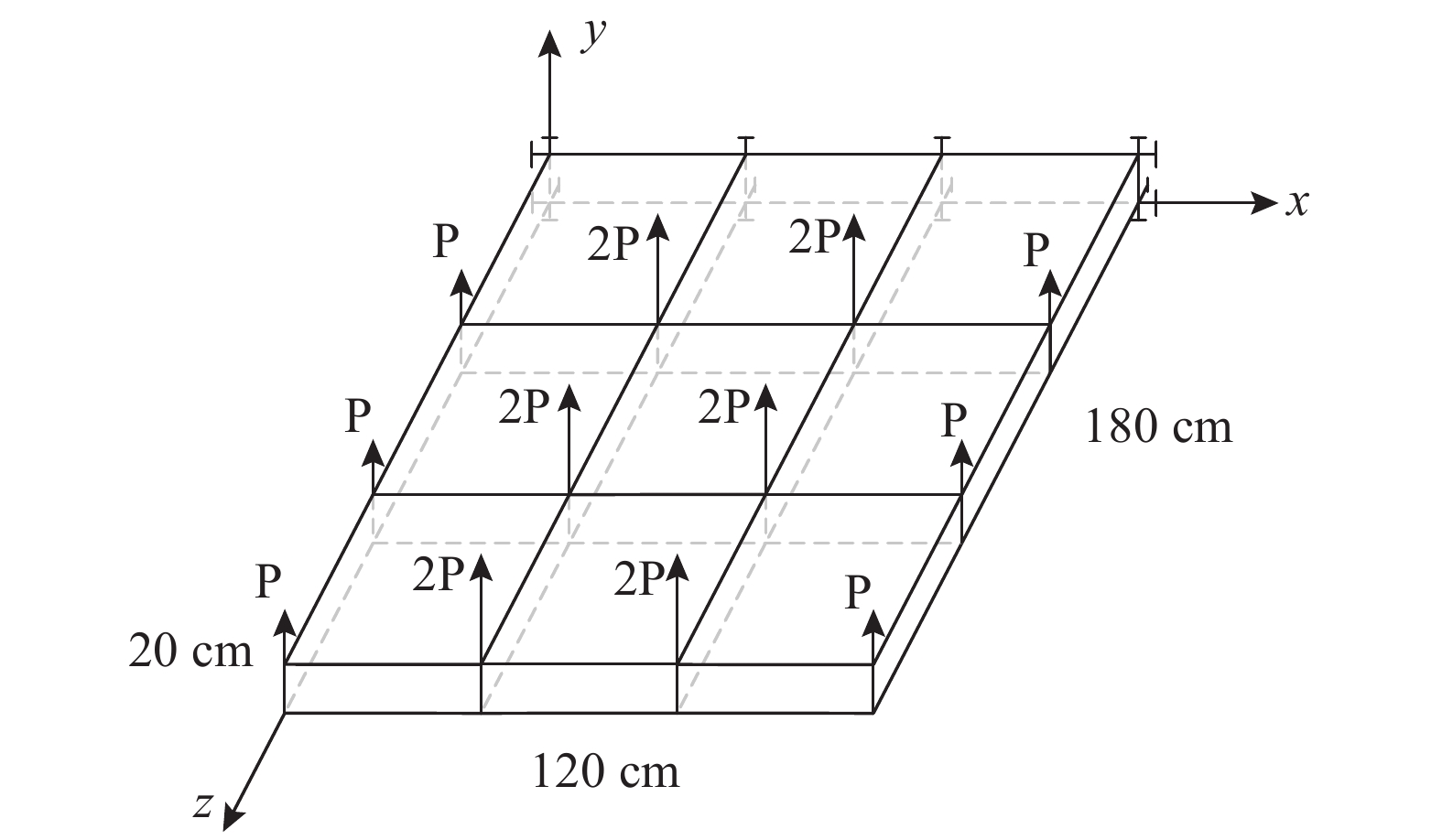
|
图 5 机翼翼盒结构示意图 Fig. 5 Wing box structure diagram |
| 表 5 机翼翼盒的输入随机变量 Table 5 Input random variables of wing box |
采用本文所提方法,取均匀映射参数
| 表 6 机翼翼盒失效概率 Table 6 Failure probabilities of wing box |
从表4、6可以看出,采用LCVT抽样方法得到的结构可靠性计算结果相较于其他抽样方法更接近MCS计算结果. 在CVT试验设计方法与LHS方法的基础上发展起来的LCVT试验设计方法兼具CVT方法的均匀性与LHS方法一定的随机性,能够更好地反映出参数设计空间的分布情况,从而避免了主观因素的干扰.
5 结 论(1)采用支持向量机回归建立代理模型,以较小的训练样本构建代理模型,可以用于结构可靠性分析中隐式极限状态函数计算量较大的问题.
(2)利用质心Voronoi网格产生分布均匀的CVT样本,对CVT样本进行拉丁化操作,得到兼具均匀性与随机性的LCVT样本. 在得到LCVT样本后,没有利用常用的逆变换法得到特定概率分布下的训练样本,而是将LCVT样本均匀映射至均值周围
(3)对结构可靠性分析中常用的抽样方法进行比较研究,包括SRS抽样、LHS抽样、CVT抽样、US抽样以及Sobol、Halton和Hammersly 3种序列抽样方法. 计算结果表明:在相同的抽样样本数及SVR参数下,LCVT抽样方法有着更高的均匀性和鲁棒性,基于LCVT构建的支持向量回归代理模型逼近精度高,可以用于结构可靠性分析.
| [1] |
QUEIPO N V, HAFTKA R T, WEI S, et al. Surrogate-based analysis and optimization[J]. Progress in Aerospace Sciences, 2005, 41(1): 1-28. DOI:10.1016/j.paerosci.2005.02.001 |
| [2] |
SONG H, CHOI K K, LEE I, et al. Adaptive virtual support vector machine for reliability analysis of high-dimensional problems[J]. Structural and Multidisciplinary Optimization, 2013, 47(4): 479-491. DOI:10.1007/s00158-012-0857-6 |
| [3] |
CHOI S K, CANFIELD R A, GRANDHI R V. Reliability-based structural design[M]. London: Springer, 2007: 207–212.
|
| [4] |
JIN R, CHEN W, SIMPSON T W. Comparative studies of metamodelling techniques under multiple modeling criteria[J]. Structural and Multidisciplinary Optimization, 2001, 23(1): 1-13. DOI:10.1007/s00158-001-0160-4 |
| [5] |
BURKARDT J, GUNZBURGER M, PETERSON J, et al. User manual and supporting information for library of codes for centroidal Voronoi point placement and associated Zeroth, first, and second moment determination[J]. Office of Scientific and Technical Information Technical Reports, 2002, 15(26): 399-406. |
| [6] |
DU Q, FABER V, GUNZBURGER M. Centroidal Voronoi tessellations: applications and algorithms[J]. Siam Review, 2006, 41(4): 637-676. |
| [7] |
RICHTER R, ALEXA M. Mahalanobis centroidal Voronoi tessellations[J]. Computers and Graphics, 2015, 46(C): 48-54. |
| [8] |
宋占杰, 张美, 何改云, 等. 基于质心Voronoi结构的自由曲面布点策略[J]. 吉林大学学报: 工学版, 2013, 43(1): 34-38. SONG Zhan-jie, ZHANG Mei, HE Gai-yun, et al. Sculptured surface point distribution strategy based on centroidal Voronoi tesssellation[J]. Journal of Jilin University: Engineering and Technology Edition, 2013, 43(1): 34-38. |
| [9] |
SAKA Y, GUNZBURGER M, BURKARDT J. Latinized, improved lhs, and cvt point sets in hypercubes[J]. International Journal of Numerical Analysis and Modeling, 2007(3/4): 729-743. |
| [10] |
ROMERO V J, BURKARDT J V, GUNZBURGER M D, et al. Comparison of pure and " Latinized” centroidal Voronoi tessellation against various other statistical sampling methods[J]. Reliability Engineering and System Safety, 2006, 91(10/11): 1266-1280. |
| [11] |
LI H S, ZHAO A L, KONG F T. Structural reliability analysis of multiple limit state functions using multi-input multi-output support vector machine[J]. Advances in Mechanical Engineering, 2016, 8(10): 1-11. |
| [12] |
CHANG C C, LIN C J. LIBSVM: a library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology (TIST), 2011, 2(3): 1-27. |
| [13] |
HURTADO J E, ALVAREZ D A. Classification approach for reliability analysis with stochastic finite-element modeling[J]. Journal of Structural Engineering, 2003, 129(8): 1141-1149. DOI:10.1061/(ASCE)0733-9445(2003)129:8(1141) |
| [14] |
HUANG B, DU X. Probabilistic uncertainty analysis by mean-value first order saddlepoint approximation[J]. Reliability Engineering and System Safety, 2008, 93(2): 325-336. DOI:10.1016/j.ress.2006.10.021 |
| [15] |
ZHOU C, LU Z, YUAN X. Use of relevance vector machine in structural reliability analysis[J]. Journal of Aircraft, 2013, 50(6): 1726-1733. DOI:10.2514/1.C031950 |



