2. 南京大学 地球科学与工程学院,江苏 南京 210046;
3. 上海地质调查研究院 国土资源部地面沉降监测与防治重点实验室,上海 200072
2. School of Earth Sciences and Engineering, Nanjing University, Nanjing 210046, China;
3. Key Laboratory of Land Subsidence Monitoring and Prevention, Ministry of Land and Resources, Shanghai Geological Survey, Shanghai 200072, China
地面沉降是全球许多大型缺水城市的主要地质环境问题,如威尼斯、墨西哥、美国加州、日本东京、泰国曼谷、中国台湾、上海、天津等地区[1-7]. 以往研究表明,过量抽取地下水,致使地下水位大幅降低,是导致区域地面沉降的主要原因[8-9]. 为此,Helm[9]建立一维有限差分地面沉降模型,用于定量刻画水位变化与地面沉降之间的关系,预测未来地面沉降量[8].
准确预测各种条件下的地面沉降量,能够为防治地面沉降提供科学依据[10]. 为了预测地面沉降量,建立区域地面沉降数值模型是有效的手段,例如上海市已经建立多个区域地面沉降模型[11-13]. 获取模型参数是一个较复杂的问题[14],许多参数不能直接使用室内或野外试验结果[15],因此参数校正或反演是模型应用中的重要环节. 本文利用敏感性分析方法,研究各模型参数对模拟沉降量的影响程度,为参数自动校正或反演提供指导.
敏感性分析方法可以分为局部和全局敏感性,以往地面沉降模型分析多采用局部敏感性分析方法,分析给定参数值情况下的局部敏感性[16-17]. 全局敏感性分析具有更多优势,可以同时分析多个参数变化及参数间相互耦合作用对模型输出结果的直接和间接影响,可以更加全面地检测参数对模拟结果的影响[18]. 近年来,全局敏感性分析及其衍生方法成为模型研究的热点,例如郑菲等[19]分析CO2地质封存模型,认为孔隙度对压力的影响最大,水平渗透率对气相CO2总量和扩散距离的影响最大;宋晓猛等[20]分析新安江水文模型,认为流域蒸发和散发折算系数对水流平衡模拟的影响较大,且各参数之间存在相互作用;张质明[21]分析WASP水质模型,认为各参数敏感性会随着时间(季节)变化,在某些时段内不敏感的参数,可能在另一时段内较敏感;Reusser等[22]分析TOPMODEL和WaSiM-ETH水文模型,认为动态全局敏感性分析是全面分析水文模型的有力工具.
本文使用上海市分层标、水位和钻孔数据,分析上海市地面沉降模型参数对模拟变形量的敏感性. 采用Sobol'法计算参数的敏感度,通过计算参数一阶敏感度,分析单个参数对模拟变形的影响;通过计算总敏感度,分析单个参数及其与其他参数组合对模拟变形的影响;通过计算交互敏感度,分析参数之间的交互影响;通过动态敏感性分析[23],分析各参数在不同模拟时间段内对模拟变形的影响.
1 地面沉降数值模型目前,区域地面沉降模型多采用一维有限差分地面沉降模型(COMPAC模型),计算土体的变形量[8, 24]. COMPAC模型[9]的理论基础为太沙基有效应力原理,对于均质黏土层(可以概化为弱透水层或者黏土夹层),孔隙水压力控制方程为
| $\frac{{{K_{\rm v}}}}{{{{S'}_{\rm{sk}}}}} \times \frac{{{\partial ^2}p'}}{{\partial {z^2}}} = \frac{{\partial p'}}{{\partial t}}.$ | (1) |
式中:当
| $\begin{split}\Delta b' = & - \frac{{\Delta z}}{2}\left[{S_{\rm{skv}}}\sum\limits_{j = 1}^{J - 1} {\left(\Delta p_{{\rm v}j}^n + \Delta p_{{\rm v}j + 1}^n\right)} -\right. \\ & \left.{S_{\rm{ske}}}\sum\limits_{j = 1}^{J - 1} {\left(\Delta p_{{\rm e}j}^n + \Delta p_{{\rm e}j + 1}^n\right)} \right].\end{split}$ | (2) |
式中:
COMPAC模型假设砂土层(可以概化为含水层)的变形是弹性变形,变形量为
| $\Delta b = {S_{\rm{sk}}}{b_0}\left( {{p^n} - {p^0}} \right).$ | (3) |
式中:pn为在时刻n(大于0)时含水层内的应力,也是弱透水层的边界应力,通常用含水层的水头表示;p0为含水层的初始应力;b0为系统内含水层厚度;Ssk为含水层贮水率. 弱透水层和含水层的变形量之和等于含水层整个含水层系统的变形量:
| $\Delta B = \Delta b + \Delta b'.$ | (4) |
涉及的地面沉降参数有5个:弱透水层垂向渗透系数Kv、弱透水层弹性贮水率Sske、弱透水层塑性贮水率Sskv、弱透水层前期最大固结应力PPmax(即前期最低水位)、含水层贮水率Ssk.
2 Sobol' 法全局敏感性分析Sobol' 法是一种较常用的定量全局敏感性分析方法[18-22]. 该方法的基本思想是将模型分解为单个参数及参数之间相互组合的函数,当参数正交时,模型具有唯一的分解形式. 此时,模型总方差可以由单个参数单独作用的方差和多个参数同时作用的方差组成[18]:
| $\begin{split}D =& \sum\limits_{i = 1}^{n} {D_i}+\sum\limits_{i = 1}^{n-1}\,\sum\limits_{j = i+1}^n\,{D_{ij}} + \sum\limits_{i = 1}^{n-2} \sum\limits_{j =i+ 1 }^{n-1} \sum\limits_{k=j+1}^{n}D_{ijk}+\cdots+\\ &\sum\limits_{i = 1}^{1} \sum\limits_{j=i+1}^{2}\sum\limits_{k=i+1}^{3} \cdots\sum\limits_{n}^{n}D_{123\cdots n}.\end{split}$ | (5) |
式中:D为模型总方差;Di为参数xi独立影响的方差,Dij为参数xi、xj共同影响的方差,D123…n为n个参数共同影响的方差. 对式(5)进行归一化处理(即式(5)两端乘以模型总方差D),定义敏感度为
| ${S_{123\cdots N}} = {{{D_{123\cdots N}}}}/{D}.$ | (6) |
| $\begin{split}&\sum\limits_{i = 1}^n {{S_i}} + \sum\limits_{i = 1}^{n-1}\sum\limits_{j = i+1}^n S_{ij}+\sum\limits_{i = 1}^{n-2}\sum\limits_{j =i+ 1}^{n-1}\sum\limits_{k =j+ 1}^n S_{ijk}+\cdots+\\ &\sum\limits_{i = 1}^1\sum\limits_{j =i+ 1}^2\sum\limits_{k = j+1}^3\cdots\sum\limits_{n}^n S_{123\cdots n} = 1 .\end{split}$ | (7) |
式中:Si为一阶敏感度,描述单个参数xi在模型中所造成的影响;Sij为二阶敏感度,描述xi和xj两个参数共同作用对模型的影响;S123…n为n阶敏感度,表征n个参数共同作用对模型的影响. 第i个参数的总敏感度为
| ${S_{{{\rm T}i}}} = \sum {{S_{(i)}}}. $ | (8) |
式中:S(i)为所有包含参数i的敏感度. Sobol'敏感性分析的优点如下:对模型的线性、单调性及输入参数的概率分布特征没有要求,且可以分析模型单个参数及参数之间相互作用对模型输出的影响[18].
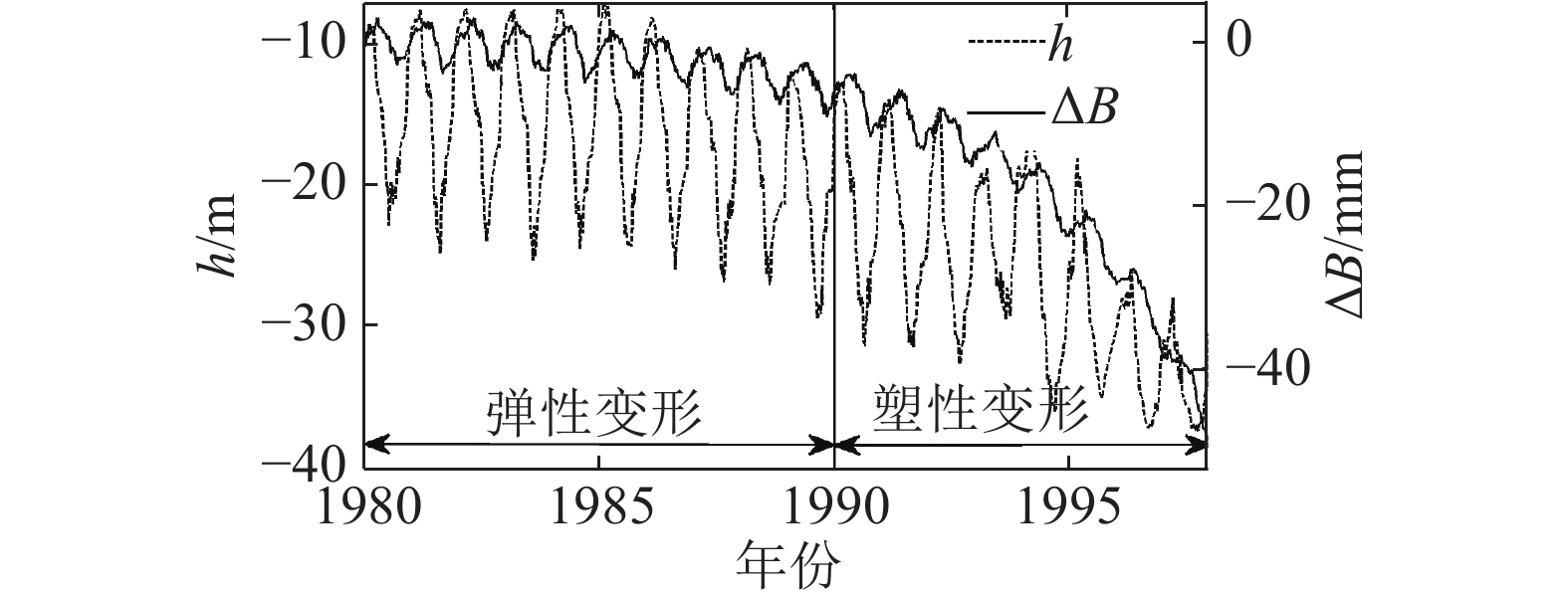
3 敏感度计算结果与讨论 3.1 算例概况上海市于90年代,大量开采地下水,尤其是第四承压含水层,致使该层发生较大压缩,于1998年达到最大压缩速率[25]. 由于严峻地地面沉降灾害带来了巨大经济损失,上海市建设27组分层标(不包括浅层分层标)用于监测上海市5个承压含水层及弱透水层的变形[25]. 使用上海市具有典型变形特征的分层标数据(选用分层标编号为F10-2[14, 25])作为示例,分析COMPAC地面沉降模型的参数敏感性. 该分层标监测埋深为165.20~210.76 m土层的变形,监测厚度为45.56 m. 钻孔数据显示该段地层为第四承压含水层,砂土厚b0=42.36 m,黏土层(弱透水层)只有一层,厚度b'0=3.20 m,顶底部都可排水,符合COMPAC模型双向排水的基本假设. 土层变形及相应的水位h见图1,模型参数取值如表1所示. 模型的模拟时间是1980~1998年,在该时间段内上海市地面沉降较严峻,是重点研究时期[12, 14]. 该时间段土层从压缩-回弹循环周期变形(称为弹性变形阶段,图1中的1980~1990年),变为总体持续压缩(称为塑性变形阶段,图1中的1990~1998年),于1998年压缩速率达到最大.
|
图 1 水位和变形历时图 Fig. 1 History of groundwater level and deformation |
| 表 1 地面沉降模型参数及范围 Table 1 Parameters and ranges for land subsidence model |
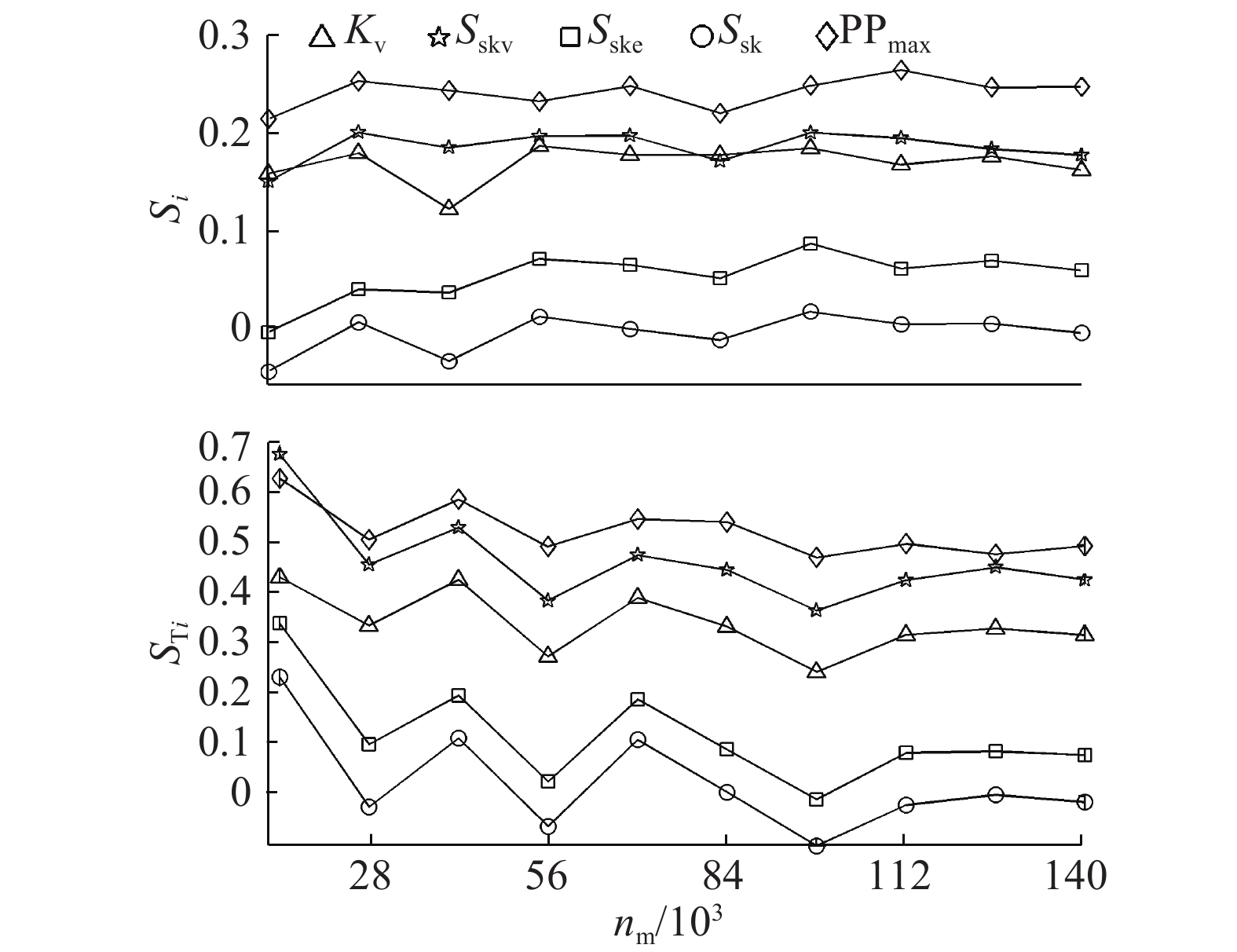
使用全局敏感性分析工具箱SAFE (sensitivity analysis for everybody)[26]计算敏感度. 该工具箱的主要特色如下:不仅提供多种方法计算敏感度,还能够查看敏感度计算的收敛过程,分析敏感度计算结果的可靠性. 首先采用均方误差(即各模拟时间步处的模拟值与观测值之差平方和的平均值)作为响应变量,使用工具箱中的Sobol’方法计算敏感度,分析COMPAC模型中5个参数的敏感性. 图2显示了Sobol’法的一阶和总敏感度及置信区间,其中含水层弹性贮水率敏感度可能出现负值,这是由数值误差引起的. 这种误差不影响分析结果,因为敏感度出现负值通常表示敏感度非常低[18]. 由于Sobol'法的结果易受到取样数量的影响,需要探讨样本数量对计算结果的影响,确保计算结果的准确性. 图3显示模型运行14 000~140 000次(即样本为2 000~20 000组)过程中,敏感度仅有少量波动,敏感度计算稳定. 图中,nm为模型运行次数. 如图2所示为敏感度的置信区间. 图中,色块上、下边表示置信区间,中间黑色横线表示敏感度. 各参数的置信区间范围较小,且总体上不改变各参数的敏感性排序,说明敏感度计算结果可靠.

|
图 2 Sobol'法敏感度计算结果 Fig. 2 Sensitivity analysis result from Sobol' method with confidence bounds |
|
图 3 Sobol'法敏感度收敛过程 Fig. 3 Convergence of sensitivity indices using Sobol' method |
一阶敏感度(或者称为主要敏感度)表征单个参数对目标函数的影响能力,总敏感度表征一个参数与其他参数结合对目标函数的影响能力. 一阶敏感度和总敏感度的差值为参数的交互敏感度,表征参数间相互耦合作用的间接影响能力,实质上反映了模型“异参同效”的可能性大小[15]. 图2显示前期最低水位、弱透水层塑性贮水率和渗透系数的一阶敏感度分别为0.243、0.187和0.174,总敏感度分别为0.493、0.430和0.309,因此交互敏感度分别为0.250、0.243和0.135. 通过敏感度计算结果可得如下结论. 1)前期最低水位、弱透水层塑性贮水率和渗透系数3个参数的敏感度显著高于其他参数,表示地面沉降主要受这3个参数的控制. 2)含水层贮水率的敏感性较小,当参数自动校正或反演时,可以固定该参数值提高反演效率和准确性. 3)前期最低水位和弱透水层塑性贮水率的交互敏感度较大,大于一阶敏感度,说明模型参数的“异参同效”性较大.
3.3 讨论上文的敏感性分析忽略了影响敏感度计算结果的2个因素. 1)时序数据影响,前文敏感性分析把模型输出的变形时序数据变换成目标函数(均方误差),综合考察参数对模拟结果的影响,忽略了模拟结果在不同时间段内会有不同特征,各参数的敏感性在不同时段内可能存在显著的不同;2)参数区间影响,计算敏感度时需要确定各参数的取值区间,不同的参数区间可能会影响敏感度的计算结果.
3.3.1 时序数据的影响与以目标函数(或者称为似然函数,例如均方误差、Nash-Sutcliffe系数)为响应变量的静态敏感性分析不同,动态敏感性分析计算每个模拟时间步处的敏感度,能够观察模型参数对输出结果的影响在时间上的变化,可以分析参数敏感性在不同模拟时间段内的特征. 为了探讨不同时段内各参数敏感性的变化,使用Sobol'法计算每个模拟时间步处的敏感度(即动态敏感性分析[26]),计算结果如图4所示. 图4显示含水层贮水率和前期最低水位在模拟初期存在较大波动,可能是由于初始时刻变形量较小引起的. 含水层贮水率敏感度在其他时间段内敏感度都不大于0.03,说明该参数在整个模拟时间段内对模拟结果的影响都非常小. 弱透水层渗透系数和塑性贮水率在时间上的总体变化规律类似,随着时间的推移,敏感度逐渐增大. 在模拟初期(1980~1981年),渗透系数对模拟结果的影响较大,塑性贮水率非常小. 这是因为在模拟初期弱透水层主要是弹性变形,与塑性贮水率无关,但渗透系数会影响弱透水层中水压传递的快慢,通过与弹性贮水率配合,影响模拟变形量. 前期最低水位的敏感度总体上呈现先增大后减小,在1994年4月达到最大值(总敏感度为0.580). 这说明前期最低水位在模拟初始阶段对模拟结果的影响较小,1994年4月达到最大,之后逐渐减小. 累积沉降量(即1980~1998年的总沉降量)主要受弱透水层塑性贮水率、渗透系数和前期最低水位的影响,因此最终地面沉降量主要受这3个参数的控制.

|
图 4 动态敏感性分析 Fig. 4 Dynamical sensitivity analysis |
动态敏感度计算结果与静态敏感性分析最大的不同体现在弱透水层弹性贮水率. 图1显示在1990年以前(视为弹性变形阶段),弱透水层弹性贮水率的总敏感度一直大于其他参数,最大值达到0.929,1980~1990年间的平均值为0.670,说明该时期的模拟变形量主要受到该参数的影响. 当使用均方误差(即目标函数)作为响应变量时,该参数的敏感度较小,不能反映该参数对弹性变形阶段的较大影响(见图2). 产生这种现象的原因如下:1980~1990年属于弹性变形阶段,变形量较小,对目标函数的贡献较小,弱化了弹性变形阶段的拟合效果对目标函数的影响,致使该参数不敏感. 为了使目标函数能够准确反映弹性变形阶段的拟合状况,通常采用加权均方误差(权重等于观测值平方的倒数)[16],此时会大幅提高该参数的敏感性,便于该参数校正. 若该算例的目标函数改为加权均方误差,则该参数的总敏感度最大(见图5),达到0.732,一定程度上增加了该参数的可识别性,但此时各参数的交互敏感度较大(见图5),增加了“异参同效”性,会给参数识别带来较大的不确定性,这说明加权均方误差作为响应变量不是最佳选择. 建议目标函数采用均方误差,但分2个变形阶段分别校正或反演模型参数.

|
图 5 更改目标函数的Sobol'敏感性分析结果 Fig. 5 Sensitivity analysis result of Sobol' with modified objective function |
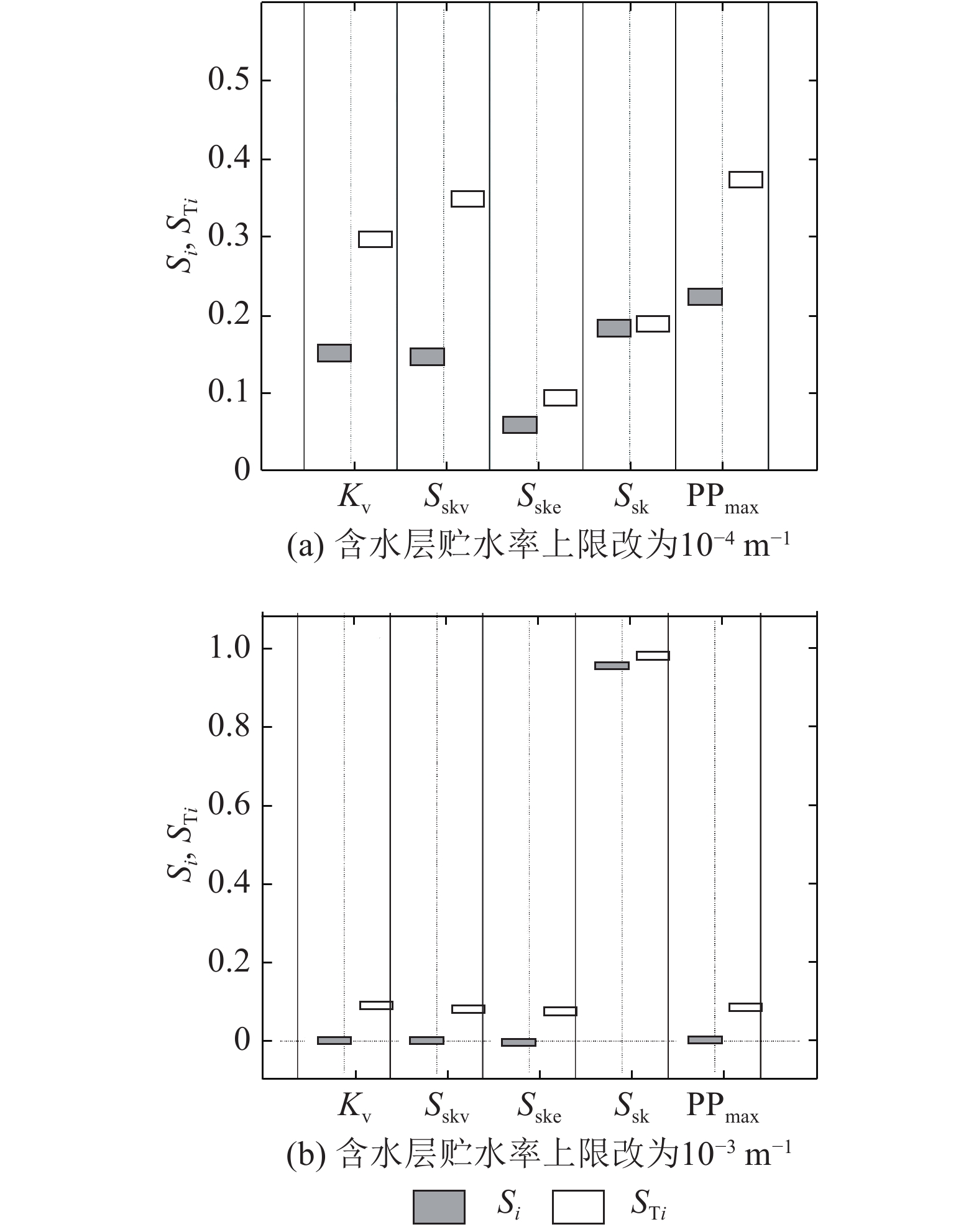
Sobol' 法的敏感度计算结果(见图2)显示含水层贮水率对模拟结果的影响非常小. 若将贮水率的上限改为10–4 m–1,则该参数的敏感度会显著增加(见图6(a));若上限改为10–3 m–1,总敏感度达到0.987,模拟结果几乎完全受该参数的影响(见图6(b)). 这是因为当贮水率最大值为10–5 m–1时,根据式(3)可知,水位下降30 m(见图1),含水层的压缩量仅为12.7 mm,相对弱透水层的变形量较小. 当贮水率上限改为10–4和10–3 m–1时,含水层压缩量分别达到127和1 271 mm,会显著影响目标函数值. 分析水位-变形历时图(见图1)发现,贮水率取值为10–5 m–1更加合理. 假设所有的变形都来自于含水层,则贮水率应该小于7.9×10–6 m–1. 若贮水率取值为10–4 m–1,则变形波动达到63.5 mm,显然大于观测变形量(见图1). 这表示贮水率上限改为10–3或者10–4 m–1不合理,会对敏感性分析带来错误结果,也会增加参数自动校正的不确定性.
|
图 6 更改贮水率范围的Sobol'敏感性分析结果 Fig. 6 Sensitivity analysis results of Sobol' with modified range of skeletal specific storage of aquifers |
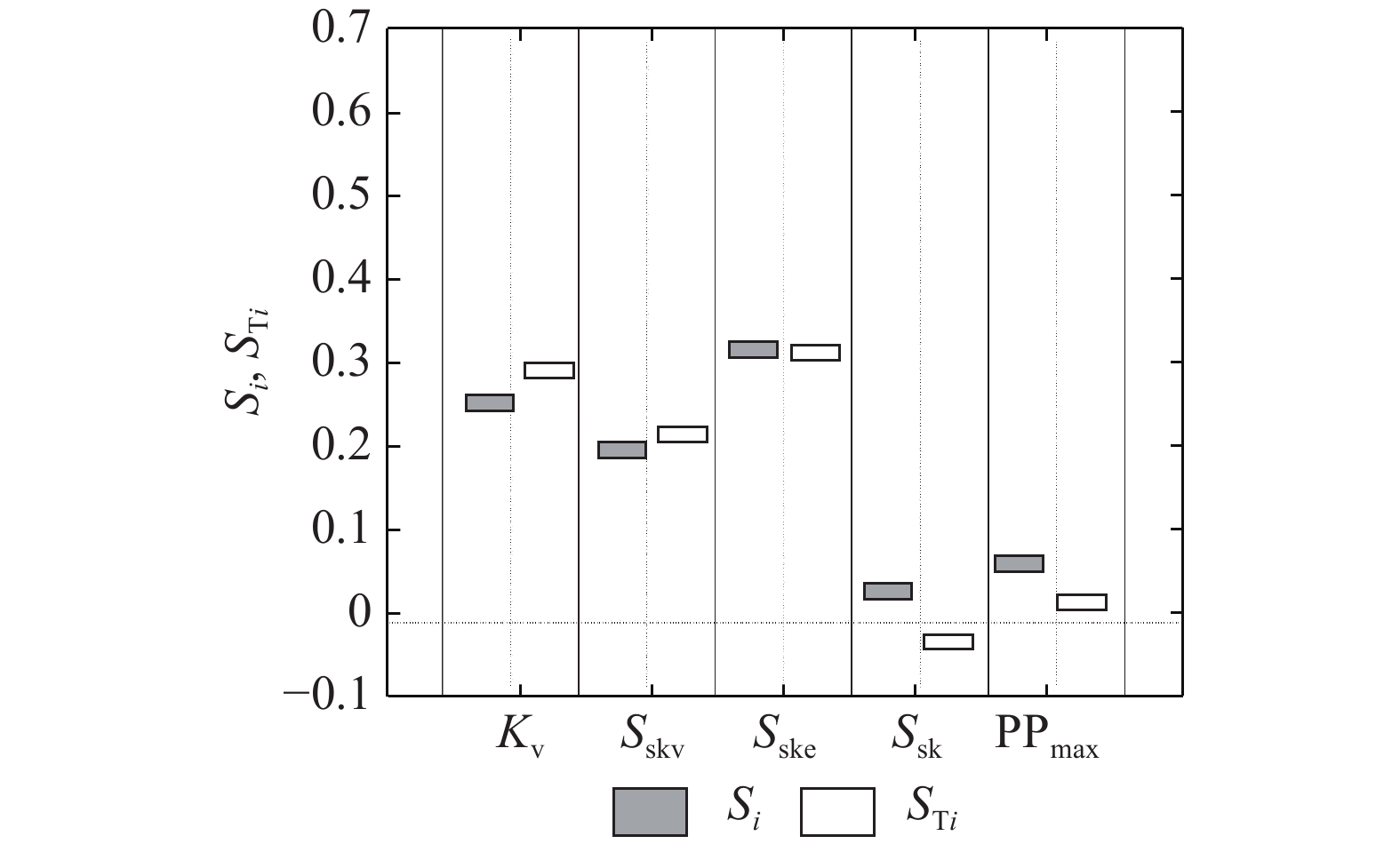
在上文的算例中,前期最低水位的范围都设置为–30~–20 m ,但如果通过研究水位和变形曲线,将其范围缩小为–28~–25 m,此时该参数的敏感度会大幅降低,如图7所示. 弱透水层渗透系数、弹性贮水率和塑性贮水率成为模拟变形的主要影响参数,且此时参数的交互敏感度降低,“异参同效”性减小,有利于参数校正和反演. 如图8所示为动态敏感度. 图中,Sint为交互敏感度. 结果显示,1980~1994年间,变形主要受弱透水层弹性贮水率的影响,前期最低水位和弱透水层塑性贮水率于1990年后产生明显的影响,更加符合实际情况. 各参数的交互敏感度在多数时间内都小于0.1(见图8),说明“异参同效”性小,有利于参数校正或反演. 此时累积沉降量主要受弱透水层渗透系数和塑性贮水率的影响. 参数自动校正或反演时不能完全依靠优化软件,需要分析变形-水位观测数据,初步判断各参数的合理区间,得到合理、可信的结果.
|
图 7 更改前期最低水位范围的Sobol'敏感性分析结果 Fig. 7 Sensitivity analysis result of Sobol' with modified range of preconsolidation stress |

|
图 8 更改前期最低水位范围的动态敏感性分析 Fig. 8 Dynamical sensitivity analysis with modified range of preconsolidation stress. |
(1)含水层贮水率的敏感度较小,说明该参数对模拟结果的影响有限,因此参数校正或反演时可以固定该参数,提高模型校正或反演的效率.
(2)在1980~1990年间(弹性变形阶段),土层变形量主要受弱透水层弹性贮水率的影响,1990~1998年间(塑性变形阶段)的变形量主要受弱透水层塑性贮水率、渗透系数和前期最低水位的影响,说明不同变形阶段各参数的敏感性差异较大. 以均方差为目标函数的敏感度计算不能体现弱透水层弹性贮水率对弹性变形的较大影响. 若直接使用1980~1998年间的全部数据进行参数自动校正或反演,则不能较好地校正或反演此参数. 为了增加弹性变形阶段对目标函数的影响,通常使用加权均方差作为目标函数. 该目标函数会增大参数的交互敏感性和“异参同效”性. 这说明加权均方差(权重等于观测值平方的倒数)作为目标函数,不是最佳的解决方法,因此建议使用均方差作为目标函数,但须在弹性和塑性变形两个阶段分别校正不同的参数.
(3)参数取值区间会显著影响参数敏感度的计算结果,主要体现在以下2个方面:当含水层贮水率上限设置过大时,会高估该参数的敏感度;当前期最低水位取值范围较大时,各参数的交互敏感度会较大. 在自动校正或反演参数前,需要分析水位和变形曲线,给出合理的含水层贮水率上限,缩小前期最低水位范围,能够大幅降低各参数的交互敏感度,减小“异参同效”性,提高参数校正的效率,降低不确定性.
| [1] |
龚士良. 国务院审批同意《全国地面沉降防治规划(2011—2020年)》[J]. 上海国土资源, 2012, 33(1): 61. GONG Shi-liang. The state council for examination and approval " the ground subsidence control plan (2011—2020)”[J]. Shanghai Land and Resources, 2012, 33(1): 61. DOI:10.3969/j.issn.2095-1329.2012.01.015 |
| [2] |
MIURA N, HAYASHI S, MADHAV M R, et al. Problems of subsidence and their mitigation in Saga Plain, Japan [C] // Proceedings of the 5th International Symposium on Land Subsidence. Netherlands: IAHS-AISH, 1995: 463-470.
|
| [3] |
PHIEN W N, GIAO P H, NUTALAYA P. Land subsidence in Bangkok, Thailand[J]. Engineering Geology, 2006, 82(4): 187-201. DOI:10.1016/j.enggeo.2005.10.004 |
| [4] |
CHEN C, HU J, LU C, et al. Thirty-year land elevation change from subsidence to uplift following the termination of groundwater pumping and its geological implications in the Metropolitan Taipei Basin, Northern Taiwan[J]. Engineering Geology, 2007, 95(1): 30-47. |
| [5] |
CALDERHEAD A I, MARTEL A, ALASSET P, et al. Land subsidence induced by groundwater pumping, monitored by D-InSAR and field data in the Toluca Valley, Mexico[J]. Canadian Journal of Remote Sensing, 2010, 36(1): 9-23. DOI:10.5589/m10-024 |
| [6] |
SNEED M. Measurement of land subsidence using interferometry, Coachella Valley, California [C] // Proceedings of the 8th International Symposium on Land Subsidence. Mexico: IAHS-AISH, 2010: 260–263.
|
| [7] |
GAMBOLATI G, PUTTI M. A comparison of lanczos and optimization methods in the partial solution of sparse symmetrical eigenproblems[J]. International Journal for Numerical Methods in Engineering, 1994, 37(4): 605-621. DOI:10.1002/(ISSN)1097-0207 |
| [8] |
GALLOWAY D L, BURBEY T J. Review: regional land subsidence accompanying groundwater extraction[J]. Hydrogeology Journal, 2011, 19(8): 1459-1486. DOI:10.1007/s10040-011-0775-5 |
| [9] |
HELM D C. One-dimensional simulation of aquifer system compaction near pixley, california.1. constant parameters[J]. Water Resources Research, 1975, 11(3): 465-478. DOI:10.1029/WR011i003p00465 |
| [10] |
薛禹群, 张云, 叶淑君, 等. 我国地面沉降若干问题研究[J]. 高校地质学报, 2006, 12(2): 153-160. XUE Yu-qun, ZHANG yun, YE Shu-jun, et al. Research on the problems of land subsidence in China[J]. Geological Journal of China Universities, 2006, 12(2): 153-160. DOI:10.3969/j.issn.1006-7493.2006.02.001 |
| [11] |
WU J, SHI X, YE S, et al. Numerical simulation of viscoelastoplastic land subsidence due to groundwater Overdrafting in Shanghai, China[J]. Journal of Hydrologic Engineering, 2010, 15(3): 223-236. DOI:10.1061/(ASCE)HE.1943-5584.0000172 |
| [12] |
YE S, LUO Y, WU J, et al. Three-dimensional numerical modeling of land subsidence in Shanghai, China[J]. Hydrogeology Journal, 2016, 24(3): 695-709. DOI:10.1007/s10040-016-1382-2 |
| [13] |
YE S, XUE Y, WU J, et al. Modeling visco-elastic–plastic deformation of soil with modified Merchant model[J]. Environmental Earth Sciences, 2012, 66(5): 1497-1504. DOI:10.1007/s12665-011-1389-x |
| [14] |
LUO Y, YE S, WU J, et al. A modified inverse procedure for calibrating parameters in a land subsidence model and its field application in Shanghai, China[J]. Hydrogeology Journal, 2016, 24(3): 711-725. DOI:10.1007/s10040-016-1381-3 |
| [15] |
BEVEN K, FREER J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology[J]. Journal of Hydrology, 2001, 249(1–4): 11-29. |
| [16] |
YAN T, BURBEY T J. The value of subsidence data in ground water model calibration[J]. Ground Water, 2008, 46(4): 538-550. DOI:10.1111/gwat.2008.46.issue-4 |
| [17] |
HOFFMANN J, ZEBKER H A, GALLOWAY D L, et al. Seasonal subsidence and rebound in Las Vegas Valley, Nevada, observed by synthetic aperture radar interferometry[J]. Water Resources Research, 2001, 37(6): 1551-1566. DOI:10.1029/2000WR900404 |
| [18] |
SALTELLI A. Global sensitivity analysis: the primer [M]. England: Wiley, 2008: 11.
|
| [19] |
郑菲, 施小清, 吴吉春, 等. 深部咸水层CO2地质封存数值模拟参数的全局敏感性分析: 以苏北盆地盐城组为例
[J]. 吉林大学学报: 地球科学版, 2014, 44(01): 310-318. ZHENG Fei, SHI Xiao-qing, WU Ji-chun, et al. Global parametric sensitivity analysis numerical simulation for CO2 geological sequestration in saline aquifers: a case study of Yancheng formation in Subei basin [J]. Journal of Jilin University: Earth Science Edition, 2014, 44(01): 310-318. |
| [20] |
宋晓猛, 孔凡哲, 占车生, 等. 基于统计理论方法的水文模型参数敏感性分析[J]. 水科学进展, 2012, 23(05): 642-649. SONG Xiao-meng, KONG Fan-zhe, ZHAN Che-sheng, et al. Sensitivity analysis of hydrological model parameters using a statistical theory approach[J]. Advances in Water Science, 2012, 23(05): 642-649. |
| [21] |
张质明. 基于不确定性分析的WASP水质模型研究[D]. 北京: 首都师范大学, 2013. ZHANG Zhi-ming. Study of WASP model based on uncertainty analysis [D]. Beijing: Capital Normal University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10028-1013289698.htm |
| [22] |
REUSSER D E, BUYTAERT W, ZEHE E. Temporal dynamics of model parameter sensitivity for computationally expensive models with the Fourier amplitude sensitivity test[J]. Water Resources Research, 2011, 47(7): 197-203. |
| [23] |
WAGENER T, MCINTYRE N, LEES M J, et al. Towards reduced uncertainty in conceptual rainfall-runoff modelling: dynamic identifiability analysis[J]. Hydrological Processes, 2003, 17(2): 455-476. DOI:10.1002/(ISSN)1099-1085 |
| [24] |
SHEN S, MA L, XU Y, et al. Interpretation of increased deformation rate in aquifer IV due to groundwater pumping in Shanghai[J]. Canadian Geotechnical Journal, 2013, 50(11): 1129-1142. DOI:10.1139/cgj-2013-0042 |
| [25] |
罗跃, 叶淑君, 吴吉春, 等. 上海市地下水位大幅抬升条件下土层变形特征分析[J]. 高校地质学报, 2015, 21(2): 243-254. LUO Yue, YE Shu-jun, WU Ji-chun, et al. Characterization of land subsidence during recovery of groundwater levels in Shanghai[J]. Geological Journal of China Universities, 2015, 21(2): 243-254. |
| [26] |
PIANOSI F, SARRAZIN F, WAGENER T. A Matlab toolbox for global sensitivity analysis[J]. Environmental Modelling and Software, 2015, 70(C): 80-85. |



