滑坡作为世界范围内发生频率最高且后果最严重的地质灾害之一,本质是一个受自身地质条件和外界因素共同影响的复杂多维非线性动态系统[1-3]. 滑坡位移是这一复杂多维非线性动态系统中多种因素共同作用的结果,是能够直接反映滑坡变形演化过程的一种综合性变量,滑坡位移与滑坡的运动特征相对应. 针对滑坡位移进行的预测工作是准确把握滑坡变形演化阶段、实现滑坡准确预警的基础和前提条件[2].
由于能够较好地表征滑坡累计位移随时间的变化关系,分离滑坡累计位移时间序列中的趋势性与周期性成分,时间序列分析法和移动平均法已经被广泛地应用于滑坡位移预测领域[4-5]. 在对非平稳时间序列进行时序分析,分离其中的趋势性与周期性成分时,一般要求数据是等时距的,在实际工程中这一要求不容易实现. 自然三次样条插值法作为一种按不同区间对原始数据进行分段低次内插的方法,具有计算简单、稳定性好、整体光滑性好等特点,能够较好地解决非等时距数据的转换问题.
基于统计学习理论建立的支持向量回归机模型(support vector regression, SVR)由于具有强大的泛化能力,目前已被广泛应用于预测滑坡的周期性位移[4-8]. 在SVR模型中,如何对惩罚因子、核函数参数和不敏感参数进行合理的设置是提升模型预测能力的关键. 在以往的研究[4-5, 8-9]中,通常只考虑前两者的作用,忽视了不敏感参数的影响. 在建立SVR模型时,有必要进行3种参数联合寻优,以提升模型的预测效果. 作为一种模仿狼群狩猎行为的新型元启发式算法,灰狼算法(grey wolf optimizer, GWO)较粒子群算法(particle swarm optimization, PSO)、遗传算法(genetic algorithm, GA)、蚁群算法等传统启发式算法而言,在研究组合式优化问题上已被证明具有显著优势,能够有效地解决多种参数的联合寻优问题.
本文以三峡库区白水河滑坡为例,采用自然三次样条插值法对地表位移监测数据进行等时距处理,应用时间序列分析法和移动平均法,将趋势性位移与周期性位移分离. 在分析滑坡位移变化特征及外界诱发因素的响应关系的基础上,实现趋势性位移和周期性位移的预测:1)基于稳健最小二乘法,利用三次多项式函数对趋势性位移进行预测;2)采用GWO-SVR耦合模型,对周期性位移进行预测. 将趋势性位移与周期性位移的预测值叠加,实现对滑坡位移的预测.
1 滑坡位移预测模型 1.1 滑坡位移分解滑坡累计位移是一种随时间变化而明显增长的非平稳时间序列[1, 7]. 大量研究表明[5],导致滑坡产生位移及位移变化的主要因素如下:1)滑坡内部地质条件,例如岩土体组成、地形地貌等,在这类因素控制下滑坡位移表现为随时间变化的近似单调增函数;2)外部诱发因素的作用(例如降雨、库水位等),在这类因素影响下的滑坡位移表现为随季节性降雨和库水位调度变化的近似周期性函数. 根据以上特性,可以采用时间序列分析理论分解滑坡的位移:
| $X(t) = \alpha (t) + \beta (t) + \gamma (t).$ | (1) |
式中:
随机性位移主要由2部分构成:1)随机荷载(如风荷载)所导致的位移;2)库水位临时调度和随机降雨过程(如非季节性降雨)所导致的位移. 其中,前者受限于目前的技术手段,在滑坡位移预测研究中一般不考虑[10];后者常常夹杂在周期性位移中作为“脉冲信号”出现,只有当其周期性较明显时,可以近似作为周期性位移的一部分考虑[7]. 滑坡的累计位移时间序列可以简化为
| $X(t) = \alpha (t) + \beta (t).$ | (2) |
对于趋势性位移而言,一般可以采用移动平均法提取,具体的计算方法如下.
假设第
| $\left.\begin{gathered} \begin{array}{*{20}{c}} {\beta (t) = \displaystyle\frac{{x\left( t \right) + x\left( {t - 1} \right) + \cdots + x\left( {t - k + 1} \right)}}{n}};& \end{array} \\ t = k,{\rm{ }}k + 1{\rm{, }}\cdots{\rm{, }}n. \\ \end{gathered} \right\}$ | (3) |
式中:
在趋势性位移提取完成后,将
由于滑坡位移监测数据一般是一组非等距的时间序列,无法直接满足时序分析法和移动平均法的要求. 在剥离趋势性与周期性位移之前,必须先采用数学方法对滑坡位移监测数据进行等时距处理. 样条插值法是一种在工程设计中获得连续光滑曲线的常用方法,三次样条是其中应用最广泛的一种插值方式. 采用自然三次样条函数插值法,对滑坡位移监测数据进行等时距处理.
支持向量回归模型是由Vapnik[9]提出的具有良好鲁棒性且用于解决函数回归问题的监督式机器学习方法. 基本思想是通过某一非线性变换函数(核函数)将低维输入向量投影到高维特征空间中,从而在高维空间中对这些向量进行线性回归,将低维非线性回归问题成功转化为高维线性回归问题,有效回避了“维数灾难”.
SVR模型中寻找支持向量的过程等价于求解一个线性约束的凸二次规划问题,可以应用Lagrange乘子法进行优化求解[1, 5, 8, 13],基于Matlab平台实现这一计算过程. SVR核函数的形式多种多样,主要有线性函数、多项式函数、高斯径向基函数(RBF函数)和sigmoid函数,其中应用最广泛的是RBF函数,因此本文中核函数为RBF函数.
1.3 灰狼优化算法GWO算法是Mirjalili等[11]提出的模拟狼群群体捕食行为的新型智能优化算法. 基本思想如下:首先在搜索空间中随机产生一群灰狼,并将狼按适应度从高到低分别划分为
定义1 灰狼与猎物之间的距离
| ${D}{\rm{ = }}\left| {{C} {{X}_{\rm p}}(t) - {X}(t)} \right|.$ | (4) |
式中:
| ${C} = 2 {{r}_1},$ | (5) |
其中,
定义2 灰狼位置
| ${X}\left( {t + {\rm{1}}} \right){ = }{{X}_{\rm p}}{\rm{(}}t{\rm{)}} - {{\mu } } {D},$ | (6) |
| ${\mu} {\rm{ = }}2{ a} {{ r}_2} - { a}.$ | (7) |
式中:
定义3 猎物位置
| ${D}_k{\rm{ = }}\left| {{{C}_i} {{X}_k}(t) - {X}(t)} \right|,$ | (8) |
| ${{X}_i} = {{X}_k} - {{\mu} _i} {D}_k.$ | (9) |
根据下式确定寻优方向:
| ${{X}_{\rm p}}\left( {t + {\rm{1}}} \right) = \frac{{{{X}_1}{\rm{ + }}{{X}_2}{\rm{ + }}{{X}_3}}}{3}.$ | (10) |
式中:
如图1所示,首先采用自然三次样条插值法和时序分解模型处理原始位移监测数据,然后通过多项式拟合和GWO-SVR模型对经过处理的位移数据分别进行建模,以预测未来滑坡位移的变化情况.
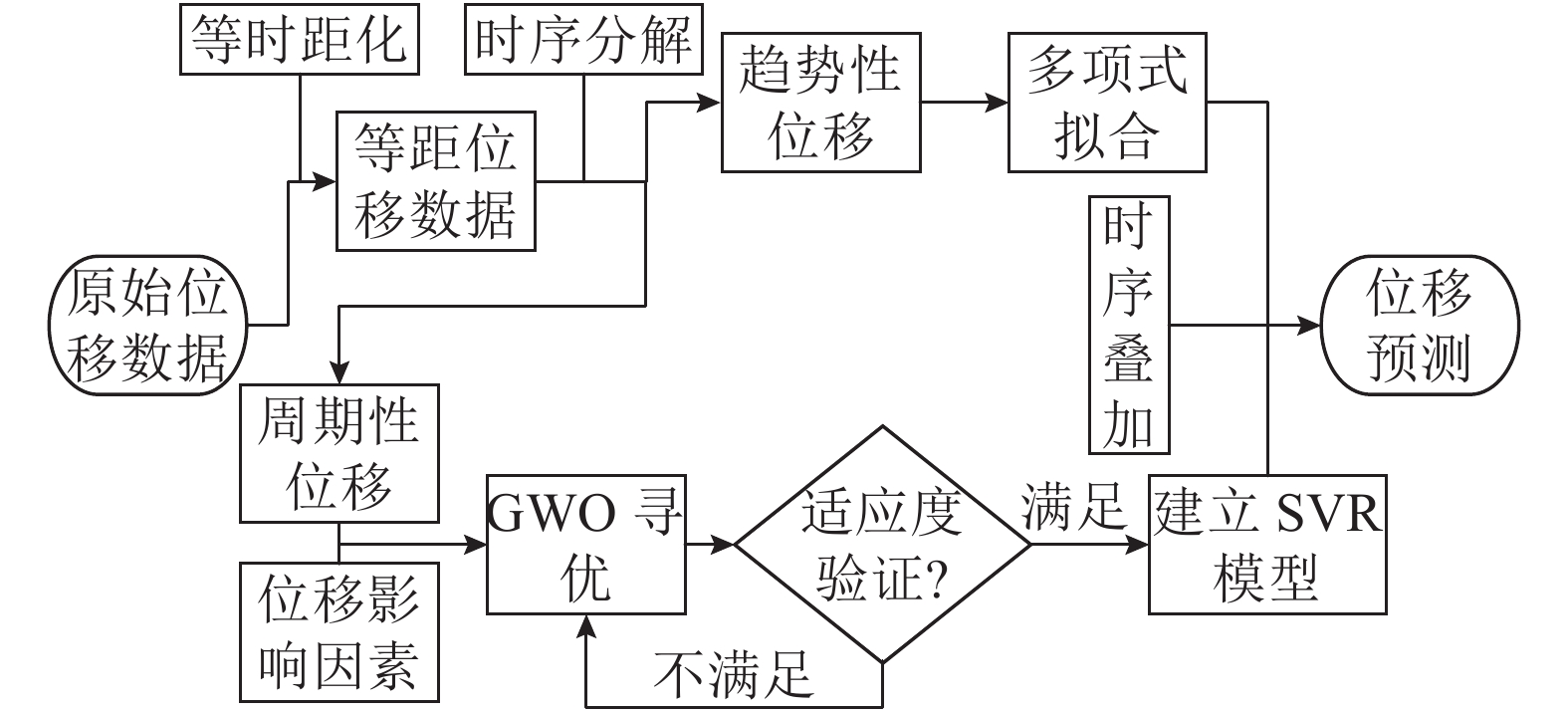
|
图 1 基于GWO-SVR的非等时距位移预测模型流程图 Fig. 1 Flow chart of displacement prediction model based on non-equidistant time series and GWO-SVR |
白水河滑坡地处湖北省秭归县沙镇溪镇,距离三峡工程坝址约60 km,发育于2条近南北向冲沟之间的单斜顺向斜坡内,南高北低,整体呈阶梯状向长江展布[2]. 白水河滑坡总体坡度约为30°,平均厚度约为30 m,体积约为1.26×104 m3,是三峡库区中典型的松散堆积层滑坡[12],地表位移GPS监测点布置如图2所示.
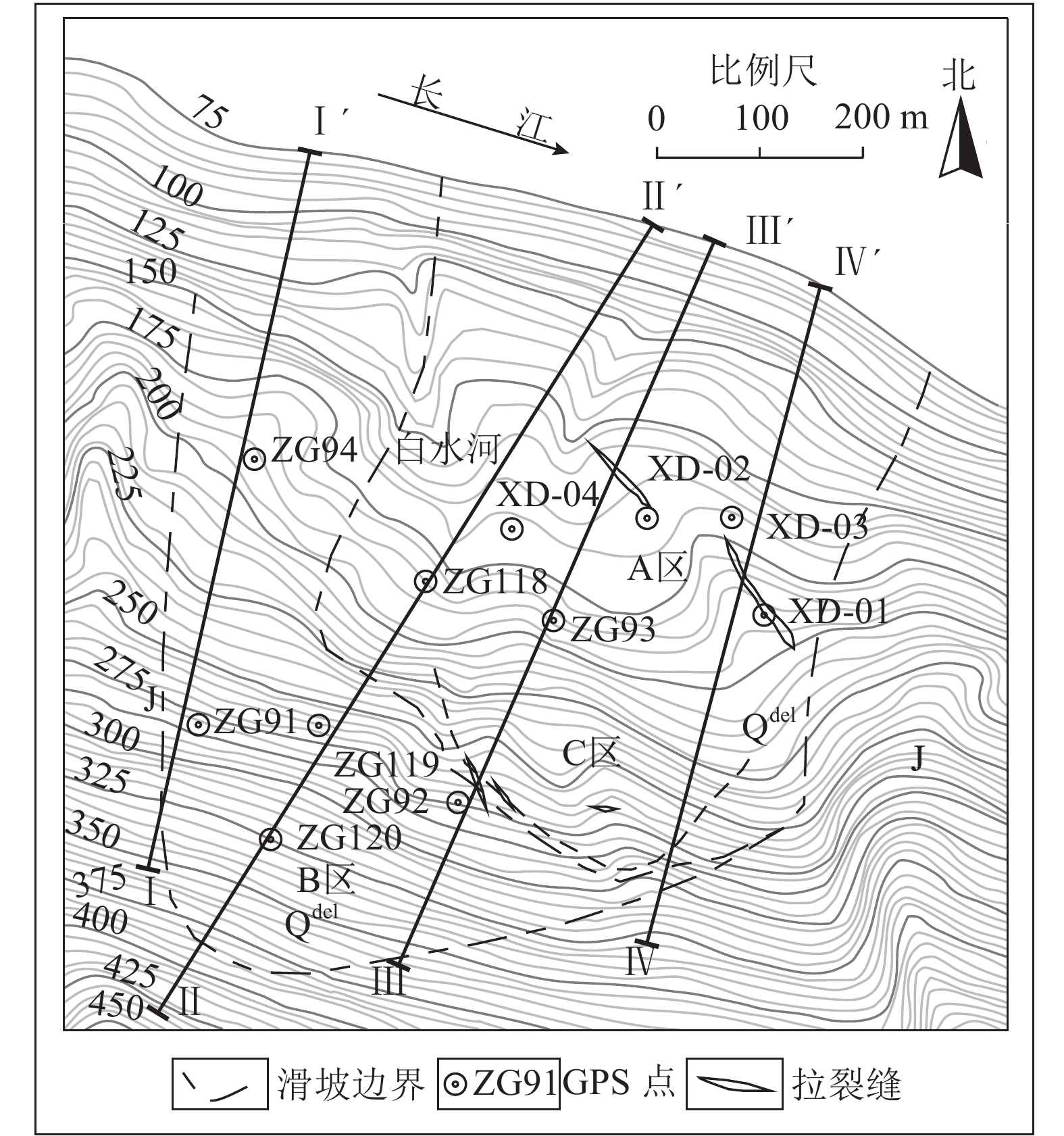
|
图 2 白水河滑坡GPS监测点布置平面图 Fig. 2 GPS monitoring arrangement of displacement in Baishuihe landslide |
如图1所示,白水河滑坡上共设置了11个GPS监测点. 其中,监测点ZG93和ZG118的布置时间最早,数据最完整,且正好位于滑坡的中部,能够有效地反映整个滑坡的运动过程,因此选取这两点的监测位移数据进行分析. 如图3所示,Dacc为累计位移,R为库水位,P为降雨量. 以2006年9月和2008年9月为界,分以下3个阶段阐述监测数据.
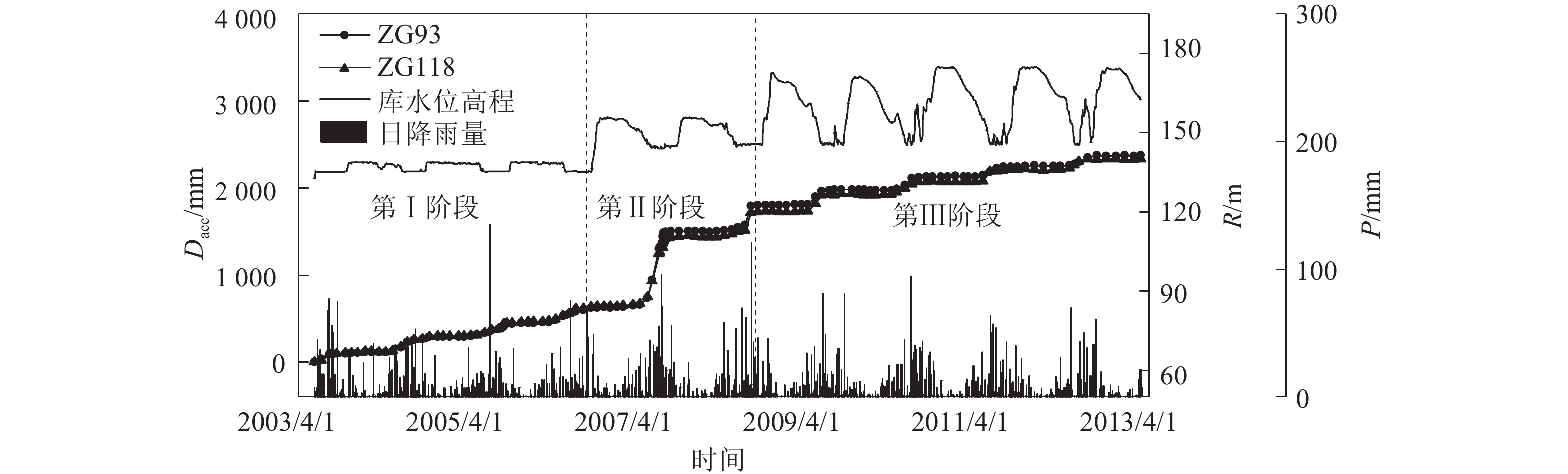
|
图 3 滑坡累计监测位移、日降雨量和库水位曲线 Fig. 3 Accumulative monitoring displacements of landslide, daily rainfall and reservoir water level |
1)第Ⅰ阶段(2003年6月—2006年9月):虽然库水位的小幅度调度使得滑坡剪出口和滑坡前缘部分被淹没,弱化了滑坡局部岩土体的抗剪强度,但是由于该阶段库水位变动幅度和滑坡前缘被淹没的面积实际相对较小(见图4(a)、(b)),且监测点累计位移增长与滑坡所属区域降雨量增长表现出强关联性(特别是每年6月~9月),故在第Ⅰ阶段中监测点位移主要由降雨所致,库水位变动的影响较小. 图4中,H为高程,d为距离.
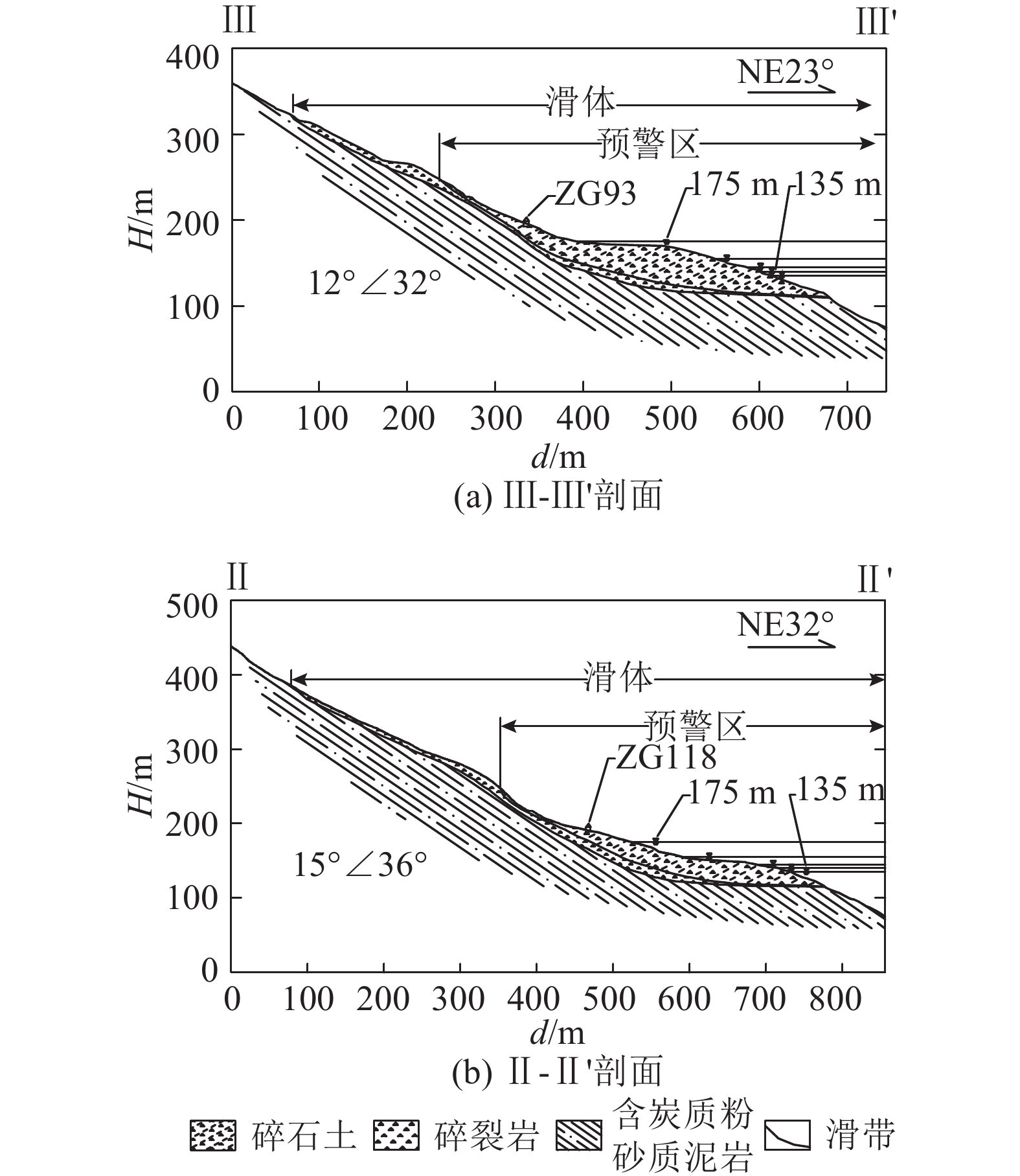
|
图 4 白水河滑坡监测剖面 Fig. 4 Geological sections of Baishuihe Landslide |
2)第Ⅱ阶段(2006年9月—2008年9月):滑坡淹没面积和库水位变动幅度大幅度增加,(见图4(a)、(b))对滑坡渗流场、应力场和岩土体的物质组成及结构特征产生较大的影响. 这种影响在库水位首次从155 m下降至145 m时最明显,且随着库水位的多年调度渐减弱并最终趋于稳定. 在第Ⅱ阶段中,降雨和库水的联合作用使得监测点在汛期发生了较大位移;在汛期过后,降雨和库水的影响逐渐减弱,监测点的位移将会再次恢复平稳.
3)第Ⅲ阶段(2008年9月—2013年12月):虽然库水位变动幅度和滑坡淹没面积进一步增大,但是由于在第Ⅱ阶段中滑坡中前部的渗流场、应力场和岩土体物质组成及结构特征均已经过了较大幅调整,当库水位首次从175 m大幅下降至145 m时,伴随着雨季的强降雨作用,监测点位移没有产生猛增. 监测点位移增幅在第Ⅱ阶段的基础上继续逐年降低并趋于稳定. 在第Ⅲ阶段中,虽然降雨和库水位的耦合作用是引起滑坡位移变化的主要因素,但是由于滑坡淹没面积和库水调度幅度的大幅增加,库水位的影响较第Ⅱ阶段时有所增强,降雨的影响相对变弱.
综上所述,可得如下结论. 1)滑坡累计位移与库水调度表现出了较强的相关性[2-3, 12]. a)由于白水河滑坡前缘(见图4(a)、(b))较平缓且滑体渗透系数较低,当库区水位大幅上升时,地下水位的抬升会明显滞后于库水位的上升,使得被库水位浸没的滑体主要受到与滑面正交的静水压力作用. 这一作用会提升滑坡的稳定性,使得监测点位移增幅趋于稳定,故在建立滑坡位移预测模型时,应当重视当前库水位的反压作用. b)当库区水位大幅下降时,地下水位的下降会明显滞后于库水位的下降,使得滑体在库水位下降后一段时间内受到一个与滑面平行且指向坡外的动水压力作用. 这一作用将会明显降低滑坡的稳定性,使得监测点位移增幅明显,故在建立滑坡位移预测模型时,应当重视库水位调度所导致的地下水位滞后. 2)白水河滑坡位移与区域降雨强度有着良好的对应关系[2, 12],当滑坡所在区域发生短时强降雨时,入渗的雨水补给了滑体内的地下水,使得岩土体物理力学参数弱化,滑体重度增大;未入渗的雨水在滑体表面汇集,形成地表径流冲刷滑体表面,从而降低坡体的稳定性,使得监测点位移增幅明显. 当建立滑坡位移预测模型时,应重视短时间内强降雨的作用,结合白水河滑坡的岩土体渗透和蒸发特性,考虑一段时间内降雨入渗的累加作用. 因此,库水和降雨的影响是诱发白水河滑坡位移运动的重要因素,但是库水和降雨对滑坡变形的影响程度不是一成不变的. 若在进行滑坡位移预测时,不区分不同阶段的监测数据,直接使用所有数据进行预测,则会影响最终的训练和预测效果.
3 白水河滑坡位移预测选择监测点ZG93和ZG118的第Ⅲ阶段累计位移作为研究对象. 其中2008年9月—2009年7月的数据为移动平均法所需的基础数据,2009年8月—2012年9月的数据作为预测模型的训练样本集,2012年10月—2013年3月的数据作为预测检验集.
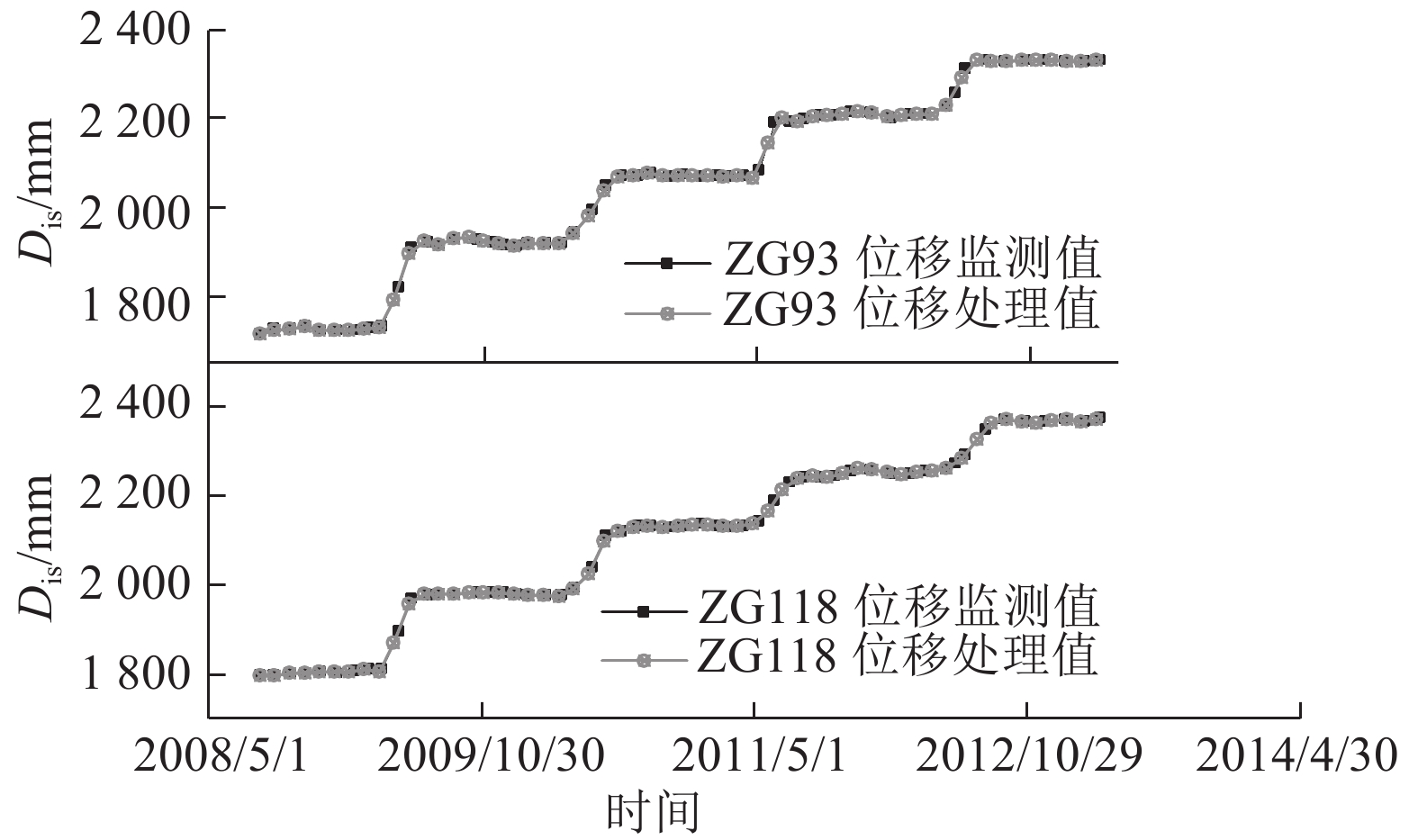
3.1 位移监测数据等时距化处理如图3所示,原滑坡位移监测数据时间间隔为1~35 d,须采用自然三次样条插值法进行等时距处理,等时距化结果如图5所示. 图中,Dis为位移. 处理后的时间间隔统一为30 d,本文中每月均按30 d计.
|
图 5 位移监测值及其等距化处理值 Fig. 5 Actual monitoring displacements and their equidistant values |
比较滑坡位移实际监测值和自然三次样条插值法处理值(见图5)可见,采用自然三次样条插法得到的数据非常接近于真实数据,不仅最大程度地保留了实际数据的变化趋势,而且将不同权重的位移数据转化为等权重数据,在避免引入人为误差的同时,满足了时序分析法和移动平均法的隐含条件.
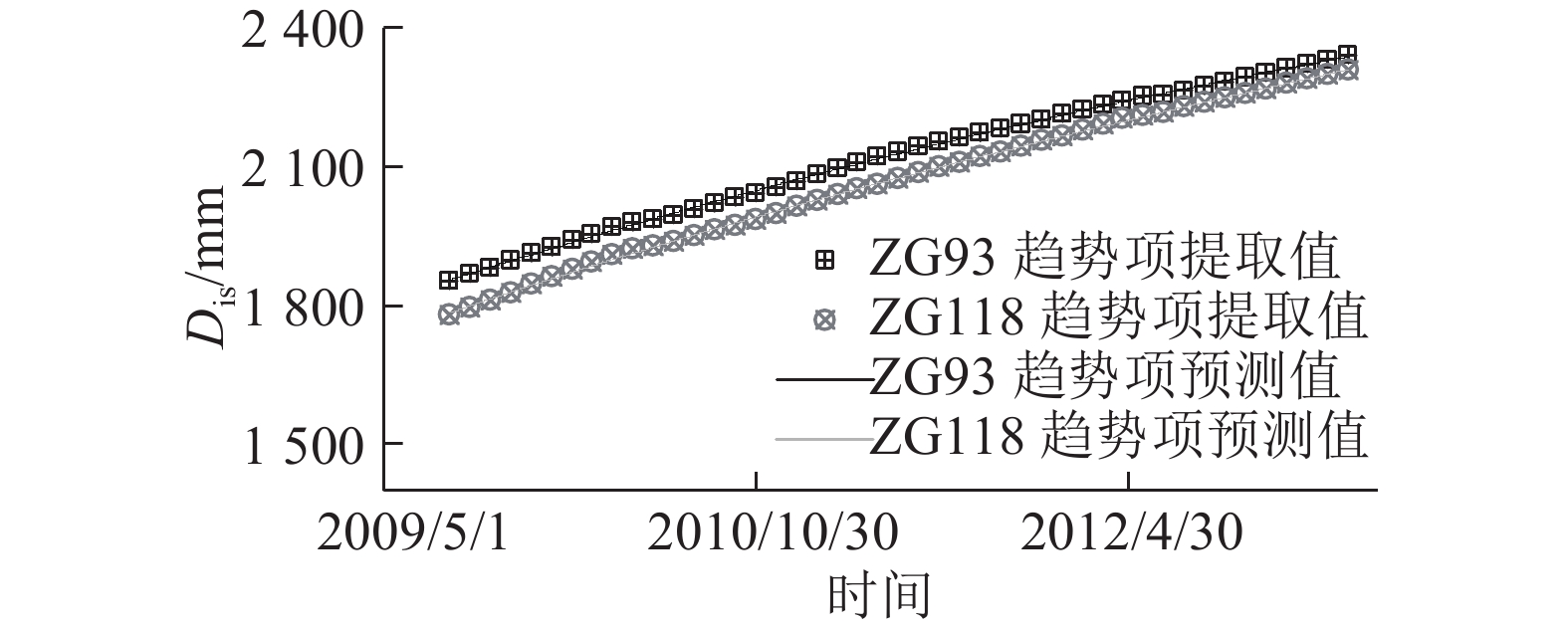
3.2 趋势性位移提取及预测利用式(3)从经过等时距处理的监测点累计位移(见图5)中提取趋势性位移,其中移动周期
|
图 6 趋势性位移实际值及预测值 Fig. 6 Actual trend displacements and their predicted values |
基于稳健最小二乘法,采用下式拟合以寻找监测点的趋势性位移与时间之间的函数关系,实现对趋势性位移的预测:
| $\alpha \left( t \right){\rm{ = }}a{t^3} + b{t^2} + ct + d.$ | (11) |
拟合结果及精度如图6和表1所示. 表中,RMSE为均方根误差,R2为拟合优度.
| 表 1 趋势性位移拟合参数、结果及误差 Table 1 Fitting parameters of trend displacements and their prediction accuracy and error |
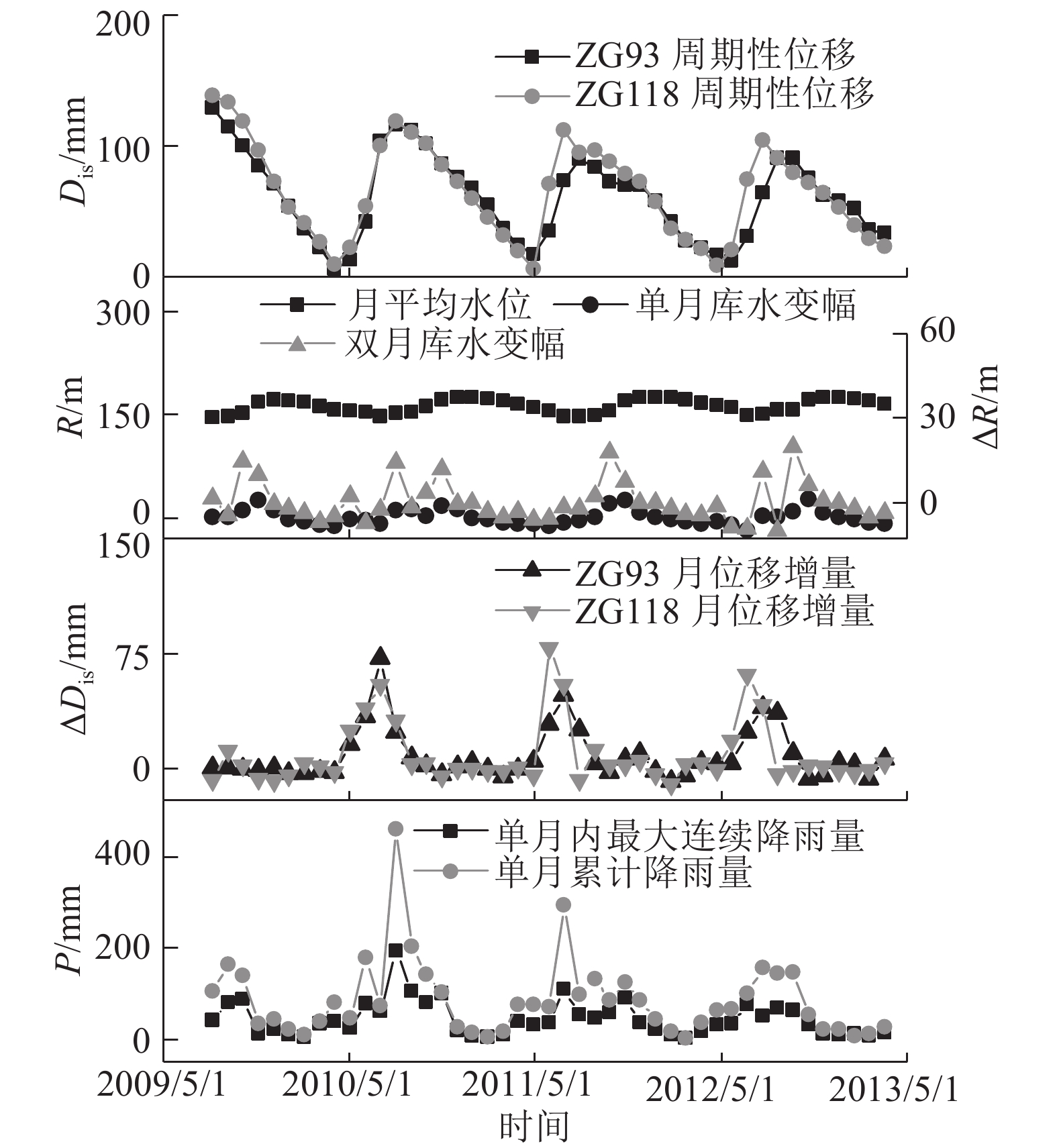
根据时间序列加法模型(式(2)),将监测点的等时距累计位移(见图5)和自身的趋势性位移(见图6)相减,得到各监测点的周期性位移(见图7). 图中,ΔR为库水位变动幅度,ΔDis为位移增幅.
|
图 7 周期性位移及其影响因子 Fig. 7 Periodic displacements and its influence factors |
模型的预测效果与影响因子的选取密切相关[6, 13-15]. 如图7所示,选取6个影响白水河滑坡周期性位移的因子建立预测模型,具体的选择依据如下.
1)降雨. 降雨对滑坡的作用是一个持续且相对缓慢的过程,除受岩土体组成及性质、坡体形态等地质条件的控制之外,主要受降雨强度和降雨时长等因素的影响. 由于白水河滑坡所属区域两次降雨过程之间的时间间隔较长(超过80%大于3 d,最长可达19 d),且雨水的入渗和蒸发是同时进行的,不宜考虑过长时间内降雨入渗的累加作用. 选取单月最大连续降雨量和单月累计降雨量作为降雨对周期性位移的影响因子.
2)库水位. 根据有关白水河滑坡对于库水位的响应分析,认为在考虑库水位对滑坡的影响时,除了考虑当前库水位对滑坡的影响(库水的反压作用)外,还应考虑过去一段时间内库水位调度所导致的地下水位滞后. 对于白水河滑坡而言,虽然缺乏相关的地下水位监测资料,但是由于地下水位的变化与库水位调度密切相关[12],故将一段时间内的库水位变动量作为预测模型的输入因素. 将月均库水位高程、单月库水位变幅和双月库水位变幅作为库水位对周期性位移的影响因子.
3)位移增量. 在库水位的周期性调度和季节性降雨的耦合作用下,滑坡的累计位移随时间呈周期性变化,滑坡的月位移增量表现出相同的变化趋势,故将月位移增量作为降雨和库水位因素的补充,表征其他周期性因素对滑坡位移的影响.
根据灰色关联度分析原理可知,当分辨系数为0.5时,若影响因子与周期性位移的灰色关联系数>0.6,则可以认为两者密切相关[16]. 如表2所示,各影响因子与周期性位移的灰色关联系数均大于0.6,证明本文中影响因子的选择具有合理性.
| 表 2 各影响因子与周期性位移的灰色关联度 Table 2 Grey relational degree between impact factors and periodic displacement |
釆用GWO-SVR耦合模型,对滑坡周期性位移进行预测,具体的预测过程如下.
1)数据预处理. 将各种影响因子和周期性位移按不同维度分别归一化到[0,l]区间.
2)模型参数寻优. 除采用GWO算法分别进行双参数寻优(惩罚因子和核函数参数)和三参数寻优(惩罚因子、核函数参数和不敏感参数)外,还采用PSO算法和GA算法进行相同工作. 各种优化算法的搜索区间如下:惩罚因子
| 表 3 各模型寻优参数及寻优结果 Table 3 Optimal parameters and results of each model |
3)训练模型和预测. 利用寻优得到的参数构建预测模型,利用该模型进行周期性位移预测,各模型的预测效果如表4和图8所示.
| 表 4 周期性位移预测精度及误差 Table 4 Prediction accuracy and error of periodic displacements |

|
图 8 周期性位移及其预测值 Fig. 8 Periodic displacements and their predicted values |
如表3和图9所示,Fit为适应度,nit为迭代次数,与PSO-SVR模型和GA-SVR模型相比,GWO-SVR模型的参数设置简单,收敛迅速,寻优耗时短;当开展三参数联合寻优时,GWO-SVR模型、PSO-SVR模型和GA-SVR模型所得的不敏感参数最优值均小于以往滑坡位移预测研究中的预设值(0.1),并且支持向量个数大于进行双参数寻优时的支持向量个数.

|
图 9 各模型收敛曲线(以ZG93为例) Fig. 9 Convergence curves of each model(ZG93) |
如表4所示,对于各种基于三参数寻优法建立的模型,该模型的预测效果优于基于双参数寻优法建立的各种模型. 无论是采用双参数法还是三参数法进行寻优,GWO-SVR模型的拟合优度均高于PSO-SVR模型和GA-SVR模型,均方根误差(RMSE)小于PSO-SVR模型和GA-SVR模型.
GWO-SVR耦合模型作为一种新型的滑坡位移预测模型,与传统PSO-SVR模型和GA-SVR模型相比,具有寻优参数设置简单、预测精度高和预测误差小的优点,能够更快速、有效地解决滑坡周期性位移的预测问题;不敏感参数同惩罚因子和核函数参数对SVR模型的预测效果影响显著,因此在模型建立过程中,有必要进行3种参数的联合寻优,以提升模型的预测效果.
虽然GWO-SVR模型的预测效果较好,但是在预测过程中个别点的预测误差较大(见图8),这主要是由于:1)部分滑坡位移影响特征(如区域短时强降雨)在因子提取过程中“淡化”或“丢失”,导致预测失准;2)滑坡是一个非常复杂的非线性动态系统,而目前的预测模型往往是静态的,在进行长期位移预测时,由于缺乏新旧数据的更替,随着预测时间的增长,预测精度会有一定的降低.
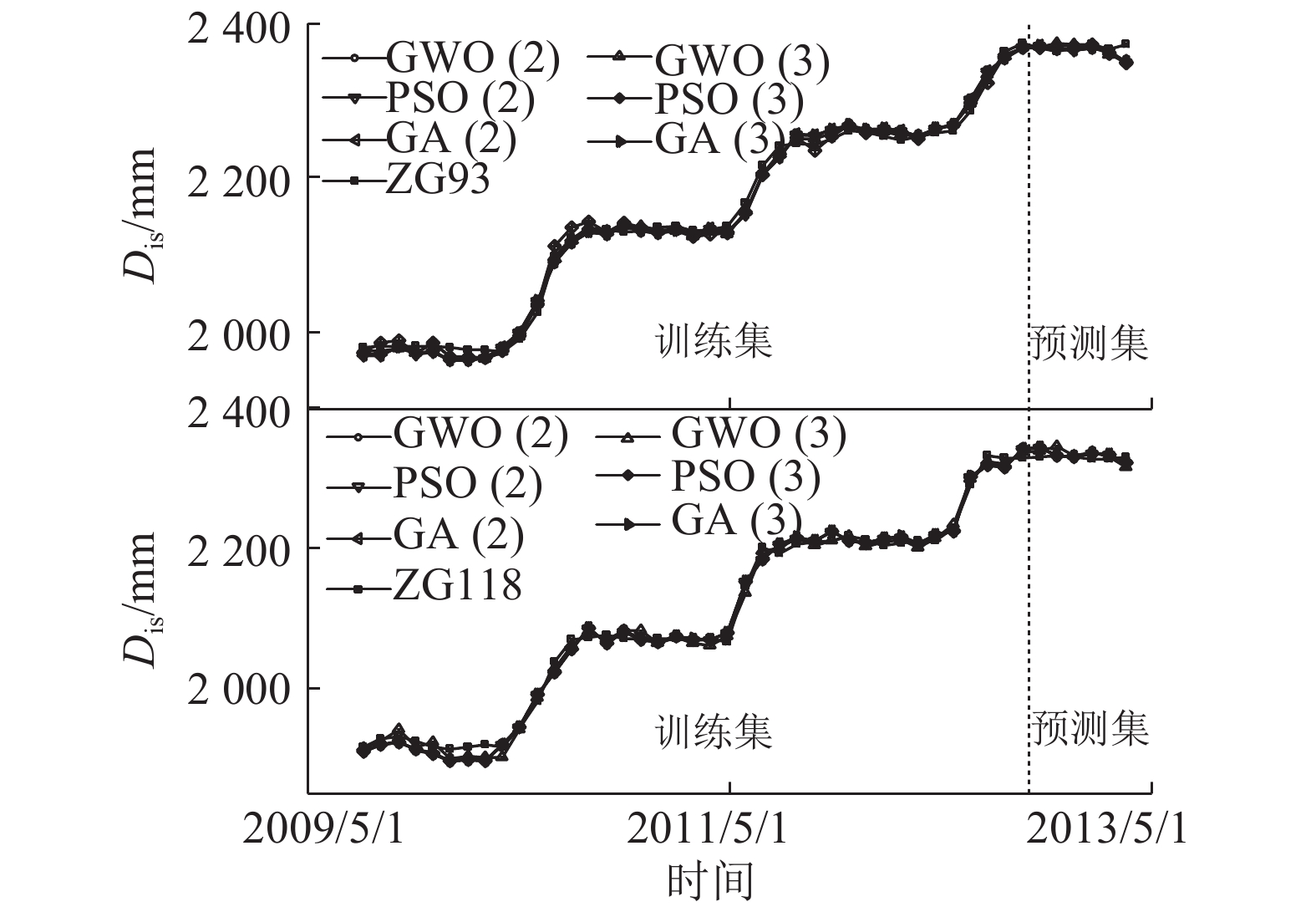
3.4 滑坡累计位移预测将滑坡趋势性与周期性位移的预测值叠加,可得累计位移的预测值. 如图10和表5所示,无论是采用GWO-SVR模型还是PSO-SVR模型进行预测,得到的位移预测曲线与等距化后的滑坡位移曲线吻合良好,R2接近1,这主要是由于趋势性位移在滑坡累计位移中占主导地位,利用较简单的数学方法能够准确地预测趋势性位移.
|
图 10 位移监测值及预测值 Fig. 10 Monitoring displacements and their predicted values |
| 表 5 累计位移预测精度及误差 Table 5 Prediction accuracy and error of accumulative displacements |
如表4、5所示,累计位移的RMSE和周期性位移的RMSE基本相等,这主要是由于周期性位移中隐含的随机性位移无法得到准确预测而使得预测误差通过时间序列加法模型累计所致.
以上结果表明,当采用时间序列分析法进行滑坡位移预测时,由于趋势性位移的变化趋势较简单且易于预测,选择合适的周期性位移预测模型成为提升滑坡位移预测效果的关键.
4 结 论(1)三峡库区滑坡的变形破坏主要受到库水位和降雨因素的共同影响,但在三峡水库不同的运行阶段,库水位和降雨对滑坡变形的影响程度不同. 在进行滑坡位移预测时,应对不同阶段的数据进行区分,以免影响模型的训练和预测效果.
(2)应用自然三次样条插值法处理滑坡位移监测数据,不仅能够最大程度地保留原始数据的变化趋势,而且能够将实际不同权重的数据转化为等权重数据,较好地满足时间序列分析法和移动平均法的隐含要求.
(3)滑坡位移的产生和演化除了受降雨和库水位等外界诱发因素的影响外,还与滑坡自身的岩土体组成及性质、坡体形态等地质条件密切相关. 在确定预测模型的输入因素时,需要重视滑坡自身地质条件对降雨、库水调度、人类工程活动等外界诱发因素的响应,针对不同滑坡的个性特征挑选合理的输入因素.
(4)基于GWO算法、PSO算法和GA算法开展的SVR模型参数寻优结果表明,不敏感参数同惩罚因子和核函数参数一样,对SVR模型的预测精度影响显著. 在利用SVR模型进行滑坡位移预测时,不应忽视不敏感参数的作用.
(5)与传统PSO-SVR模型和GA-SVR模型相比,GWO-SVR耦合模型的预测效果较理想,寻优参数设置简单,收敛迅速,计算耗时短,在滑坡位移预测领域具有较高的应用价值.
| [1] |
彭令, 牛瑞卿, 吴婷. 时间序列分析与支持向量机的滑坡位移预测[J]. 浙江大学学报: 工学版, 2013, 47(9): 1672-1679. PENG Ling, NIU Rui-qing, WU Ting. Time series analysis and support vector machine for landslide displacement prediction[J]. Journal of Zhejiang University: Engineering Science, 2013, 47(9): 1672-1679. |
| [2] |
许强, 汤明高, 徐开祥, 等. 滑坡时空演化规律及预警预报研究[J]. 岩石力学与工程学报, 2008, 27(6): 1104-1112. XU Qiang, TANG Ming-gao, XU Kai-xiang, et al. Research on space-time evolution laws and early warning-prediction of landslides[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6): 1104-1112. DOI:10.3321/j.issn:1000-6915.2008.06.003 |
| [3] |
LI D, YIN K, LEO C. Analysis of Baishuihe landslide influenced by the effects of reservoir water and rainfall[J]. Environmental Earth Sciences, 2010, 60(4): 677-687. DOI:10.1007/s12665-009-0206-2 |
| [4] |
ZHOU C, YIN K, CAO Y, et al. Application of time series analysis and PSO–SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir, China[J]. Engi-neering Geology, 2016, 204: 108-120. DOI:10.1016/j.enggeo.2016.02.009 |
| [5] |
张俊, 殷坤龙, 王佳佳, 等. 基于时间序列与PSO-SVR耦合模型的白水河滑坡位移预测研究[J]. 岩石力学与工程学报, 2015, 34(2): 382-391. ZHANG Jun, YIN Kun-long, WANG Jia-jia, et al. Displacement prediction of Baishuihe landslide based on time series and PSO-SVR model[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 382-391. |
| [6] |
CAI Z, XU W, MENG Y, et al. Prediction of landslide displacement based on GA-LSSVM with multiple factors[J]. Bulletin of Engineering Geology and the Environ-ment, 2016, 75(2): 637-646. DOI:10.1007/s10064-015-0804-z |
| [7] |
DU J, YIN K, LACASSE S. Displacement prediction in colluvial landslides, Three Gorges Reservoir, China[J]. Landslides, 2013, 10(2): 203-218. DOI:10.1007/s10346-012-0326-8 |
| [8] |
黄发明, 殷坤龙, 张桂荣, 等. 多变量PSO-SVM模型预测滑坡地下水位[J]. 浙江大学学报: 工学版, 2015, 49(6): 1193-1200. HUANG Fa-ming, YIN Kun-long, ZHANG Gui-rong, et al. Prediction of groundwater level in landslide using multivariable PSO-SVM model[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(6): 1193-1200. |
| [9] |
VAPNIK V N. 统计学习理论的本质[M]. 张学工, 译. 北京: 清华大学出版社, 2000: 96–101.
|
| [10] |
苗发盛, 吴益平, 谢媛华, 等. 基于多算法参数优化与SVR模型的白水河滑坡位移预测[J]. 工程地质学报, 2016, 24(6): 1136-1144. MIAO Fa-sheng, WU Yi-ping, XIE Yuan-hua, et al. Displacement prediction of Baishuihe landslide based on multi algorithm optimization and SVR model[J]. Journal of Engineering Geology, 2016, 24(6): 1136-1144. |
| [11] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69(3): 46-61. |
| [12] |
卢书强, 易庆林, 易武, 等. 库水下降作用下滑坡动态变形机理分析--以三峡库区白水河滑坡为例[J]. 工程地质学报, 2014, 22(5): 869-875. LU Shu-qiang, YI Qing-lin, YI Wu, et al. Study on dynamic deformation mechanism of landslide in drawdown of reservoir water level: take Baishuihe landslide in three gorges reservoir area for example[J]. Journal of Engineering Geology, 2014, 22(5): 869-875. |
| [13] |
彭令, 牛瑞卿, 赵艳南, 等. 基于核主成分分析和粒子群优化支持向量机的滑坡位移预测[J]. 武汉大学学报: 信息科学版, 2013, 38(2): 148-592. PENG Ling, NIU Rui-qing, ZHAO Yan-nan, et al. Prediction of landslide displacement based on KPCA and PSO-SVR[J]. Geomatics and Information Science of Wuhan University, 2013, 38(2): 148-592. |
| [14] |
吴益平, 滕伟福, 李亚伟. 灰色-神经网络模型在滑坡变形预测中的应用[J]. 岩石力学与工程学报, 2007, 26(3): 632-636. WU Yi-ping, TENG Wei-fu, LI Ya-wei. Application of grey-neural network model to landslide deformation prediction[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 632-636. DOI:10.3321/j.issn:1000-6915.2007.03.028 |
| [15] |
REN F, WU X, ZHANG K, et al. Application of wavelet analysis and a particle swarm-optimized support vector machine to predict the displacement of the Shuping land-slide in the Three Gorges, China[J]. Environmental Earth Sciences, 2015, 73(8): 4791-4804. DOI:10.1007/s12665-014-3764-x |
| [16] |
汪洋, 殷坤龙, 安关峰. 滑坡敏感因子的灰色关联分析[J]. 岩土力学, 2004, 25(1): 91-93. WANG Yang, YIN Kun-long, AN Guan-feng. Grey correlation analysis of sensitive factors of landslide[J]. Rock and Soil Mechanics, 2004, 25(1): 91-93. DOI:10.3969/j.issn.1000-7598.2004.01.019 |



