2. 东南大学 交通学院, 江苏 南京 210096
2. School of Transportation, Southeast University, Nanjing 210096, China
网络节点重要性辨识作为研究复杂网络重要属性的核心指标之一, 被广泛地应用与研究[1-3]. 节点重要性广泛应用于多种领域, 例如交通网络中的核心枢纽节点决定整个交通网络的有效运转[4]; 电网中关键区域的电路维保是保证整个电网正常运转的核心工作[5]. 简单的节点重要性评估方法是用节点的度值来表示该节点的重要性[6], 节点的度值越大, 该节点越重要; 该方法易于操作, 但存在片面性.
近年来, 很多学者从邻居节点对待评估节点的影响进行多角度研究. Ugander等[7]研究Facebook朋友关系网发现, 影响节点重要性的因素不是邻居节点的绝对数目, 起决定作用的是邻居节点之间形成的联通子图的数量. Chen等[8]提出多级邻居评估指标, 综合考虑待评估节点的一阶邻居和二阶邻居的度值; 任卓明等[9]提出基于邻居信息与集聚系数的节点重要性评估方法, 该方法综合考虑节点邻居个数及集聚系数. 张喜平等[10]定义m阶邻居节点概念, 将节点的重要性归为节点自身及节点的邻居节点两方面来源. 苏晓萍等[11]提出基于节点及领域结构洞的节点重要性评估方法. 韩忠明等[12]研究节点与邻居节点之间的三角结构, 给出节点影响力度量指标模型. 阮逸润等[13]定义节点的相似性, 同时考虑节点的度值及邻居节点的拓扑重合度双重因素来研究节点的重要性.
部分学者从网络中节点所在位置对节点重要性的影响角度进行分析研究. 谭跃进等[14]定义网络的凝聚度, 提出节点重要度评估的节点收缩方法. 赵毅寰等[15]定义节点重要性贡献矩阵, 但该方法不适用于有向网络中节点的评估. Kitsak等[16]从新的角度出发, 提出比度值、节点介数等更精确的节点重要性指标. 张小娟等[17]针对传统用移除某一节点研究网络的受影响程度来研究节点的重要性的不足, 提出计算网络节点重要性的评价公式.
从网络节点层级划分与定性定量角度研究. 肖俐平等[18]基于聚类思想, 利用势场拓扑的层次聚类方法, 对网络中节点的重要性程度进行划分; 陈静等[19]定义节点的接近度、关键度及重要度, 提出针对无向无权网络的节点接近度及关键度评估节点重要性的方法; 王甲生等[20]在文献[15]的基础上, 改进凝聚度研究节点与其他节点的连接特性对节点重要度的影响, 定义节点连边的重要度. 周漩等[21-23]从效率角度研究网络节点的重要性.
上述文献研究网络节点重要性存在以下不足. 1)以单独的指标或因素进行节点重要性评估, 使评估结果缺乏合理性; 2)部分研究方法具有较好的评估结果, 但计算时间复杂度较高, 不利于推广和应用; 3)经典的节点度值对节点重要性的评测方法较单一和笼统, 部分研究方法只适用于无向网络.
为了更准确地对网络节点重要性进行评估, 本文基于ISM模型针对有向网络进行节点重要性研究, 给出网络待评估节点重要性及所在网络层级辨识方法. 通过定义网络层级、网络层级权重、出入度节点影响系数和节点重要性综合值, 对网络待评估节点进行更细致的定量分析.
1 理论基础 1.1 ISM模型引入系统结构模型是通过探寻系统构成要素, 定义要素间的关联意义, 给出要素间以二元关系为基础的具体关系, 并且将系统要素间的关系整理成图、矩阵等较直观、易于理解和便于处理的形式, 逐步建立复杂系统的结构模型.
解释结构模型(interpretive structure model, ISM)广泛应用于各个领域, Hasteer等将ISM用于软件开发过程中属性识别、分析和调查研究, 利用ISM方法识别出属性之间的上下级关系, 进而建立层次结构模型[24]. Kato等在产品开发员共享产品信息过程中引入ISM, 使用描述需要考虑的设计元素之间的关系的质量矩阵来共享产品信息, 通过矩阵表达设计元素之间的复杂关系[25]. Liu等[26]以森林生态系统的开放性、复杂性和规模化为特征, 与社会系统、经济系统和其他自然生态系统相互交织, 使研究与管理决策复杂化.
ISM是美国J.N. 沃菲尔德教授于1973年作为分析复杂的社会经济系统结构问题而开发的一种方法. ISM是一种系统工程的理论分析方法, 该方法的特点是将影响系统的所有要素进行层级划分, 找出不同要素之间的相互关系(有因果关系、上下级关系等), 最后形成关系矩阵和递阶有向图. ISM广泛地运用于现代系统工程中[27]. ISM具有用矩阵的手段, 将各要素间零乱、复杂、无规律等关系经过区域、级位划分后呈现较清晰的结构关系的优点[28].
1.2 ISM模型构建在复杂网络的研究中, ISM将复杂网络看成一个系统, 网络的节点即为组成系统要素, 节点之间的关系为系统要素之间的关联关系, 以节点之间的二元关系将各节点之间的关系以矩阵的形式表达. ISM在复杂网络中的具体模型构建如图 1所示.

|
图 1 ISM模型在复杂网络中模型构建 Fig. 1 Model construction of ISM model in complex network |
不同网络类型具有相应的结构特征, 明确所研究的网络类型有助于对网络性质进行归纳和整理; 网络的节点作为组成网络的基本要素, 是网络最重要的组成部分, 明确节点的数量是研究网络性质的必要环节; 节点间的关系是网络的研究基础和重要影响要素, 节点间的关系虽然体现网络局部的性质, 但与网络的整体结构性质密不可分; 明确节点间的相互关系, 以矩阵形式建立邻接矩阵, 结合整个网络节点之间的关系建立网络的可达矩阵; 对网络进行区域、级位划分, 找出网络中联系较密切的节点和网络中没有联系的节点; 在划分区域后, 对网络建立多级递阶结构模型, 进行级位划分; 在级位划分后, 针对网络中形成的环, 即某两节点之间存在强连接关系, 要进行强连接要素缩减, 简化网络中各节点之间的关系; 网络中各节点关系简化后, 针对越级关系, 例如: 节点A影响节点B, 节点B影响节点C, 则节点A对节点C的影响为越级关系. 要剔除网络中存在的越级关系, 进一步约简网络中各节点之间的关系; 节点自身对自身的影响忽略不计, 去掉自身关系; 根据以上具体步骤, 绘制网络的递阶有向图.
2 基于ISM模型的复杂网络节点重要性辨识分析为了便于研究网络的性质, 基于ISM模型的复杂网络节点重要性评价ISM模型, 给出以下相关定义.
定义1(网络层级) 通过ISM系统模型在网络中的应用, 得到网络节点所属的不同层级.
为了更好地描述网络节点的重要性, 定义网络层级的概念, 通过ISM在所研究网络中的应用, 最终得到一个层级分明的网络, 处于较高层级的节点在网络中的重要度更大. 假设网络最终被分为N层, 网络的层级序号为
| ${L_1} \succ {L_2} \succ \ldots \succ {L_N}.$ | (1) |
定义2(网络层级重要性权重) 通过ISM在网络中的应用, 得到网络不同层级间重要性的权重大小指标.
不同节点的网络层级在网络中的重要性不同, 定性的大小关系不能准确地描述不同网络层级之间的差异, 网络层级权重能够很好地反映各层级的重要性. 假设网络有N个层级, 网络的层级序号为
| ${Q_i} = \frac{{1/{L_i}}}{{\displaystyle\mathop \sum \nolimits_1^N \;(1/{L_i})}}.$ | (2) |
例如在有5个网络层级的网络中, 各层级的权重为
| ${Q_1} = \frac{{1/{L_1}}}{{\displaystyle\mathop \sum \nolimits_1^5 \;1/{L_i}}} = \frac{{1/1}}{{\left( {1/1 + 1/2 + 1/3 + 1/4 + 1/5} \right)}} \approx 0.44.$ |
同理可得,
| ${Q_2} \approx 0.22,{Q_3} \approx 0.15,{Q_4} \approx 0.11,{Q_5} \approx 0.09$ |
定义3(节点出、入度重要性影响权重系数) 与待评估节点相连接的2种节点(出度节点和入度节点)对待评估节点的影响大小.
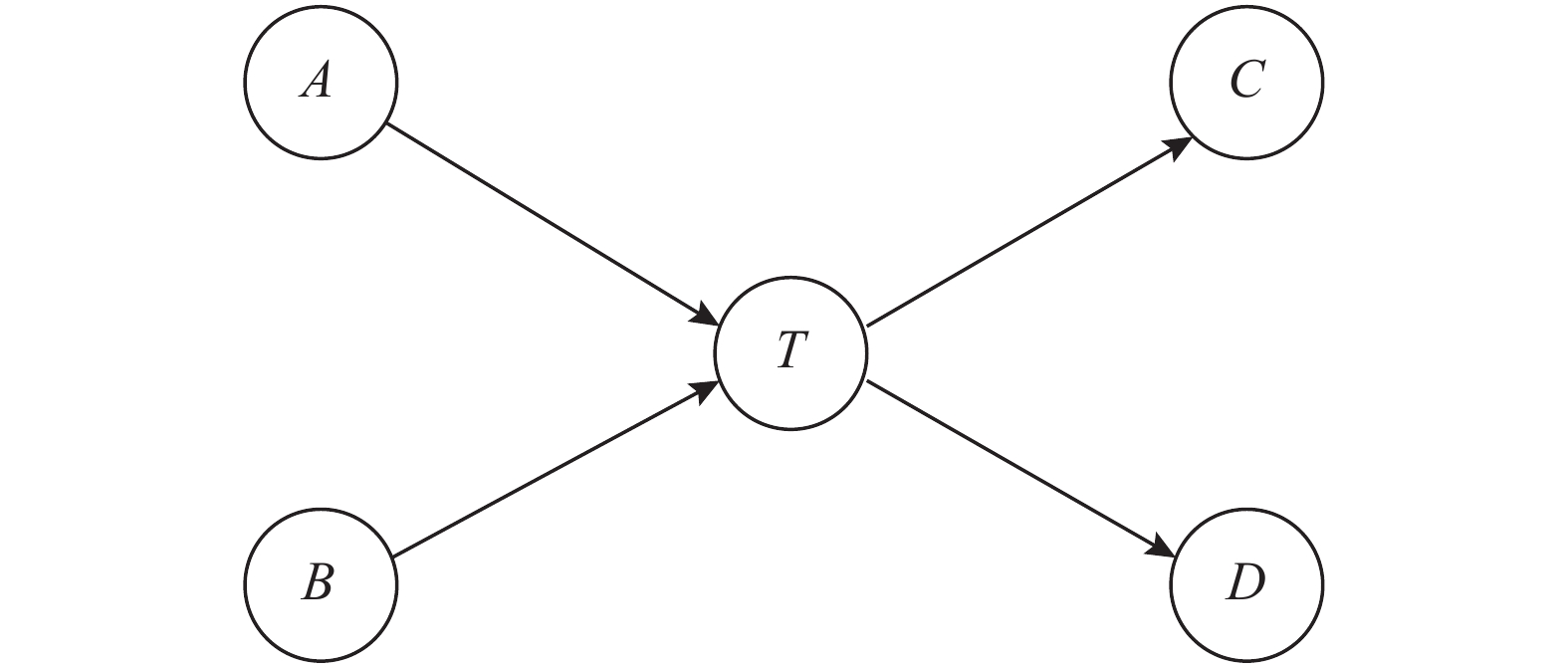
在分析网络节点重要性的过程中, 不仅要考虑待评估节点自身所处的网络层级, 而且要考虑与待评估节点相连的节点所处的网络层级. 设入度节点的系数为I, 出度节点的系数为O, 与待评估节点相连的节点有以下2种情况: 1)指向待评估节点的节点, 即待评估节点的入度节点; 2)由待评估节点指向相连的节点, 即待评估节点的出度节点, 如图 2所示, 节点A、B为节点T的入度节点, 节点C、D为节点的出度节点.
|
图 2 节点的出度节点和入度节点 Fig. 2 Node's exit node and entry node |
命题1 网络节点的入度节点对待评估节点的影响大于出度节点, 即I > O.
例如, 在微博用户中, 别人转发自己的微博比自己转发别人的微博更能体现自己的重要性; 在论文写作过程中, 别人引用自己的论文比自己引用别人的论文更能显示自己论文的重要性等.
定义4(节点重要性综合值) 考虑待评估节点所在网络层级和与待评估节点相连节点所在网络层级对待评估节点重要性的影响, 同时考虑待评估节点的出、入度节点对待评估节点影响的差异性来定义节点重要性综合值, 能够更加细致地评估各节点在网络中的重要性.
以节点的综合值来判断节点的重要性, 综合值越大则节点越重要; 反之, 则节点重要程度越低. 综合值的计算公式为
| ${T_i} = {Q_i}\left( {I\sum\nolimits_k \;{{Q_{k \to i}}{D_{k \to i}}} + O\sum\nolimits_j \;{{Q_{i \to j}}{D_{i \to j}}} } \right).$ | (3) |
式中:Ti为节点i的综合值; Qi为节点i所在的等级权重; O和I分别为出度和入度的权重, 假设O<I, 且O+I=1, 参数O和I通过层次分析法得到, 本文取I=0.75, O=0.25, 根据不同网络中节点出度和入度重要性的大小程度, 可以适当调整参数; Qk→i为指向节点i的节点k(即节点i的入度节点)所在网络等级的权重, Qi→j为节点i指向的节点j(即节点i的出度节点)所在网络等级的权重; Dk→i为指向节点i的节点k的数量, Di→j为节点i指向的节点j的数量.
由上述定义可以得到以下2个公理.
公理1 若待评估节点处于相同层级且与其相连的邻接节点处于相同层级, 则待评估节点的度值越大, 重要性越高.
公理2 处于同一网络层级的节点之间互相不影响, 即只有待评估节点所在网络层级、与待评估节点相连接节点所在网络层级和待评估节点的出、入度3个因素影响节点的重要性.
由上述相关定义可知, 计算网络中各个节点的节点重要性综合值, 通过比较综合值的大小来判断节点的重要性程度, 即节点重要性综合值越大, 节点在网络中的重要性越大, 反之则节点重要性越小.
本文提出的方法基于解释结构模型, 解释结构模型基于网络的邻接矩阵. 在提取骨架矩阵的环节中, 为了减少工作量, 将具有强连接关系的节点进行融合, 即将2个节点看作一个整体. 强连接的节点之间会形成环, 所以该方法对无环的有向复杂网络中节点重要性的计算效率更高.
3 基于ISM模型的有向复杂网络节点重要性评估比较 3.1 ARPA有向网络节点重要性评估对美国的ARPA(Advanced Research Project Agency, ARPA)网络中节点重要性进行研究, 张小娟等[17]对ARPA网络节点重要度进行评估, 但是没有考虑节点之间的有向性问题; 在文献[17]的基础上, 李鹏翔等[29]给出边定向方法, 将无向的ARPA网络转化为有向的ARPA网络, 研究网络中各节点的重要性. 按照上述ISM在复杂网络中的应用顺序, 开展网络节点重要度的研究.
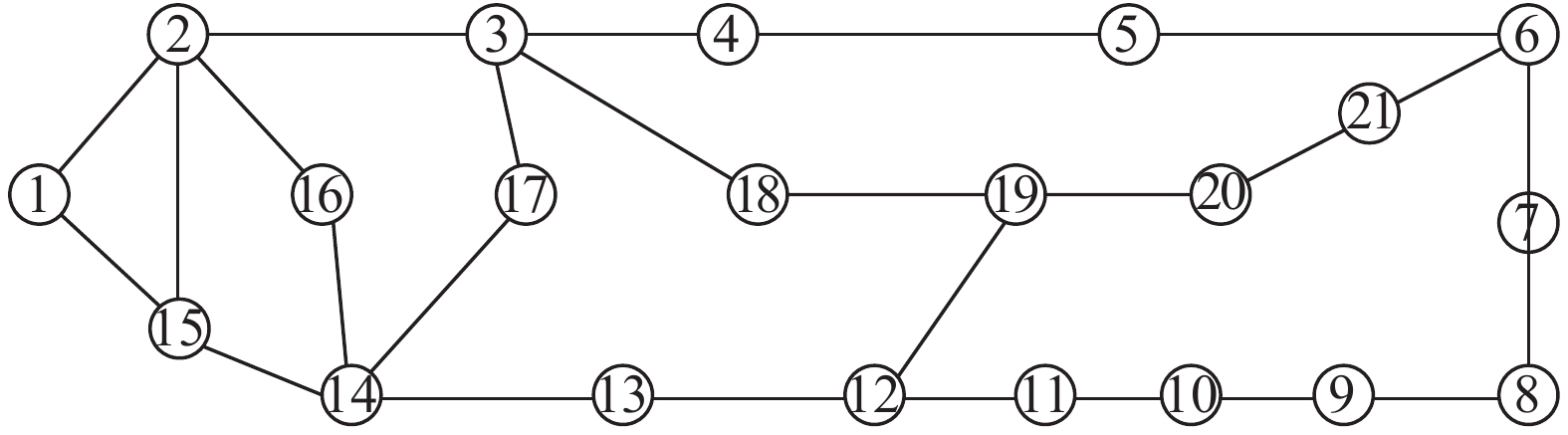
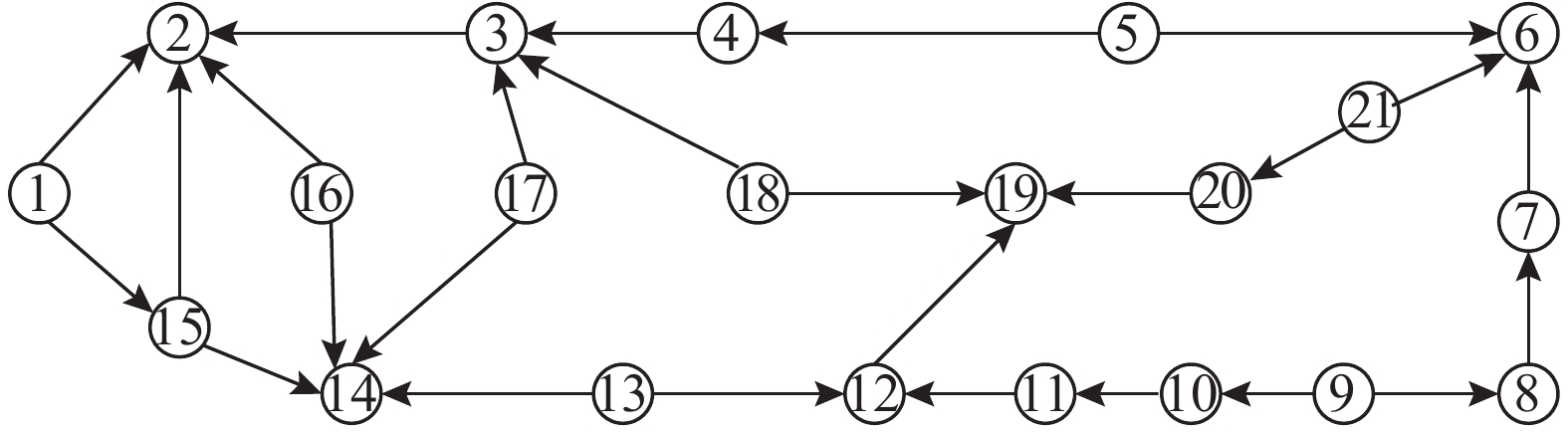
1)ARPA网络简述.ARPA网络属于无向网络, 先对网络进行定向处理, 得到有向的ARPA网络[29], 如图 4所示. 网络由21个节点构成, 节点间的关系如图 3所示.
|
图 3 无向的ARPA网络 Fig. 3 Undirected ARPA network |
|
图 4 有向的ARPA网络 Fig. 4 Directed ARPA network |
2)构建ARPA有向网络递阶结构. 根据ISM模型, 在复杂网络中的建模步骤如下. 1)建立网络的邻接矩阵和可达矩阵; 2)对网络进行区域划分; 3)在区域划分的基础上进行级位划分; 4)在区域、级位划分后, 对可达矩阵进行缩减, 提取骨架矩阵; 5)以骨架矩阵为基础, 建立网络的多级递阶有向图.
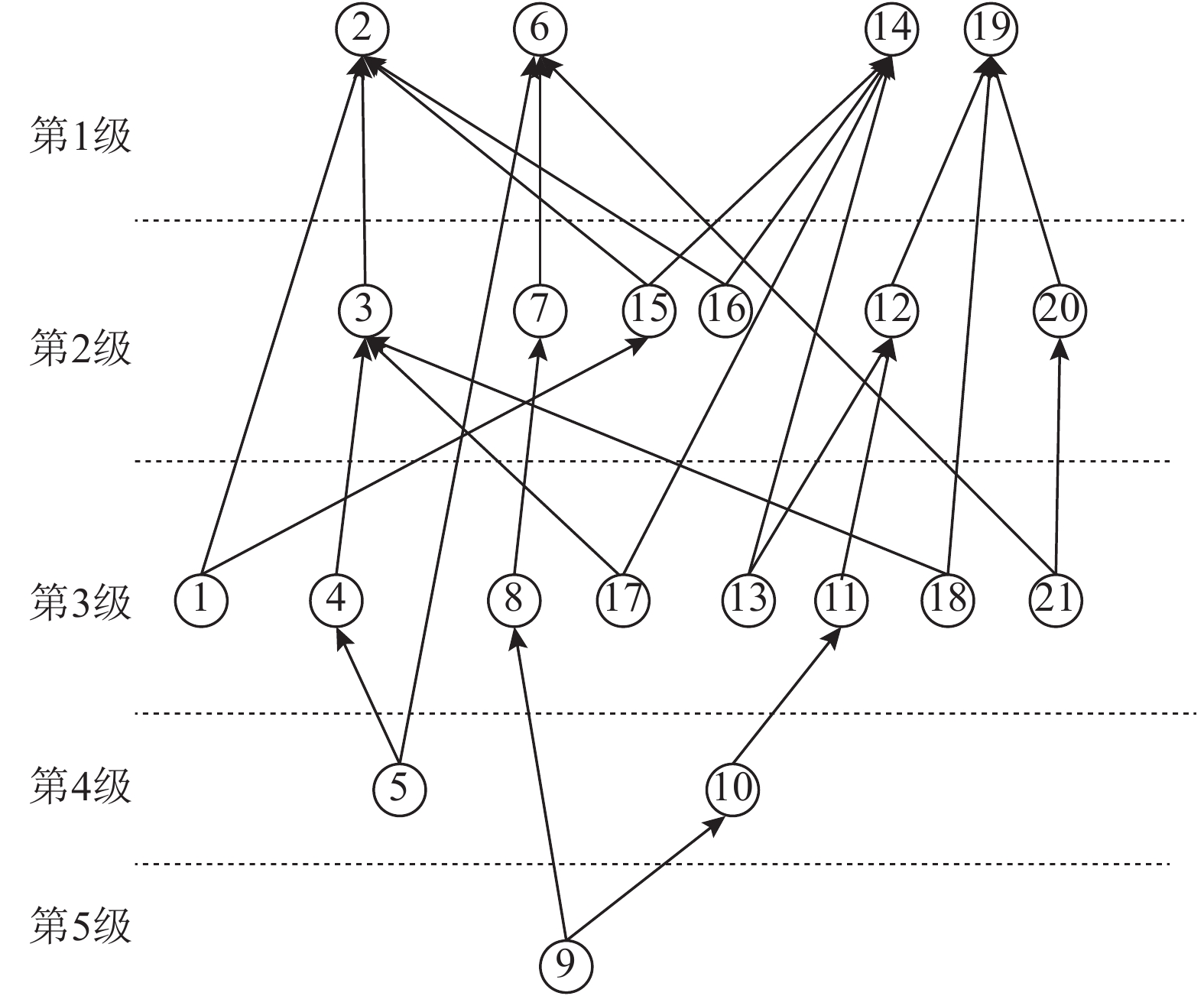
通过以上步骤, 得到ARPA有向网络的多级递阶有向图, 如图 5所示.
|
图 5 基于ISM的网络递阶有向图 Fig. 5 Hierarchical directed graph based on ISM |
1)节点出、入度统计分析. 对递阶化网络中不同层级的节点度进行统计. 度值的统计不仅仅是出度和入度的数值大小, 还要统计某节点所连接的出度节点和入度节点所在的层级. 各节点的出、入度统计如表 1所示, 例如出度为2的节点记为2(1Ⅰ1Ⅱ), 表示该节点有两条边指向别的节点, 一条指向的节点在第一层级, 另一条边所指向的节点在第二层级, 同理可以统计入度.
| 表 1 各节点出、入度统计表 Table 1 Statistical table of admission and departure degree of each node |
2)ARPA有向网络中各节点重要度综合值计算. 根据节点重要度评价方法, 通过计算ARPA有向网络中各个节点的节点重要性综合值, 可得网络各节点的重要度排序, 如表 2所示.
| 表 2 各节点重要性综合值统计表 Table 2 Statistical table of importance degree of each node |
为了更清楚地演化O、I参数对节点综合值及节点重要度排序的影响程度, 根据判断矩阵标度的不同[30 ], 分别取8组数值, 演化出不同参数对节点重要度排序的影响趋势,具体结果如图 6所示.
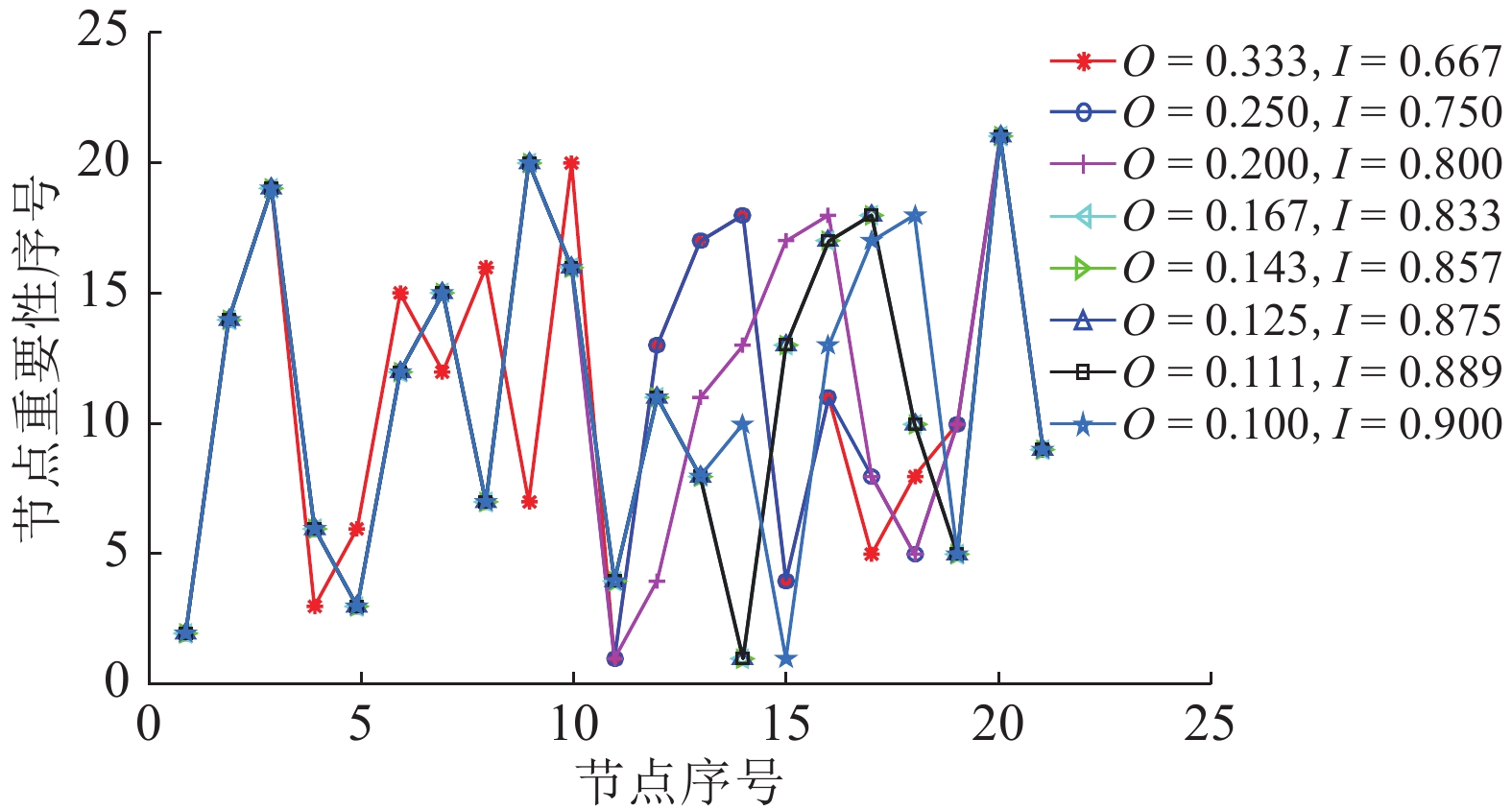
|
图 6 不同参数对节点重要度排序的影响 Fig. 6 Influence of different parameters on node importance ranking |
3)与其他文献节点重要性评估结果比较, 如表 3所示. 表中, “●”、“◢”、“▲”、“◆”、“★”分别表示文献[22, 23, 31, 32]及本文中重要度为“1”、“2”、“3”、“4”、“5”的节点, “○”为非前5的节点.
| 表 3 本文方法与其他文献节点重要度排序比较表 Table 3 Comparison of proposed method and ranking degree of other documents |
4)4种节点重要性评估方法比较分析. 文献[22, 32]的方法是针对无向ARPA网络中节点的重要性进行评估, 该方法不适用于有向复杂网络, 本文算法针对有向复杂网络; 文献[23, 31]虽然是针对有向ARPA网络中节点进行重要性分析, 但不能很好地将网络中的所有节点进行排序. 例如, 在文献[23]中, 节点8、10都排在第10位, 节点16、17都排在第14位, 节点1、13和18都排在第16位, 节点5、21都排在第19位; 文献[23]的算法只考虑了节点的度值和节点连边上的权重, 没有考虑节点的邻居节点和邻居节点的度值与权重. 文献[31]中存在只考虑节点度的问题, 节点5、21都属于第7位, 节点8、10和11属于第11位.
根据ISM对网络节点层级划分, 得到节点2、6、14、19属于第1层级, 且这4个节点只有入度, 没有出度; 节点2、4的出度和入度都为4, 节点6、19的入度分别为2和3, 故节点2、14比节点6、19更重要; 同时, 节点2有3条来自第2层的连边, 节点14只有2条, 故节点2比节点14更重要. 范文礼等[22, 32]认为节点3的重要度大于节点19, 因只考虑节点3的度数大于节点19, 未考虑节点所处的层级位置, 故虽然节点3的度数为4, 出度为1, 入度为3, 但其中有3条连边处于较低的第3层级, 节点3本身处于第2层级; 节点19虽然度数较小, 但是本身处于较高的第1层级, 且其中有2条连边来自第2层级, 1条连边来自第3层级. 综上分析可知, 节点19比节点3更重要; 同理, 节点6的重要性大于节点3. 表 5的最后一列为文献[22, 23, 31, 32]中节点重要度排序的平均值. 可知,利用本文的节点重要度评价方法得到的排序结论与平均值基本契合, 体现了该评价方法的合理性.
4 ISM模型在有向随机网络与无标度网络中的推广应用为了说明该网络节点重要性评估方法的适用性, 通过Pajek软件仿真出21个节点的有向随机网络和无标度网络, 利用该方法对网络中节点进行重要性评估.
4.1 有向随机网络节点重要性评估分析1)在Pajek软件中生成21个节点的随机网络, 如图 7所示.
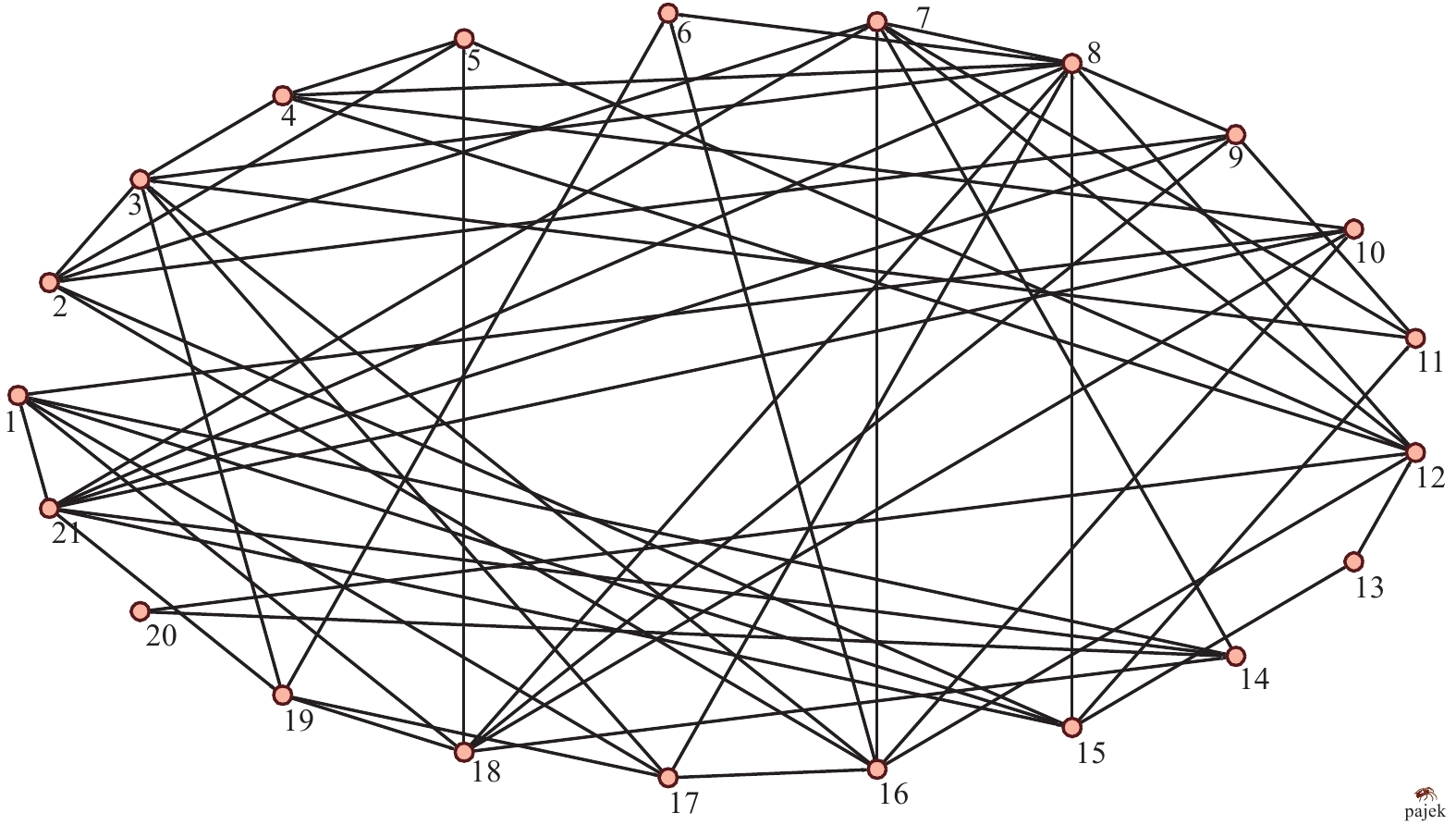
|
图 7 Pajek仿真的有向随机网络 Fig. 7 Directed random network based on Pajek simulation |
2)提取网络的邻接矩阵.
3)在MATLAB中得到网络的可达矩阵, 并使用ISM对网络分层, 具体分层结果如图 8所示.

|
图 8 有向随机网络的递阶有向图 Fig. 8 Hierarchical directed graphs of directed random network |
对分层后的有向随机网络进行节点综合值计算, 根据计算结果对节点进行重要性排序, 如表 4所示.
| 表 4 有向随机网络相应指标统计表 Table 4 Statistical table of directed random network corresponding index |
1) 在Pajek软件中生成21个节点的无标度网络, 如图 9所示.
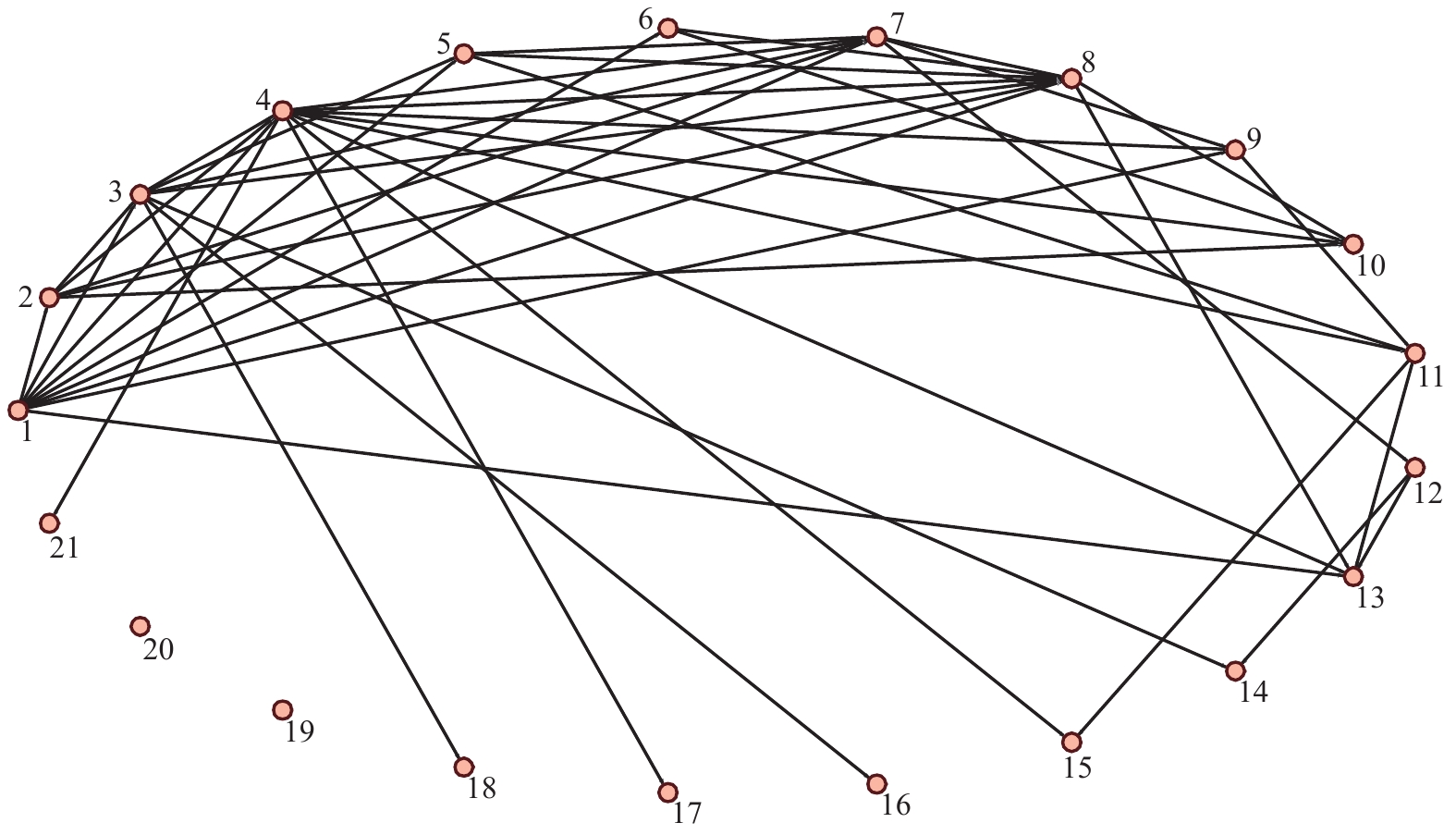
|
图 9 Pajek仿真的有向无标度网络 Fig. 9 Directed scale-free network based on Pajek simulation |
2)提取网络的邻接矩阵.
3)在MATLAB中得到网络的可达矩阵, 使用ISM对网络分层, 具体的分层结果如图 10所示.

|
图 10 有向无标度网络的递阶有向图 Fig. 10 Hierarchical directed graphs of directed scale-free network |
对分层后的有向随机网络进行节点综合值计算, 根据计算结果对节点进行重要性排序, 如表 5所示.
| 表 5 有向无标度网络相应指标统计表 Table 5 Statistical table of directed scale-free network corresponding index |
通过上述研究与实验可知, 本文算法能够很好地应用于有向随机网络和有向无标度网络, 说明该算法在复杂网络节点重要性计算与排序方面具有一定的普适性与有效性. 通过对随机网络和无标度网络的实验分析可知, ISM模型能够根据网络的性质进行层级划分, 例如在随机网络中, 每一层级的节点数量分布较均匀, 节点数最多的为5, 节点数最少的为1, 平均每一层级节点数为2.3; 在无标度网络中, 除了第一层级, 其他层级节点数分布较均匀, 节点数最多的为8, 节点数最少的为1, 平均每层节点数为2.6, 该结果体现了随机网络节点分布的均匀分布特征与无标度网络核心节点分布的幂率分布变化特征.
5 结 语本文基于ISM系统模型, 给出综合考虑节点出、入度以及节点所在网络层级的节点重要性辨识与评估方法. 该方法能够将网络进行层级划分, 赋予不同网络层级节点不同的重要性权重, 且处于相同网络层级的节点因度值差异具有不同的重要性; 定义网络节点出、入度影响系数, 细化节点度值的重要性. 将该方法应用于ARPA有向网络、有向随机网络和有向无标度网络节点重要性评估中, 与文献[22, 23, 30, 31]结果相比, 本文方法更细致地刻画了节点的重要度. 通过模型的推广实验可以看出, 本文方法具有一定的普适性与有效性. 根据ISM模型的特点, 本文方法更加适用于无环的有向网络. 如何基于该方法对加权有向网络开展网络快速分块演化计算、网络序贯抗毁性和结构稳性研究, 将是进一步的研究方向.
| [1] |
WATTS D J, STROGATZ S H. Collective dynamics of small-world networks[J]. Nature, 1998, 393(6684): 440-442. DOI:10.1038/30918 |
| [2] |
BARABÁ SI A L, ALBERT R. Emerging of scaling in random networks[J]. Science, 1999, 286(5439): 509-512. DOI:10.1126/science.286.5439.509 |
| [3] |
LIU Y Y, SLOTINE J J, BARABÁ SI A L. Controllability of complex networks[J]. Nature, 2011, 473(7346): 167. DOI:10.1038/nature10011 |
| [4] |
OROSZ G, WILSON R E, STÉPÁN G. Traffic jams: dynamics and control[J]. Philosophical Transactions Mathematical Physical and Engineering Sciences, 2010, 368(1928): 4455. DOI:10.1098/rsta.2010.0205 |
| [5] |
WANG J W, RONG L L. Cascade-based attack vulnerability on the US power grid[J]. Safety Science, 2009, 47(10): 1332-1336. DOI:10.1016/j.ssci.2009.02.002 |
| [6] |
BONACICH P. Taylor & Francis Online: factoring and weighting approaches to status scores and clique identification[J]. Journal of Mathematical Sociology, 1972, 2(1): 113-120. DOI:10.1080/0022250X.1972.9989806 |
| [7] |
UGANDER J, BACKSTROM L, MARLOW C, et al. Structural diversity in social contagion[J]. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109(16): 5962. DOI:10.1073/pnas.1116502109 |
| [8] |
CHEN D, LÜ L, SHANG M S, et al. Identifying influential nodes in complex networks[J]. Physica A Statistical Mechanics and its Applications, 2012, 391(4): 1777-1787. DOI:10.1016/j.physa.2011.09.017 |
| [9] |
任卓明, 邵凤, 刘建国, 等. 基于度与集聚系数的网络节点重要性度量方法研究[J]. 物理学报, 2013, 62(12): 000522-526. REN Zhuo-ming, SHAO Feng, LIU Jian-guo, et al. Study on the importance measure of network nodes based on degree and clustering coefficients[J]. Acta Physica Sinica, 2013, 62(12): 000522-526. |
| [10] |
张喜平, 李永树, 刘刚, 等. 节点重要度贡献的复杂网络节点重要度评估方法[J]. 复杂系统与复杂性科学, 2014, 11(3): 26-32. ZHANG Xi-ping, LI Yong-shu, LIU Gang, et al. Method for evaluating the importance of complex network node with contribution to node importance[J]. Journal of Complex Systems and Complexity, 2014, 11(3): 26-32. |
| [11] |
苏晓萍, 宋玉蓉. 利用邻域"结构洞"寻找社会网络中最具影响力节点[J]. 物理学报, 2015, 64(2): 1-11. SU Xiao-ping, SONG Yu-rong. Application of neighborhood "structure cave" to find the most influential node in social networks[J]. Acta Physica Sinica, 2015, 64(2): 1-11. |
| [12] |
韩忠明, 陈炎, 李梦琪, 等. 一种有效的基于三角结构的复杂网络节点影响力度量模型[J]. 物理学报, 2016, 65(16): 285-296. HAN Zhong-ming, CHEN Yan, LI Meng-qi, et al. An effective model of complex network node influence based on triangular structure[J]. Acta Physica Sinica, 2016, 65(16): 285-296. |
| [13] |
阮逸润, 老松杨, 王竣德, 等. 基于领域相似度的复杂网络节点重要度评估算法[J]. 物理学报, 2017, 66(3): 365-373. RUAN Yi-run, LAO Song-yang, WANG Jun-de, et al. Complexity evaluation of complex network node based on domain similarity[J]. Acta Physica Sinica, 2017, 66(3): 365-373. |
| [14] |
谭跃进, 吴俊, 邓宏钟. 复杂网络中节点重要度评估的节点收缩方法[J]. 系统工程理论与实践, 2006, 26(11): 79-83. TAN Yue-jin, WU Jun, DENG Hong-zhong. Node shrinkage method for node importance assessment in complex networks[J]. Systems Engineering-Theory and Practice, 2006, 26(11): 79-83. DOI:10.3321/j.issn:1000-6788.2006.11.011 |
| [15] |
赵毅寰, 王祖林, 郑晶, 等. 利用重要性贡献矩阵确定通信网中最重要节点[J]. 北京航空航天大学学报, 2009, 35(9): 1076-1079. ZHAO Yi-huan, WANG Zu-lin, ZHENG Jing, et al. Using the importance contribution matrix to determine the most important nodes in communication network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(9): 1076-1079. |
| [16] |
KITSAK M, GALLOS L K, HAVLIN S, et al. Identification of influential spreaders in complex networks[J]. Nature Physics, 2010, 6(11): 888-893. DOI:10.1038/nphys1746 |
| [17] |
张小娟, 王旭峰. 一种通信网络节点重要性的计算公式[J]. 东北大学学报: 自然科学版, 2014, 35(5): 663-666. ZHANG Xiao-juan, WANG Xu-feng. A formula for calculating the importance of communication network nodes[J]. Journal of Northeastern University: Natural Science Edition, 2014, 35(5): 663-666. |
| [18] |
肖俐平, 孟晖, 李德毅. 基于拓扑势的网络节点重要性排序及评价方法[J]. 武汉大学学报: 信息科学版, 2008, 33(4): 379-383. XIAO Li-ping, MENG Hui, LI De-yi. Importance ranking and evaluation method of network nodes based on topological potential[J]. Journal of Wuhan University: Information Science Edition, 2008, 33(4): 379-383. |
| [19] |
陈静, 孙林夫. 复杂网络中节点重要度评估[J]. 西南交通大学学报, 2009, 44(3): 426-429. CHEN Jing, SUN Lin-fu. Evaluation of node importance in complex networks[J]. Journal of Southwest Jiao Tong University, 2009, 44(3): 426-429. DOI:10.3969/j.issn.0258-2724.2009.03.021 |
| [20] |
王甲生, 吴晓平, 廖巍, 等. 改进的加权复杂网络节点重要度评估方法[J]. 计算机工程, 2012, 38(10): 74-76. WANG Jia-sheng, WU Xiao-ping, LIAO Wei, et al. Improved method for evaluating the importance of nodes in weighted complex networks[J]. Computer Engineering, 2012, 38(10): 74-76. DOI:10.3969/j.issn.1000-3428.2012.10.021 |
| [21] |
周漩, 张凤鸣, 李克武, 等. 利用重要度评价矩阵确定复杂网络关键节点[J]. 物理学报, 2012, 61(5): 1-7. ZHOU Xuan, ZHANG Feng-ming, LI Ke-wu, et al. The importance evaluation matrix to determine the key nodes of the complex network[J]. Journal of Physics, 2012, 61(5): 1-7. |
| [22] |
范文礼, 刘志刚. 基于传输效率矩阵的复杂网络节点重要度排序方法[J]. 西南交通大学学报, 2014, 49(2): 337-342. FAN Wen-li, LIU Zhi-gang. Ranking method of node importance in complex networks based on transfer efficiency matrix[J]. Journal of Southwest Jiao Tong University, 2014, 49(2): 337-342. DOI:10.3969/j.issn.0258-2724.2014.02.023 |
| [23] |
王雨, 郭进利. 基于多重影响力矩阵的有向加权网络节点重要性评估方法[J]. 物理学报, 2017, 66(5): 13-24. WANG Yu, GUO Jin-li. Evaluation method of node importance of directed weighted network based on multiple influence matrix[J]. Journal of Physics, 2017, 66(5): 13-24. |
| [24] |
HASTEER N, BANSAL A, MURTHY B K. Assessment of cloud application development attributes through interpretive structural modeling[J]. International Journal of System Assurance Engineering and Management, 2017, 8(2): 1-10. |
| [25] |
KATO T, MATSUOKA Y. Quality function deployment using improved interpretive structural modeling: human interface and the management of information [M]. Cham: Springer, 2014: 352–363.
|
| [26] |
LIU S, GAO X, ZEN Q, et al. Studies on interpretive structural model for forest ecosystem management decision-making: complex sciences [M]. Berlin: Springer, 2009: 944–953.
|
| [27] |
GOVINDAN K, PALANIAPPAN M, ZHU Q, et al. Analysis of third party reverse logistics provider using interpretive structural modeling[J]. International Journal of Production Economics, 2012, 140(1): 204-211. DOI:10.1016/j.ijpe.2012.01.043 |
| [28] |
CHANDRAMOWLI S, TRANSUE M, FELDER F A. Analysis of barriers to development in landfill communities using interpretive structural modeling[J]. Habitat International, 2011, 35(2): 246-253. DOI:10.1016/j.habitatint.2010.09.005 |
| [29] |
李鹏翔, 任玉晴, 席酉民. 网络节点(集)重要性的一种度量指标[J]. 系统工程, 2004, 22(4): 13-20. LI Peng-xiang, REN Yu-qing, XI You-min. An importance measure of actor(set) within a network[J]. Systems Engineering, 2004, 22(4): 13-20. |
| [30] |
汪应洛. 系统工程[M]. 北京: 机械工业出版社, 2008: 122–123.
|
| [31] |
王班, 马润年, 王刚, 等. 改进的加权网络节点重要性评估的互信息方法[J]. 计算机应用, 2015, 35(7): 1820-1823. WANG Ban, MA Run-nian, WANG Gang, et al. Improved mutual information method for weighted network node importance evaluation[J]. Computer Applications, 2015, 35(7): 1820-1823. |
| [32] |
HU P, FAN W, MEI S. Identifying node importance in complex networks[J]. Physica A Statistical Mechanics and its Applications, 2015, 429(1): 169-176. |


