跑动是人类最基本的运动方式之一，对于假肢穿戴者而言，跑动运动有助于恢复身体运动机能，可以有效地避免残肢肌肉萎缩.近几年，动力型下肢假肢的发展使穿戴者进行跑动运动成为可能，因此对假肢穿戴者跑动意图识别的研究十分关键.在国外，智能假肢性能不断提高，相应产品及样机的功能逐渐完善.冰岛Ossur公司的Power Knee系列假肢、德国Otto Bock公司的Genium智能仿生腿等^[1-2]，在运动状态识别、人机交互、能量效率等方面各有特色，尤其是Genium X3的智能仿生膝关节，不仅实现不同步速下的行走与跑动，而且克服了其他智能假肢无法在水中运行的缺点.此外，Shultz等^[3]一直致力于下肢假肢跑动模式控制方法的研究，设计出动力型下肢跑动运动控制器，能够实现跑动与行走之间的转换；Rigney等^[4]通过有限元分析假肢跑动模式下能量峰值的变化，判断假肢性能.在国内，动力型假肢研究的进步十分明显，但是主要侧重于不同路况下行走步态的识别和控制方面. 黄岩等^[5]研究动态行走机理的“机器人假肢”，所设计的位姿估算器能够有效提高“机器人假肢”行走稳定性；王启宁等^[6-10]以下肢假肢在不同路况下行走的步态识别与控制为研究重点.此外，陈国兴等^[11]设计跌倒预警系统，能够完成假肢穿戴者异常步态的识别与预警；杨建坤等^[12-13]针对假肢穿戴者在不同情况下的跌倒，提出相应的跌倒恢复策略.以上均是对假肢配合穿戴者在不同路况下正常行走及安全预警的相关研究，对于下肢假肢跑动运动的研究十分匮乏.

下肢假肢穿戴者的跑动状态与行走状态有很大的不同，步态周期缩短，使得支撑期的频率增高；造成跑动过程出现更强的颠振现象，使安装在假肢和残肢上的传感器发生信号振动问题.为了保证下肢运动信息的可靠性，单一的运动信息特征已无法满足要求.在结合已有研究报告的基础上发现，大腿残肢端股直肌部位与膝关节部位是不同运动模式下较典型的信号区^[14-15]，因此将多个肌电传感器、加速度计安装在股直肌和膝关节部位，采集大腿残肢端加速度信息、肌电信息及假肢膝关节加速度信息；结合双下肢足底压力信息，组成多维特征向量作为跑动步态识别模型的输入.另外，多特征参数的处理问题关系到分类器的识别率和稳定性^[16]，SVM在多种特征输入的故障检测问题上有着良好的分类效果^[17-19]，且在假肢跌倒异常步态识别中有所应用，故选取SVM作为跑动步态分类器，并利用PSO优化分类模型参数，解决全局优化问题^[20-21]，提高SVM次序分类模型的准确率.

1 步态分析与数据采集

在识别下肢假肢跑动步态之前，首先分析人体下肢的跑动运动模式.下肢跑动与行走都是人体交替换步的运动，但在动作结构方面存在根本区别.在下肢行走的运动过程中不会出现腾空现象，始终有一条腿与地面接触，行走的动作特点可以描述为单脚支撑与双脚支撑相互交替.在跑动运动过程中，在支撑末期单脚瞪伸离地后，下肢会出现腾空现象；紧接着另一只腿下落着地，出现与行走状态完全不同的单脚轮流支撑与腾空反复交替的运动过程.

下肢假肢跑动步态的识别是以假肢侧为研究对象，讨论以假肢侧为主的单步跑动周期，因此将健肢侧支撑阶段划分至假肢侧腾空中期当中，并将整个跑动周期划分为支撑期与腾空期. 腾空期分为3个阶段，分别为腾空前期、腾空中期、腾空末期，形体表现分别为腾空后折、支撑摆腿、腾空前伸，如图1所示.通过分析人体跑动运动特点发现，在跑动过程中，下肢支撑期状态与跑动速度有关. 当低步速跑动时，支撑期是脚跟先着地；当步速达到一定程度时，支撑期转变为前脚掌先着地，但是该临界值受不同群体的身高、年龄等众多因素影响而没有严格的标准.在实际调研中，与假肢穿戴者和康复师交流发现，下肢假肢穿戴者跑动时身体协调性与正常人存在一定的差异.基于安全考虑，跑动以低步速为宜，故只研究假肢穿戴者低速跑动状态下支撑期脚跟先着地的情况.

数据采集实验在电动跑步机上开展，假肢穿戴者以5 km/h的步速进行跑动，跑步机跑道与地面水平，受试者双手扶在跑步机前方扶手上.考虑到残疾人即便穿戴动力型假肢，若安装诸多有线传感器，则会给假肢穿戴者的生活带来诸多不便，因此选用高性能、高精度的TrignoTM wire-less EMG无线采集仪，如图2(a)所示.EMG智能传感器模块可以嵌入到假肢接受腔中，集成了肌电传感器和加速度计的数据采集功能，肌电信号的采样频率为2 000 Hz，加速度信号的采样频率为150 Hz.足底压力信息采集选用stm32无线数据采集模块，如图2(b)所示，采样频率为150 Hz.

在假肢穿戴者进行跑动实验之前，以待测速度热身1.0~2.0 min，待跑动运动稳定后，再采集数据，以提高数据采集的稳定性和可靠性.如图3所示为受试者进行数据采集的实验照片.

2 数据预处理与多特征提取 2.1 数据预处理

在下肢运动信息采集过程中，因身体颠振会产生较多的噪声信号，而在腾空中期健肢侧支撑；在假肢侧腾空摆腿过程中，因关键部位信息不突出，很容易被当成噪声信号去除.为了避免跑动运动信息边缘局部特征丢失的问题，采用基于改进的小波包去噪方法对跑动运动信息进行预处理，由原来单一的硬阈值或软阈值去噪转换为两者相结合的去噪方法.首先根据Donoho等^[22]提出的阈值函数变换方法，确定软、硬阈值变换的临界阈值；再通过软硬阈值结合的去噪函数，对多层小波包分解系数进行阈值判断，得到具有量化特性的小波包系数；将小波包系数进行反变换，重构消噪后的信号，其中软硬阈值结合的去噪函数为

$\mu = \sigma \sqrt {2{\rm{lg}} \,N } /\left( {1 + {\rm{lg }}\;f} \right);$

(1)

${M_{x,y}} = \left\{ \begin{gathered} {\rm{sgn}}\left( {{m_{x,y}}} \right)\begin{array}{*{20}{c}} {\left( {\left| {{m_{x,y}}} \right| - p\mu } \right){\rm{ ,}}}&{\left| {{m_{x,y}}} \right|> \mu }, 0 \leqslant p \leqslant 1;\end{array} \\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!0,{\rm{ }}\begin{array}{*{20}{l}} {\left| {{m_{x,y}}} \right| \leqslant \mu },\;0 \leqslant p \leqslant 1.\end{array} \\ \end{gathered} \right.$

(2)

式中：μ为阈值；N为小波包变换系数的个数；f为小波包分解尺度； $\sigma $ 为噪声因子， $\sigma $ 根据第一层小波包分解系数估计获取；m_x,y为小波包系数；M_x,y为调节阈值处理后的小波包系数；p为阈值函数的调节因子.

当p设置为0时，式(2)为硬阈值去噪函数；当p设置为1时，式(2)为软阈值去噪函数；当0<p< 1时，M_x,y介于软、硬阈值函数计算的结果之间.通过适当变换p，可以有效地避免因颠振导致跑动运动信息边缘模糊失真的问题.根据大量的实验数据对比分析，将p设置为0.6，获取了较理想的跑动运动信息，降低了跑动步态分析过程中的不确定性.

以5 km/h的跑动实验数据为例，在速度稳定状态下，取其中相同时间段的数据进行软硬阈值结合去噪处理. 如图4所示为在相同时刻，大腿侧股直肌、膝关节的竖直方向和水平方向加速度和调节阈值去噪处理后的信号对比. 图中，t_s为采样时间， $a_{{\rm h}z}$ 、 $a_{{\rm h}z}^{\rm p}$ 分别为大腿股直肌竖直方向加速度原始信号和去噪处理后信号， $a_{{\rm h}x}$ 、 $a_{{\rm h}x}^{\rm p}$ 分别为大腿股直肌水平方向加速度原始信号和去噪处理后信号， $a_{{\rm k}z}$ 、 $a_{{\rm k}z}^{\rm p}$ 分别为膝关节竖直方向加速度原始信号和去噪处理后信号， $a_{{\rm k}x}$ 、 $a_{{\rm k}x}^{\rm p}$ 分别为膝关节水平方向加速度原始信号和去噪处理后信号.

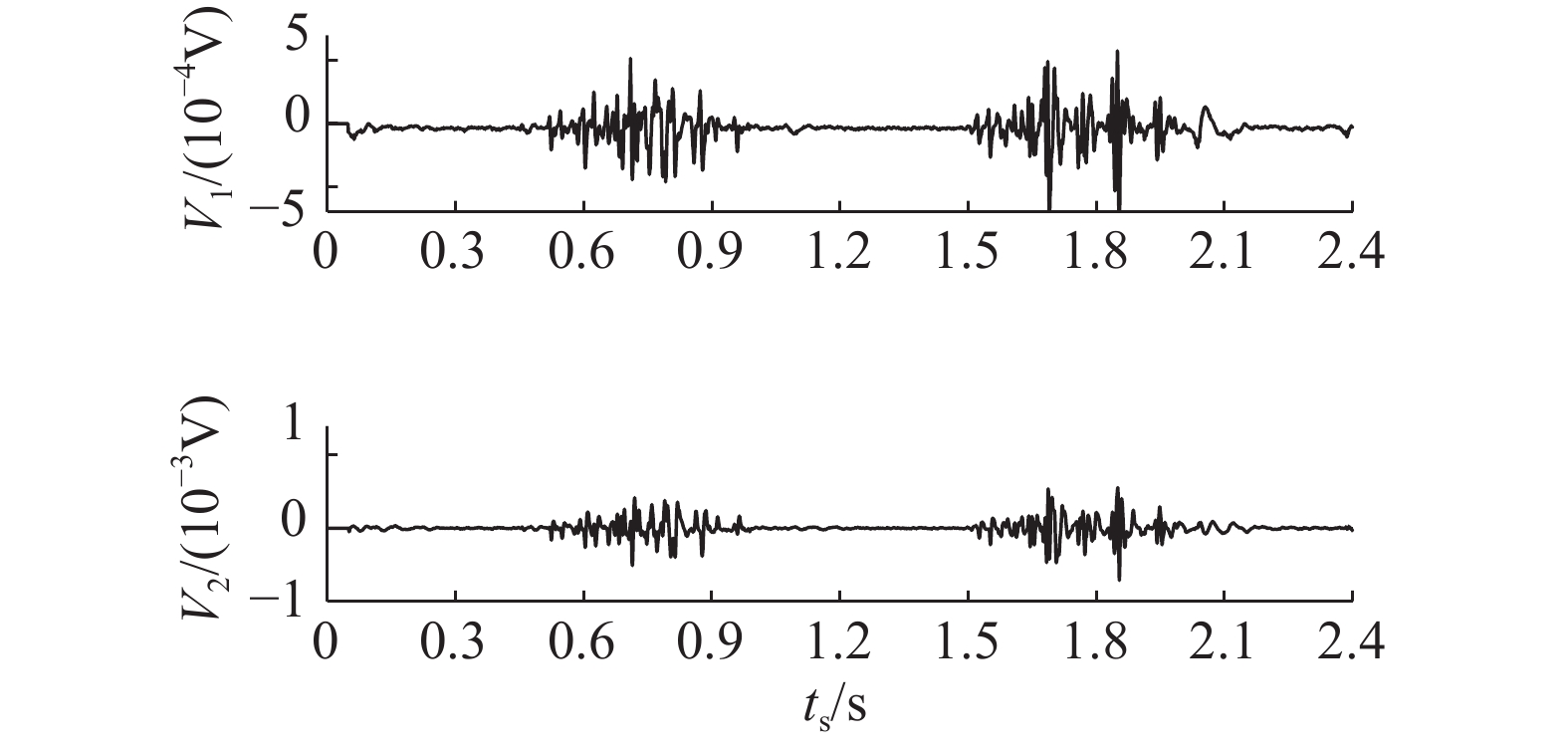
在表面肌电信号（surface electromyography, sEMG）中，20~450 Hz频段数据被认为是肌电信号最有效的组成部分；利用切比雪夫I型滤波方法，对大腿股直肌部位的肌电信号数据进行预处理，将滤波类型设置为带通滤波，通带频率设定为20~450 Hz，波动小于3 dB. 将肌电信号滤波前、后的数据进行对比，如图5(a)、(b)所示分别为5 km/h跑动状态下的大腿侧sEMG原始信号 ${V_1}$ 和滤波处理的sEMG信号 ${V_2}$ .

2.2 多特征值提取

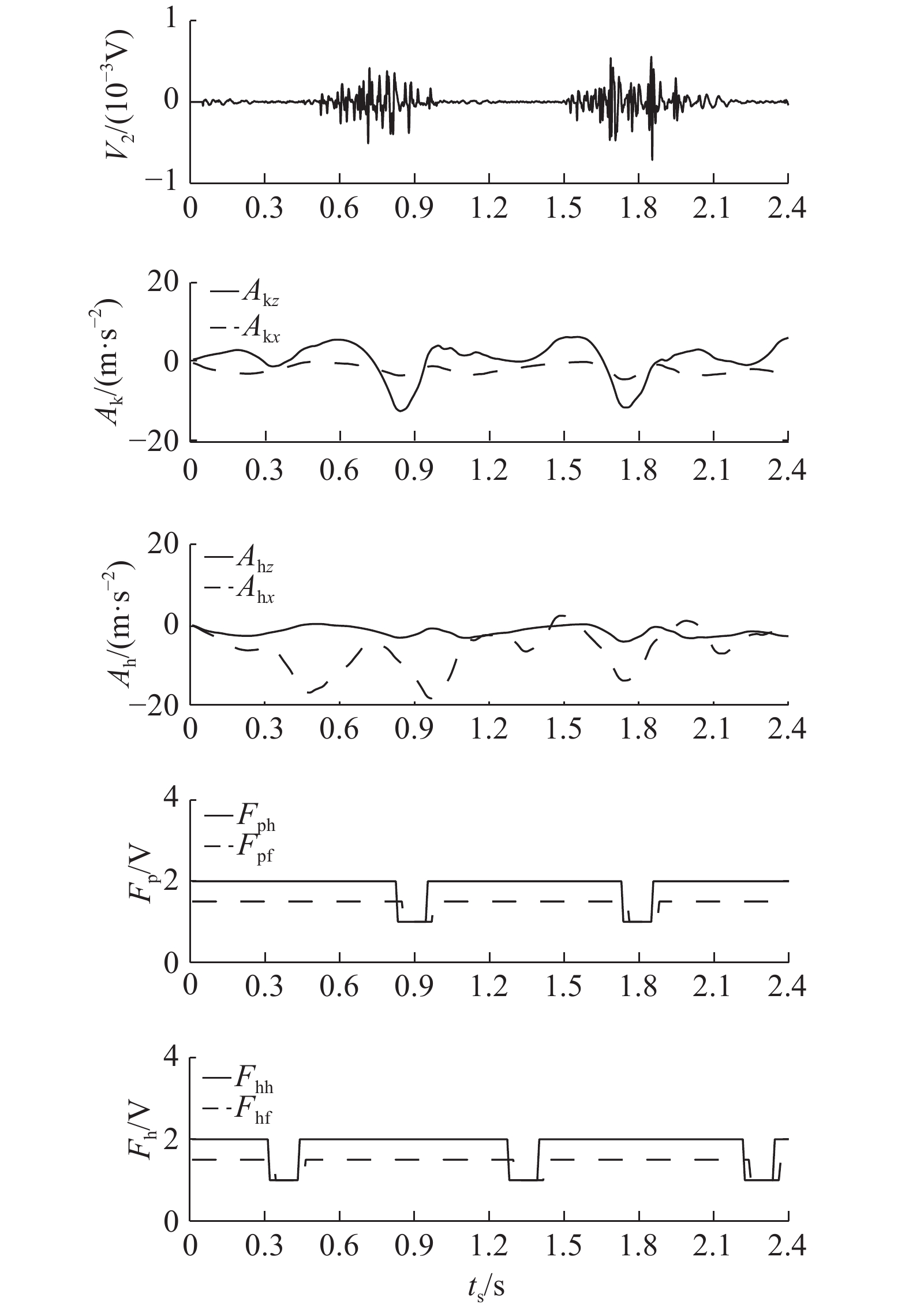
为了针对性地提取下肢跑动状态下不同相位的特征，需要对运动信号相位进行详细划分.以其中一组5 km/h跑动状态下大腿侧股直肌及膝关节部位的样本数据为例，如图6所示. 图中，A_k、A_h分别为膝关节和大腿股直肌加速度阈值处理信号，下标x、z分别表示水平方向和竖直方向；F_ph、F_pf分别为假肢侧脚底压力和前脚掌压力，F_hh、F_hf分别为健肢侧脚底压力和前脚掌压力. 一个完整的跑动步态周期被划分为支撑前期、支撑中期、支撑末期和腾空前期、腾空中期、腾空末期，共6个步态相位，分别由A、B、C、D、E、F表示，可以结合双下肢足底压力信息进行划分.为了便于区分腿部传感器信息，将右侧腿假设为假肢侧作为研究对象，左侧腿作为健肢侧提供辅助信息，双下肢运动信息相结合，为整体跑动步态划分提供依据.设假肢侧后脚跟与前脚掌的逻辑值分别为 ${x_1}$ 、 ${x'_1}$ ，健肢侧后脚跟与前脚掌的逻辑值分别为 ${y_1}$ 、 ${y'_1}$ ，向量 $\left\{ {{x_1},{{x'}_1},{y_1},{{y'}_1}} \right\}$ 可以作为下肢跑动步态不同相位开始和结束的判断信号. 其中前脚掌和后脚跟着地时，逻辑值均为1，后脚跟抬起时逻辑值为2，前脚掌抬起时逻辑值为1.5. 由步态分析可知，健肢侧支撑期阶段被划分至腾空期中，根据足底压力信息，完整跑动状态的各阶段步态相位划分如下.

支撑前期：A={1,1.5,2,1.5}；支撑中期：B={1,1,2,1.5}；支撑末期：C={2,1,2,1.5}；腾空前期：D={2,1.5,2,1.5}；腾空中期：E={2,1.5,1,1.5}U{2,1.5,1,1}U{2,1.5,2,1}；腾空末期F={2,1.5,2,1.5}.

选取60组数据作为实验样本，根据足底压力信息所划分的步态相位，对预处理后的样本集进行分解，对大腿股直肌与膝关节部位的数据分别提取竖直方向加速度偏度和水平方向加速度平均值，对大腿侧股直肌部位的肌电信号提取均方根，与足底压力信息相结合组成多维特征向量，为后续步态识别提供有效数据信息.其中，偏度s(skew)主要衡量跑动运动数据分布的偏斜方向和偏斜程度；平均值m(mean)表征加速度信号的平均强度；肌电信号均方根r(rms)是表面肌电信号的有效度量参数，能够有效反映表面肌电信号的功率.相应公式如下所示：

$s = {{N\sum{_{i = 1}^n} {{{({V_i} - \bar V)}^3}} } \left/ \left[{(N - 1)(N - 2){\sigma ^3}}\right]\right.}{\text{，}}$

(3)

$m = {{\sum{_{i = 1}^n} {{H_i}^2} } / N}{\text{，}}$

(4)

$r = \sqrt {{{\sum{_{i = 1}^n} {{E_i}^2} } / N}} {\text{。}}$

(5)

式中：N为传感器采样点数， $\sigma $ 为肌电信号的方差，V_i、H_i、E_i分别为加速度竖直方向、水平方向和肌电信号的采样值.

支撑期和腾空期共6个不同相位，不同相位的数据段共提取9个特征值，组成特征向量 ${\phi _i}\left( { x} \right)$ . 令 ${\phi _i}\left( { x} \right) =[ {{s_i},{{s'}_i},{m_i},{{m'}_i},{r_i},{x_i},{{x'}_i},{y_i},{{y'}_i}} ]$ .其中 ${s_i}$ 、 ${m_i}$ 分别为大腿股直肌部位竖直和水平方向加速度信号， ${s'_i}$ 、 ${m'_i}$ 分别为膝关节部位竖直和水平方向加速度信号， ${r_i}$ 为大腿股直肌部位的肌电信号， ${x_1}$ 、 ${x'_1}$ 分别为假肢侧后脚跟与前脚掌的逻辑值， ${y_1}$ 、 ${y'_1}$ 分别为健肢侧后脚跟与前脚掌的逻辑值.

3 下肢假肢跑动步态识别方法 3.1 粒子群优化算法

粒子群优化算法（(particle swarm optimization, PSO）通过迭代实现全局寻优，粒子以适应度作为评判标准，利用每次迭代跟踪个体极值及全局极值，确定粒子的最新位置和速度.粒子速度及位置的更新公式如下：

$v_{id}^{k + 1} = \omega v_{id}^k + {c_1}{r_1}\left( {p_{id}^k - x_{id}^k} \right) + {c_2}{r_2}\left( {p_{gd}^k - x_{id}^k} \right){\text{，}}$

(6)

$x_{id}^{k + 1} = x_{id}^k + v_{id}^k{\text{。}}$

(7)

式中： ${r_1}$ 、 ${r_2}$ 为独立的随机数， ${r_1}$ 、 ${r_2} \in \left[ {0,1} \right]$ ； ${c_1}$ 、 ${c_2}$ 分别为局部、全局加速度常数； $k$ 为当前的迭代次数； ${V_i}\left( {{v_{i1}},{v_{i2}}, \cdots ,{v_{id}}} \right)$ 、 ${X_i}\left( {{x_{i1}},{x_{i2}}, \cdots ,{x_{id}}} \right)$ 分别为不同粒子的运动速度和位置； ${P_i}\left( {{p_{i1}},{p_{i2}}, \cdots ,{p_{id}}} \right)$ 为粒子的局部最优位置， ${P_{\rm{g}}}\left( {{p_{{\rm{g}}1}},{p_{{\rm{g}}2}}, \cdots ,{p_{{\rm{g}}d}}} \right)$ 为粒子的全局最优位置； $\omega $ 为惯性系数，表征粒子在解空间追随最优过程时受惯性作用的影响程度，与目标函数和适应度函数有关，

$\omega = \left\{ \begin{array}{l}\displaystyle\frac{{\left( {{\omega _{\max }} - {\omega _{\min }}} \right)\left( {F - {F_{\min }}} \right)}}{{{F_{\rm{avg}}} - {F_{\min }}}} + {\omega _{\min }},\begin{array}{*{20}{c}}{}&{F \leqslant {F_{\rm{avg}}}};\end{array}\\{\omega _{{\rm{max}}}},\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}&{}&{}\end{array}}&{}&{}&{}\end{array}}&{}&{}&{F > {F_{\rm{avg}}}}.\end{array}\end{array} \right.$

(8)

其中， ${\omega _{\max }}$ 、 ${\omega _{\min }}$ 分别为最大和最小惯性系数； $F$ 为粒子的适应度函数， ${F_{\min }}$ 和 ${F_{\rm avg}}$ 分别为适应度函数的最小值和平均值，本文将SVM分类过程中的十折交叉验证识别率作为PSO的适应度函数，

$F = \displaystyle\frac{1}{K}\sum\limits_{l = 1}^K {\displaystyle\frac{{{x_{l{\rm{r}}}}}}{{{x_{l{\rm{r}}}} + {x_{l{\rm{w}}}}}}} ,$

(9)

其中 $K$ 为优化的样本集数目，设置为10，由十折交叉验证方法决定， ${x_{l{\rm{r}}}}$ 和 ${x_{l{\rm{w}}}}$ 分别为SVM第 $l$ 次验证样本集中被正确和错误分类的样本数量，适应度函数值越大，表示寻优效果越显著.

设计的PSO优化SVM模型的跑动步态分类算法流程如图7所示.

3.2 基于PSO-SVM模型的跑动步态识别 3.2.1 SVM多分类模型设计

SVM是在多维非线性数据处理方面应用较广泛的机器学习算法. SVM根据决策函数构造最优超平面，具有良好的泛化性能与分类精度. 以两类数据的分类问题为例，具体的操作方法如下.

首先，假设训练样本集T={( ${{x}}_i$ , ${y_i}$ )}， ${{x}}_i \in {{\bf R}^n}$ ， ${y_i} \in $ {±1}， $i$ =1,2,3,···,l，其中 ${{{x}}_i}$ 为特征向量.根据先验知识选取SVM核函数 $K\left( {{{{x}}_i} \cdot {{x}}} \right)$ 和惩罚因子C，将寻找最优超平面问题转换为求解最优化问题：

$\min \displaystyle\frac{1}{2}\sum\limits_{i = 1}^j {\sum\limits_{j = 1}^l {{y_i}{y_j}{\alpha _i}} } {\alpha _j}K\left( {{{ x}_i},{ x}} \right) - \sum\limits_{j = 1}^l {{\alpha _j}};$

(10)

${\rm{s}} . {\rm{t}}. \sum\limits_{i = 1}^l {{y_i}{\alpha _i} = 0,}\, {\rm{ }}0 \leqslant {\alpha _i} \leqslant C,\,{\rm{ }}i = 1,2, \cdots ,l .$

(11)

可得最优解： ${{{\alpha}} ^ * }= [{ {\alpha _1^ * , \cdots ,\alpha _l^ * } ]^{\rm T}}$ .

然后，选取 ${{{\alpha}} ^ * }$ 的一个正分量 $0 < \alpha _j^ * < C$ ，据此计算最优权值向量和阈值，分别为

${w^ * } = \sum\limits_{j = 1}^l {\alpha _i^ * } {y_j}{x_j},$

(12)

${b^ * } = {y_i} - \sum\limits_{i = 1}^l {{y_i}\alpha _i^ * } K\left( {{{{x}}_i} \cdot {{x}}} \right).$

(13)

最后，由式(12)、(13)构造决策函数：

$f\left( {{x}} \right) = {\rm{sgn}}\left( {\left( {{{{w}}^ * } \cdot {{x}}} \right) + {b^ * }} \right) = \operatorname{sgn} \left( {\sum\limits_{i = 1}^l {{y_i}\alpha _i^ * K\left( {{{{x}}_i},{{x}}} \right) + {b^ * }} } \right).$

(14)

SVM根据决策函数构造最优分类面实现分类，本文所采集的加速度和肌电信号属于线性不可分情况. 针对这类问题，通过组合多个二分类器来完成多分类的构造，建立基于SVM的次序二叉树多分类模型，利用空间映射的方法来确定最优分类面，在高维特征空间解决线性不可分问题.

根据式(14)可知，以多维特征向量作为SVM的输入， ${ x}$ 从输入空间 ${{\bf{R}}^n}$ 到特征空间 $H$ 的变换，即： ${ x} \to {\phi} \left( { x} \right) = {[ {{{\phi} _1}\left( { x} \right),{{\phi} _2}\left( { x} \right), \cdots ,{{\phi} _l}\left( { x} \right)} ]^{\rm T}}\;$ . 利用多维特征向量 ${\phi} \left( { x} \right)$ 取代输入向量 ${{x}}$ ，可得最优分类函数：

$f\left( {{x}} \right) = \operatorname{sgn} \left( {\sum\limits_{i = 1}^l {{y_i}\alpha _i^ * K\left( {{{\phi} _i}({ x}),{\phi} ({ x})} \right) + {b^ * }} } \right).$

(15)

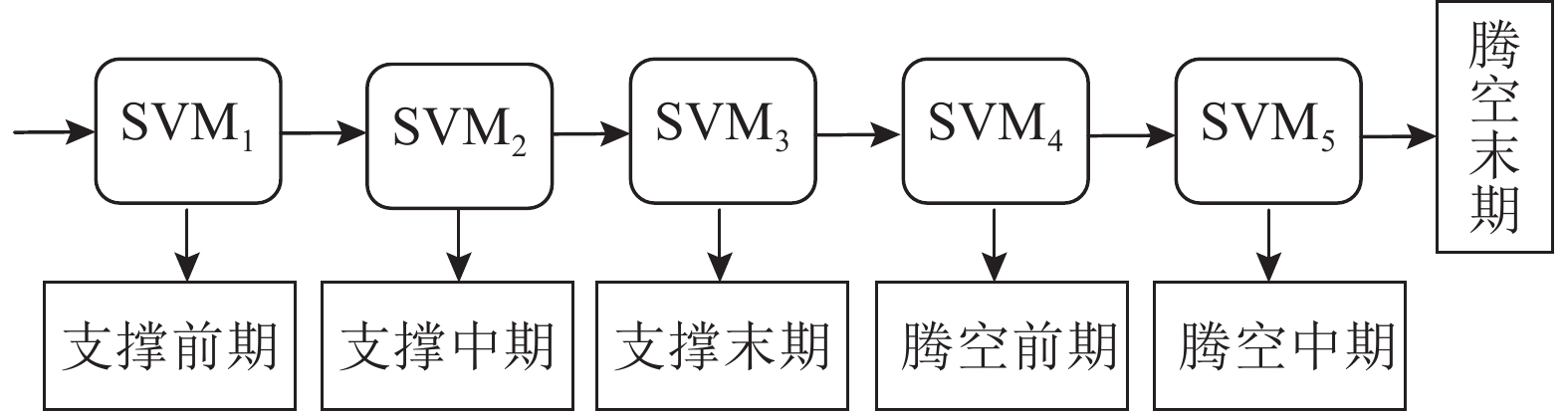
将 ${{\phi} _i}\left( { x} \right) = \left[ {{s_i},{{s'}_i},{m_i},{{m'}_i},{r_i},{x_i},{{x'}_i},{y_i},{{y'}_i}} \right]$ 作为特征向量，构成新的特征子空间，用于SVM的训练与识别. 建立如图8所示的SVM次序二叉树多分类模型，开展跑动步态相位辨识.

3.2.2 SVM核函数的选择

SVM通过非线性变换在低维空间完成复杂运算，在高维空间建立最优分类面，而这种非线性变化依靠核函数完成. SVM核函数的选择对于跑动步态相位的辨识十分关键，SVM算法中常用的核函数如下.

多项式核函数(polynomial)为

$k({{x}},{{{x}}_i}) = {[\gamma({{x}} \cdot {{{x}}_i}) + {\rm{coef}}]^a}.$

(16)

Sigmoid核函数(sigmoid)为

$k({{x}},{{x}}_i) = {\rm{tanh}}\;[\gamma ({{x}} \cdot {{x}}_i) + {\rm{coef}}].$

(17)

线性核函数(linear)为

$k({{x}},{{x}}_i) = \gamma ({{x}} \cdot {{x}}_i).$

(18)

径向基核函数(RBF)为

$k({{x}},{{x}}_i) = {\rm{exp}}\;\left( {{\rm{ - }}\gamma\, {{\left|| {{{x}} \cdot {{x}}_i} \right.\left|| \right.}^2}} \right).$

(19)

式中：coef为核函数偏置系数；a为多项式的核阶数，a<0； $\gamma $ 为核函数的宽度.

根据经验法，预先选定符合所设计的SVM二叉树分类模型训练程度的惩罚因子C和核函数参数，设置C=2，coef=0， $\gamma $ =1，定义t表示核函数类型.建立LIBSVM与MATLAB接口，选取不同的核函数，在MATLAB环境下完成模型的训练与测试.选取60组跑动实验样本、6种不同的跑动相位，共提取360组数据，开展滤波和归一化处理. 为了避免分类数据集偏斜问题，选取其中180组数据. 每个相位各30组，用于模型训练，剩下的180组数据用于模型测试.不同的核函数测试结果如表1所示. 表中，P为准确率.

根据不同核函数测试的结果对比可知，多项式核函数与RBF核函数均有较高的识别准确率；从响应时间方面考虑，RBF核函数优于多项式核函数，因此选用RBF核函数作为PSO优化SVM次序二叉树多分类模型的核函数.

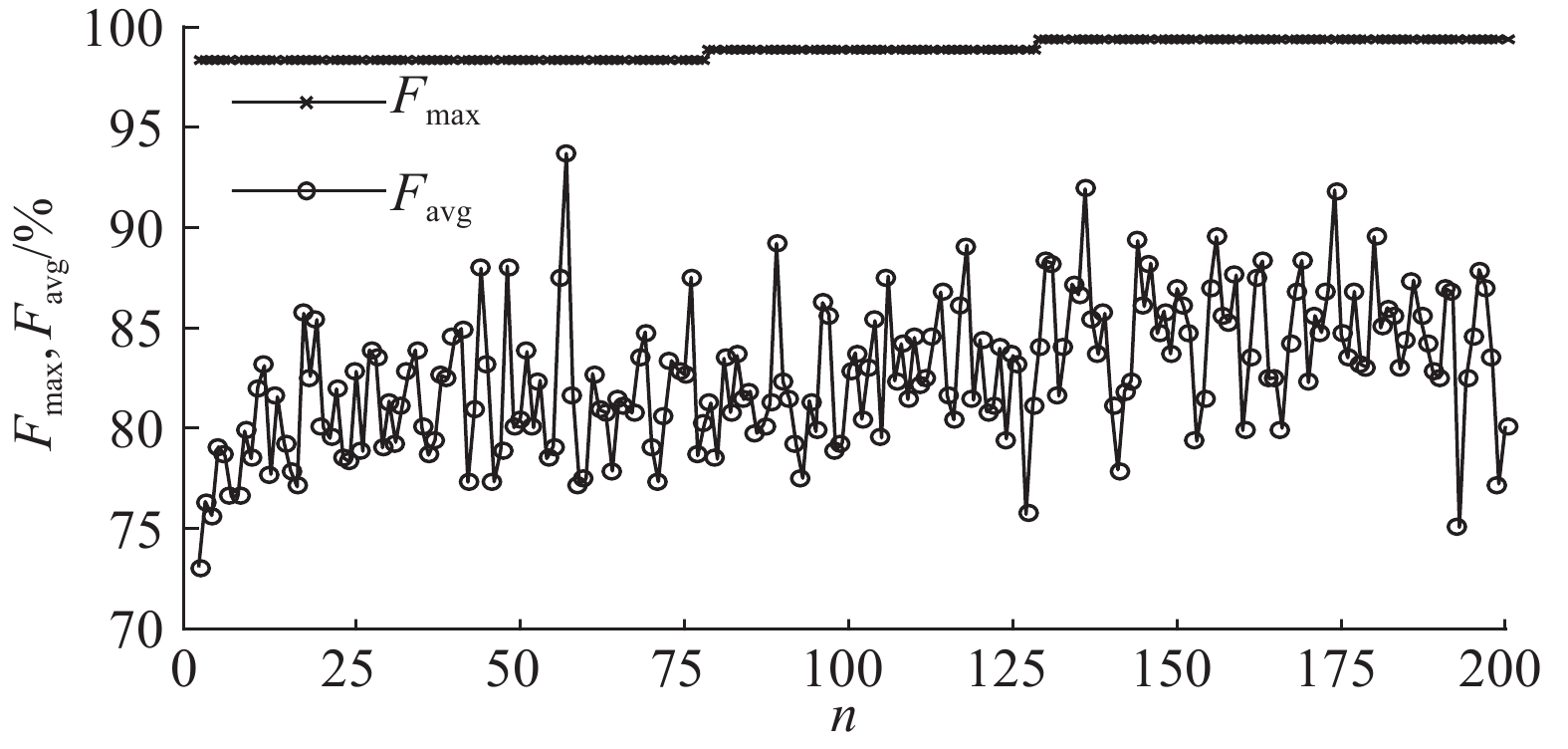
3.2.3 PSO优化SVM核函数参数

SVM分类模型包含5个分类器，须利用PSO算法对5个核函数参数进行优化. 首先设置PSO算法的种群规模为20，粒子的维数为5，最大迭代次数为200，设置局部加速度因子和全局加速度因子的系数分别为1.5和1.7. 通过十折交叉验证的方法，将用于训练及优化的样本数据随机分为10组，每组数据的样本数相等，且包含6种跑动步态的特征数据. 从10组数据中依次轮流选取9组作为训练集，剩下1组作为测试集，10次迭代后求取10次平均交叉验证识别率，因此每组数据都得到验证，从而提高了算法的可靠性，减小了核函数参数误差. 通过寻优得到的5个RBF核函数参数依次为2.161/1.234/1.982/0.325/0.652，SVM的惩罚因子依次为5.202/4.746/3.281/3.011/3.278. PSO对SVM模型进行参数优化的适应度收敛曲线如图9所示. 图中，平均适应度F_avg为每一代中所有粒子的目标函数平均值，最佳适应度F_max为每一代中所有粒子的目标函数最大值，n为进化代数.

由图9可知，随着进化次数的增加，平均适应度为80%~90%，验证了PSO的优化性能，说明了模型的核参数变化对分类模型准确性的影响.

4 实验分析与结果

为了验证PSO优化SVM算法对假肢穿戴者跑动步态识别的可行性和有效性，将基于PSO-SVM多分类模型与算法与基于SVM次序二叉树多分类模型、典型的BP神经网络分类方法分别进行对比.

选取60组跑动数据样本，每组样本包括6种不同的步态相位，共360组数据. 在预处理后用于对比实验，其中的180组数据用于模型的训练，剩下的180组数据分别输入训练后的SVM多分类模型、PSO-SVM多分类模型和BP神经网络中进行对比测试.其中，PSO优化前、后的SVM核函数数量、类型、核参数及惩罚因子等相关参数按上文的研究结果配置；BP神经网络的结构设计如下：9个节点的输入层，6个节点的输出层，另外根据经验风险最小化原则，选取学习率为0.7，隐含层激励函数为通用的S型函数.通过试凑法确定隐含层最佳节点数，使BP神经网络达到最优识别结果，提高不同算法的对比效果.

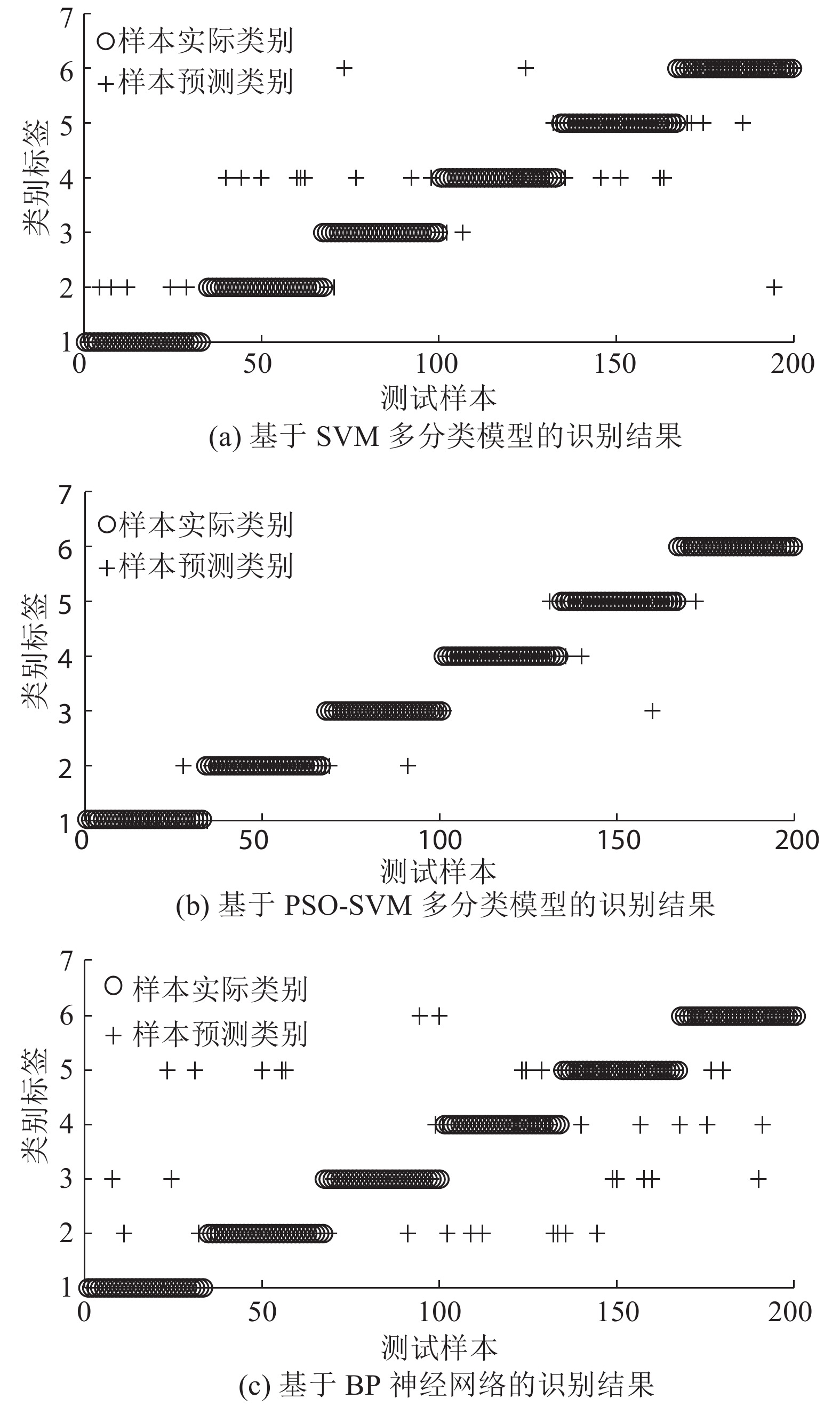
如图10(a)~(c)所示分别为SVM多分类模型、PSO-SVM多分类模型和BP神经网络的识别结果. 图中，数值1、2、3、4、5、6分别对应跑动过程的支撑前期、支撑中期、支撑末期、腾空前期、腾空中期、腾空末期，实际的步态相位以空心圆的形式输出，模型预测的步态相位以十字符号形式输出. 若模型输出的空心圆与十字符号重合，则表示模型识别准确；反之，则识别错误.

6种不同跑动步态的测试数据各取30组，共计180组测试样本中，SVM多分类模型共准确识别出146组跑动实验样本，PSO-SVM多分类模型共准确识别出167组跑动实验样本，BP神经网络方法共准确识别出138组跑动实验样本，相应的识别率分别为81.11%、92.78%、76.67%. 对比3种不同算法的识别结果，如表2所示. 利用PSO-SVM算法准确识别的6种跑动步态样本数量最多，优于SVM多分类模型和BP神经网络.BP神经网络建立于经验风险最小化基础之上，预测误差函数易陷入局部最小化，使训练过程随误差变化出现欠学习或过学习状态；SVM是基于结构风险最小化原理，相对于传统BP神经网络而言，具有更高的泛化性能和稳定性，结合PSO算法对SVM核参数进行全局寻优，使得步态识别率进一步提高.上述结果表明，根据针对性提取和处理的假肢穿戴者跑动运动样本数据，采用PSO优化SVM次序二叉树多分类模型实现不同跑动步态识别的方法是有效的，具有较高的识别率和实用参考价值，在跑动步态识别技术的基础上，该方法对于控制智能假肢实现不同的跑动动作转换具有重要的作用.

5 结　语

本文分析下肢跑动运动模式，将跑动周期分为支撑前期、支撑中期、支撑末期和腾空前期、腾空中期、腾空末期；通过假肢接受腔装配的肌电传感器、加速度计和足底的压力传感器采集假肢穿戴者下肢多个部位的跑动运动信息，克服了单信息源的片面性和偶然性，更全面地反映下肢跑动运动状态.针对不同部位的运动特征参数，采取不同的去噪方法. 利用小波包软、硬阈值结合的去噪方法，能够有效地避免因颠振导致跑动运动信息边缘模糊失真的问题，降低了下肢假肢跑动步态分析过程中的不确定性.介绍PSO优化算法的概念、参数和算法实现，将该算法融入SVM模型识别步态的过程中. 从实验结果可以看出，PSO优化的平均适应度为80%~90%，能够有效地消除核参数选择的局部最优，使基于SVM次序二叉树分类模型的识别正确率由81.11%上升到92.78%；识别准确率高于SVM和BP神经网络，有效解决了假肢穿戴者跑动状态下的步态识别问题.