2. 西安电子科技大学 计算机学院,陕西 西安 710071
2. School of Computing, Xidian University, Xi'an 710071, China
无线传感器与执行器网络是无线传感器网络的一种,由大量的异构传感节点和能够对感知到的物理信息作出响应的执行器构成. WSANs在工业进程中广泛应用,由普通低能量、性能资源的传感器节点和性能、容量远超普通节点的执行器构成[1]. 传感节点感知数据,并周期性或自发性地将数据传输给临近的执行器节点,执行器对此作出响应,可以用于工业自动化、实时目标追踪、环境监控等应用. 由于传感节点的低花费、灵活性和可拓展性等优点,迅速取代了有线的工业设施.
工业环境恶劣、噪声的干扰给WSANs的可靠、实时传输带来巨大的挑战. 多跳通信增大了通信延时,信道状况的动态改变给路由选取带来巨大的麻烦. WSANs需要高效的通信设计. 由于传感节点通常稠密部署在感知区域来保证覆盖范围和拓扑连通性[2],如文献[1]、[3]、[4]所示,WSANs中存在许多实时通信的开放性问题,尤其是关于异构的网络模型、资源限制和可拓展性问题.
当前无线传感网中大多数路由协议不能很好地利用资源丰富的设备来减少普通节点的通信压力,如地理路由、AODV[5]、DSR[6]等. 再如考虑链路故障的路由算法[4,7-10],由于这些方法是针对普通传感网,它们并不适合
之前对于
设计容错、实时、高效、可靠的先验式路由FRER来解决以上问题. 本文的贡献如下:1)阐述了
定义 1
在无线网络拓扑设计中,要考虑节点度和网络直径对网络性能的影响. 较高的节点度能够保证较好的容错性、较低的网络直径和传输时延,但同时会造成较大的开销和干扰. 传统的互联网络拓扑有着节点数目和不支持节点加入或离开的限制,
定理1[18] 对于给定的度数d和直径n,一个拓扑至多可容纳的节点数受
证明:给定度数
定理2[17] 对于给定的节点度数和节点总数为N的任意网络拓扑,根据
证明:根据
| $\begin{split}\left\lceil {{{\log }_d}(({d^n} + {d^{n - 1}})(d - 1) + 1)} \right\rceil - 1 = \quad\quad\quad\\\left\lceil {{{\log }_d}({d^n} + {d^{n - 1}} + 1)} \right\rceil - 1 = n + 1 - 1 = n.\end{split}$ |
定理1和2说明
假定
|
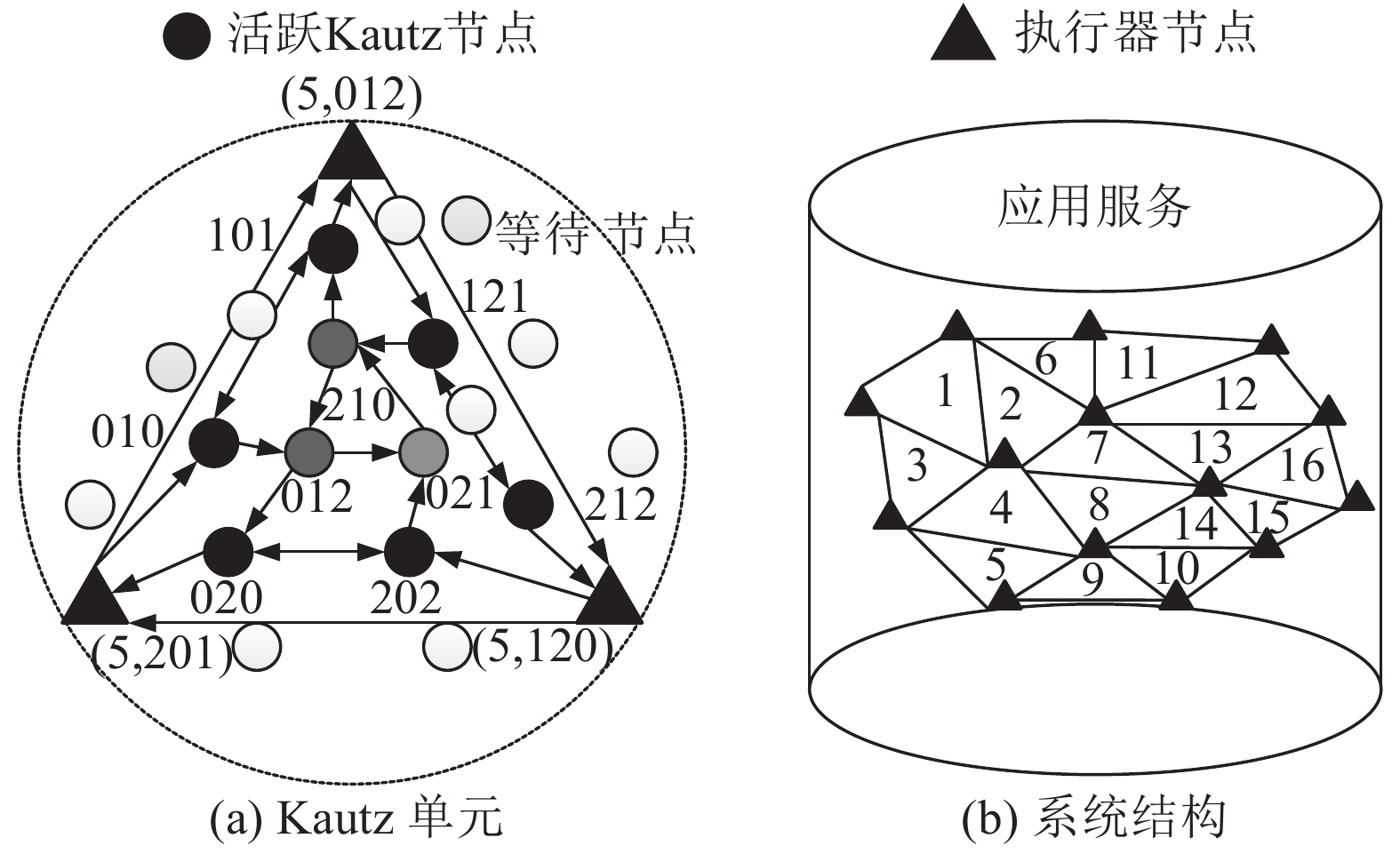
图 1 网络整体结构 Fig. 1 Network architecture |
每个Kautz单元包含一个单元ID(CID),每个传感节点在每个单元包含一个节点ID(KID),即WSAN中每个节点可以用(CID, KID)表示,其中KID={u1, ···ui, ···|ui
在所有Kautz单元构建完成之后,需要给每个Kautz单元中的传感节点赋予ID,即Kautz图的构建. 如图1(a)所示为图1(b)的区域5. 为了明确地表示路由,尽管节点间的通信是双向的,仍将WSAN表示为有向图
如图1所示为K(2,3)的例子,即节点的入度和出度都为2,网络的直径为3,包含12个节点. 首先是执行器间的互联,例如,对于执行器(5,012),它挑选后继(5,120). 同时,它广播一个到(5,120)TTL(存活时间)为2的路径请求信息,保证直径
每个节点只能被一组执行器节点选取,当节点被选中为图1中黑色节点所在路径之后,其他执行器节点不能再选取该节点为作为到后继执行器节点的路径. 在图1中黑色节点选取完毕之后,开始选取深灰色节点. 例如执行器(5,012)的后继为(5,121),执行器(5,201)的前驱为(5,020),为了保证信息能够穿越不同的执行器对,(5,121)选取到(5,020)的路径,并给它们赋予
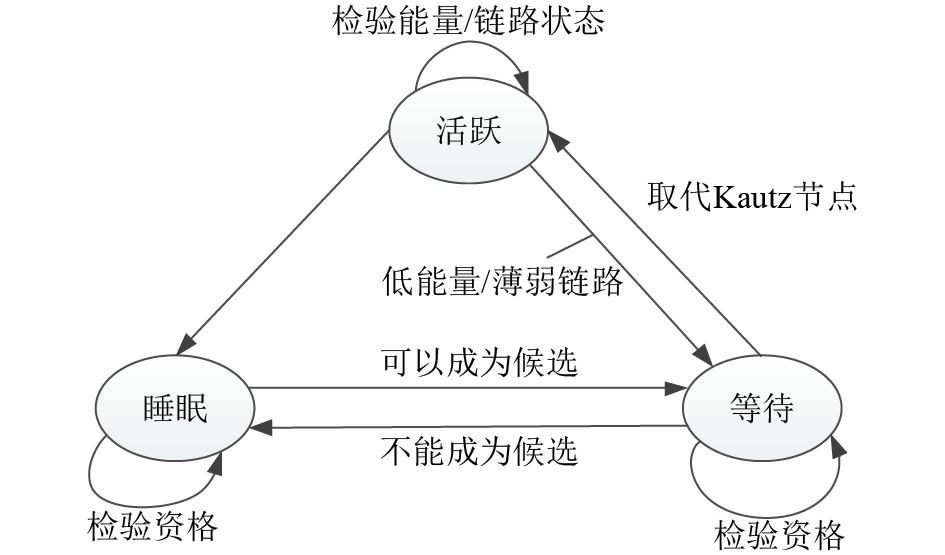
研究大规模的WSAN,传感节点密集部署. 如图2所示,传感节点包含3种状态:活跃、睡眠和等待. 活跃节点为Kautz节点,它们周期性地发送“Hello”数据包来更新与邻居节点的连通性状态. 当节点的能量低于某一阈值或链路质量下降到某一阈值时,规定节点能量低于20%或链路PDR连续20个时间片低于0.6,进行Kautz节点更新. 睡眠的传感节点周期性地唤醒,并与Kautz节点交换信息,检查自身能否成为Kautz节点候选. 成为Kautz节点候选需要满足3种要求:1)它必须能与一个Kautz节点通信;2)它必须有至少一个Kautz邻居节点能量低于20%或链路连续20个时间片不可用;3)它能够与该Kautz节点的其他邻居Kautz节点连通. 当一个节点检查自身时,发现自身能量或链路质量降低到某一水平,它通知邻居节点并选择满足要求的邻居节点代替自身作为Kautz节点,将自身的ID信息交给该节点,则进入睡眠状态. 为了避免出现节点未转交ID发生故障的情况,邻居Kautz节点周期性地发送“Hello”数据包检测邻居Kautz节点的状况. 若发现找不到邻居节点的情况,则通知邻居传感节点唤醒,选取链路质量最高的节点作为新的Kautz节点.
|
图 2 传感节点的3种状态 Fig. 2 Three states of sensor nodes |
对于本文的网络构架,在网络分成多个
定理3 当节点
证明:根据
定理4[17] 当节点
| $\left\{ {\begin{array}{*{20}{l}} {(1)\,{u_2}\cdots{u_n}{u_{n - l}},\quad }&{n + 2},&{\;{u_{n - l}} \ne {v_{l + 1}}} ;\\ {(2)\,{u_2}\cdots{u_{n - l}}\cdots{u_n}{v_{l + 1}}},&{n - l},&{\text{最短路径}}; \\ {(3)\,{u_2}\cdots{u_n}{v_1}, \quad \,\,\,}&n,&{{u_n} \ne {v_1}}; \\ {(4)\,{u_2}\cdots{u_n}{\alpha _i}, \quad \;\,}&{n + 1},&{\text{其他}}. \end{array}} \right.$ | (1) |
式中:
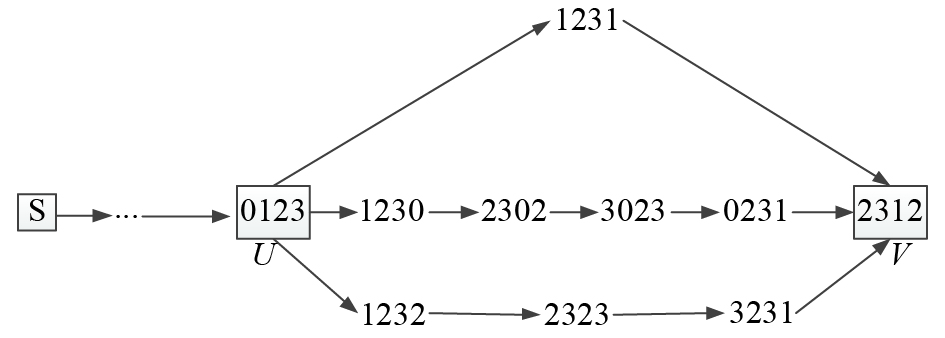
当任意节点对要发送数据时,节点通过目标节点ID,根据定理4可知,源节点能够快速、高效地找到目的节点的最短路. 任意节点对之间包含
该传输方法存在一定的问题. 当
|
图 3 Kautz图路由范例 Fig. 3 Kautz routing paradigm |
针对这一问题的解决方法是允许节点沿
定理5 当节点
| $\left\{ {\begin{array}{*{20}{l}} {(1)\,{u_{l + 1}}{u_1}\cdots{u_{n - 1}}, }&{n + 2},&{\;{u_{l + 1}} \ne {v_{n - l}}}; \\ {(2){v_{n - l}}{u_1} \cdots {u_{n - 1}}, \;}&{n - l},&{\text{最短路径}} ;\\ {(3){v_n}{u_1}\cdots{u_{n - 1}},\quad \quad \,\,\,}&n,&{{u_1} \ne {v_n}}; \\ {(4)\,\alpha {u_1}\cdots{u_{n - 1}}, \;\,}&{n + 1},&{\text{其他}}. \end{array}} \right.$ | (2) |
式中:
证明:1)根据定理3证明可知,最短路径中
为了充分利用无线介质的广播特性,拓展路由路径的多样性,在网络节点数据传输过程中发生节点故障时,由于任意节点间存在
由于节点周期性地发送“
数据包的格式如图4所示. 数据包的包头包含源节点ID、目的节点ID、数据包类型、数据包序列号及正、反向标记位和绕道标记位. 正、反向标记位为0和1两种,0表示正向传输,1表示方向传输. 绕道标记位包含2部分:标记和ID;标记为0,表示没有绕道,标记为1表示绕道,在ID位记录绕道节点ID信息. 最后的FCS位是校验位,用于检测接收数据包是否误码. 当节点通过“Hello”数据包评估邻居节点间链路质量时,要评估不存在于Kautz拓扑中的链路质量;当绕道链路质量高于原链路,绕道节点的下一跳节点有更优的匹配长度时,可以使用绕道链路.

|
图 4 FRER数据包格式 Fig. 4 FRER packet format |
可用性历史表示链路可用性随时间变化的记录,将时间分为l个时间片,节点i和j之间链路第r个时间片所对应的可用性为
| $a_{ij}^s = \left\{ {\begin{aligned} & {\begin{array}{*{20}{l}}1,{{\;\;\;{\rm{PDR}}}_{ij}^s \geqslant {\gamma _0}}\;; \end{array}} \\ & {\begin{array}{*{20}{l}} 0,{\;\;\;\text{其他}}; \end{array}} \end{aligned}} \right.$ | (3) |
路径的可用性是所有该路径上链路的可用性进行逻辑位运算
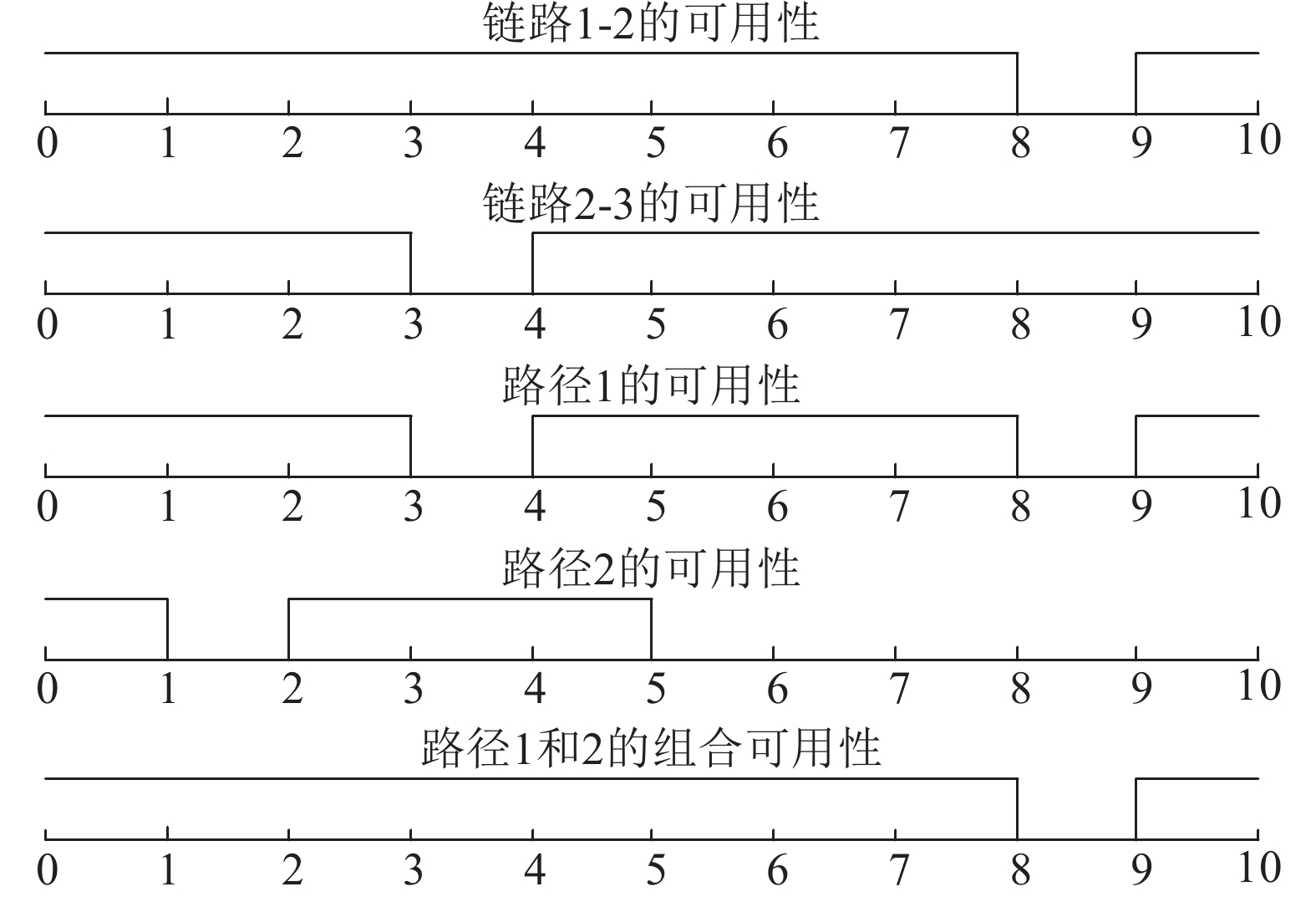
如图5所示,路径1包含链路1-2和2-3. 在某一时期网络的可用性如图5所示,链路1-2在第9个时间片不可用,链路2-3在第4个时间片不可用,则路径1在第4和第9个时间片不可用. 路径2与路径1有着相同的源节点和目标节点,路径2在第1和第3~5时间片可用,则它们的组合可用性只在第9个时间片不可用. 利用组合路径的方法,可以增大传输的可用性.
|
图 5 网络的可用性 Fig. 5 Network availability |
多路径挑选的具体流程如下. 算法总共分为2个阶段:路径预挑选阶段和贪婪多路径挑选阶段. 在路径预挑选阶段,通过上文所述的挑选最小编号下一跳节点的方法,寻找正、反向匹配的最短和次最短路径,存放于集合H中. 在贪婪多路径挑选过程中,旨在挑选组合可用性最大的k条路径用作数据传输,本文设定
| 表 1 基于可用性历史的多路径挑选 Table 1 Availability based multiple path selection |
使用NS-2来评估FRER性能,并与REFER[17]和DeBruijn图进行比较. 当节点发生故障时,发送广播信息来重建路径. 10个执行器节点均匀分布在500
对于未受干扰的网络环境,使用以下标准进行评估.
1)吞吐量:目标节点每秒钟成功接收的数据包的数量. 更高的吞吐量意味着更高的容错性和实时性能.
2)时延:平均端到端数据传输延时.
3)数据包传输比PDR:成功传输的数据包与总发送数据包的比值. 更高的PDR意味着更高的传输效率.
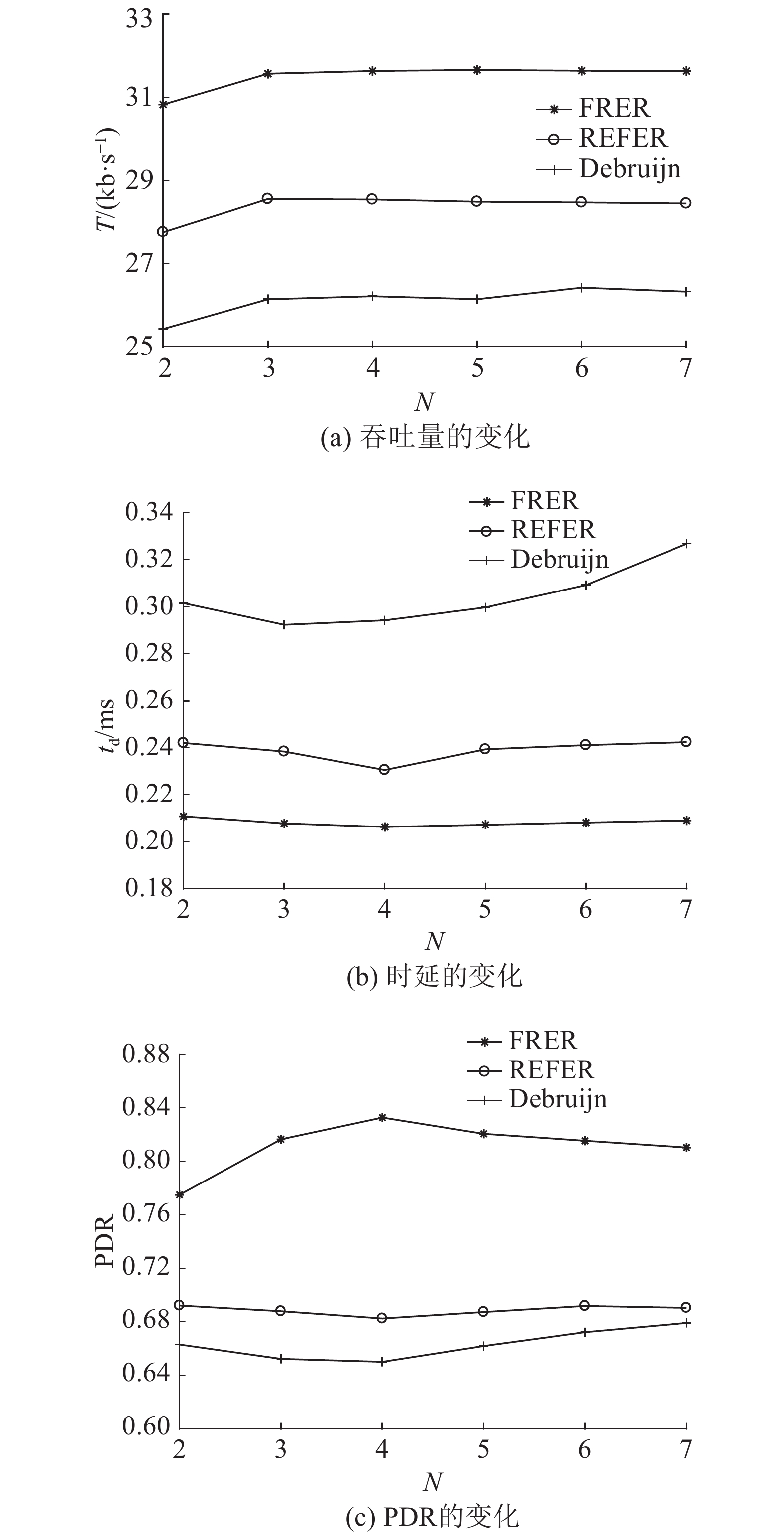
在仿真过程中,随机挑选2x个故障节点,x服从[1, 5]上的均匀分布,每过10 s,修复网络中之前的故障节点. 如图6(a)所示为吞吐量T随源目标节点对数N的变化. 可以看出,REFER和DeBruijn图的吞吐量低于本文的算法FRER,但Kautz图的吞吐量远高于DeBruijn图. 随着源目标节点对数的增长,网络吞吐量先上升后平稳下降. 这是因为最初时,随着网络中源节点数目的增多,网络吞吐量相应增长;随着源节点的增多,每个Kautz单元中重合的链路数量增多,从而影响端到端的数据传输. 从图6(a)可以看出,当每个Kautz单元中源节点的数量为4时,网络吞吐量最大. 如图6(b)所示为端到端平均传输时延随源目标节点对数的变化. 可以看出,当网络中源节点数增大时,网络端到端时延先下降;当节点对数为4时达到最小,之后增长,这是因为仿真时随机挑选源目标节点对,当节点对数较小时,所选取的可能是与REFER相同的较长路径;当节点对数增大时,FRER的路径长度小于等于REFER的路径长度,因此随着节点对数的增长,网络时延下降;随着节点对数的增加,每个Kautz单元和DeBruijn图中重合的链路增多,造成网络时延增大. 与Kautz图相比,DeBruijn图变化最明显,当本文的FRER算法在每个Kautz单元中重合的链路数量较少,时延变动较平滑. 如图6(c)所示为PDR随网络中源目标节点对数的变化. 随着源目标节点对的增多,本文算法的FRER先增长后平稳下降,当源目标节点对的数量为4时达到最高值,之后平稳下降;REFER的PDR变化不大,当网络中源目标节点对数增大时,呈现出下降趋势,整体来说,Kautz图的PDR高于DeBruijn图,本文算法的传输效率高于REFER.
|
图 6 吞吐量、时延和PDR随源目标节点对数的变化 Fig. 6 Throughput, delay, and PDR vary with number of source destination pair |
由于WSANs一般用于工业环境,相较于REFER,本文考虑网络中链路的故障. 当链路故障时,仅通过替换节点无法解决该问题,需要使用多路径的方法来提高网络传输的可靠性.
工业环境中包含诸多噪声. 考虑其中一种高斯白噪声,对于其他噪声,可以使用本文方法降低噪声对数据传输的影响. 使用Nakagami分布来描述接收到的信号强度,Nakagami分布定义为
| $f(x,m,\varOmega ) = \frac{{{m^m}{x^{m - 1}}}}{{\varGamma (m){\varOmega ^m}}}\exp \left( - \frac{{mx}}{\varOmega }\right).$ | (4) |
式中:
| $\varOmega (d) = \frac{{{P_{\rm t}}{G_{\rm t}}{G_{\rm r}}h_{\rm t}^2h_{\rm r}^2}}{{{d^n}L}}.$ | (5) |
式中:
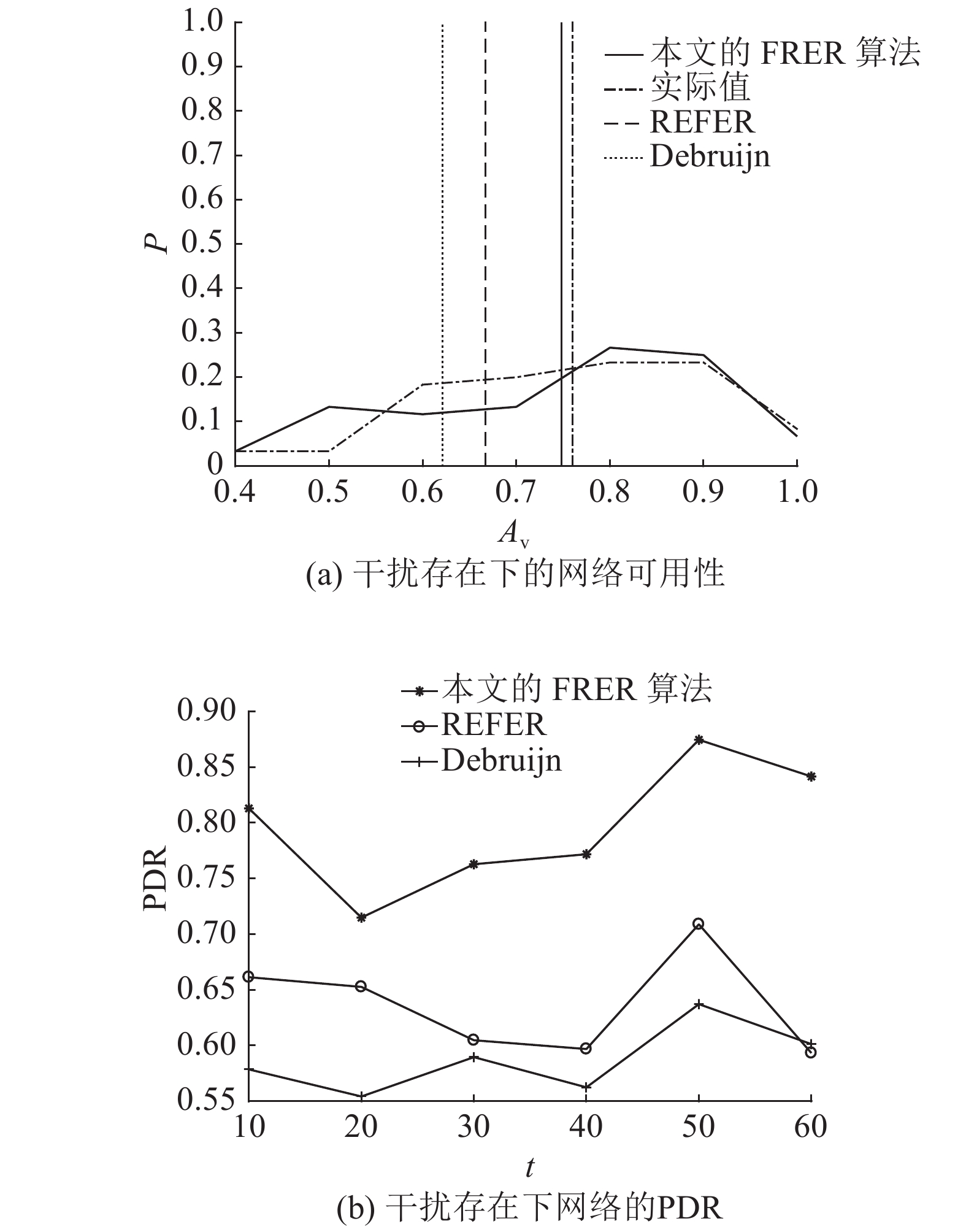
如图7所示为在干扰情况下的网络可用性和性能情况. 在仿真过程中,将时间划分为10个时间片;每过一个时间片,可用性信息左移一位,由新的可用性信息补全最后一位. 如图7(a)所示为干扰存在下的网络端到端可用性情况. 图中,Av为可用性,P为分布概率,垂直线表示均值,其他曲线表示累积分布. 为了与REFER算法进行对比,REFER算法和DeBruijn图按照路由选取规则挑选2条最短路进行数据传输. 从图7(a)可以看出,基于可用性历史的FRER算法与实际情况较接近,可以预测实际情况;2种基于Kautz图的可用性高于DeBruijn图,与REFER算法和DeBruijn图进行对比可知,FRER的平均可用性明显高于REFER算法和DeBruijn图,这说明利用基于可用性历史的FRER算法能够挑选出k条最优可用性的路径组合来提高网络传输的可靠性. 如图7(b)所示为干扰存在下网络端到端的数据包传输比. 图中,t为时间. 可以看出,在干扰存在的情况下,本文算法的数据包传输比明显优于REFER算法和基于DeBruijn图的算法,即网络整体传输效率高于以上2种算法.
|
图 7 干扰存在情况下网络可用性的分布和PDR Fig. 7 Network availability and PDR in the presence of interference |
本文提出的FRER算法能够利用邻居节点信息,在已存在的网络拓扑中拓展网络的路径多样性;与当前的无线传感网路由算法相比,本文的FRER算法基于Kautz图,能够以最小花费找到最短路径. 与基于Kautz图的REFER算法及基于DeBruijn图的算法相比,本文的FRER算法利用拓展路径多样性的方法,找到的路由路径长小于等于REFER算法. 本文算法考虑了REFER算法没有考虑的链路故障情况,使用可用性历史来预测未来链路的可用性,通过组合k条最优可用性组合的路径来提高网络整体传输效率. 大量的仿真实验表明,在链路故障存在的情况下,利用本文的FRER算法能够提高网络的可用性;FRER算法在提高网络可靠性、降低延时和丢包率、提高网络吞吐量方面优于REFER算法和DeBruijn图. 下一步的研究方向是考虑拥塞情况对FRER算法的影响,评估并设计拥塞避免的算法.
| [1] |
CHACZKO Z, CHIU C, ASLANZADEH S, et al. Software infrastructure for wireless sensor and actuator networks [C] // Proceedings of the 21st International Conference on Systems Engineering (ICSEng). Las Vegas: IEEE, 2011: 474–479.
|
| [2] |
ZHU J, ZOU Y, ZHENG B. Physical-layer security and reliability challenges for industrial wireless sensor networks[J]. IEEE Access, 2017, 5(99): 5313-5320. |
| [3] |
ZENG Y, LI D, VASILAKOS A V. Real-time data report and task execution in wireless sensor and actuator networks using self-aware mobile actuators[J]. Computer Communications, 2013, 36(9): 988-997. DOI:10.1016/j.comcom.2012.07.016 |
| [4] |
LU C, SAIFULLAH A, LI B, et al. Real-time wireless sensor-actuator networks for industrial cyber-physical systems[J]. Proceedings of the IEEE, 2016, 104(5): 1013-1024. DOI:10.1109/JPROC.2015.2497161 |
| [5] |
NATH S, BANIK S, SEAL A, et al. Optimizing MANET routing in AODV: an hybridization approach of ACO and firefly algorithm [C] // 2016 2nd International Conference on Research in Computational Intelligence and Communication Networks (ICRCICN). Kolkata: IEEE, 2016: 122–127.
|
| [6] |
BAKHT H. A comparative study of MAODDP with ZRP and DSR routing protocols for mobile AD-HOC network[J]. Computer Science and Telecommunications, 2016, 1(47): 64-68. |
| [7] |
NIU J, CHENG L, GU Y, et al. R3E: Reliable reactive routing enhancement for wireless sensor networks[J]. IEEE Transactions on Industrial Informatics, 2014, 10(1): 784-794. DOI:10.1109/TII.2013.2261082 |
| [8] |
PRADITTASNEE L, CAMTEPE S, TIAN Y C. Efficient route update and maintenance for reliable routing in large-scale sensor networks[J]. IEEE Transactions on Industrial Informatics, 2017, 13(1): 144-156. DOI:10.1109/TII.2016.2569523 |
| [9] |
SEPULCRE M, GOZALVEZ J, COLL-PERALES B. Multipath QoS-driven routing protocol for industrial wireless networks[J]. Journal of Network and Computer Applications, 2016, 8(74): 121-132. |
| [10] |
LI Z, SHEN H. A QoS-oriented distributed routing protocol for hybrid wireless networks[J]. IEEE Transactions on Mobile Computing, 2014, 13(3): 693-708. DOI:10.1109/TMC.2012.258 |
| [11] |
LI D, LU X, WU J, et al. A scalable constant degree and low congestion DHT scheme based on Kautz [C]//IEEE Conference on Computation Communication. Miami: IEEE, 2005: 1677–1688.
|
| [12] |
FABREGA J, MARTÍ-FARRÉ J, MUNOZ X. Layer structure of DeBruijn and Kautz digraphs: an application to deflection routing[J]. Electronic Notes in Discrete Mathematics, 2016, 9(54): 157-162. |
| [13] |
GUO D, LIU Y, KI X. Bake: a balanced kautz tree structure for peer-to-peer networks [C] // The 27th Conference on Computer Communications. Phoenix: IEEE, 2008: 351–355.
|
| [14] |
ZUO K, HU D, WANG H, et al. An efficient clustering scheme in mobile peer-to-peer networks [C] // International Conference International Conference on Information Networking. Busan, South Korea: IEEE, 2008: 1–5.
|
| [15] |
RAVIKUMAR C P, RAI T, VERMA V. Kautz graphs as attractive logical topologies in multihop lightwave networks[J]. Elsevier Science, 1997, 20(14): 1259-1270. |
| [16] |
CHIANG W K, CHEN R J. Distributed fault-tolerant routing in Kautz networks[J]. Parallel Distributed Computing, 1994, 6(20): 99-106. |
| [17] |
SHEN H, LI Z. A Kautz-based wireless sensor and actuator network for real-time, fault-tolerant and energy-efficient transmission[J]. IEEE Transactions on Mobile Computing, 2016, 15(1): 1-16. DOI:10.1109/TMC.2015.2407391 |
| [18] |
刘盛云. 基于Kautz图的数据中心网络拓扑结构研究[D]. 长沙: 国防科学技术大学, 2010: 1–67. LIU Sheng–yun. Research on the topology of Kautz based data centers network [D]. Changsha: National University of Defense Technology, 2010: 1–67. http://cdmd.cnki.com.cn/Article/CDMD-90002-1011279667.htm |
| [19] |
GROSS J L, YELLEN J. Graph theory and its applications [M]. [S. 1.]: CRC, 2005: 1–767.
|


