2. 长沙市规划设计院有限责任公司,湖南 长沙 410007
2. Changsha Planning and Design Institute Limited Company, Changsha 410007, China
正交异性钢桥面与钢-混凝土组合结构在桥梁工程中应用广泛,但一方面,正交异性钢桥面存在疲劳开裂和铺装层易损坏两大难题[1-2];另一方面,普通的钢-混凝土组合桥梁存在自重较大和混凝土桥面板易开裂的弊端[3]. 采用高强度、高性能材料是世界大桥未来发展的趋势之一[4].
超高性能混凝土(ultra high performance concrete, UHPC)是一类纤维增强水泥基复合材料,具有较高的材料强度和良好的耐久性能. 钢纤维的掺入增强了UHPC基体的韧性,阻碍和延缓了混凝土裂缝的产生和发展,提高了UHPC抗拉强度和延性[5-6].
将UHPC与正交异性钢桥面通过栓钉剪力连接件连接,形成一种新型的钢-UHPC组合桥面板. 研究结果表明,该新型桥面结构体系可以大幅度降低钢结构应力,基本消除疲劳开裂风险,同时UHPC层开裂拉应力达到42.7 MPa,远高于设计荷载下的拉应力[7];以虎门大桥桥面改造工程为依托的钢-UHPC组合桥面板足尺条带模型抗弯疲劳试验表明,在200万次疲劳荷载下,UHPC层未出现新裂缝,试件刚度基本不下降,证明该桥面结构具有优良的抗弯疲劳性能[8].
对钢-UHPC轻型组合桥面板纵、横2个方向的试验分析表明,纵向桥面板具有更高的抗拉强度,横向受力更加不利[9]. 进一步的研究结果表明,钢-UHPC组合桥面板在车轮荷载作用下,横向受力局部效应明显,以第三体系受力为主,即由钢-UHPC组合板直接承受荷载[10]. Yuguang等[11]研究配筋UHPC板的受弯性能,李文光等[12]对钢-UHPC组合板进行受弯试验研究与理论分析,测试钢-UHPC组合板的开裂强度、裂缝发展情况和破坏形态等.
钢-UHPC组合板的受力复杂且非线性效应明显,仅依靠试验分析或解析方法难以全面地了解其整个受力过程中的内力和变形情况. 本文在开展钢-UHPC组合板正、负弯矩试验的基础上,采用有限元分析软件ABAQUS进行全过程有限元分析,为钢-UHPC组合板的设计与计算提供参考.
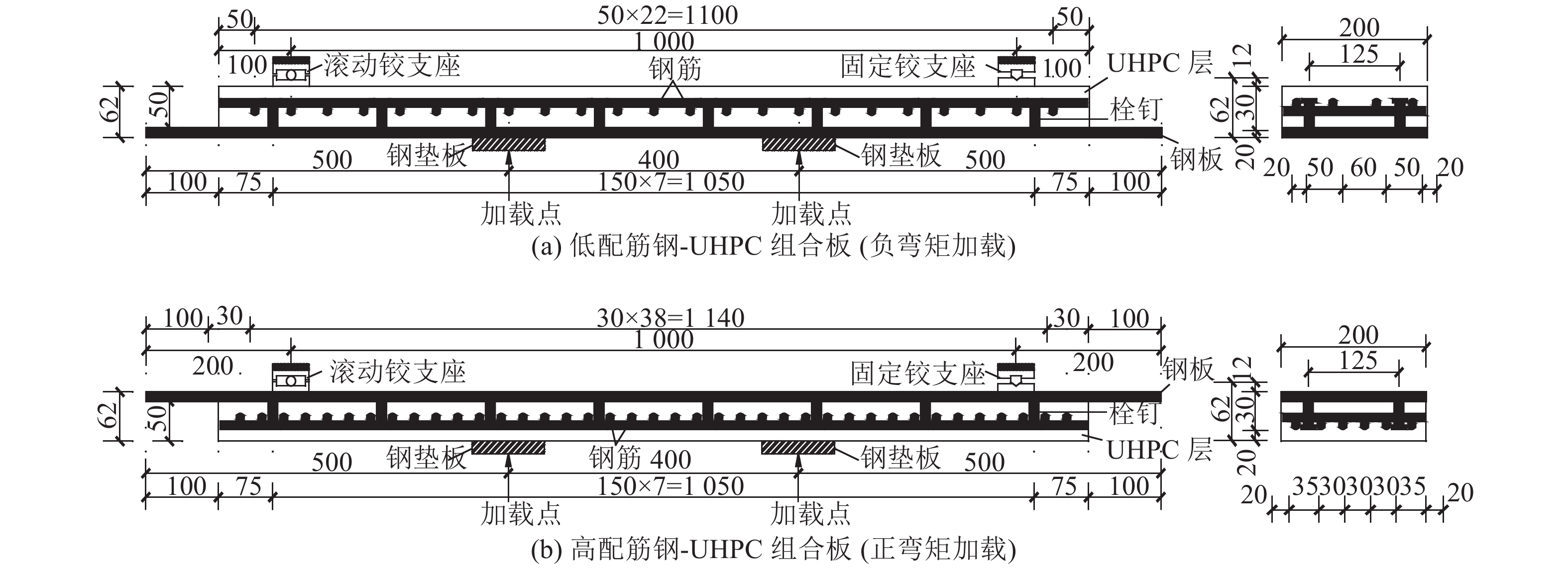
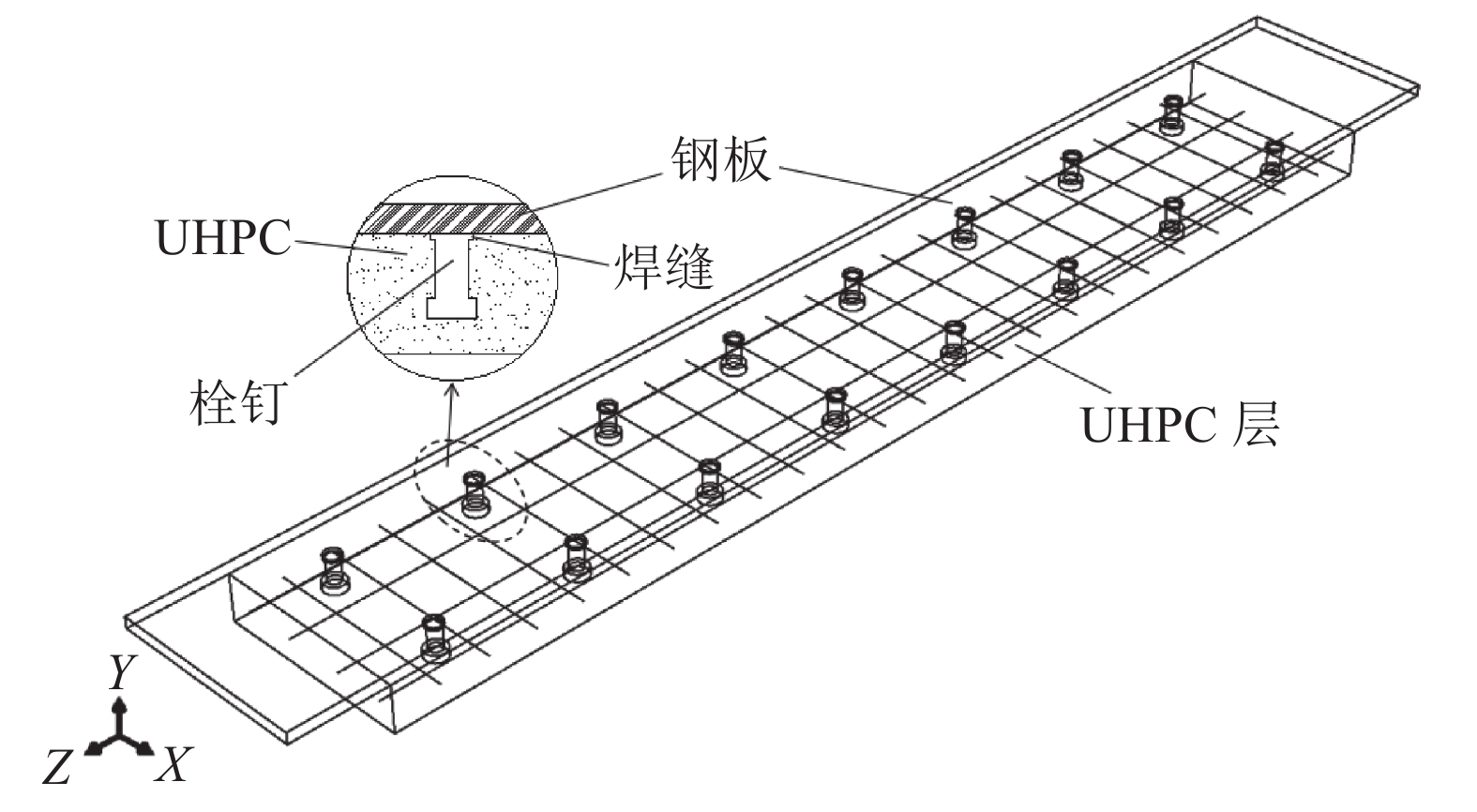
1 试验概况开展8块钢-UHPC组合板的试验研究,各试件尺寸相同,长1 400 mm,宽200 mm,UHPC层厚50 mm,钢板厚12 mm. 变化的参数为纵筋配筋率和加载方式,试件编号、钢筋布置、配筋率等具体参数及详细尺寸如表1、图1所示. 表1中,“4”和“6”表示纵筋数目分别为4根和6根,对应的试件分别称为低配筋钢-UHPC组合板和高配筋钢-UHPC组合板;P和N分别表示正弯矩加载和负弯矩加载.
| 表 1 钢-UHPC组合板试验参数 Table 1 Experimental parameters of steel-UHPC composite slabs |
|
图 1 钢-UHPC组合板一般构造图 Fig. 1 General structure of steel-UHPC composite slabs |
为了降低试验结果的离散性影响并兼顾成本问题,相同尺寸、配筋率和加载方式的试件各制作2个,分别编号为“1”和“2”;8块组合板的栓钉布置情况相同,栓钉纵、横向间距分别为150、125 mm. 钢板均为Q345钢,纵、横向钢筋均为HRB400,栓钉为Φ13 mm×35 mm的短栓钉,UHPC中钢纤维体积掺量为3.5%,其中端钩型钢纤维长度和直径分别为13和0.2 mm,体积掺量为2.0%;圆直型钢纤维长度和直径分别为8和0.12 mm,体积掺量为1.5%. 通过材性试验,测得UHPC立方体抗压强度fcu为134.2 MPa.
2 有限元分析利用有限元分析软件ABAQUS,能够较好地模拟结构的非线性全过程. 研究钢-UHPC组合板的受弯全过程性能并进行因素分析,采用ABAQUS开展组合板非线性全过程的有限元模拟.
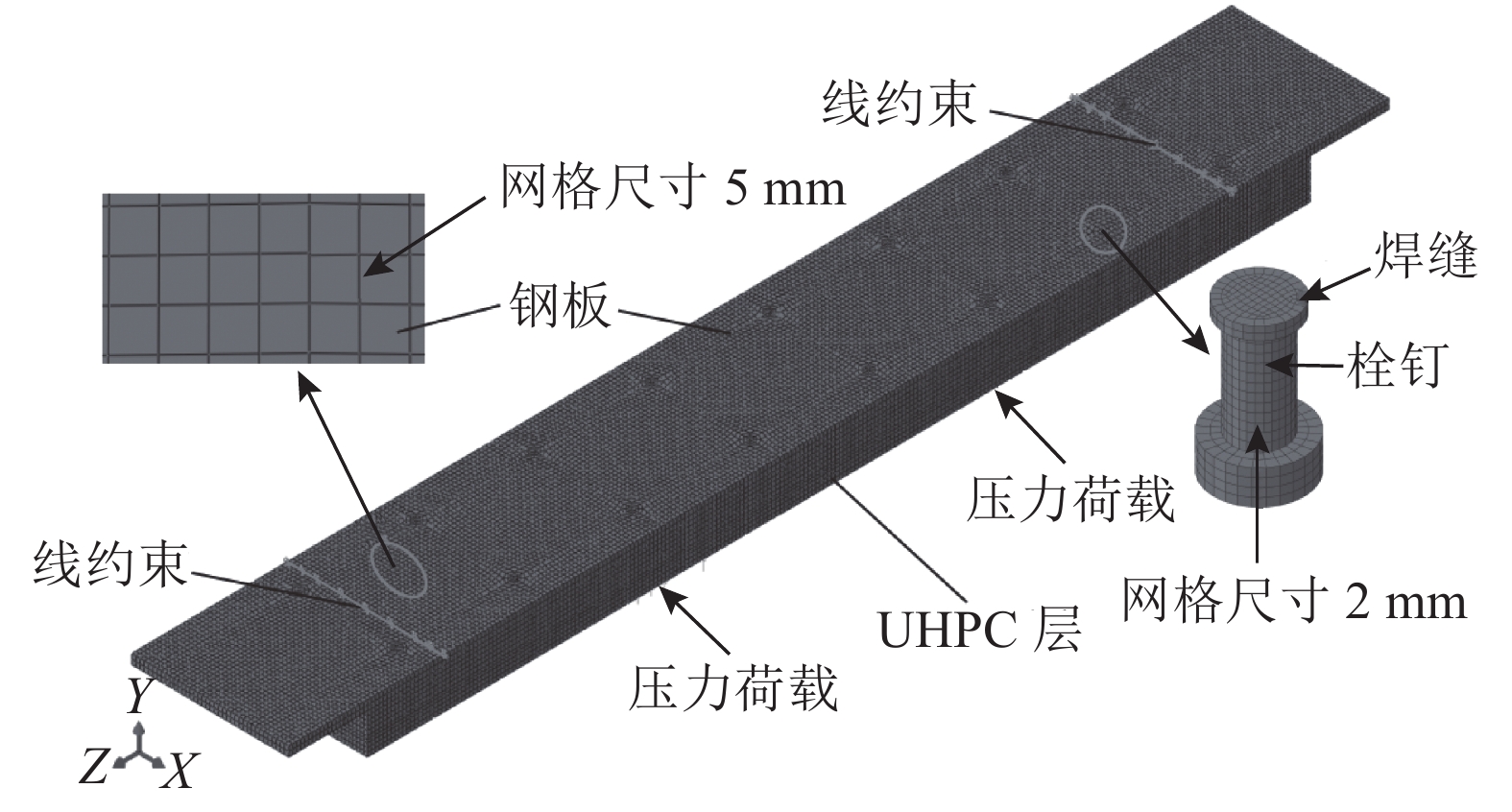
2.1 单元选取钢板、UHPC、栓钉、焊缝均采用三维实体单元C3D8R模拟,C3D8R为三维8节点线性实体缩减积分单元,是ABAQUS有限元计算分析中常用的一种实体单元. 每个单元具有8个节点,每个节点具有3个平动自由度,采用的积分方式比普通的完全积分单元在每个方向上少用一个积分点,可以提高计算效率. 钢板和UHPC网格尺寸为5 mm,栓钉和焊缝网格尺寸为2 mm;钢筋采用两节点三维桁架单元T3D2模拟,网格尺寸为10 mm并以“Embedded”的方式嵌入UHPC中. 各模型的网格划分情况基本相同,如图2所示. 通过试算可知,选用的网格尺寸能够保证计算精度和结果收敛.
|
图 2 有限元模型网格划分 Fig. 2 Mesh partition of finite element model |
UHPC弹性模量Ec=42.6 GPa[13],泊松比μ=0.2. 选择ABAQUS材料库中的损伤塑性(concrete damaged plasticity,CDP)模型来模拟UHPC. CDP模型假设混凝土的两种破坏模式为受拉开裂和受压压溃,适用于模拟由损伤引起的无法恢复的材料退化. 这种退化主要体现在材料抗拉压屈服强度的不同,受拉屈服后材料进入软化阶段及受压屈服后材料先硬化后软化,拉伸和压缩选取不同的损伤和刚度折减因子[14-15]. 相关参数均按ABAQUS的推荐取值[16]:剪切角为36°,偏心率为0.1,双轴与单轴抗压强度的比值为1.16,K为0.666 7,黏性系数为0.
UHPC的应力-应变关系采用张哲等[17]提出的UHPC双线性受拉应力-应变关系,如下所示:
| ${\sigma \rm _t} = \left\{ {\begin{aligned} & {\frac{f_{\rm ct}}{\varepsilon _{\rm ca}}\varepsilon, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < \varepsilon \leqslant {\varepsilon _{\rm ca}}}; \\ & {{f_{\rm ct}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\varepsilon _{\rm ca}} < \varepsilon < {\varepsilon _{\rm pc}}.} \end{aligned}} \right.$ | (1) |
式中:fct为应变硬化阶段平均应力,εca为弹性阶段峰值应变,εpc为极限应变,本文中fct=8.0 MPa,εca=2×10–4,εpc=1.941×10–3.
采用杨剑等[18]提出的UHPC受压应力-应变关系,如下所示:
| ${\sigma _{\rm c}} = \left\{ {\begin{aligned}& {{f_{\rm c}}\frac{{n\xi - {\xi ^2}}}{{1 + \left( {n - 2} \right)\xi }},\;\;\;\varepsilon \leqslant {\varepsilon _0}}\,; \\ & {{f_{\rm c}}\frac{\xi }{{2{{\left( {\xi - 1} \right)}^2} + \xi }},\;\;\;\varepsilon > {\varepsilon _0}\,.\;} \end{aligned}} \right.$ | (2) |
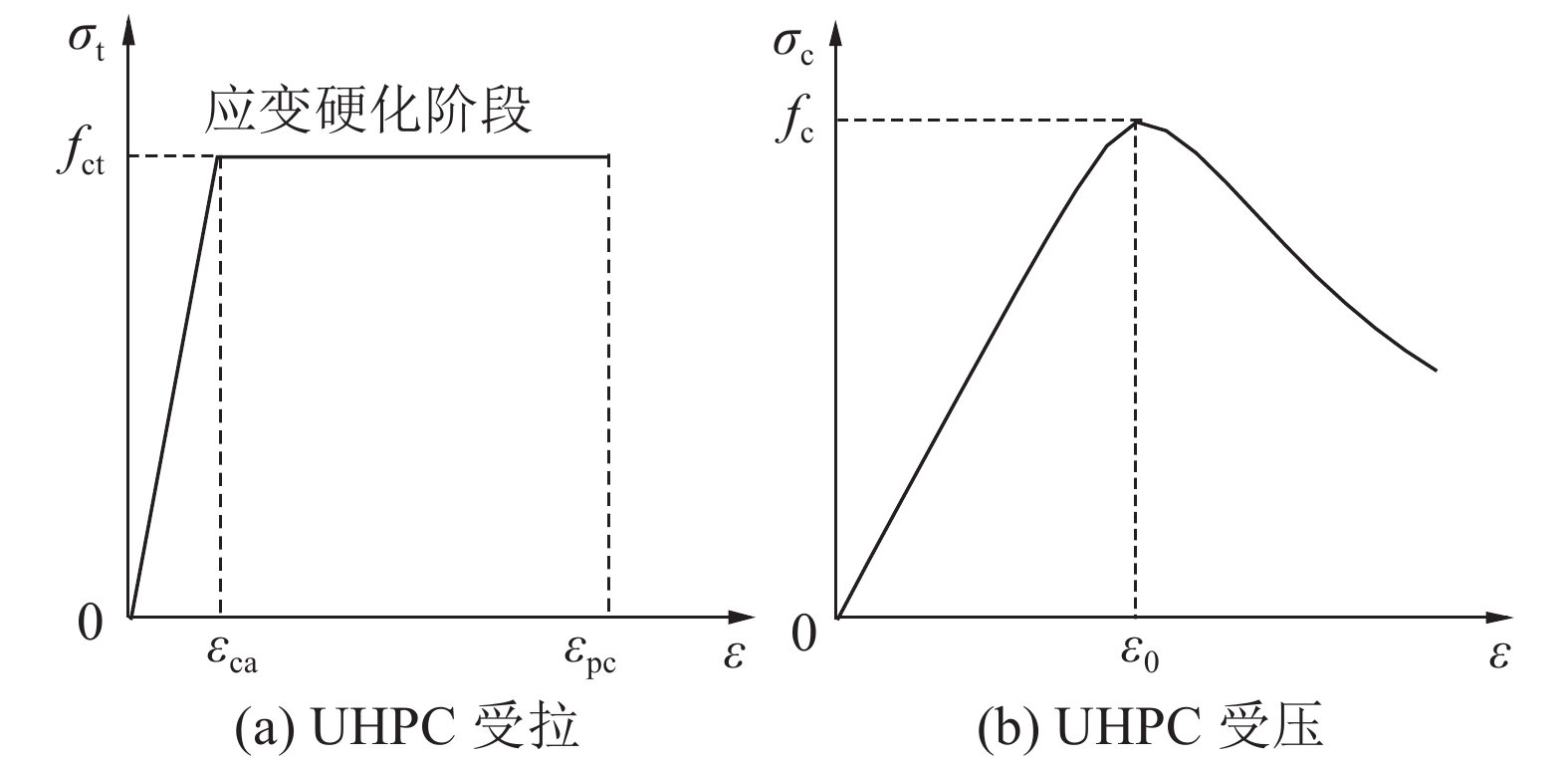
式中:ε0=3.5×10-3,ξ=ε/ε0,fc为圆柱体抗压强度,n=Ec/Es,Ec为初始弹性模量,Es为峰值点的割线模量. 研究表明,UHPC圆柱体抗压强度与立方体抗压强度之间的换算系数约为0.95[19],故取fc=0.95fcu=127.5 MPa. 由式(1)、(2),可得UHPC本构关系,如图3所示.
|
图 3 UHPC本构关系曲线 Fig. 3 Stress-strain curve of UHPC |
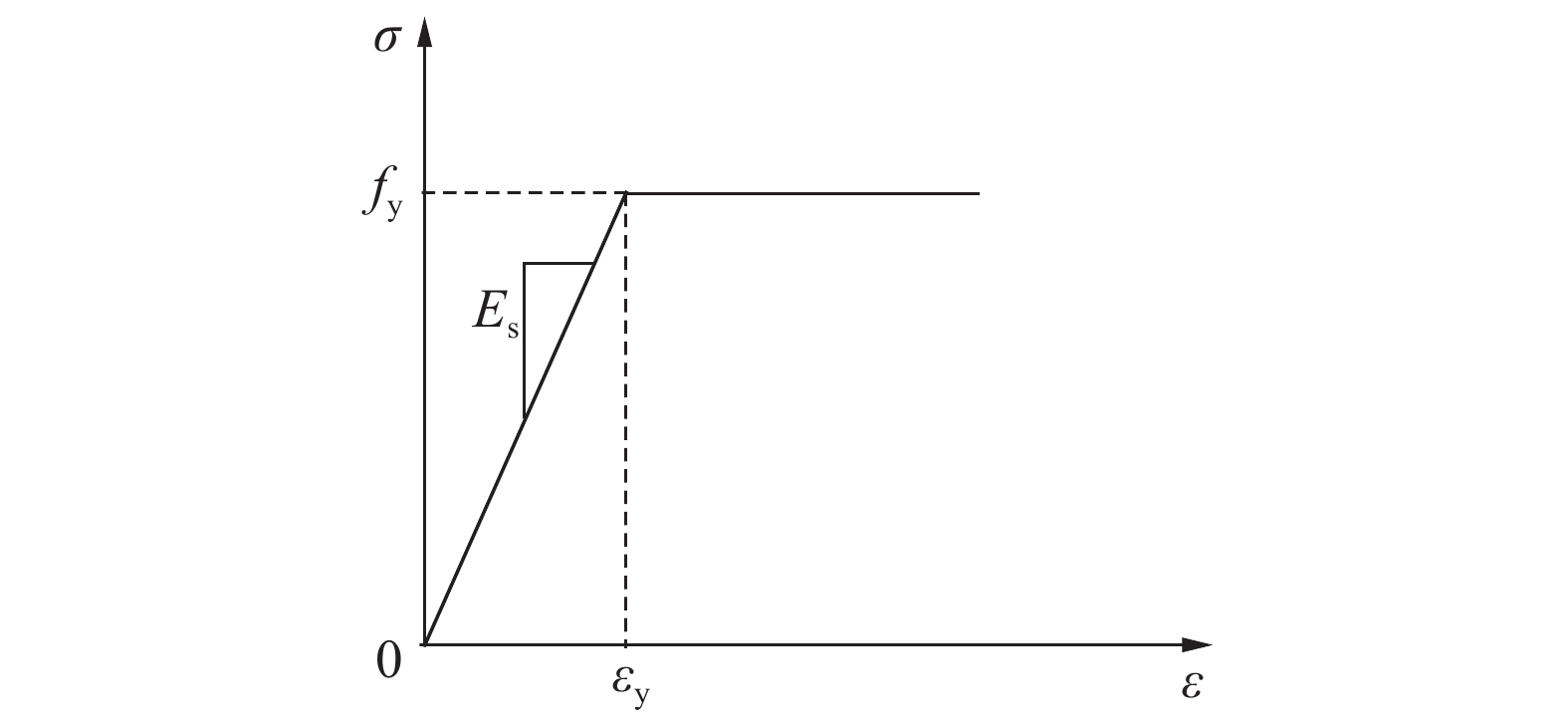
钢板和钢筋均采用理想弹塑性本构模型,如图4所示. 钢板为Q345钢材,屈服强度fy=345 MPa,弹性模量Es=206 GPa,μ=0.3;纵横向钢筋为HRB400,fy=400 MPa,Es=200 GPa,μ=0.3.
|
图 4 钢材本构关系曲线 Fig. 4 Stress-strain curve of steel |
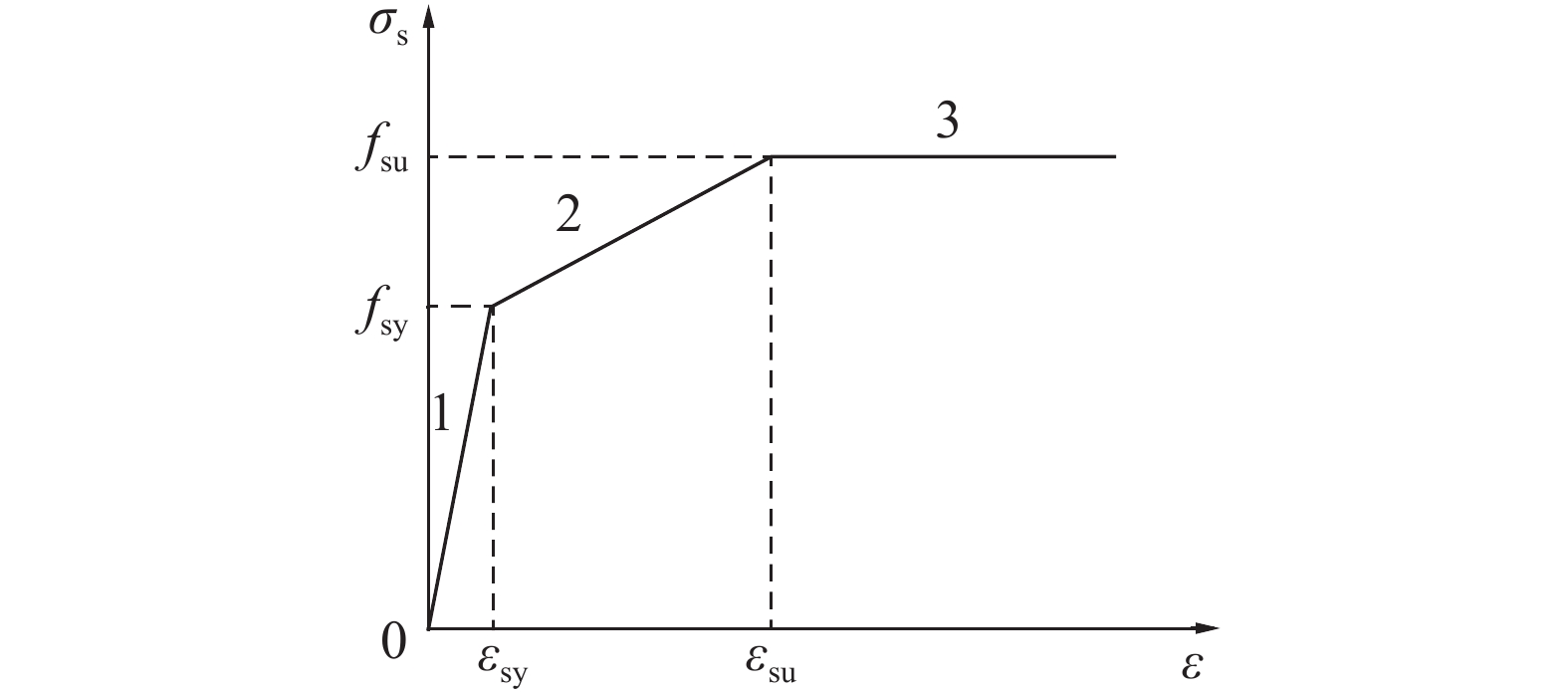
有限元模型根据文献[20]的焊缝尺寸规定建立焊缝,焊缝采用与栓钉相同的材料进行模拟. 栓钉的应力-应变关系一般采用三折线模型[21-22],表达式为
| ${\sigma _{\rm s}} = \left\{ {\begin{array}{*{20}{l}}&\!\!\!\!\!\!\!\!\!\!\!\!{\rm{I}}, & {{E_{\rm ss}}\varepsilon }, \;& {\varepsilon \leqslant {\varepsilon _{\rm sy}}};\\ &\!\!\!\!\!\!\!\!\!\!\!\!{\rm{II}}, & {{f_{\rm sy}} + 0.01{E_{\rm ss}}( \varepsilon - {\varepsilon _{\rm sy}})}, \;& {{\varepsilon _{\rm sy}}< \varepsilon \leqslant {\varepsilon _{\rm su}}};\\ &\!\!\!\!\!\!\!\!\!\!\!\!{\rm{III}}, & {1.2{f_{\rm sy}}}, \;& {\varepsilon > {\varepsilon _{\rm su}}}.\end{array}} \right. $ | (3) |
式中:Ess为栓钉的弹性模量,取值为206 GPa;εsy为屈服应变,εsy=fsy/Ess=1.82×10–3;εsu为栓钉达到极限强度时的应变,根据文献[21]取值为εsu=21εsy=3.822×10–2.
由式(3)得到栓钉的应力-应变关系曲线,如图5所示.
|
图 5 栓钉本构关系曲线 Fig. 5 Stress-strain curve of stud |
钢板-UHPC、栓钉-UHPC界面接触以及栓钉的模拟方式均影响钢-UHPC组合板界面滑移的大小,从而影响组合板的整体力学性能. 定义界面的面面接触,法向采用软件默认的“硬”接触,切向采用罚函数接触,摩擦系数为0.4[23];栓钉根部底面与钢板“Tie”固结,并以“Embedded”方式嵌入UHPC层.
有限元计算模型尺寸与实际的试验模型一致,采用线约束来模拟实际边界情况. 滚动铰支座处约束X、Y方向自由度,固定铰支座处约束X、Y和Z方向自由度,采用面压力模拟外荷载,建立的有限元模型如图6所示.
|
图 6 钢-UHPC组合板有限元模型 Fig. 6 Finite element model of steel-UHPC composite slabs |
8块钢-UHPC组合板正、负弯矩试验测量了结构跨中挠度、端部界面滑移以及纯弯段跨中截面钢板和UHPC表面应变等数据. 将试验结果与ABAQUS有限元计算结果进行对比分析,研究组合板受弯破坏的全过程,同时检验有限元模型的合理性,为进一步的影响因素分析奠定基础.
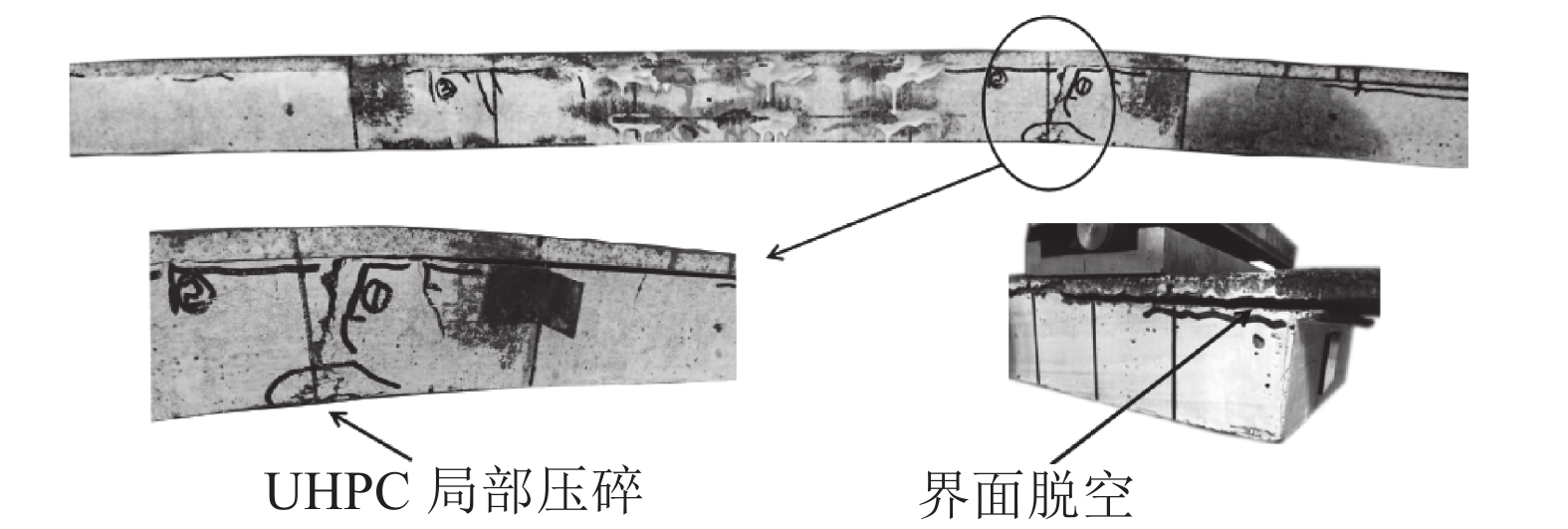
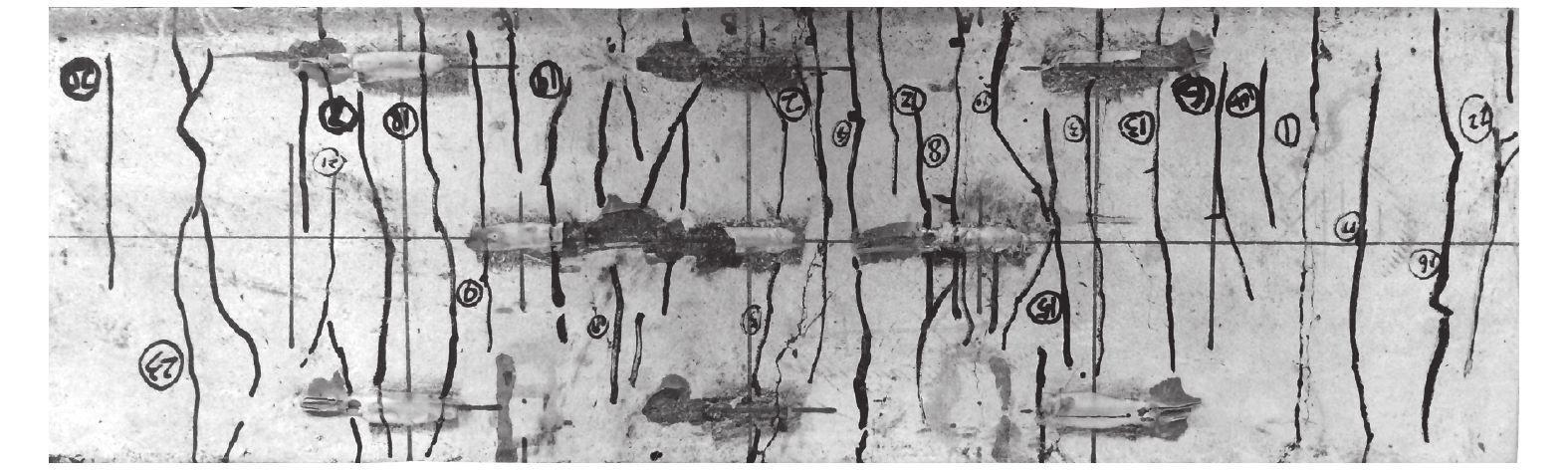
3.1 组合板破坏形态和试验结果汇总组合板在正弯矩作用下,加载点附近UHPC局部压碎且剪弯段与端部钢-UHPC界面出现脱空而导致试件破坏,典型的破坏形态如图7所示;在负弯矩作用下,试件因UHPC主裂缝宽度过大,结构刚度衰减明显而破坏,破坏时UHPC表面的裂缝分布形态如图8所示. 组合板受弯试验结果的汇总情况如表2所示. 表中,Fe为弹性极限荷载,εs为钢板表面应变,εc为UHPC表面应变,Fu为极限荷载,δ为跨中挠度,Δ为端部滑移. 对于正弯矩作用,弹性极限荷载为端部产生滑移时对应的荷载;对于负弯矩作用,弹性极限荷载为试验中观测到第一条裂缝(裂缝宽度为0.02 mm)时的前一级荷载;试件6-P-2因偏早卸载引起实测极限荷载、跨中挠度和端部滑移偏小.
|
图 7 正弯矩典型破坏形态 Fig. 7 Typical failure patterns of positive bending moments |
|
图 8 负弯矩UHPC裂缝分布图 Fig. 8 Distribution of UHPC cracks in negative bending moments |
| 表 2 组合板受弯试验结果汇总 Table 2 Summary of bending test results for composite slabs |
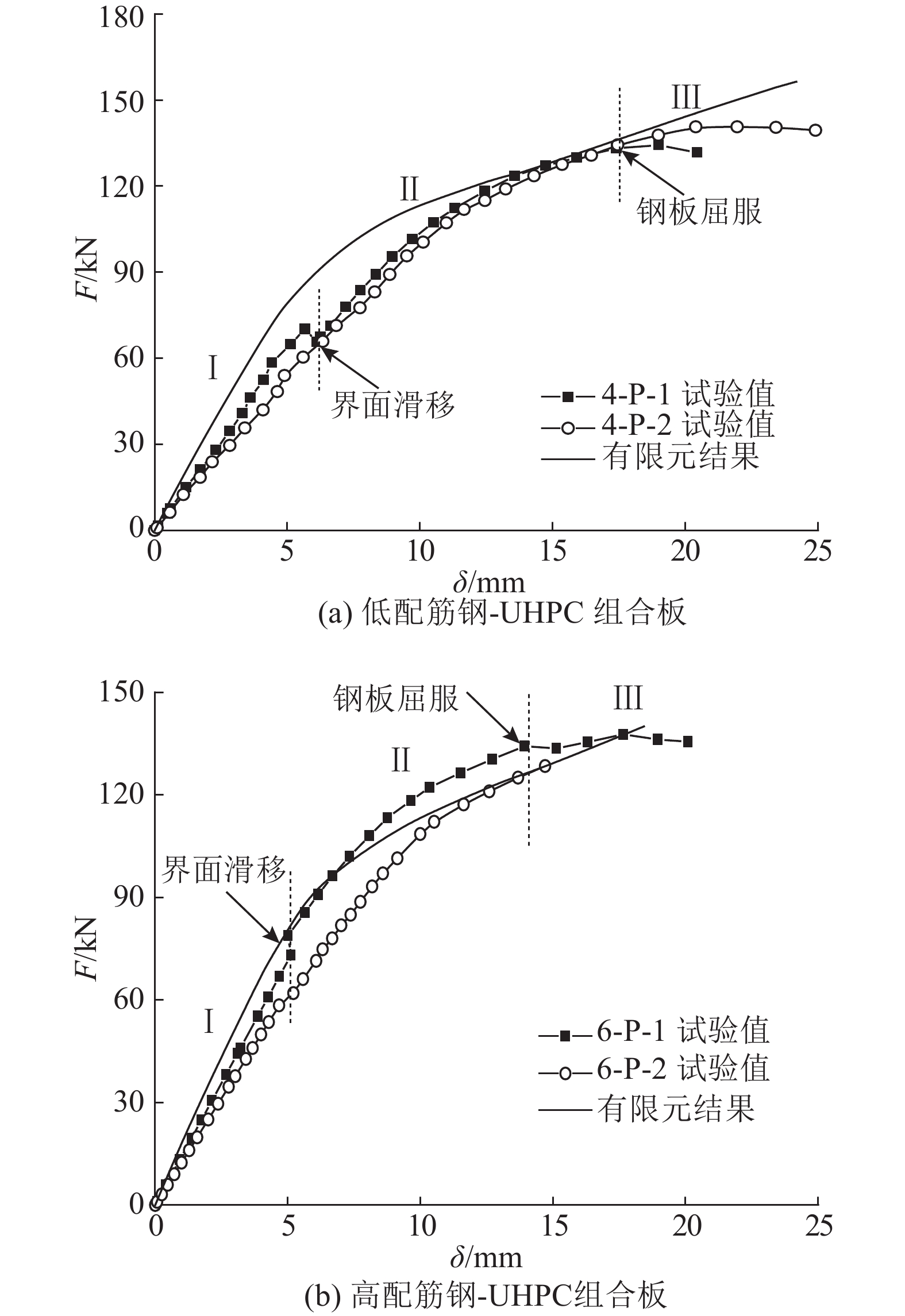
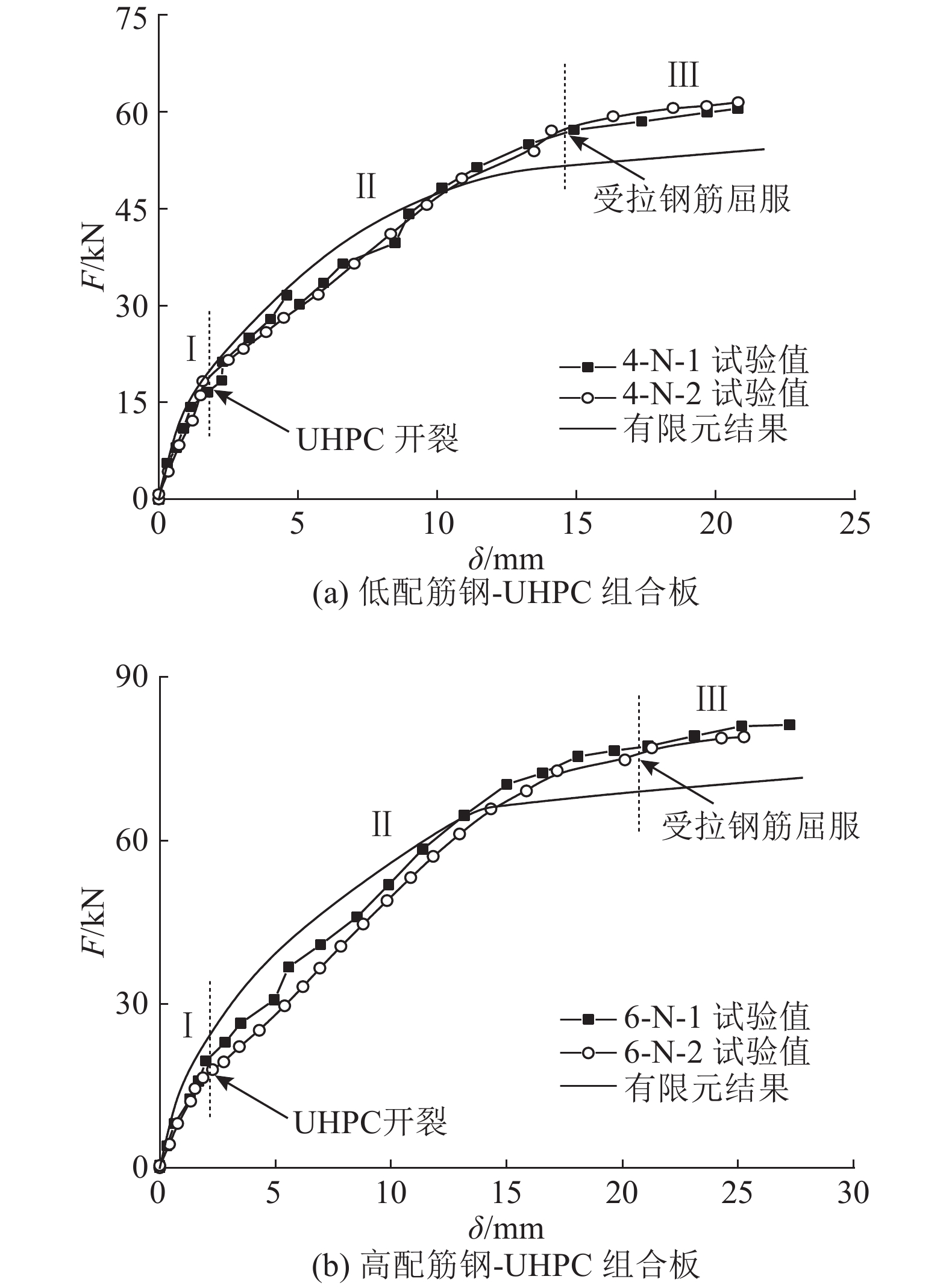
通过试验实测得到的荷载-跨中挠度关系曲线和ABAQUS有限元的计算曲线对比结果如图9、10所示.图中,F为荷载.
|
图 9 正弯矩荷载-挠度曲线 Fig. 9 Load-deflection curves of positive bending moments |
|
图 10 负弯矩荷载-挠度曲线 Fig. 10 Load-deflection curves of negative bending moments |
从图9、10可知,相同配筋和加载方式的2个试件的试验曲线十分接近,说明试验结果的离散性较小. 采用ABAQUS模拟得到的结果与试验曲线的整体趋势一致且初始阶段两者吻合良好,从荷载-挠度曲线的走势分析结构受力的全过程.
在正弯矩作用下,荷载-挠度曲线可以分为3个阶段. Ⅰ)线弹性阶段,荷载与挠度呈线性关系,结构刚度保持不变. Ⅱ)裂缝发展阶段,随着荷载的增加,在阶段Ⅰ的末端,试验观测到组合板端部界面产生滑移;此时,钢-UHPC界面黏结发生破坏,结构组合效应下降,结构刚度减小而进入非线性;随后试验观测到加载点附近UHPC层侧面产生斜裂缝,斜裂缝萌芽于加载点附近的界面处并斜向板底发展. Ⅲ)屈服阶段,随着裂缝的发展,组合板界面滑移持续增大,钢板应力不断增大直至屈服,结构刚度明显衰减;此后,结构承载力不再增加而变形持续增大,加载点附近UHPC局部压碎,组合板剪弯段及端部界面出现脱空而导致试件破坏.
在负弯矩作用下,荷载-挠度曲线可以分为3个阶段:Ⅰ)线弹性阶段;Ⅱ)裂缝发展阶段;Ⅲ)屈服阶段. 线弹性阶段荷载与跨中挠度近似为线性关系,与正弯矩受力不同,在负弯矩作用下,纯弯段UHPC层表面首先出现横向裂缝,结构刚度减小而进入非线性;随着裂缝数量和宽度的增大,结构刚度持续下降,截面应力重分布导致受拉区钢筋应力增加直至钢筋屈服,结构进入屈服阶段,最终组合板因UHPC层主裂缝宽度过大而破坏.
综上所述,正弯矩和负弯矩受弯全过程均可以分为3个阶段,下文统一以Ⅰ、Ⅱ和Ⅲ阶段简明表述.
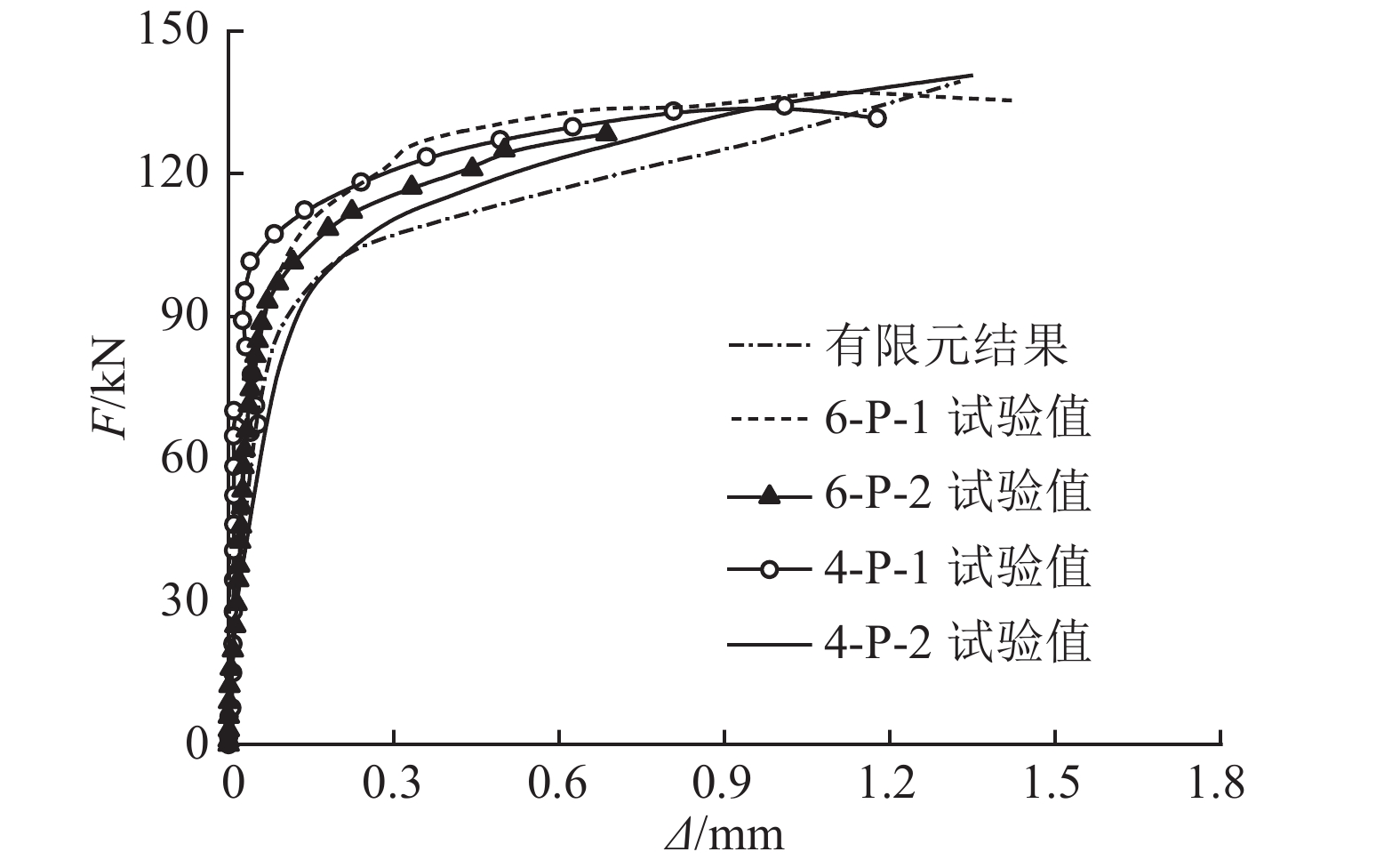
3.3 组合板界面滑移情况在组合板中,钢与UHPC之间采用短栓钉抗剪件连接,由于连接件的变形和界面黏结的破坏,钢-混凝土界面势必发生相对滑移. 关于滑移效应对组合梁抗弯性能影响的研究,已有较多的报道. 研究表明,滑移效应降低了截面组合效应,将引起截面应力重分布,导致结构抗弯刚度和极限承载力下降[24-25]. 在试验中,在组合板端部界面布置千分表来测量滑移,由于负弯矩作用下实测滑移极小(约为正弯矩滑移的1/20),仅研究正弯矩滑移随荷载的变化关系,如图11所示.
|
图 11 正弯矩荷载-端部滑移曲线 Fig. 11 Load-end slip curves of positive bending moments |
由图11可知,在正弯矩作用下,实测的不同配筋率试件荷载-端部滑移曲线基本重合. 当实测荷载约为70 kN时,试件端部界面开始产生滑移,这与正弯矩作用下荷载-挠度曲线由Ⅰ阶段进入Ⅱ阶段的拐点正好对应. 有限元结果与试验曲线整体吻合良好,但在界面滑移产生后,有限元计算的端部滑移与试验值出现偏差. 原因是在界面产生滑移后,钢-UHPC接触面进入了复杂的非线性阶段,而ABAQUS接触模拟中作了简化处理. 采用切向摩擦系数模拟界面黏结情况. 若想更加准确地模拟非线性阶段的荷载-滑移关系,则需要掌握钢-UHPC界面脱粘前、后的接触非线性本构关系,这有待进一步的研究.
除试件6-P-2因偏早卸载引起实测屈服阶段较短,端部滑移仅约为0.7 mm外,其余3个试件滑移为1.2 ~ 1.5 mm.
4 影响因素分析模型试验受限于经济成本及时间的因素,难以考虑周全,有限元模型计算可以弥补模型试验的不足,通过影响因素分析可以进一步揭示结构的力学性能,从而得到更多可靠的结论. 分析影响钢-UHPC组合板抗弯性能的主要计算与设计因素,包括界面黏结方式、纵筋配筋率、栓钉数及布置等.
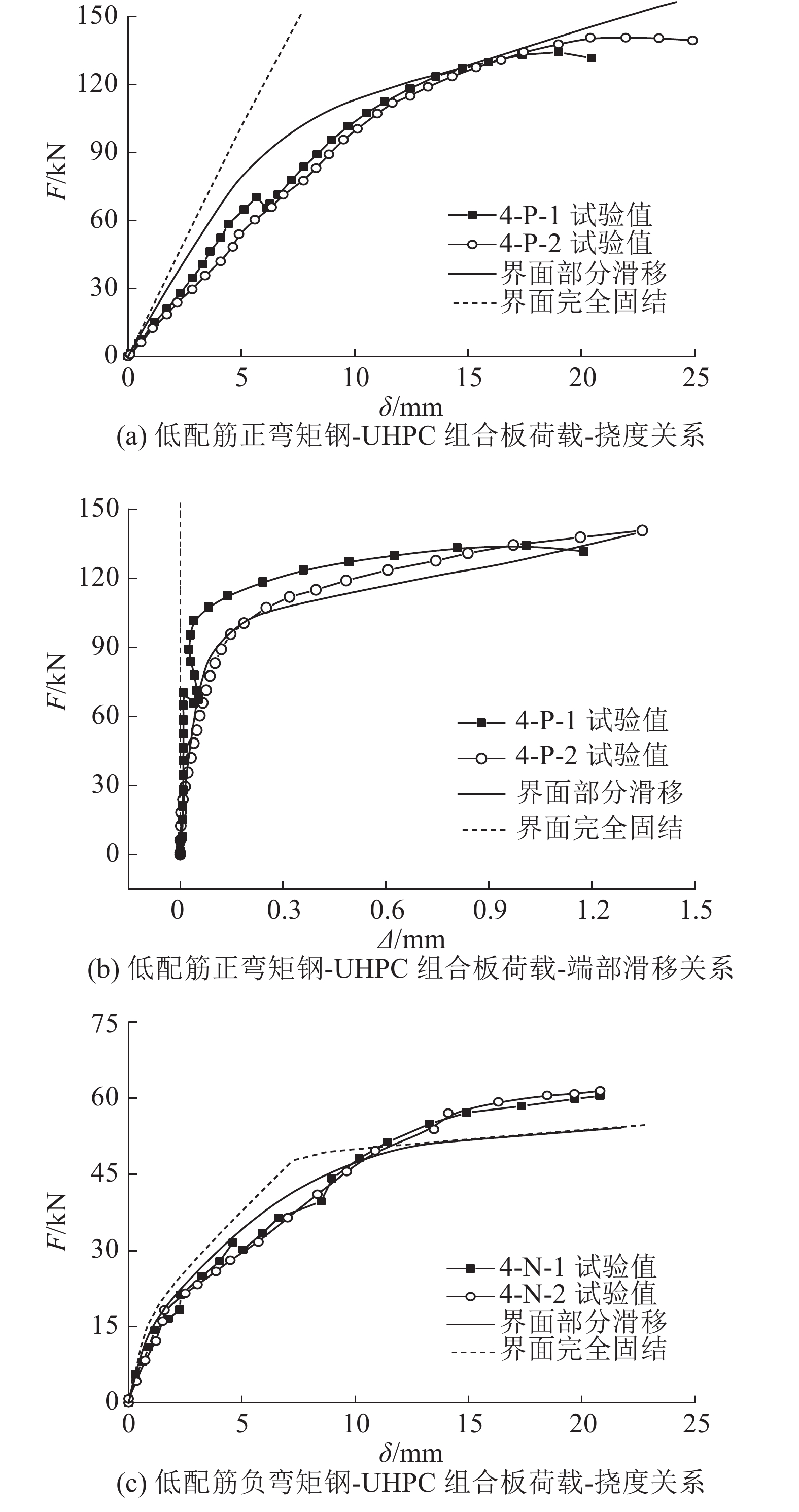
4.1 钢-UHPC界面黏结方式为了研究界面黏结方式对钢-UHPC组合板受弯性能的影响,考虑部分滑移和完全固结两种黏结方式开展有限元模拟,模拟情况如表3所示. 以低配筋组合板试件为例,有限元模拟与试验对比结果如图12所示.
| 表 3 界面黏结方式模拟 Table 3 Simulation of interfacial bonding mode |
|
图 12 界面黏结方式对比 Fig. 12 Comparison of interfacial bonding mode |
对于正弯矩受力模式,界面完全固结极大地高估了结构整体刚度,荷载-挠度呈线性关系,结构刚度远大于部分滑移的计算结果且无衰减趋势;界面完全固结计算得到的结构端部滑移几乎为零,部分滑移计算结果与试验值吻合良好. 在负弯矩作用下,完全固结、部分滑移模型的Ⅰ阶段刚度均与试验值吻合良好,完全固结模拟稍高估了结构在阶段Ⅱ的刚度;总体而言,负弯矩作用下的2种黏结方式均与试验曲线吻合较好,部分滑移黏结方式的吻合程度更高.
4.2 纵筋配筋率表2的试验结果表明,纵筋配筋率由3.14%提高到4.71%,对组合板正弯矩作用下的抗弯性能几乎没有影响,对负弯矩作用下的抗弯性能有明显的提高. 当正弯矩作用时,纵筋位于受压区,无法发挥钢筋良好的受拉性能;当负弯矩作用时,受拉区纵筋能够有效限制和延缓UHPC裂缝的产生和发展,显著提高组合板的延性和极限承载力.
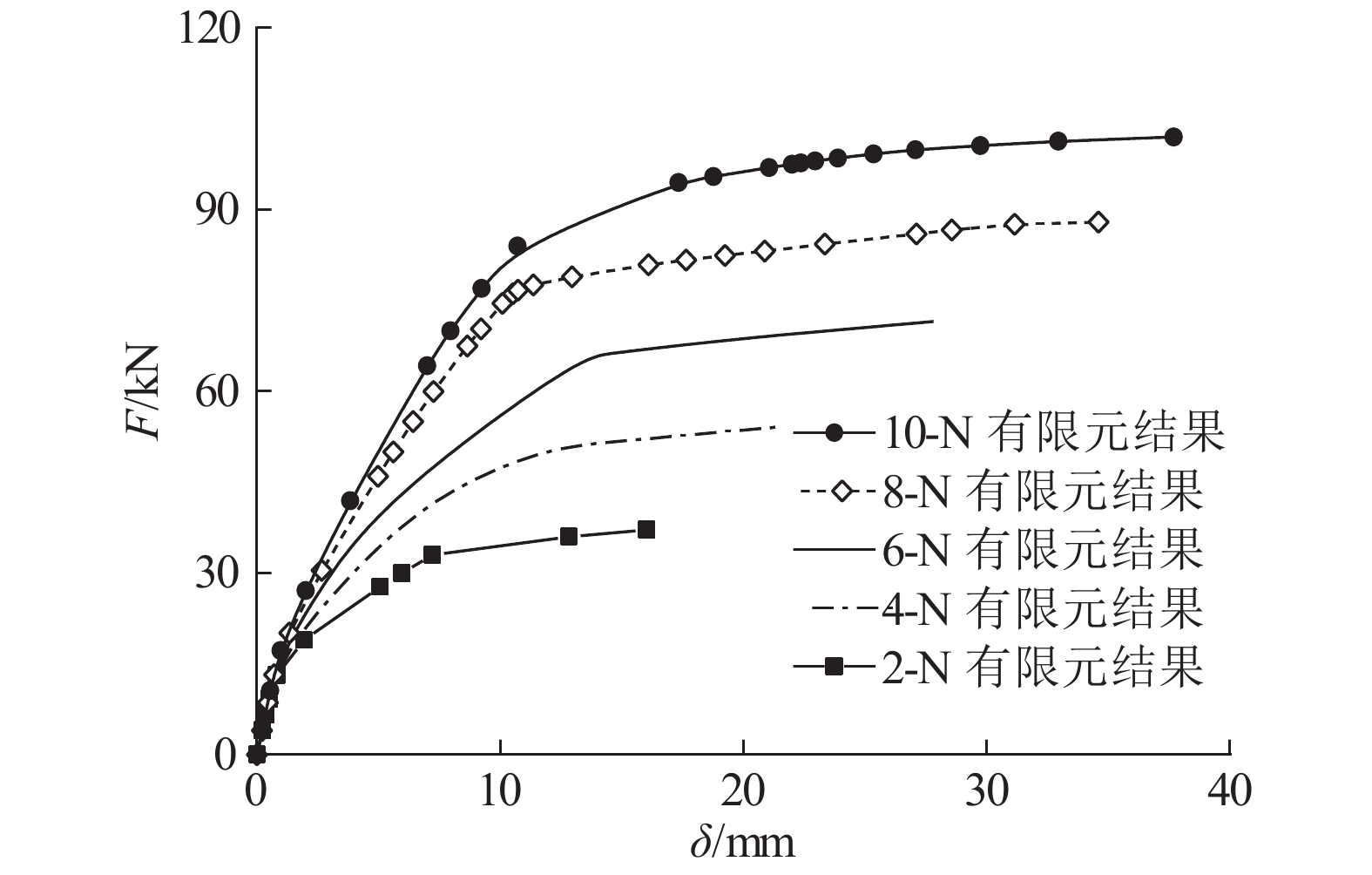
如图13所示为负弯矩作用下不同配筋率模型的荷载-挠度变化关系. 纵筋数量由2增加至4、6、8和10根(对应的纵筋配筋率由1.57%增加至3.14%、4.71%、6.28%和7.85%),Ⅰ阶段的结构初始刚度基本不变,但线弹性极限荷载提高;阶段Ⅱ刚度增大,结构极限承载力显著提高且延性更优.
|
图 13 纵筋配筋率变化 Fig. 13 Change of longitudinal reinforcement ratio |
试验模型栓钉布置为横向2排,间距为125 mm,纵向8列,间距为150 mm,栓钉数为2×8,沿板纵向均匀布置. 如图14所示为组合板栓钉布置情况. 以低配筋组合板模型为例,为了研究栓钉数对组合板性能的影响,分别对栓钉数为 2×15、2×8、1×8、1×4和无栓钉5种情况进行模拟分析;为了研究不同受力区段栓钉布置对组合板性能的影响,分别去除纯弯段、剪弯段栓钉进行模拟分析,分析结果如图15、16所示.

|
图 14 组合板栓钉布置 Fig. 14 Stud arrangement of composite slabs |
|
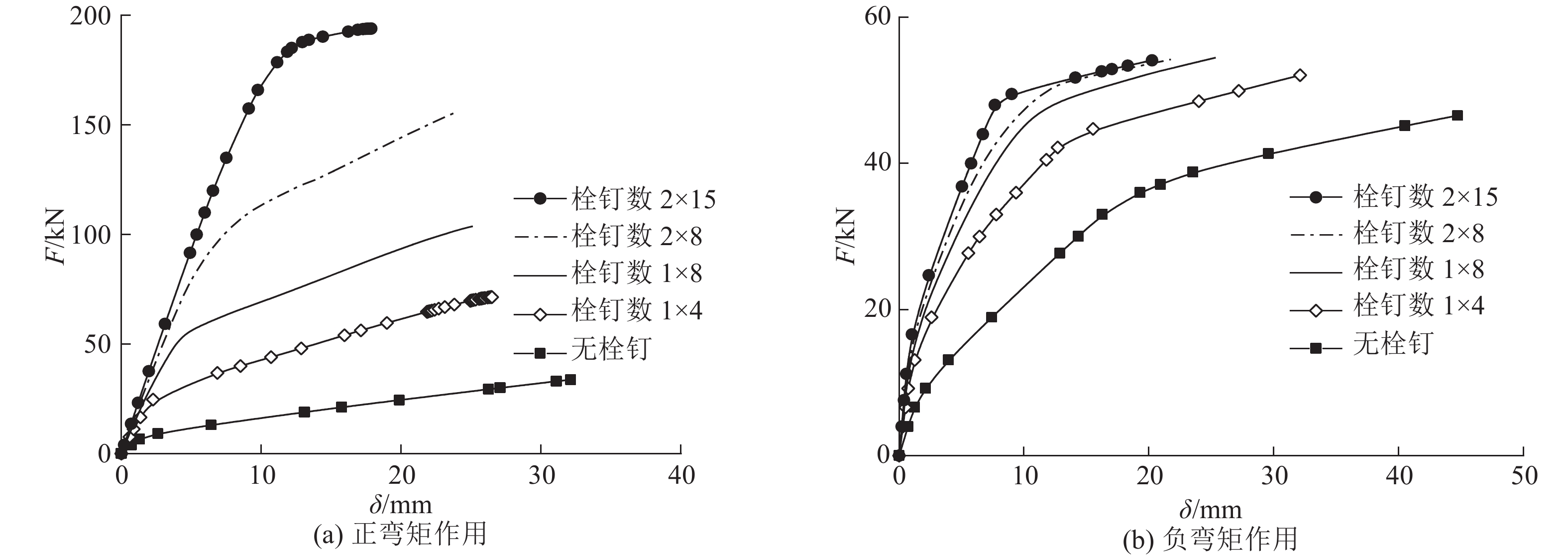
图 15 正、负弯矩下栓钉数的变化 Fig. 15 Change of stud quantity under positive and negative bending moments |
|
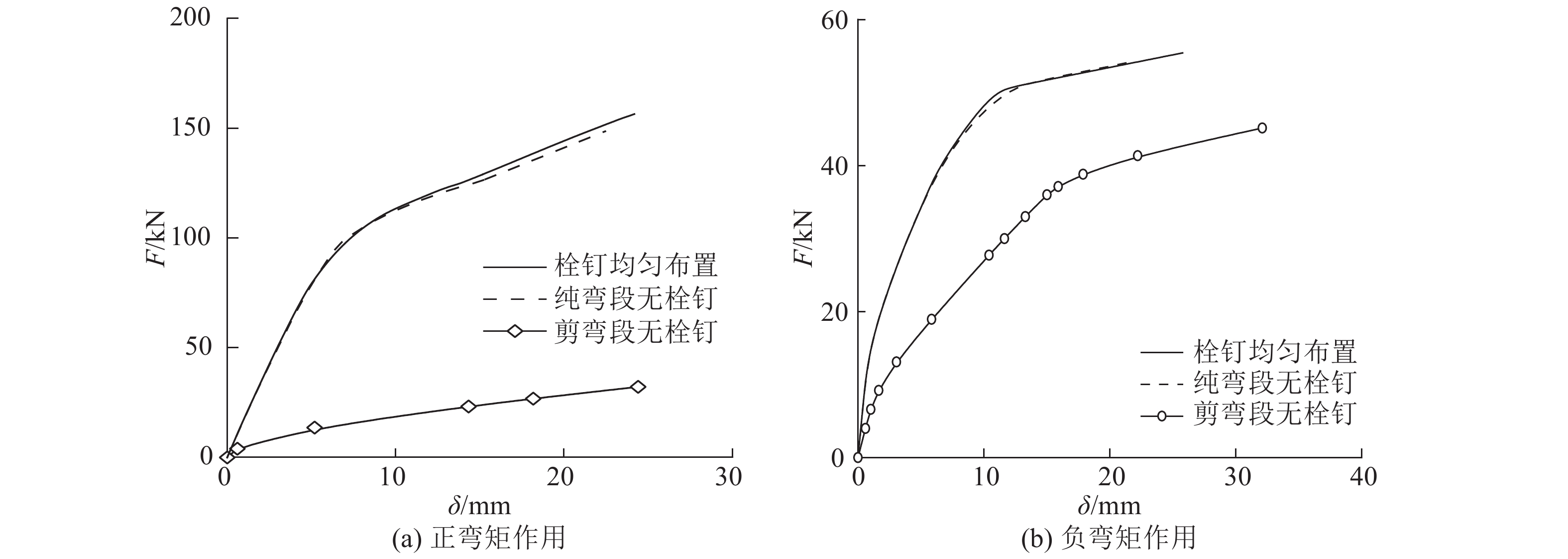
图 16 正、负弯矩下栓钉布置的变化 Fig. 16 Change of stud arrangement under positive and negative bending moments |
图15表明,在正弯矩作用下,栓钉数的增加提高了组合板的弹性极限荷载,延长了结构的线弹性阶段,阶段Ⅱ的结构刚度明显增大,在相同荷载下结构的挠度显著下降;在负弯矩作用下,结构刚度随栓钉数的增加有所提高,但提高幅度不如正弯矩作用模式明显. 原因是正、负弯矩受力模式不同,正弯矩作用下结构刚度衰减与界面滑移量增加关系密切,栓钉数的增加能够有效地限制界面滑移,从而明显提高组合板的刚度;在负弯矩作用下,结构刚度的衰减主要取决于UHPC层裂缝的萌生与发展,界面滑移量极小,因此栓钉数的增加对结构刚度的影响没有正弯矩模式明显.
图16表明,无论是正弯矩还是负弯矩受力模式,纯弯段栓钉对结构抗弯刚度的贡献十分有限;剪弯段栓钉起着关键性作用,去除剪弯段栓钉将大幅度降低组合板刚度,结构的极限承载力有明显降幅,这一点值得在设计中注意.
5 结 论(1) 在正弯矩作用下,组合板受弯破坏全过程分为线弹性阶段、裂缝开展阶段和屈服阶段. 结构刚度两次下降的拐点分别对应于界面滑移发生与钢板屈服,结构破坏时加载点附近UHPC局部压碎且剪弯段与端部钢-UHPC界面出现脱空现象.
(2) 在负弯矩作用下,组合板纯弯段UHPC层表面最早产生横向裂缝,随着荷载的增加,裂缝数量不断增加且宽度增大,截面应力发生重分布,钢筋的应力持续增大直至屈服,最终组合板因主裂缝宽度过大导致刚度衰减严重而破坏. 不同于普通的钢-混凝土组合板,钢-UHPC组合板在负弯矩作用下具有良好的延性.
(3) 通过组合板受弯全过程试验实测得到的荷载-跨中挠度及荷载-端部滑移曲线与ABAQUS有限元计算结果整体趋势一致,且初始阶段两者吻合良好,之后受限于接触非线性本构的影响,两者出现一定的偏差,该类影响因素有待进一步的研究.
(4) 影响组合板抗弯性能的因素分析表明,不同界面黏结方式的有限元模拟结果差别明显,部分滑移计算更符合试验曲线;增加纵筋配筋率能够显著提高负弯矩模式下的组合板刚度、承载力和延性. 试验结果显示,配筋率从3.14%增加至4.71%,组合板承载力和延性分别增加了31.3%和26.0%;栓钉数的增加可以提高组合板刚度,剪弯段栓钉对组合结构传力起着关键性作用,在设计中应予以重视.
(5) 钢-UHPC组合板在负弯矩作用下具备的良好延性揭示了UHPC材料优良的抗拉性能,这有望解决组合桥梁负弯矩区混凝土易开裂的难题.
| [1] |
崔冰, 吴冲, 丁文俊, 等. 车辆轮迹线位置对钢桥面板疲劳应力幅的影响[J]. 建筑科学与工程学报, 2010, 27(3): 19-23. CUI Bing, WU Chong, DING Wen-jun, et al. Influence of acting position of vehicle wheels on fatigue stress range of steel deck[J]. Journal of Architecture and Civil Engineering, 2010, 27(3): 19-23. |
| [2] |
王春生, 成锋. 钢桥腹板间隙面外变形疲劳应力分析[J]. 建筑科学与工程学报, 2010, 27(1): 65-72. WANG Chun-sheng, CHENG Feng. Out-of-plane distortional fatigue stress analysis at web gaps of steel bridges[J]. Journal of Architecture and Civil Engineering, 2010, 27(1): 65-72. |
| [3] |
李辉. 钢-混凝土组合梁斜拉桥病害及其影响分析[D]. 哈尔滨: 哈尔滨工业大学, 2008: 25-29. LI Hui. The analysis of disease and its effect on cable stayed bridge with composite girder [D]. Harbin: Harbin Institute of Technology, 2008: 25-29. http://d.wanfangdata.com.cn/Thesis/D255197 |
| [4] |
项海帆. 世界大桥的未来趋势-2011年伦敦国际桥协会议的启示[C]//第二十届全国桥梁学术会议论文集(上册). 武汉: 人民交通出版社, 2012: 10–17. XIANG Hai-fan. Future trends of the world bridge: implications of the 2011 London Inter-national Bridge conference [C] // Academic Conference Papers of the 20th National Conference on Bridge (The First Volume). Wuhan: China Communications Press, 2012: 10–17. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-OGTY201205002004.htm |
| [5] |
LARRARD D F, SEDRAN T. Optimization of ultra-high-performance concretes[J]. Cement and Concrete Research, 1995, 25(7): 1501-1511. DOI:10.1016/0008-8846(95)00144-2 |
| [6] |
AFGC-SETRA. Ultra high performance fiber reinforced concretes [S]. Pairs: AFGC&SETRA Working Group, 2013.
|
| [7] |
邵旭东, 曹君辉, 易笃韬, 等. 正交异性钢板-薄层RPC组合桥面基本性能研究[J]. 中国公路学报, 2012, 25(2): 40-45. SHAO Xu-dong, CAO Jun-hui, YI Du-tao, et al. Research on basic performance of composite bridge deck system with orthotropic steel deck and thin RPC layer[J]. China Journal of Highway and Transport, 2012, 25(2): 40-45. DOI:10.3969/j.issn.1001-7372.2012.02.007 |
| [8] |
刘梦麟, 邵旭东, 张哲, 等. 正交异性钢板-超薄RPC组合桥面板结构抗弯疲劳性能试验研究[J]. 公路交通科技, 2012, 29(10): 46-53. LIU Meng-lin, SHAO Xu-dong, ZHANG Zhe, et al. Experiment on flexural fatigue performance of composite deck system composed of orthotropic steel deck and ultra-thin RPC layer[J]. Journal of Highway and Transportation Research and Development, 2012, 29(10): 46-53. DOI:10.3969/j.issn.1002-0268.2012.10.009 |
| [9] |
邵旭东, 张哲, 刘梦麟, 等. 正交异性钢-RPC组合桥面板弯拉强度的实验研究[J]. 湖南大学学报: 自然科学版, 2012(10): 7-13. SHAO Xu-dong, ZHANG Zhe, LIU Meng-lin, et al. Research on bending tensile strength for composite bridge deck system composed of orthotropic steel deck and thin RPC topping[J]. Journal of Hunan University: Natural Sciences, 2012(10): 7-13. |
| [10] |
邵旭东, 郑晗, 黄细军, 等. 钢-UHPC轻型组合桥面板横向受力性能[J]. 中国公路学报, 2017, 30(9): 1. SHAO Xu-dong, ZHENG Han, HUANG Xi-jun, et al. Transversal mechanical behavior of steel-UHPC light-weighted composite bridge deck system[J]. China Journal of Highway and Transport, 2017, 30(9): 1. DOI:10.3969/j.issn.1001-7372.2017.09.001 |
| [11] |
YUGUANG Y, WALRAVEN J, UIJL J D. Study on bending behavior of an UHPC overlay on a steel orthotropic deck [C] // 2nd International Symposium on Ultra High Performance Concrete. Kassel: Kassel University Press, 2008.
|
| [12] |
李文光, 邵旭东, 方恒, 等. 钢-UHPC组合板受弯性能的试验研究[J]. 土木工程学报, 2015, 48(11): 93-102. LI Wen-guang, SHAO Xu-dong, FANG Heng, et al. Experimental study on flexural behavior of steel-UHPC composite slabs[J]. China Civil Engineering Journal, 2015, 48(11): 93-102. |
| [13] |
SHAO X D, YI D T, HUANG Z Y, et al. Basic performance of the composite deck system composed of orthotropic steel deck and ultra thin RPC layer[J]. Journal of Bridge Engineering, 2013, 18(5): 417-428. DOI:10.1061/(ASCE)BE.1943-5592.0000348 |
| [14] |
HUU T N, SEUNG E K. Finite element modeling of push-out tests for large stud shear connectors[J]. Journal of Constructional Steel Research, 2009(65): 1909-1920. |
| [15] |
张劲, 王庆扬, 胡守营. ABAQUS混凝土损伤塑性模型参数验证[J]. 建筑结构, 2008, 38(8): 127-130. ZHANG Jin, WANG Qing-yang, HU Shou-ying, et al. Parameters verification of concrete damaged plastic model of ABAQUS[J]. Building Structure, 2008, 38(8): 127-130. |
| [16] |
KMIECIK P, KAMISKI M. Modeling of reinforced concrete structures and composite structures with concrete strength degradation taken into consideration[J]. Archives of Civil and Mechanical Engineering, 2011, 11(3): 623-635. DOI:10.1016/S1644-9665(12)60105-8 |
| [17] |
张哲, 邵旭东, 李文光, 等. 超高性能混凝土轴拉性能试验[J]. 中国公路学报, 2015, 28(8): 50-58. ZHANG Zhe, SHAO Xu-dong, LI Wen-guang, et al. Axial tensile behavior test of ultra high performance concrete[J]. China Journal of Highway and Transport, 2015, 28(8): 50-58. DOI:10.3969/j.issn.1001-7372.2015.08.007 |
| [18] |
杨剑, 方志. 超高性能混凝土单轴受压应力-应变关系研究[J]. 混凝土, 2008(7): 11-15. YANG Jian, FANG Zhi. Research on stress-strain relation of ultra high performance concrete[J]. Concrete, 2008(7): 11-15. DOI:10.3969/j.issn.1002-3550.2008.07.004 |
| [19] |
GRAYBEAL B A. Characterization of the behavior of ultra-high performance concrete [D]. Maryland: University of Maryland College Park, 2005: 36-64. http://adsabs.harvard.edu/cgi-bin/nph-data_query?bibcode=2005PhDT........72G&db_key=PHY&link_type=ABSTRACT&high=08011
|
| [20] |
国家质量监督检验检疫总局. GB/T 10433-2002, 电弧螺柱焊用圆柱头焊钉[S]. 北京: 中国标准出版社, 2002: 1-5. State Administration of Quality Supervision, Inspection and Quarantine. GB/T 10433-2002, Cylindrical head welding nails for arc stud welding [S]. Beijing: China Standard Press, 2002: 1-5. |
| [21] |
丁发兴, 倪鸣, 龚永智, 等. 栓钉剪力连接件滑移性能试验研究及受剪承载力计算[J]. 建筑结构学报, 2014, 35(9): 98-106. DING Fa-xing, NI Ming, GONG Yong-zhi, et al. Experimental study on slip behavior and calculation of shear bearing capacity for shear stud connectors[J]. Journal of Building Structures, 2014, 35(9): 98-106. |
| [22] |
曹君辉. 钢-薄层超高性能混凝土轻型组合桥面结构基本性能研究[D]. 长沙: 湖南大学, 2016: 47-48. CAO Jun-hui. Research on basic performance of steel-thin UHPC lightweight composite deck [D]. Changsha: Hunan University, 2016: 47-48. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y3165838 |
| [23] |
LUO Y, HOKI K, HAYASHI K, et al. Behavior and strength of headed stud-SFRCC shear connection, II: Strength evaluation[J]. Journal of Structural Engineering, 2015, 142(2): 1. |
| [24] |
樊健生, 聂建国. 负弯矩作用下考虑滑移效应的组合梁承载力分析[J]. 工程力学, 2005, 22(3): 177-182. FAN Jian-sheng, NIE Jian-guo. Effects of slips on load-carrying capacity of composite beams under negative bending[J]. Engineering Mechanics, 2005, 22(3): 177-182. DOI:10.3969/j.issn.1000-4750.2005.03.031 |
| [25] |
苗林, 陈德伟. 考虑层间滑移效应的组合梁解析计算[J]. 同济大学学报: 自然科学版, 2011, 39(8): 1113-1119. MIAO Lin, CHEN De-wei. Closed-form solution of composite beam considering interfacial slip effects[J]. Journal of Tongji University: Natural Science, 2011, 39(8): 1113-1119. |



