钢筋的应力-应变滞回本构模型是影响钢筋混凝土结构有限元分析精度的重要因素之一. 迄今为止,许多学者对钢筋的滞回性能进行了研究,提出多种本构模型,其中双折线随动强化、等向强化、Ramberg-Osgood模型等传统的计算模型存在计算精度低或参数确定困难、计算效率差等问题. Menegotto[1]提出Giuffre-Menegotto-Pinto钢筋滞回本构模型(MP模型). 该模型采用应变的显函数表达形式,计算简便,精度较高,可以模拟Bauschinger效应,在钢筋混凝土结构地震反应分析中得到了广泛应用.
除了MP模型以外,Monti等[2]提出考虑非弹性屈曲的钢筋滞回本构模型;Chang等[3-4]提出考虑钢筋横截面积变化的Chang-Mander钢筋滞回本构模型;Dodd等[5]基于自然坐标系,提出预测钢筋滞回循环性能的宏观模型;Dhakal等[6]提出专门模拟钢筋屈曲的滞回本构模型模型;Hoehler等[7]提出可考虑屈服平台的简化单轴钢筋滞回本构模型. 这些研究在某些方面改进了钢筋的滞回履历特性,但计算效率较MP模型低,没有得到推广,完善MP模型具有重要的现实意义.
目前,常用的MP模型是经Ciampi等[8-9]修正的计算模型,除改进了原模型中部分卸载、加载不合理履历路径外,还考虑了钢筋等向强化效应. Sakai等[10]发现上述模型在小幅循环荷载下存在不合理的履历路径,提出对小幅循环后应力路径重新赋值的修正方法. 该修正方法对于小幅循环的判断以是否越过初始平衡点作为条件,对小幅循环的定义不够明确,不能避免不合理的履历曲线. 本文通过定义钢筋材料的弹性域半径,引入通用性较强的循环判别方法,将循环分为2种不同的类型,提出对反转点重新赋值的修正方法,从根本上消除了不合理的履历路径,避免了小幅定义困难的问题. 通过与钢筋试验结果的对比,验证了修正方法的合理性. 应用修正MP模型和Mander混凝土模型,开发基于空间纤维梁单元的钢筋混凝土结构非线性分析程序;根据RC柱拟静力试验模拟曲线与结果数据的对比,验证了模型修正的有效性,提高了MP模型的模拟精度.
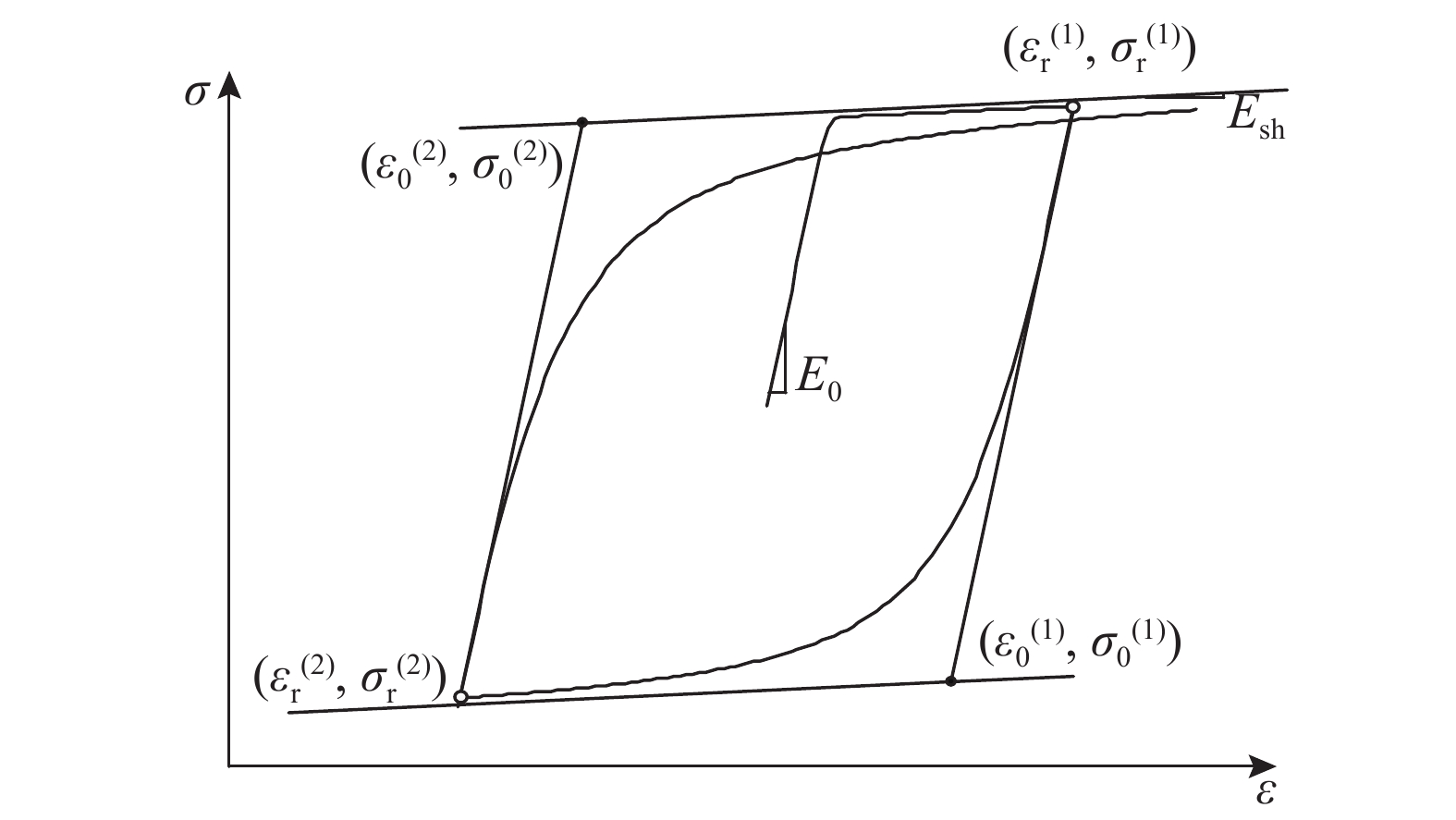
1 MP模型及相关改进 1.1 MP模型如图1所示为MP模型的滞回曲线. 图中,上标(1)、(2)为荷载循环周次编号,每当应变反向后,该类参数都须进行更新. 滞回曲线的方程为
| ${\sigma ^*} = b{\varepsilon ^*} + \frac{{\left( {1 - b} \right){\varepsilon ^*}}}{{{{\left( {1 + {\varepsilon ^*}^R} \right)}^{1/R}}}}.$ | (1) |
式(1)表示从斜率为E0的直线渐近线到斜率为Esh的直线渐近线之间的过渡曲线方程. 式中:b为应变强化系数,是硬化模量Esh和初始弹性模量E0的比值;R为影响过渡曲线形状的曲率参数;
| $\left. \begin{aligned} &{\varepsilon ^*} = {{\left( {\varepsilon - {\varepsilon _{\rm r}}} \right)} / {\left( {{\varepsilon _0} - {\varepsilon _{\rm r}}} \right)}}, \\ &{\sigma ^*} = {{\left( {\sigma - {\sigma _{\rm r}}} \right)} / {\left( {{\sigma _0} - {\sigma _{\rm r}}} \right)}}. \end{aligned} \right\}$ | (2) |
其中,σ和ε为当前应力、应变,σr和εr为应变反向点的应力、应变,σ0和ε0为2条渐近线交点的应力、应变.
|
图 1 MP钢筋滞回本构模型 Fig. 1 MP hysteretic constitutive model of reinforcement |
R反映Bauschinger效应的程度,R越小,Bauschinger效应越显著,计算公式为
| $R = {R_0}\left( {1 - \frac{{c{R_1} \xi }}{{c{R_2} + \xi }}} \right).$ | (3) |
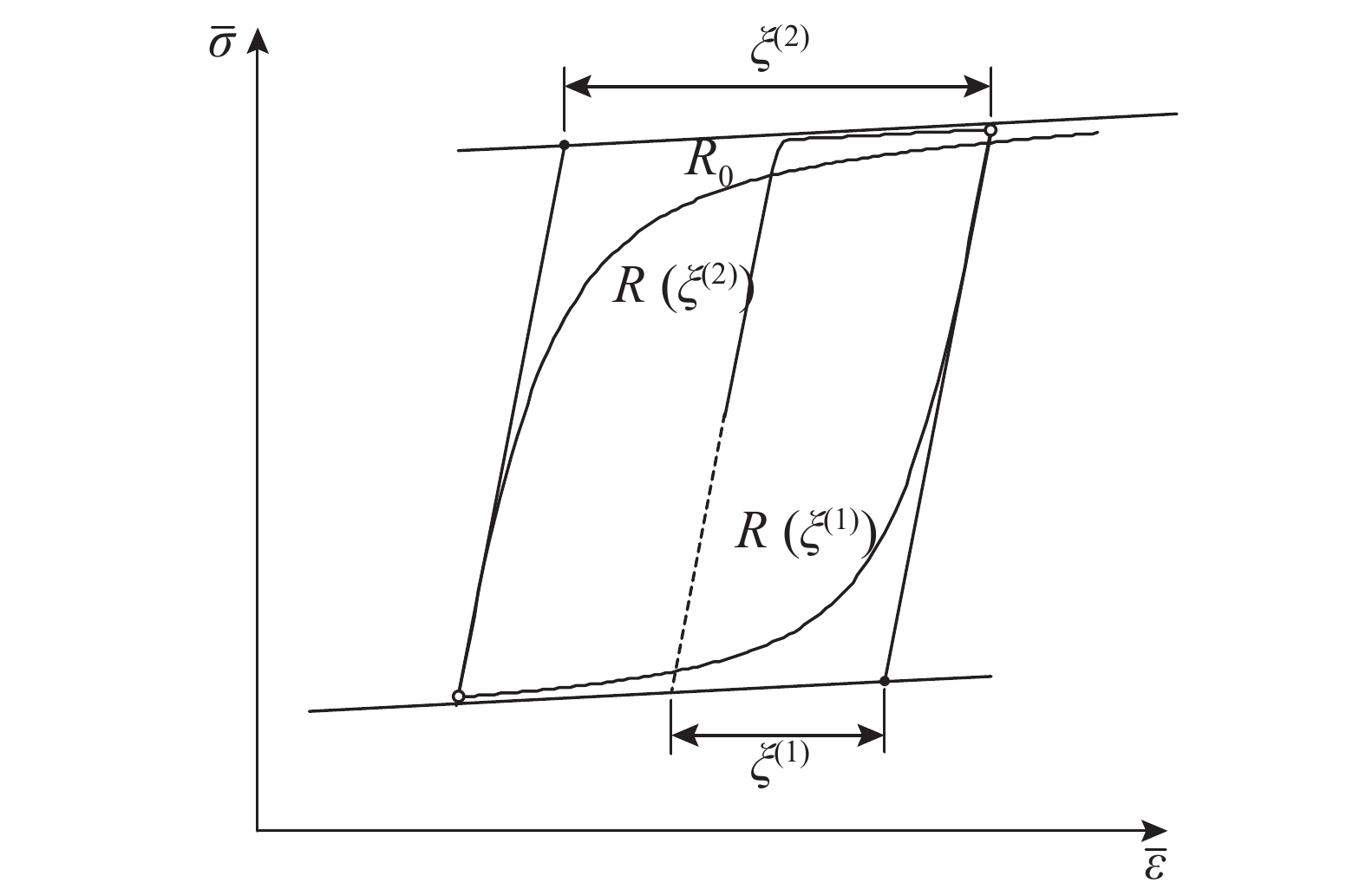
式中:R0、cR1和cR2为材料常数,通过试验测定;ξ为当前循环半周期的塑性应变(见图2),且每次应变反向后都根据下式更新:
| $\xi = \left|{ ({{{\varepsilon _{\rm m}} - {\varepsilon _0}}})/{{{\varepsilon _{\rm y}}}}} \right|,$ | (4) |
其中,εm为加载历史的应变极值,εy为钢筋的屈服应变. 图2中,
|
图 2 曲率参数R的定义 Fig. 2 Definition of curvature parameter R |
在履历曲线中,点(ε0,σ0)用来确定屈服渐近线的位置,当应变增量
| $\left. {\begin{aligned} &{{\varepsilon _0} = \displaystyle\frac{{ - {\sigma _{\rm y}}{\varDelta _{\rm N}} + {E_{{\rm sh}}}{\varepsilon _{\rm y}}{\varDelta}_{\rm N} - {\sigma _{\rm r}} + {E_0}{\varepsilon _{\rm r}}}}{{{E_0} - {E_{{\rm sh}}}}}}, \\ &{{\sigma _0} = - {\sigma _{\rm y}}{\varDelta _{^{\rm N}}} + {E_{{\rm sh}}}\left( {{\varepsilon _0} + {\varepsilon _{\rm y}}{\varDelta _{^{\rm N}}}} \right) }. \end{aligned}} \right\}$ | (5) |
当
| $\left. {\begin{aligned} &{{\varepsilon _0} = \displaystyle\frac{{{\sigma _{\rm y}}{\varDelta _{\rm P}} - {E_{{\rm sh}}}{\varepsilon _{\rm y}}{\varDelta _{\rm P}} - {\sigma _{\rm r}} + {E_0}{\varepsilon _{\rm r}}}}{{{E_0} - {E_{{\rm sh}}}}}}, \\ &{{\sigma _0} = {\sigma _{\rm y}}{\varDelta _{\rm P}} + {E_{{\rm sh}}}\left( {{\varepsilon _0} - {\varepsilon _{\rm y}}{\varDelta _{\rm P}}} \right) }. \end{aligned}} \right\}$ | (6) |
式中:σy为钢筋的屈服应力;εmax、εmin为加载历史中的最大和最小应变;参数ΔN和ΔP为
| $\left. {\begin{aligned} &{{\varDelta _{\rm N}} = 1 + {a_1}{{\left( {\displaystyle\frac{{{\varepsilon _{\max }} - {\varepsilon _{\min }}}}{{2{a_2}{\varepsilon _{\rm y}}}}} \right)}^{0.8}}}, \\ &{{\varDelta _{\rm P}} = 1 + {a_3}{{\left( {\displaystyle\frac{{{\varepsilon _{\max }} - {\varepsilon _{\min }}}}{{2{a_4}{\varepsilon _{\rm y}}}}} \right)}^{0.8}}},\end{aligned}} \right\}$ | (7) |
其中,a1、a2、a3、a4为考虑等向强化效应的材料常数,由实验测定.
1.2 MP模型在小幅循环时的履历缺陷当出现小幅卸载再加载路径时,MP模型的履历曲线会发生应变和刚度的突变,导致应力履历偏大,削弱R的作用.
为了方便说明上述现象,以HRB400钢筋的应力-应变曲线为例进行分析,材料参数见表1. 表中,E0、σy按规范确定[11],b、R0、cR1及cR2按Opensees官网(http://opensees.berkeley.edu/index.php)说明取值.
| 表 1 HRB400钢筋材料参数表 Table 1 Material parameter of HRB400 reinforcing steel |
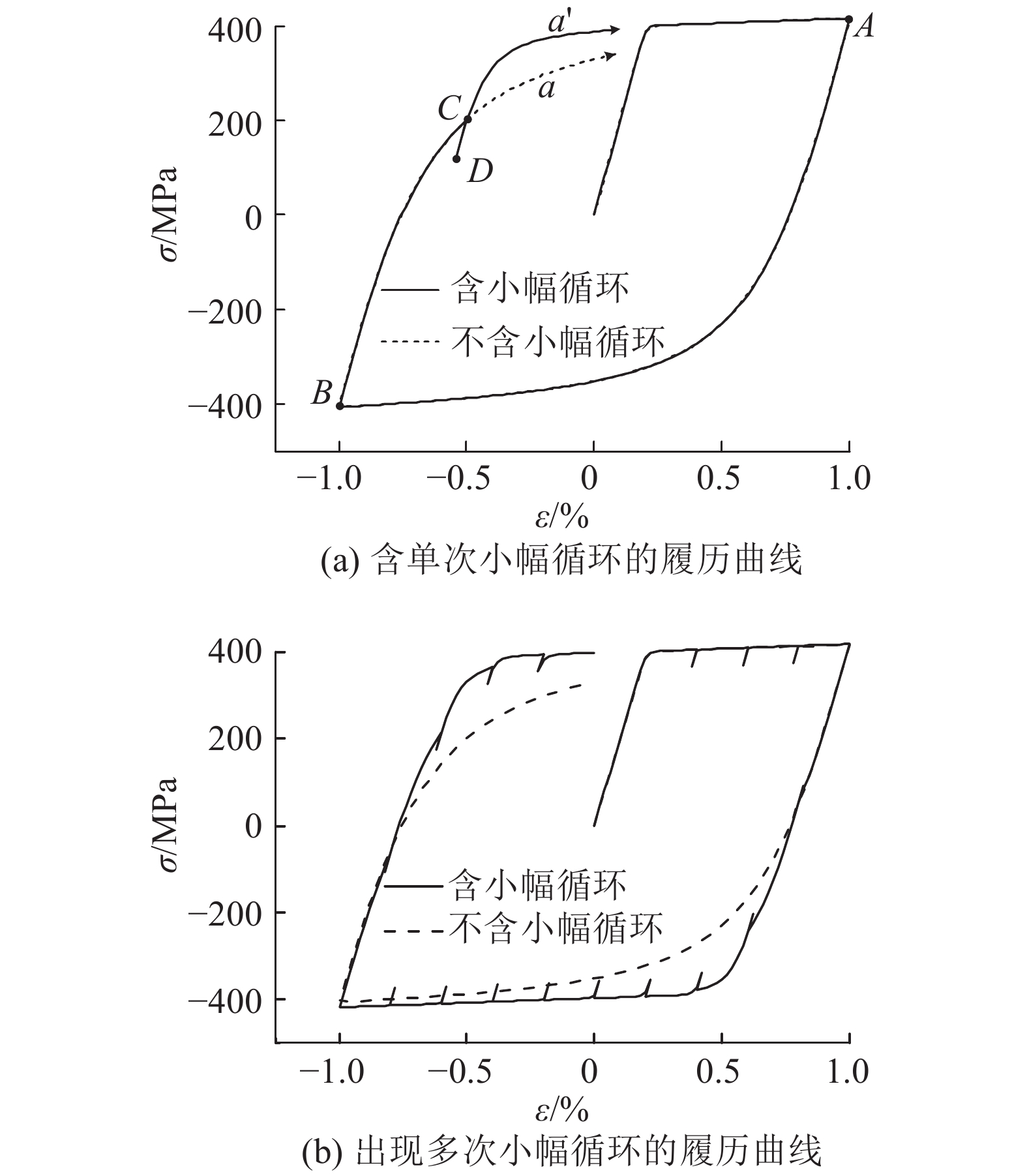
如图3(a)所示为含单次小幅循环的钢筋应力-应变曲线. 当应变履历达到C点、小幅卸载至D点后再次加载时,曲线经过C点后沿路径a'行进,偏离了原路径a(见图3的虚线). 由于卸载幅度较小,在弹性范围内反向加载,路径a为合理的履历. 经小幅循环后,MP模型在C点处计算得到的刚度偏大,此后的应力结果偏大. 如图3(b)所示为钢筋加载过程中出现多次小幅循环后的计算结果,曲线逐渐接近双直线模型,无法体现Bauschinger效应.
|
图 3 小幅卸载后再加载时的履历曲线 Fig. 3 Hysteretic curve under small strain vibration |
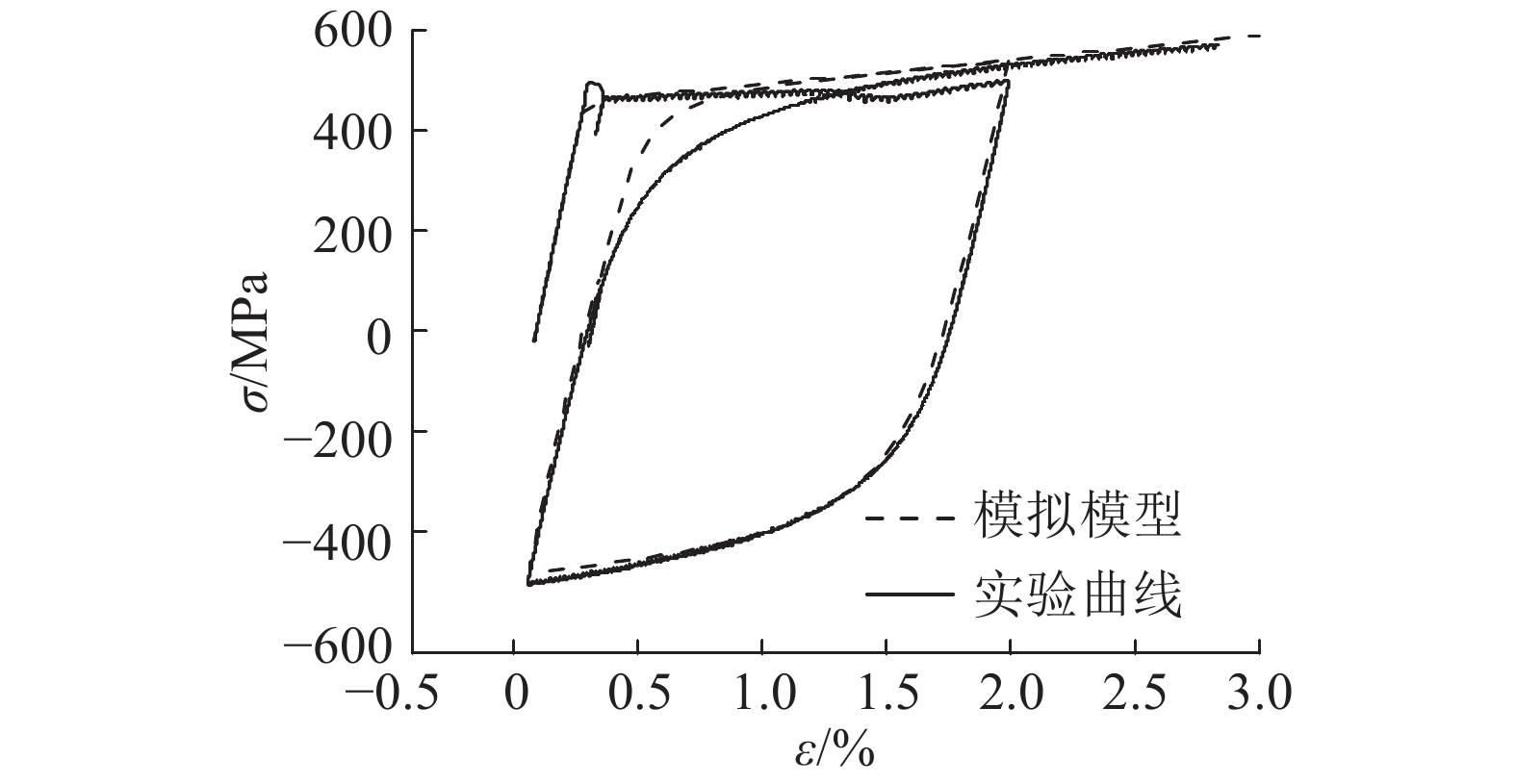
如图4所示为直径为12 mm的HRB400钢筋应力-应变曲线试验结果与既有MP模型的模拟曲线对比. 加载履历为0→ 2.0%→ 0.0%→ 0.3%→ 0.25%→ 3.0%. 由图4可知,当加载履历中存在小幅循环时,应力超过原反转点的履历曲线未发生应变和刚度突变,既有MP模型的计算结果沿着不合理的路径变形.
|
图 4 MP模型的应力-应变履历曲线与试验结果对比 Fig. 4 Comparison of test stress-strain hysteretic curve and MP model |
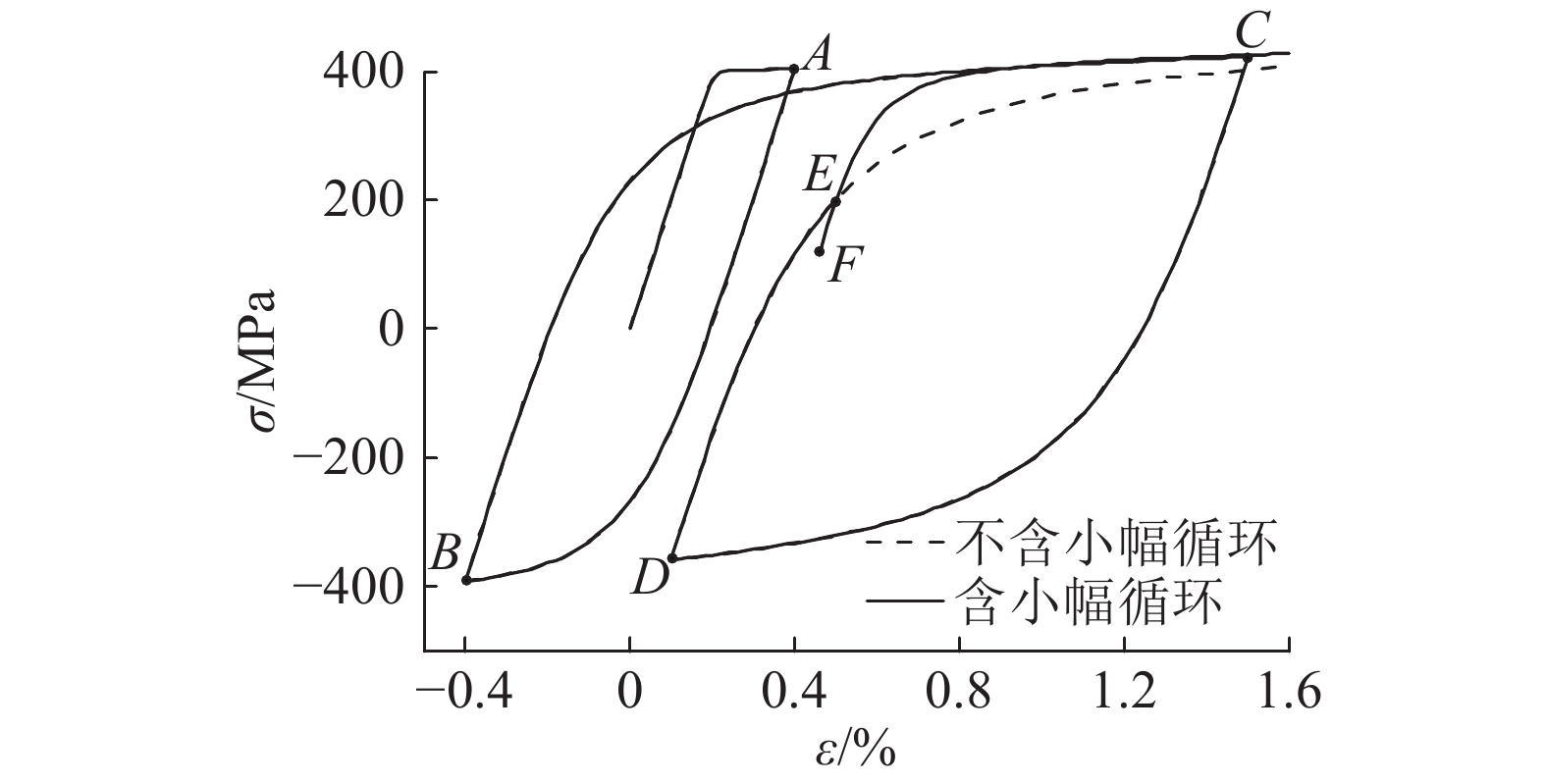
为了解决上述缺陷,Ciampi等[8]对MP模型进行改进. 方法是以应变历史中反转点的正、负极值作为临界值,将该点所确定的加载履历作为上、下边界线;若加载应变没有超过临界值则卸载,应力履历到达边界线后沿边界线继续行进. 该修正模型被Opensees软件所采用[12]. 由于模型通过记忆骨架曲线和上、下边界面来修正当前的应力-应变履历,对小幅循环的定义不够准确,导致结果与试验不符. 如当钢筋应变履历为0→ 0.4%→ –0.4%→ 1.5%→ 0.1%→ 0.5%→ 0.46%→ 1.6%时,根据上述修正模型计算得到的钢筋应力-应变曲线为 图5的实线,在E点出现小幅循环后,履历曲线偏离合理的路径(图5的虚线),向上边界线BC靠拢.
|
图 5 Ciampi修正的MP模型存在的履历缺陷 Fig. 5 Anomaly strain history in modified model by Ciampi |
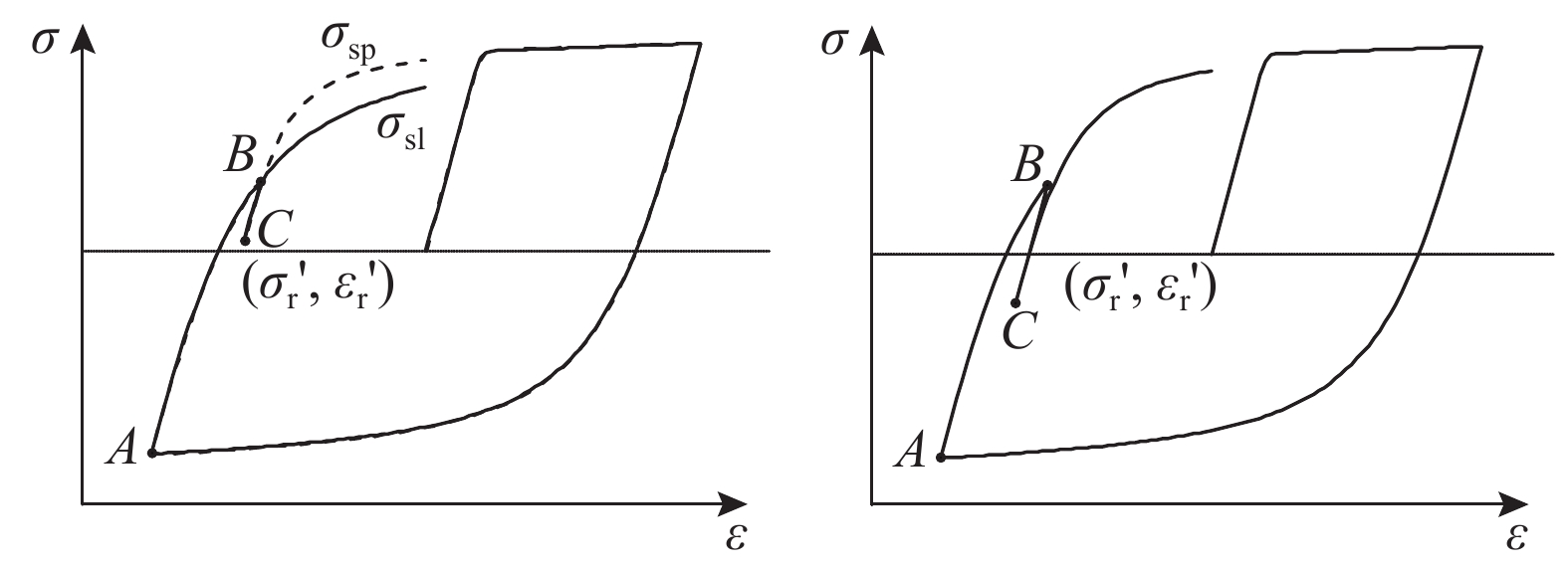
Sakai等[10]提出小幅循环后应力履历按式(8)、(9)计算,如图6所示. 当应变增量为正时,
| $ \sigma = \left\{ {\begin{aligned}&{{\sigma _{{\rm sl}}},\begin{array}{*{20}{c}}{}&{{{\sigma _{{\rm sl}}} \leqslant {\sigma _{{\rm sp}}}}};\end{array}}\\&{{\sigma _{{\rm sp}}},\begin{array}{*{20}{c}}{}&{{{\sigma _{{\rm sl}}} > {\sigma _{{\rm sp}}}}}.\end{array}}\end{aligned}} \right. $ | (8) |
当应变增量为负时,
| $ \sigma = \left\{ {\begin{aligned}&{{\sigma _{{\rm sl}}},\begin{array}{*{20}{c}}{}&{{{\sigma _{{\rm sl}}} \geqslant {\sigma _{{\rm sp}}}}};\end{array}}\\&{{\sigma _{{\rm sp}}},\begin{array}{*{20}{c}}{}&{{{\sigma _{{\rm sl}}} < {\sigma _{{\rm sp}}}}}.\end{array}}\end{aligned}} \right.$ | (9) |
式中:σsl为反转点A开始的履历曲线上的应力,σsp为反转点C开始的履历曲线上的应力.
关于小幅循环的定义,Sakai等[10]以应力是否越过初始平衡点作为判断的依据. 如图6所示,应力-应变履历卸载至点C(εr',σr')后再加载,若σr'>0,此次循环为小幅循环,对应力履历进行修正;若σr'<0,此次循环为正常履历,无需修正. 当应变增量为负时,情况与上述相反.
|
图 6 应力应变路径的判断 Fig. 6 Judgment of stress-strain path |
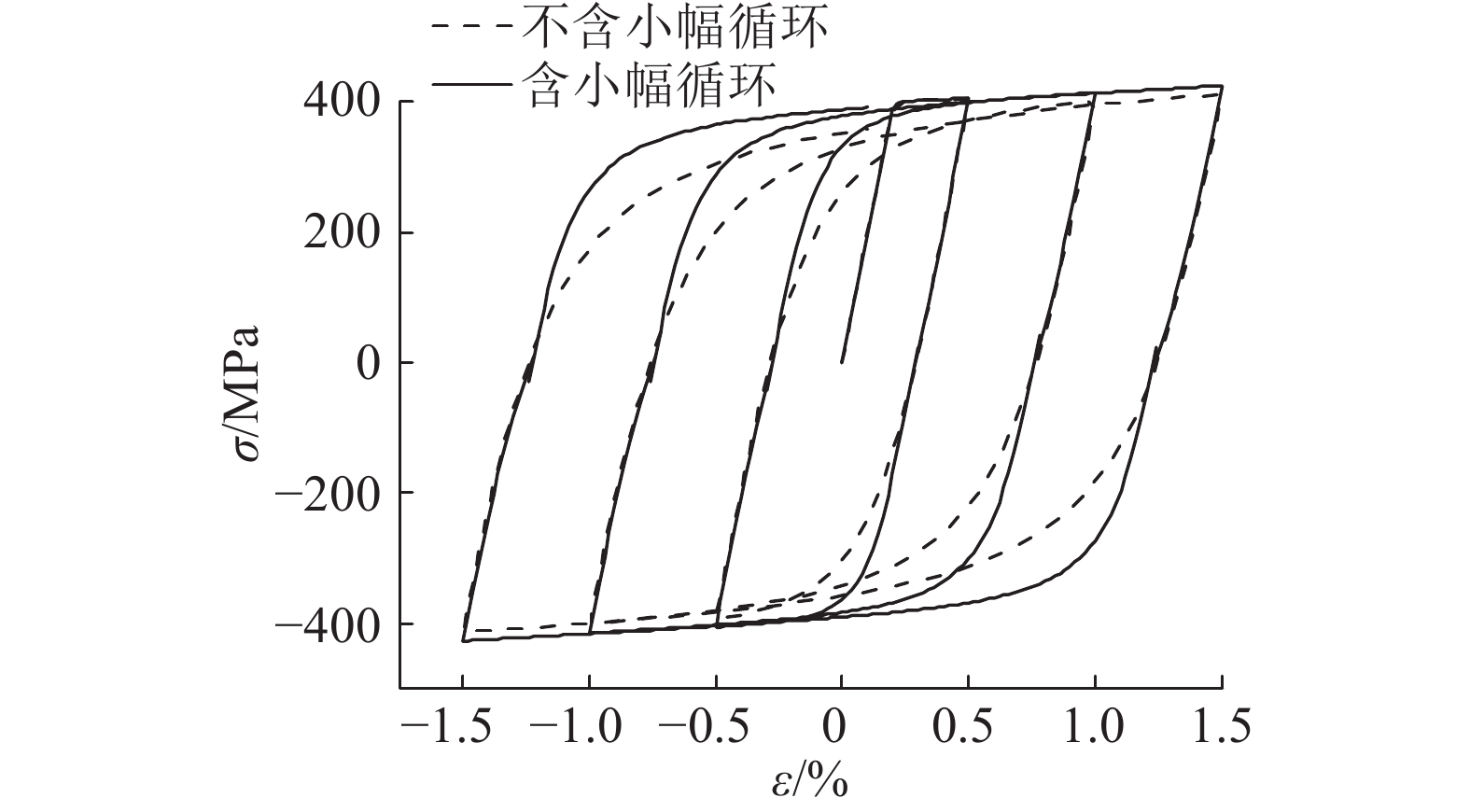
Sakai等[10]对于小幅循环的判断,只简单地根据应力是否变号;当加载履历在0应力附近出现振荡时,仍会出现如图7实线所示的不合理应力-应变曲线,过大地评价了钢筋的应力.
|
图 7 Sakai修正模型出现的不合理履历 Fig. 7 Anomaly strain history in modified model by Sakai |
虽然一些学者对既有MP模型小幅循环后不合理的履历曲线进行修正,但是问题未得到根本解决. 本文参考文献[13],修正双曲面滞回本构模型的做法,提出基于弹性域判断小幅循环的MP模型修正方法.
2.1 修正方法将MP模型的小幅循环履历曲线分成以下2种情形进行修正.
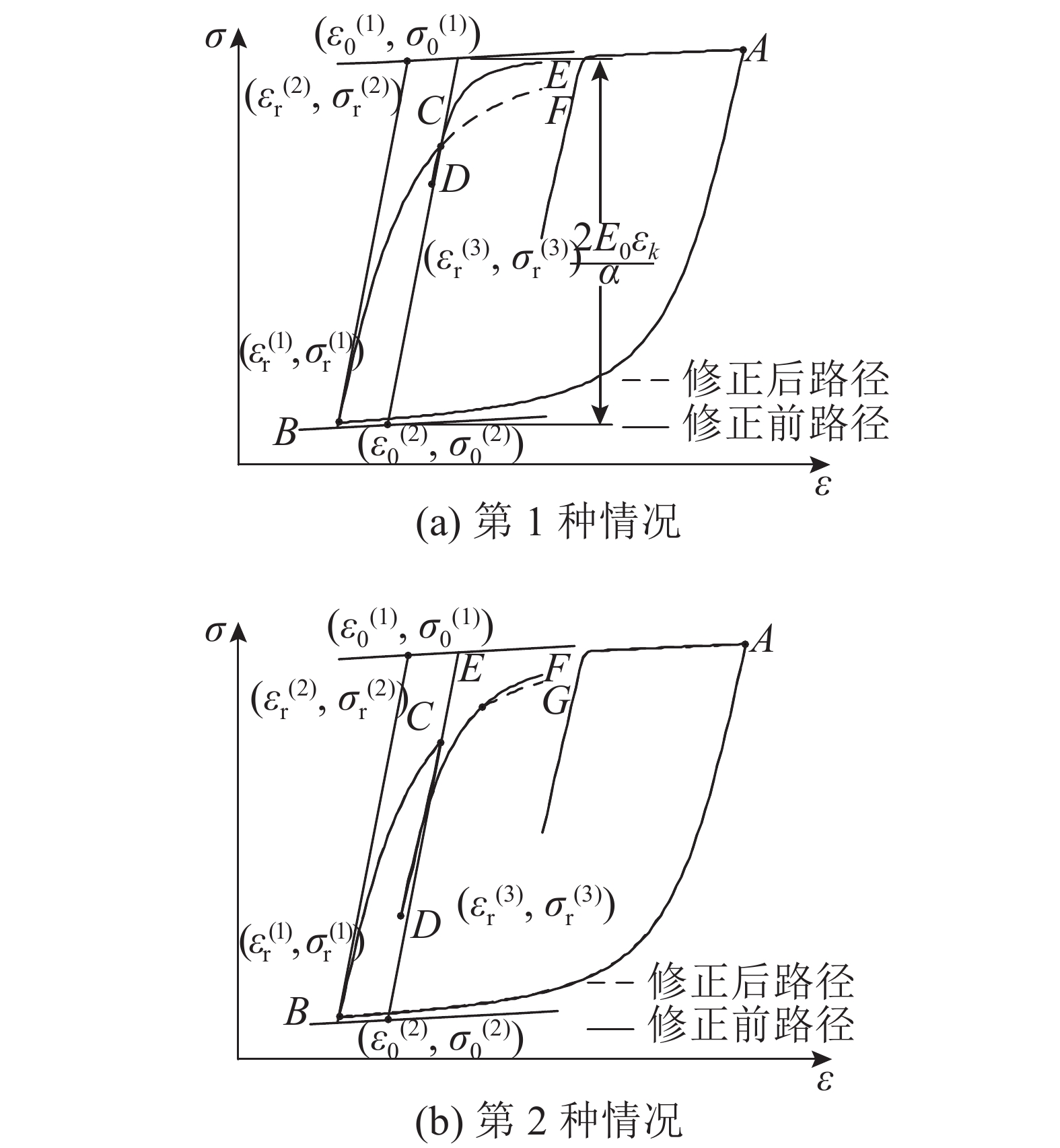
1)钢筋应力由塑性状态反向加载,尚在弹性范围内就卸载,重新加载至屈服,即应力-应变履历沿图8(a)的A-B-C-D-C路径发展.
|
图 8 2种小幅循环应力-应变履历 Fig. 8 Two kinds of stress-strain curve after reloading from low-amplitude unloading |
2)钢筋应力由塑性状态卸载后,小幅加载至塑性范围,再次卸载后沿同向加载至屈服,即应力-应变履历沿图8(b)的A-B-C-D-E路径发展.
为了区分上述2种情况,判断钢筋加载至D点后是否进入塑性,引入计量弹性应变范围的参数. 将上、下屈服渐近线间的应力差值按比例换算为应变差,取中间部分定义为弹性域,弹性域应变直径为2εk. 记反转点C点为(εr(2),σr(2)),渐近线交点为(ε0(2),σ0(2)),前一反转点B点为(εr(1),σr(1)),渐近线交点为(ε0(1),σ0(1)),反转点D点为(εr(3),σr(3)). 弹性域应变半径εk根据下式计算:
| ${\varepsilon _k} = \alpha \frac{{{E_{{\rm sh}}}\left| {\varepsilon _0^{(2)} - \varepsilon _0^{(1)}} \right| + \left| {\sigma _0^{(2)} - \sigma _0^{(1)}} \right|}}{{2E\left( {1 - b} \right)}}.$ | (10) |
式中:α为小于1的正常数,取值根据下文的分析确定.
设参数n按下式计算:
| $n = \left| {\frac{{\varepsilon _{\rm r}^{(3)} - \varepsilon _{\rm r}^{(2)}}}{{{\varepsilon _k}}}} \right|.$ | (11) |
若n≤1,表示该循环为第1种情况下的小幅循环;若1<n<β(β>1),即考虑为第2种情况下的小幅循环.
针对上述2种情形的履历路径,分别提出相应的修正方法.
对于图8(a)所示的第1种情况,规定履历DCF段按如下规则发展.
当应变增量为正时,取反向点为
| $ \left( {{\varepsilon _{\rm r}},{\sigma _{\rm r}}} \right) = \left\{ {\begin{aligned}&{\left( {\varepsilon _{\rm r}^{(3)},\sigma _{\rm r}^{(3)}} \right),\begin{array}{*{20}{c}}{}&{{{\sigma _{{\rm sl}}} \leqslant {\sigma _{{\rm sp}}}}};\end{array}}\\&{\left( {\varepsilon _{\rm r}^{(1)},\sigma _{\rm r}^{(1)}} \right),\begin{array}{*{20}{c}}{}&{{{\sigma _{{\rm sl}}} > {\sigma _{{\rm sp}}}}}.\end{array}}\end{aligned}} \right.$ | (12) |
当应变增量为负时,取反向点为
| $ \left( {{\varepsilon _{\rm r}},{\sigma _{\rm r}}} \right) = \left\{ {\begin{aligned}&{\left( {\varepsilon _{\rm r}^{(3)},\sigma _{\rm r}^{(3)}} \right),\begin{array}{*{20}{c}}{}&{{{\sigma _{{\rm sl}}} \geqslant {\sigma _{{\rm sp}}}}};\end{array}}\\&{\left( {\varepsilon _{\rm r}^{(1)},\sigma _{\rm r}^{(1)}} \right),\begin{array}{*{20}{c}}{}&{{{\sigma _{{\rm sl}}} < {\sigma _{{\rm sp}}}}}.\end{array}}\end{aligned}} \right.$ | (13) |
对于图8(b)所示的第2种情况,假设加载至D点时,已进入塑性,加载段CD对反向段的应力履历产生影响. 规定履历DEG段按如下规则发展.
当应变增量为正时,取反向点为
| $\left( {{\varepsilon _{\rm r}},{\sigma _{\rm r}}} \right) = \left\{ {\begin{aligned} &{\left( {\varepsilon _{\rm r}^{(3)},\sigma _{\rm r}^{(3)}} \right){\rm{,}}\begin{array}{*{20}{c}} {}&{{{\sigma _{{\rm sl}}} \leqslant {\sigma _{{\rm sp}}}}}; \end{array}} \\ &{\left( {\varepsilon _{\rm r}^*,\sigma _{\rm r}^*} \right) ,\begin{array}{*{20}{c}} {}&\quad{{{\sigma _{{\rm sl}}} > {\sigma _{{\rm sp}}}}}. \end{array}} \end{aligned}} \right.$ | (14) |
当应变增量为负时,取反向点为
| $ \left( {{\varepsilon _{\rm r}},{\sigma _{\rm r}}} \right) = \left\{ {\begin{aligned}&{\left( {\varepsilon _{\rm r}^{(3)},\sigma _{\rm r}^{(3)}} \right),\begin{array}{*{20}{c}}{}&{{{\sigma _{{\rm sl}}}\geqslant {\sigma _{{\rm sp}}}}};\end{array}}\\&{\left( {\varepsilon _{\rm r}^*,\sigma _{\rm r}^*} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} \begin{array}{*{20}{c}}{}&{{{\sigma _{{\rm sl}}} < {\sigma _{{\rm sp}}}}}.\end{array}}\end{aligned}} \right.$ | (15) |
变量εr*、σr*为
| $\left. {\begin{aligned}& {\varepsilon _{\rm r}^* = \varepsilon _{\rm r}^{(1)} - \displaystyle\frac{{n - 1}}{{\beta - 1}}\left( {\varepsilon _{\rm r}^{(1)} - \varepsilon _{\rm r}^{(3)}} \right) }; \\ &{\sigma _{\rm r}^* = \sigma _{\rm r}^{(1)} - \displaystyle\frac{{n - 1}}{{\beta - 1}}\left( {\sigma _{\rm r}^{(1)} - \sigma _{\rm r}^{(3)}} \right)}. \end{aligned}} \right\}$ | (16) |
式中:β为控制过渡区域大小的参数,取值根据下文的分析确定.
2.2 参数α与β对修正模型的影响上述修正方法中含有新定义的参数α与β. 通过分析这2个参数对钢筋应力-应变曲线的影响,讨论合理的取值方法.
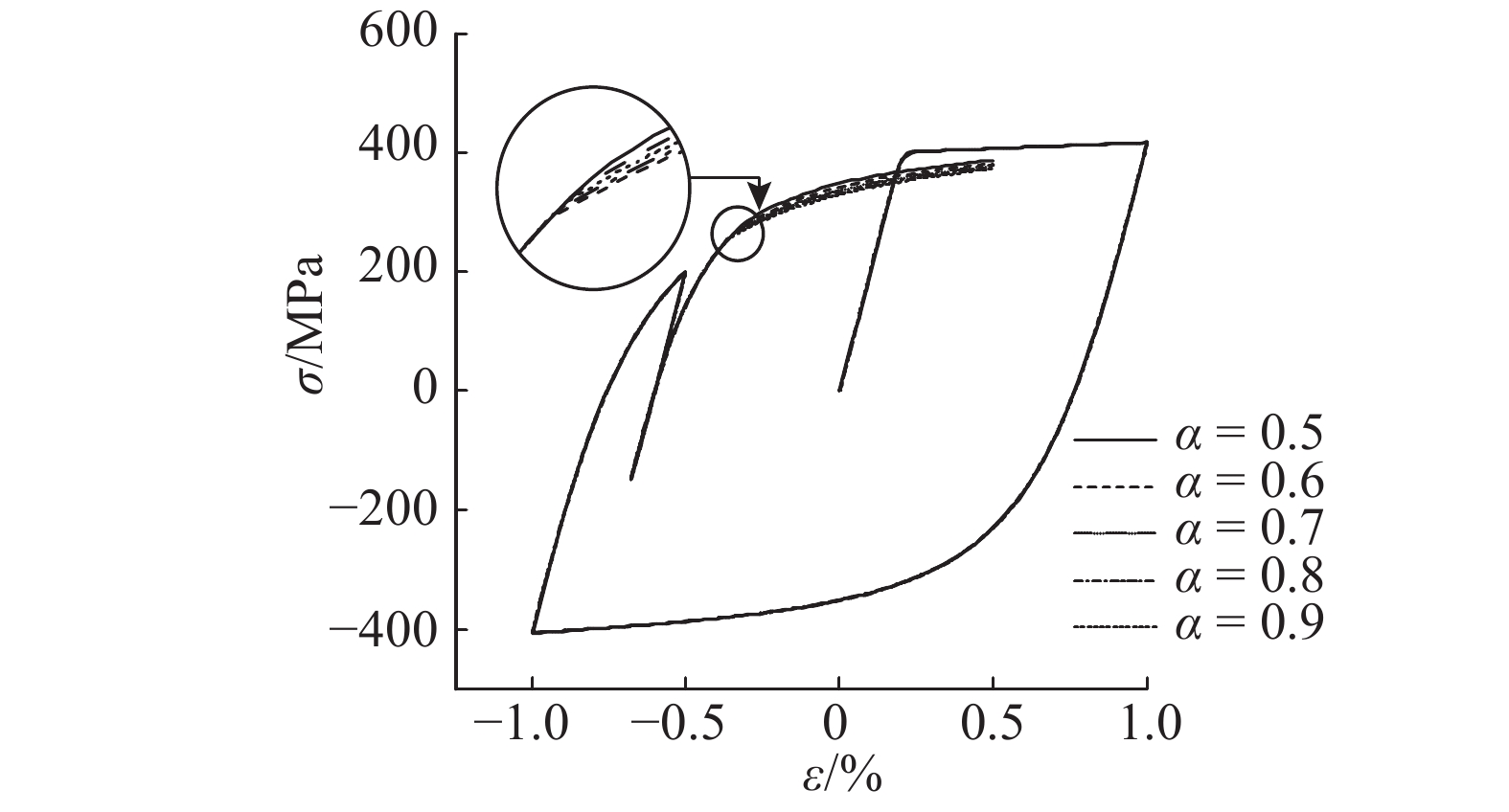
参数α表示弹性域占上、下屈服渐近线间距离的比例. 为了比较不同α对应力-应变曲线的影响,设计钢筋应变履历0→1.0%→–1.0%→–0.5%→–0.68%→0.5%,分别取α为0.5、0.6、0.7、0.8、0.9进行计算(β取值为2,钢筋参数取表1). 如图9所示为结果曲线. 当α=0.9时,计算可得n=1,该循环为第1种情况下的小幅循环,其余曲线的n为1.0~2.0,发生第2种情况下的小幅循环. 计算结果表明,随着α的增大,应力逐渐增大,但对应力计算结果的影响较小. 根据经验,可以取α为0.8.
|
图 9 参数α对应力计算结果的影响 Fig. 9 Influence of parameter α on stress calculation results |
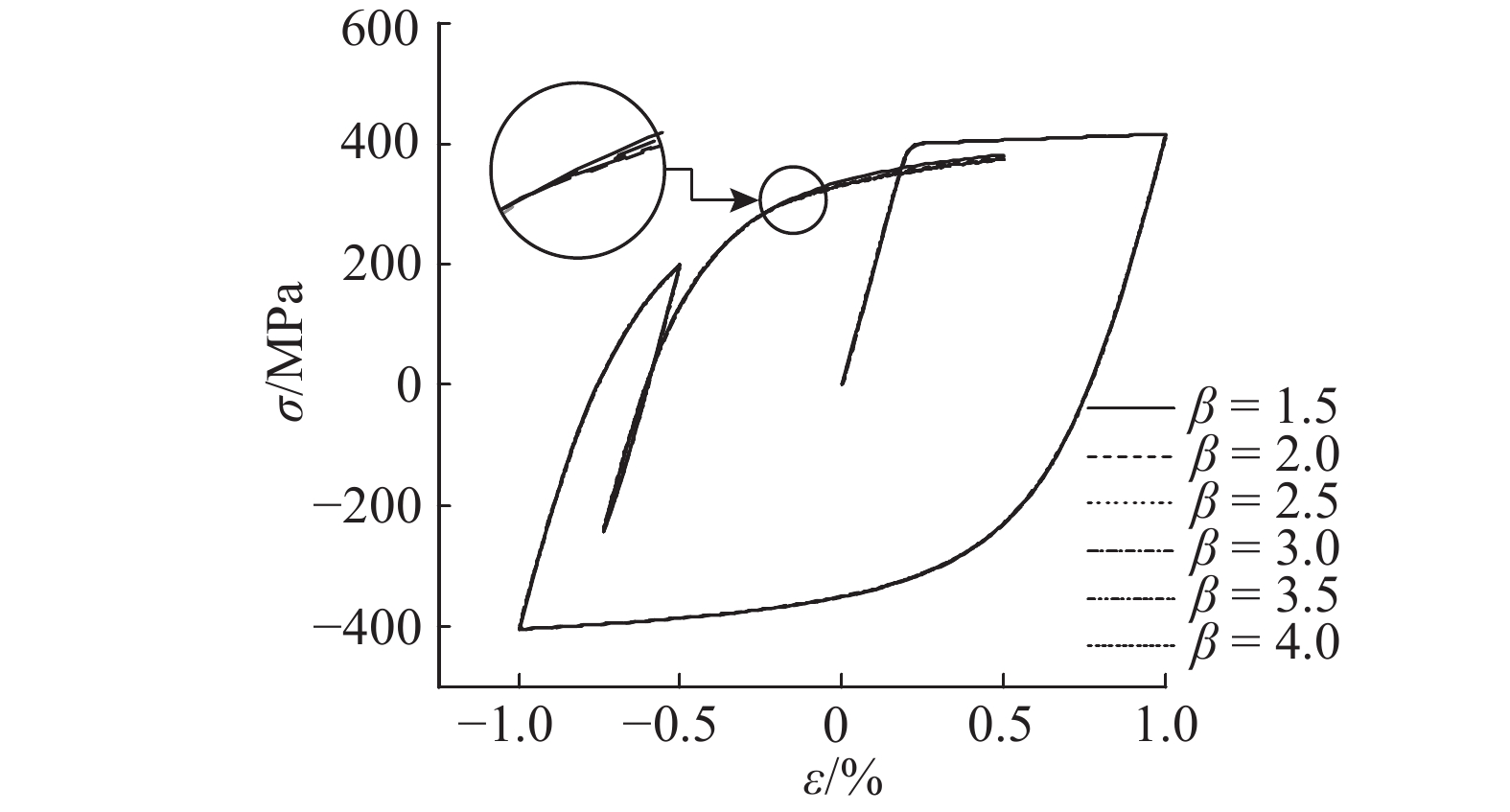
参数β用于控制过渡区域的大小,即控制图3(a)中履历曲线在a与a'之间过渡. 为了比较不同β对应力-应变曲线的影响,设计钢筋应变履历0→1.0%→–1.0%→–0.5%→–0.74%→0.5%,分别取β为1.5、2.0、2.5、3.0、3.5、4.0进行计算(α取值为0.8,钢筋参数取表1),结果如图10所示. 除了取n=1.5,β=1.5的曲线发生非小幅循环外,其余曲线均发生第2种情况下的小幅循环. 结果表明,随着β的增大,应力逐渐减小;在β超过2.0后趋于稳定,对结果的影响较小. 因此,取β为2.0.
|
图 10 参数β对应力计算结果的影响 Fig. 10 Influence of parameter β on stress calculation results |
修正MP模型在钢筋层面的验证主要分为以下2个方面:1)与试验结果进行对比;2)验算各种含小幅循环履历下的钢筋滞回曲线是否合理.
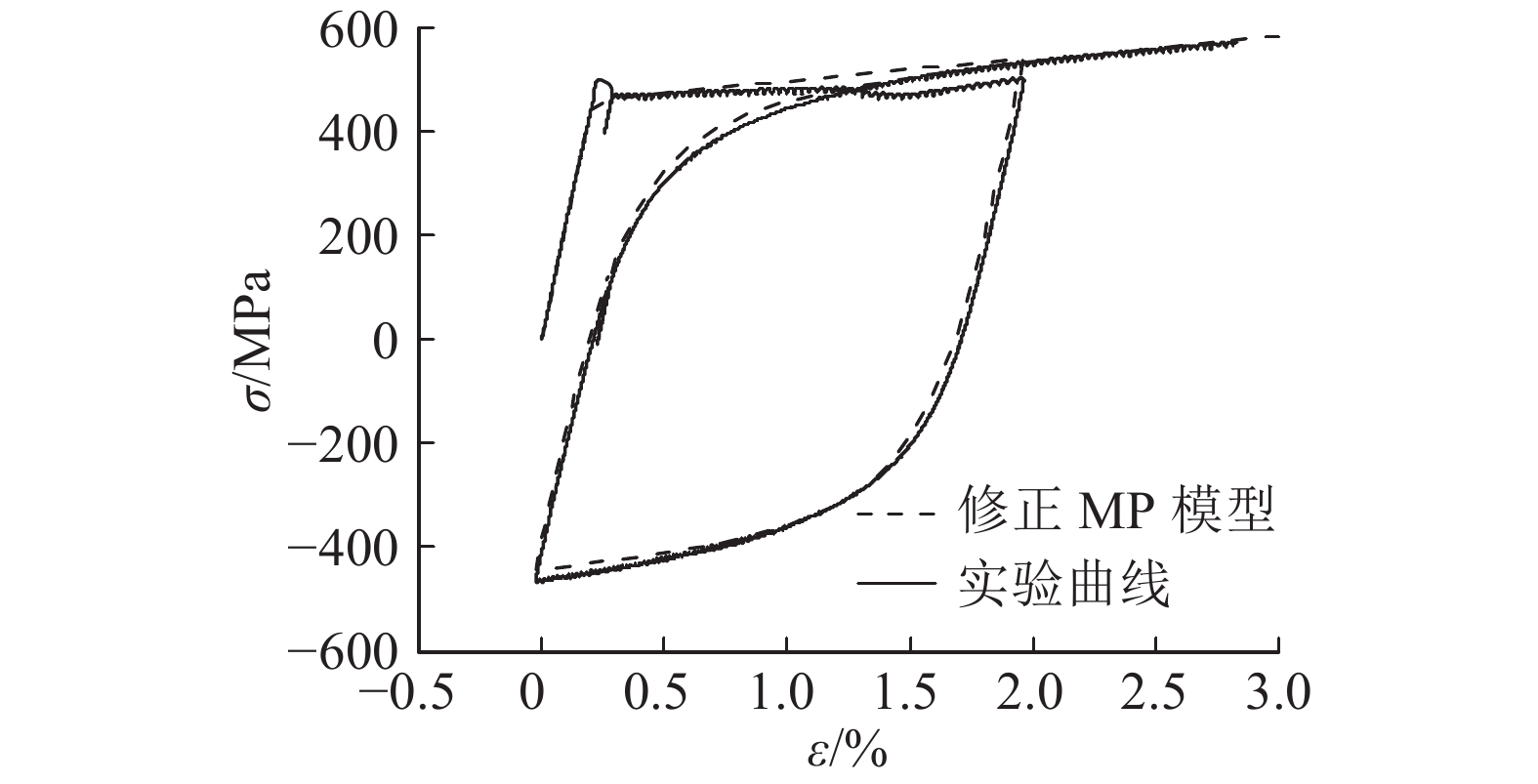
为了与试验结果进行对比,以图4的钢筋反复荷载实验结果为例进行模拟,比较结果如图11所示. 可见,修正MP模型可以改进原MP在小幅循环后出现的不合理应力履历,履历结果符合实际情况.
|
图 11 修正MP模型与试验结果对比 Fig. 11 Comparison of test curve and modified MP model |
为了验算各种含小幅循环履历下的钢筋滞回曲线,计算以下4种不同加载路径的钢筋应力-应变曲线(材料参数取表1),与原模型的计算结果进行对比.
1)应变路径为0→0.4%→–0.4%→1.5%→0.1%→0.5%→0.46%→1.6%(例1).
2)应变路径为0→0.4%→–0.4%→1.5%→0.1%→0.5%→0.3%→1.6%(例2).
3)与图7相同的应变履历(例3).
4)与图3(b)相同的应变履历(例4).
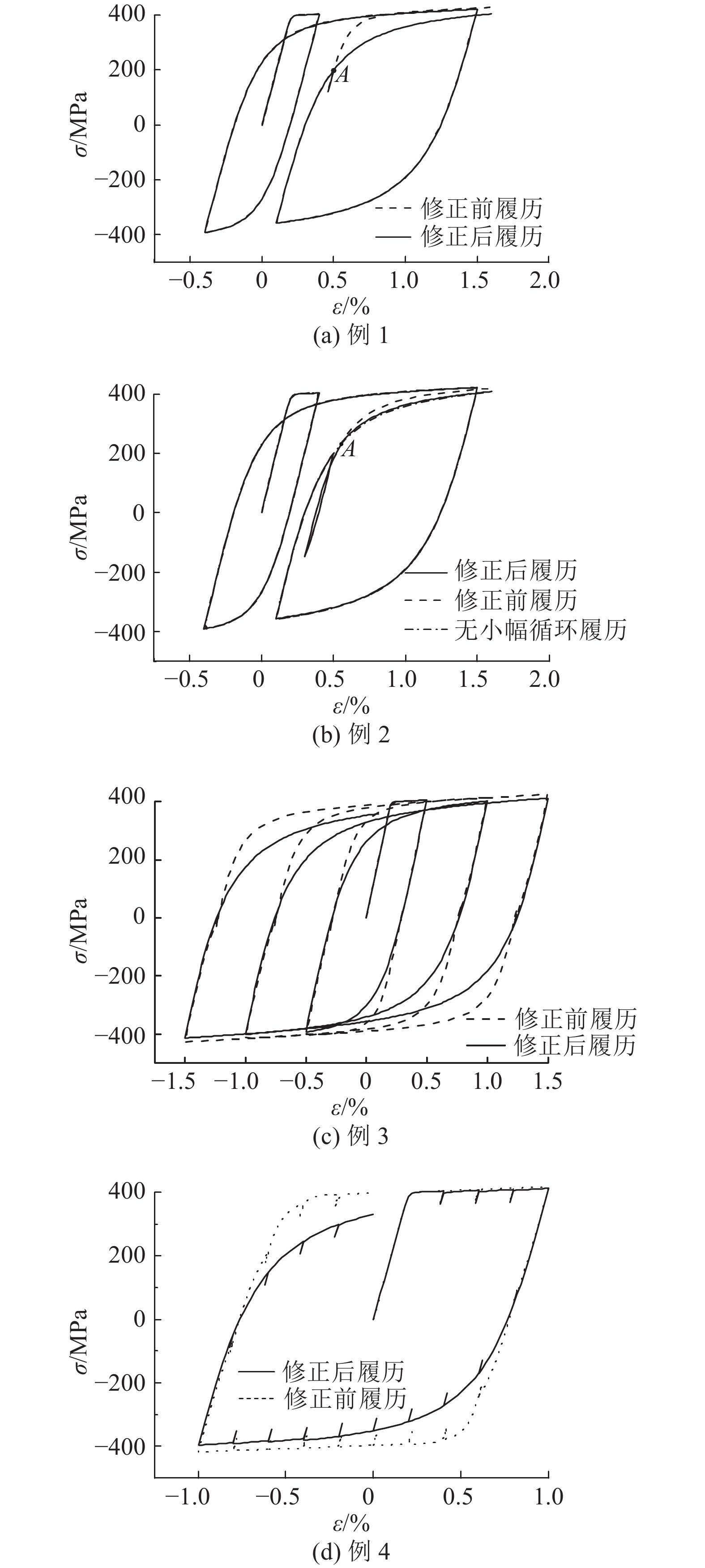
如图12所示为4种路径的计算结果对比. 修改后的MP模型经单次(A点)或多次小幅循环后,计算结果均符合预期的轨迹,修正后的履历曲线(图12的实线)正常反映Bauschinger效应.
|
图 12 修正MP模型和原MP模型经单次或多次小幅循环后的应力-应变路径对比 Fig. 12 Comparison of stress-strain path for modified MP model and former model after single or multiple small strain vibration |
基于上述修正的MP模型和Mander混凝土本构模型,开发钢筋混凝土空间纤维梁单元弹塑性分析程序. 为了验证修正MP模型的适用性,以图13所示的2011年清华大学完成的RC柱拟静力试验结果[14-16]为例进行分析.
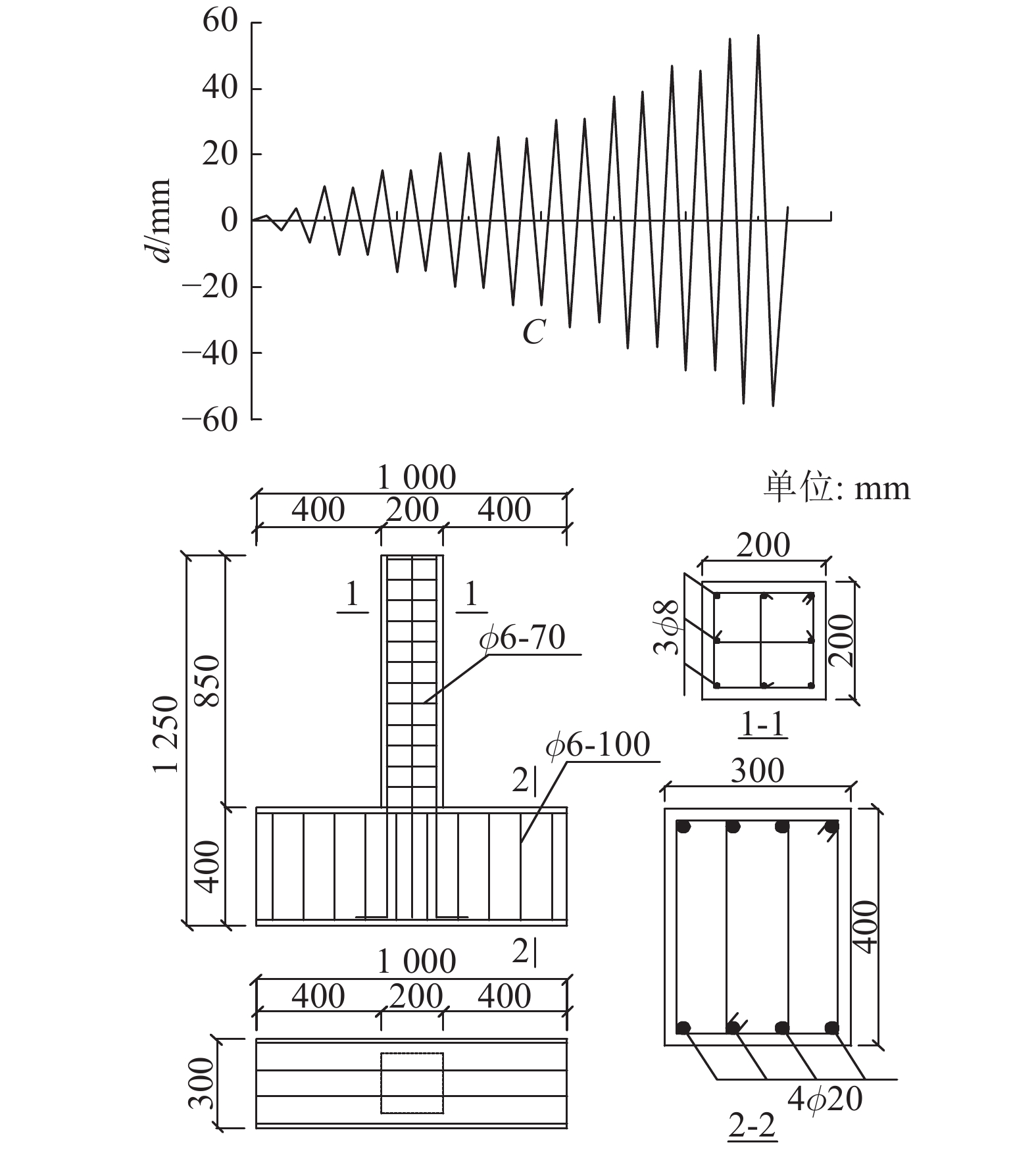
试验柱的柱长850 mm,柱截面尺寸为200 mm×200 mm. 混凝土强度等级为C30,纵筋HRB335,箍筋HPB235;150 mm混凝土立方体抗压强度fcu=30.1 MPa,钢筋材料参数见表2. 表中,D为直径,σu为极限强度,△为伸长率. 试验装置见文献[16],试件底部与混凝土基础整浇,轴压力通过柱顶千斤顶施加,大小为141 kN,往复水平力加载点至柱底距离为750 mm. 加载制度与配筋如图13所示. 图中,d为柱顶水平位移,C为循环周次.
| 表 2 试验钢筋材料参数表 Table 2 Material parameter of reinforcing steel |
|
图 13 节点设计及加载方式 Fig. 13 Description of joint and loading protocol |
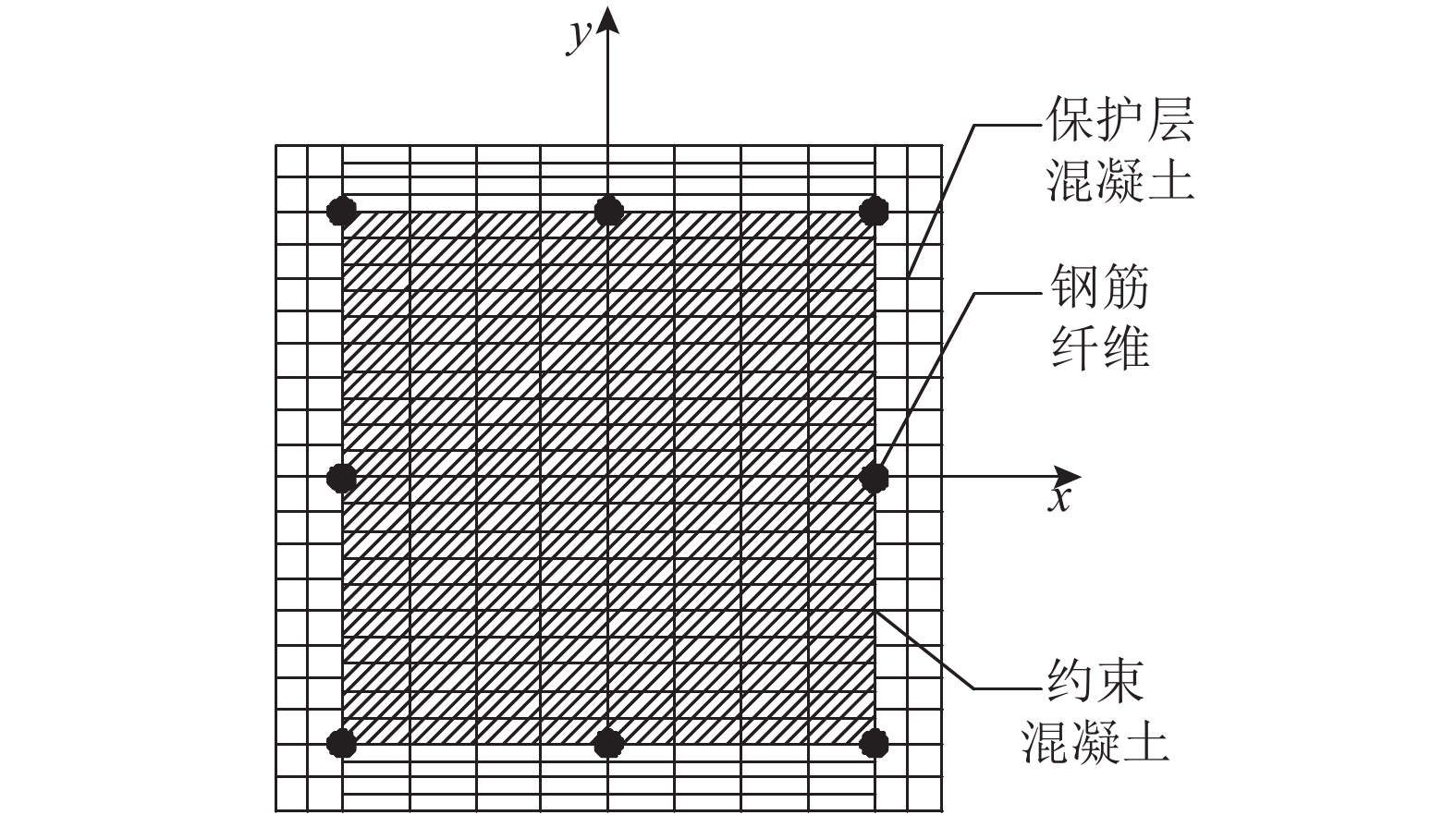
柱采用弹塑性纤维梁单元. 全柱分为5个单元,每个单元设6个Gauss积分点. 混凝土截面分为保护层混凝土和核心区约束混凝土,保护层厚度取20 mm. 如图14所示为截面纤维划分情况,共312根纤维.
|
图 14 柱截面纤维划分 Fig. 14 Fiber division of pier in transverse section |
采用Mander模型[3,17-18]作为混凝土本构模型,材料参数如表3所示[17]. 表中,fc'、εc'为混凝土的抗压强度和极限压应变,ft、εt为混凝土的抗拉强度和极限拉应变,Ec为混凝土的初始弹性模量.
| 表 3 Mander模型控制参数表 Table 3 Controling parameter of Mander model |
MP模型中的材料参数R0、cR1、cR2如表1所示,b取0.6%.
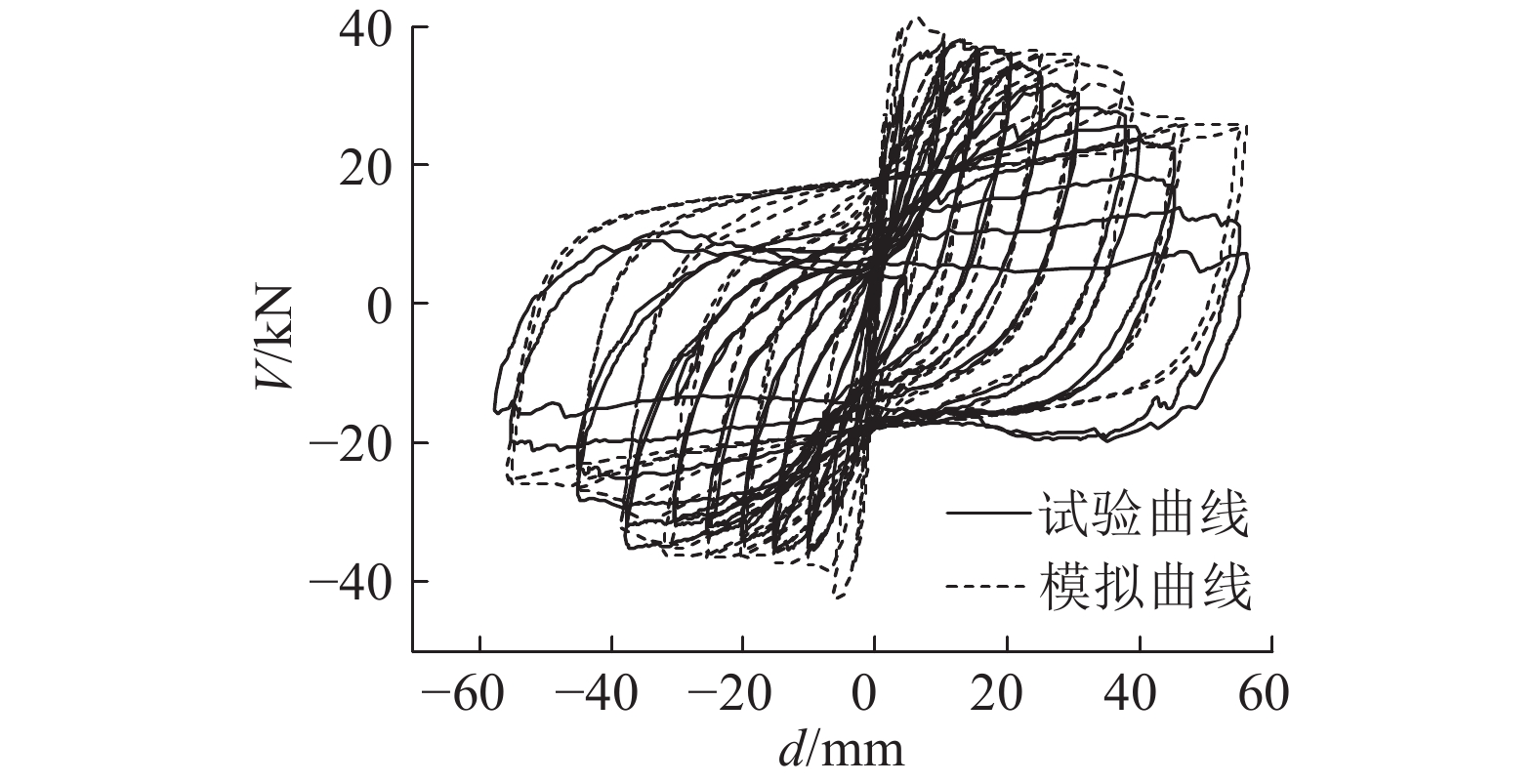
如图15所示为试验结果与本文模拟结果的对比. 图中,V为柱底剪力,计算时不考虑混凝土与钢筋间的黏结滑移现象以及P-
1)模拟曲线和试验曲线形状接近,能够模拟出水平承载力的退化,表明计算结果可以较准确地模拟钢筋混凝土结构的弹塑性力学行为.
2)当水平位移较大时,由于本构模型没有考虑保护层混凝土剥落后钢筋屈曲的影响,高估了构件的承载力.
3)与试验结果相比,模拟曲线的捏拢效应不明显. 原因是计算时没有考虑混凝土与钢筋间的黏结滑移现象.
|
图 15 本文模拟结果与试验结果的对比 Fig. 15 Comparison of load-displacement curves from numerical and experimental results |
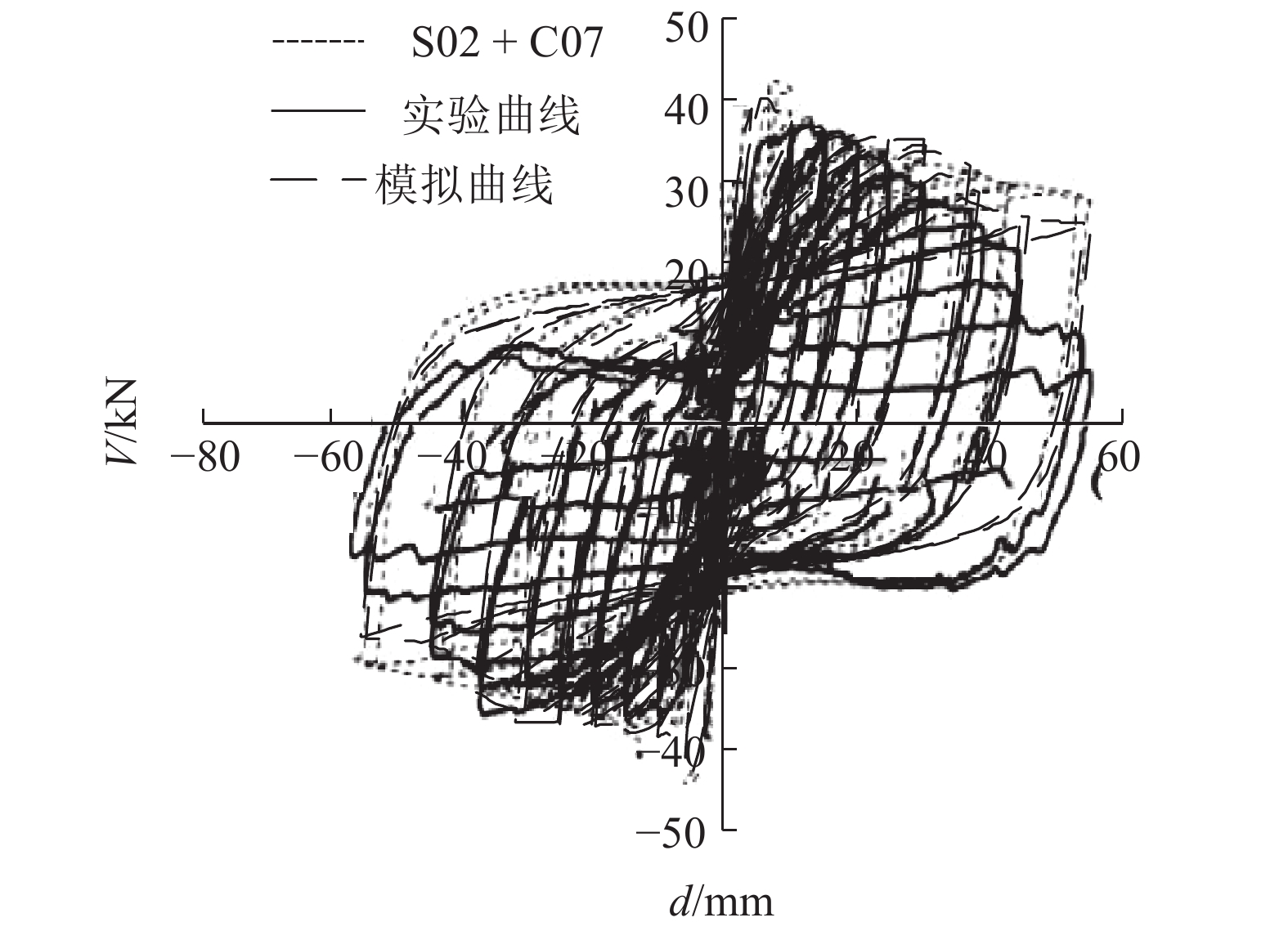
图16中,细虚线为Opensees对相同试验结果的模拟曲线,计算采用MP模型和Mander模型[19]. 可知,本文的计算精度略优于Opensees.
|
图 16 本文模拟结果与Opensees模拟结果的比较 Fig. 16 Comparison with simulated results of Opensees |
以3.2节所用的构件为对象,根据图17所示含小幅循环的加载制度进行计算,分析修正模型对构件力学滞回性能的影响.

|
图 17 含小幅循环的加载制度 Fig. 17 Loading protocol with small strain vibration |
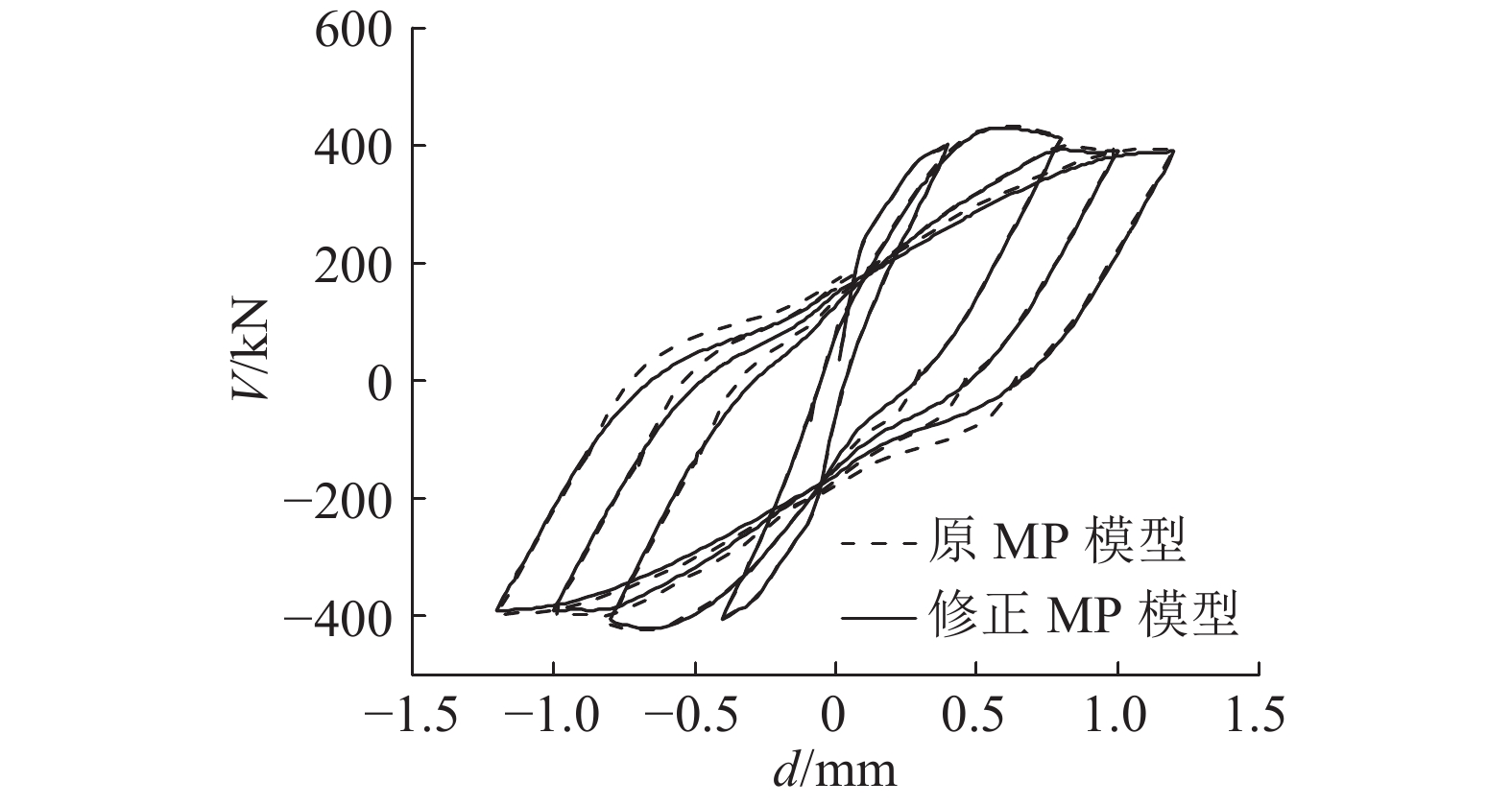
如图18所示为2种MP模型的荷载-位移曲线对比. 总体来看,MP模型修正对结构的荷载-位移履历影响不显著,但原MP模型发生小幅循环后,模拟曲线有一定的突变,承载力和耗能均略有增加,累计耗能增大了6.25%.
|
图 18 含小幅循环加载制度下的荷载-位移曲线 Fig. 18 Load-displacement curve under specific displacement |
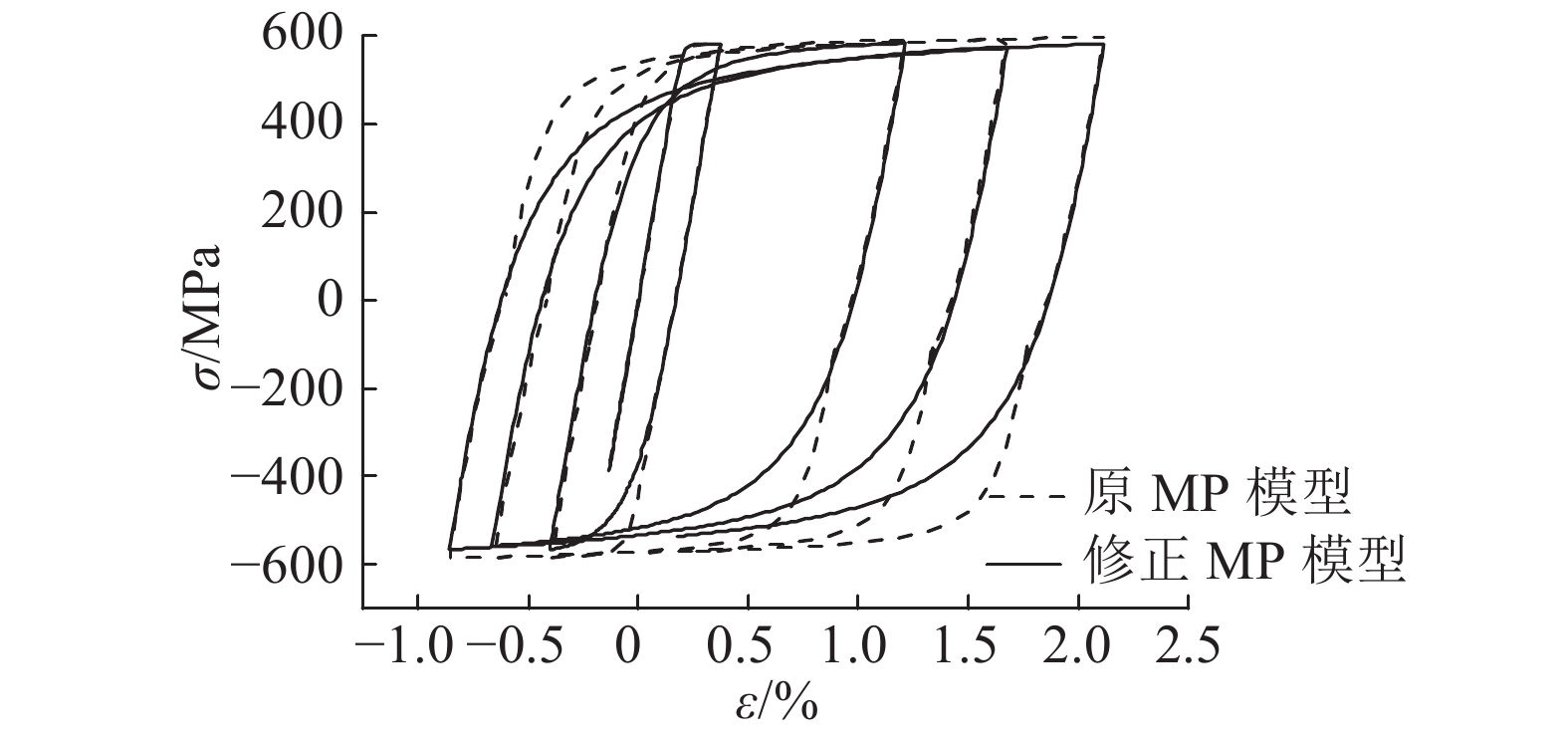
如图19所示为截面中位于外侧第一排纵筋的应力-应变曲线. 当出现小幅循环时,原MP模型的应力履历偏大,导致耗能增加;修正MP模型的应力-应变曲线保持较合理的路径,与实际情况接近.
|
图 19 含小幅循环加载制度下的钢筋应力-应变曲线 Fig. 19 Stress-strain curve of reinforcing steel under specific displacement |
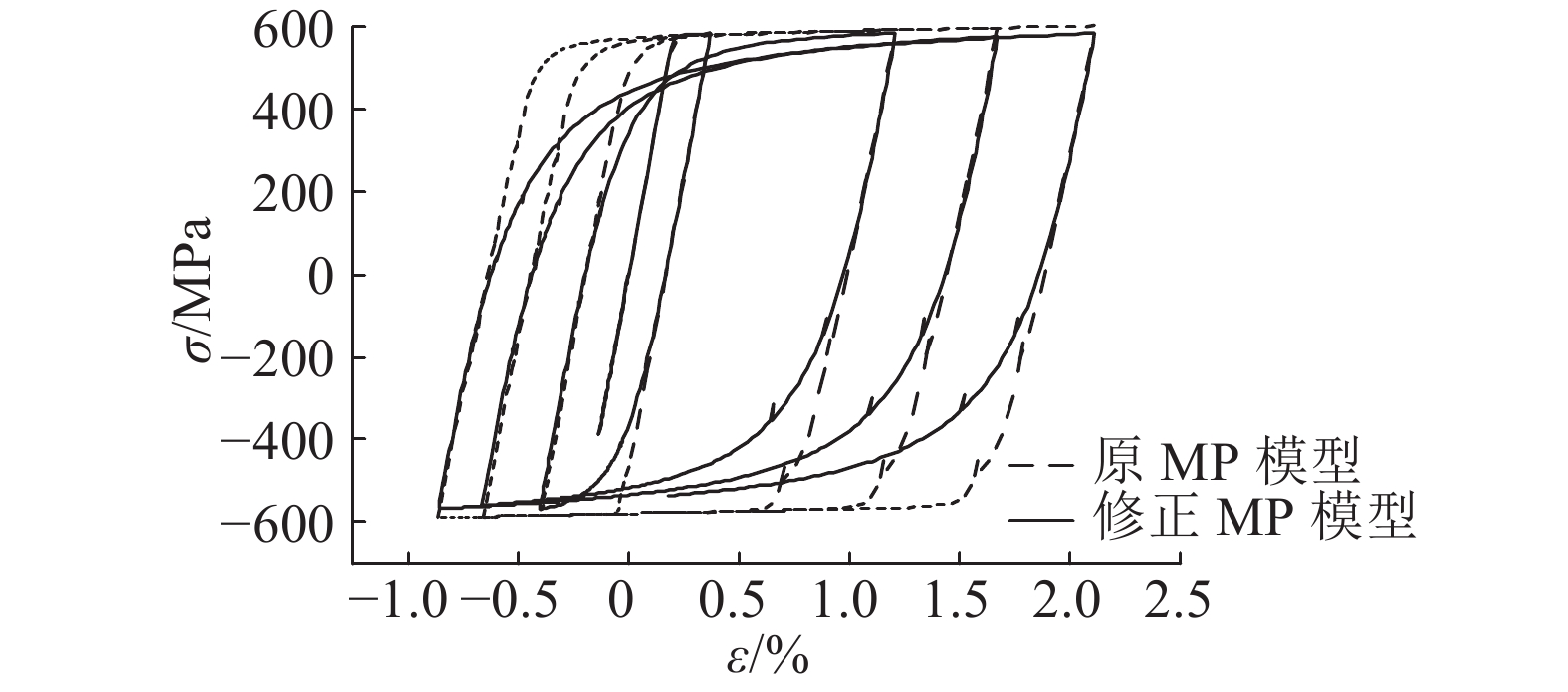
为了分析小幅循环次数对构件耗能及钢筋应力-应变履历曲线的影响,增加图17加载制度中每个荷载周期中小幅循环的次数,利用2种MP模型计算所得的构件耗能结果相差9.6%,原MP模型计算所得的钢筋履历不再反映Bauschinger效应. 钢筋的应力-应变履历如图20所示.
|
图 20 含多次小幅循环加载制度下的钢筋应力-应变曲线 Fig. 20 Stress-strain curve of reinforcing steel under specific displacement |
若将柱的配筋率提高至0.5%,则按图17所示的加载制度计算可知,2种MP模型得到的耗能结果相差7.78%.
上述结果表明,虽然MP模型的修正对构件承载能力和变形性能的影响不显著,但是对钢筋的应力-应变履历有较大的影响,对构件耗能计算结果也有一定的影响. MP模型的修正有益于改进地震作用下钢筋履历的计算结果,合理评价钢筋超低周疲劳强度.
4 结 论(1)既有研究对MP模型的修正没有根本解决小幅循环时应力-应变路径不合理的问题.
(2)用弹性域半径定义小幅循环,提出新的小幅循环判断及修正方法;通过含小幅循环的钢筋应力-应变曲线与试验结果对比等方法,验证了修正方法的有效性.
(3)基于修正的MP模型和Mander混凝土模型,开发RC空间纤维梁单元弹塑性分析程序,验证了利用修正MP模型可以合理地模拟构件中的钢筋应力-应变履历.
(4)修正MP模型对构件承载能力计算结果的影响较小,但对构件的耗能结果有一定的影响.
| [1] |
MENEGOTTO M. Method of analysis for cyclically loaded R. C. plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending [C] // Proceedings of IABSE Symposium on Resistance and Ultimate Deformability of Structures. Lisbon: [s. n.], 1973: 15–22.
|
| [2] |
MONTI G, NUTI C. Nonlinear cyclic behavior of reinforcing bars including buckling[J]. Journal of Structural Engineering, 1992, 118(12): 3268-3284. DOI:10.1061/(ASCE)0733-9445(1992)118:12(3268) |
| [3] |
CHANG G A, MANDER J B. Seismic energy based fatigue damage analysis of bridge columns: part I - evaluation of seismic capacity. technical report [R]. Buffalo: National Center for Earthquake Engineering Research, 1994, nceer-94-0006.
|
| [4] |
KUNNATH S K, HEO Y A, MOHLE J F. Nonlinear uniaxial material model for reinforcing steel bars[J]. Journal of Structural Engineering, 2009, 135(4): 335-343. DOI:10.1061/(ASCE)0733-9445(2009)135:4(335) |
| [5] |
RESTREPOPOSADA J I, DODD L L. Model for predicting cyclic behavior of reinforcing steel[J]. Journal of Structural Engineering, 1995, 121(3): 433-445. DOI:10.1061/(ASCE)0733-9445(1995)121:3(433) |
| [6] |
DHAKAL R P, MAEKAWA K. Path-dependent cyclic stress-strain relationship of reinforcing bar including buckling[J]. Engineering Structures, 2002, 24(11): 1383-1396. DOI:10.1016/S0141-0296(02)00080-9 |
| [7] |
HOEHLER M S, STANTON J F. Simple phenomenological model for reinforcing steel under arbitrary load[J]. Journal of Structural Engineering, 2006, 132(7): 1061-1069. DOI:10.1061/(ASCE)0733-9445(2006)132:7(1061) |
| [8] |
CIAMPI V, ELIGEHAUSEN R, BERTERO V, et al. Analytical model for concrete anchorages of reinforcing bars under generalized excitations, Report No. UCB/EERC-82/23 [R]. Berkeley: Earthquake Engineering Research Center, University of California at Berkeley, 1982.
|
| [9] |
FILIPPOU E, POPOV E, BERTERO V. Effects of bond deterioration on hysteretic behavior of reinforced concrete joints, Report No. UCB/EERC-83/19 [R]. Berkeley: Earthquake Engineering Research Center, University of California at Berkeley, 1983.
|
| [10] |
SAKAI J, KAWASHIMA K. Modification of the giuffre, menegotto and pinto model for unloading and reloading paths with small strain variations[J]. Doboku Gakkai Ronbunshu, 2003, 738(738): 159-169. |
| [11] |
GB 50010-2010, 混凝土结构设计规范[S]. 北京: 中华人民共和国住房与城乡建设部, 2010.
|
| [12] |
KOLOZVARI K, TRAN T A, ORAKCAL K, et al. Modeling of cyclic shear-flexure interaction in reinforced concrete structural walls. I: theory[J]. Journal of Structural Engineering, 2015, 141(5): 04014136. DOI:10.1061/(ASCE)ST.1943-541X.0001083 |
| [13] |
王彤, 谢旭, 唐站站, 等. 考虑复杂应变历史的钢材修正双曲面滞回模型[J]. 浙江大学学报: 工学版, 2015, 49(7): 1305-1312. WANG Tong, XIE Xu, TANG Zhan-zhan, et al. Modified two-surface steel hysteretic model considering complex strain history[J]. Journal of Zhejiang University: Engineering Science, 2015, 49(7): 1305-1312. |
| [14] |
陆新征, 叶列平, 潘鹏, 等. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛I: 框架试验[J]. 建筑结构, 2012, 42(11): 19-22. LU Xin-zheng, YE Lie-ping, PAN Peng, et al. Pseudo-static collapse experiments and numerical prediction competition of RC frame structure I: RC frame experiment[J]. Building Structure, 2012, 42(11): 19-22. |
| [15] |
陆新征, 叶列平, 潘鹏, 等. 钢筋混凝土框架结构拟静力倒塌试验研究及数值模拟竞赛II: 关键构件试验[J]. 建筑结构, 2012, 42(11): 23-26. LU Xin-zheng, YE Lie-ping, PAN Peng, et al. Pseudo-static collapse experiments and numerical prediction competition of RC frame structure II: key elements experiment[J]. Building Structure, 2012, 42(11): 23-26. |
| [16] |
中国建筑学会抗震防灾分会建筑结构抗倒塌专业委员会. 钢筋混凝土框架柱拟静力试验竞赛结果[EB/OL]. 2011-08-01[2017-08-01]. http://www.collapse-prevention.net/show.asp?ID=11&adID=2.
|
| [17] |
MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804-1826. DOI:10.1061/(ASCE)0733-9445(1988)114:8(1804) |
| [18] |
WAN T T. Uniaxial compressional stress-strain relation of concrete[J]. Journal of Structural Engineering, 1988, 114(9): 2133-2136. DOI:10.1061/(ASCE)0733-9445(1988)114:9(2133) |
| [19] |
卜海峰, 胡思康, 张耀庭, 等. 基于OpenSees的RC柱拟静力数值分析模型[J]. 土木工程与管理学报, 2016, 33(5): 21-27. BU Hai-feng, HU Si-kang, ZAHNG Yao-ting, et al. Numerical analysis model for pseudo-static RC columns based on OpenSees[J]. Journal of Civil Engineering and Management, 2016, 33(5): 21-27. DOI:10.3969/j.issn.2095-0985.2016.05.004 |



