海工结构中因为钢筋锈蚀，导致混凝土结构耐久性退化日益严重，故不锈钢筋逐渐成为一些重要工程的可靠选择. 不锈钢筋与碳素钢筋相比，轧制时掺入了许多合金元素，这些元素使得钢筋能够有效抵挡有害离子的侵蚀. 对于海洋环境或是除冰盐环境下的混凝土结构，不锈钢的使用能够大大减少由钢筋锈蚀带来的结构安全问题，增大结构的使用年限.

目前，国内外有一些海港及桥梁工程采用不锈钢筋，如最早把不锈钢运用到钢筋混凝土结构的墨西哥Yucatan Progresso海港工程，至今仍在安全服役，没有因钢筋锈蚀问题进行大的检修^[1]. 混凝土结构中最常用的不锈钢种类是奥氏体304、316和双相型2205不锈钢^[2-3]. 我国目前有两座已建成使用的大桥运用了不锈钢筋，分别是连接香港鳌磡石和深圳西部的通道大桥和香港的昂船洲大桥，两座大桥均可以保证使用120年而无需进行大的维护^[4]，即将建成通车的港珠澳大桥部分结构采用了不锈钢筋. 已有一些工程运用了不锈钢筋，但是目前对于不锈钢筋力学性能、不锈钢筋混凝土的工作机理研究不是很充分；已有不锈钢的研究多集中于耐蚀性能或者工字钢、槽钢等不同截面的不锈钢结构的力学性能、高温度下的耐受性等，包括欧、美、日已出的关于不锈钢的设计规范，都没有提到不锈钢作为钢筋作用于混凝土结构的适用性^[5]. 由于不锈钢材料与普通碳素钢材料在力学性能上存在一定的差异，比如应力-应变曲线的线性段特别短，初始弹性模量较小，没有屈服平台等^[6-8]，有必要开展针对性试验研究，验证其应用于混凝土结构的可行性或修正现有的结构设计规范. 本文采用具有更好耐蚀性能的新型双相型不锈钢筋作为受力主筋. 为了探讨其应用于混凝土结构的适用性，开展不锈钢筋混凝土柱的小偏心抗压试验研究，讨论不锈钢钢筋的适用本构模型，建立该类偏心受压构件正截面承载能力的计算方法.

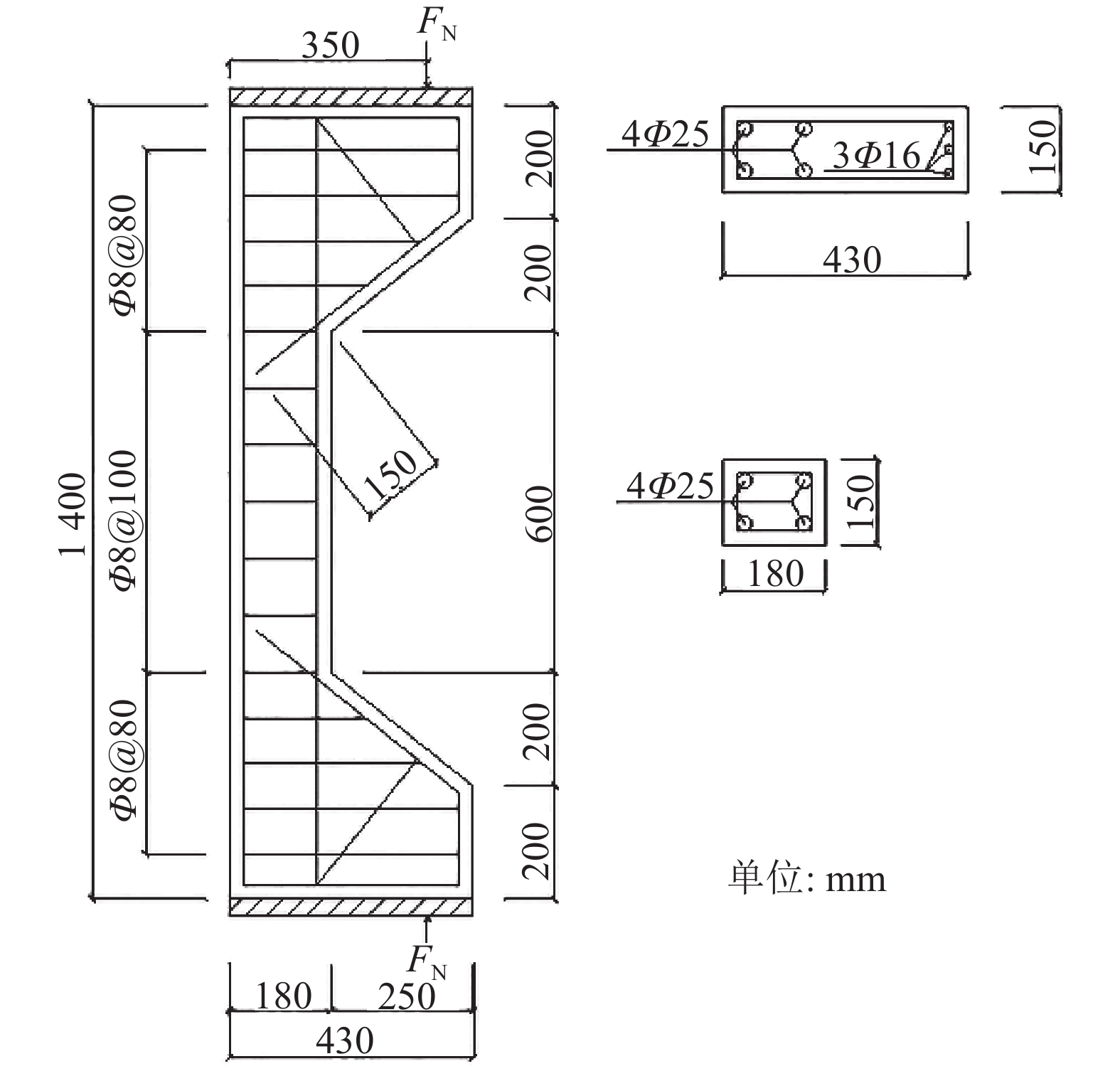
该试验采用偏心受压构件作为带牛腿的不锈钢筋混凝土柱，试件截面尺寸为150 mm×180 mm，高度为1 400 mm. 试验柱纵向钢筋采用新型2205不锈钢筋，对称配筋为4Φ25 mm，箍筋采用Φ8@100 mm，保护层厚度为20 mm. 沿牛腿顶部配置纵向受力筋3Φ16 mm，并沿牛腿外边缘向下伸入下柱内150 mm后截断，牛腿处箍筋加密Φ8@80 mm. 具体尺寸及配筋如图1所示. 混凝土保护层厚度取20 mm，设计的受压偏心距为260 mm.

图 1

图 1 不锈钢筋小偏心柱尺寸及配筋 Fig. 1 Size and reinforcement distribution of stainless steel reinforced concrete column with small eccentricity

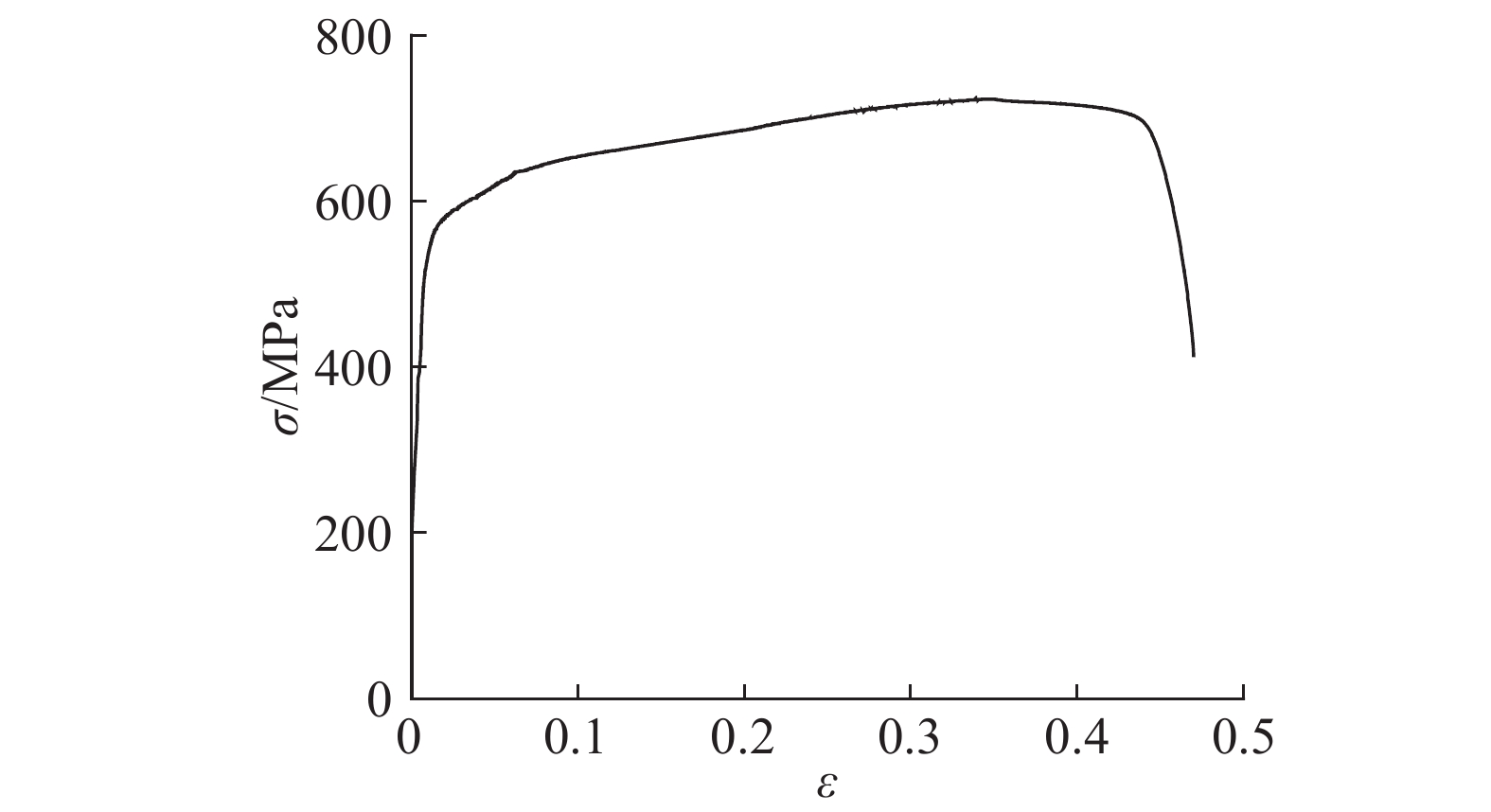
试验选用的2205双相型不锈钢是在原有的2205不锈钢基础上调整元素含量而特制的新型耐蚀2205双相不锈钢（简称新2205）. 根据钢筋拉伸试验，可得该种不锈钢筋的应力应变曲线，如图2所示. 可以看出，该不锈钢没有明显的屈服平台，名义屈服强度σ_0.2=511 MPa，极限抗拉强度σ_u=714 MPa，名义屈服强度对应的应变ε_0.2=0.005 4，弹性模量E_s=151 GPa，延性明显高于普通碳素钢.

图 2

图 2 新2205不锈钢σ-ε曲线 Fig. 2 σ-ε curves of new 2205 stainless steel

该次试验荷载由100 t液压千斤顶提供，加载点处采用单刀铰支座放置在反力架上. 为了防止加载点处因应力集中而发生局部破坏，在支座和柱子之间增加一块30 mm厚的钢板，扩散应力. 在柱子中部布置3个百分表，2个支座处各布置1个百分表. 混凝土侧面布置5个应变片，受拉区和受压区各布置1个应变片，用来测量截面应变. 百分表数据及应变数据采用DH3816N静态应变测试系统自动采集. 试验装置及测点布置见图3.

图 3

图 3 实验装置及测点布置图 Fig. 3 Experiment device and layout of measure-point

试验柱预加载后卸载，再缓慢连续加载直到柱子破坏，采用分级加载. 初期每级荷载约为5 kN，等到混凝土开裂后，每级荷载为10 kN，到达破坏荷载附近，每级荷载减至5 kN. 荷载稳定后，采集应变、位移、裂缝开展情况等数据.

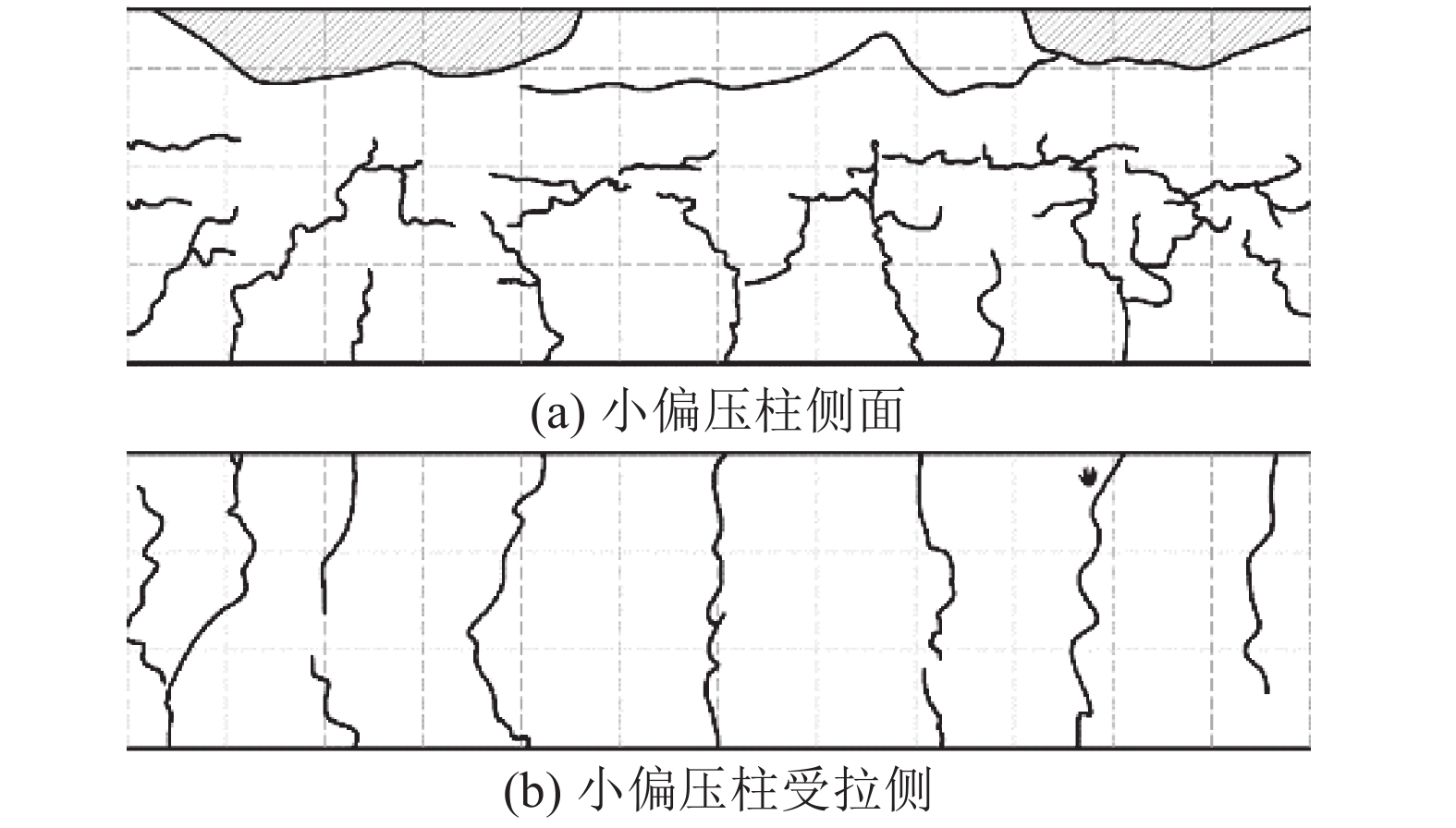
试件受拉区（远离加载点一侧）横向裂缝在加荷初期开始开展，裂缝最先出现在跨中部位，后随着荷载的增加，新裂缝出现位置逐渐向两侧发展，同时旧裂缝不断向受压区延伸，大约为0.6倍极限荷载，裂缝延伸到截面中上部，随后荷载继续增加，裂缝长度基本不再延伸，宽度逐渐增大. 当加载到0.80~0.90倍极限荷载时，横向裂缝宽度持续增加，并且集中在某一、两根主裂缝上；同时横向裂缝顶端开始纵向发展，新的纵向裂缝在中上部及受压区出现，构件开始发出“噼啪”的响声，构件整体弯曲变形明显. 在到达极限荷载后，受压区混凝土被压碎，无法继续承受荷载，受拉区钢筋未屈服，表现出小偏压柱偏心受压破坏模式，此时最大裂缝宽度为0.40~0.50 mm. 如图4所示为柱C-2非牛腿部分的裂缝开展与分布图，能够反映上述小偏压柱的破坏过程与破坏模式.

图 4

图 4 柱C-2裂缝分布图 Fig. 4 Crack distribution of column C-2

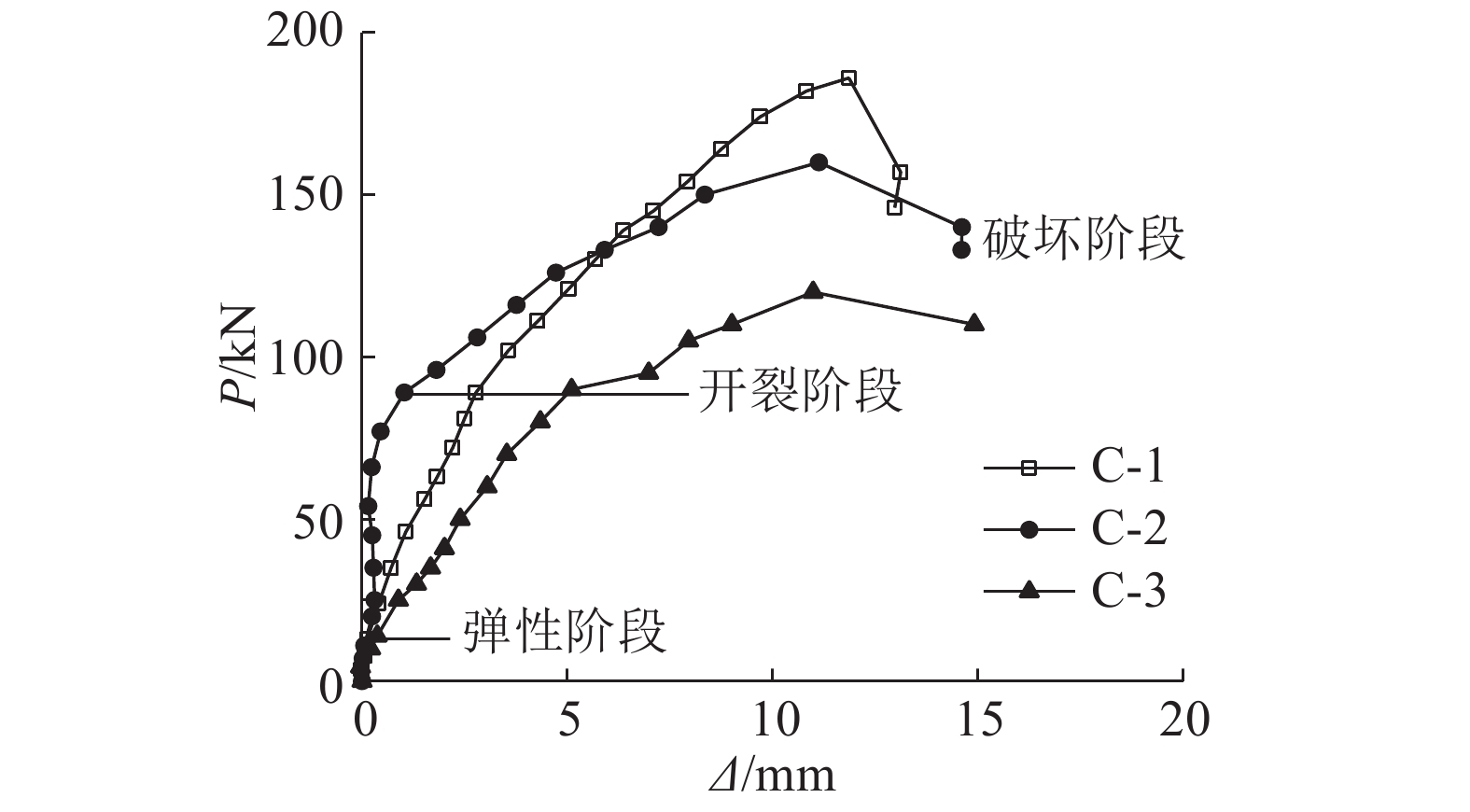
3根小偏心受压柱的荷载P-挠度Δ曲线如图5所示. 破坏过程可以大致分为以下3个阶段.

图 5

图 5 3根试验柱的荷载-挠度曲线 Fig. 5 Load-displacement curves of three columns

第1阶段：弹性阶段. 在加载初期，荷载较低，混凝土未开裂，钢筋应力较低，荷载挠度曲线基本呈直线.

第2阶段：开裂阶段. 在加载到开裂荷载后，偏压柱的跨中首先出现裂缝；随着荷载的增加，裂缝缓慢向上发展，但是宽度基本保持不变，由跨中向牛腿方向陆续出现裂缝. 此时混凝土柱受拉区混凝土退出工作，受拉部分逐渐转由钢筋独自承担，柱子截面刚度减小，故开裂后荷载-挠度曲线的斜率减小. 由于每根柱子的开裂情况不同，开裂后荷载挠度曲线的斜率变化不一.

第3阶段：破坏阶段. 由图5可以看出，当3根柱子加载到80 kN左右时，荷载继续增大，挠度的增加速度变快. 此时主裂缝已经产生，并且随荷载增加不断扩大. 图6中，ε为应变. 由图6可以看出，受拉区钢筋远没有达到名义屈服应变（大约为5.4×10^-3），但是构件在破坏前表现出较大的变形，原因在于不锈钢的弹性模量与普通碳素钢相比较小，这导致不锈钢在较小的荷载作用下呈现出较大的变形.

图 6

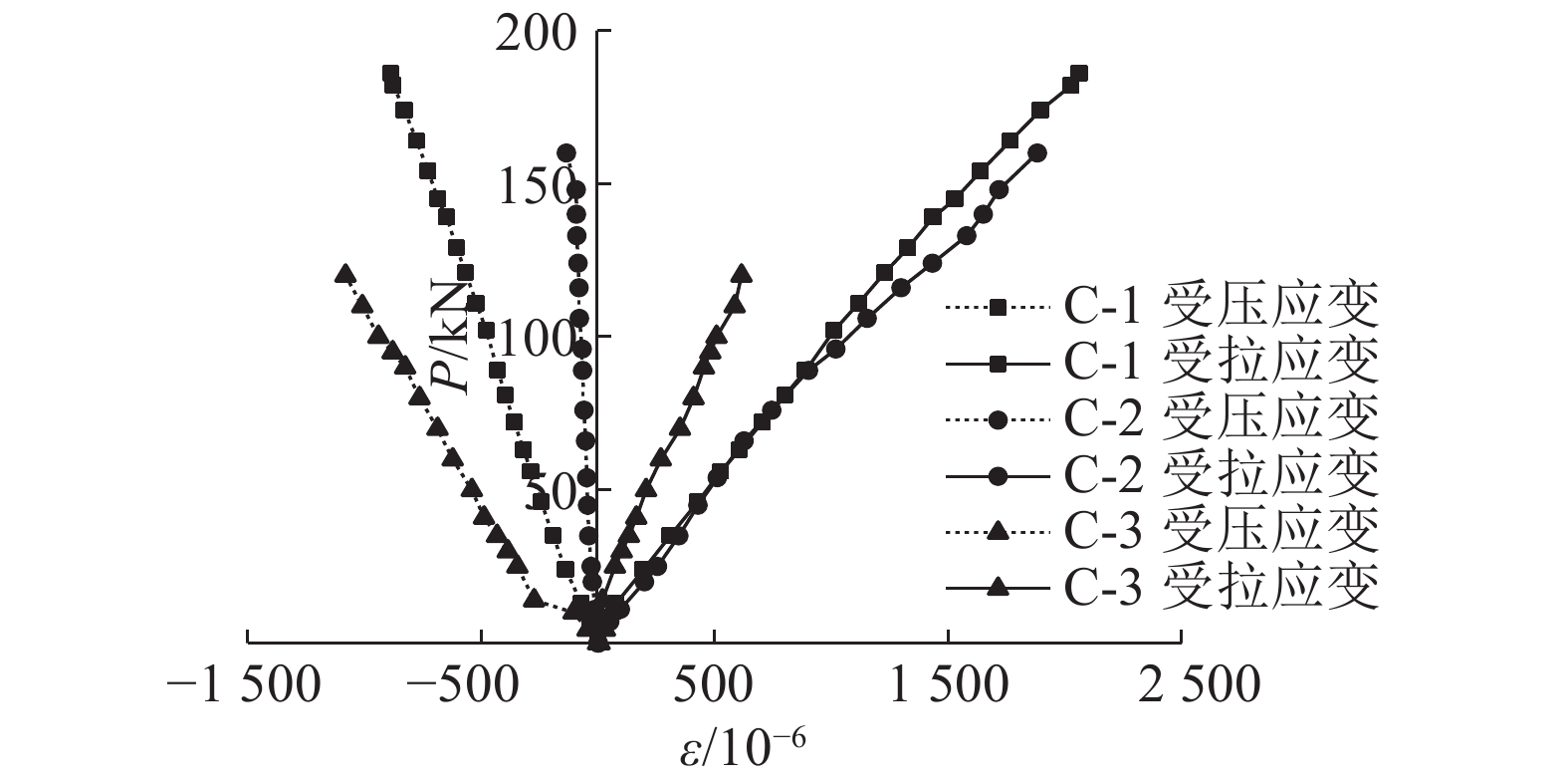
图 6 3根试验柱的荷载-应变曲线 Fig. 6 Load-strain curves of three columns

柱C-3前期的裂缝与挠度发展情况与其他2根柱子相同，到开裂阶段后期，主裂缝产生在牛腿处，斜向变截面处延伸，如图7所示，此时挠度有一个突然增大的过程，同时构件受压区钢筋和受拉区钢筋都处于较低的应力状态. 在裂缝扩展到一定宽度后，荷载无法继续增加，构件破坏. 主要原因是牛腿处纵向受力钢筋因为直径较粗，两端没有弯起，导致纵向受力钢筋与水平受力筋未能较好锚固，牛腿处钢筋笼整体性不足，因而后期混凝土被拉裂而无法继续加载. 牛腿完好的C-1和C-2柱子因为受压区混凝土被压碎而破坏，属于典型的小偏压破坏特征.

图 7

图 7 C-3柱牛腿处被拉裂 Fig. 7 Fracture in corbel of column C-3

李强等^[9-11]给出类似普通钢筋偏压柱受力性能的研究结果，其中普通钢筋小偏压柱极限相对挠度（侧向挠度/柱高）为0.08%~0.138%，用碳纤维加固后的小偏压柱极限相对挠度最高为0.6%，大偏压柱极限相对挠度为0.2%~0.33%. 该试验的不锈钢筋小偏压柱极限相对挠度最小为0.78%. 对比研究可以发现：虽然从配筋及破坏模式上来看，不锈钢筋试验柱属于小偏压柱，但是荷载-挠度曲线的发展阶段与大偏压柱类似，并且破坏前具有较大的变形，相对挠度可以达到普通钢筋大偏压柱的2倍以上，表现出良好的延性.

典型的不锈钢混凝土柱跨中截面在各级荷载下的应变沿高度h分布如图8所示. 可见，跨中截面应变基本呈直线分布，符合平截面假定，后续承载力计算可以在平截面假定的基础上进行分析.

图 8

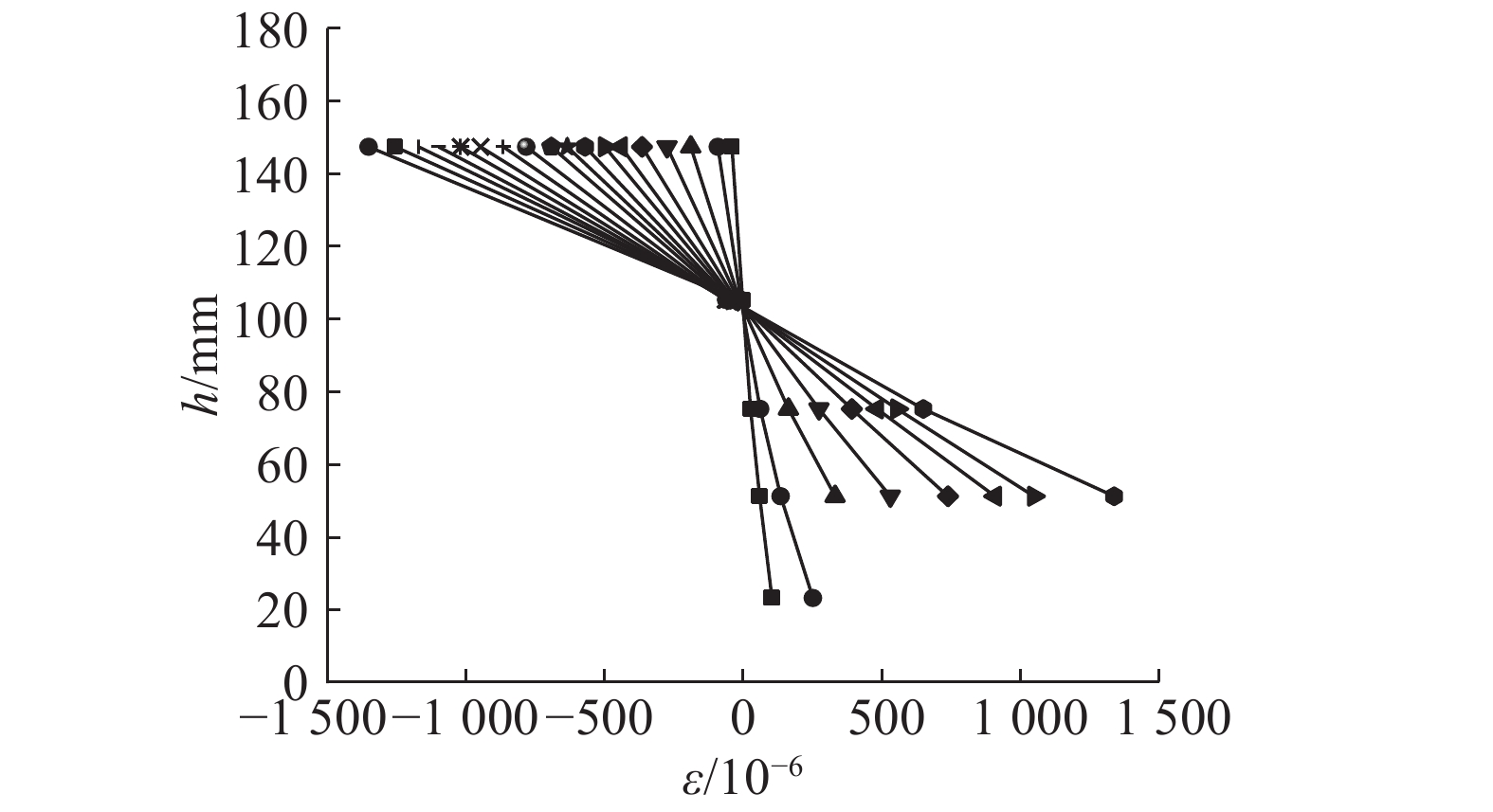
图 8 试验柱C-1跨中截面应变沿高度分布 Fig. 8 Strain distribution along height in mid-span section of column C-1

因为钢筋强度较高，为了与之匹配，该试验偏心柱选用C55混凝土，配比如表1所示. 实测标准养护28 d后的棱柱体抗压强度为34.41 MPa，相当于标号为C53的混凝土. 根据《混凝土结构设计规范GB50010-2010》^[12]可得，混凝土极限压应变ε_cu=0.003 27. 混凝土与不锈钢筋的力学性能如表2所示. 表中，f_ck为混凝土棱柱体抗压强度，ε_cu、ε_u分别为混凝土和钢筋的极限拉应变.

表 1

表 1 混凝土配合比 Table 1 Concrete composition of experiment ρ（水） ρ（水泥） ρ（砂） ρ（石子） ρ（减水剂） 220 611.6 486.4 1 033.5 4.5

表 1 混凝土配合比 Table 1 Concrete composition of experiment

表 2

表 2 混凝土与不锈钢筋材料的力学性能 Table 2 Mechanical properties of concrete and stainless steel rebar 混凝土 新2205不锈钢筋 fck εcu ε0.2 σ0.2 εu σu Es 34.41 MPa 0.003 27 0.005 4 511 MPa 0.284 728 MPa 151 GPa

表 2 混凝土与不锈钢筋材料的力学性能 Table 2 Mechanical properties of concrete and stainless steel rebar

不锈钢的本构选用双斜线模型和针对不锈钢进行优化过的Rasmussen模型^[13].

双斜线模型的数学表达式为

式中：E₀为初始弹性模量；ε_py为残余应变，ε_py=0.002；E_s1为曲线上名义屈服强度与极限强度两点间的斜率.

Rasmussen模型屈服前半段沿用Ramberg-Osgood的模型，对大于名义屈服强度的部分进行修正^[14]，数学表达式为

式中： $n = \ln 20/\ln \left(\displaystyle{{{\sigma _{0.2}}}}/{{{\sigma _{0.01}}}}\right)$ ，其中σ_0.01为残余应变等于0.01%时对应的应力；E_0.2为名义屈服强度点的切线斜率； $m = 1 + 3.5\displaystyle{{{\sigma _{0.2}}}}/{{{\sigma _{\rm u}}}}$ ； ${\varepsilon _{\rm u}} = 1 - \displaystyle{{{\sigma _{0.2}}}}/{{{\sigma _{\rm u}}}}$ .

取拉伸曲线特征值的平均值获得相关系数，代入式（1）、（2），可以获得该次试验钢筋材料的2个本构模型表达式如下.

双斜线模型：

Rasmussen模型：

本构模型对比如图9所示. 可以看出，在名义屈服点之前，2个模型和拉伸试验曲线吻合；在名义屈服点之后，Rasmussen模型与拉伸曲线吻合更好，双斜线模型取值较保守. 根据破坏截面的受力平衡与受拉钢筋中心点的力矩平衡（见图10），可得

图 9

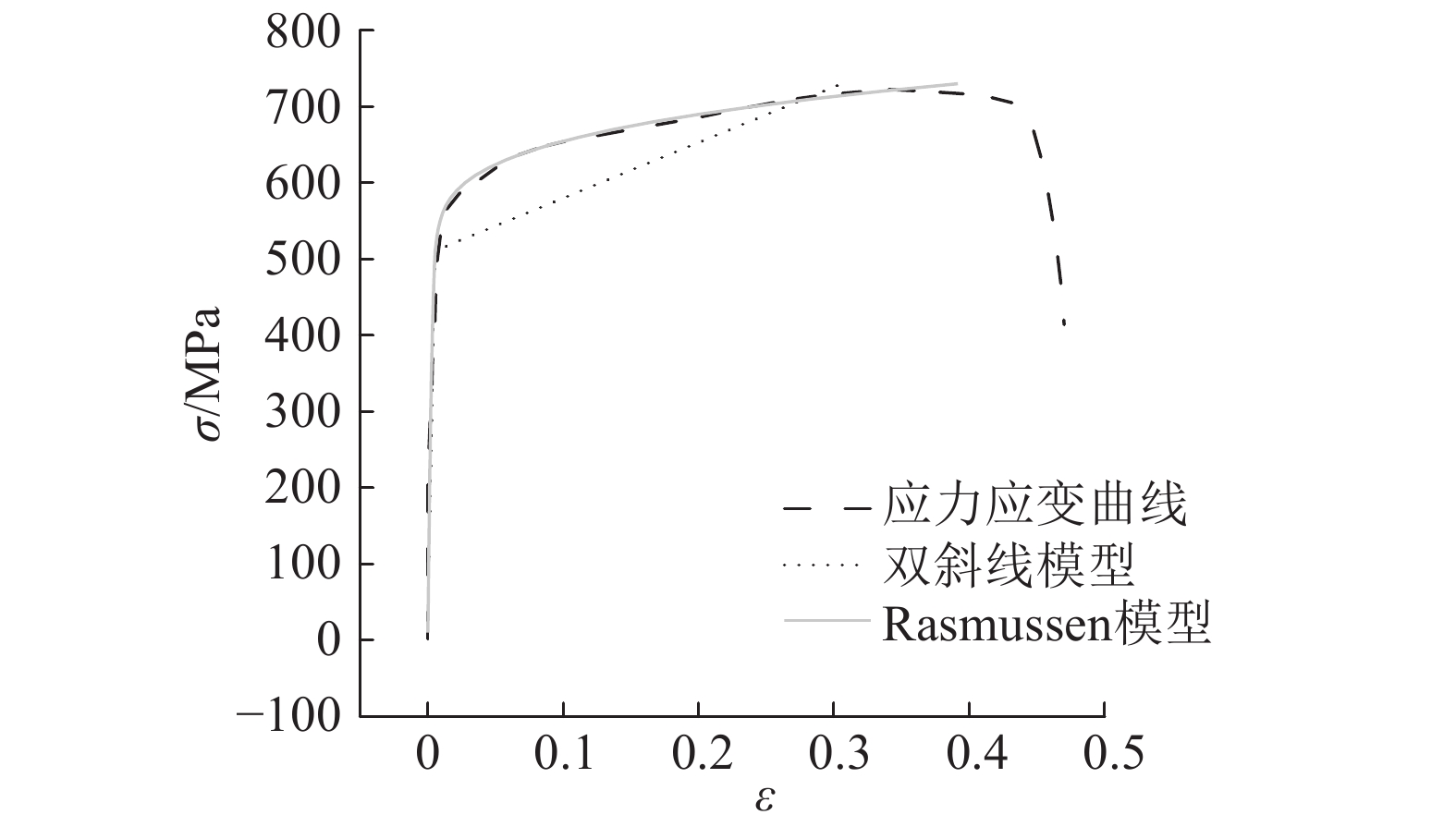
图 9 双斜线模型与Rasmussen模型对比图 Fig. 9 Comparison diagram of double slash model and Rasmussen model

图 10

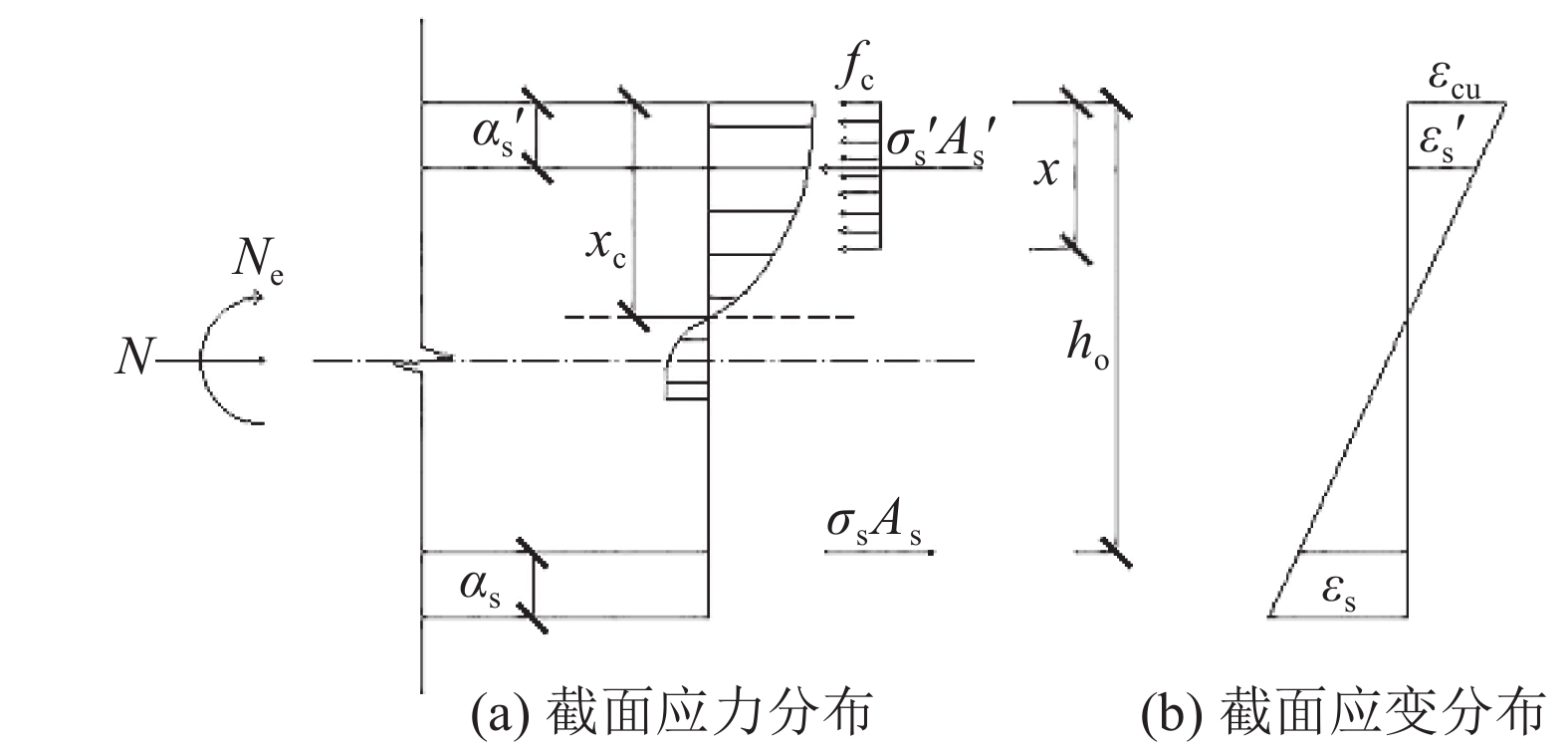
图 10 小偏压柱破坏截面应力应变分布 Fig. 10 Stress and strain distribution of failure cross section

求解可得2种本构模型下的极限承载能力理论值，如表3所示.

表 3

表 3 2种本构模型的理论计算值 Table 3 Theoretical values based on two constitutive models 模型 N/kN x/mm σ's/MPa σs/MPa 双斜线模型 167.5 59.03 174.7 305.4 Rasmussen 模型 204.2 61.28 270.2 376.6

表 3 2种本构模型的理论计算值 Table 3 Theoretical values based on two constitutive models

共开展3根柱子的小偏心受压试验，其中C-3柱因为牛腿部分破坏而提前失效，不进行理论分析，剩余2根柱子的极限承载能力分别为166和180 kN，接近双斜线本构模型的计算值，低于Rasmussen本构模型的计算值. 从安全性考虑，用双斜线模型来进行计算较合适，且留有一部分的安全储备，同时双斜线模型公式简单，方便确定相关系数.

观察分析受拉区和受压区钢筋应力可知，由于小偏心受压，受拉区钢筋未屈服，且受压区钢筋应力较低，没有充分利用高强钢筋的优势. 在双斜线本构模型的基础上，维持现有的截面及配筋，计算分析混凝土强度对钢筋利用率和小偏压柱极限承载力的影响，计算结果如表4 所示. 选取高于本试验混凝土强度的3种标号混凝土，分别为C60、C70和C80混凝土的材料性能，开展承载力N_i与破坏时受拉钢筋强度σ_i、受压钢筋强度σ'_i的反算. 表4中，i为混凝土标号，比值为不同标号下模型计算值与C53混凝土模型计算值的比.

表 4

表 4 混凝土强度提升对承载能力以及钢筋应力的影响 Table 4 Inference on ultimate load capacity and reinforcement stress with increase of concrete strength i $\frac{{{N_i}}}{{{N_{53}}}}$ $\frac{{{\sigma _i}'}}{{{\sigma _{53}}'}}$ $\frac{{{\sigma _i}}}{{{\sigma _{53}}}}$ 53（试验值） 1.00 1.00 1.00 60 1.03 0.96 1.02 70 1.07 0.91 1.05 80 1.10 0.86 1.06

表 4 混凝土强度提升对承载能力以及钢筋应力的影响 Table 4 Inference on ultimate load capacity and reinforcement stress with increase of concrete strength

从表4可以看出，混凝土强度增大小偏压柱的极限承载能力增大、受拉区钢筋的利用率也随之增加. 但是混凝土强度增大使其脆性变大，即混凝土极限压应变减小，导致受压区钢筋利用率越来越低. 观察3个比值随着混凝土强度增加的变化率可以看出，当混凝土强度约为C70时，极限承载力与受拉钢筋的强度利用率最好. 若小偏压柱受压侧腐蚀条件不恶劣，设计时建议受压侧钢筋采用同强度等级的碳素钢筋或降低不锈钢受压钢筋的配筋量.

（1）不锈钢筋混凝土小偏压柱的极限状态破坏模式与碳素钢筋小偏压混凝土柱相同，但是荷载-挠度曲线发展与碳素钢筋大偏压混凝土柱类似，加载过程可以分为弹性阶段、开裂阶段和破坏阶段. 虽然是以受压区混凝土压碎作为破坏标准，但是与碳素钢筋构件不同，不锈钢筋混凝土小偏压柱在破坏前有明显的挠度增长，且极限挠度较碳素钢筋大偏压混凝土柱增大许多.

（2）不锈钢筋混凝土小偏压柱跨中截面应变沿高度分布基本符合平截面假定，可以按照平截面假定进行理论计算.

（3）双斜线模型与Rasmussen模型是现在常用的2种不锈钢筋本构模型，在名义屈服点之后，Rasmussen本构模型与拉伸曲线符合较好，双斜线本构模型的取值偏保守. 在不锈钢筋屈服之前，用双斜线模型计算出的极限承载能力理论值与试验值较接近，且有一定的安全保证；双斜线模型公式较简单，方便计算，推荐使用.

（4）为了与高强钢筋匹配，所采用的混凝土应为高强混凝土，对比混凝土强度提升对极限承载能力和受拉区钢筋、受压区钢筋应力变化的影响. 当混凝土强度约为C70时，对极限承载能力与受拉区钢筋利用率的提升效果最佳；若小偏压柱受压侧腐蚀条件不恶劣，建议受压侧钢筋采用同强度等级的碳素钢筋或降低不锈钢受压钢筋配筋量.