荷载分项系数调整对砌体结构设计的影响

引用本文 [复制中英文]

吴柯娴, 金伟良, 夏晋. 荷载分项系数调整对砌体结构设计的影响[J]. 浙江大学学报(工学版), 2018, 52(10): 1901-1910.
dx.doi.org/10.3785/j.issn.1008-973X.2018.10.009

[复制中文]

WU Ke-xian, JIN Wei-liang, XIA Jin. Influence of load partial factors adjustment on design of masonry structures[J]. Journal of Zhejiang University(Engineering Science), 2018, 52(10): 1901-1910.
dx.doi.org/10.3785/j.issn.1008-973X.2018.10.009

[复制英文]

作者简介

吴柯娴（1998—），女，博士生，从事工程结构全寿命设计的研究.
orcid.org/0000-0003-0231-1657.
E-mail: 11612040@zju.edu.cn.

通信联系人

金伟良，男，教授.
orcid.org/0000-0002-8475-8032.
E-mail: jinwl@zju.edu.cn.

文章历史

收稿日期：2018-04-17

Contents Abstract Full text Figures/Tables PDF

荷载分项系数调整对砌体结构设计的影响

吴柯娴, 金伟良, 夏晋

浙江大学建筑工程学院，浙江杭州 310058

收稿日期：2018-04-17

作者简介：吴柯娴（1998—），女，博士生，从事工程结构全寿命设计的研究.
orcid.org/0000-0003-0231-1657.
E-mail: 11612040@zju.edu.cn.

通讯作者：金伟良，男，教授.
orcid.org/0000-0002-8475-8032.
E-mail: jinwl@zju.edu.cn.

摘要: 为了确定《建筑结构可靠性设计统一标准》(GB 50068)征求意见稿中的荷载分项系数调整对砌体结构设计安全性和材料用量的影响，以《砌体结构设计规范》（GB 50003–2011）中的无筋砌体和配筋砌体构件为研究对象，通过综合安全系数法和可靠指标法，分别计算荷载分项系数调整后砌体结构设计安全度的变化幅度. 计算无筋砌体构件的横截面积增率和配筋砌体构件的配筋量增率，得到砌体结构设计材料用量的变化幅度. 结果表明，荷载分项系数调整使砌体结构设计的综合安全系数提高5%，可靠指标提高5%~6.5%，无筋砌体构件的砌块材料用量提升6%~8%，配筋砌体构件的配筋量提升10%~23%.

关键词: 砌体结构规范修订分项系数安全系数可靠指标材料用量

Influence of load partial factors adjustment on design of masonry structures

WU Ke-xian , JIN Wei-liang , XIA Jin

College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

Abstract: Unreinforced and reinforced masonry components from Code for Design of Masonry Structures (GB 50003-2011) were analyzed in order to illustrate the influence of load partial factor adjustment on safety level and material consumption of the masonry structures in the draft of Unified Standard for Reliability Design of Building Structures (GB 50068). The comprehensive safety factor method and the reliability index method were used to calculate the change range of the masonry structures design safety after the adjustment of the load partial factors. The increase rate of cross-sectional area of the unreinforced components and the reinforcement rate of the reinforced components were calculated to obtain the variation of the material consumption. Results showed that the adjustment of load partial factors improved the comprehensive safety factors of the masonry structures by 5% and the reliability indexes by 5%~6.5%. The block material consumption of unreinforced components was increased by 6%~8%, and the reinforcement consumption of reinforced components was increased by 10%~23%.

Key words: masonry structure code revision partial factor safety factor reliability index material consumption

砌体结构在我国是一种历史悠久、量大面广的传统结构形式，作为城镇化建设的主要结构体系，砌体结构在我国的住宅建设中占据着较大比重^[1]. 自20世纪50年代起，我国砌体结构研究经历了60多年的发展^[2]，从借鉴苏联的设计标准起步，经过全国性的调研、理论与试验^[3]，砌体结构研究在结构体系^[4-5]、新型材料^[6]、抗震设计^[7-8]、工程应用^[9]等方面取得了巨大的成就. 随着理论成果和实验数据的积累，我国砌体结构设计规范从1973年颁布的第一版《砖石结构设计规范》GBJ 3–73^[10]（以下简称《73规范》）开始，经历了《砌体结构设计规范》GBJ 3–88^[11]（以下简称《88规范》）、《砌体结构设计规范》GB 50003–2001^[12]（以下简称《2001规范》）、《砌体结构设计规范》GB 50003–2011^[13]（以下简称《2011规范》）等多次修订，规范内容不断丰富，理论体系更加完善，先后增加了配筋砌体、抗剪理论、抗裂措施、耐久性及抗震设计^[14]，设计方法从单一安全系数法到半概率半经验的总安全系数法，再发展成为以概率理论为基础、以分项系数为表达形式的极限状态设计方法^[15]，为我国房屋建筑结构与国际主流设计规范的一致性奠定了基础.

随着我国经济建设的发展和社会财富的积累，人们对建筑结构安全性不断提出更高的要求，因此砌体结构设计规范的每一次修订都伴随着设计可靠度一定程度的提升. 在实际工程中，可靠度与材料用量是一对矛盾因素，提高结构的可靠度意味着更高的造价，为了获得更经济、合理的设计可靠度水平，多位学者对砌体结构设计规范中的可靠度与材料用量进行试算分析. 刘立新等^[16]对《73规范》和《88规范》的受压构件可靠度进行校核，认为当可靠度水平明显提高（失效概率降低一个数量级）时，材料用量增加15%~20%，并给出了3组可靠度水平的设计参数. 苑振芳等^[17]认为对于大面积的住宅建筑而言，《88规范》与《73规范》的材料用量基本持平，保持了可靠度水平的连续性，对于多层纵墙承重房屋和单层厂房，材料用量增加15%~30%. 严家熺等^[18]通过分析《88规范》与《2001规范》中的墙体轴心抗压性能得到，住宅楼的安全度水平总体提高了16%，材料用量提高了1.40~1.50级砂浆强度等级耗用量的水平. 蒋利学等^[19]全面分析我国1970~2015年修订的一系列混凝土和砌体结构设计规范的安全系数和可靠指标，认为相对安全系数由0.85逐步提高到1.00，且砌体结构《2011规范》与《2001规范》的可靠度基本维持在同一水平. 通过以上分析可以看出，《砌体结构设计规范》的每一次修订都需要对结构可靠度和材料用量这两个指标进行重点研究，进而反映规范有关条文调整前、后结构设计安全性和经济性的变化幅度. 本文在《建筑结构可靠性设计统一标准》(GB 50068)征求意见稿修订的基础上，探讨荷载分项系数调整对砌体结构设计的安全性和经济性影响，通过实际工程案例，分析结构层次上砌体结构设计的变化.

1 《建筑结构可靠性设计统一标准》对荷载分项系数的调整

随着《建筑结构可靠性设计统一标准》GB 50068^[20]（以下简称《统一标准》）修订工作的开展，2017年2月规范修订组公布了针对《统一标准》全面修订后的征求意见稿. 在荷载效应的基本组合中，取消了对永久荷载为主的结构起控制作用的组合式，通过提高永久荷载与可变荷载的分项系数来提升建筑结构安全度的设置水平. 其中，永久作用分项系数由原标准的 ${\gamma _{\rm{G}}}$ =1.2提高到 ${\gamma _{\rm{G}}}$ =1.3，可变作用分项系数由原标准的 ${\gamma _{\rm{Q}}}$ =1.4提高到 ${\gamma _{\rm{Q}}}$ =1.5，调整前、后建筑结构作用分项系数的对比如表1所示. 表中，括号内数值为永久荷载控制条件下的永久荷载分项系数.

表 1 建筑结构作用分项系数对比 Table 1 Partial factors comparison of building structures

对于承载能力极限状态，在持久设计状况下应选择荷载效应的基本组合，当仅有一个可变荷载时，荷载效应的基本组合如下.

${\text{当}}\;\rho > 0.357{\text{时}},\;\;{S_{\rm{d}}} = {\gamma _0}\left( {1.2{S_{{\rm{Gk}}}} + 1.4{S_{{\rm{Qk}}}}} \right);$

(1)

${\text{当}}\;\rho \leqslant 0.357{\text{时}},\;\;{S_{\rm{d}}} = {\gamma _0}\left( {1.35{S_{{\rm{Gk}}}} + 0.98{S_{{\rm{Qk}}}}} \right).$

(2)

调整后荷载效应的基本组合为

${S_{\rm{\!d}}} = {\gamma _0}\left( {1.3{S_{{\rm{Gk}}}} + 1.5{S_{{\rm{Qk}}}}} \right).$

(3)

式中： $\rho $ 为效应比，即可变荷载效应与永久荷载效应标准值的比值； ${S_{\rm{\!d}}}$ 为荷载组合效应设计值； ${\gamma _0}$ 为结构重要性系数； ${S_{{\rm{\!Gk}}}}$ 为永久荷载标准值； ${S_{{\rm{\!Qk}}}}$ 为可变荷载标准值.

为了确定荷载效应设计值的增加幅度，设定 $\rho $ 为0~1.0，计算荷载分项系数调整前、后的荷载效应设计值与永久荷载效应标准值的比值 ${{{S_{\rm{\!d}}}} / {{S_{{\rm{\!Gk}}}}}}$ ，如图1所示. 可以看出，当 $\rho $ =0.096时，分项系数调整前、后的荷载组合值相等；随着 $\rho $ 的增大，调整前、后荷载组合值的相对增率先线性上升，在 $\rho $ =0.357之后基本保持不变，荷载效应增率 ${\varDelta _{\rm{\!S}}}$ 稳定为8%. 这说明调整荷载分项系数后，施加在结构上的荷载增长幅度与效应比有关.

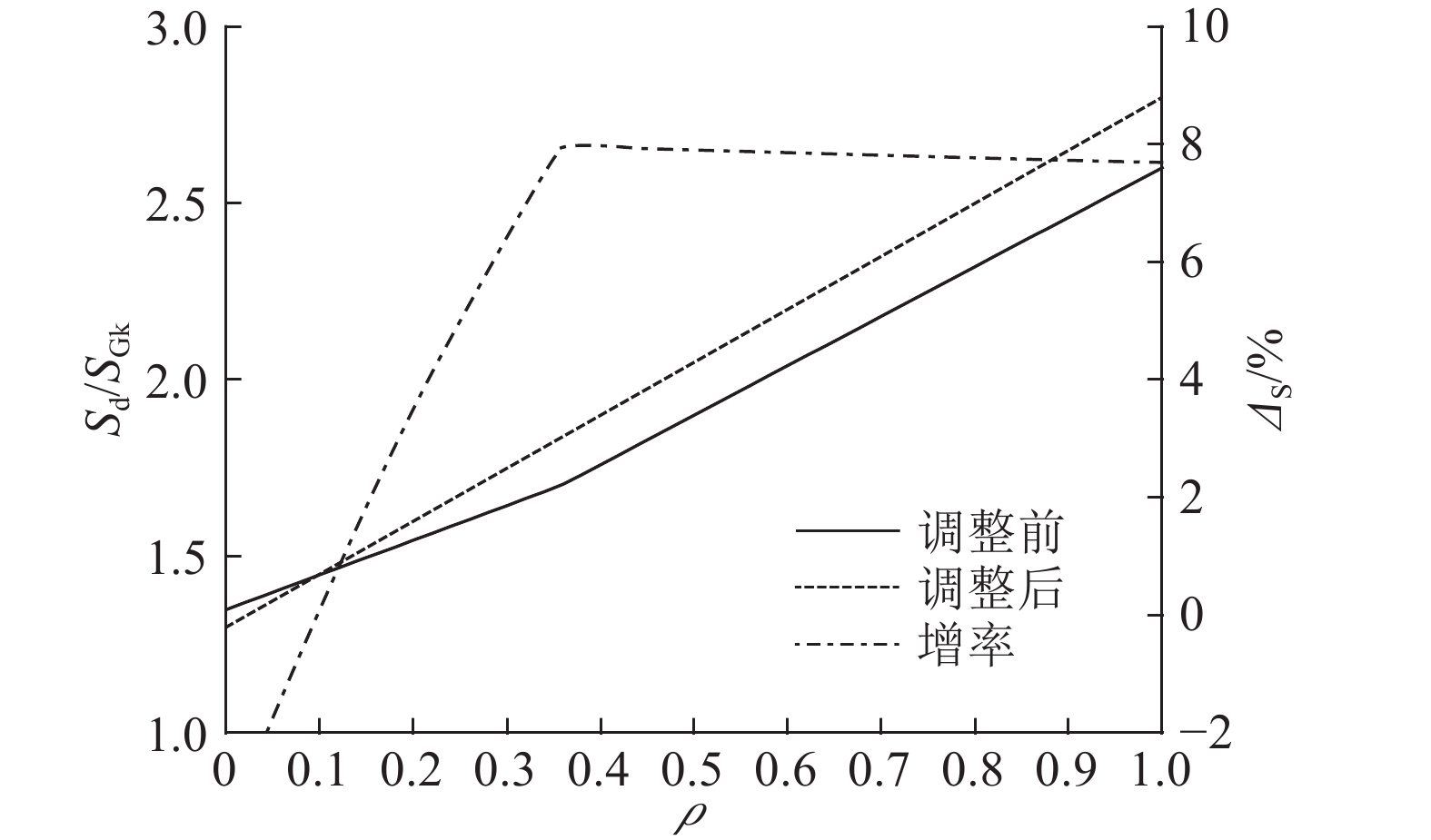
图 1 荷载效应设计值增率随效应比的变化趋势 Fig. 1 Variation trends of increment rate for load effect design value with effect ratio

一般而言，《统一标准》^[20]是各种材料及结构设计规范所共同遵守的准则，条文的改动将产生广泛而深远的影响，调整后需要对各类设计规范进行试算，分析设计安全度和材料用量的变化幅度. 为了说明《统一标准》征求意见稿中荷载分项系数的变化对砌体结构设计的影响，开展构件和结构层次上的可靠度分析和材料用量变化计算.

2 荷载分项系数调整后砌体结构设计安全性的变化

采用安全系数法和可靠指标法，衡量荷载分项系数调整对砌体结构设计安全性的影响. 相对而言，安全系数法是综合考虑荷载效应和抗力的多个系数并得到综合安全系数的方法，简明直观，计算方便，但所得结果较粗糙. 利用基于概率理论的可靠指标法，能够准确衡量结构可靠度的变化，但该方法要求统一的相关参数取值，需要进行大量试验和实际工程数据的收集和统计，工作量较大，且计算复杂，无法从设计表达式中直观地体现设计安全度.

2.1 砌体结构安全系数的变化

为了对比我国各时期砌体规范的安全度，除《73规范》^[10]已给出总安全系数外，还可以根据 ${\gamma _{\rm{G}}}$ 、 ${\gamma _{\rm{Q}}}$ 和 $\rho $ 计算出《88规范》^[11]、《2001规范》^[12]、《2011规范》^[13]和《统一标准》征求意见稿的综合安全系数 $K$ 并进行比较.

为了方便计算，设置综合荷载分项系数 ${\gamma _{\rm{S}}}$ ，即

${S_{\rm{\!d}}} = {\gamma _0}\left( {{\gamma _{\rm{G}}}{S_{{\rm{\!Gk}}}} + {\gamma _{\rm{Q}}}{S_{{\rm{\!Qk}}}}} \right) = {\gamma _0}{\gamma _{\rm{S}}}\left( {{S_{{\rm{\!Gk}}}} + {S_{{\rm{\!Qk}}}}} \right),$

(4)

${\gamma _{\rm{S}}} = \frac{{{\gamma _{\rm{G}}} + {\gamma _{\rm{Q}}}\rho }}{{1 + \rho }}.$

(5)

综合安全系数 $K$ ^[19]如下. 对于《73规范》，

$K = 1.1\left( {1 - 1.645{\delta _{\rm{f}}}} \right){K_0};$

(6)

对于其他规范，

$K = {\gamma _{\rm{S}}}{\gamma _{\rm{R}}}.$

(7)

式中： ${K_0}$ 为《73规范》^[10]中砌体受压构件的安全系数， ${K_0}$ =2.3； ${\gamma _{\rm{R}}}$ 为抗力分项系数，砌块可以看作是由块体和砂浆共同组成的一种综合材料，因此抗力分项系数等于材料分项系数，取 ${\gamma _{\rm{R}}}$ =1.6； ${\delta _{\rm{f}}}$ 为砌体强度变异系数，对于砌体结构受压构件为0.17，受剪构件为0.2.

从式（5）、（7）可以看出， ${\gamma _{\rm{G}}}$ 、 ${\gamma _{\rm{Q}}}$ 和 ${\gamma _{\rm{R}}}$ 越大，相应的结构可靠度设置水平越高. 另外，《73规范》^[10]和《88规范》^[11]中办公楼和住宅楼面可变荷载为1.5 kN/m²，《2001规范》^[12]、《2011规范》^[13]和《统一标准》征求意见稿中规定的办公楼和住宅楼面可变荷载为2 kN/m²，对 $\rho $ 进行计算并综合确定《73规范》^[10]和《88规范》^[11]相对于《2001规范》^[12]、《2011规范》^[13]的荷载换算系数 ${\xi _{\rm{S}}}$ =0.965^[19]. 砌体结构系列规范中的受压构件安全度设置水平如表2所示. 表中，K为综合安全系数，安全系数相对值 $k$ 指各规范与现行《2011规范》^[13]安全系数的比值，括号内数值表示考虑楼面可变荷载取值变化的计算结果.

表 2 砌体结构系列规范中受压构件设计安全度的对比 Table 2 Design safety comparison of compressed components in masonry structure series specifications

通过分析安全系数的相对值可以看出，砌体结构系列规范安全度的相对大小逐年增长，当考虑楼面可变荷载的变化时，《73规范》^[10]和《88规范》^[11]的受压构件设计安全度分别比《2001规范》^[12]小14%和12%，《2011规范》^[13]和《2001规范》^[12]的安全度保持一致，《统一标准》征求意见稿中荷载分项系数的调整使得砌体结构的设计安全性增大5%.

2.2 砌体结构可靠指标的变化

当按照承载能力极限状态设计结构时，应采用荷载作用效应和结构抗力作为基本变量，极限状态函数 $Z = g\left( {R,S} \right) = R - {S_{\rm{G}}} - {S_{\rm{\!Q}}} = 0$ ，其中 $R$ 为结构抗力， $S$ 为荷载组合效应， ${S_{\rm{\!G}}}$ 为永久荷载， ${S_{\rm{\!Q}}}$ 为可变荷载.

作为结构可靠度分析的基础，统计参数的取值需要研究人员通过大量试验数据和工程数据统计得到，但现阶段荷载效应参数的统计很薄弱^[21]. 本文采用文献[22]的荷载效应统计值（见表3），计算荷载分项系数调整前、后砌体结构的可靠指标变化幅度. 表中， ${Q_{\rm{k}}}$ 为荷载标准值， ${\kappa _{\rm{S}}}$ 、 ${\delta _{\rm{S}}}$ 分别为荷载效应的均值系数与变异系数. 采用文献[15]、[22]和[23]的抗力统计数据，根据误差传递原理，考虑材料、几何和计算公式的不确定性，计算得到抗力统计参数值（见表4）. 表中， ${\kappa _{\rm{R}}}$ 、 ${\delta _{\rm{R}}}$ 分别为结构抗力的均值系数与变异系数.

表 3 荷载效应参数的取值 Table 3 Value of load effect parameters

表 4 抗力相关参数的取值 Table 4 Value of resistance parameters

根据《统一标准》^[20]中的分项系数设计方法可知，承载能力极限状态设计时的基本要求为 ${R_{\rm{d}}} \geqslant {\gamma _0}{S_{\rm{\!d}}}$ ，即

${R_{\rm{d}}} \geqslant {\gamma _0}{S_{\rm{\!d}}} = {\gamma _0}\left( {{\gamma _{\rm{G}}}{S_{{\rm{\!Gk}}}} + {\gamma _{\rm{Q}}}{S_{{\rm{\!Qk}}}}} \right).$

(8)

式中： ${R_{\rm{d}}}$ 为结构抗力设计值. 一般安全等级为二级或设计使用年限为50 a的结构， ${\gamma _0}$ =1.0. 在计算可靠指标的过程中，首先选定 $\rho $ 及荷载组合，已知 ${S_{{\rm{Qk}}}}$ ，计算得到 ${S_{{\rm{Gk}}}} = {{{S_{{\rm{Qk}}}}} / \rho }$ . 根据表3的均值系数和变异系数，求得永久荷载及可变荷载的平均值和标准差 ${\mu _{{{{S}}_{\rm{G}}}}}$ 、 ${\sigma _{{{{S}}_{\rm{G}}}}}$ 、 ${\mu _{{{{S}}_{\rm{Q}}}}}$ 、 ${\sigma _{{{{S}}_{\rm{Q}}}}}$ . 由式（8），可以求得 ${R_{\rm{d}}}$ ，抗力平均值 ${\mu _{\rm{R}}} = {\kappa _{\rm{R}}}{\gamma _{\rm{R}}}{R_{\rm{d}}}$ ，标准差 ${\sigma _{\rm{R}}}{\rm{ = }}{\mu _{\rm{R}}}{\delta _{\rm{R}}}$ .

采用当量正态化和验算点法计算可靠指标 $\beta $ ，结果如表5、6所示. 表中， $\rho $ 为效应比. 砖砌体和混凝土砌块砌体的平均可靠指标在荷载分项系数调整后的可靠指标增率 ${\varDelta _\beta }$ 如图2、3所示.

表 5 砖砌体的可靠指标 $\beta $ Table 5 Reliability index $\beta $ of brick masonry

$\rho $	调整前, 轴压		调整前, 偏压		调整前, 受剪		调整后, 轴压		调整后, 偏压		调整后, 受剪
$\rho $	办公	住宅	办公	住宅	办公	住宅	办公	住宅	办公	住宅	办公	住宅
0.1	4.103	4.024	4.206	4.171	4.068	4.032	4.108	4.071	4.211	4.175	4.073	4.037
0.25	4.211	4.126	4.311	4.229	4.176	4.091	4.390	4.305	4.484	4.401	4.353	4.269
0.4	4.321	4.197	4.418	4.298	4.286	4.162	4.598	4.475	4.685	4.566	4.560	4.438
0.5	4.430	4.286	4.523	4.384	4.394	4.251	4.701	4.559	4.786	4.648	4.664	4.522
0.6	4.515	4.355	4.606	4.452	4.479	4.321	4.781	4.624	4.864	4.711	4.743	4.587
0.75	4.605	4.431	4.695	4.526	4.571	4.397	4.862	4.691	4.944	4.778	4.825	4.655
1.0	4.688	4.503	4.778	4.597	4.657	4.471	4.929	4.750	5.013	4.837	4.896	4.717

表 5 砖砌体的可靠指标 $\beta $ Table 5 Reliability index $\beta $ of brick masonry

表 6 混凝土砌块砌体的可靠指标 $\beta $ Table 6 Reliability index $\beta $ of concrete masonry

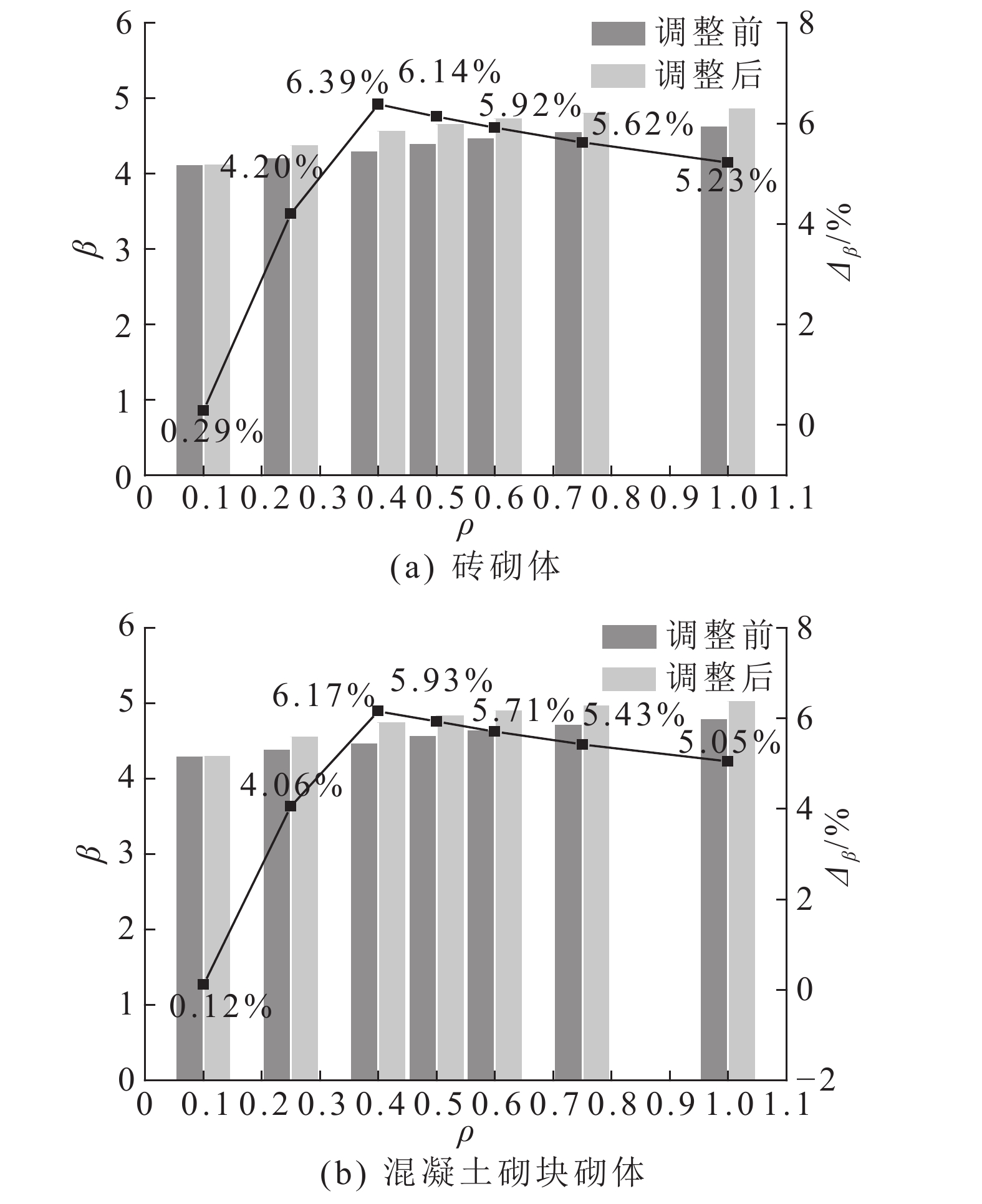
图 2 砖砌体与混凝土砌块砌体的平均可靠指标增率随效应比的变化 Fig. 2 Increment rate variations of average reliability index for brick masonry and concrete masonry with effect ratio

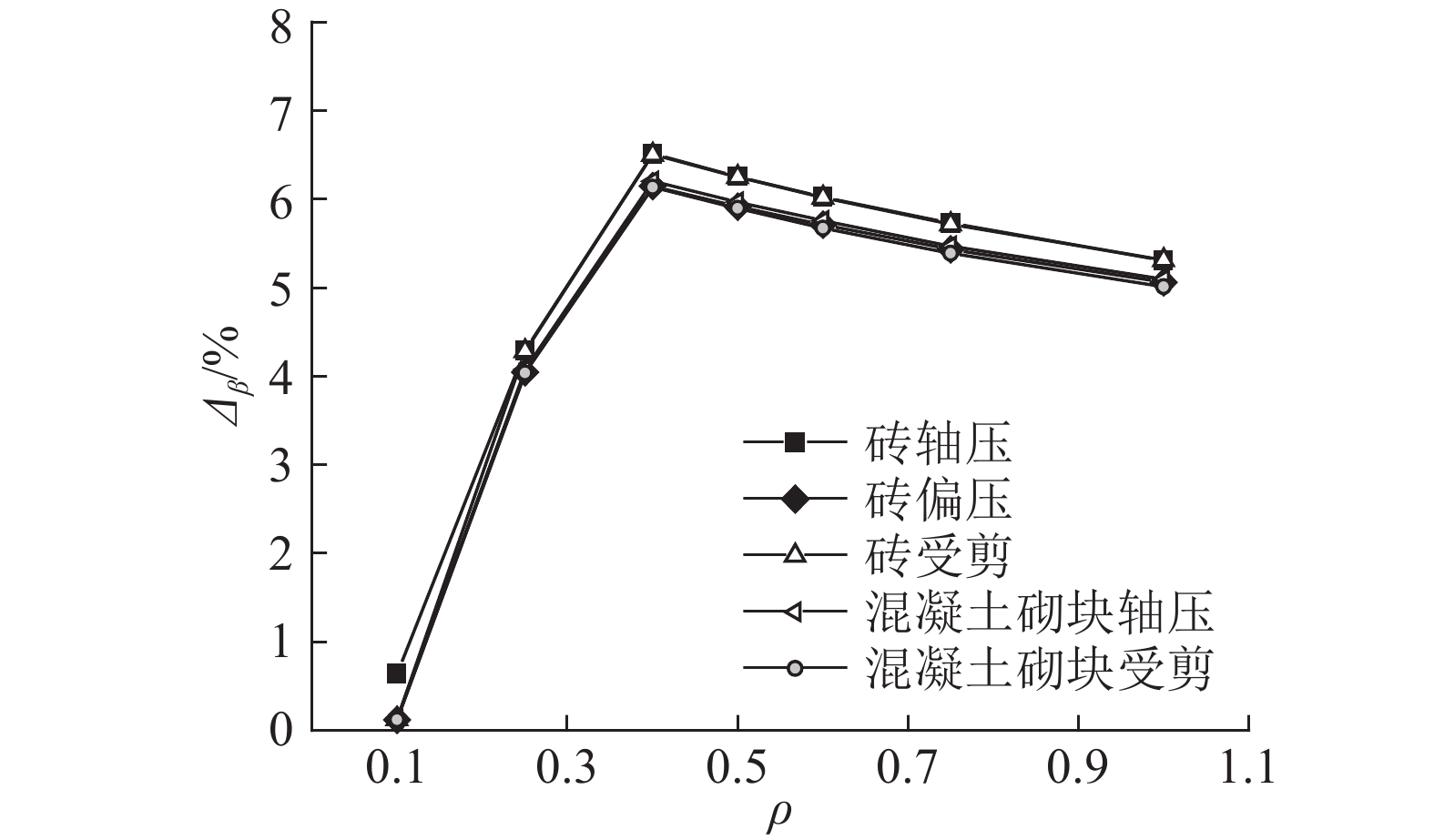
图 3 不同砌块在不同受力情况下的可靠指标增率随效应比的变化趋势 Fig. 3 Increment rate variations of reliable index under different masonry types and different stress conditions with effect ratio

从图2、3可得如下结论. 1）荷载分项系数调整前、后的平均可靠指标在不同效应比时均满足 $\beta \geqslant 3.7$ 的目标要求. 2）可靠指标增率随 $\rho $ 的增大先增大后略微减小，当 $\rho $ =0.1时，调整前、后的可靠指标大小基本不变；随着 $\rho $ 的增长，可靠指标增率不断增加并维持为5%~6.5%. 3）砖砌体和混凝土砌体的可靠指标增率几乎重合，说明荷载分项系数的调整对于不同砌体种类和不同受力状态的砌体构件设计安全度的影响效果是相同的. 4）从荷载分项系数调整前、后指标的增长趋势曲线可以看出，可靠指标的增长趋势与荷载组合值的增长趋势类似，且与采用安全系数法计算所得的安全度增率基本一致，2种方法相互得到验证.

3 荷载分项系数调整后砌体结构材料用量的变化

按照构件内部是否配置钢筋，砌体结构可以分为无筋砌体和配筋砌体. 仅由块体和砂浆组成的砌体称为无筋砌体，在砌体中设置了钢筋或钢筋混凝土材料的砌体称为配筋砌体，配筋砌体的抗压、抗剪和抗弯承载力远大于无筋砌体. 为了考虑不同荷载分项系数和效应比情况下砌体的材料用量变化，对无筋砌体和配筋砌体构件进行试设计计算，本文不考虑抗震设计要求.

3.1 无筋砌体构件的材料用量变化

由于砌体材料有砖、砌块和石三大类，为了减小由砌块种类引起的误差，选取4种常见砌体材料—烧结普通砖、混凝土砖、混凝土砌块、毛料石，开展构件试设计计算. 受压强度设计值大小如下：混凝土砌块>毛料石>混凝土砖>烧结普通砖. 考虑构件纵向弯曲对承载力的影响，将受压构件分为受压短柱和受压长柱，按照《2011规范》^[13]中的设计方法，计算承载能力极限状态下砌体结构不同受力构件在荷载分项系数调整前、后的材料用量增率 ${\varDelta _{\rm{c}}}$ ，对不同砌体材料的截面积增率取平均值得到综合增率 ${\varDelta _{{\rm{c}}1}}$ ，结果如表7所示.

表 7 无筋砌体构件的截面积增率 Table 7 Increment rate of cross-sectional area for unreinforced masonry components

构件类型	受力类型	砌块种类	${\varDelta _{\rm{c}}}$ /%							${\varDelta _{{\rm{c}}1}}$ /%
构件类型	受力类型	砌块种类	$\rho=$ 0.1	$\rho=$ 0.25	$\rho=$ 0.4	$\rho=$ 0.5	$\rho=$ 0.6	$\rho=$ 0.75	$\rho=$ 1.0	$\rho=$ 0.1	$\rho=$ 0.25	$\rho=$ 0.4	$\rho=$ 0.5	$\rho=$ 0.6	$\rho=$ 0.75	$\rho=$ 1.0
短柱	轴压	烧结普通砖	0.12	4.15	6.43	6.11	5.97	5.78	5.49	0.11	4.24	6.03	5.83	5.87	6.12	7.14
短柱	轴压	混凝土砖	0.11	5.04	5.93	5.77	5.62	5.42	7.69	0.11	4.24	6.03	5.83	5.87	6.12	7.14
短柱	轴压	混凝土砌块	0.11	4.01	6.00	5.84	5.70	5.49	7.69	0.11	4.24	6.03	5.83	5.87	6.12	7.14
短柱	轴压	毛料石	0.11	3.76	5.77	5.60	6.19	7.78	7.69	0.11	4.24	6.03	5.83	5.87	6.12	7.14
短柱	偏压	烧结普通砖	0.12	4.10	7.64	5.86	5.61	7.78	7.69	0.12	4.19	6.80	6.35	7.28	7.78	7.69
短柱	偏压	混凝土砖	0.11	3.80	5.76	6.08	7.84	7.78	7.69	0.12	4.19	6.80	6.35	7.28	7.78	7.69
短柱	偏压	混凝土砌块	0.11	3.84	5.83	5.57	7.84	7.78	7.69	0.12	4.19	6.80	6.35	7.28	7.78	7.69
短柱	偏压	毛料石	0.14	5.02	7.95	7.89	7.84	7.78	7.69	0.12	4.19	6.80	6.35	7.28	7.78	7.69
长柱	轴压	烧结普通砖	0.11	4.06	7.67	5.94	5.80	5.60	6.79	0.11	3.71	6.55	6.42	6.30	7.42	7.69
长柱	轴压	混凝土砖	0.11	3.83	5.89	5.73	5.58	6.70	7.69	0.11	3.71	6.55	6.42	6.30	7.42	7.69
长柱	轴压	混凝土砌块	0.11	3.77	5.79	5.63	5.47	7.78	7.69	0.11	3.71	6.55	6.42	6.30	7.42	7.69
长柱	轴压	毛料石	0.10	3.52	7.95	7.89	7.84	7.78	7.69	0.11	3.71	6.55	6.42	6.30	7.42	7.69
长柱	偏压	烧结普通砖	0.11	5.02	7.95	7.89	7.84	7.78	7.69	0.11	4.31	8.04	7.89	7.84	7.78	7.69
长柱	偏压	混凝土砖	0.11	3.63	8.29	7.89	7.84	7.78	7.69	0.11	4.31	8.04	7.89	7.84	7.78	7.69
长柱	偏压	混凝土砌块	0.10	3.57	7.95	7.89	7.84	7.78	7.69	0.11	4.31	8.04	7.89	7.84	7.78	7.69
长柱	偏压	毛料石	0.13	5.02	7.95	7.89	7.84	7.78	7.69	0.11	4.31	8.04	7.89	7.84	7.78	7.69
–	受剪	烧结普通砖	0.88	6.87	7.92	7.80	7.76	7.94	7.64	0.92	6.93	7.90	7.82	7.75	7.94	7.63
–	受剪	混凝土砖	0.90	6.89	7.92	7.84	7.75	7.94	7.62	0.92	6.93	7.90	7.82	7.75	7.94	7.63
–	受剪	混凝土砌块	0.94	7.02	7.87	7.83	7.76	7.93	7.61	0.92	6.93	7.90	7.82	7.75	7.94	7.63
–	受剪	毛料石	0.97	6.93	7.91	7.82	7.74	7.94	7.63	0.92	6.93	7.90	7.82	7.75	7.94	7.63

表 7 无筋砌体构件的截面积增率 Table 7 Increment rate of cross-sectional area for unreinforced masonry components

对4类常见砌体材料的截面积增率取平均值，得到 ${\varDelta _{{\rm{c}}1}}$ 随 $\rho $ 的变化规律，如图4所示. 可以看出，各类受力构件的变化规律基本一致，随着 $\rho $ 的增大， ${\varDelta _{{\rm{c}}1}}$ 逐渐增大并趋于平缓；当 $\rho $ 较大时，砌体材料的 ${\varDelta _{{\rm{c}}1}}$ 稳定于6%~8%，这与荷载效应设计值的变化趋势相似. 此外，受力不同的砌体构件的材料用量增幅不同，图4中显示受剪构件的材料用量增幅最大，其次是偏心受压构件，轴心受压构件最小，考虑构件纵向弯曲效应的受压长柱的材料用量增幅大于受压短柱.

图 4 无筋砌体构件截面积的综合增率随效应比的变化趋势 Fig. 4 Comprehensive increment rate variations of cross-sectional area for unreinforced masonry components with effect ratio

3.2 配筋砌体构件的材料用量变化

配筋砌体可以分为网状配筋砖砌体和组合砖砌体. 网状配筋砌体是指在砌体的水平灰缝中配置钢筋网，组合砖砌体是指在砖砌体内配置纵向钢筋或设置部分钢筋混凝土或钢筋砂浆以共同工作^[24]的砌体结构. 除了构件截面积的变化外，配筋砌体构件材料用量还应当考虑配筋量的增加幅度，通过计算不同受力条件下的砌体构件配筋率来评价钢材用量. 由于工程实例计算量过大，仅给出网状配筋砖砌体构件、组合砖砌体构件以及配筋砌块砌体剪力墙的计算结果，如表8所示. 表中，网状配筋砌体的偏心距不宜超过截面核心范围，较大偏心受压仅指偏心距较大的小偏心受压构件，不等同于大偏心受压.

表 8 配筋砌体构件配筋率的增率 Table 8 Increase rate of reinforcement ratio for reinforced masonry components

配筋类型	受力类型	${\varDelta _{\rm{c}}}/$ %
配筋类型	受力类型	$\rho=$ 0.1	$\rho=$ 0.25	$\rho=$ 0.4	$\rho=$ 0.5	$\rho=$ 0.6	$\rho=$ 0.75	$\rho=$ 1.0
网状配筋砌体	轴压	0.44	12.67	20.71	20.09	20.51	19.69	19.54
	小偏压	0.42	12.55	19.71	19.88	19.39	19.28	19.24
	较大偏压	0.55	12.42	19.57	19.49	19.05	18.18	18.36
组合砖砌体	轴压	0.51	17.07	22.40	21.80	21.58	20.61	18.71
	小偏压	0.33	14.94	21.05	21.15	20.39	19.03	17.38
	大偏压	0.21	7.97	13.04	12.92	13.35	13.60	14.02
配筋砌块砌体剪力墙	轴压	0.34	12.94	19.77	19.73	19.54	17.79	17.96
	小偏压	0.30	11.41	17.55	17.49	18.15	16.72	16.13
	大偏压	0.28	10.76	17.46	17.34	16.96	17.12	16.45
	受剪	0.19	7.28	11.48	11.49	11.07	11.01	10.31

表 8 配筋砌体构件配筋率的增率 Table 8 Increase rate of reinforcement ratio for reinforced masonry components

由图5可知，随着荷载效应比的增大，砌体构件的配筋量逐渐增大并趋于平缓. 当 $\rho $ =0.1时，由于荷载效应几乎没有增长，砌体构件的配筋量增率为0. 当 $\rho $ 较大时，配筋砌体的钢材用量增率为10%~23%. 由图5(a)~(c)可以看出，配筋砌体构件在不同受力条件下钢材用量的增长幅度与无筋砌体砌块材料用量的增长幅度相反，受剪构件的增幅最小，其次是偏心受压构件，轴心受压构件最大. 这是由于配筋砌体构件与无筋砌体构件的受力体系和破坏方式不同，当配筋砌体构件轴心受压时，往往是竖向钢筋受压屈服或面层混凝土和砌块被压碎导致的破坏；当配筋砌体构件小偏心受压时，受拉侧钢筋可能受压未屈服，面层混凝土或部分砖砌体先压碎，发生受压破坏；当配筋砌体构件大偏心受压时，受拉侧钢筋先受拉屈服，随后由于裂缝开展使得受压区面积减小，导致面层混凝土或砌块受压破坏. 当计算荷载分项系数调整前、后配筋砌体材料用量增量时，假设面层混凝土和砌块材料的强度与截面积不变，仅计算荷载效应增加导致的配筋率增率，由于在构件受剪或大偏心受压时，相比小偏心受压或轴心受压更能够发挥钢筋受拉强度高、延性好的优势，因此配筋率相对增率较小.

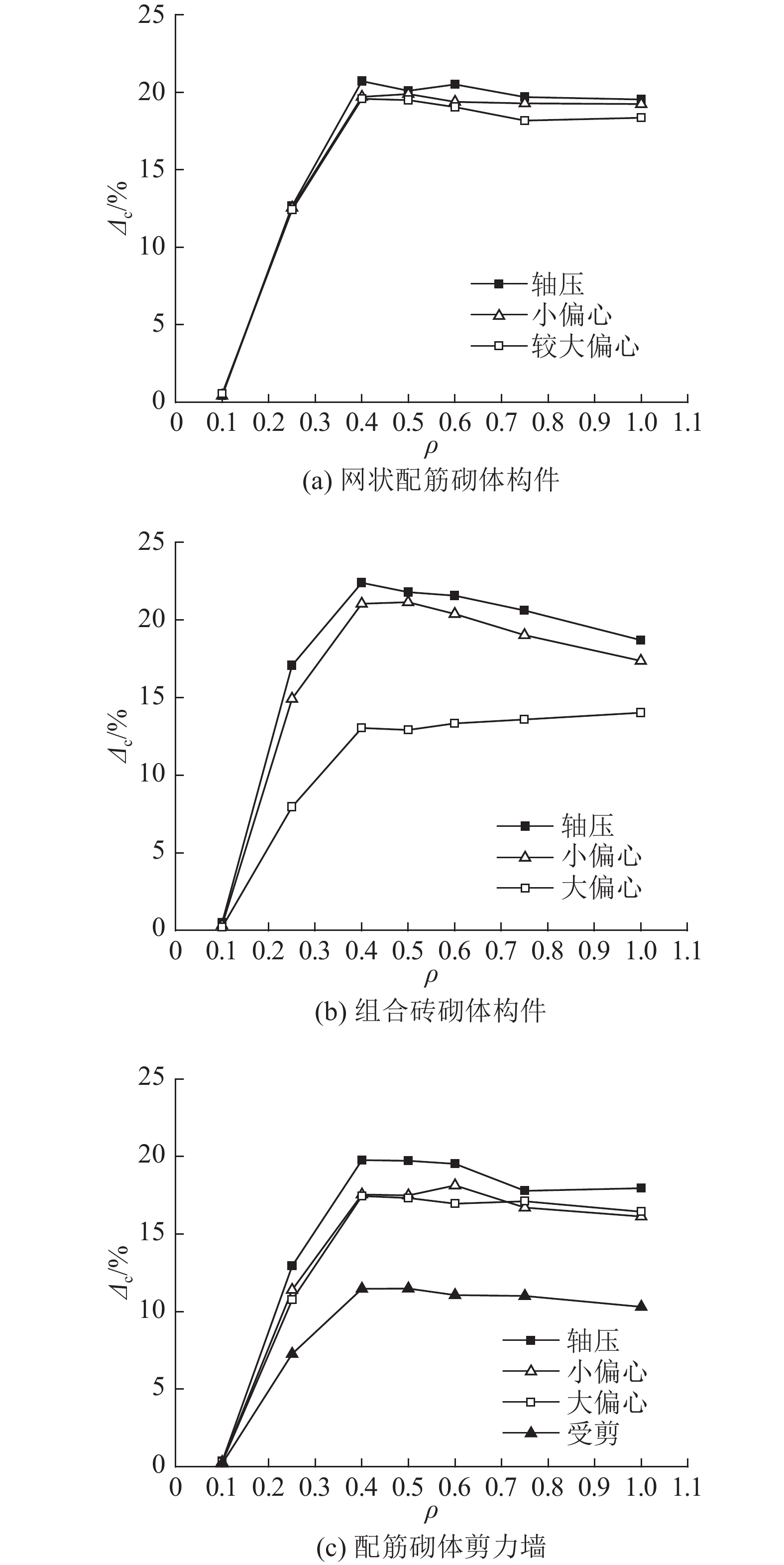
图 5 配筋砌体构件的配筋率增量随效应比的变化趋势 Fig. 5 Increment rate variations of reinforcement ratio for reinforced masonry components with effect ratio

4 砌体结构实例试算分析

计算一座6层砖混结构的教学楼，其中墙体为砌体结构，楼屋盖为钢筋混凝土结构. 层高为3.9 m（第6层）、3.6 m（第2~5层）和4.6 m（第1层），女儿墙高0.9 m，标准开间3.3 m. 墙体采用MU10实心黏土砖、强度等级为M7.5的混合砂浆进行砌筑，施工质量控制等级为B级.

图 6 教学楼平面图及剖面图 Fig. 6 Plan and section of teaching building

选取外纵墙作为计算单元，按照无筋砌体结构的设计方法，确定墙体厚度以保证最不利截面的承载力满足要求，计算该墙体厚度下每层结构的荷载组合、墙体内力和承载力. 通过《2011规范》^[13]与《统一标准》征求意见稿的轴心受压承载力比值，确定修订前、后设计安全度的变化.

各楼层墙体轴心压应力从上到下逐渐累积，荷载效应比不断变化，第6层主要承受屋盖荷载，荷载效应比很小，因此有轴力增率为负值的情况. 在第1~5层中，由于荷载分项系数调整后的荷载效应设计值增加，纵向墙体内部轴力和弯矩在荷载分项系数调整后均有增加. 按照最薄弱截面的承载能力要求，对砌体结构纵向墙体宽度进行设计，通过对比各楼层的抗力设计值 $\varphi Af$ 与墙体内力 $N$ 的比值分析设计安全度，如表9所示. 表中， ${\varDelta _{\rm{s}}}$ 为设计安全度增率. 为了对每层材料用量变化进行更准确的描述，在计算经济指标时，假设每一层纵墙厚度不同，通过试算得到该层纵墙的最小厚度，对比荷载分项系数调整前、后砌体结构墙体的材料用量变化，如表10所示. 表中，d为纵墙厚度.

表 9 砌体结构墙体受压承载力比值和设计安全度对比 Table 9 Bearing capacity and design safety comparison of masonry structure walls

表 10 砌体结构墙体设计厚度和材料用量对比 Table 10 Design thickness and material consumption comparison of masonry structure walls

由表9可知，荷载分项系数调整后的砌体结构设计安全度增加1%~3%，由表10可知，各层墙体厚度相对增率为0.2%~4.2%. 一般砌体结构的 $\rho $ 为0.1~0.5，本例中的效应比为0.14~0.15，因此本例中的设计安全度增率与前文可靠指标法计算所得的安全度增率基本吻合，材料用量增率符合无筋砌体的材料用量增率.

5 结　论

（1）荷载分项系数调整后，砌体结构设计的总安全系数提高5%，可靠指标增率受 $\rho $ 的影响，随着 $\rho $ 的增大而增大并趋于平缓. 当 $\rho $ =0.1时，可靠指标大小基本不变；当 $\rho $ 较大时，设计可靠指标增率基本为5%~6.5%，与总安全系数增率基本吻合.

（2）荷载分项系数调整后，砌体材料用量增率与 $\rho $ 有关. 当 $\rho $ =0.1时，调整前、后的砌体材料用量相对持平；当 $\rho $ 较大时，无筋砌体的截面积增量稳定为6%~8%，其中受剪构件的截面积增幅最大，其次是偏心受压构件，轴心受压构件最小.

（3）当 $\rho $ 较大时，荷载分项系数调整后配筋砌体的配筋率增量为10%~23%，且由于配筋砌体构件与无筋砌体构件的受力体系和破坏方式不同，在不同受力条件下，配筋砌体受剪构件的配筋率增幅最小，其次是偏心受压构件，轴心受压构件的配筋率增幅最大.

参考文献

[1]	李永梅, 孙国富. 适当提高砌体结构设计可靠度[J]. 建筑科学, 2004, 20(02): 24-27. LI Yong-mei, SUN Guo-fu. Reliability has been enhanced appropriately for design of masonry structures[J]. Building Science, 2004, 20(02): 24-27. DOI:10.3969/j.issn.1002-8528.2004.02.006
[2]	苑振芳. 《砌体结构设计规范》的发展历程和展望[J]. 工程建设标准化, 2015(07): 46-53. YUAN Zhen-fang. The development and prospect of code for design of masonry structures[J]. Standardization of Engineering Construction, 2015(07): 46-53.
[3]	徐建, 梁建国, 石柳, 等. 我国砌体结构发展的若干问题探讨[J]. 建筑结构, 2016, 46(15): 91-97. XU Jian, LIANG Jian-guo, SHI Liu, et al. Discussion on some problems of development of masonry structures in China[J]. Building Structure, 2016, 46(15): 91-97.
[4]	王凤来, 陈再现. 配筋砌块砌体结构承重墙体系发展概况及应用效益分析[J]. 墙材革新与建筑节能, 2009(3): 43-46. WANG Feng-lai, CHEN Zai-xian. Development overview and analysis of benefits for reinforced concrete block load bearing walls system[J]. Wall Materials Innovation and Energy Saving in Buildings, 2009(3): 43-46. DOI:10.3969/j.issn.1006-9135.2009.03.024
[5]	高连玉. 高层配筋砌块砌体结构体系的关键技术研究[J]. 混凝土, 2001(09): 12-18. GAO Lian-yu. Key techniques of high-rise reinforced block masonry structure system[J]. Concrete, 2001(09): 12-18. DOI:10.3969/j.issn.1002-3550.2001.09.003
[6]	李国忠. 新型墙体材料应用现状与发展趋势[J]. 21世纪建筑材料, 2009(1): 31-33. LI Guo-zhong. The application current situations and development trend for new wall material[J]. 21st Century Building Materials, 2009(1): 31-33. DOI:10.3969/j.issn.1003-1324.2009.01.009
[7]	林立, 杨伟军. 基于概率烈度的结构抗震损伤可靠性分析[J]. 重庆交通大学学报: 自然科学版, 2012, 31(06): 1121-1124. LIN Li, YANG Wei-jun. Structure seismic damage reliability analysis based on probabilistic seismic intensity[J]. Journal of Chongqing Jiaotong University: Natural Science, 2012, 31(06): 1121-1124.
[8]	杜东升, 苗启松, 梁羽, 等. 老旧砌体房屋加固及顶部加层隔震的理论分析及振动台试验[J]. 土木工程学报, 2013, 46(08): 45-54. DU Dong-sheng, MIAO Qi-song, LIANG Yu, et al. Theoretical analysis and shaking table tests of old masonry structure reinforced by external frames with added stories on the top using seismic isolation technology[J]. China Civil Engineering Journal, 2013, 46(08): 45-54.
[9]	肖建庄, 黄江德, 李宏, 等. 灾后重建再生砌块砌体结构性能和设计研究[J]. 四川大学学报: 工程科学版, 2009, 41(03): 202-208. XIAO Jian-zhuang, HUANG Jiang-de, LI Hong, et al. Structural performance and design investigation on recycled concrete block masonry during post-earthquake reconstruction[J]. Journal of Sichuan University: Engineering Science Edition, 2009, 41(03): 202-208.
[10]	砖石结构设计规范: GBJ 3–73 [S]. 北京: 中国建筑工业出版社, 1973.
[11]	砌体结构设计规范: GBJ 3–88 [S]. 北京: 中国建筑工业出版社, 1988.
[12]	砌体结构设计规范: GB 50003–2001 [S]. 北京: 中国建筑工业出版社, 2001.
[13]	砌体结构设计规范: GB 50003–2011 [S]. 北京: 中国建筑工业出版社, 2011.
[14]	金伟良, 岳增国, 高连玉. 《砌体结构设计规范》的回顾与进展[J]. 建筑结构学报, 2010, 31(06): 22-28. JIN Wei-liang, YUE Zeng-guo, GAO Lian-yu. State-of-art development on Code for design of masonry structures[J]. Journal of Building Structures, 2010, 31(06): 22-28.
[15]	严家熺. 砌体结构可靠度的发展——砌体规范可靠度编制的背景材料[J]. 武汉大学学报: 工学版, 2015, 48(增刊): 10. YAN Jia-xi. Development of reliability of masonry structures: background materials for compiling the reliability of masonry code [J]. Engineering Journal of Wuhan University, 2015, 48(Suppl.): 10. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGQT201504001004.htm
[16]	刘立新, 谢丽丽. 砌体结构可靠度分析及可靠度水平调整的建议[J]. 郑州工业大学学报, 1999, 20(04): 10-13. LIU Li-xin, XIE Li-li. Reliability analysis of masonry structure and suggestion of reliability level adjustment[J]. Journal of Zhengzhou University of Technology, 1999, 20(04): 10-13. DOI:10.3969/j.issn.1671-6833.1999.04.003
[17]	苑振芳, 严家熺. 《砌体结构设计规范》GBJ3–88可靠度水平修订的意见[J]. 建筑科学, 1999, 15(05): 30-31. YUAN Zhen-fang, YAN Jia-xi. Opinions on the revision of the reliability level of GBJ3–88 for Masonry Structure Design Code[J]. Building Science, 1999, 15(05): 30-31.
[18]	严家熺, 金伟良, 邹道勤, 等.无筋砌体的可靠度分析[C] // 2000年全国砌体结构学术会议. 重庆: [s.n.], 2000: 11. YAN Jia-xi, JIN Wei-liang, ZOU Dao-qin, et al. Reliability analysis of nonreinforced masonry [C] // National Masonry Structure Conference in 2000. Chongqing: [s.n.], 2000: 11. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=4862822
[19]	蒋利学, 王卓琳. 我国近几代混凝土和砌体结构设计规范的可靠度比较[J]. 结构工程师, 2015, 31(02): 80-88. JIANG Li-xue, WANG Zhuo-lin. Reliability comparison on national codes of recent generations for design of concrete and masonry structures[J]. Structural Engineers, 2015, 31(02): 80-88. DOI:10.3969/j.issn.1005-0159.2015.02.009
[20]	建筑结构可靠度设计统一标准: GB 50068—2001[S]. 北京: 中国建筑工业出版社, 2001.
[21]	李杰. 论第三代结构设计理论[J]. 同济大学学报: 自然科学版, 2017, 45(5): 617-624. LI Jie. On the third generation of structural design theory[J]. Journal of Tongji University: Natural Science, 2017, 45(5): 617-624.
[22]	严家熺. 无筋砌体结构的可靠度分析和工程试设计[C] // 1988年中国工程建设标准化协会砌体结构委员会年会. 沈阳: [s.n.], 1988: 13. YAN Jia-xi. Reliability analysis and engineering design of non-reinforced masonry structures [C] // Association for Engineering Construction Standardization Masonry Committee Annual Meeting. Shenyang: [s.n.], 1988: 13. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGQT198806001003.htm
[23]	黄靓, 黄凯, 施楚贤. 基于数据库的配筋砌块砌体剪力墙受剪承载力计算公式可靠度分析[J]. 建筑结构, 2015, 45(12): 96-100. HUANG Liang, HUANG Kai, SHI Chu-xian. Reliability analysis of shear bearing capacity formula of reinforced concrete masonry shear wall based on database[J]. Building Structure, 2015, 45(12): 96-100.
[24]	唐岱新. 砌体结构[M]. 3版. 北京: 高等教育出版社, 2013: 108–112.